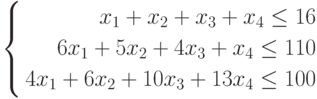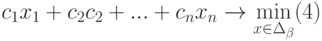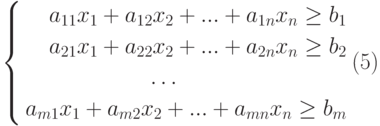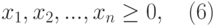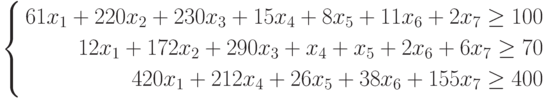Решение математических задач в системе excel

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Решение различных
математических задач, используя надстройки
«Подбор параметра» и «Поиск решения» в MS Excel.

Цель работы. Изучить:

·      надстройку «Подбор параметра» для нахождения корней нелинейных
уравнений;

·      надстройку «Поиск решения» для нахождения корней систем уравнений.

Пользуясь приемами выполнения простейших
расчетов и построения графиков функций в Excel, можно
находить решение различных математических задач. Рассмотрим это на примере
наиболее часто встречающихся задач нахождения корней нелинейных уравнений и
решения систем линейных уравнений. Указанные математические задачи легко
решаются с помощью надстроек Excel Поиск решения и Подбор параметра.

Подбор параметра

Надстройка Microsoft Excel Подбор параметра служит для нахождения
оптимального желаемого решения за счет изменения одного из параметров. С
формальной точки зрения такие задачи описываются уравнением с одной переменной,
которое в общем случае можно представить в следующем каноническом виде:

F(x) = 0,

где функция F(x) определена и непрерывна на интервале [a, b]. Таким образом, можно сказать, что
инструмент Подбор параметра служит для нахождения корня уравнения x. В этой надстройке реализован алгоритм метода
половинного деления.

Пример 1. Решим
уравнение x² – 3 =
0, используя надстройку Подбор параметра.

В ячейку А1 вводится начальное приближение
для поиска одного из корней уравнения. Лучше найти его графически, хотя можно подставить и произвольное значение (например,
ноль). В ячейку В2 записывается в виде формулы левая часть решаемого уравнения.
Диалоговое окно данного инструмента вызывается через меню Данные
/ Что-если / Подбор параметра и имеет
следующий вид (рис. 2.7.1, 2.7.2):

Рис. 2.7.1. Надстройка Подбор параметра

В поле Установить в ячейке вводится
ссылка на ячейку, содержащую левую часть уравнения. В поле Значение
непосредственно (т.е. без ссылок на ячейки) вводится правая часть уравнения.
Причем правая часть уравнения должна обязательно представлять собой конкретное
числовое значение. Если правая часть уравнения содержит переменную или
какое-либо выражение, то такое уравнение должно быть предварительно
преобразовано к равносильному виду (в общем случае, к каноническому виду F(x) = 0). Нажав кнопку ОК, получаем в
ячейке А1 значение искомого корня: 1,731856.

Рис. 2.7.2. Надстройка Подбор параметра

Поиск решения

Нелинейные
уравнения также можно решать, используя надстройку Поиск решения. Для
того чтобы ее подключить, следует в меню Office (рис. 2.7.3) выбрать пункт Параметры Excel (рис. 2.7.4) и в раскрывшемся списке войти в меню Надстройки,
далее активировать Поиск решения, установив флажок против пункта Поиск
решения (рис. 2.7.5).

Рис. 2.7.3 Кнопка Office

Рис. 2.7.4. Меню Office

Рис. 2.7.5. Надстройки

После нажатия кнопки ОК
соответствующий значок появится во вкладке Данные (рис. 2.7.6).

Рис. 2.7.6. значок Поиск решения

Пример 2. Решим
уравнение x² – 3 =
0, используя надстройку Поиск решения.

В ячейку А1
заносится начальное приближение корня, в ячейку В1 – левая
часть уравнения в виде формулы. Для предыдущего примера она имеет вид =А1*А1-3.

Далее из вкладки меню Данные
запускается надстройка Поиск решения.

В открывшемся диалоговом окне Поиск
решения устанавливается целевая ячейка $B$1, равная
нулевому значению. В текстовом поле Изменяя ячейки устанавливается адрес
$А$1 и нажимается кнопка Выполнить (рис. 2.7.7).

Рис. 2.7.7. Надстройка Поиск
решения

В ячейке А1 получается значение корня
1,732051 (рис. 2.7.8).

Рис. 2.7.8. Результаты работы
надстройки Поиск решения

Как видим, оно совпало с точностью до 0,001
с найденным ранее значением.

Обращает на
себя внимание неточность решения. Мы получаем очень близко приближающиеся к
точным, но все же неточные корни уравнения. Это происходит потому, что решение
уравнений на вычислительной технике происходит не аналитическими методами, как
это делает человек, а специально разработанными методами, получившими название
численных. В отличие от аналитических (точных) методов численные методы
обладают определенной погрешностью. В Excel с целью повышения точности решения
пользователь может уменьшить погрешность вычислений, но при этом может
потребоваться увеличение количества итераций. При этом надо помнить, что тем
самым увеличивается время на поиск решения. Установленные по умолчанию значения подходят для большинства практических задач, относительная
погрешность вычислений составляет 0,001 (рис. 2.7.9).

Рис. 2.7.9. Изменение
погрешности

Следует отметить, что найден только один из
двух корней данного уравнения. Для нахождения второго корня, следует в ячейку
А1 ввести новое приближение, близкое ко второму корню, и повторить поиск
решения.

Пример 3. Решим
систему уравнений, используя надстройку Поиск решения.

Для того, чтобы использовать рассматриваемую
надстройку Поиск решения для нахождения решения системы линейных
алгебраических уравнений, следует ввести в
столбец А начальное приближение для значений всех неизвестных. Пусть это будут
нули. В столбец В ввести формулы, описывающие левые части уравнений. В столбец
С вводят значения правых частей уравнений. Курсор ставят на ячейку В1 и
запускают надстройку Поиск решения. Значение целевой ячейки $B$1устанавливают равным значению ячейки С1. Изменяют значения ячеек
столбца А. К ограничениям добавляют все уравнения, кроме первого. Для системы
уравнений:

настроенный на
показ формул лист Excel с диалоговым окном Поиск решения
будут выглядеть так, как это показано на рисунках 2.7.10, 2.7.11.

Рис. 2.7.10. добавление ограничения

Рис. 2.7.11. Поиск решения
системы уравнений

Нажав кнопку Выполнить, получается в
столбце А значение неизвестных (рис. 2.7.12):

Как видно, надстройка Поиск решения
очень удобна для решения рассмотренных задач. Однако следует помнить, что
алгоритмы, реализованные в ней, предназначались не для них, а для решения задач
оптимизации. Поэтому возможны сбои в работе надстройки, и к полученным
результатам необходимо подходить критически.

.

Рис. 2.7.12. Результаты
работы с надстройкой Поиск решения

Задания для выполнения

Варианты заданий для работы приведены в
таблице 2.7.1, 2.7.2.

Задание1.

1.                 
Используя надстройку «Подбор параметра», найти все
корни уравнения (по вариантам) на отрезке [-2; +2] (табл. 2.7.1).

Таблица 2.7.1

Варианты заданий

Задание 2.

1.                 
Используя надстройку «Поиск решения», решить
систему линейных уравнений AX = B (по вариантам) (табл. 2.7.2)
и проверить правильность решения в Excel, подставив найденные значения неизвестных в систему уравнений. A – матрица коэффициентов при x1, x2, x3, x4. В- матрица свободных членов уравнений.

 Таблица 2.7.2

Варианты заданий

Использование Excel при решении математических задач

       Любому человеку в ходе практической деятельности приходится совершать операции над количественными данными, которые осуществляются в соответствии с математическими законами. Поэтому для человека, который не свяжет дальнейшую жизнь с математикой, наиболее важным является практический аспект математики. Для него это — прикладная наука, близкая к технологии. Здесь наиболее важным является умение провести необходимые вычисления. Математическая теория изменяется сравнительно медленно, однако технология применения математических методов претерпела значительно более существенные изменения. Буквально за последние десятилетия пройден путь от расчетов в уме и на бумаге к применению счетов, арифмометров, калькуляторов и далее — к расчетам на компьютере. Поэтому в настоящее время специалист, даже хорошо знающий математику, но не умеющий применять математические методы на компьютере, не может считаться специалистом современного уровня.

       Использование компьютера при проведении расчетов сдвигает акценты в математической подготовке специалиста. Если раньше основное внимание было сосредоточено на математических методах, которые предусматривали проведение расчетов вручную, то теперь, с появлением специализированных математических программ, необходимо научиться проводить требуемые вычисления на компьютере.

      Для решения задач на компьютерах чаще всего применяется метод решения «в лоб», опирающийся на основное определение и использующий самый общий подход. Снижается значение частных случаев, различных свойств описываемых математических объектов, ориентированных на облегчение решений вручную.

      Например, при решении вручную квадратного уравнения ax2+bx+c=0 помимо общего решения требовалось знать решения для частых случаев: когда квадратное уравнение разлагается на множители, когда b —четное, когда а = 1, по формулам Виета. При этом было принято считать, что решение «рационально», если для него используется, подходящая частная формула. В настоящее время при применении компьютера, по-видимому, рациональным следует считать решение с использованием общих подходов, по общей формуле. В то же время традиционное преподавание классической математики все еще ориентировано на дальнейшую работу с карандашом и бумагой.

      Наиболее важной отличительной особенностью предлагаемого материала должно являться рассмотрение основных разделов курса математики не в традиционном изложении, а с перспективой дальнейшего применения компьютера. Причем, в отличие от курсов информатики, изложение материала должно вестись не «от пакетов программ и их возможностей», а «от математических задач к способам их решения на компьютере». При этом основное внимание должно быть сосредоточено на реализации способов решения математических задач, на том, как решать типовые задачи.

     Компьютерный математический анализ данных предполагает некоторое математическое преобразование данных с помощью определенных программных средств. Следовательно, необходимо иметь представление как о математических методах обработки данных, так и о соответствующих программных средствах, то есть необходимо опираться на определенный программный пакет.

     Существует значительное количество специализированных математических пакетов, таких как MatLab, MatbCad, Math, Mathematica, Maple и др. Все они охватывают основные разделы математики и позволяют производить подавляющее большинство необходимых. математических расчетов. Однако освоение этих пакетов самостоятельно — достаточно трудоемкая задача. В то же время в курс информатики в большинстве вузов включено изучение электронной таблицы Excel. Поэтому представляется оправданным реализовать в старших классах подход, основанный на применении математических методов именно с помощью пакета Excel. Конечно, Excel сильно уступает специализированным математическим пакетам. Тем не менее. большое количество математических задач может быть решено с его помощью.

     Изложение учебного материала в 10-11-х классах может осуществляться в следующей последовательности (из расчета 1час в неделю – факультативный или элективный курс)^

1. Основные операции в Excel — 12 часов.

Запуск Excel, окно Excel, открытие таблицы, создание новой рабочей книги, ввод данных, выделение блока ячеек, построение диаграмм, редактирование диаграмм, копирование, автозаполнение, автосуммирование, ввод математических формул, копирование формул, печать результатов, форматирование рамки таблицы, работа с простейшими базами данных, отмена действий, сохранение результатов, закрытие рабочей книги, завершение работы, получение справочной информации, сообщение об ошибках.

2. Построение графиков функций — 4 часа.

Линейная, квадратичная, кубическая, обратная пропорциональность, со знаком корня, модуля, дробно-рациональная, тригонометрическая, логарифмическая, показательная функции.

3. Построение кривых 2 порядка — 2 часа.

Построение окружности, эллипса.

4. Графическое решение систем уравнений — 2 часа.

5 Построение плоскости — 1 час.

6. Построение поверхностей второго порядка в пространстве — 3 часа.

Построение эллипсоида, гиперболоида, параболоида, конуса.

7. Решение уравнений с одним неизвестным —2 часа.

8. Элементы линейной алгебры — 10 часов.

Операции с матрицами, решение систем линейных уравнений.

9. Элементы математического анализа — 8 часов.

Производная, определенный интеграл, числовые и функциональные ряды.

10. Элементы теории вероятности — 10 часов.

Понятие случайного события, вероятности события, условная вероятность, перестановка, сочетания, размещение.

11. Элементы статистики — 10 часов.

Понятие математической статистики, выборочный метод, выборочная функция распределения, выборочная характеристика, проверка статистических гипотез.

Итого — 64 часа.

В старших классах нашей школы на уроках информатики меньше времени уделяют программированию, больше – Word, Excel , с 2007 года проводится элективный курс по следующей программе (из расчета 1час в неделю во втором полугодии 10 класса и в первом полугодии 11 класса):

1. Основные операции в Excel — 6 часов.

Запуск Excel, окно Excel, открытие таблицы, создание новой рабочей книги, ввод данных, выделение блока ячеек, построение диаграмм, редактирование диаграмм, копирование, автозаполнение, автосуммирование, ввод математических формул, копирование формул, печать результатов, форматирование рамки таблицы, работа с простейшими базами данных, отмена действий, сохранение — результатов, закрытие рабочей книги, завершение работы, получение справочной информации, сообщение об ошибках

2. Построение графиков функций — 4 часа

Линейная, квадратичная, кубическая, обратная пропорциональность, со знаком корня, модуля, дробно-рациональная, тригонометрическая, логарифмическая, показательная функции.

3. Построение кривых 2 порядка — 2 часа.

Построение окружности, эллипса.

4. Элементы теории вероятности — 10 часов.

Понятие случайного событии, вероятности события,  условная вероятность, перестановка, сочетания, размещение

5. Элементы статистики — 10 часов.

Понятие математической статистики, выборочный метод, выборочная функция распределения, выборочная характеристика, проверка статистических гипотез.

Итого — 32 часа.

К этим курсам имеется приложение, где подробно описаны задания и их решения.

Приведу лишь некоторые из них.

Для лучшего восприятия материала, все названия клавиш, кнопок, диалоговых окон и их полей, команды меню в приложении выделены специальным стилем.

Приложение см

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

1. В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
2. В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

• Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
• Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
• Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х1	х2	x3	х4	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

1. Максимум прибыли в зависимости от оптимального распределения затрат.
2. Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

1. Создание математической модели задачи ЛП.
2. Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
3. Ввод данных из формы в окно Excel Поиск решения из меню Данные.
4. Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

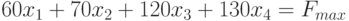
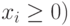
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

• Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х7	х2	x3	х4	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

• Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
• Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

• в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
• в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
• в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

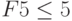
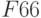
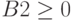
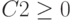
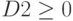
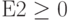
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

• Трудовые – 16 (У₁)
• Сырьевые – 84 (У₂)
• Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j (j in <1,2. т>) человека в каждом из видов питательных веществ. Задана калорийность с_i одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n>).

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 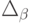формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

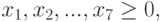
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
2. В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
3. В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
4. В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

1. В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
2. В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
3. Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
4. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
4. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
   • для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
   • в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
   • в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
   • в качестве значения правой части ограничения выбрать ячейку $J$5 ;
   • для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
   • аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

1. Составить математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования в Excel с помощью Поиска решения.
3. Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

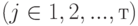
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.