Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
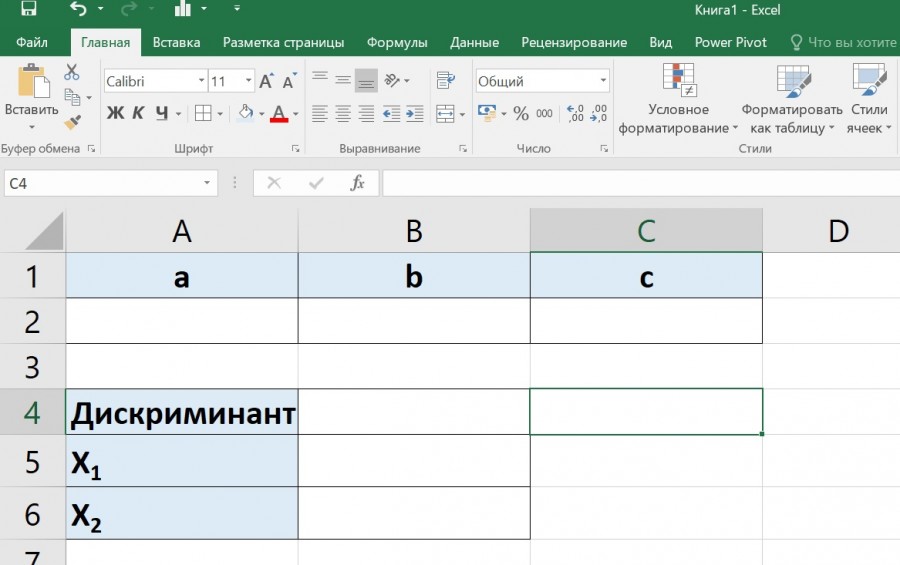
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
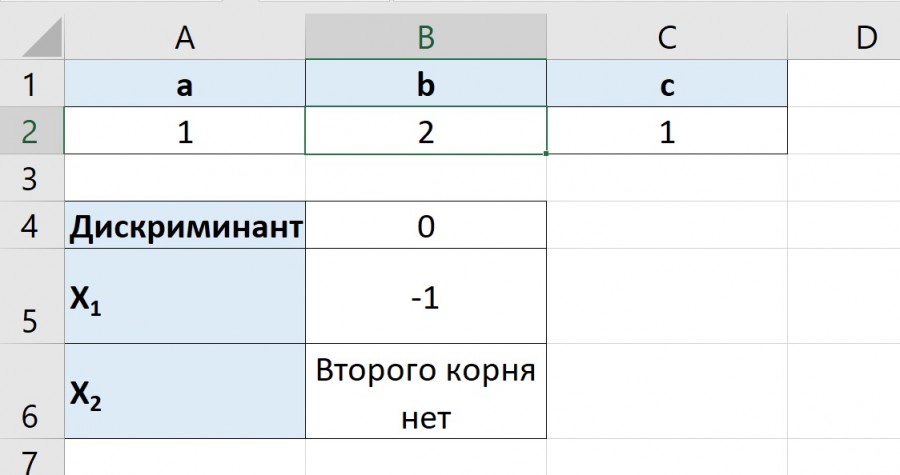
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
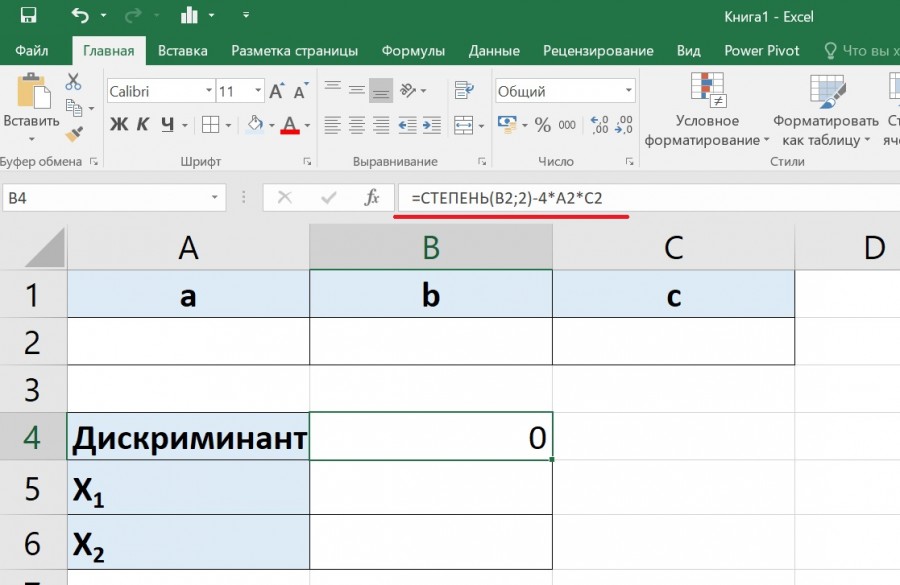
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
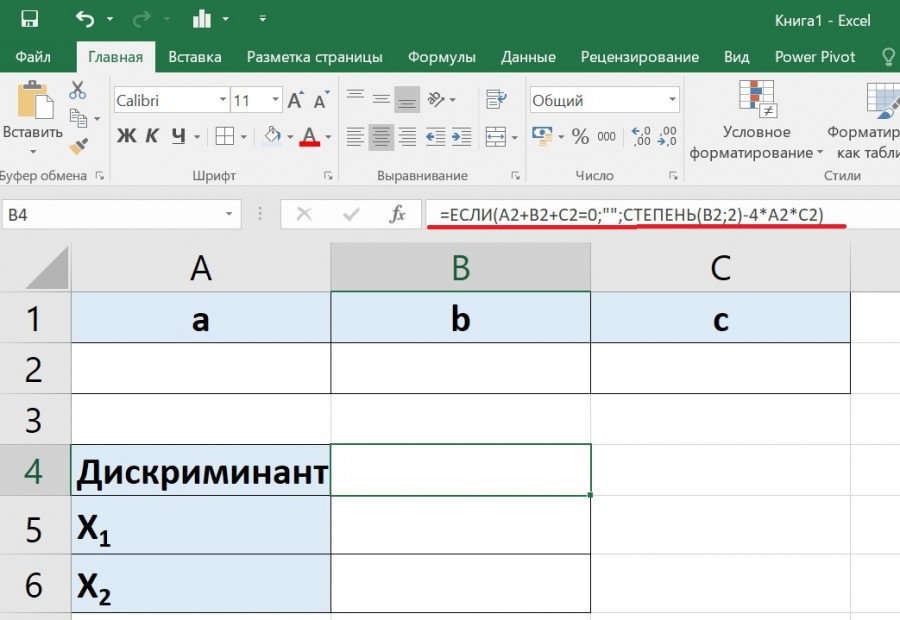
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
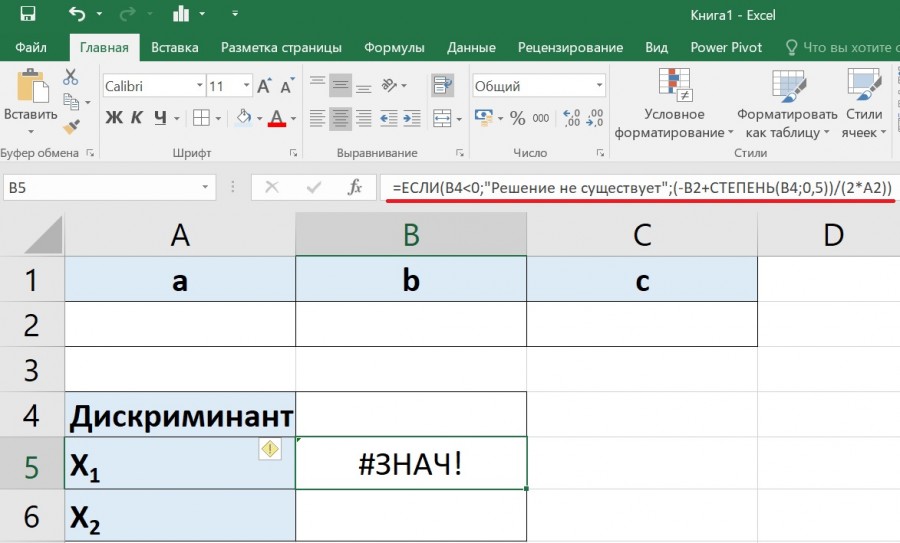
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Квадратное уравнение. Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D 2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень

Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
источники:
http://portalonline.ru/kompyutery-i-programmy/5337-kak-reshit-kvadratnoe-uravnenie-v-eksele.html
http://wpcalc.com/kvadratnoe-uravnenie-excel/
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
A quadratic function is a type of equation that contains a squared variable. It is called quadratic because quad means square in Latin. The quadratic functions usually have a structure like ax² + bx + c = 0, where x represents an unknown variable, and a, b, and c represent known constants. In this guide, we are going to show you how to solve quadratic equations in Excel.
Download Workbook
Thanks to Excel’s features, we can list you 3 different way to solve quadratic equations. These ways includes Goal Seek feature of Excel as well as a manual calculation method and a custom formula which can be created via VBA.
The first part of our guide focuses on Goal Seek feature. You can find the manual and VBA methods in the the second part.
Goal Seek
Goal Seek is among Excel’s most important features. Its purpose is exactly what we’re looking to do here — to find the variable in an equation. Goal Seek uses an iterative calculation process to «guess» the value of a cell value used in the workbook formulas. Based on this, a quadratic equation can be formulated to be run in Excel. Let’s now see how you can do this.
Creating a quadratic equation in Excel
A quadratic equation should at least have one squared variable. To do this, you can simply multiply the variable by itself, calculate he 2nd power of the variable using the power operator ^ or use the POWER function as in our example.
The other important part is to refer a cell as variable, x. Our formula uses named range x and y for the unknown variables and the formula result respectively (x is C7 and y is D7).
5x² + 6x + 1 = 0 => =5*POWER(x,2) + 6*x + 1 — y
Note: Although adding y into the calculation isn’t necessary if you always set it 0, we included it in our example for versatility.
Using Goal Seek to solve quadratic equations in Excel
Once the formula is ready in your spreadsheet, it is time to use Goal Seek to solve the quadratic function. Follow the steps below to find one of the variables of the equation:
- Select the cell that contains the formula
- Open the Goal Seek dialog in Data > Data Tools > What-If Analysis > Goal Seek
- Set cell is the formula cell (It should be automatically selected)
- To value should be 0, which is the right end of the equation
- Select the cell of the x value to the By changing cell
- Click OK to start Goal Seek
- After Excel finished the Goal Seek execution, the Goal Seek Status dialog will display the calculated value
- Click OK to close the dialog
Results of Goal Seek
Although the process is pretty straightforward, there are some downsides to using Goal Seek. As you may have noticed in our screenshots, Goal Seek may fail to find the exact value you want. For example, in our example we wanted Goal Seek to find a value that makes our formula 0. However, the value makes the formula return a number close to 0, 0.000121893.
If you check the x value, you will see a value very close to -0.2, -0.199969528007691. You need to manually enter -0.2 to see the formula return 0.
This difference comes from calculation logic of Goal Seek. Goal Seek continues searching a certain number of times until it finds a value closer to the target value within the precision limits specified. The default limits for the iteration number and precision value are 100 and 0.001. You can adjust these from File > Options > Formulas.
Note: Decrease the Maximum Change value to increase the precision.
Another important point while using Goal Seek is that you need to choose (guess) a starting point for Goal Seek. Goal Seek finds a single variable, but a quadratic function can have 2 variable options. We found -0.2 value when we set 0 to x. If you’re satisfied with the results, you can change the x and run Goals Seek again. For example, setting 10 to x, and running Goal Seek finds another x value, -1.
Please see out the second part to see how to solve quadratic equations using regular functions and VBA macros.
17 авг. 2022 г.
читать 2 мин
Квадратное уравнение принимает следующий вид:
ах 2 + Ьх + с = у
Часто вам будет дано значение y и вас попросят найти значение x .
Например, предположим, что у нас есть следующее квадратное уравнение:
4x 2 – 20x + 16 = -8
Оказывается, установка x = 3 или x = 2 решит это уравнение.
Для решения квадратных уравнений в Excel можно использовать функцию поиска цели .
В следующем пошаговом примере показано, как использовать функцию поиска цели на практике.
Шаг 1: введите уравнение
Во-первых, давайте введем случайное значение для x и формулу квадратного уравнения для y:
Шаг 2: Найдите первое значение X, используя поиск цели
Затем щелкните вкладку « Данные » на верхней ленте, затем нажмите кнопку « Анализ «что, если»» и выберите «Поиск цели »:
В появившемся новом окне укажите, что вы хотите установить ячейку B2 равной -8 , изменив значение в ячейке A2 :
Как только мы нажмем OK , функция поиска цели автоматически найдет значение x, которое решает уравнение:
Goal Seek находит, что значение x=2 (при условии, что 1,9999 округляется до 2) решает квадратное уравнение.
Шаг 3: Найдите второе значение X, используя поиск цели
Чтобы найти второе значение x, которое решает квадратное уравнение, установите начальное значение x на другое число.
Например, мы могли бы установить начальное значение x равным 4:
Затем мы можем снова запустить функцию поиска цели и увидеть, что она находит новое решение x=3 :
Таким образом, два значения x, которые могут решить это квадратное уравнение, равны x=2 и x=3 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как решить систему уравнений в Excel
Как построить уравнение в Excel
Содержание
- 0.1 Шаг 1. Организация таблицы
- 0.2 Шаг 2. Проверка равенства Дискриминанта.
- 0.3 Формула дискриминанта
- 0.4 Шаг 3. Вычисляем корни уравнения.
- 1 Перейдем к вводу формул для решения
- 1.1 Защита листа в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
В этой статье вы узнаете как решить квадратное уравнение на конкретном примере.
Постановка задачи: решить квадратное уравнение в Excel
Ход решения: Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,cсначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c,то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK,подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
На примере квадратного уравнения х2 — 3х + 2 = 0 рассмотрим как решить квадратное уравнение в Excel.
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4=0;«х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;«х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
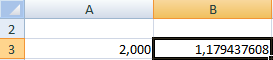
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Решение квадратных уравнений с использованием электронных таблиц
Решение квадратных уравнений с использованиемэлектронных таблиц EXCEL
Работу выполнила ученица 9 класса
МБОУ « Бичурга-Баишевская СОШ»
Гаврилова Анна
Руководитель: учитель информатики Симурзина Н.Н.
Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
«Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
Готфрид Лейбниц
Цель исследования : изучить и создать программы для автоматического вычисления корней квадратного уравнения
Цель исследования: изучить и создать программы для автоматического вычисления корней квадратного уравнения.
Поставленная цель исследования предполагает решения ряда задач:
Изучить способы решения квадратных уравнений
Разработать вычислительные программы для решения квадратных уравнений
Проанализировать результаты вычислений
Сформулировать выводы и рекомендации по выбору программы для решения квадратных уравнений с помощью компьютера
Проблема: создать программу для автоматического решения квадратных уравнений
Проблема: создать программу для автоматического решения квадратных уравнений
Объект исследования: решение уравнений с помощью компьютера
Предмет исследования: компьютерные программы
Гипотеза: считаю, что компьютерные программы для решения квадратных уравнений автоматизируют вычисление корней
Методы исследования : сравнение и анализ, эксперимент, метод визуализации данных
Методы исследования: сравнение и анализ, эксперимент, метод визуализации данных.
Новизна исследования заключается в экспериментальной проверке компьютерных вычислений с помощью табличного процессора MS Excel.
Практическая значимость состоит в том, что созданные для проведения эксперимента программы можно будет использовать и в дальнейшем для нахождения корней квадратного уравнения
В своей работе, я решила остановиться на квадратных уравнениях, так как эти виды уравнений – самые распространенные
В своей работе, я решила остановиться на квадратных уравнениях, так как эти виды уравнений – самые распространенные. Они используются в таких науках, как алгебра, физика, геометрия и химия.
Программу, которую я решила взять для решения квадратных уравнений – это
Программу, которую я решила взять для решения квадратных уравнений – это MS Excel
Microsoft Еxcel – программа для работы с электронными таблицами, созданная компанией Microsoft. Она представляет возможности экономико – статистических расчетов, графические инструменты
Я буду исследовать решение трех квадратных уравнений:
Я буду исследовать решение
трех квадратных уравнений:
Технология решения квадратного уравнения в
Технология решения квадратного уравнения в MS Excel
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4<0; «нет»;»да»).
6. В ячейку В6 введите формулу = ЕСЛИ(В4>=0;»х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;»х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае- Microsoft Excel 2010, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней квадратного уравнения с заданной точностью
Подбор параметра Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в рассмотренных примерах
Подбор параметра
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в рассмотренных примерах.
Возможности электронных таблиц позволяют находить приближенные значения корней уравнения с заданной точностью .Для этого используется метод Подбор параметра.
Подбор параметра — х2+5х-3 = 0
Подбор параметра
—х2+5х-3=0
Построение диаграммы типа График
Определение приближенных значений корней уравнения
Поиск приближенного решения уравнения с заданной точностью методом Подбора параметра
Подбор параметра Решение уравнения -х2+5х-3=0
Подбор параметраРешение уравнения -х2+5х-3=0
Выводы Используя информационные технологии можно очень быстро и качественно решить квадратные уравнения
Выводы
Используя информационные технологии можно очень быстро и качественно решить квадратные уравнения.
Мы убедились, что построенные нами модели работают для всех случаев: есть два решения квадратного уравнения, единственное решение; решений нет.
Созданные программы можно будет использовать и в дальнейшем для нахождения корней квадратного уравнения на уроках математики.
Литература Н.Д. Угринович «Информатика и
Литература
Н.Д. Угринович «Информатика и ИКТ: учебник для 9 класса», М.:БИНОМ. Лаборатория знаний, 2013.
http://ru.wikipedia.org/wiki/Квадратное уравнение
Спасибо за внимание
Спасибо за внимание