Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
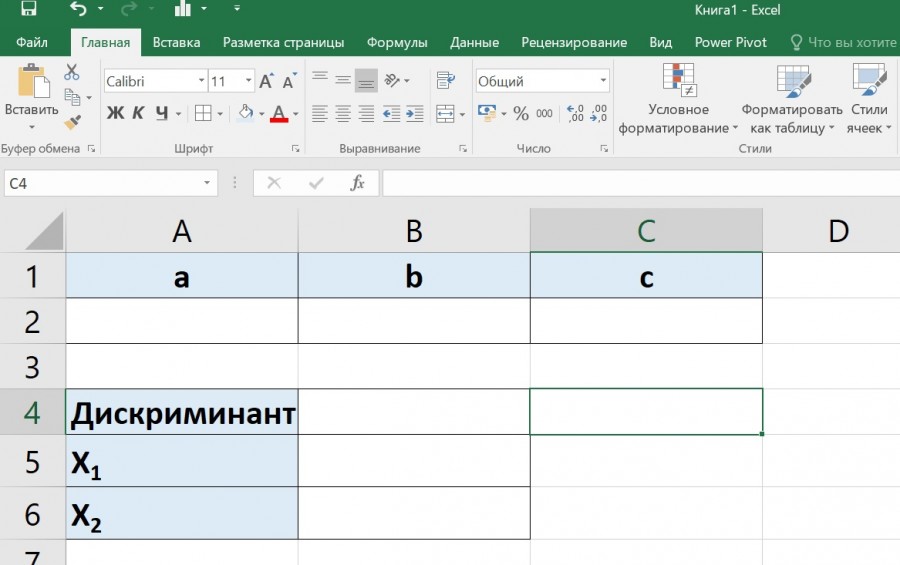
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
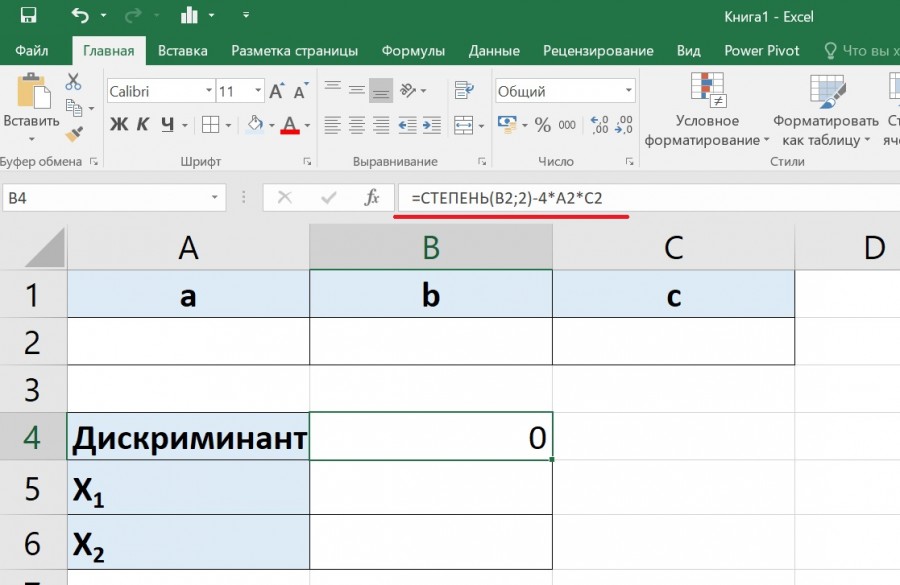
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
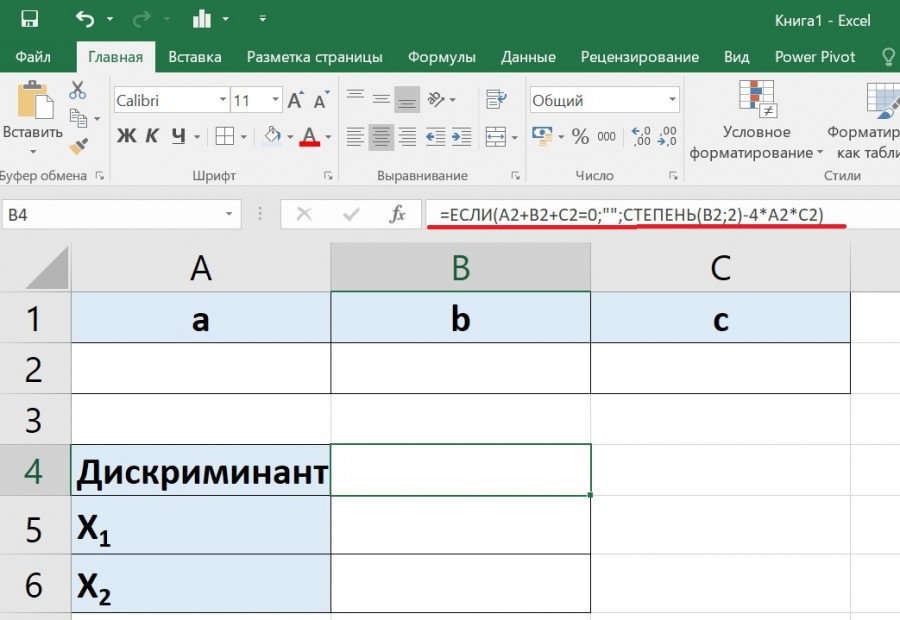
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
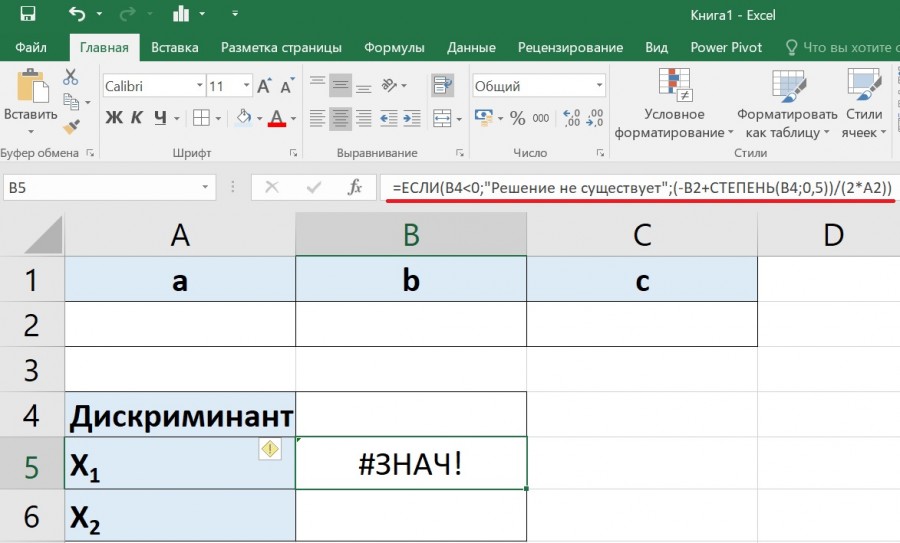
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Квадратное уравнение. Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D 2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень

Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
источники:
http://portalonline.ru/kompyutery-i-programmy/5337-kak-reshit-kvadratnoe-uravnenie-v-eksele.html
http://wpcalc.com/kvadratnoe-uravnenie-excel/
17 авг. 2022 г.
читать 2 мин
Квадратное уравнение принимает следующий вид:
ах 2 + Ьх + с = у
Часто вам будет дано значение y и вас попросят найти значение x .
Например, предположим, что у нас есть следующее квадратное уравнение:
4x 2 – 20x + 16 = -8
Оказывается, установка x = 3 или x = 2 решит это уравнение.
Для решения квадратных уравнений в Excel можно использовать функцию поиска цели .
В следующем пошаговом примере показано, как использовать функцию поиска цели на практике.
Шаг 1: введите уравнение
Во-первых, давайте введем случайное значение для x и формулу квадратного уравнения для y:
Шаг 2: Найдите первое значение X, используя поиск цели
Затем щелкните вкладку « Данные » на верхней ленте, затем нажмите кнопку « Анализ «что, если»» и выберите «Поиск цели »:
В появившемся новом окне укажите, что вы хотите установить ячейку B2 равной -8 , изменив значение в ячейке A2 :
Как только мы нажмем OK , функция поиска цели автоматически найдет значение x, которое решает уравнение:
Goal Seek находит, что значение x=2 (при условии, что 1,9999 округляется до 2) решает квадратное уравнение.
Шаг 3: Найдите второе значение X, используя поиск цели
Чтобы найти второе значение x, которое решает квадратное уравнение, установите начальное значение x на другое число.
Например, мы могли бы установить начальное значение x равным 4:
Затем мы можем снова запустить функцию поиска цели и увидеть, что она находит новое решение x=3 :
Таким образом, два значения x, которые могут решить это квадратное уравнение, равны x=2 и x=3 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как решить систему уравнений в Excel
Как построить уравнение в Excel
A quadratic function is a type of equation that contains a squared variable. It is called quadratic because quad means square in Latin. The quadratic functions usually have a structure like ax² + bx + c = 0, where x represents an unknown variable, and a, b, and c represent known constants. In this guide, we are going to show you how to solve quadratic equations in Excel.
Download Workbook
Thanks to Excel’s features, we can list you 3 different way to solve quadratic equations. These ways includes Goal Seek feature of Excel as well as a manual calculation method and a custom formula which can be created via VBA.
The first part of our guide focuses on Goal Seek feature. You can find the manual and VBA methods in the the second part.
Goal Seek
Goal Seek is among Excel’s most important features. Its purpose is exactly what we’re looking to do here — to find the variable in an equation. Goal Seek uses an iterative calculation process to «guess» the value of a cell value used in the workbook formulas. Based on this, a quadratic equation can be formulated to be run in Excel. Let’s now see how you can do this.
Creating a quadratic equation in Excel
A quadratic equation should at least have one squared variable. To do this, you can simply multiply the variable by itself, calculate he 2nd power of the variable using the power operator ^ or use the POWER function as in our example.
The other important part is to refer a cell as variable, x. Our formula uses named range x and y for the unknown variables and the formula result respectively (x is C7 and y is D7).
5x² + 6x + 1 = 0 => =5*POWER(x,2) + 6*x + 1 — y
Note: Although adding y into the calculation isn’t necessary if you always set it 0, we included it in our example for versatility.
Using Goal Seek to solve quadratic equations in Excel
Once the formula is ready in your spreadsheet, it is time to use Goal Seek to solve the quadratic function. Follow the steps below to find one of the variables of the equation:
- Select the cell that contains the formula
- Open the Goal Seek dialog in Data > Data Tools > What-If Analysis > Goal Seek
- Set cell is the formula cell (It should be automatically selected)
- To value should be 0, which is the right end of the equation
- Select the cell of the x value to the By changing cell
- Click OK to start Goal Seek
- After Excel finished the Goal Seek execution, the Goal Seek Status dialog will display the calculated value
- Click OK to close the dialog
Results of Goal Seek
Although the process is pretty straightforward, there are some downsides to using Goal Seek. As you may have noticed in our screenshots, Goal Seek may fail to find the exact value you want. For example, in our example we wanted Goal Seek to find a value that makes our formula 0. However, the value makes the formula return a number close to 0, 0.000121893.
If you check the x value, you will see a value very close to -0.2, -0.199969528007691. You need to manually enter -0.2 to see the formula return 0.
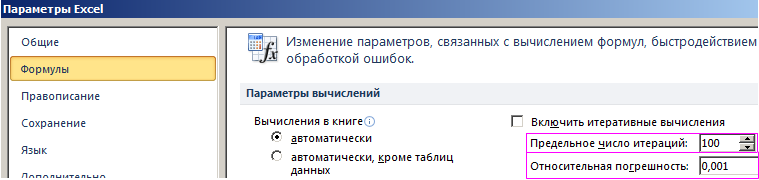
This difference comes from calculation logic of Goal Seek. Goal Seek continues searching a certain number of times until it finds a value closer to the target value within the precision limits specified. The default limits for the iteration number and precision value are 100 and 0.001. You can adjust these from File > Options > Formulas.
Note: Decrease the Maximum Change value to increase the precision.
Another important point while using Goal Seek is that you need to choose (guess) a starting point for Goal Seek. Goal Seek finds a single variable, but a quadratic function can have 2 variable options. We found -0.2 value when we set 0 to x. If you’re satisfied with the results, you can change the x and run Goals Seek again. For example, setting 10 to x, and running Goal Seek finds another x value, -1.
Please see out the second part to see how to solve quadratic equations using regular functions and VBA macros.
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
людей нашли эту статью полезной. А Вы?
Содержание
- 0.1 Шаг 1. Организация таблицы
- 0.2 Шаг 2. Проверка равенства Дискриминанта.
- 0.3 Формула дискриминанта
- 0.4 Шаг 3. Вычисляем корни уравнения.
- 1 Перейдем к вводу формул для решения
- 1.1 Защита листа в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
В этой статье вы узнаете как решить квадратное уравнение на конкретном примере.
Постановка задачи: решить квадратное уравнение в Excel
Ход решения: Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,cсначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c,то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK,подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
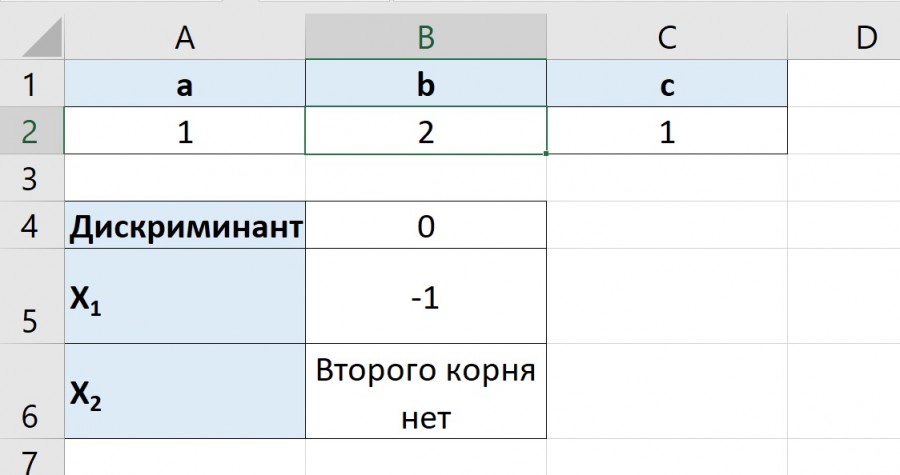
На примере квадратного уравнения х2 — 3х + 2 = 0 рассмотрим как решить квадратное уравнение в Excel.
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4=0;«х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;«х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
Содержание
- Как решить квадратное уравнение в экселе?
- Видео как решить квадратное уравнение в экселе.
- Квадратное уравнение в Excel
- Ход решения
- Перейдем к вводу формул для решения
- Защита листа в Excel
- Решить квадратное уравнение в excel подбор параметра
- Квадратное уравнение в Excel
- Ход решения
- Перейдем к вводу формул для решения
- Защита листа в Excel
- Подбор параметра в EXCEL
- Простейший пример
- Калькуляция, подбираем значение прибыли
- Подбор суммы кредита
- Уравнения и задачи на подбор параметра в Excel
- Подбор параметра и решение уравнений в Excel
- Второй пример использования подбора параметра для уравнений
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Источник
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Источник
Решить квадратное уравнение в excel подбор параметра
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Подбор параметра в EXCEL
history 18 ноября 2012 г.
- Группы статей
- Другие Стандартные Средства
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .
Простейший пример
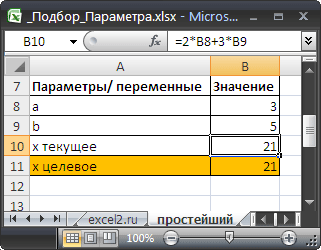
Найдем значение параметра b в уравнении 2*а+3*b=x , при котором x=21 , параметр а= 3 .
Подготовим исходные данные.
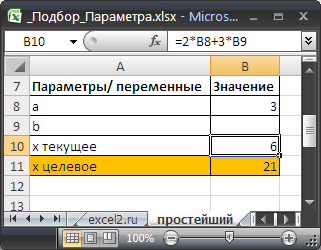
Значения параметров а и b введены в ячейках B8 и B9 . В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x ). Целевое значение x в ячейке B11 введено для информации.
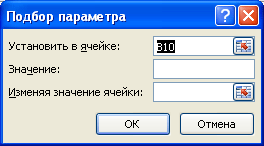
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …) .
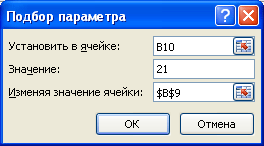
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b ).
Инструмент Подбор параметра подобрал значение параметра b равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно .
Примечание : Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b , которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший .
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
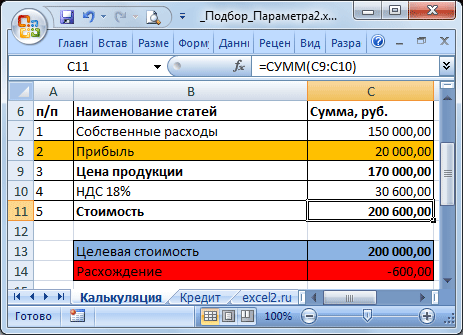
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13 ). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли ( С8 ), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение ( С14 ) равно 0.
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11 ) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра .
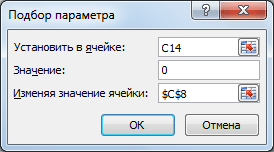
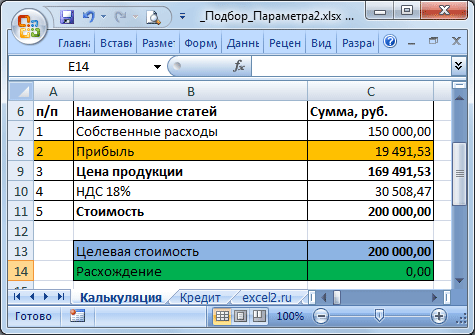
Выделите ячейку С14 , вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).
Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
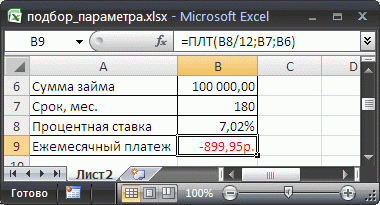
Предположим, что нам необходимо определить максимальную сумму кредита , которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет ). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.
Введем в ячейку B 6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B 7 , % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
- на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …;
- в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9 ;
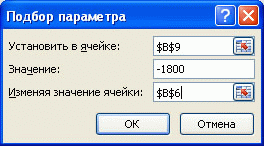
- введите искомый результат в поле Значение . В данном примере он равен -1800 ;
- В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6 ;
- Нажмите ОК
Что же сделал Подбор параметра ? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения . Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.
Уравнения и задачи на подбор параметра в Excel
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y =7 является функцией x ;
- нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
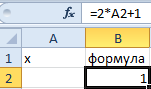
- Заполните ячейки листа, так как показано на рисунке:
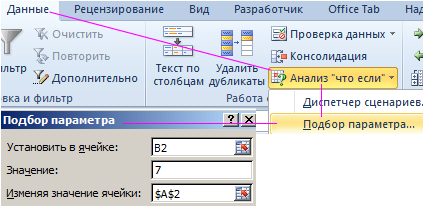
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
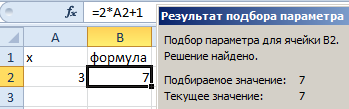
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
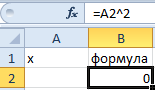
- Заполните ячейку B2 формулой как показано на рисунке:
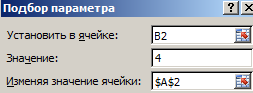
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
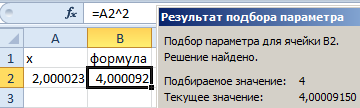
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
Источник
Скачать материал

Скачать материал


- Сейчас обучается 121 человек из 40 регионов


- Сейчас обучается 36 человек из 26 регионов


- Сейчас обучается 122 человека из 48 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Графический способ решения квадратных уравнений с помощью Excel
Интегрированный урок математики и информатики
Учитель информатики
(по специальности математика и информатика)Шихмагомедов Эльбрус Асланбекович
-
2 слайд
Цель урока:
Обеспечить умение решить расчетные задачи с использованием математических функций для решения квадратного уравнения в среде электронных таблиц Excel, повторение относительных и абсолютных ссылок, отработка навыков построения графиков функций в среде электронных таблиц Excel; повторение формул нахождения дискриминанта и корней квадратного уравнения. -
3 слайд
«Дорогу осилит идущий,
а информатику – мыслящий»Гюстав Гийома
-
4 слайд
«Графический способ решения квадратных уравнений с помощью Excel»
Тема урока: -
5 слайд
2х2+10х-6=0
а=2
b=10
с=-6
x0=-2,5 -
-
7 слайд
-х2-14х+23=0
а=-1
b=-14
с=23
x0=-7 -
8 слайд
17-х2-х=0
а=-1
b=-1
с=17
x0=-0,5 -
-
10 слайд
Определить количество корней в уравнении:
Вариант I
9y2+6y+1=0;
2×2+8x+13=0.Вариант II
4y2-4y+1=0;
3×2+32x+80=0;Вариант III
x2+10x+25=0;
3×2+5x+15=0. -
11 слайд
«Недостойно одаренному человеку, тратить подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
Готфрид Лейбниц (1646 – 1716) – немецкий
математик, физик, философ, юрист, языковед. -
12 слайд
Электронные таблицы (ЭТ)
1) Для чего предназначены электронные таблицы?
(ЭТ – это инструмент для табличных расчетов)
2) Из чего состоит имя ячейки?
(Из имени столбца и номера строки. Например, А1, В7, F12.)
3) Что может быть содержимым ячейки?
(Текст, числовое значение или формула.)
4) Каковы правила записи формул в ячейках?
(Ввод формулы начинается со знака =, вся формула пишется в строку.)
5) Как выглядят знаки арифметических операций в ЭТ?
(«+» сложение, «–» вычитание, «*» умножение, «^» возведение в степень, «/» – деление) -
13 слайд
Устные упражнения (по информатике)
Какой вид примет содержащая абсолютную и относительную ссылку формула =$A$1*B1, записанная в ячейке С1, после ее копирования в ячейку С2?
=$А$1*B2 -
14 слайд
3. Дан фрагмент электронной таблицы:
В ячейку D2 введена формула =А2*В1+С1. В результате в ячейке D2 появится значение:
1) 62) 143) 164) 2424
-
15 слайд
4. Дан фрагмент электронной таблицы:
В ячейку D1 введена формула =$А$1*В1+С2, а затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?
1) 10 2) 143) 16 4) 2414
-
16 слайд
Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс.
-
17 слайд
Решим квадратное уравнение
2×2+10x-6=0.Для этого построим график функции y=2×2+10x-6
1. Откройте файл
Рабочий стол/Заготовка2. Введите коэффициенты a, b, c.
-
-
-
20 слайд
Найдите координаты вершины параболы
x0=-b/(2*a);
-
-
-
23 слайд
Найдите дискриминант
=b^2 – 4*a*c -
-
-
26 слайд
Введите начало интервала
-
27 слайд
Введите конец интервала
-
28 слайд
Заполните промежуточные значения х
-
-
30 слайд
Найдите соответствующие значения у
-
-
-
-
-
35 слайд
Физминутка
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто». Сократ
«Здоровье — не все, но все без здоровья — ничто».
Сократ
Простейшие упражнения для глаз:
вертикальные движения глаз вверх – вниз;
горизонтальное вправо – влево;
вращение глазами по часовой стрелке и против;
закрыть глаза и представить по очереди цвета радуги как можно отчетливее;
глазами «нарисовать» эти фигуры несколько раз в одном, а затем в другом направлении. -
36 слайд
Самостоятельная работа
-
-
38 слайд
Рефлексия
Как может располагаться парабола относительно оси x? -
39 слайд
Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет корней.
D<0 -
40 слайд
Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один корень (также говорят, что уравнение имеет два совпадающих корня).
D=0 -
41 слайд
Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два корня.
D>0
-
42 слайд
Домашнее задание
Написать программу на Excel для вычисления:
процентов успеваемости и качества;
среднего балла. -
43 слайд
Спасибо за урок!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 212 200 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 08.04.2016
- 496
- 0
- 08.04.2016
- 970
- 2
- 08.04.2016
- 594
- 0
- 08.04.2016
- 687
- 0
- 08.04.2016
- 2594
- 1
- 08.04.2016
- 4730
- 433
- 08.04.2016
- 1203
- 4
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
Лабораторная
работа № 1
«Решение
квадратного уравнения в Ms.excel»
Задание (по Excel).
Решение квадратного уравнения.
Необходимо изобразить общую схему для
решения уравнений вида ax2
+ bx + c =
0.
1. В ячейке А1 записать – Решение
уравнения вида:
Объедините ячейки А1, В1, С1, Д1 измените
шрифт и цвет надписи.
В ячейке В2 записать ax2+bx+c=0.
Выделите цифру 2, щелкните правой кнопкой
мыши, выберете команду Формат ячеек
и во вкладке Шрифт команду Верхний
индекс. Измените цвет и размер шрифта
по вашему усмотрению.
2. Введите следующие значения в
ячейки:
В А3 а= В А5 с= В А7 х1=
В А4 b= В А6 D=
В А8 х2=
Выровняйте
текст в этих ячейках по правому краю, а
в ячейках А7 и А8 сделайте цифры 1 и 2
нижними индексами (аналогично как
написано в пункте 1).
3. В ячейку В6 введем формулу для
вычисления дискриминанта (b2
-4*a*c)
Формулу вводим с использованием мастера
функций:
В ячейках В7 и В8 напишите формулы для
вычисления х1 и х2 ()
4. Отобразите корни уравнения с
точностью до четвертого знака после
запятой. Выделите ячейки в которых
содержится вычисление корней уравнения.
Щелкаем правой кнопкой мыши. В появившемся
меню выбираем Формат ячеек. Выбираем
вкладку число и числовой формат.
Устанавливаем число десятичных знаков
– 4.
5. С использованием логической
функции ЕСЛИ в ячейках для расчета
корней уравнения отобразить “решения
нет” для случая, когда дискриминант
отрицательный.
6.
Попробуйте несколько вариантов решения
уравнения.
Пример исполнения работы представлен
на рисунках (см ниже)
Соседние файлы в папке Lab_R_Excel
- #
- #
- #
- #
- #
- #
- #