Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
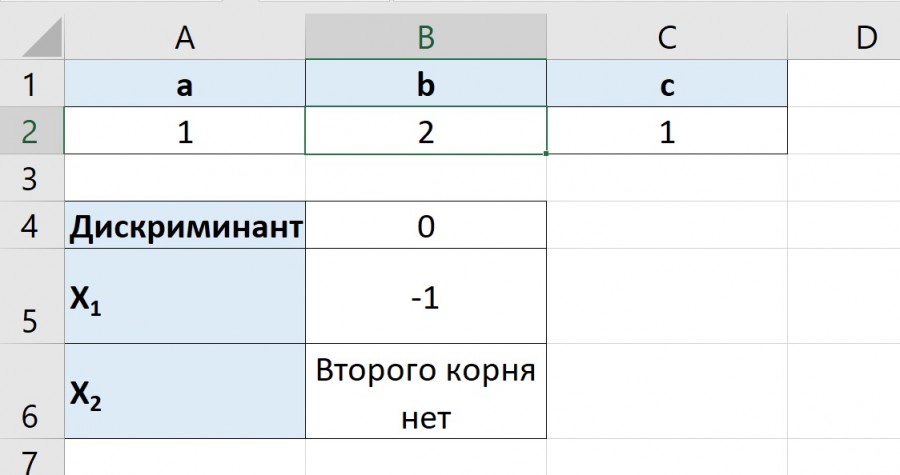
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
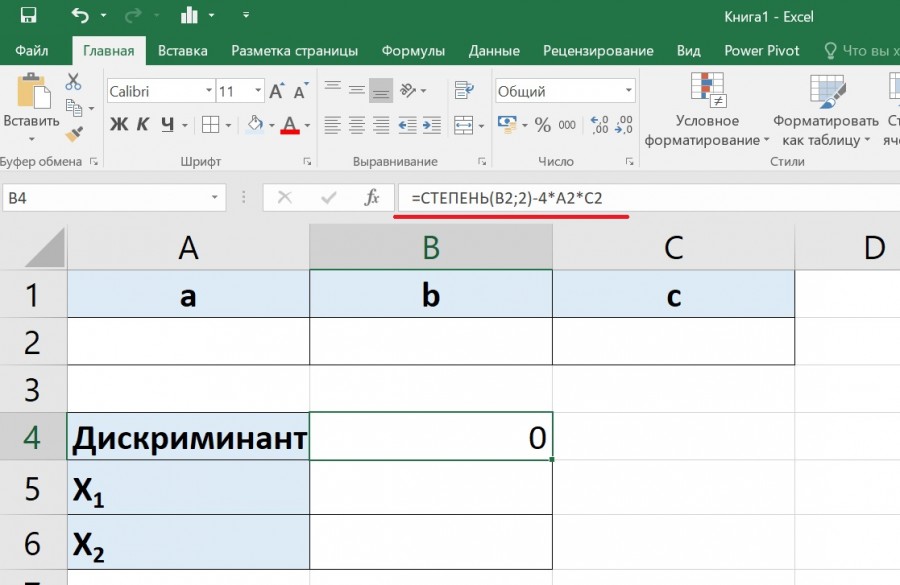
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
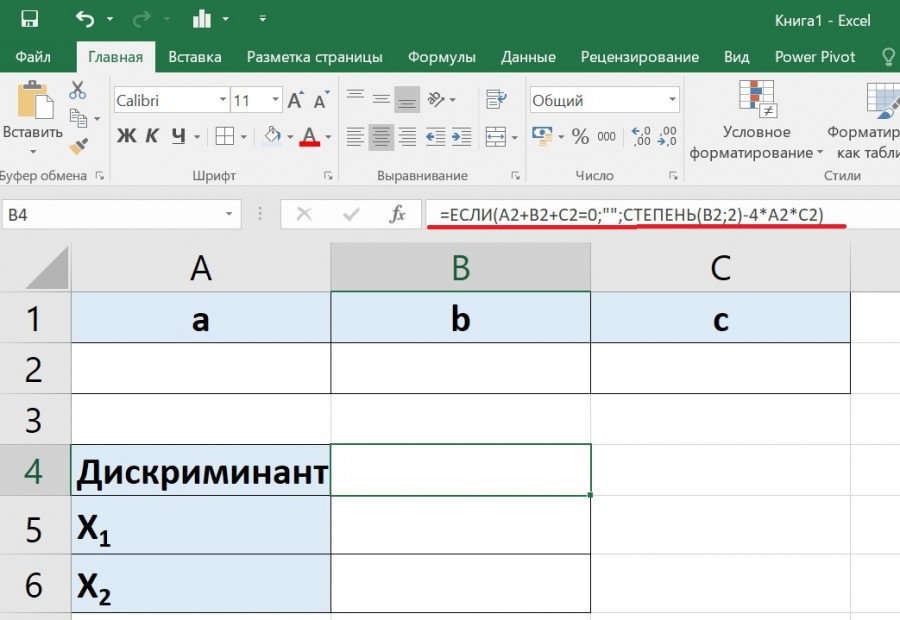
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
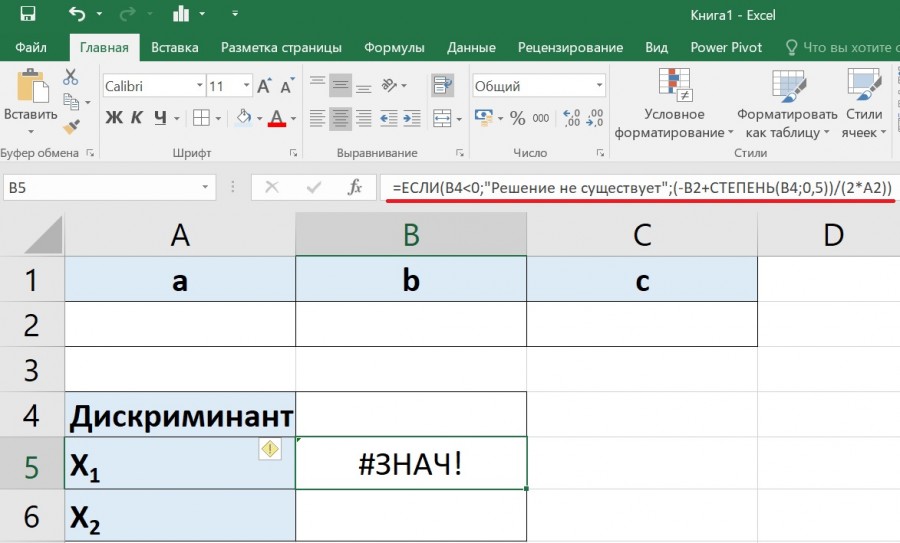
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Квадратное уравнение. Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D 2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень

Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
источники:
http://portalonline.ru/kompyutery-i-programmy/5337-kak-reshit-kvadratnoe-uravnenie-v-eksele.html
http://wpcalc.com/kvadratnoe-uravnenie-excel/
17 авг. 2022 г.
читать 2 мин
Квадратное уравнение принимает следующий вид:
ах 2 + Ьх + с = у
Часто вам будет дано значение y и вас попросят найти значение x .
Например, предположим, что у нас есть следующее квадратное уравнение:
4x 2 – 20x + 16 = -8
Оказывается, установка x = 3 или x = 2 решит это уравнение.
Для решения квадратных уравнений в Excel можно использовать функцию поиска цели .
В следующем пошаговом примере показано, как использовать функцию поиска цели на практике.
Шаг 1: введите уравнение
Во-первых, давайте введем случайное значение для x и формулу квадратного уравнения для y:
Шаг 2: Найдите первое значение X, используя поиск цели
Затем щелкните вкладку « Данные » на верхней ленте, затем нажмите кнопку « Анализ «что, если»» и выберите «Поиск цели »:
В появившемся новом окне укажите, что вы хотите установить ячейку B2 равной -8 , изменив значение в ячейке A2 :
Как только мы нажмем OK , функция поиска цели автоматически найдет значение x, которое решает уравнение:
Goal Seek находит, что значение x=2 (при условии, что 1,9999 округляется до 2) решает квадратное уравнение.
Шаг 3: Найдите второе значение X, используя поиск цели
Чтобы найти второе значение x, которое решает квадратное уравнение, установите начальное значение x на другое число.
Например, мы могли бы установить начальное значение x равным 4:
Затем мы можем снова запустить функцию поиска цели и увидеть, что она находит новое решение x=3 :
Таким образом, два значения x, которые могут решить это квадратное уравнение, равны x=2 и x=3 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как решить систему уравнений в Excel
Как построить уравнение в Excel
This is the second part of the how to solve quadratic equations in Excel guide. Here, we are going to be focusing on how to do this manual and VBA method, whereas the first part shows how to do this using the Goal Seek feature. In this guide, we are going to show you a different approach to solving quadratic equations in Excel using formulas and VBA.
If you missed the first part:
A quadratic function is a type of equation that contains a squared variable. It is called quadratic because quad means square in Latin. The quadratic functions usually have a structure like ax² + bx + c = 0, where x represents an unknown variable, and a, b, and c represent known constants. Excel can help you easily solve these types of equations for x.
Download Workbook
The Quadratic Formula
A quadratic function’s variable can take 2 values, meaning that there can be 2 solutions. To find these values, you can use the quadratic formula:
The plus/minus operator (±) means the formula should be executed twice. Once with plus (+):
And once with minus (-):
The a, b and c values are known numbers where a ≠ 0. Since we know the formula representation and the values, we can now create a formula for solving quadratic equations.
The Standard Formula
For this first approach, you essentially need to replicate the quadratic formula in Excel. You can enter the known values (a, b and c) right away into the formula. However, this means that the formula will be static and you will need to change the values one-by-one again when you need to solve for another equation.
Alternatively, you can pull the input values from cells to place the constants a, b and c and use those references inside the formula. Changing the cell value is usually a lot easier than changing all values one-by-one, especially with complex formulas.
Let’s assume that our constant values are in cells C7, D7 and E7. In this example, we also named these cells as a_1, b_1 and c_1 to make the formula easier to read. The formulas will be,
=(-b_1 + SQRT(POWER(b_1,2) — 4*a_1*c_1)) / (2*a_1)
=(-b_1 — SQRT(POWER(b_1,2) — 4*a_1*c_1)) / (2*a_1)
As you can see, one of the formulas uses plus and the other uses minus. This is how you can create a structure to solve the quadratic equations using traditional formulas. You can learn more about the POWER and SQRT functions in the respective pages.
Solving Quadratic Equations using VBA
The standard formula method is effective and dynamic. However, it may be hard to remember or use. While Excel doesn’t have a function that allows solving quadratic equations with one click, you can create yourself one!
To start working with VBA, you need to enable the Visual Basic for Applications (VBA) window. When your workbook is open, press the Alt + F11 key combination. Once the VBA window is active, add a module. Modules are pages where you can write your VBA code.
Copy and paste the code below into the module you’ve just added:
Function SolveQuadraticEquation(a As Integer, b As Integer, c As Integer, result As Integer)
If result = 1 Then
SolveQuadraticEquation = (-b + Sqr(b * b — 4 * a * c)) / (2 * a)
ElseIf result = 2 Then
SolveQuadraticEquation = (-b — Sqr(b * b — 4 * a * c)) / (2 * a)
Else
SolveQuadraticEquation = «Invalid result value. It should be 1 or 2.»
End If
End Function
This code creates a new function named SolveQuadraticEquation. This function has 4 arguments — 3 for known values, and 1 for selecting the plus/minus sign.
After pasting the code, return to the Excel window and test your new function. First, enter the 3 known values, a, b and c. Set 1 or 2 to select between plus and minus respectively.
Содержание
- 0.1 Шаг 1. Организация таблицы
- 0.2 Шаг 2. Проверка равенства Дискриминанта.
- 0.3 Формула дискриминанта
- 0.4 Шаг 3. Вычисляем корни уравнения.
- 1 Перейдем к вводу формул для решения
- 1.1 Защита листа в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
В этой статье вы узнаете как решить квадратное уравнение на конкретном примере.
Постановка задачи: решить квадратное уравнение в Excel
Ход решения: Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,cсначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c,то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK,подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
На примере квадратного уравнения х2 — 3х + 2 = 0 рассмотрим как решить квадратное уравнение в Excel.
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4=0;«х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;«х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
Оглавление
Введение.
Решение квадратных уравнений через дискриминант с помощью табличного процессора MS Excel.
Решение квадратных уравнений по теореме Виета с помощью табличного процессора MS Excel
Решение квадратного уравнения графическим методом с помощью табличного процессора MS Excel
Решение биквадратного уравнения в EXCEL.
Заключение
Литература
«Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
Готфрид Лейбниц в XVII в
Введение.
Уравнения, зачем они нам нужны и где вообще встречаются? В поисках ответа на этот вопрос я просмотрела учебники химии, физики, алгебры и геометрии за 8 класс и оказалось, что в учебнике химии многие задачи решаются уравнением, в учебнике физики некоторые задачи решаются уравнением. В учебнике алгебры большинство задач можно решить уравнением, в геометрии 1-2%. Теория уравнений интересовала и интересует математиков всех времён и народов.
Первобытная мама по имени (впрочем, у неё и имени- то не было) сорвала с дерева 12 яблок и решила поделить их между своими четырьмя детьми. Она не умела считать ни до четырёх, ни до двенадцати. Она поступила так: дала каждому по одному яблоку, потом ещё по одному, потом ещё по одному, и увидела, что и яблок больше нет, и никто из детей не обижен.
Сегодня эту задачу можно решить уравнением 4х=12. Таким образом, уравнение, как метод решения задач, появился очень давно.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Я задалась вопросом. А можно ли использовать компьютер для быстрого решения квадратного и биквадратного уравнений и как это сделать?
В данном проекте затрагиваются вопросы решения квадратных и биквадратных уравнений с помощью табличного процессора MS Excel. Я попыталась построить модель для решения квадратных уравнений с помощью алгебраического метода, по теореме Виета и графического метода, а также построила модель биквадратного уравнения.
Решение квадратных уравнений через дискриминант с помощью табличного процессора MS Excel.
Итак, моя задача сводилась к следующему: по известным коэффициентам квадратного уравнения вычислить дискриминант, сделать вывод о наличии корней и, если корни есть, найти их.
Начала я с составления блок-схемы:
да нет
В электронной таблице пользователю предоставляется возможность ввести любые коэффициенты квадратного уравнения. Благодаря введенным формулам в ЭТ вычисляется дискриминант и корни квадратного уравнения, если таковы имеются.
Ниже представлена технология решения квадратного уравнения в MS Excel : х2 — 3х + 2 = 0
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4<0; «нет»;»да»).
6. В ячейку В6 введите формулу = ЕСЛИ(В4>=0;»х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;»х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
Вот скриншот моей таблицы:
Решение квадратных уравнений по теореме Виета с помощью табличного процессора MS Excel
Нет формул важней
Для приведенного уравнения:
— b– Это сумма его корней,
c — Его корней произведение.
Франсуа Виет заметил некоторую закономерность между корнями квадратного уравнения и его коэффициентами. Сегодня эта теорема в школьном учебнике алгебры звучит так: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Ниже представлена технология решения приведённого уравнения в MS Excel:
х2 + 2х — 3 = 0
1. В ячейки А3:А6 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В3:В5 введите соответствующие значения коэффициентов: 1, 2, -3.
3. В ячейку В6 введите формулу =ЕСЛИ($B$3=1;$B$4^2-4*$B$5)
(Если все сделали правильно, то в ячейке В6 будет число 16).
- В ячейку А7 введите текст «Есть ли корни?».
- В ячейку В7 введите формулу =ЕСЛИ($B$6<0;»Корней нет!»;»Корни есть!»)
(Данная формула проверяет наличие корней у уравнения)
- В ячейку В8 введите формулу =ЕСЛИ($B$3=1;(-$B$4+КОРЕНЬ($B$6))/2)
(Вычисляем первый корень)
- В ячейку В9 введите формулу =ЕСЛИ($B$3=1;(-$B$4-КОРЕНЬ($B$6))/2)
(Вычисляем второй корень)
Но оказывается, теорема Виета рассматривается шире, для любого квадратного уравнения.
Действительно, если: ах² + bх + с=0
Сделаем дополнения в нашу таблицу. Чтобы сделать уравнение приведённым, разделим каждое слагаемое на первый коэффициент и к полученному уравнению применим теорему Виета.
- В ячейку С4 введем формулу =$B$4/$B$3
(делим второй коэффициент на первый b/a)
- В ячейку С5 введем формулу =$B$5/$B$3
(делим третий коэффициент на первый с/a)
- В ячейке В6 в формулу добавим =ЕСЛИ($B$3=1;$B$4^2-4*$B$5; $C$4^2-4*$C$5)
(дополненная формула позволяет вычислить дискриминант, при условии, если, а
- В ячейке B8 в формулу вносим дополнения, =ЕСЛИ($B$3=1;(-$B$4+КОРЕНЬ($B$6))/2;(-$C$4+КОРЕНЬ($B$6))/2)
(Вычисляем первый корень)
- В ячейке B9 в формулу вносим дополнения, =ЕСЛИ($B$3=1;(-$B$4-КОРЕНЬ($B$6))/2;(-$C$4-КОРЕНЬ($B$6))/2)
(Вычисляем второй корень)
Есть ещё способ, благодаря которому можно при определённых условиях сразу назвать корни уравнения.
Предположим, что а + b + с = 0, тогда b = -а — с
дискриминант D=(-а-с)²-4ас=а²+2ас+с²-4ас=(а-с)2
тогда , а
т. е если сумма коэффициентов квадратного уравнения равна нулю, то мы сразу можем назвать корни. Внесем необходимые изменения в уже существующую таблицу:
- В ячейку D3 введем формулу =ЕСЛИ($B$3+$B$4+$B$5=0;ИСТИНА;ЛОЖЬ)
(Данная формула проверяет условие, а+в+с=0 и если условие верно, то присваивается значение «ИСТИНА», в обратнос случае – «ЛОЖЬ»)
- В ячейку D8 введем формулу =ЕСЛИ(D3=ИСТИНА;1;»данный способ не подходит»)
(это позволит при условии «ИСТИНА» первому корню уравнения присваивается 1, если «ЛОЖЬ», то данным способом уравнение решаться не будет)
- В ячейку D9 введем формулу ЕСЛИ(D3=ИСТИНА;$B$5/$B$3;»данный способ не подходит»)
(это позволит при условии «ИСТИНА» вычислить второй корень уравнения как если «ЛОЖЬ», то данным способом уравнение решаться не будет).
Ну а если сумма первого коэффициента и свободного члена равна второму коэффициенту а + с = b, тогда:
D= (а+с) ²-4aс = а²+2ас+с²-4ас = (а-с) 2
Внесём необходимые формулы в табличный процессор MS Excel:
- В ячейку Е3 введём формулу =ЕСЛИ(B3+B5=B4;ИСТИНА;ЛОЖЬ)
- В ячейку Е8 введём формулу =ЕСЛИ(E3=ИСТИНА;-$B$5/$B$3;»данный способ не подходит»)
(при условии «ИСТИНА» вычисляет первый корень как ( — ) если «ЛОЖЬ», то данным способом уравнение решаться не будет)
- В ячейку Е9 введём формулу =ЕСЛИ(E3=ИСТИНА;-1;»данный способ не подходит»)
(при условии «ИСТИНА» второму корню уравнения присваивается ‘-1’, если «ЛОЖЬ», то данным способом уравнение решаться не будет)
Также в таблицу можно добавить проверку формул теоремы Виета, если
x1 + x2 = -b
x1 * x2 = c
то уравнение является приведённым:
- В ячейку А11 и А12 введём соответственно текст «x1 + x2 = -b?» «x1 * x2 = c?»
- В ячейку В11 введём =ЕСЛИ(И($B$8+$B$9=-$B$4;B8*B9=B5);»Уравнение приведённое»;»Уравнение не является приведённым» )
Здесь представлен скриншот моей таблицы:
Решение квадратного уравнения графическим методом с помощью табличного процессора MS Excel
Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
Если в уравнении х2 + bx + c = 0 перенести второй и третий члены в правую часть, то получим х2 = -bx — c. Построив графики зависимости у = х2 и у = — bx – c, на пересечении двух графиков можно определить не только количество корней, но и их значение.
Решим уравнение: х2 + 2х – 3 = 0.
Представим данное уравнение в следующем виде: х2 = – 2х + 3.
Чтобы решить данное уравнение, нужно найти такое значение х, при котором левая часть уравнения была бы равна правой. Введем две функции у1, равной левой части уравнения и у2, равной правой части уравнения. Теперь нужно найти такое значение х, при котором у1 = у2, т. е. общую точку, принадлежащую графику функции у1 и графику функции у2. Эта точка будет являться точкой пересечения графиков функций у1= х2 и у2= –2х + 3. Абсцисса точки пересечения будет являться решением исходного уравнения. Для этого составим таблицы их значений в MS Excel:
|
x |
у1=х^2 |
у2=-2х+3 |
|
-4 |
16 |
11 |
|
-3,5 |
12,25 |
10 |
|
-3 |
9 |
9 |
|
-2,5 |
6,25 |
8 |
|
-2 |
4 |
7 |
|
-1,5 |
2,25 |
6 |
|
-1 |
1 |
5 |
|
-0,5 |
0,25 |
4 |
|
0 |
0 |
3 |
|
0,5 |
0,25 |
2 |
|
1 |
1 |
1 |
|
1,5 |
2,25 |
0 |
|
2 |
4 |
-1 |
|
2,5 |
6,25 |
-2 |
|
3 |
9 |
-3 |
|
3,5 |
12,25 |
-4 |
|
4 |
16 |
-5 |
у1 = х2 – график первой зависимости — парабола, проходящая через начало координат, у2 = –2х + 3 – график второй зависимости – пряма
Выделим столбцы у1 и у2 и построим график функций:
А(–3;9) и В (1;1) –точки пересечения.
Абсциссы этих точек равны –3 и 1.
Значит х1 = –3 и х2 = 1 – решение уравнения
Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Решение биквадратного уравнения в EXCEL.
Уравнение вида: ax4 + bx2 + c = 0, где a, b, c — любые действительные числа, называется биквадратным.
Изложим основные пункты алгоритма решения биквадратного уравнения:
- Прежде всего сделаем замену y = x2. Получим квадратное уравнение ay2 + by + c = 0. Решим полученную систему квадратных уравнений.
Начнем с решения квадратного уравнения.
Далее в зависимости от значения переменной y будем решать второе уравнение y=x2 и находить значения переменной x. - С этой целью первым делом вычислим дискриминант квадратного уравнения: D = b2 — 4ac.
Далее в зависимости от значения дискриминанта D и от значений переменной y могут встретиться случаи, показанные в блок-схеме решения биквадратного уравнения:
Опишем действия, необходимые для того, чтобы составить модель решения задачи в MS Excel:
- В ячейку A1 записать наименование задачи «Биквадратное уравнение».
- В третьей строке указать заголовки столбцов: № ; a= ; b= ; c= ; d= ; y1 ; y2 ; x1= ; x2= ; x3= ; x4= ;
- Начиная с 4-ой строки, будем располагать соответственно числовые значения коэффициентов a, b, c и необходимые формулы для вычисления значений расчетных величин: D, y1, y2, x1, x2, x3, x4:
- В ячейку E4 поместить формулу для вычисления D
= =C4^2-4*B4*D4 - В ячейку F4 поместить формулу для вычисления y1 =ЕСЛИ(E4<0;»Решений нет»;(-C4-КОРЕНЬ(E4))/(2*B4))
- В ячейку G4 поместить формулу для вычисления y2 =ЕСЛИ(E4<0;»Решений нет»;(-C4+КОРЕНЬ(E4))/(2*B4))
- В ячейку H4 поместить формулу для вычисления x1
=ЕСЛИ(E4<0;»решений нет»; ЕСЛИ(И(F4<0;G4<0); «решений нет»;ЕСЛИ(И(F4>=0;G4>=0);-КОРЕНЬ(F4) - В ячейку I4 поместить формулу для вычисления x2
=ЕСЛИ(E4<0;»решений нет»; ЕСЛИ(И(F4<0;G4<0); «решений нет»;ЕСЛИ(И(F4>=0;G4>=0);-КОРЕНЬ(F4) - В ячейку J4 поместить формулу для вычисления x3
=ЕСЛИ(E4<0;»решений нет»; ЕСЛИ(И(F4<0;G4<0); «решений нет»;ЕСЛИ(И(F4>=0;G4>=0);-КОРЕНЬ(G4); - В ячейку K4 поместить формулу для вычисления x4
=ЕСЛИ(E4<0; «решений нет»; ЕСЛИ(И(F4<0;G4<0); «решений нет»; ЕСЛИ(И(F4>=0;G4>=0); + КОРЕНЬ(G4); ЕСЛИ(И(G4>=0;H4<0);»решений нет»;»решений нет»)))) - Скопируем формулы Е4:К4 в диапазон ячеек соответственно Е5:К8
Поместим в таблицу MS Excel коэффициенты а, b, c следующих пяти исходных биквадратных уравнений:
8x4 — 6x2 + 200 = 0
x4 + 5x2 + 6 = 0
x4 — 5x2 + 6 = 0
x4 + x2 — 6 = 0
x4 — x2 — 6 = 0
Скриншот таблицы:
Здесь предусмотрены все пять случаев, которые могут встретиться при решении биквадратного уравнения.
Заключение
Исследуя мир, познавая его, мы нередко встречаемся с разного рода задачами.
Данная творческая работа позволила мне понять, что любую проблему можно решить. В школе нас этому учат. Мы знакомимся с различного рода задачами, и для их решения составляем уравнение. Также в школе нас знакомят с методами решения уравнений, открытыми великими математиками. Я научилась решать эти уравнения с помощью компьютерных технологий.
В итоге изучения материала о квадратных и биквадратных уравнениях я не только овладела применением алгоритмических предписаний к решению конкретных заданий, но и научилась использовать логические средства для обоснования решений в случаях, когда это необходимо.
Список используемых источников
- Л.Ф. Пичурин «За страницами алгебры», Москва: Просвещение, 1990.
- Д.И. Аверьянов и др. Большой справочник «Математика» для школьников и поступающих в ВУЗы, Москва: Дрофа, 1999.
- Н.В. Макарова «Информатика и ИКТ. Практикум 8-9», СПб.: Питер, 2008.
- Н.Д. Угринович «Информатика и ИКТ: учебник для 9 класса», М.:БИНОМ. Лаборатория знаний, 2010.
- Л.А. Залогова и др.; под ред. И.Г. Семакина, Е.К. Хеннера «Информатика и ИКТ. Задачник практикум», том 2, М.:БИНОМ. Лаборатория знаний, 2011.
Применение табличного процессора MS Excel для решения квадратных и биквадратных уравненийСтраница
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
людей нашли эту статью полезной. А Вы?
Решение квадратных уравнений с использованием электронных таблиц
Решение квадратных уравнений с использованиемэлектронных таблиц EXCEL
Работу выполнила ученица 9 класса
МБОУ « Бичурга-Баишевская СОШ»
Гаврилова Анна
Руководитель: учитель информатики Симурзина Н.Н.
Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
«Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
Готфрид Лейбниц
Цель исследования : изучить и создать программы для автоматического вычисления корней квадратного уравнения
Цель исследования: изучить и создать программы для автоматического вычисления корней квадратного уравнения.
Поставленная цель исследования предполагает решения ряда задач:
Изучить способы решения квадратных уравнений
Разработать вычислительные программы для решения квадратных уравнений
Проанализировать результаты вычислений
Сформулировать выводы и рекомендации по выбору программы для решения квадратных уравнений с помощью компьютера
Проблема: создать программу для автоматического решения квадратных уравнений
Проблема: создать программу для автоматического решения квадратных уравнений
Объект исследования: решение уравнений с помощью компьютера
Предмет исследования: компьютерные программы
Гипотеза: считаю, что компьютерные программы для решения квадратных уравнений автоматизируют вычисление корней
Методы исследования : сравнение и анализ, эксперимент, метод визуализации данных
Методы исследования: сравнение и анализ, эксперимент, метод визуализации данных.
Новизна исследования заключается в экспериментальной проверке компьютерных вычислений с помощью табличного процессора MS Excel.
Практическая значимость состоит в том, что созданные для проведения эксперимента программы можно будет использовать и в дальнейшем для нахождения корней квадратного уравнения
В своей работе, я решила остановиться на квадратных уравнениях, так как эти виды уравнений – самые распространенные
В своей работе, я решила остановиться на квадратных уравнениях, так как эти виды уравнений – самые распространенные. Они используются в таких науках, как алгебра, физика, геометрия и химия.
Программу, которую я решила взять для решения квадратных уравнений – это
Программу, которую я решила взять для решения квадратных уравнений – это MS Excel
Microsoft Еxcel – программа для работы с электронными таблицами, созданная компанией Microsoft. Она представляет возможности экономико – статистических расчетов, графические инструменты
Я буду исследовать решение трех квадратных уравнений:
Я буду исследовать решение
трех квадратных уравнений:
Технология решения квадратного уравнения в
Технология решения квадратного уравнения в MS Excel
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4<0; «нет»;»да»).
6. В ячейку В6 введите формулу = ЕСЛИ(В4>=0;»х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;»х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Графический способ решения квадратных уравнений
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае- Microsoft Excel 2010, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней квадратного уравнения с заданной точностью
Подбор параметра Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в рассмотренных примерах
Подбор параметра
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в рассмотренных примерах.
Возможности электронных таблиц позволяют находить приближенные значения корней уравнения с заданной точностью .Для этого используется метод Подбор параметра.
Подбор параметра — х2+5х-3 = 0
Подбор параметра
—х2+5х-3=0
Построение диаграммы типа График
Определение приближенных значений корней уравнения
Поиск приближенного решения уравнения с заданной точностью методом Подбора параметра
Подбор параметра Решение уравнения -х2+5х-3=0
Подбор параметраРешение уравнения -х2+5х-3=0
Выводы Используя информационные технологии можно очень быстро и качественно решить квадратные уравнения
Выводы
Используя информационные технологии можно очень быстро и качественно решить квадратные уравнения.
Мы убедились, что построенные нами модели работают для всех случаев: есть два решения квадратного уравнения, единственное решение; решений нет.
Созданные программы можно будет использовать и в дальнейшем для нахождения корней квадратного уравнения на уроках математики.
Литература Н.Д. Угринович «Информатика и
Литература
Н.Д. Угринович «Информатика и ИКТ: учебник для 9 класса», М.:БИНОМ. Лаборатория знаний, 2013.
http://ru.wikipedia.org/wiki/Квадратное уравнение
Спасибо за внимание
Спасибо за внимание
Содержание
- Как решить квадратное уравнение в экселе?
- Видео как решить квадратное уравнение в экселе.
- Квадратное уравнение в Excel
- Ход решения
- Перейдем к вводу формул для решения
- Защита листа в Excel
- Решить квадратное уравнение в excel подбор параметра
- Квадратное уравнение в Excel
- Ход решения
- Перейдем к вводу формул для решения
- Защита листа в Excel
- Подбор параметра в EXCEL
- Простейший пример
- Калькуляция, подбираем значение прибыли
- Подбор суммы кредита
- Уравнения и задачи на подбор параметра в Excel
- Подбор параметра и решение уравнений в Excel
- Второй пример использования подбора параметра для уравнений
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Источник
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Источник
Решить квадратное уравнение в excel подбор параметра
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Подбор параметра в EXCEL
history 18 ноября 2012 г.
- Группы статей
- Другие Стандартные Средства
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .
В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .
Простейший пример
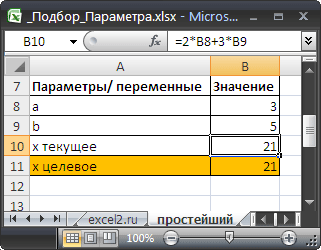
Найдем значение параметра b в уравнении 2*а+3*b=x , при котором x=21 , параметр а= 3 .
Подготовим исходные данные.
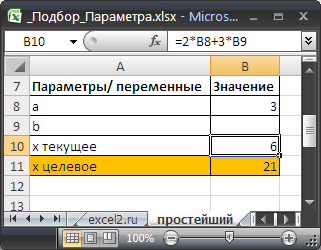
Значения параметров а и b введены в ячейках B8 и B9 . В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x ). Целевое значение x в ячейке B11 введено для информации.
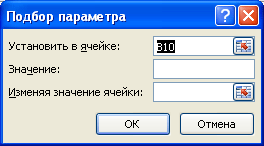
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …) .
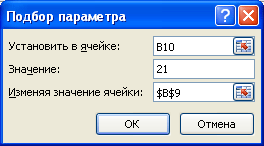
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b ).
Инструмент Подбор параметра подобрал значение параметра b равное 5.
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно .
Примечание : Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b , которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший .
Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).
Калькуляция, подбираем значение прибыли
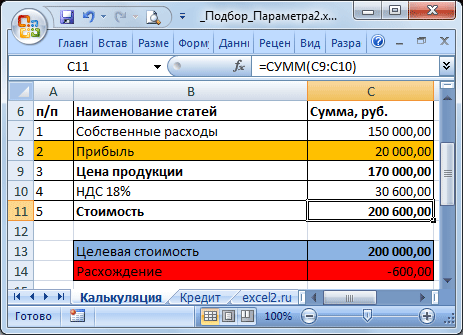
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13 ). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли ( С8 ), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение ( С14 ) равно 0.
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11 ) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра .
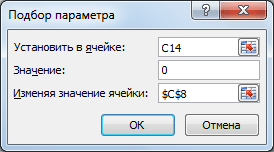
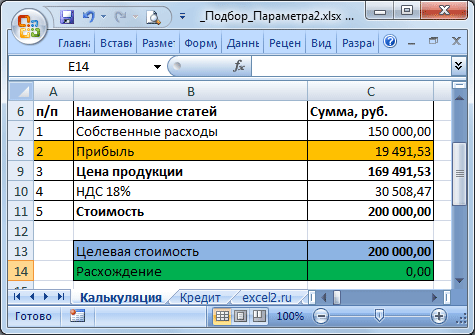
Выделите ячейку С14 , вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).
Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0
Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.
Подбор суммы кредита
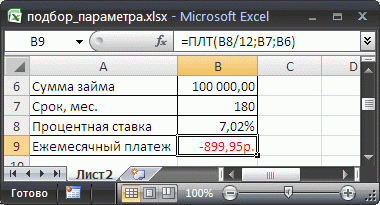
Предположим, что нам необходимо определить максимальную сумму кредита , которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).
В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет ). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.
Введем в ячейку B 6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B 7 , % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:
- на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …;
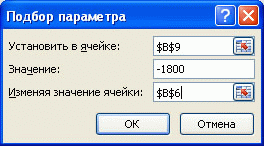
- в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9 ;
- введите искомый результат в поле Значение . В данном примере он равен -1800 ;
- В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6 ;
- Нажмите ОК
Что же сделал Подбор параметра ? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.
Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения . Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.
Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.
Уравнения и задачи на подбор параметра в Excel
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y =7 является функцией x ;
- нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
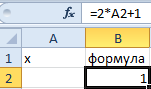
- Заполните ячейки листа, так как показано на рисунке:
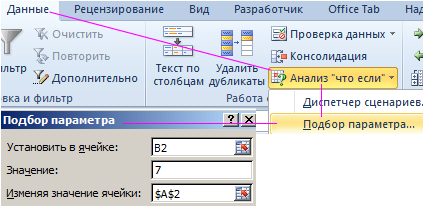
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
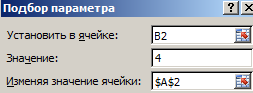
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
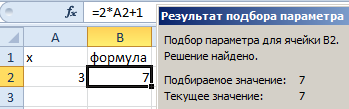
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
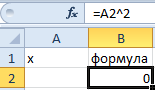
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
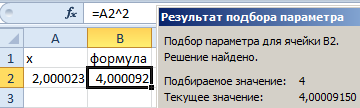
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
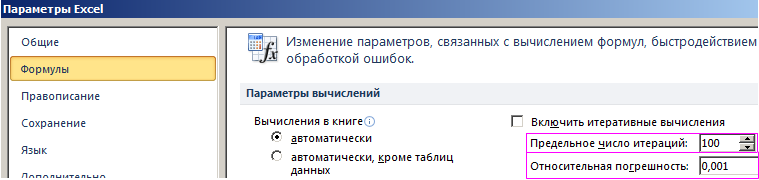
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
Источник