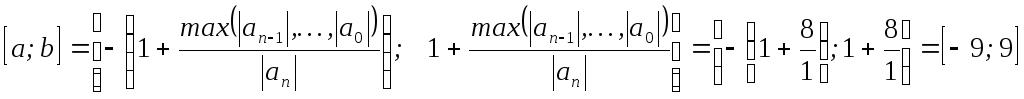Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Excel. Решение уравнений n-ой степени
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
ПОИСК РЕШЕНИЯ В EXCEL
Программа Microsoft Office Excel предназначена и широко используется для вычислений, предполагающих представление данных в табличном виде.
На уроках алгебры часто приходится решать квадратные, кубические уравнения, системы уравнений.
Цель — решать уравнения n -ой степени и системы уравнений с помощью Excel .
Для достижения данной цели поставим следующие задачи :
изучить возможности инструмента «Поиск решения»;
создать в Excel шаблоны для решения различных типов задач;
разработать инструкции нахождения решений;
Программа « Поиск решения» позволяет получить результат на основе изменения значения нескольких ячеек. Кроме того, при выполнении поиска решения можно задать условия – ввести ограничения. Эти возможности позволяют использовать программу Excel для решения системы уравнений и уравнений, при решении которых необходимо учитывать область допустимых значений, для нахождения точек, в которых достигается максимум или минимум значения целевой функции нескольких переменных, определенных на множестве с линейными и нелинейными ограничениями. Другими словами – находить оптимальное решение задачи с ограничениями.
Модели всех задач на оптимизацию состоят из следующих элементов:
Переменные — неизвестные величины, которые нужно найти при решении задачи.
Целевая функция — величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
Ограничения — условия, которым должны удовлетворять переменные.
Поиск решения рассмотрим на примерах.
Найти минимальное значение функции 
В 
Получен результат: минимальное значение функции 
Найти максимальное значение функции 

Как решить кубическое уравнение эксель
Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).
Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.
Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

|
| Рис. 8. График функции |
Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:
где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).
- В ячейку Хнач (В4) заносим начальное приближение — 5.
- В ячейку Хтекущ (С4) записываем формулу:
=ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)). - В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
- Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
- Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
Рис. 9. Определение начальных установок значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.
2.2. Подбор параметра
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:
- В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
Рис. 10. Окно диалога Подбор параметра стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
- В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
- После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.
Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):
- В ячейку Х (С2) вводим начальное приближение.
- В ячейку Хi (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
=X-(X^2-5*X+6)/(2*X-5). - В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Хi.
- После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).
Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.
2.3. Поиск решения
Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.
Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:
Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х1, х2, … , хn), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:
- найти максимум целевой функции F(х1, х2, … , хn);
- найти минимум целевой функции F(х1, х2, … , хn);
- добиться того, чтобы целевая функция F(х1, х2, … , хn) имела фиксированное значение: F(х1, х2, … , хn) = a.
Функции G(х1, х2, … , хn) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.
Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.
Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
|
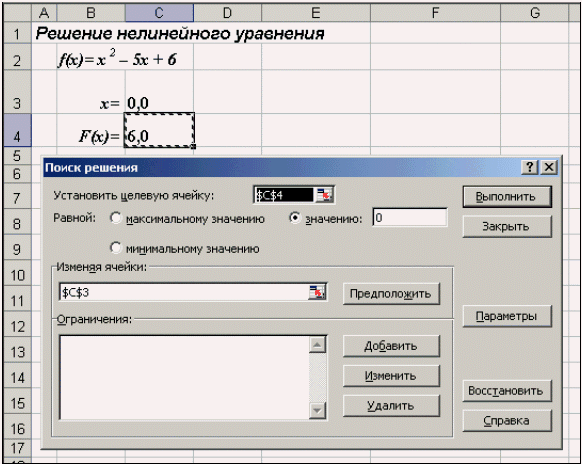
| Рис. 12. Окно диалога Поиск решения |
После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:
- в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
- для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
- в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
- в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
- для запуска процесса поиска решения нажать кнопку Выполнить.

|
| Рис. 13. Результаты поиска |
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
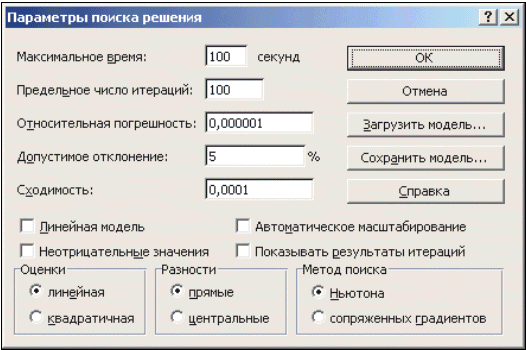
Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):
|
| Рис. 14. Настройка параметров Решателя |
- Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
- Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
- Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
- Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
- Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
- Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
- Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
- Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
- Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
- Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
- Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
- Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Сохранить модель поиска решения можно следующими способами:
- при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
- если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
- еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.
Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.
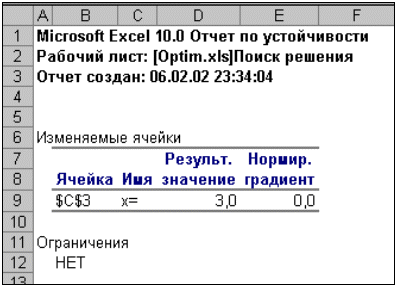
|
| Рис. 15. Отчет по устойчивости |
Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

|
| Рис. 16. Отчет по результатам |
Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.
Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
источники:
http://infourok.ru/ecel-reshenie-uravneniy-noy-stepeni-1487724.html
http://old.exponenta.ru/EDUCAT/systemat/pimonov/Equations/gl2.asp
ПОИСК
РЕШЕНИЯ В EXCEL
Программа Microsoft Office Excel
предназначена и широко используется для вычислений, предполагающих
представление данных в табличном виде.
На уроках алгебры часто приходится решать квадратные,
кубические уравнения, системы уравнений.
Цель — решать
уравнения n-ой
степени и системы уравнений с помощью Excel.
Для достижения данной цели поставим следующие задачи:
—
изучить
возможности инструмента «Поиск решения»;
—
создать
в Excel шаблоны для решения различных типов задач;
—
разработать
инструкции нахождения решений;
Программа «Поиск решения» позволяет получить
результат на основе изменения значения нескольких ячеек. Кроме того, при
выполнении поиска решения можно задать условия – ввести ограничения. Эти
возможности позволяют использовать программу Excel для решения системы
уравнений и уравнений, при решении которых необходимо учитывать область
допустимых значений, для нахождения точек, в которых достигается максимум или
минимум значения целевой функции нескольких переменных, определенных на
множестве с линейными и нелинейными ограничениями. Другими словами – находить
оптимальное решение задачи с ограничениями.
Модели всех задач на оптимизацию состоят из следующих
элементов:
1.
Переменные
— неизвестные величины, которые нужно найти при решении задачи.
2.
Целевая
функция — величина, которая зависит от переменных и является целью, ключевым
показателем эффективности или оптимальности модели.
3.
Ограничения
— условия, которым должны удовлетворять переменные.
Поиск решения рассмотрим на примерах.
Пример 1. (1; -9)
Найти
минимальное значение функции .

найти с помощью инструмента Поиск решения, заполнив поля, как
показано на рис. 2.
Рис. 2
Рис.
1
Получен результат: минимальное значение
функции y = -9 при x = 1. Так как исследована квадратичная функция, графиком которой
является парабола, ветви направлены вверх, тогда точка (1, -9) является
вершиной параболы. Значит, с помощью инструмента Поиск
решения также можно найти и координаты вершины параболы, что в свою
очередь сокращает время в их нахождении.
Пример 2. (-1; -1)
Найти
максимальное значение функции .
Пример 3. x= — 0,5
и y = 2,5

уравнение
Рис. 3 Рис.4

Рис.
5
Таким образом, с помощью Excel можно
решать квадратные уравнения, допускающие два решения. Рассмотрена задача поиска
значения параметра, позволяющего достичь конкретной цели. Но решаемые задачи
могут быть более сложными. Например, поиск нескольких параметров,
обеспечивающих некоторый, наперед заданный результат.
Пример 4. x= 12, y = 6 и z
=3
Решить
систему уравнений
Рис. 6
Рис.7
Пример 5. ,
,
Решить
кубическое уравнение .
 Воспользовавшись инструментом
Воспользовавшись инструментом
Поиск решения, получены
корни.
.
Рис. 8
Пример 6. x = 0,5
5x – 8 lnx = 8
Самостоятельная работа
Пример 7. x = —
1, y = —
1, z = — 1
Решить
систему уравнений
x + 5y + z = — 7,
2x – y – z = 0,
x – 2y – z = 0.
Пример 8. x = 2,
y = 3
Решить
уравнение x² + 5x + 6 = 0
Пример 9. x = 2, y = 28
Решить
уравнение x² + 30x + 56 = 0
Решение разнообразных задач позволяет расширить
представление о возможностях электронных таблиц, продемонстрировать
практическое применение программы Excel на уроках математики.
Содержание | Назад
Рассмотрим пример нахождения всех корней уравнения
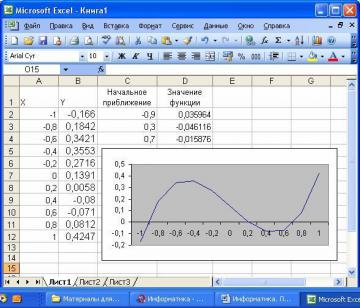
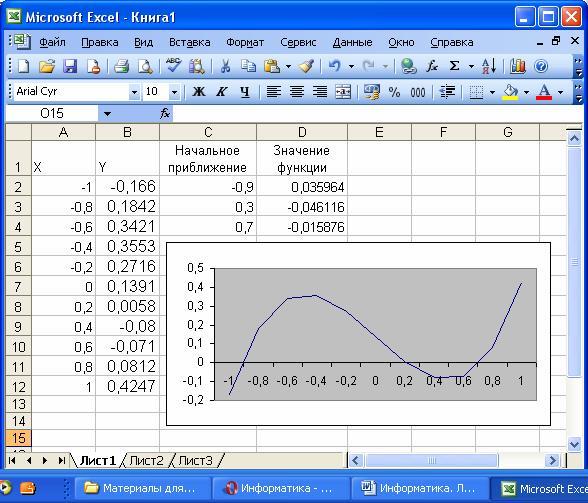
Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно надо локализовать. С этой целью необходимо полином протабулировать. Построим таблицу значений полинома на отрезке [—1,1] с шагом 0,2 и график полинома. Результат приведен на рис. 29, где в ячейку В2 введена формула
=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.
На рис. 29 видно, что полином меняет знак на интервалах [—1,—0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни.
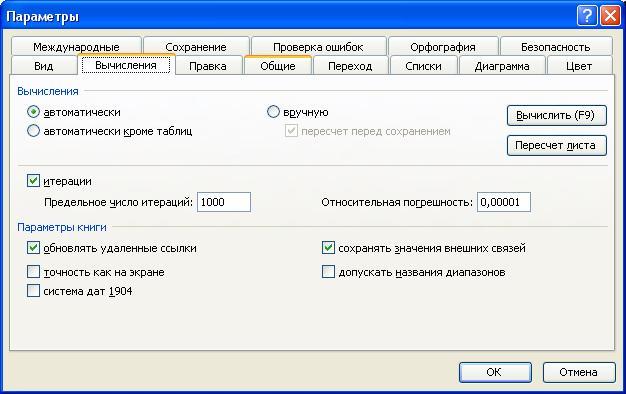
Найдем корни полинома методом последовательных приближений с помощью команды Сервис / Подбор параметров. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис / Параметры (рис. 30).
Зададим относительную погрешность и предельное число итераций равными 0,00001 и 1000 соответственно. В качестве начальных приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем в качестве начальных приближений их средние точки: —0.9, 0.3, 0,7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу
=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.
Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. В ячейках D2:D4 будут вычислены значения полинома при значениях аргумента, введенных в ячейки C2:C4.
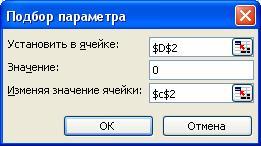
Теперь выберем команду Сервис / Подбор параметров и заполним диалоговое окно Подбор параметров следующим образом (рис. 31).
В поле Установить в ячейке введем D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).
Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере в $D$2 и $C$2).
После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помещается в ячейку С2. В данном случае оно равно —0,920. Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0,210 и 0,720.
Содержание | Назад
|
smelovvvv Пользователь Сообщений: 47 |
Знатоки, помогите с макросом для решения кубического уравнения итерациями…ну или другим способом! |
|
Radioalex Пользователь Сообщений: 73 |
Наверно както так… Изменено: Radioalex — 27.10.2013 23:25:13 |
|
А что мешает воспользоваться солвером? Задача вполне тривиальная. На худой конец можно построить график прилагаемой функции и найти все пересечения с осью иксов. С уважением, |
|
|
smelovvvv Пользователь Сообщений: 47 |
ну построить график без проблем да и вручную итерациями я решить могу… |
|
Radioalex Пользователь Сообщений: 73 |
Если объем данных большой, то решатель малоэффективен, так как необходимо будет находить по 3 корня в каждом варианте. В этом случае Вам целесообразно воспользоваться стандартными формулами (Кардано, Виета) для решения кубических уравнений |
|
smelovvvv Пользователь Сообщений: 47 |
Спасибо попробую. А что такое решатель? |
|
smelovvvv Пользователь Сообщений: 47 |
Из всех корней обязательно будет вещественный положительный лежащий в диапазоне от 0 до 200…именно он и нужен…может это поможет упростить задачу… |
|
Kuzmich Пользователь Сообщений: 7998 |
#8 28.10.2013 00:12:06
Сервис — поиск решения |
||
|
jakim Пользователь Сообщений: 1947 |
#9 28.10.2013 01:48:29 Посмотрите, что получается графически. Прикрепленные файлы
|
Страницы работы
Содержание работы
Балтийский
Государственный Технический Университет «ВоенМех» им. Д.Ф. Устинова
Кафедра
прикладной математики и информатики
Курсовая
работа по дисциплине «Информатика»
Нахождение
корней кубического уравнения в среде Microsoft
Office Excel
2003, Mathcad 13, Turbo
Pascal 7.0.
Студент Ефимов
Евгений Михайлович Е19108
Преподаватель
Гнидин Вячеслав Васильевич
Санкт
– Петербург 2010
Решение
кубического уравнения
· Работа
в
среде
Microsoft Office Excel 3
· Работа
в среде Mathcad 13
4
· Работа
в среде Turbo
Pascal
7.0 5
· Вывод
по результатам работы 9
Работавсреде
Microsoft Office Excel
|
-2,7 |
-1,74568 |
|
-2,6 |
-1,04055 |
|
-2,5 |
-0,44582 |
|
-2,4 |
0,044506 |
|
-2,3 |
0,436436 |
|
-2,2 |
0,735966 |
|
-2,1 |
0,949096 |
|
-2 |
1,081826 |
|
-1,9 |
1,140156 |
|
-1,8 |
1,130086 |
|
-1,7 |
1,057616 |
|
-1,6 |
0,928746 |
|
-1,5 |
0,749476 |
|
-1,4 |
0,525806 |
|
-1,3 |
0,263736 |
|
-1,2 |
-0,03073 |
|
-1,1 |
-0,3516 |
|
-1 |
-0,69287 |
|
-0,9 |
-1,04854 |
|
-0,8 |
-1,41261 |
|
-0,7 |
-1,77908 |
|
-0,6 |
-2,14195 |
|
-0,5 |
-2,49522 |
|
-0,4 |
-2,83289 |
|
-0,3 |
-3,14896 |
|
-0,2 |
-3,43743 |
|
-0,1 |
-3,6923 |
|
0 |
-3,90757 |
|
0,1 |
-4,07724 |
|
0,2 |
-4,19531 |
|
0,3 |
-4,25578 |
|
0,4 |
-4,25265 |
|
0,5 |
-4,17992 |
|
0,6 |
-4,03159 |
|
0,7 |
-3,80166 |
|
0,8 |
-3,48413 |
|
0,9 |
-3,073 |
|
1 |
-2,56227 |
|
1,1 |
-1,94594 |
|
1,2 |
-1,21801 |
|
1,3 |
-0,37248 |
|
1,4 |
0,596646 |
|
1,5 |
1,695376 |
|
1,6 |
2,929706 |
|
1,7 |
4,305636 |
С помощью графика,
построенного по точкам в среде Excel,
я нахожу промежутки, при которых корни уравнения находятся внутри этих
промежутков.
Кубическое уравнение
вида a + b
+ cx
+ d = 0 имеет коэффициенты, равные:
A = 1 B=
2,28 C= -1,9347 D=
-3,907574
Работа
в среде Mathcad
13
1) Постановка
задачи
A:=
1
B:=
2,28
C:=
-1,9347
D:=
-3,907574
2) Построение
графика
Задав
функцию и промежутки в среде MathCAD 13, я построил график.
С
помощью встроенной функции «Given -Find» в среде MathCAD 13 вычислил
корни кубического уравнения.
Работа
в среде TurboPascal
7.0
1) Задача
Составление программы, позволяющую
находить корни кубического уравнения с заданной точностью на известных
промежутках.
2) Описание
алгоритма.
Т.к. с достаточно высокой точностью
известны промежутки, на которых находятся корни уравнения, то решено было
использовать наиболее простой алгоритм: нахождение минимального по модулю
значения функции на заданном промежутке с помощью прямой подстановки; шаг
значений переменной задаёт необходимую точность.
3) Блок
– схема

4) Текст
программы
program roots3;
const k1=1;
k2=2.28; k3=-1.9347; k4=-3.907574;
var
a,b,c,fa,fc,eps:real; key:integer; f:text;
procedure input;
begin
write(‘Border
left= ‘);
readln(a);
write(‘Border
right= ‘);
readln(b);
write(‘Input
eps= ‘);
readln(eps);
end;
begin
assign(f,’D:rezult.txt’);
rewrite(f);
append(f);
repeat
input;
writeln(f,’
Boundaries a= ‘,a:4:4,’ b=’,b:4:4,’ Accuracy eps =’,eps:4:4);
while
(b-a)>eps do
begin
fa:=a*a*a*k1+a*a*k2+a*k3+k4;
c:=(a+b)/2;
fc:=c*c*c*k1+c*c*k2+c*k3+k4;
if
(fa*fc)<=0 then b:=c else a:=c;
end;
writeln(f, ‘Root
of the equation c= ‘,c);
writeln(‘c=
‘,c);
writeln(‘ New
boundaries? 1-yes, 0-no’);
readln(key);
until key=0;
close(f)
end.
5) Вывод
результатов
Border left= -2.5
Border right= -2.4
Input eps= 0.001
C= -2.4101562500E+00
New boundaries? 1-yes,
0-no
1
Border left= -1.3
Border right= -1.2
Input eps= 0.001
C= -1.2101562500E+00
New boundaries? 1-yes,
0-no
1
Border left= 1.3
Border right= 1.4
Input eps= 0.001
C= 1.33984375+00
New boundaries? 1-yes,
0-no
0
6) Вывод
результата в файл
Boundaries a= -2.5000 b=-2.4000 Accuracy
eps =0.0010
Root of the equation c=
-2.4101562500E+00
Boundaries a= -1.3000 b=-1.2000
Accuracy eps =0.0010
Root of the equation c=
-1.2101562500E+00
Boundaries a= 1.3000 b=1.4000 Accuracy
eps =0.0010
Root of the equation c=
1.3398437500E+00
Вывод по результатам работы
Ознакомившись
с работой программ, по итогам данной курсовой работы могу отметить для себя
следующий момент: наиболее удобной и быстрой в освоении я считаю программу MathCAD
13.
Удобный ввод
переменных, вывод графика, удобство изменения обозримых границ координат на
графике и подсчет корней уравнения по итогам работы показались мне наиболее
быстрым способом работы.
Похожие материалы
- Табличный процессор Excel. Основные понятия и общие принципы работы с электронной таблицей. Создание и заполнение таблиц постоянными данными и формулами
- Ответы на вопросы к зачету по дисциплине «Информатика» (Место ЭВМ в деятельности человека. Структура программы типовой вычислительной задачи)
- Запись специальных математических формул в Microsoft Office Word. Решение трансцендентных уравнение с помощью Mathcad
Информация о работе
Разнообразные
проблемы механики, физики, техники
сводятся к вопросу о нахождении корней
многочлена, причем, иногда достаточно
высоких степеней. Точные решения известны
для квадратных уравнений, кубических
(формула Кардано) и уравнений 4-й степени
(метод Феррари). Для уравнений выше 5-й
степени не существует формул для
выражения корней многочлена. Однако в
технических приложениях обычно достаточно
знать лишь приближенные значения корней
с некоторой заранее заданной точностью.
В
общем
же
случае
надежд
на
простое
аналитическое
решение
нет. Более
того,
доказано,
что
даже
алгебраическое
уравнение
выше
четвертой
степени
неразрешимо
в
элементарных
функциях.
Поэтому
решение
уравнения
проводят
численно
в
два
этапа
(здесь
разговор
идет
лишь
о
вещественных
корнях
уравнения).
На
первом
этапе
производится
отделение
корней
– поиск
интервалов,
в
которых
содержится
только
по
одному
корню.
Второй
этап
решения
связан
с
уточнением
корня
в
выбранном
интервале
(определением
значения
корня
с
заданной
точностью).
В
общем виде уравнение n-й
степени выглядит следующим образом:
,
где
n
− некоторое положительное число,
− произвольные числа, причем старший
коэффициентдолжен быть не равен нулю.
Выражение
называется многочленом (полиномом)n
− й степени от неизвестного x.
Если
при некотором x
= x0
выполняется равенство
,
тоx0
называется корнем многочлена
.
Приведем
некоторые рекомендации по отысканию
действительных корней многочленов с
действительными коэффициентами:
-
Действительными
корнями многочлена будут абсциссы
точек пересечения его графика с осью
Х
и только они; -
Число
положительных корней многочлена равно
числу перемен знаков в системе
коэффициентов этого многочлена
(коэффициенты, равные нулю, не учитываются)
или меньше этого числа на четное число; -
Число
отрицательных корней многочлена равно
числу сохранения знаков в системе
коэффициентов этого многочлена или
меньше этого числа на четное число; -
Если
многочлен не имеет отрицательных
коэффициентов, то многочлен не имеет
положительных корней; -
О
трезок
локализации всех корней многочлена
определяется по выражению:
Для границы a
формула справедлива если
Решение
отыскания корней многочлена с помощью
электронной таблицы MS
Excel
предполагает следующие шаги:
-
Провести
табулирование заданного многочлена
на интервале
.
-
Выявить
интервалы локализации каждого корня
многочлена (перемена знака в значении
).
При необходимости, следует использовать
табуляцию многочлена, неоднократно
уменьшая шаг табуляции для более точных
оценок. -
После
локализации корней произвести их
уточнение.
При последующем
уточнении корня на обнаруженном
интервале не надейтесь никогда найти
точное
значение и добиться обращения функции
в нуль при использовании калькулятора
или компьютера, где сами числа
представлены ограниченным числом
знаков. Здесь критерием может служить
приемлемая абсолютная
или относительная
погрешность
корня. Если корень близок к нулю, то лишь
относительная погрешность даст
необходимое число значащих цифр. Если
же он весьма велик по абсолютной величине,
то критерий абсолютной погрешности
часто дает совершенно излишние верные
цифры. Для функций, быстро изменяющихся
в окрестности корня, может быть
привлечен и критерий: абсолютная
величина значения функции
не превышает заданной допустимой
погрешности.
Пример
Найти
все действительные корни уравнения:
f(x)
= Х5
+
2Х4
+
5Х3
+
8Х2
−
7Х –
3
= 0,
где
а5
= 1, а4
= 2, а3
= 5, а2
= 8, а1
= −7, а0
= −3.
-
Число сохраненных
знаков =
4 (в уравнение отрицательных корней 4
или 2) -
Число перемены
знаков = 1 (в уравнение один положительный
корень) -
Определяем отрезок
[a;
b],
на котором существуют корни уравнения..
-
Выполняем
приближенное табулирование функции
на отрезке [−9; 9]
с шагом 1. -
Определяем, что
функция меняет знак на отрезке [−3; 1]. -
Производим
табулирование функции на отрезке [−3;
1] с шагом 0,1. -
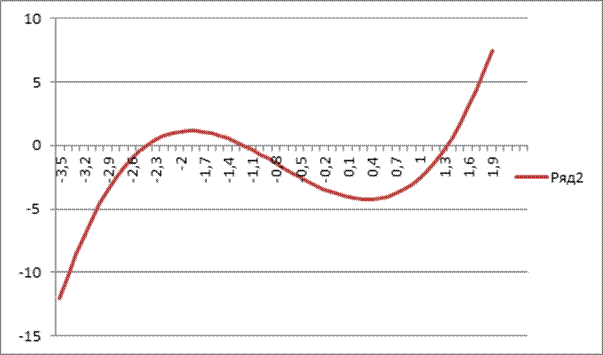
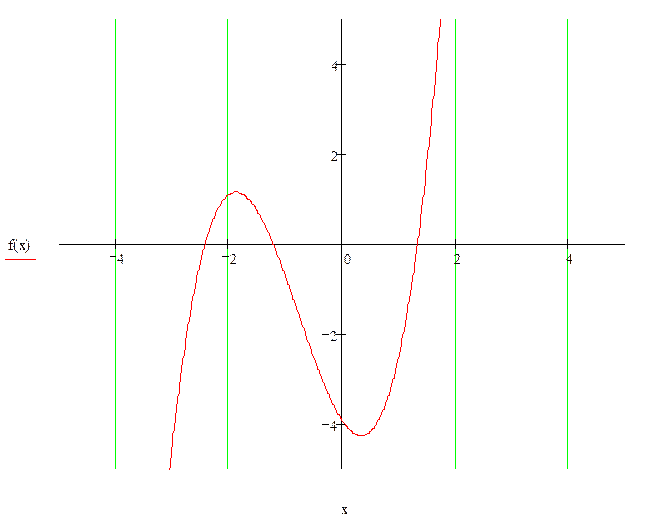
Строим график
функции. -
Используя, таблицу
и график функции определяем положение
корней уравнения (на рис. 1. отрезки
локализации корней выделены желтым
цветом).
Р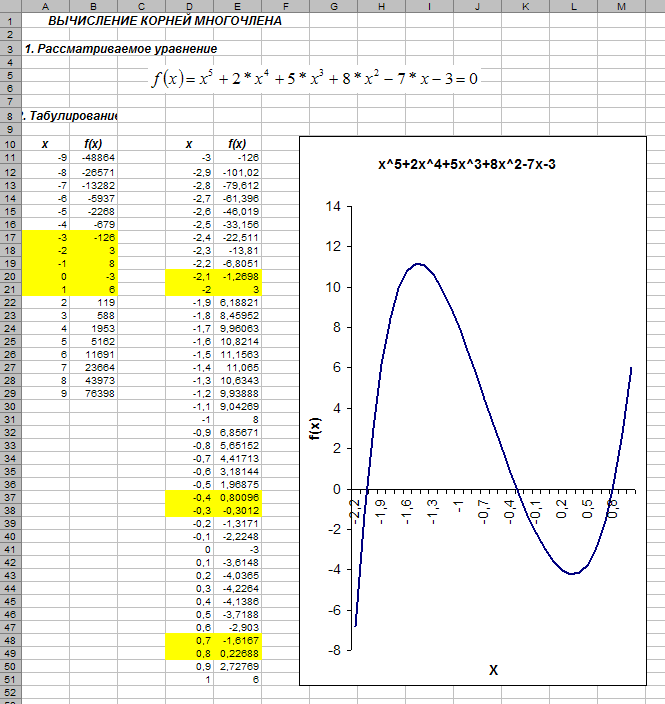
1. Локализация корней уравнения
Из таблицы и графика
видно, что многочлен f(x)
содержит 3 корня, находящихся в границах
отрезков: 1-й корень
,
;
2-й корень,
;
3 — й корень,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
0
1 ответ:
0
0
Надо воспользоваться надстройкой «Поиск решения». С её помощью можно решить не только кубическое уравнение, но и уравнение любой другой степени. А также любую систему уравнений, как линейных, так и нелинейных.
Читайте также
Время, в Excel является числом, точнее, десятичной дробью меньше единицы. (Соответственно дата — число, больше единицы. А дата с временем — это сумма этих чисел.).
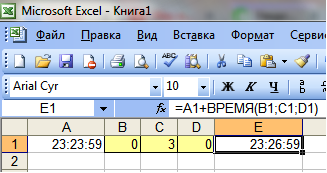
Что бы данное число смотрелось в клетке как Дата, или Время, или Дата с Временем — для этого необходимо задать определенный формат с свойствах ячейки (Втор. кл. мыши по ячейке — пункт «Формат Ячейки»). Следственно, над любой датой и над любым временем можно производить операции сложения и вычитания. Так же надо помнить, что в Excel есть функция (ВРЕМЯ()), которая преобразовывает три значения (часы,минуты,секунды) в специальную десятичную дробь, которая, по сути, является временем «чч:мм:сс», если изменить формат ячейки на «Время-13:30:55».
Итак, например:
- Пусть в ячейке A1 у нас есть время «23:23:59«, тогда
- Пусть, клетках B1,C1,D1 у нас будет количество часов,минут,секунд, (целые числа) которое мы хотим добавить к нашему времени.
- Для получения результата, запишем в клетке E1 формулу: =A1+ВРЕМЯ(B1;C1;D1)
- Если мы поставим в клетку С1 значение 3, тогда мы получим десятичную дробь, которая соответствует 23:26:59. (или «00.01.1900 23:26»).
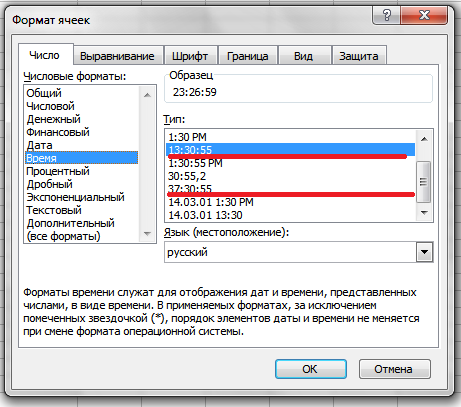
- Для того, что бы получить в клетке «только время» (без даты, или без дроби), откройте настройки формата ячейки (Правая кл мыши по ячейке и пункт «Формат ячейки») и задайте для нее формат «Время — 13:30:55». Если же у вас в сумме получается время, которое превышает сутки (24 часа), тогда поставьте формат «Время — 37:30:55»
- Как можно понять из приведенного примера, более простая формула в вашем случае (надо добавить 3 минуты к ячейке A1) — будет иметь вид: =A1+ВРЕМЯ(0;3;0)
График можно перенести как картинку обычным копированием.
Для того, что бы перенести график из EXCEL в Power Point. В Excel выделить график, выполнить «копировать», открываем Power Point, открываем нужный слайд, выполняем операцию «вставить».
Сохранить можно множеством способов:
1 — Горячие клавиши. Shift+F12 — сохранить. F12 — сохранить как.
Contrl + S — Сохранить.
2 — Нажав на клавишу альт и управляя стрелочками, выбрать нужное меню затем нажать копку Enter.
Чтобы уметь использовать макросы в excel нужно уметь программировать. Если вы программировать не умеете, то и макрос скорей всего написать не сможете.
Если вы берете макрос с интернета, то скорей всего там будет подробная инструкция что и куда надо вставить. Лично я не пользуюсь ими. Мне, как обычному пользователю, хватает стандартных команд в виде IF, SUMM и т.д.
В общем-то это просто делается. Когда копируете в буфер обмена содержимое ячейки (не важно с помощью меню, ленты или просто CTRL+C), то потом, когда в другую ячейку надо будет вставить только данные надо кликнуть по стрелочке расположенной рядом с кнопочкой в меню «Вставить». Там выпадет менюшка с запросом чтот именно вы хотите вставить. Если нет прямого указания (например, есть только иконки разные), то копайте глубже через пункт «Специальная вставка». Дальше думаю сами разберетесь…
Лично мне там нравится опция «Вставить ширину колонок». Часто, когда копируешь блок в новое место, в этом месте ширина колонок остается оригинальной, что сильно мешает восприятию информации. Так вот когда скопируешь туда ширины исходных колонок, все становится на свои места.
































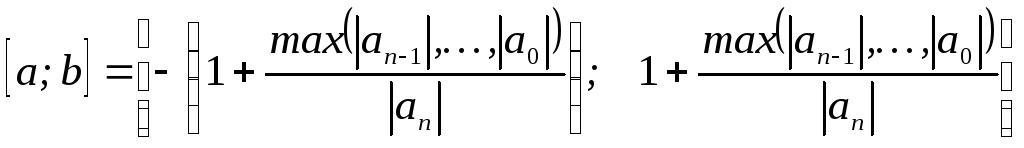 трезок
трезок