Содержание
- Использование табулирования
- Создание таблицы
- Построение графика
- Вопросы и ответы
Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.
Использование табулирования
Табулирование применяется путем создания таблицы, в которой в одной колонке будет записано значение аргумента с выбранным шагом, а во второй — соответствующее ему значение функции. Затем на основе расчета можно построить график. Рассмотрим, как это делается на конкретном примере.
Создание таблицы
Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.
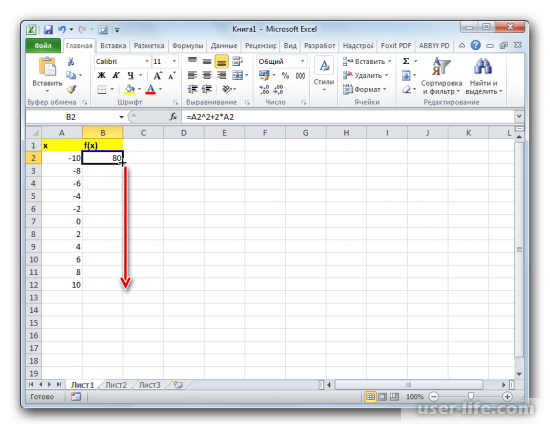
- В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.
- Все дальнейшие значения можно заполнить вручную, придерживаясь шага 2, но удобнее это сделать с помощью инструмента автозаполнения. Особенно этот вариант актуален, если диапазон аргументов большой, а шаг — относительно маленький.
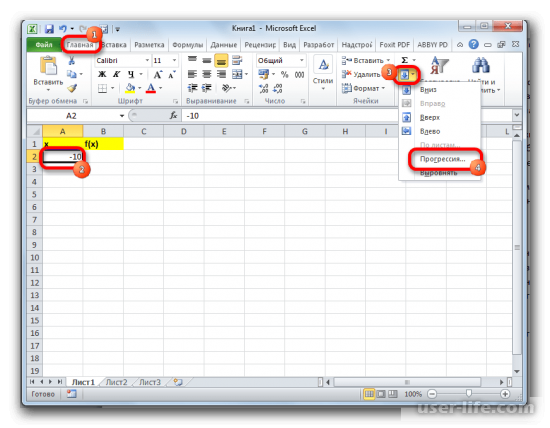
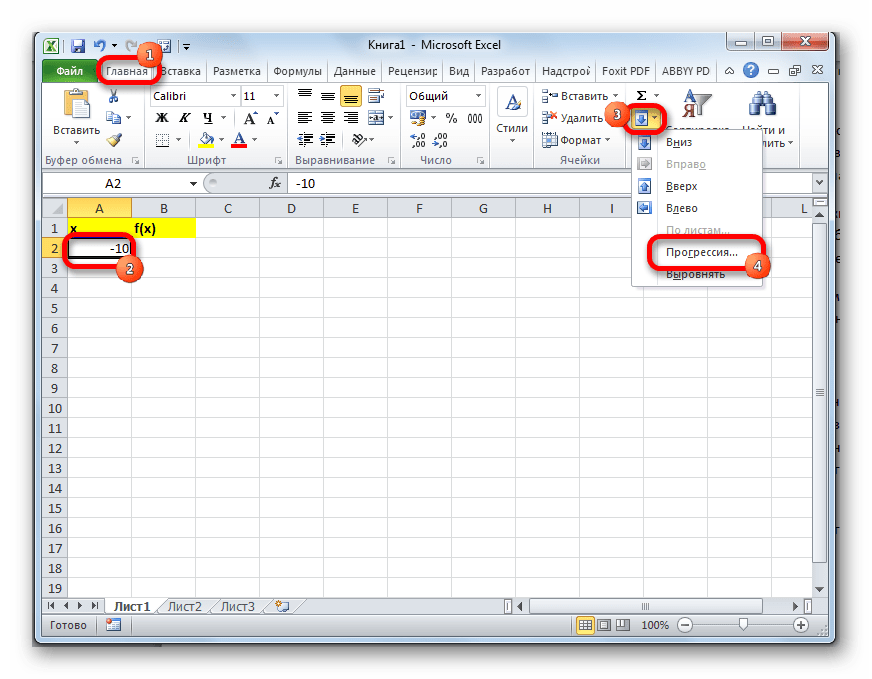
Выделяем ячейку, в которой содержится значение первого аргумента. Находясь во вкладке «Главная», кликаем по кнопке «Заполнить», которая размещена на ленте в блоке настроек «Редактирование». В появившемся списке действий выбираем пункт «Прогрессия…».
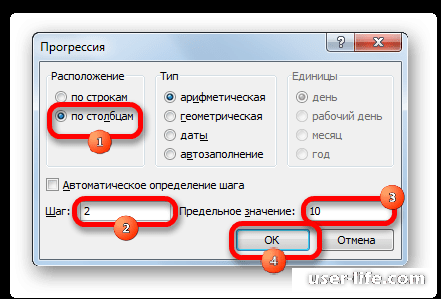
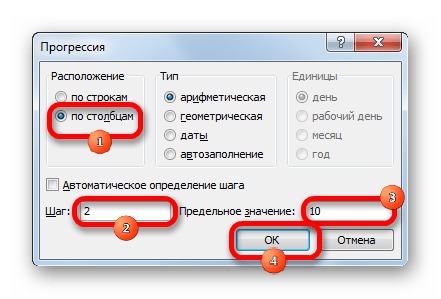
- Открывается окошко настройки прогрессии. В параметре «Расположение» устанавливаем переключатель в позицию «По столбцам», так как в нашем случае значения аргумента будут размещаться именно в колонке, а не в строке. В поле «Шаг» устанавливаем значение 2. В поле «Предельное значение» вписываем число 10. Для того чтобы запустить прогрессию, жмем на кнопку «OK».
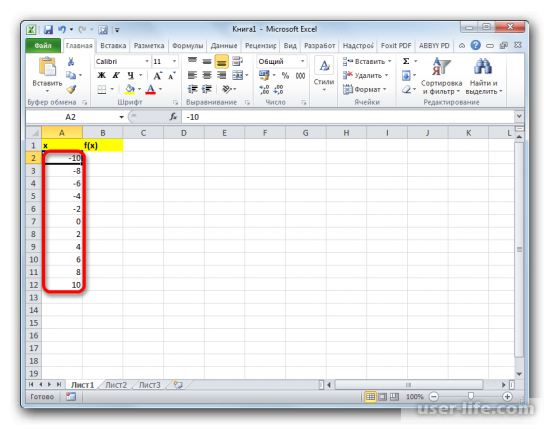
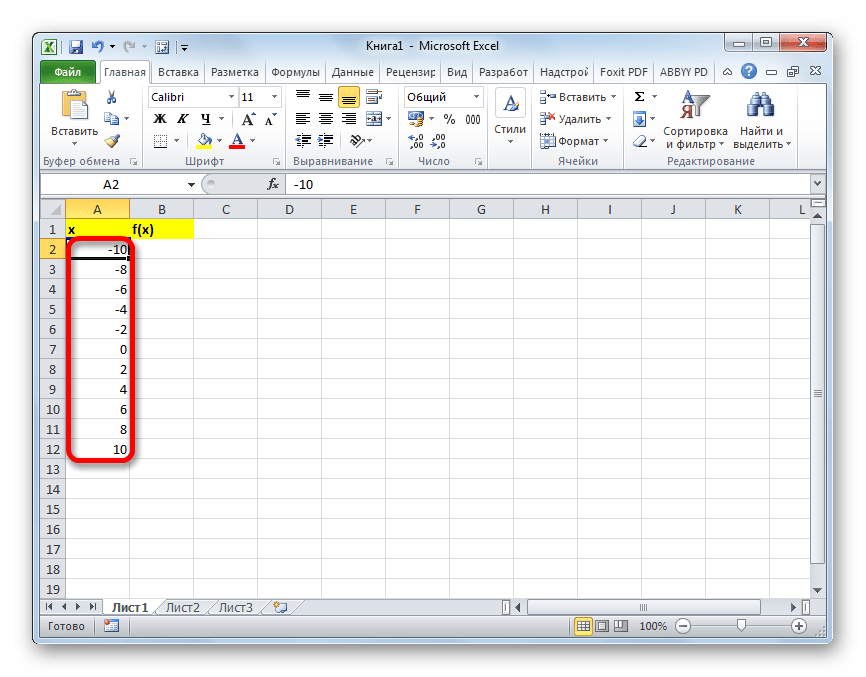
- Как видим, столбец заполнен значениями с установленными шагом и границами.
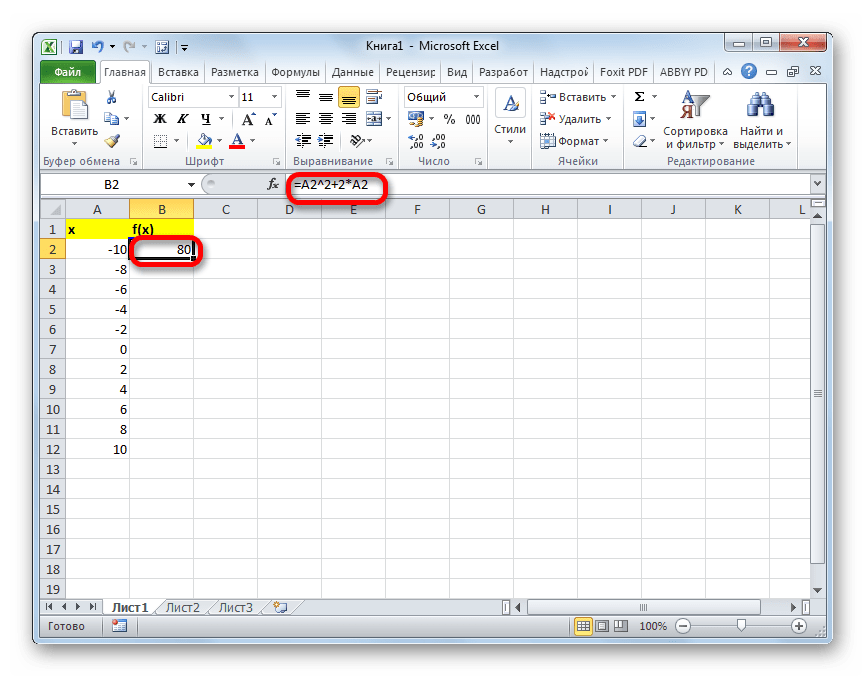
- Теперь нужно заполнить столбец функции f(x)=x^2+2x. Для этого в первую ячейку соответствующей колонки записываем выражение по следующему шаблону:
=x^2+2*xПри этом, вместо значения x подставляем координаты первой ячейки из столбца с аргументами. Жмем на кнопку Enter, чтобы вывести результат вычислений на экран.
- Для того, чтобы произвести вычисление функции и в других строках, снова воспользуемся технологией автозаполнения, но в данном случае применим маркер заполнения. Устанавливаем курсор в нижний правый угол ячейки, в которой уже содержится формула. Появляется маркер заполнения, представленный в виде небольшого по размеру крестика. Зажимаем левую кнопку мыши и протягиваем курсор вдоль всего заполняемого столбца.
- После этого действия вся колонка со значениями функции будет автоматически заполнена.
Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и 0. Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.
Урок: Как сделать автозаполнение в Эксель
Построение графика
На основе произведенной табуляции в таблице можно построить график функции.
- Выделяем все значения в таблице курсором с зажатой левой кнопкой мыши. Перейдем во вкладку «Вставка», в блоке инструментов «Диаграммы» на ленте жмем на кнопку «Графики». Открывается список доступных вариантов оформления графика. Выбираем тот вид, который считаем наиболее подходящим. В нашем случае отлично подойдет, например, простой график.
- После этого на листе программа выполняет процедуру построения графика на основе выделенного табличного диапазона.
Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.
Урок: Как построить график в Эксель
Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Иногда трудно понять, как вложенная формула вычисляет конечный результат, поскольку в ней выполняется несколько промежуточных вычислений и логических проверок. Но с помощью диалогового окна Вычисление формулы вы можете увидеть, как разные части вложенной формулы вычисляются в заданном порядке. Например, формулу =ЕСЛИ(СПБ(F2:F5)>50;СУММ(G2:G5);0) проще понять, если вы увидите промежуточные результаты:
|
Шаги, показанные в диалоговом окне |
Описание |
|
=ЕСЛИ(СРЗНАЧ(F2:F5)>50;СУММ(G2:G5);0) |
Сначала выводится вложенная формула. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ. |
|
=ЕСЛИ(40>50;СУММ(G2:G5);0) |
Диапазон ячеек F2:F5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(F2:F5) возвращает результат 40. |
|
=ЕСЛИ(Ложь;СУММ(G2:G5);0) |
40 не больше 50, поэтому выражение в первом аргументе функции ЕСЛИ (аргумент logical_test) ложно. |
|
0 |
Функция ЕСЛИ возвращает значение третьего аргумента (аргумент значение_если_ложь). Функция СУММ не вычисляется, так как она является вторым аргументом функции ЕСЛИ (value_if_true) и возвращается только в том случае, если выражение истинно. |
-
Выделите ячейку, которую нужно вычислить. За один раз можно вычислить только одну ячейку.
-
На вкладке Формулы в группе Зависимости формул нажмите кнопку Вычислить формулу.
-
Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычисления отображается курсивом.
Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться к предыдущей ячейке и формуле.
Примечание: Кнопка Шаг с заходом недоступна для ссылки, если ссылка используется в формуле во второй раз или если формула ссылается на ячейку в отдельной книге.
-
Продолжайте этот процесс, пока не будут вычислены все части формулы.
-
Чтобы посмотреть вычисление еще раз, нажмите кнопку Начать сначала.
Чтобы закончить вычисление, нажмите кнопку Закрыть.
Примечания:
-
Некоторые части формул, в которые используются функции ЕСЛИ и ВЫБОР, не вычисляются, и в поле «Оценка» #N/Д.
-
Если ссылка пуста, в поле Вычисление отображается нулевое значение (0).
-
Формулы с циклыми ссылками могут не оцениваться, как ожидалось. При желании можно включить итеративные вычисления.
-
Следующие функции пересчитываются каждый раз при внесении изменений в ячейку и могут привести к тому, что инструмент «Вычислите формулу» дает результаты, отличаные от результатов в ячейке: СЛЧИС, СМЕДЕН, ЯЧЕЙКА, ДВЕ, СЕГОДНЯ, СЛЧИСЛО, МНИМ.СТ.ЕСЛИ (в некоторых случаях).
-
Нужна дополнительная помощь?
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
На чтение 11 мин Просмотров 4.5к. Опубликовано 31.07.2020
Содержание
- Использование табулирования
- Создание таблицы
- Построение графика
Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.
Использование табулирования
Табулирование применяется путем создания таблицы, в которой в одной колонке будет записано значение аргумента с выбранным шагом, а во второй — соответствующее ему значение функции. Затем на основе расчета можно построить график. Рассмотрим, как это делается на конкретном примере.
Создание таблицы
Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.
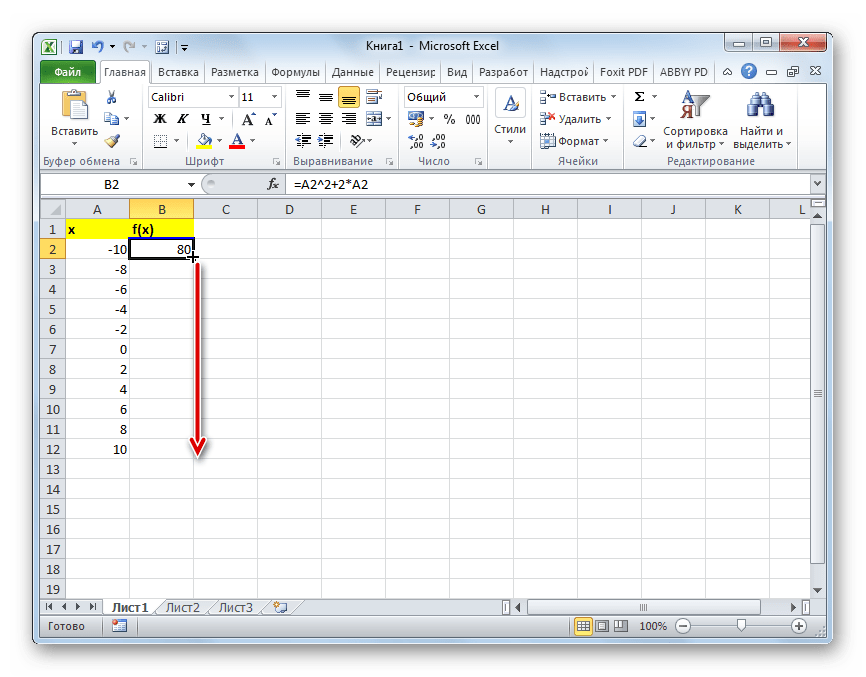
- В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.
Все дальнейшие значения можно заполнить вручную, придерживаясь шага 2, но удобнее это сделать с помощью инструмента автозаполнения. Особенно этот вариант актуален, если диапазон аргументов большой, а шаг — относительно маленький.
Выделяем ячейку, в которой содержится значение первого аргумента. Находясь во вкладке «Главная», кликаем по кнопке «Заполнить», которая размещена на ленте в блоке настроек «Редактирование». В появившемся списке действий выбираем пункт «Прогрессия…».
Открывается окошко настройки прогрессии. В параметре «Расположение» устанавливаем переключатель в позицию «По столбцам», так как в нашем случае значения аргумента будут размещаться именно в колонке, а не в строке. В поле «Шаг» устанавливаем значение 2. В поле «Предельное значение» вписываем число 10. Для того чтобы запустить прогрессию, жмем на кнопку «OK».
Теперь нужно заполнить столбец функции f(x)=x^2+2x. Для этого в первую ячейку соответствующей колонки записываем выражение по следующему шаблону:
При этом, вместо значения x подставляем координаты первой ячейки из столбца с аргументами. Жмем на кнопку Enter, чтобы вывести результат вычислений на экран.
Для того, чтобы произвести вычисление функции и в других строках, снова воспользуемся технологией автозаполнения, но в данном случае применим маркер заполнения. Устанавливаем курсор в нижний правый угол ячейки, в которой уже содержится формула. Появляется маркер заполнения, представленный в виде небольшого по размеру крестика. Зажимаем левую кнопку мыши и протягиваем курсор вдоль всего заполняемого столбца.
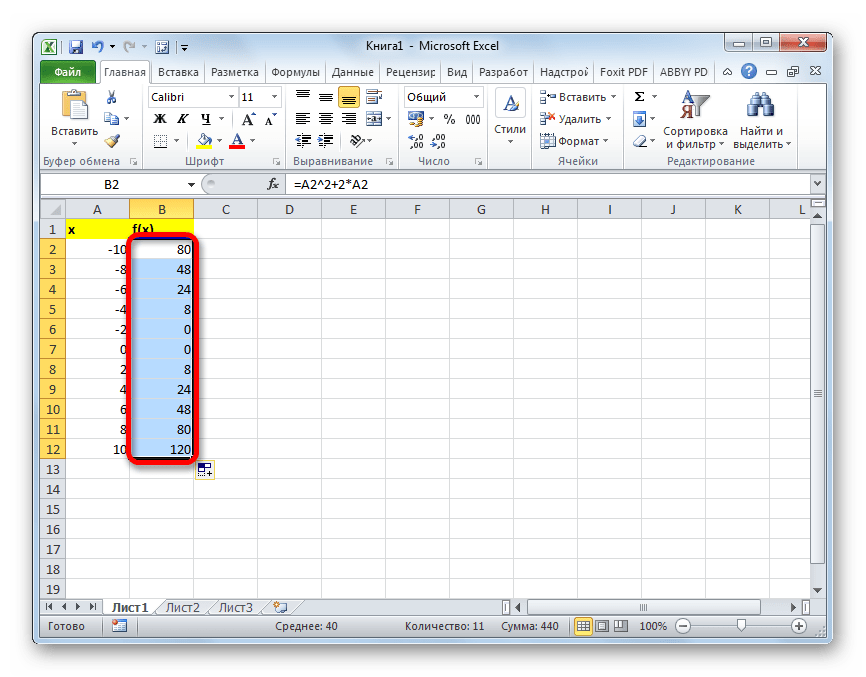
Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и . Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.
Построение графика
На основе произведенной табуляции в таблице можно построить график функции.
-
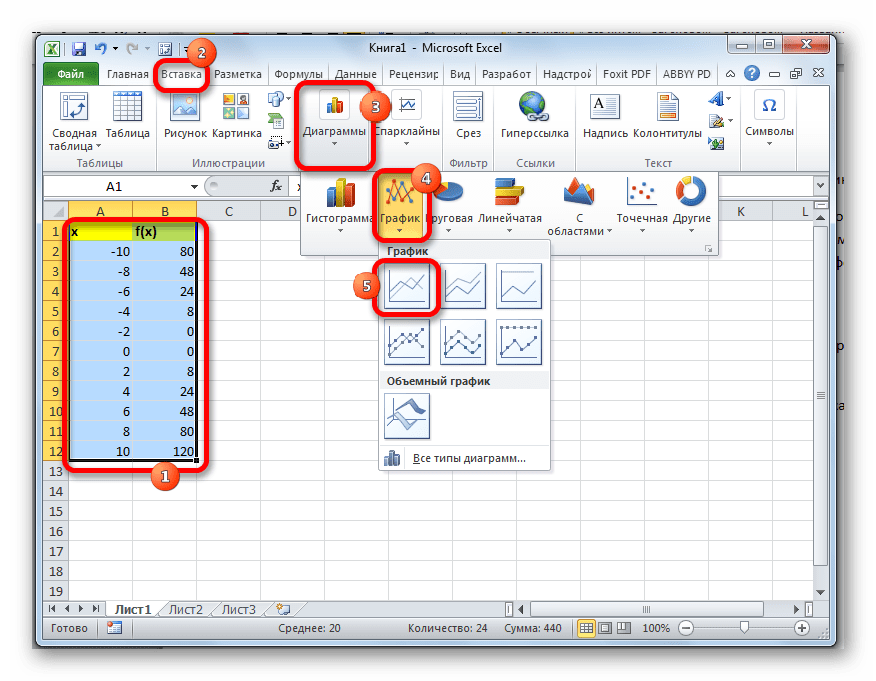
Выделяем все значения в таблице курсором с зажатой левой кнопкой мыши. Перейдем во вкладку «Вставка», в блоке инструментов «Диаграммы» на ленте жмем на кнопку «Графики». Открывается список доступных вариантов оформления графика. Выбираем тот вид, который считаем наиболее подходящим. В нашем случае отлично подойдет, например, простой график.
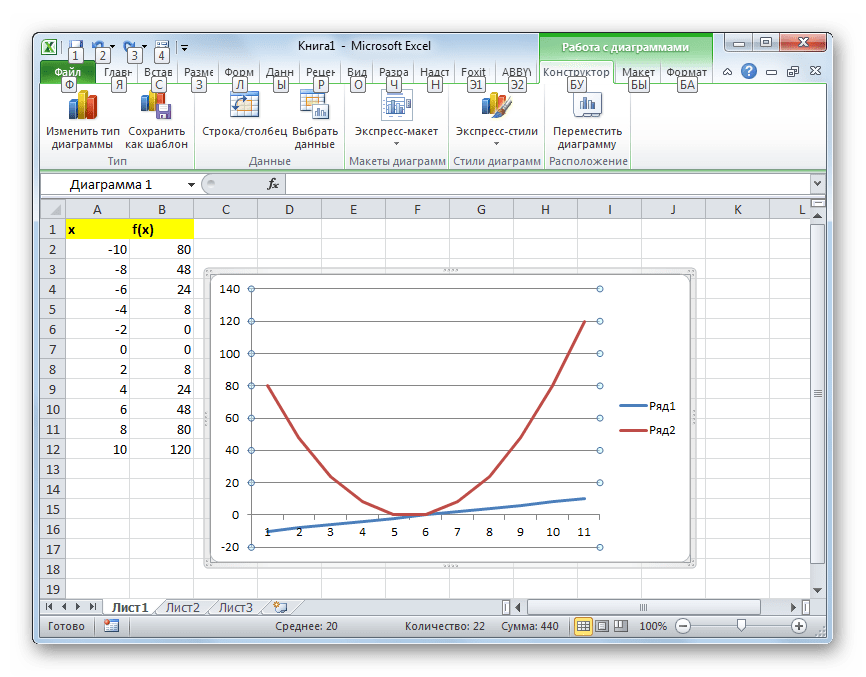
Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.
Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.
Отблагодарите автора, поделитесь статьей в социальных сетях.
EXCEL: табулирование функций, построение графиков функций.
Цель работы:закрепить навыки заполнения и редактирования таблиц,познакомиться со способами адресации, научиться использовать абсолютные ссылки.
Теоретическая часть.
Абсолютная, относительная и смешанная адресация ячеек и блоков.
При обращении к ячейке можно использовать описанные ранее способы: B3, A1: G9 и т.д. Такая адресация называется относительной. При ее использовании в формулах Excel запоминает расположение относительно текущей ячейки. Так, например, когда вы вводите формулу =B1+B2 в ячейку B4, то Excel интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки, расположенной двумя рядами выше».
Если вы скопировали формулу =B1+B2 из ячейки B4 в C4, Excel также интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки двумя рядами выше». Таким образом, формула в ячейке C4 примет вид =C1+C2.
Если при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или область, то вам необходимо воспользоваться абсолютной адресацией. Для ее задания необходимо перед именем столбца и перед номером строки ввести символ $. Например: $B$4 или $C$2:$F$48 и т.д.
Смешанная адресация. Символ $ ставится только там, где он необходим. Например:B$4 или $C2. Тогда при копировании один параметр адреса изменяется, а другой – нет. Т.е иногда возникает необходимость зафиксировать определенные ссылки, указав, что число можно брать только из указанного столбца или строки.
Практическая часть.
Рассмотрим задачу табулирования функции: вычислить значение функции 
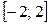
Решение должно быть получено в виде таблицы:
| № | x | k | y1=x^2-1 | y2=x^2+1 | y=k*(y1/y2) |
Задание 1. Запустите Microsoft Excel.
Задание 2.Заполните основную и вспомогательную таблицы.
2.1. Заполните шапку основной таблицы начиная с ячейки A1:
в ячейку A1 занести N;
в ячейку B1 занести X;
в ячейку C1 занести K и т.д.
установите ширину столбцов такой, чтобы надписи были видны полностью.
2.2. Заполните вспомогательную таблицу начальными исходными данными начиная с ячейки H1:
где x0 – начальное значениеx; step – шаг изменения x; k – коэффициент (константа).
Данный пункт при решении задачи табулирования функции является не обязательным и введен искусственно – для демонстрации способа адресации.
2.3. Используя функцию автозаполнения, заполните столбец A числами от 1 до 21, начиная с ячейки A2 и заканчивая ячейкой A22.
2.4. Заполните столбец B значениями x:
· в ячейку B2 занесите =$H$2. Это означает, что в ячейку B2 заносится значение из ячейки H2 (начальное значение x), знак $ указывает на абсолютную адресацию;
· в ячейку B3 занесите =B2+$I$2. Это означат, что начальное значение x будет увеличено на величину шага, которая берется из ячейки I2;
· скопируйте формулу из ячейки B3 в ячейки B4:B22. Столбец заполнится значениями x от –2 до 2 с шагом 0,2.
2.5. Заполните столбец C значениями коэффициента k:
· в ячейку C2 занесите =$J$2;
· в ячейку C3 занесите =C2.
· скопируйте формулу из ячейки C3 в ячейки C4:C22. Весь столбец заполнился значением 10.
2.6. Заполните столбец D значениями функции y1=x^2-1:
· в ячейку D2 занесите =B2*B2-1;
· скопируйте формулу из ячейки D2 в ячейки D3:D22. Столбец заполнился как положительными, так и отрицательными значениями функции y1. Начальное и конечное значения равны 3.
2.7. Аналогичным образом заполните столбец E значениями функции y2=x^2+1.
Проверьте! Все значения положительные; начальное и конечное значения равны 5.
2.8. Заполните столбец F значениями функции y=k*(x^2-1)/(x^2+1):
· в ячейку F2 занесите =C2*(D2/E2);
· скопируйте формулу из F2 в ячейки F2:F22.
Проверьте! Значения функции как положительные, так и отрицательные; начальные и конечные значения равны 6.
Задание 3. Понаблюдайте за изменениями в основной таблице при смене данных во вспомогательной.
3.1. Измените во вспомогательной таблице начальное значение x: в ячейку H2 занесите значение –5.
3.2.Измените значение шага: в ячейку I2 занесите 2.
3.3. Измените значение коэффициента: в ячейку J2 занесите 1.
Внимание! При всех изменениях данных во вспомогательной таблице в основной таблице пересчет производится автоматически.
3.4. Прежде чем продолжить работу, верните прежние начальные значения во вспомогательной таблице: x0= -2, step=0,2, k=10.
Задание 4. Оформите основную и вспомогательную таблицы.
4.1. Вставьте две пустые строки сверху для оформления заголовков:
· установите курсор на строку номер 1;
· выполните команды меню Вставка, Строки (2 раза).
4.2. Введите заголовки:
в ячейку A1– «Таблицы»;
в ячейку A2 – «основная»;
в ячейку H2 – «вспомогательная».
4.3. Объедините ячейки A1:J1 и разместите заголовок «Таблицы» по центру:
выделите блок A1:J1; используйте кнопку “Центрировать по столбцам” панели инструментов Форматирование.
4.4. Аналогичным образом разместите по центру заголовки «основная» и «вспомогательная».
Задание 5. Шрифтовое оформление текста.
Символы любой ячейки или любого блока можно оформить разными шрифтами. Для этого необходимо выделить ячейку или блок, а затем воспользоваться кнопками из панели Форматирование или командой меню Формат, Ячейки, Шрифт.
5.1. Для заголовка «Таблицы» задайте шрифт Courier New Cir, размер шрифта 14, полужирный.
5.2. Для заголовков «основная» и «вспомогательная» задайте шрифт Courier New Cir, размер шрифта 12, полужирный.
5.3. Для шапок таблиц установите шрифт Courier New Cir, размер шрифта 12, курсив.
5.4. Подгоните ширину столбцов так, чтобы текст помещался полностью. Произведите выравнивание надписей шапок по центру.
Содержимое любой ячейки можно выровнять по левому или правому краю, по центру (по горизонтали и вертикали), а также можно задать необходимую ориентацию текста (снизу вверх, сверху вниз и т. д.). Для задания необходимой ориентации используются кнопки в панели Форматирование или команда меню Формат, Ячейки, Выравнивание.
6.1. Задайте рамки для основной и вспомогательной таблиц, используя кнопку панели инструментов Форматирование. Для задания рамки используется кнопка в панели Форматирование или команда меню Формат, Ячейки, Рамка.
6.2. Задайте фон заполнения внутри таблиц – желтый, фон заполнения шапок таблиц – малиновый. Для задания фона используется кнопка в панели Форматирование или команда меню Формат, Ячейки, Вид.
Задание 7. Завершите работу в Excel.
1) Для чего предназначен мастер функций и как его вызвать?
2) Что такое относительная ссылка?
3) Что такое абсолютная ссылка?
4) Какими инструментами вы пользовались при оформлении заголовка таблицы?
5) Какие средства служат для оформления таблицы?
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10236 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Табулирование применяется благодаря созданию таблицы. В одной ее колонке записываются значения аргумента с выбранным шагом, а в другой – соответствующее ему значение функции. На основе расчета далее можно построить график. Для начала необходимо создать шапку таблицы, в которой должны быть колонки х и указано значение аргумента f(x). Для процедуры табулирования может применяться функция любого вида. В первую ячейку столбца «х» вносится значение «-10» и нажимается Enter.
Далее значения можно заполнять вручную, но лучше делать это с помощью инструмента автозаполнения. Выделите ячейку со значением первого аргумента. Находясь во вкладке «Главная» нажмите «Заполнить» (кнопка расположена в блоке настроек «Редактирование»). Появится список, в котором следует выбрать «Прогрессия…».
Должно появиться окно настройки прогрессии. В параметре «Расположение» установите переключатель в позиции «По столбцам». В поле «Шаг» установите значение 2. В поле «Предельное значение» — 10. Для запуска прогрессии нажмите ОК.
Столбец будет заполнен значениями с установленными границами и шагом.
Далее заполняете столбец функции f(x)=x^2+2x. В первую ячейку, которая соответствует колонки, внесите выражение по такому шаблону — =x^2+2*x. Вместо значения х следует подставить координаты ячейки со столбца с аргументами. Нажимаете Enter, и результаты вычислений выведутся на экран.
Для вычисления функции и в других строках можно снова применить технологию автозаполнения, но лучше задействовать маркер заполнения. В нижний правый угол ячейки установите курсор с уже внесенной формулой, должен появиться маркер заполнения, который представлен в виде маленького крестика. Зажмите левую кнопку мыши и протяните курсор вдоль все столбца, который будет заполняться.
Когда действие будет выполнено, то вся колонка со значениями функции автоматически заполнится. Табуляция функции проведена.


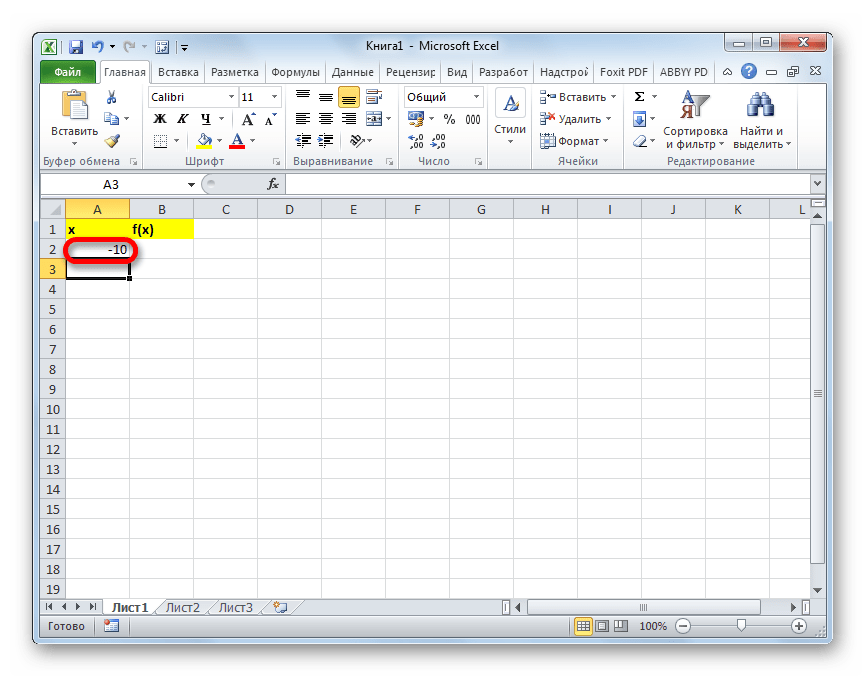



























 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):