Решение экономико математической модели в excel

Решение задач экономико-математического моделирования с помощью программы Excel

Решение задач
экономико-математического моделирования с помощью программы Excel

Определить оптимальное сочетание
трех зерновых культур: пшеницы, ячменя и овса

Производство культур характеризуется
показатели таблицы.

Показатели	Озимая пшеница	Яровой ячмень	Овес
Урожайность с 1 га, ц.	40	35	30
Затраты труда на 1 га, чел.-ч.	20	15	13
Затраты удобрений на 1 га, руб.	80	50	40

Производственные ресурсы: пашня-1600
га, труд — 27000 чел.-ч., удобрения — 99000 руб.

В структуре посевов площадь под оз.
пшеницы должна составлять не менее 50 %. Критерий оптимальности максимальное
производство зерна.

Решение.

Обозначим через:

х1-площадь оз. пшеницы, га.

х2-площадь яр. ячмень, га.

х3-площадь овса, га.

Запишем условие задач в виде системы
ограничений (уравнений и неравенств).

)        По уборки площади посевов
трех зерновых, га

Х1+х2+х3=1600

)        По использовании ресурсов
труда

*х1+15*х2+13*х3≤27000

)        По затратам удобрений, руб.

*х1+50*х2+40*х3≤99000

)        По структуре посевной
площади

х1≥0,5(х1+х2+х3)

х1≥0,5*х1+0,5*х2+0,5*х3

,5х1-0,5х2-0,5х3≥0

ЦФ= критерий max производства зерна.

ЦФ=40*х1+35*х2+30*х3→max

Решение задачи в Excel

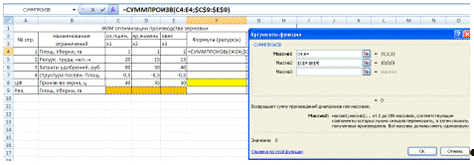
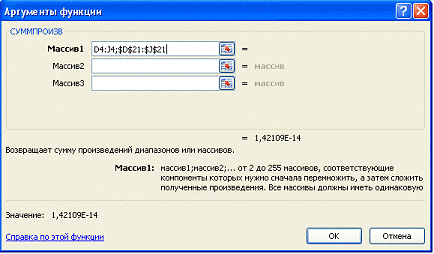
В ячейку F4 вставим формулу «
=СУММПРОИЗВ(С4:Е4;$C$9:$E$9)», затем растянем форму до целевой ячейки
включительно.

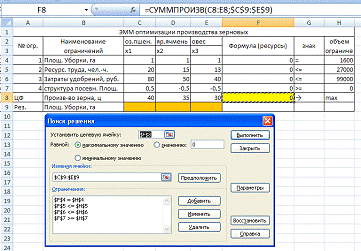
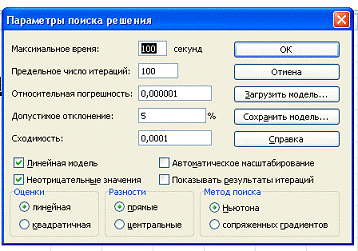
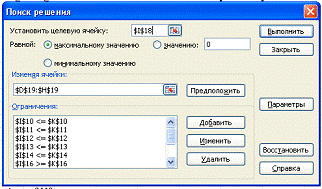
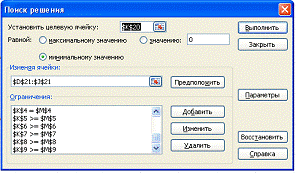
Затем находим решение задачи с
помощью «поиска решения». Находим: Данные→Анализ→Поиск решения. Как
видно на рисунке: устанавливаем целевую ячейку; равный- max значению; изменяя
ячейки и ограничение.

программирование excel оптимальный
модель

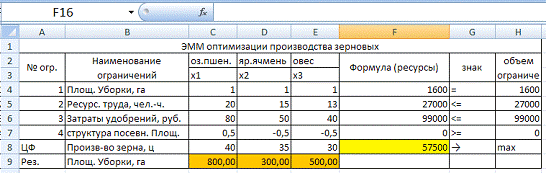
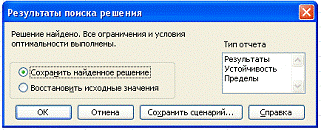
После выполненных операций нажимаем,
на «выполнить» и получаем возможное решение задачи:

Вывод: Оптимальное сочетание трех
зерновых культур, максимальное производства зерна будет при площади уборки: оз.
пшеницы — 800 га, яр. ячмень — 300 га, овес — 500 га.

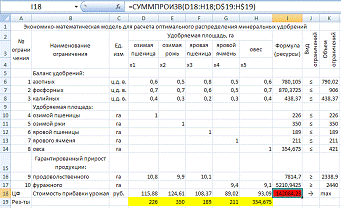
Экономико-математические модели для
расчета оптимального распределения минеральных удобрений

Рассчитать план распределения
минеральных удобрений, при котором достигается максимум стоимости прибавки
урожая. При этом по плану необходимо получить не менее 23 000 ц
продовольственного и 17 000 ц фуражного зерна. Площадь посева культур,
рекомендуемые дозы внесения удобрений и прибавка урожая показаны в табл.7.1.
Сведения о количестве, качестве и стоимости минеральных удобрений приведены в
табл.7.2.

Таблица 7.1

Показатели	Озимая пшеница	Озимая  рожь	Яровая пшеница	Яровой ячмень	Овес
Площадь посева, га	226	350	189	211	421
Урожайность без внесения удобрений с 1 га, ц	29,7	26,3	25,1	28,9	20,1
Азотных	0,6	0,5	0,8	0,5	0,6
Фосфорных	0,7	0,7	0,6	0,5	0,7
Калийных	0,4	0,3	0,2	0,3	0,4
Прибавка урожая за счет внесения удобрений с 1 га:
ц	10,8	9,9	10,1	9,4	9,1
руб	115,88	124,61	108,37	89,02	93,09

Таблица 7.2

показатели	Сульфат аммония N	Суперфосфат Р2О5	Хлористый калий  К2О
Количество, ц	3762	4530	743
Содержание действующего вещества, %	21	20	59
Цена 1 ц, руб	4,00	2,39	1,10
Стоимость внесения 1 ц, руб	0,25	0,19	0,26

Решение:

ЭММ для расчета оптимальных рационов
кормления с/х животных

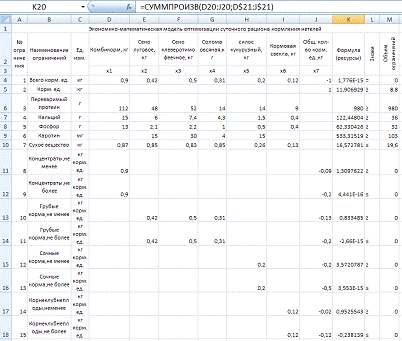
Рассчитать оптимальный суточный
рацион кормления нетелей средней живой массой 480 кг. В рационе должно
содержаться не менее 8,8 кг кормовых единиц, 980 г переваримого протеина, 36 г
кальция, 32 г фосфора, 103 мг каротина и не более 19,6 кг сухого вещества.

Рацион составляется из комбикорма,
сена лугового, сена клеверотимофеечного, соломы овсяной, силоса кукурузного и
кормовой свеклы. Содержание питательных веществ в кормах и их себестоимость
представлены в таблице 9.5.

В соответствии с зоотехническими
требованиями отдельные группы кормов в рационе могут изменяться в следующих
пределах, % к общему количеству кормовых единиц: концентрированные — от 9 до
20, грубые — от 13 до 20, сочные — от 20 до 50 и корнеклубнеплоды — от 2 до 12.
Удельный вес соломы в грубых кормах должен составлять не менее 50%.

Таблица 9.5

Корма	Содержание в 1 кг корма	Себестоимость 1 кг корма, коп
	Кормовых единиц, кг	Переваримого протеина, г	Кальция, г	Фосфора, г	Каротина, мг
Комбикорм	0,9	112	15	13	—	0,87	14,5
Сено луговое	0,42	48	6	2,1	15	0,85	3,4
Сено клеверотимофеечное	0,5	52	7,4	2,2	30	0,83	2,1
Солома овсяная	0,31	14	4,3	1	4	0,85	0,2
Силос кукурузный	0,2	14	1,5	0,5	15	0,23	0,6
Кормовая свекла	0,12	9	0,4	0,4	—	0,13	2,1

Решение:

Определим перечень переменных.
Количество кормов, которая может войти в рацион нетелей, обозначим через:

Х1-количество комбикорма в рационе,
кг

Х2-количество сена лугового в
рационе, кг

Х3-количество сена
клеверотимофеечного в рационе, кг

Х4-количество соломы овсяной в
рационе, кг

Х5-количество силоса кукурузного в
рационе, кг

Х6-количество кормовой свеклы в рационе,
кг

Х7-общее количество кормовых единиц
в рационе, кг

Запишем систему ограничений в
развернутом виде.

. Ограничения по балансу питательных
веществ в рационе:

) общее количество кормовых единиц

,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6=х7

или после преобразования

,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6-х7=0

) кормовые единицы не менее

Х7 ≥ 8,8

) переваримого протеина не менее

х1+48х2+52х3+14х4+14х5+9х6 ≥
980

) кальция не менее

х1+6х2+7,4х3+4,3х4+1,5х5+0,4х6 ≥
36

) фосфора не менее

) каротина не менее

х2+30х3+4х4+15х5 ≥ 103

. Ограничения по содержанию сухого
вещества в рационе:

)
0,87х1+0,85х2+0,83х3+0,85х4+0,26х5+0,13х6 ≤ 19,6

. Ограничения по содержанию
отдельных групп кормов в рационе:

) концентрированных не менее

,9х1 ≥ 0,09х7

или после преобразований

,9х1-0,2х7 ≥ 0

) концентрированных не более

,9х1 ≤ 0,2х7

или после преобразований

,9х1-0,2х7 ≤ 0

) грубых не менее

,42х2+0,5х3+0,31х4 ≥ 0,13х7

или после преобразований

,42х2+0,5х3+0,31х4-0,13х7 ≥ 0

) грубых не более

,42х2+0,5х3+0,31х4 ≤ 0,2х7

или после преобразований

,42х2+0,5х3+0,31х4-0,2х7 ≤ 0

) сочных не менее

,2х5≥0,2х7

или 0,2х5-0,2х7≥0

) сочных не более

,2х5≤0,5х7

или 0,2х5-0,5х7≤0

) корнеклубнеплодов не менее

,12х6≥0,02х7

или 0,2х6-0,02х7≥0

)корнеклубнеплодов не более

,12х6≤0,12х7

или 0,12х6-0,12х7≤0

. ограничения по содержанию
отдельных видов кормов

) удельный вес соломы в группе
грубых

,31х4≥0,5*(0,42х2+0,5х3+0,31х4)

или после преобразований

,21х2-0,25х3+0,155х4≥0

Целевая функция — минимальная
себестоимость рациона=14,5х1+3,4х2+2,1х3+0,2х4+0,6х5+2,1х6→min

Определить оптимальную структуру
посевных площадей, обеспечивающую получение максимума валовой продукции. В
хозяйстве имеется 2377 га пашни. Ресурсы труда — 98700 чел.-ч.

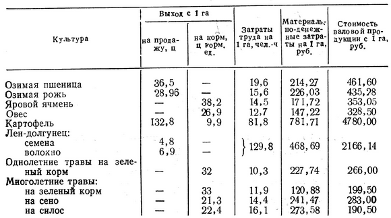
Данные при возделывании культур
представлены в таблице:

Сельскохозяйственные культуры могут
размещаться по двум вариантам севооборотов:

Севооборот №1

. однолетние травы

. озимые зерновые

. картофель

. ячмень с подсевом многолетних трав

. многолетние травы

. озимые зерновые

. лен

. овес

Севооборот №2

. однолетние травы

. озимые зерновые с подсевом
многолетних трав

. многолетние травы

. лен

. картофель

. ячмень

. озимые зерновые

. картофель

. ячмень

Плановое задание по продажи
продукции государству, ц:

) картофель 56120

) льносемена 1050

) льноволокно 1830

Для обеспечения животноводства
кормами необходимо произвести следующее количество кормов, ц корм.ед.:

концентрированных 17930

грубых 2380

сочных 7280

зеленых 8760

Основные переменные:

В севообороте №1:

х11 — озимая пшеница

х21 — озимая рожь

х31 — яровой ячмень

х41 — овес

х51 — картофель

х61 — лен

х71 — однолетние травы

х81 — многолетние травы на зеленый
корм

х91 — многолетние травы на сено

х101 — многолетние травы на силос

х1 — площадь севооборота №1

В севообороте №2

х12 — озимая пшеница

х22 — озимая рожь

х32 — яровой ячмень

х52 — картофель

х62 — лен

х72- однолетние травы

х82 — многолетние травы на зеленый
корм

х92 — многолетние травы на сено

х102 — многолетние травы на силос

х2 — площадь севооборота №2

х3 — материально-денежные затраты,
руб.

х4 — Валовая продукция, руб.

Система ограничений:

. По площади пашни:

) х1+х2<=2377

. По площади севооборота №1:

)
х11+х21+х31+х41+х51+х61+х71+х81+х91+х101-х1<=0

. По площади отдельных
сельскохозяйственных культур внутри севооборота №1:

) озимые зерновые в севообороте
№1+x21=0,25×1

) ячмень-0,125×1=0

) овес-0,125×1=0

) картофель-0,125×1=0

) лен-0,125×1=0

) однолетние травы-0,125×1=0

) многолетние
травы+x91+x101-0,125×1=0

. По площади севооборота №2:

) x12+x22+x32+x52+x62+x72+x82+x92+x102-x2<=0

. По площади отдельных
сельскохозяйственных культур внутри севооборота №2:

) озимые зерновые+x22-0,22×2=0

) ячмень-0,22×2=0

) картофель-0,22×2=0

) лен-0,11×2=0

) однолетние травы-0,11×2=0

) многолетние
травы+x92+x102-0,11×2=0

. По использованию трудовых
ресурсов:

)
19,6×11+15,6×21+14,5×31+12,7×41+81,8×51+ 129,8×61+
10,37×71+11,9×81+14,4×91+16,1×10,1+19,6×12+15,6×22+14,5×32+81,8×52+129,8×62+10,37×72+11,9×82+14,4×92+16,1×10,2<=98700

. На продажу:

) зерно, ц+x21+x12+x22>=18030

) картофель, ц+x52>=56120

) льносемена

,8×6,1+4,8×6,2>=1050

) льноволокно

,9×61+6,9×62>=1830

. По производству кормов:

) концентрированные корма,
ц.корм.ед.

,2×3+26,9×41+38,2×32>=17930

) грубые корма

,3×91+21,3×92>=2380

,9×51+22,4×101+9,9×52+22,4×102>=7280

) зеленый корм

x71+33×81+32×72+33×82>=8760

. Материально-денежные затраты, руб.

)
214,27×11+226,03×21+171,72×31+147,22×41+781,71×51+468,69×61
+227,74×71+120,88×81+241,47×91+273,58×101+214,27×12+226,03×22+171,72×32+781,71×52+468,69×62+227,74×72+120,88×82+241,47×92+273,58×102-x3=0

. Валовая продукция, руб.

)
461,6×11+435,28×21+…+190,5×10,1+461,6×12+…+190,5×10,2-x4=0

ЦЕЛЕВАЯ ФУНКЦИЯ: х4 стремится к
максимуму

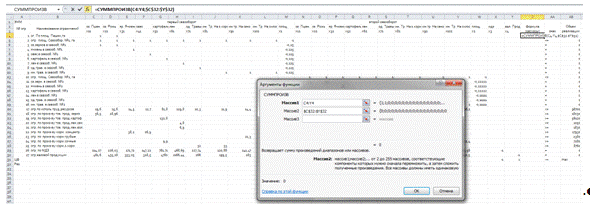
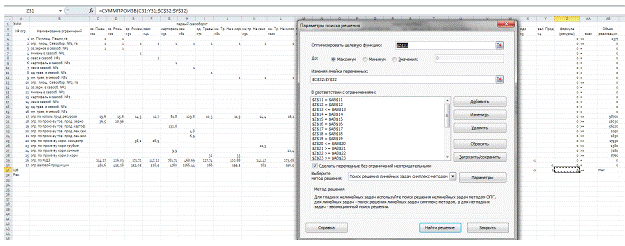
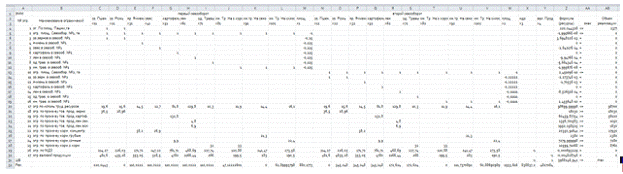
Решение задачи:

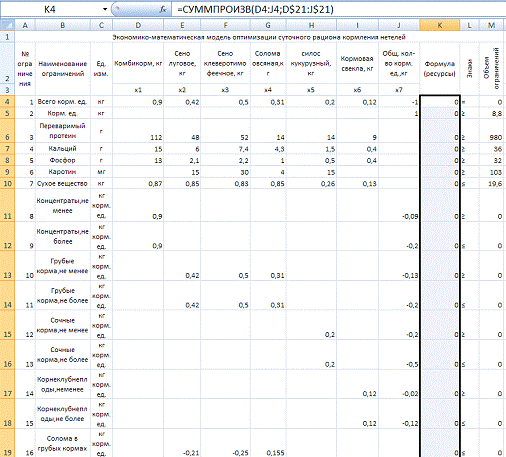
В ячейку Z4 вставим формулу «
=СУММПРОИЗВ(С4:Y4;$C$31:$Y$31)», затем растянем форму до целевой ячейки
включительно.

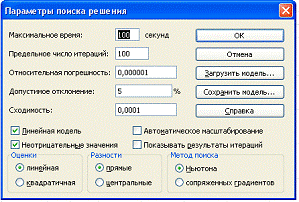
Затем находим решение задачи с помощью «поиска решения». Находим:
Данные→Анализ→Поиск решения. Как видно на рисунке: устанавливаем
целевую ячейку; равный- max значению; изменяя ячейки и ограничение.

Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).

Решить задачи линейного программирования в Excel достаточно просто:

• составить математическую модель задачи,
• внести исходные данные задачи и ограничения,
• выделить место под ячейки решения и целевую функцию, ввести ее формулу,
• запустить надстройку Поиск решения,
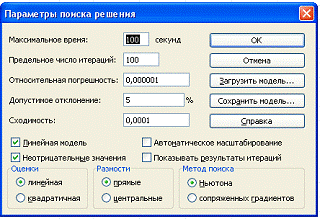
• установить нужные параметры решения и запустить выполнение.

Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.

Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.

Помогаем студентам: Работы по линейному программированию на заказ

Линейное программирование: примеры в Excel

Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.

Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?

Может пригодиться: транспортные задачи в Excel

Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.

Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.

Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?

Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).

Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.

Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).

Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?

Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.

Полезные ссылки

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)