Обзор методов решения в Excel
Введение
Уравнение 

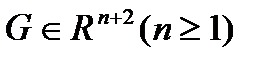

Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2)
k1 = Fk h = F(xk , yk )h
Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:


Разобьём промежуток [a,b] на N частей 

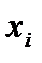
1. явные: 
2. неявные: 
Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение 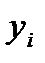
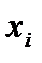


1.3 Метод Эйлера
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием
Требуется найти решение уравнения (7) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку Мi. Если правая часть уравнения (7) в некотором прямоугольнике R<|x-x0|£a, |y-y0|£b>удовлетворяет условиям:
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
где у(хn)-значение точного решения уравнения (7) при х=хn, а уn— приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.4 Модифицированный метод Эйлера
Рассмотрим дифференциальное уравнение (7) y / =f(x,y) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.
Рисунок 1 Метод Эйлера в графическом виде
Получаем точку Мк(хк,ук). Через Мк проводим касательную:
Получаем точку Nk / . В этой точке строим следующую касательную:
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой Хк1. Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
(14)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2, затем находят значение правой части уравнения (11) в средней точке y / k+1/2=f(xk+1/2, yk+1/2) и определяют ук+1.
Для оценки погрешности в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y // =f(y / ,y,x) c начальными условиями y / (x0)=y / 0, y(x0)=y0, выполняется замена
Тем самым преобразуются начальные условия
1.5 Практическая часть
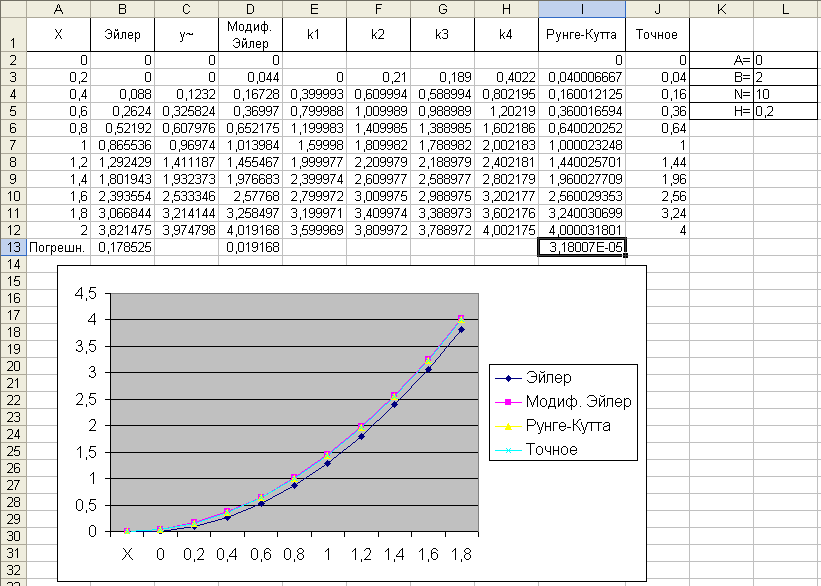
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в нормеL1, как и принято в данном случае
Численное решение дифференциальных уравнений в excel
Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x .
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L1 , как и принято в данном случае.

Рунге-Кутта VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube
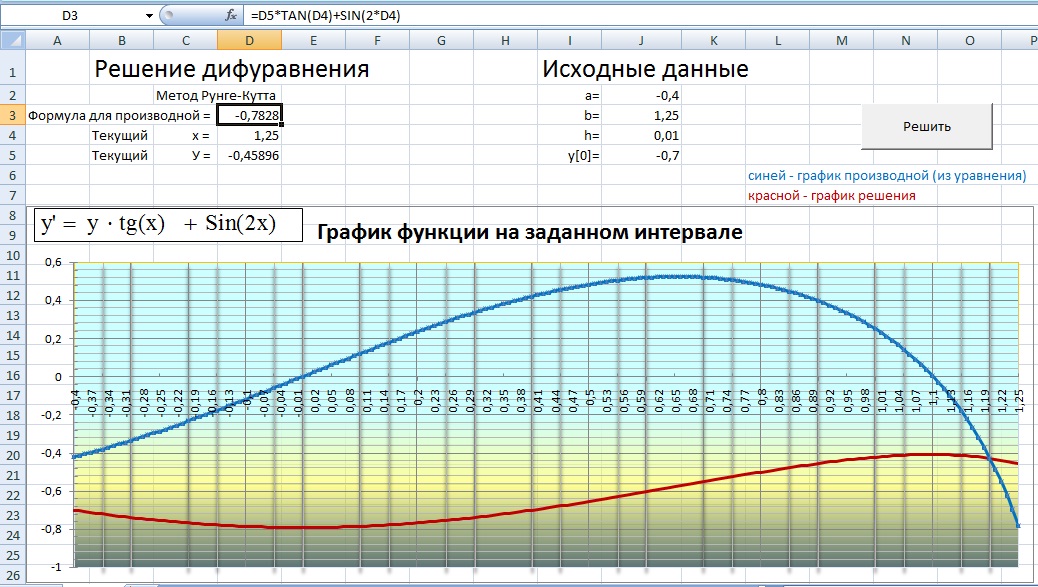
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)
Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function
Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer
For i = 1 To n ‘нулевые значения уже есть
x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)
y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
источники:
http://pers.narod.ru/study/excel_odu.html
http://orenstudent.ru/RungeKuttaVBA_change_formula.htm
Обзор методов решения в Excel
Введение
Уравнение 

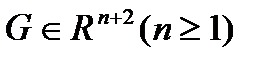

Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
Решение дифференциальных уравнений в эксель
Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x .
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L1 , как и принято в данном случае.

Рунге-Кутта VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)
Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function
Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer
For i = 1 To n ‘нулевые значения уже есть
x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)
y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
источники:
http://pers.narod.ru/study/excel_odu.html
http://orenstudent.ru/RungeKuttaVBA_change_formula.htm
Использование
дифференциальные уравнений находит
широкое применение для компьютерного
моделирования динамических процессов
в автоматизированных системах управления,
в механике, других математических
моделях. Практическое применение в
различных областях науки и техники
находят как обыкновенные дифференциальные
уравнения, так и уравнения в частных
производных. Ниже будет рассмотрен
пример решения обыкновенных дифференциальных
уравнений с заданными начальными
условиями, то есть для таких уравнений
значения функции и ее производных до
n-1
порядка являются известными при Х=0. Для
обыкновенных дифференциальных
уравнений,как правило, решается задача
Коши, то есть задаются уравнения вида
y=f
(x,y)
с начальными условиями x0,
y0
при x0
≤ x
≤ xкон.
Численное решение
таких уравнений заключается в разбиении
интервала х точками xi
с шагом h
для i=1,2,…n
и нахождении значений yi
по формуле
yi
= yi-1
+ ∆yi,
где ∆yi
— приращение
переменной у на каждом шаге.
Формула данного
приращения определяется выбранным
численным методом, Для метода Эйлера
∆yi
= h∙f(xi,yi),
а в инженерных методах (Рунге-Кутта и
других) она записывается более сложным
образом. При этом уравнение 2-го и более
высоких порядков предварительно должны
быть сведены к нормальной системе
обыкновенных дифференциальных уравнений
1-го порядка. Так уравнение y»=xy’
+y2
с начальными условиями x0
=0, y0
=3, y’
=1 преобразуется к системе двух уравнений
1-го порядка:
y1′
=y2,
y2′
=xy2
+ y12
с начальными
условиями y10
= 3, y20
= 1.
Один из вариантов
решения этой системы обыкновенных
дифференциальных уравнений на интервале
(0, 1) с шагом 0, 1 методом Эйлера приведен
на рис.4.47.
Рис.4.47. Решение
дифференциального уравнения
В столбце А создан
диапазон изменения аргумента х от 0 до
1 с шагом 0, 1. Столбец В содержит вычисленные
по формуле Эйлера значения Y1(=B2
+ 0,1*C2),
столбец С – значения Y2
(=C2
+ 0,1*(A2*C2+B2^2)).
Графики изменения
функций Y1(х)
и Y2(х)
представлены на диаграмме.
4.8.9. Финансовые вычисления в Excel
Для выполнения
различных финансовых вычислений Excel
содержит группу финансовых функций,
реализуемых с помощью Мастера функций.
Они включают такие функции как: вычисление
амортизации активов, ставку доходности
по вкладу, вычисление процентов за
определенный инвестиционный период и
многие другие. Ниже рассмотрим примеры
реализации некоторых финансовых
функций.
Расчет амортизационных отчислений
Для расчета
амортизационных отчислений необходимо
знать три основных параметра:
-
начальная стоимость
имущества; -
остаточная
стоимость имущества — стоимость в конце
периода амортизации, иногда называемая
остаточной стоимостью имущества после
завершения эксплуатации; -
время эксплуатации
— количество периодов, в течение которых
имущество амортизируется, иногда
называемые периодами амортизации.
Для расчета
амортизационных отчислений могут быть
использованы различные подходы и способы
и в зависимости от этого могут быть
применены и различные финансовые
функции. В наиболее простом подходе
амортизация распределяется равномерно
на каждый год эксплуатации имущества
и для расчета величины амортизационных
отчислений используют функцию АПЛ,
которая имеет следующий синтаксис:
АПЛ(А;В;С), где:
-
А — начальная
стоимость имущества; -
В — остаточная
стоимость имущества; -
С — продолжительность
эксплуатации.
Рассмотрим пример
расчета амортизационных отчислений.
Пусть имеется приобретенное имущество
стоимостью 400000 руб., продолжительность
его эксплуатации составляет 8 лет, а
остаточная стоимость равняется 50000 руб.
Величина амортизационных отчислений
составит 43,500 руб. за каждый год эксплуатации
Рис.4.48. Вычисление
амортизационных отчислений
Соседние файлы в папке Информатика
- #
- #
- #
- #
- #
- #
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x.
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x2.
Оценка погрешности делается в норме L1, как и принято в данном случае.
Скачать пример в Excel XP/2003 (28 Кб)