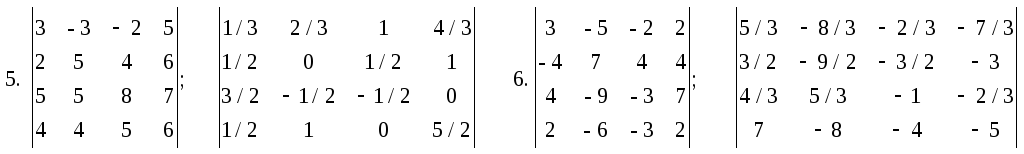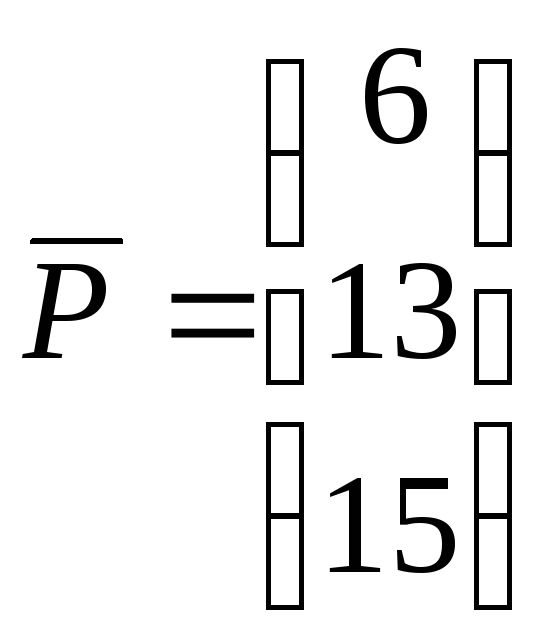Решение алгебраических задач в excel - Word и Excel - помощь в работе с программами

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

f(x)

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

«равно»

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

«равно»

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12701 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.
Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

источники:

http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/

http://exceltable.com/otchety/reshenie-uravneniy

Источник

Тема “Решение математических задач средствами
EXCEL”, является значимой в курсе “Информатика и
информационные технологии”, которая возникает
на различных этапах изучения предмета. Например,
вычисления алгебраических выражений, решения
квадратных уравнений в различных средах,
построение графиков функций и т.д.

На протяжении почти всего курса математики
учащиеся изучают различные методы решения
уравнений и систем уравнений. Когда школьники
изучат методы решения систем уравнений на уроках
алгебры, на уроках информатики целесообразно
рассмотреть дополнительные, более эффективные,
по времени, инструменты для выполнения таких
заданий. Данная тема не является сложной для
учащихся, но очень трудоемкая для учителя,
необходимо делать много записей на доске,
фактически учитель весь урок стоит спиной к
учащимся. Для оптимизации и эффективности
учебной деятельности учителя на уроке была
создана презентация, которая может применяться
на любом этапе прохождения темы фрагментарно или
полностью учителями математики, а особенно
полезна учителям информатики из-за
ограниченного количества часов по предмету.

Данный урок можно отнести к интегрированным
урокам, построенным на деятельной основе с
применением проблемно-исследовательской
технологии. Ценность урока заключается в том, что
ученики решают стандартные математические
задачи нестандартным способом – применяя
современные компьютерные технологии. Этим
достигается мотивационная цель – побуждение
интереса, показ необходимости знаний по
математике и информатики в реальной жизни. На
уроке ученики покажут владение компьютером,
умение работать с пакетом программ Microsoft Office,
знания, умения и навыки, полученные на уроках
математики. В результате будет достигнута
образовательная цель урока: по математики
обобщение знаний по темам: “Матрицы. Действия с
матрицами. Решение систем линейных уравнений
методом Крамера, Гаусса”, по информатике у
учащихся формируется навык работы с табличными
формулами, познакомятся с возможностями Excel для
решения различных уравнений и систем уравнений.

11 класс, информатика.

Тема: “Применение табличного процессора MS
Excel для решения систем линейных алгебраических
уравнений”.

Тема рассчитана на два урока.

Тип урока: комбинированный урок,
совершенствование знаний, умений и навыков.

Вид урока: интегрированный.

Цели урока:

обучающие:

повторение и закрепление знаний учащихся
математического аппарата по теме;
отработать умение переходить от математической
записи выражений к записи в среде электронных
таблиц;
продемонстрировать учащимся рациональность
использования электронных таблиц для решения
систем п линейных уравнений с п неизвестными;

Развитие внимания, памяти, представления,
мышления, речи. Развитие интереса к предмету,
навыка самостоятельной работы.

Развивающие и воспитательные:

формирование умений анализировать, выделять
главное, сравнивать, строить аналогии;

развитие умения применять имеющиеся знания и
умения в новой ситуации;
развивать гибкость мышления, отыскивать
наиболее краткий путь достижения цели развивать
целенаправленность, рациональность, критичность
мышления.
умение устанавливать межпредметные связи.
формирование способностей, позволяющих
осуществлять быструю смену видов учебной
деятельности.

Формы организации познавательной
деятельности: фронтальная, индивидуальная,
групповая, коллективная.

Методы и приемы обучения:
объяснительно-иллюстративный, проблемного
изложения, наглядно-иллюстративный,
практический, эвристическая беседа.

Оборудование: доска, компьютеры,
мультимедийный проектор и экран, презентация,
карточки с индивидуальным заданием, папка с
электронным материалом для урока.

Средства обучения: презентация учителя MS
PowerPoint “Решение математических задач средствами
Excel”, ресурсы Интернет.

Компьютерное программное обеспечение: пакет
программ Microsoft Office 2007.

Структура урока

№	Название этапа	Приемы педагогической техники	Время (мин.)
1	Организационный момент. Постановка цели урока и проблемы исследования	Вступительное слово учителя. Рефлексия. Ознакомление с темой, постановка цели.	2
2	Актуализация опорных знаний	Фронтальная работа с классом. Работа с формулами в Excel. Относительные и абсолютные ссылки. Применение логических функций. Приложение 2.	10
4	Изучение нового материала	Формирование понятие табличной формулы. Частично-поисковая работа. Презентация учителя.	10
5	Подготовка к осмысление и применение изученного материала. Повторение, обобщение математических знаний, дополненных демонстрацией новых функций Excel. Тренировочная практическая работа.	Объяснительно — иллюстративный, повторение и обобщение необходимых знаний из математики с дополнениями новых функций в Excel. Эвристическая беседа Презентация учителя. Задания для практической работы. (Выполняется вместе с учителем. Приложение 3)	25
6	Закрепление (тренировка, отработка умений). Практическая работа.	Беседа по вопросам из презентация учителя. Практическая работа. Приложение 3.	25
10	Итог урока. Контроль.	Анализ работы на уроке. Проверка достижений поставленной цели урока: обобщение изученного материала, выполнение практической работы, активность учащихся на всех этапах урока.	3
9	Постановка домашнего задания.	Домашнее задание творческое. Приложение 4.	3
11	Самооценка деятельности.	Рефлексия.	2
Резерв времени 10 минут на индивидуальную работу при выполнении практической работы

Приложение 1

Описание урока

1. Организационный момент.

Учитель сообщает учащимся тему и цель урока.
Учащиеся записывают тему урока Слайд Титульный
лист.
Рассказывает о том, как будет построен урок.
Знакомит с задачами, которые должны быть решены
в ходе урока.

2. Актуализация опорных знаний.

Учитель. Для успешного проведения занятия по
теме нам необходимо будет вспомнить и повторить
материал из уроков математики “Методы решения
линейных систем уравнений” и из информатики
“Работа с формулами в Excel. Логические формулы.
Относительные и абсолютные ссылки”.

Откройте файл D://Уроки_11/Решение
СЛАУ/Приложение 2. У учащихся файл без листа
Решение.

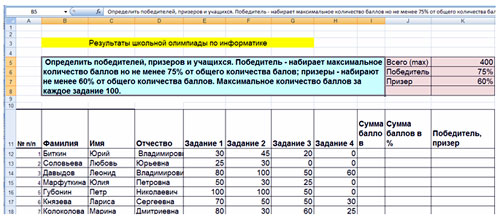
Заполните все поля таблицы.

Фронтальная работа с учащимися по проверки
знаний и умений работы с формулами и функциями в
Excel. На экране демонстрируется пример таблицы,

в которой необходимо заполнить все поля.
Учащиеся предлагают алгоритмы заполнения полей.
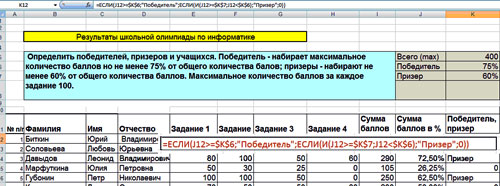
В тетради выписывают формулу для заполнения
столбца K (победители, призеры), далее сравнивают
свое решение с решением, представленным на
экране (лист Решение, Приложение 2).

3. Изучение нового материала.

Учитель

Какие методы решения линейных уравнений вы
знаете? Если не просмотрели файл выложенный в
домашнее задание предыдущего урока, то можете
открыть файл D://Уроки_11/Решение СЛАУ/Приложение
1.

Учащиеся

Метод последовательного исключения
неизвестных, метод Крамера.

Учитель

Посмотрите описание метода Крамера, с какими
элементами нужно уметь работать при применении
этого метода?

Учащиеся

С определителями.

Учитель

Т.е. с матрицами, на экране демонстрируется
пример матрицы . Откройте файл D://Уроки_11/Решение
СЛАУ/Приложение 3, лист Пример и выполните
задание.

Учащиеся открывают документ Приложение
3 (лист Пример 1).

Выполняются задания, представленные на экране.

Учитель

Для работы с матрицами в Excel существуют
специальные формулы, формулы для работы с
массивом или их ещё называют табличные формулы.

Презентация. Слайд 3, 4. Учащиеся записывают
понятие табличной формулы и особенности её
ввода.

4. Подготовка к осмысление и применение
изученного материала. Практическая работа.

Эвристическая беседа.

Учитель

1. Для решения, каких задач можно применять
табличные формулы?

Ответ может быть предопределен заданием,
которое они выполняли – действия с матрицами,
если решением должна получиться тоже матрица.

2. Дайте понятие матрицы? Может ли сказать, что
любая прямоугольная таблица, заполненная
числовыми значениями, есть матрица?

Ответ утвердительный. Слайд 5

3. Какие виды матриц вы знаете, чем они
отличаются друг от друга? (заполнение,
размерность и т.д.)

После обсуждения представить Слайд 6.

4. Можно ли с матрицами производить какие-либо
действия?

Учащиеся могу перечислить некоторые действия с
матрицами, сложение, умножение на число и т.д.
Слайд 7.

Учитель информирует учащихся , о широких
возможностях табличного процессора Excel для
работы с матрицами.

Ученики записывают тему пункта темы Слайд8.

Повторение, обобщение математических знаний,
дополненных демонстрацией новых функций Excel.

Презентация Слайды 9-14.

Демонстрация каждого слайда предопределяется
вопросами по теме слайда.

В тетрадь учащиеся записывают только функции
Excel для работы с матрицами и одновременно
выполняют тренировочные практические задания из
Приложение 3 Листы: пример 2, пример 3, пример 4.
Подробно остановиться на примере 5, Приложение 3,
Слайд 14.

Учитель

Теперь непосредственно перейдем к решению СЛАУ
и познакомимся с методом, который вы
рассматривали на уроках математики, это
матричный метод. Слайд 16. Как вы думаете
почему вы не решали системы матричным методом?

Учащиеся

Сложность вычисления обратной матрицы

Учитель

Запишите в тетрадь алгоритм решения системы
матричным способом.

Откройте новую книгу Excel и решим вместе систему
представленную на экране. Слайды 18-21.

Учитель открывает файл – заготовку упражнения
и вместе с учащимися решает упражнение.

Решение сопровождается подробным объяснением.
Решение учащихся сравнивается с предложенным
решением в презентации. Слайды 18-21.

Учитель

Рассмотрим теперь решение СЛАУ методом
Крамера, этот метод вам знаком, но на уроках
математики вы решали, в основном, системы из двух
уравнений с двумя неизвестными, почему? Слайд
22.

Ученики

Нужно много времени для вычисления
определителей.

Учитель

Возможности Excel решают эту проблему.
Откройте новый лист в книге и вместе решим
систему уравнений представленную на экране.

Свои решения учащиеся сравнивают с решением,
представленным в презентации. Слайды 23-25.

5. Закрепление (эвристическая беседа,
тренировка, отработка умений).

Обсуждение темы по вопросам. Презентация. Слайд
26.

Практическая работа по группам: группа
(практики) Приложение 3 Листы пример 6, пример 7,
группа (технологи) Лист пример 8 решить систему
методом Гаусса ( можно воспользоваться
Интернет-ресурсами), группа (программисты)
создать программу на языке программирования
Паскаль или С# решение системы уравнений методом
Крамера, можно для ограниченного количества
строк и столбцов.

6. Итог урока.

Проверка практической работы, обсудить
проблемы в выполнении с каждой группой, если были
выполнены не все задания, то откорректировать
домашнее задание. Выставление оценок за урок.

Домашнее задание. На выбор:

1. (Приложение 4) Выполнить один из
вариантов из карточки , разобрать программы
решения систем уравнений на языке Паскаль из
теоретического материала (Приложение 1)

2. Выполнить один из вариантов из карточки.
Создать отдельно программу для решения систем
методом Гаусса или матричным методом, группе
программистов доработать программу метод
Крамера.

7. Заключение.

Опыт работы с интегрированными уроками
показывает, что у учащихся повышается качество
знаний, оно может и не выражаться в оценках, но
расширяется кругозор, развиваются творческие
способности, повышается интерес к предметам, и
вообще интерес к обучению, формируется
убеждение, что учащиеся могут изучить больше, чем
дается по программе.

Предложенное занятие по содержанию и
выполнению заданий, кажется, насыщенным и
перегруженным теорией и практическими
упражнениями, но применение презентации,
заготовок файлов (приложение 3) помогает
выполнить все запланированные действия. Такое
занятие рекомендуется проводить в
математических классах, когда учащиеся уже
изучили методы решения СЛАУ. За неделю до
изучения этой темы выложить в эл. дневник, для
ознакомления, информационный материал по
методам решения систем уравнений и описание
создания программ для решения систем уравнений
на языке программирования.

Литература

1. Воронина Т.П. Образование в эпоху новых
информационных технологий / Т.П. Воронина.- М.: АМО,
2008. -147 с.

2. Глинская Е. А. Межпредметные связи в обучении /
Е.А. Глинская, С.В. Титова. – 3-е изд. – Тула: Инфо,
2007. — 44 с.

3. Данилюк Д. Я. Учебный предмет как
интегрированная система /Д.Я. Данилюк
//Педагогика. — 2007. — № 4. — С. 24-28.

4. Иванова М.А. Межпредметные связи на уроках
информатики / М.А. Иванова, И.Л. Карева //
Информатика и образование. – 2005. — №5. – С. 17-20.

5. А.В. Могилев, Н.И. Пак, Е.К. Хеннер
«Информатика», Москва, ACADEMA, 2000 г.

6. С.А. Немнюгин, «Турбо ПАСКАЛЬ», Практикум,
Питер, 2002 г.

Ресурсы Интернет

http://www.excelworld.ru/publ/hacks/tools/solver/27-1-0-122

http://www.uchportal.ru/publ/23-1-0-1832

http://math.immf.ru/lections/003.html

Источник

Среда
MS
Excel
представляет собой набор инструментов
для обработки данных, как правило,
числовых. Ядром данной прикладной
программы являются функции MS
Excel
(финансовые, математические, статистические,
баз данных и т.д.), предназначение которых
ясно из названий. В этом параграфе мы
применим средства Excel
для выполнения действий над матрицами,
что, надеемся, облегчит студентам решение
задач.

Итак,
в Excel
существуют следующие функции действий
над матрицами:

МУМНОЖ
– возвращает произведение матриц
(матрицы хранятся в массивах). Результатом
является массив с таким же числом строк,
как массив 1, и с таким же числом столбцов,
как массив 2.

МОПРЕД
– возвращает определитель матрицы
(матрица хранится в массиве).

ТРАНСП
– транспонирование матрицы.

МОБР
– возвращает обратную матрицу для
матрицы, хранящейся в массиве.

Для
простейших действий над матрицами,
такими как:

сложение/вычитание
двух матриц;
умножение
матрицы на число –

использование
встроенных функций MS
Excel
не требуется. Для выполнения арифметических
действий, но не над числами, а над
массивами чисел (матрицами), достаточно
составить необходимую формулу для
одного из элементов, а затем скопировать
ее для всех остальных. За счет индексации
(адреса) каждой ячейки листа MS
Excel
будет получен корректный результат.

Пример
2.15.
Найдем матрицу С = А + В и D
= 4*A,
где А и В – матрицы вида:

Решение. В данном случае необходимо
ввести значения матрицы А и В (рис. 2.1).

К оформлению никаких строгих правил
не предъявляется:

Рис.
2.1.
Исходные
данные для примера

Для
нахождения матрицы С запишем в первый
элемент результирующей матрицы формулу.
Поскольку сложение матриц происходит
поэлементно, то первый элемент матрицы
С будет суммой первых элементов матриц
А и В (рис. 2.2).

Рис.2.2.
Сумма
первых элементов

После
нажатия клавиши «ENTER»
в первой ячейке области, отведенной под
матрицу С, появится результат сложения.
Формулу, составленную для первого
элемента, используем для нахождения
оставшихся элементов. Для этого формулу
необходимо скопировать и «забить» в
нужные ячейки. Копирование и вставку
можно провести тремя способами:

– поставив
курсор в первую клетку, вызвать в пункте
главного меню «Правка» подпункт
«Копировать/Вставить»;

– правой
кнопкой «мышки» нажать на первую ячейку
и в появившемся меню выбрать
«Копировать/Вставить»;

– воспользоваться
«горячими» клавишами: копировать –
Ctrl+C;
вставить – Ctrl+V.

После
копирования (занесения в буфер памяти)
формулы, необходимо выделить область
результирующей матрицы, в данном случае
3 клетки х 3 клетки, и вставить формулу
перечисленными тремя способами или
просто нажав клавишу «ENTER».

В
результате должна получиться результирующая
матрица С (рис. 2.3).

Рис.
2.3.
Результат
сложения матриц

Аналогичным
образом получим матрицу D
= 4*A
(рис. 2.4).

Рис.
2.4.
Результат
умножения матрицы на число

Все
перечисленные выше функции можно найти
в полном алфавитном списке функций MS
Excel,
который можно вызвать тремя способами:

– в
пункте главного меню «Вставка» выбрать
пункт «Функции» (рис. 2.5).

Рис.
2.5.

– нажатием
на панели инструментов иконки со значком
f^х(рис.
2.6).

Рис.
2.6.

– после
ввода в желаемую ячейку символа «=»
справа под панелью инструментов
появляется выпадающее меню, в котором
отображены последние 10 использованных
функций (рис. 2.7 и рис. 2.8).

Рис.
2.7

Рис.
2.8

Рассмотрим
использование данных функций на примерах.

Пример
2.16. Найти
произведение
матриц
А и В из примера 2.15.

Решение.
В
задаче перемножения матриц прежде всего
необходимо определить размерность
итоговой матрицы. В нашем случае, матрица
Е = А*В будет содержать 3 строки и 3 столбца.
На листе Excel
необходимо
выделить область 3х3 и в первой ячейке
вызвать функцию МУМНОЖ (рис. 2.9).

Рис.
2.9.
Вызов
функции МУМНОЖ

В
окне функции МУМНОЖ заносятся адреса
перемножаемых массивов. Для этого в
верхнем окне для адреса первого массива
необходимо нажать кнопку
и указать выделением на рабочем листе
расположение элементов первого массива
(рис. 2.10 и 2.11).

Рис.
2.10

Рис.
2.11

Аналогично
заполнить адрес второго массива в строке
«Массив 2» (рис. 2.12).

Рис.
2.12

Следующей
задачей является перенос полученных
результатов на рабочий лист. Поскольку
в данном действии результатом является
не одна ячейка, а девять, то вместо
клавиши «ENTER»
нажимается комбинация клавиш
Ctrl+Shift+Enter.
В результате должен получиться заполненный
массив Е (рис. 2.13).

Рис.
2.13

Аналогичным
образом производится работа с функцией
МОБР, которая служит для нахождения
обратной матрицы.

Пример
2.17. С
помощью Excel
найти обратную матрицу для матрицы В
из примера 2.15.

Решение.
Для
отыскания матрицы В^-1
выделить на рабочем листе область 3х3 и
вызвать функцию МОБР. Синтаксис этой
функции предполагает адрес одного
массива (рис. 2.14).

Рис.
2.14.
Нахождение
обратной матрицы

В
результате нажатия комбинации клавиш
(поскольку требуется заполнить не одну
ячейку) Ctrl+Shift+Enter
в выделенной области будет размещаться
обратная матрица для массива В (рис.
2.15).

Рис.
2.15

Аналогично
выполняется транспонирование матрицы
с единственным отличием – используется
функция ТРАНСП.

Пример
2.18.
Найти определитель матрицы А из примера
2.15.

Решение.
Для
нахождения определителей любых порядков
используется функция МОПРЕД. Поскольку
опредилитель – это число,
характеризующее квадратную матрицу,
нет необходимости в выделении области
для ответа. Решением будет число,
помещенное в одну ячейку (рис. 2.16).

Рис.
2.16.

Необходимо
помнить, что в случае, когда в результате
действий над матрицами ответом будет
являться массив, а не число, следует
следить за выполнением двух требований:

перед
вызовом функции выделять область, в
которой ожидается решение;
после
заполнения необходимой информации в
окне таких функций, как МУМНОЖ, МОБР и
ТРАНСП, следует нажимать комбинацию
Ctrl+Shift+Enter.

Контрольные
вопросы

Дайте
определение матрицы.
Перечислите
виды матриц.
Какие
матрицы можно складывать, умножать?
Дайте
определение n-мерного вектора.
Является
ли вектор матрицей или наоборот?
Что
такое минор M_ijматрицы А?
Что
такое алгебраическое дополнение A_ij?
Что
такое определитель матрицы?
Как
вычислить определитель квадратной
матрицы второго порядка, третьего
порядка?
Для
всех ли матриц существует понятие
определителя?
Дайте
определение обратной матрицы.
Что
такое неособенная матрица?
Как
вычислить обратную матрицу?
Как
проверить, является ли матрица В обратной
к А?
Запишите
СЛАУ в матричной форме.
Как
решить СЛАУ методом Крамера?
Как
решить СЛАУ методом обратной матрицы?
Запишите
решение матричного уравнения AX = B.
Какие
системы можно решать методом Гаусса?
Какие
случаи возможны при решении СЛАУ?
Что
такое однородная СЛАУ?
Дайте
определение общего решения СЛАУ.
Дайте
определение частного решения СЛАУ.
Дайте
определение базисного решения СЛАУ.
Сколько
базисных решений может иметь СЛАУ.
Что
называется линейной комбинацией системы
векторов?
Какая
система векторов называется
линейно-зависимой (независимой)?
Что
называется базисом n-мерного пространства?
Как
определить линейную зависимость или
независимость системы векторов?
Как
перейти от одного базиса векторного
пространства к другому?

Задание
№2

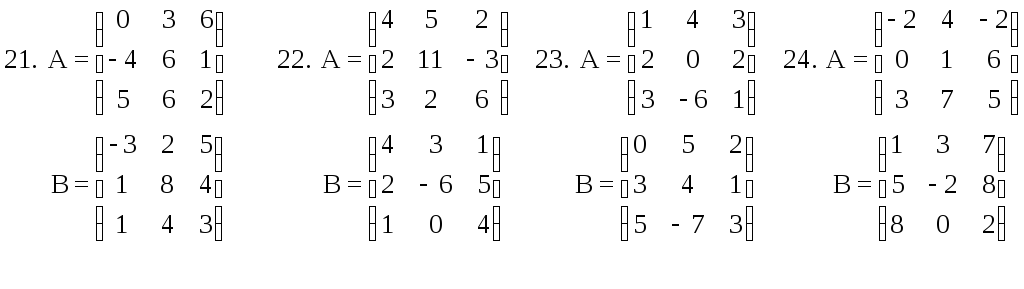
Для
матриц А
и В
определить:

а)
3А
+
4В;

б)
АВ
– ВА;

в)
(А—В)^-1.

Задание
№3

Вычислить
следующие определители:

Задание
№4

Решите
систему линейных уравнений двумя
способами (после решения необходимо
выполнить проверку):

по
формулам Крамера;

матричным
способом.

1)
2X₁
+ 5X₂
— 8X₃
= 8 2) X₁
+ 8X₂
— 7X₃
= 12

4X₁
+ 3X₂
— 9X₃
= 9 2X₁
+ 3X₂
— 5X₃
= 7

2X₁
+ 3X₂
— 5X₃
= 7 6X₁
+ 8X₂
-17X₃
= 17

3)
2X₁
+ 3X₂
— 5X₃
= 7 4) 6X₁
+ 6X₂
-14X₃
= 16

5X₁
+11X₂
-16X₃
= 21 2X₁
+ 5X₂
— 8X₃
= 8

4X₁
+ 3X₂
— 9X₃
= 9 4X₁
+ 3X₂
+ 9X₃
= 9

5)
-7X₁
+ 3X₂
+8X₃
= 75 6) 13X₁
— 6X₂
= 32

9X₁
— 4X₂
= -3 8X₁
+4X₂
+ 1X₃
= 12

X₁
— 7X₂
— 3X₃
= 12 2X₁
+ 9X₂
+ 5X₃
= -5

7)
7X₁
— 4X₂
= 61 6X₁
+ 3X₂
+ 9X₃
= -111

8X₁
+9X₂
— 6X₃
= 48 -7X₁
— 4X₂
— 2X₃=
52

9X₁
— 6X₂
— 2X₃
= 99 X₁
— 7X₂
+ 3X₃
= -47

9)
-5X₁
+ 7X₂
+11X₃
= -2 10) 2X₁
+ X₂
+ 3X₃
= 11

2X₁
+ 6X₂
+ 3X₃
= 11 3X₁
+ 2X₂
— 5X₃
= -20

3X₁
— 5X₂
+ 4X₃
= 11 5X₁
— 2X₂
+3X₃
= -4

11)
2X₁
+ 3X₂
— 6X₃
= 18 12) X₁
+ 7X₂
— 5X₃
= 25

4X₁
+ 3X₂
— 9X₃
= 9 X₁
+ 3X₂
— 5X₃
= 15

2X₁
+ 2X₂
— 5X₃
= 10 6X₁
+ 8X₂
-17X₃
= 17

13)
2X₁
+ 5X₂
— 5X₃
= 25 14) 6X₁
+ 2X₂
-X₃
= 16

5X₁
+11X₂
-16X₃
= 21 2X₁
+ X₂
— 8X₃
= 36

4X₁
+ 2X₂
— X₃
= 8 4X₁
+ 3X₂
+ 9X₃
= 90

15)
-X₁
+ 3X₂
+8X₃
= 24 16) 12X₁
— 6X₂
= 45

9X₁
— 4X₂
= -36 8X₁
+X₂
+ 7X₃
= 56

X₁
— 7X₂
— 3X₃
= 12 2X₁
+ 9X₂
+ 5X₃
= -5

17)
7X₁
— 4X₂
= 60 18) 6X₁
+ 2X₂
+ 9X₃
= -81

8X₁
+9X₂
— 3X₃
= 48 -7X₁
— 4X₂
— 2X₃=
52

9X₁
— 6X₂
— 2X₃
= 99 X₁
— 5X₂
+ 3X₃
= -45

19)
-3X₁
+ 7X₂
+5X₃
= -20 20) 2X₁
+ 5X₂
+ 3X₃
= 110

2X₁
+ 6X₂
+ 2X₃
= 120 3X₁
+ 2X₂
— 3X₃
= -20

3X₁
— 5X₂
+ 4X₃
= 90 5X₁
— 12X₂
+3X₃
= -4

21)
2X₁
+ 7X₂
— 8X₃
= 80 22) X₁
+ 8X₂
— 3X₃
= 90

14X₁
+ 3X₂
— 9X₃
= 90 2X₁
+ 3X₂
— 5X₃
= 70

2X₁
+ 3X₂
— 5X₃
= 70 X₁
+ 8X₂
-15X₃
= 120

23)
2X₁
+ 3X₂
— X₃
= 7 24) 6X₁
+ 6X₂
-X₃
= 16

5X₁
+5X₂
-16X₃
= 25 5X₁
+ 5X₂
— 8X₃
= 80

X₁
+ 3X₂
— 9X₃
= 9 4X₁
+ 3X₂
+ 9X₃
= 90

25)
-7X₁
+ 3X₂
+8X₃
= 64

9X₁
— 4X₂
= -30

X₁
— 7X₂
— 2X₃
= 14

Задание
№5

Решить
системы линейных уравнений методом
Жордана–Гаусса

Вариант
№1 – решить системы №1, 6, 11

Вариант
№2 – решить системы №2, 7, 12

Вариант
№3 – решить системы №3, 8, 13

Вариант
№4 – решить системы №4, 9, 14

Вариант
№5 – решить системы №5, 10, 15

Вариант
№6 – решить системы №1, 7, 13

Вариант
№7 – решить системы №2, 8, 14

Вариант
№8 – решить системы №3, 9, 15

Вариант
№9 – решить системы №4, 10, 11

Вариант
№10 – решить системы №5, 6, 12

Вариант
№11 – решить системы №1, 7, 12

Вариант
№12 – решить системы №2, 9, 13

Вариант
№13 – решить системы №3, 10, 11

Вариант
№14 – решить системы №4, 8, 14

Вариант
№15 – решить системы №5, 9, 12

Вариант
№16 – решить системы №1, 8, 14

Вариант
№17 – решить системы №2, 10, 12

Вариант
№18 – решить системы №3, 9, 15

Вариант
№19 – решить системы №4, 7, 11

Вариант
№20 – решить системы №5, 6, 13

Вариант
№21 – решить системы №1, 6, 15

Вариант
№22 – решить системы №2, 8, 15

Вариант
№23 – решить системы №3, 6, 14

Вариант
№24 – решить системы №4, 10, 15

Вариант
№25 – решить системы №5, 7, 11

1.
2Х₁
+ Х₂
+ Х₃
= 2 2. 2Х₁
— Х₂
+ 3Х₃
= 3

Х₁+3Х₂
+ Х₃
= 5 3Х₁
+ Х₂
— 5Х₃
= 0

Х₁
+Х₂
+5Х₃
= -7 4Х₁
— Х₂
+ Х₃
= 3

2Х₁+3Х₂
— 3Х₃
= 14 Х₁
+ 3Х₂
-13Х₃
= -6

3.
Х₁
+ Х₂
+ Х₃
+ Х₄
= 6 4. 2Х₁
— Х₂
+ Х₃
— Х₄
= 1

Х₁
+ Х₂
— Х₃
— Х₄
= 0 2Х₁
— Х₂
— 3Х₄
= 2

Х₁
— Х₂
+ Х₃
— Х₄
= 4 3Х₁
— Х₃
+ Х₄
= -3

Х₁
— Х₂
— Х₃
+ Х₄
= 2 2Х₁+2Х₂
-2Х₃+
5Х₄
= -6

11Х₁
-Х₂
— Х₃+
Х₄
= -5

5.
Х₁
+ Х₂
+ Х₃
+ Х₄
= 0 6. Х₁
+5Х₂
— 9Х₃
+ 8Х₄
= 1

Х₂
+ Х₃
+Х₄
+Х₅
= 0 5Х₁+18Х₂
+ 4Х₃
+ 5Х₄
= 12

Х₁
+2Х₂
+3Х₃
= 2 2Х₁
+7Х₂
+3Х₃
+ 4Х₄
= 5

Х₂
+ Х₃+3Х₄
= -2 1Х₁
+3Х₂
+5Х₃
— 2Х₄
= 3

Х₃+2Х₄
+Х₅
= 2

7. 2Х₁
+ 3Х₂
+ 9Х₃
-7Х₄
= 3 8. 9Х₁
+4Х₂
+ Х₃
+ 7Х₄
= 2

8Х₁
+12Х₂
— 9Х₃
+8Х₄
= 3 2Х₁+
7Х₂
+ 3Х₃
+ Х₄
= 6

4Х₁
+ 6Х₂+
3Х₃
— 2Х₄
= 3 3Х₁
+5Х₂
+2Х₃
+ 2Х₄
=4

2Х₁+
3Х₂
— Х₃+
Х₄
= 1

9.
2Х₁
— 3Х₂
— 11Х₃
-15Х₄
= 1 10. 9Х₁+12Х₂
+ 3Х₃
+10Х₄
= 13

2Х₁
— 3Х₂
+ 5Х₃
+ 7Х₄
= 1 3Х₁+
4Х₂
+ Х₃
+ 2Х₄
= 3

4Х₁
— 6Х₂+
2Х₃
+ 3Х₄
= 2 6Х₁
+ 8Х₂
+2Х₃
+ 5Х₄
= 7

11.
7Х₁
— 4Х₂
+ Х₃
+ 3Х₄
= 5 12. 3Х₁+3Х₂
+ 5Х₃
-2Х₄+3Х₅
= 1

3Х₁—
5Х₂
+2Х₃
+4Х₄
= 2 2Х₁+2Х₂
+ 4Х₃
-Х₄
+3Х₅
= 2

5Х₁
+ 7Х₂
— 4Х₃
— 6Х₄
= 3 Х₁
+ Х₂+
3Х₃
-2Х₄+5Х₅
= 1

2Х₁+2Х₂+
8Х₃
-3Х₄+9Х₅
= 2

13.
Х₁
+ 2Х₂
+ 3Х₃
= 2 14. Х₁+
Х₂
— 3Х₃
= -1

Х₁+
Х₂
+ 2Х₃
= 1 2Х₁+
Х₂
— 2Х₃
= 1

3Х₁
+ 5Х₂
+ 8Х₃
= 0 Х₁
+ Х₂+
Х₃
= 3

-Х₁
+ Х₂
+ 4Х₃
= 2 Х₁
+2Х₂-3Х₃
= 1

15.
2Х₁
— Х₂
+ Х₃
— 3Х₄
= 4

3Х₁—
2Х₂
+2Х₃
— 3Х₄
= 2

2Х₁
+ Х₂
— Х₃
+ Х₄
= 1

5Х₁
+ Х₂
— Х₃
+ 2Х₄
= 1

Задание
№6

В
естественном базисе заданы векторы.
Установить, составляют ли они базис.
Если составляют, то найти связь между
новым и старым базисами, а также в новом
базисе найти компоненты вектора
.

Для
вариантов 1–10

Для
вариантов 11–20

Для
вариантов 21–30

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.

Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.

Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.

Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.

Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.

В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

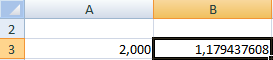
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Источник

Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.

В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:

Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?

Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» Но весьма скоро, я уверен, вы сообразите, что на самом деле всё не так примитивно и для получения ответа нужно решить простую систему уравнений (здесь b — это бита, а m — это мяч):

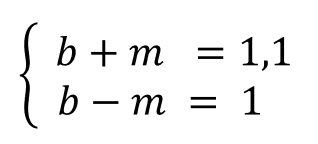
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:

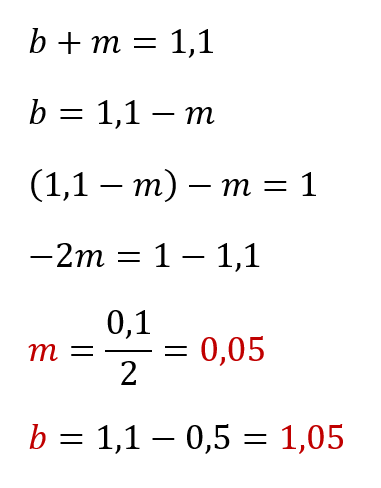
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.

Способ 1. Матричные функции МУМНОЖ и МОБР

Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.

Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).

Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):

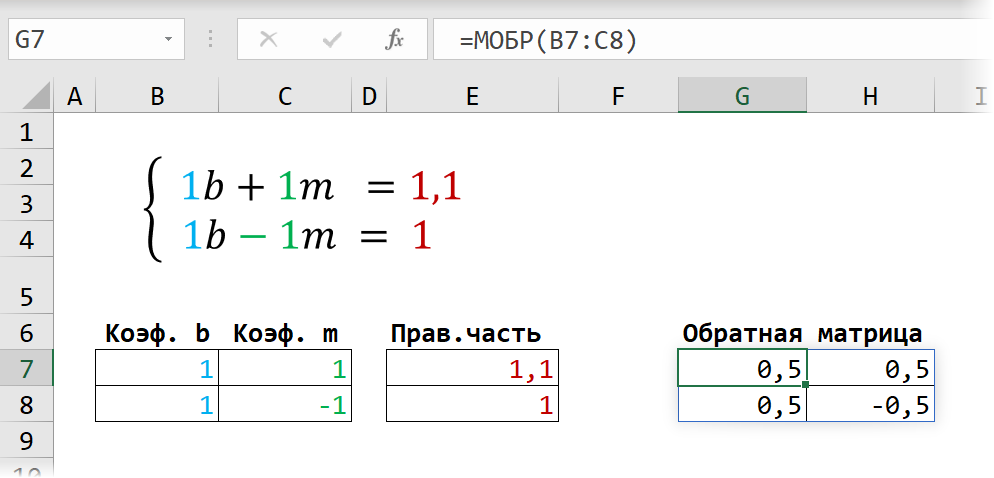
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:

Выделить диапазон для результатов — G7:H8
Ввести функцию =МОБР(B7:C8) в строку формул
Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter

Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):

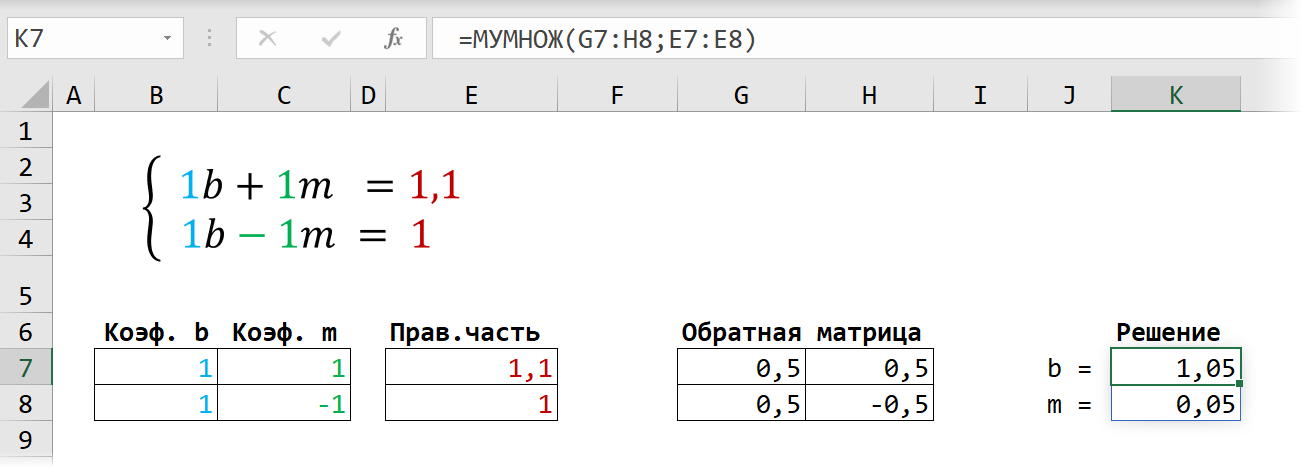
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.

Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:

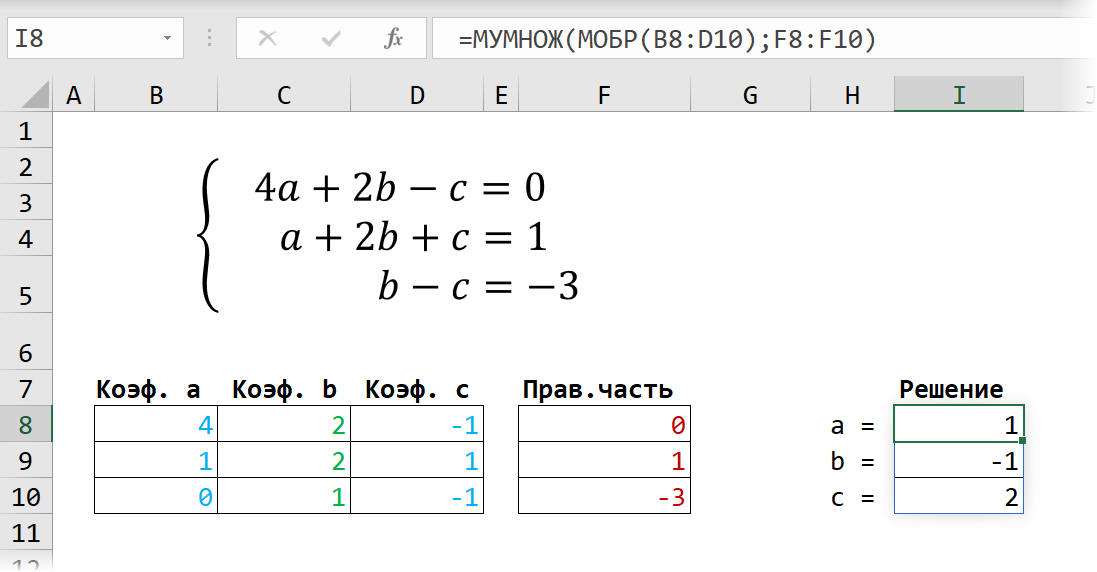
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.

Способ 2. Подбор надстройкой «Поиск решения» (Solver)

Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.

В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).

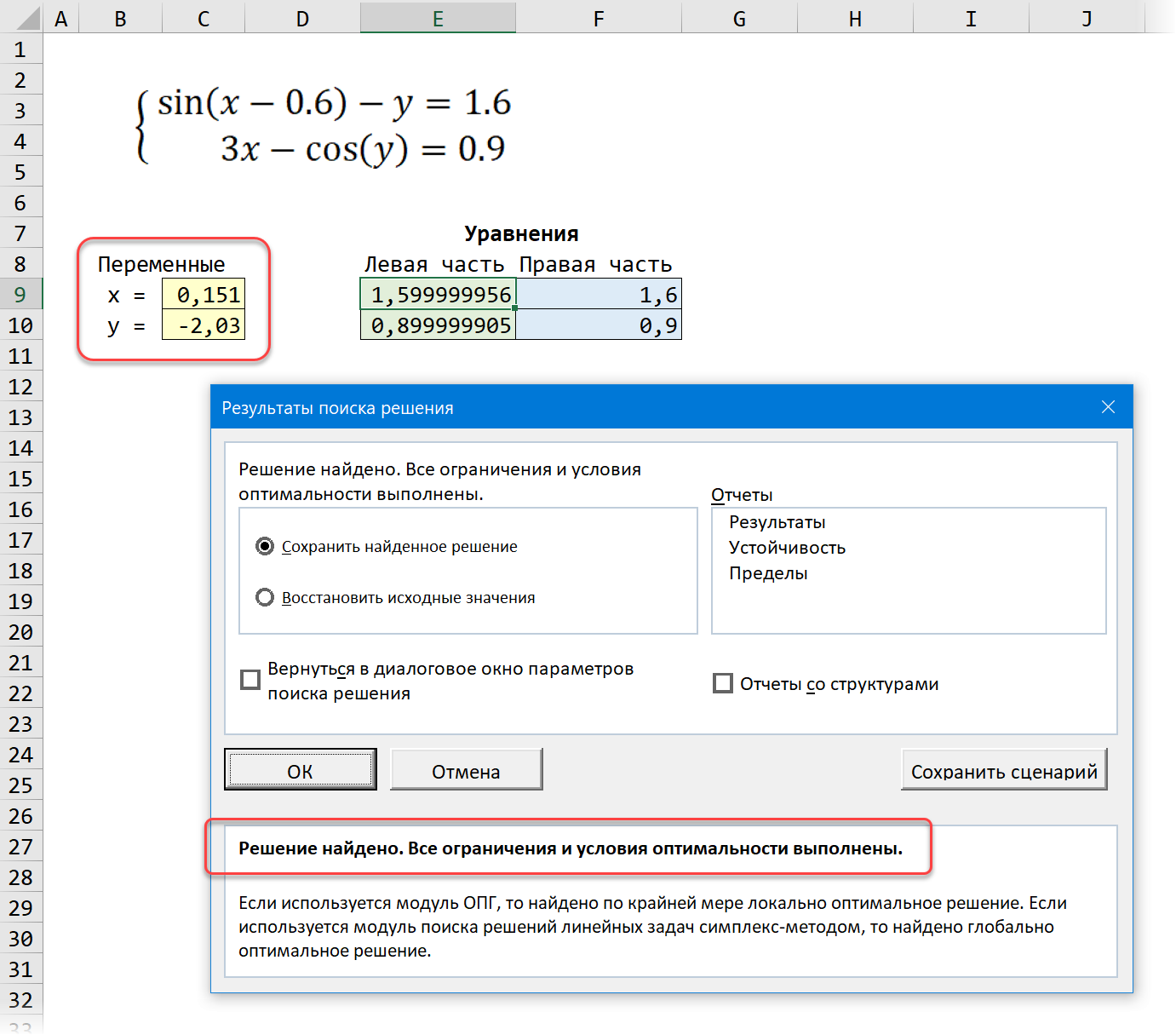
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:

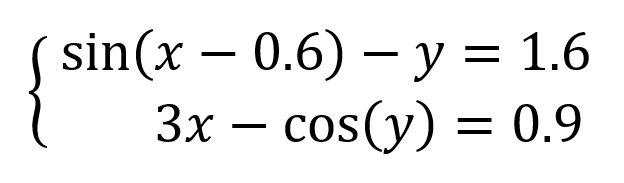
Подготавливаем основу для оптимизации в Excel:

Здесь:

В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.

Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:

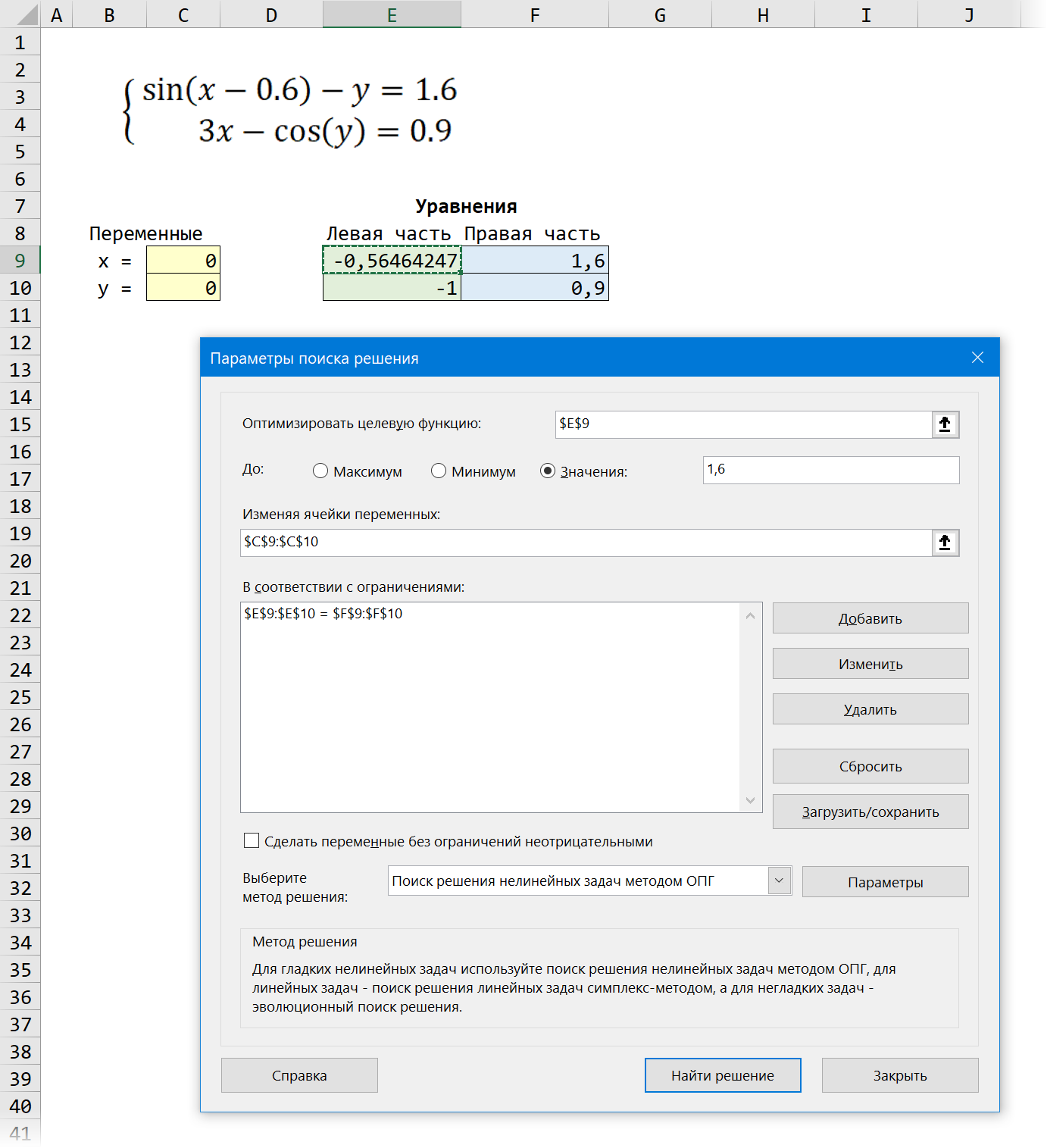
Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.

После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:

Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).

Источник

МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ В MICROSOFT EXCEL

Автор: Мурзин Дмитрий Алексеевич, студент 2 курса ГБПОУ МО «Серпуховский колледж» г. Серпухов Московской области.

Научный руководитель: Соколова Марина Анатольевна, преподаватель специальных дисциплин ГБПОУ МО «Серпуховский колледж» г. Серпухов Московской области.

Аннотация.

В данной статье рассматриваются методы решения алгебраических и трансцендентных уравнений, с применением электронных таблиц Microsoft Excel.

Annotation.

This article shows methods for solving algebraic and transcendental equation comparison using Microsoft Excel spreadsheets.

Ключевые слова: трансцендентные, алгебраические, уравнения, электронная таблица

Keywords: transcendental, algebraic, equations, spreadsheet

Актуальность

На практике при решении различных физических и технических задач составляются и решаются уравнения. Уравнения – аналитическая запись задачи о нахождении значений аргументов, при которых значения двух данных функций равны. Аргументы-неизвестные, а значение неизвестных-корни уравнения. В школьном курсе математике рассматриваются различные способы аналитического решения простейших уравнений. Но существуют алгебраические уравнения, для которых нет общего случая решения в радикалах, их решение можно найти только приближенно.

Например, шар радиуса r плавает в воде, погрузившись на глубину d.Пусть r =10см, сделан он из сосны, имеющей плотность 0,638 г/. Плотность воды 1 г/. Требуется найти глубину погружения шарика d.

В своей работе я буду рассматривать различные методы решения алгебраических и трансцендентных уравнений, с применением электронных таблиц Microsoft Excel.

Объект исследования: уравнения;

Предмет исследования: методы решения уравнений.

Цель работы: выполнить в Microsoft Excel различные методы решения алгебраических и трансцендентных уравнений.

Задачи работы:

1. Изучить и провести анализ литературы, интернет-ресурсов теоретической и практической основы методов решения уравнений;

2. Исследовать различные методы решения трансцендентных и алгебраических уравнений;

3. Выполнить в Microsoft Excel различные методы решения алгебраических и трансцендентных уравнений.

Введение:

Возможности электронных таблиц не ограничиваются вычислениями по формулам и построением графиков и диаграмм. В своей работе я рассмотрю практическое применение Microsoft Excel. Остановимся на решении уравнений. Конечно, это не означает, что Microsoft Excel решит уравнение в алгебраическом виде и выдаст все его корни. В Microsoft Excel встроены методы нахождения приближенных значений. Один из них называется методом подбора параметра. Она подберет один из корней уравнения. Электронные таблицы располагают серьезными возможностями по оптимизации решений, то есть нахождению наилучшего результата при заданных условиях. Для этого в Microsoft Excel можно рассмотреть различные методы приближенного решения уравнений. [4]

Общая постановка задачи

Найти действительные корни уравнения f(x) = 0, где f(x) – алгебраическая или трансцендентная функция. Точные методы решения уравнений подходя только для узкого класса уравнений (квадратные, биквадратные и т. д.).

Задача численного нахождения корней уравнения состоит из двух этапов:

1. Отделение (локализация) корня;

2. Приближенное вычисление корня до заданной точности (уточнение корней).

Уточнение корня может производить разными методами[1][3]:

1. Графический метод;

2.Метод подбора параметра;

3. Метод половинного деления;

4. Метод итераций;

5. Метод хорд (метод секущих);

6. Метод касательных (метод Ньютона);

7. Комбинированный метод.

Применяя электронные таблицы Microsoft Excel, я выполнил решение задачи перечисленными методами.

Пример:

Шар радиуса r плавает в воде, погрузившись на глубину d.Пусть r =10см, сделан он из сосны, имеющей плотность 0,638 г/.Плотность воды 1 г/. Требуется найти глубину погружения шарика d, применяя электронные таблицы Microsoft Excel.

Результаты:

Исследование методов показало различные методы решения алгебраических и трансцендентных уравнений с помощью электронной таблицы Microsoft Excel. Следующие методы были изучены:

• Графический метод;

• Подбор параметра;

• Метод половинного деления;

• Метод итераций;

• Метод хорд (метод секущих);

• Метод касательных (метод Ньютона);

• Комбинированный метод.

Вывод

Я изучил методы решения алгебраических и трансцендентных уравнений на примере задачи с физическим содержанием с помощью Microsoft Excel. В данной работе я показал методы решение алгебраических и трансцендентных уравнений в среде Microsoft Excel:

1) методом бисекции;

2) методом итераций;

3) методом секущих;

4) методом Ньютона;

5) метод подбора параметра;

Список использованных источников

1. Lectures on Numerical Analysis /Dennis Deturck, Herbert S. Wilf. — 1-е издание. — Philadelphia: Department of Mathematics University of Pennsylvania, 2002. — 125с.

2. Numerical analysis [Электронный ресурс] / Wikipedia contributors. — Электрон. текстовые дан. — San Francisco: Wikipedia, The Free Encyclopedia, 2019. — Режим доступа: https://en.wikipedia.org/w/index.php?title=Numerical_analysis&oldid=895278527, свободный. — Online encyclopedia (Дата обращения: 13.05.2019);

3. Numerical methods /John D. Fenton. — 1-е издание. — Vienna: Institute of Hydraulic Engineering and Water Resources Management. Vienna University of Technology, 2019. — 33с.;

4. Numerical Methods for Physicists [Электронный ресурс] / Anthony O’Hare. — Электрон. текстовые дан. — Belton: MMHB. Department of Computer Science and Engineering, 2005. — Режим доступа: http://mars.umhb.edu/~wgt/engr2311/NMfP.pdf, свободный (Дата обращения: 12.05.2019)

Источник