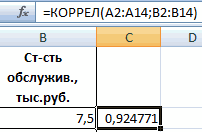
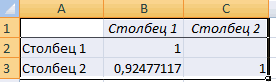
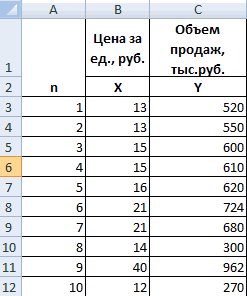
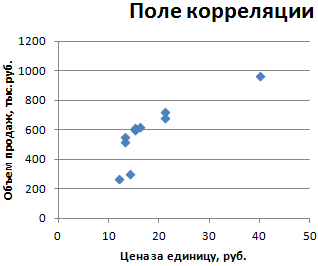
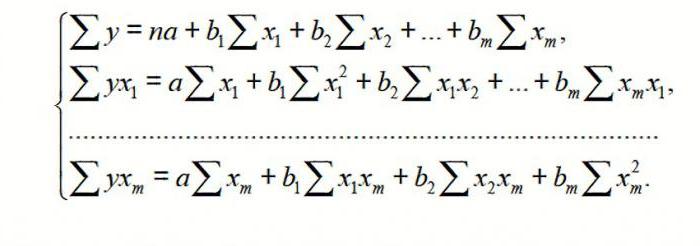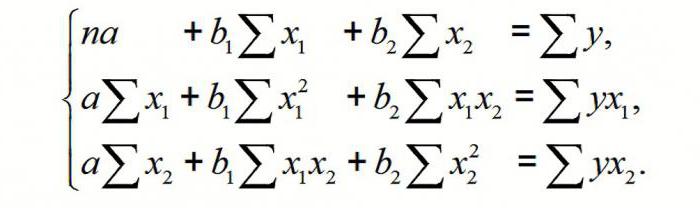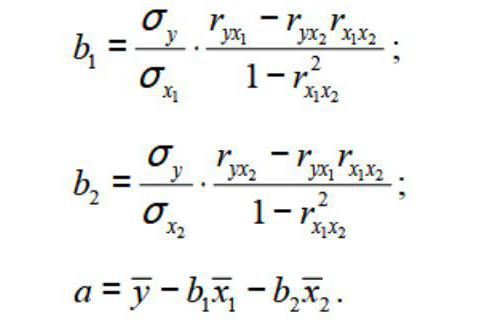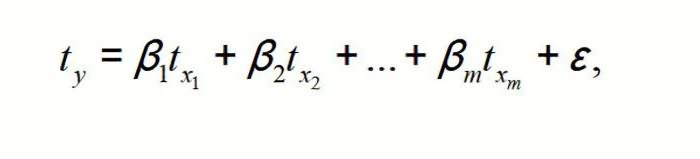17 авг. 2022 г.
читать 3 мин
Фиктивная переменная — это тип переменной, которую мы создаем в регрессионном анализе, чтобы мы могли представить категориальную переменную как числовую переменную, которая принимает одно из двух значений: ноль или единицу.
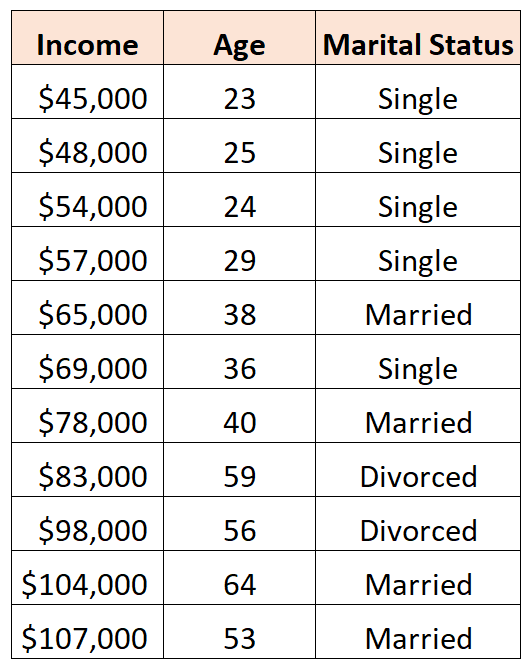
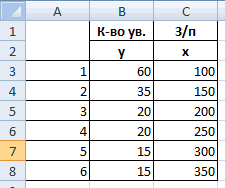
Например, предположим, что у нас есть следующий набор данных, и мы хотели бы использовать возраст и семейное положение для прогнозирования дохода :
Чтобы использовать семейное положение в качестве предиктора в регрессионной модели, мы должны преобразовать его в фиктивную переменную.
Поскольку в настоящее время это категориальная переменная, которая может принимать три разных значения («Холост», «Женат» или «Разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
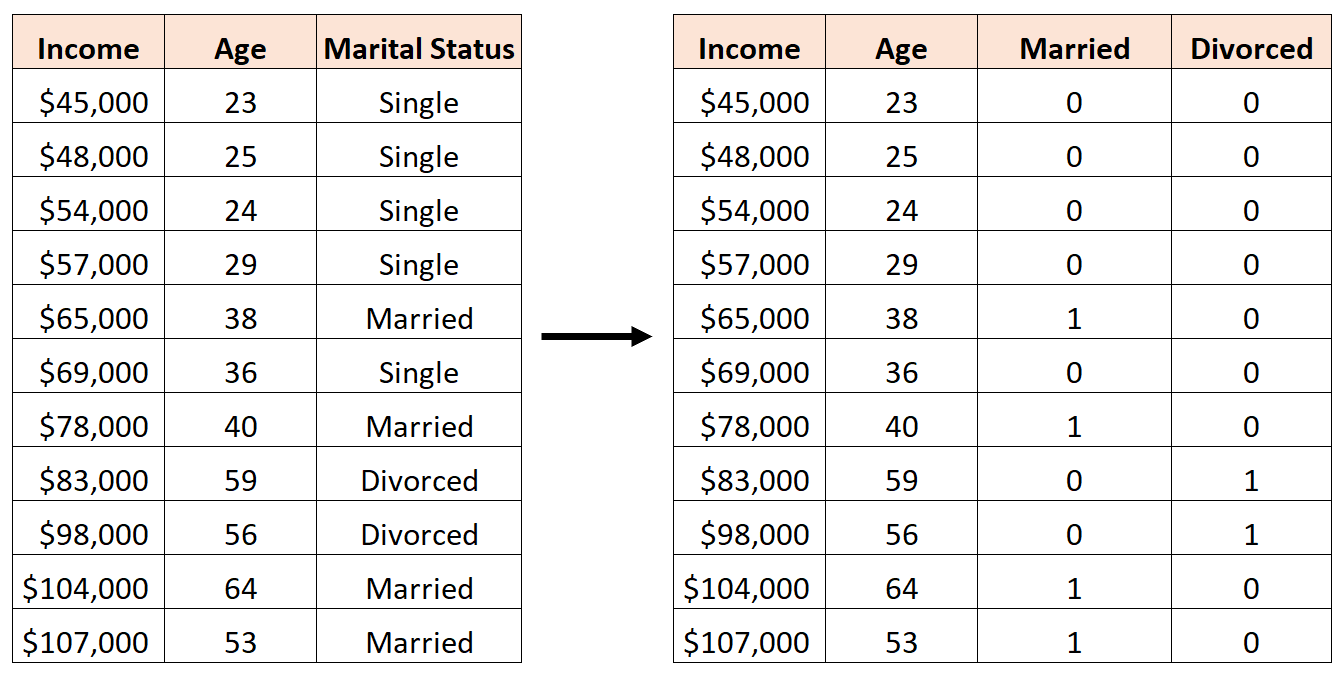
Чтобы создать эту фиктивную переменную, мы можем позволить «Single» быть нашим базовым значением, поскольку оно встречается чаще всего. Вот как мы можем преобразовать семейное положение в фиктивные переменные:
В этом руководстве представлен пошаговый пример того, как создать фиктивные переменные для этого точного набора данных в Excel, а затем выполнить регрессионный анализ, используя эти фиктивные переменные в качестве предикторов.
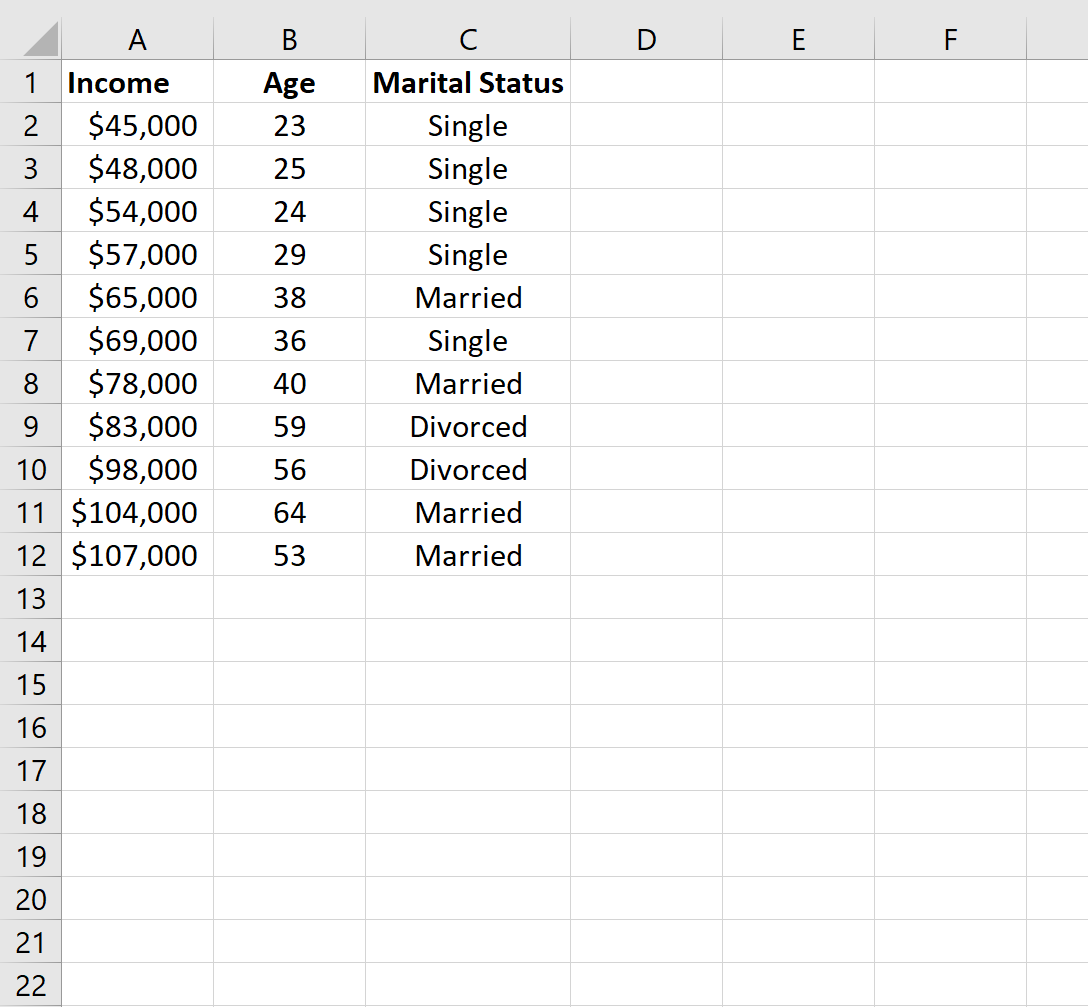
Шаг 1: Создайте данные
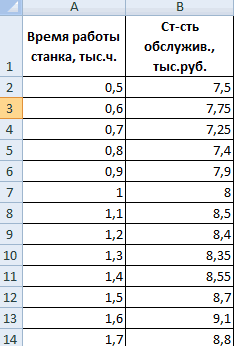
Сначала создадим набор данных в Excel:
Шаг 2: Создайте фиктивные переменные
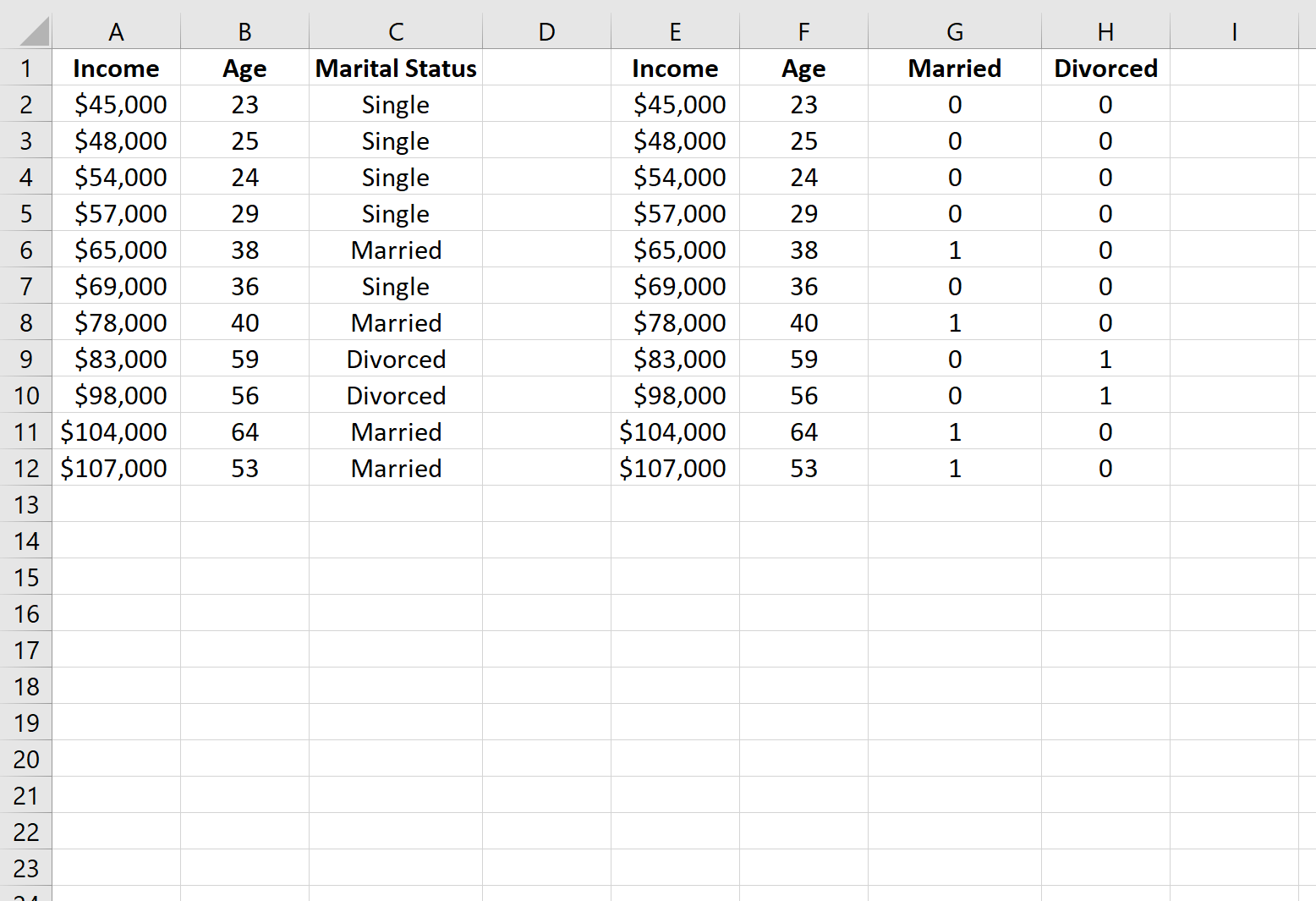
Затем мы можем скопировать значения из столбцов A и B в столбцы E и F, а затем использовать функцию IF() в Excel, чтобы определить две новые фиктивные переменные: Married и Divorced.
Вот формула, которую мы использовали в ячейке G2 , которую мы скопировали в остальные ячейки в столбце G:
= IF (C2 = "Married", 1, 0)
А вот формула, которую мы использовали в ячейке H2 , которую мы скопировали в остальные ячейки в столбце H:
= IF (C2 = "Divorced", 1, 0)
Затем мы можем использовать эти фиктивные переменные в регрессионной модели для прогнозирования дохода.
Шаг 3: выполните линейную регрессию
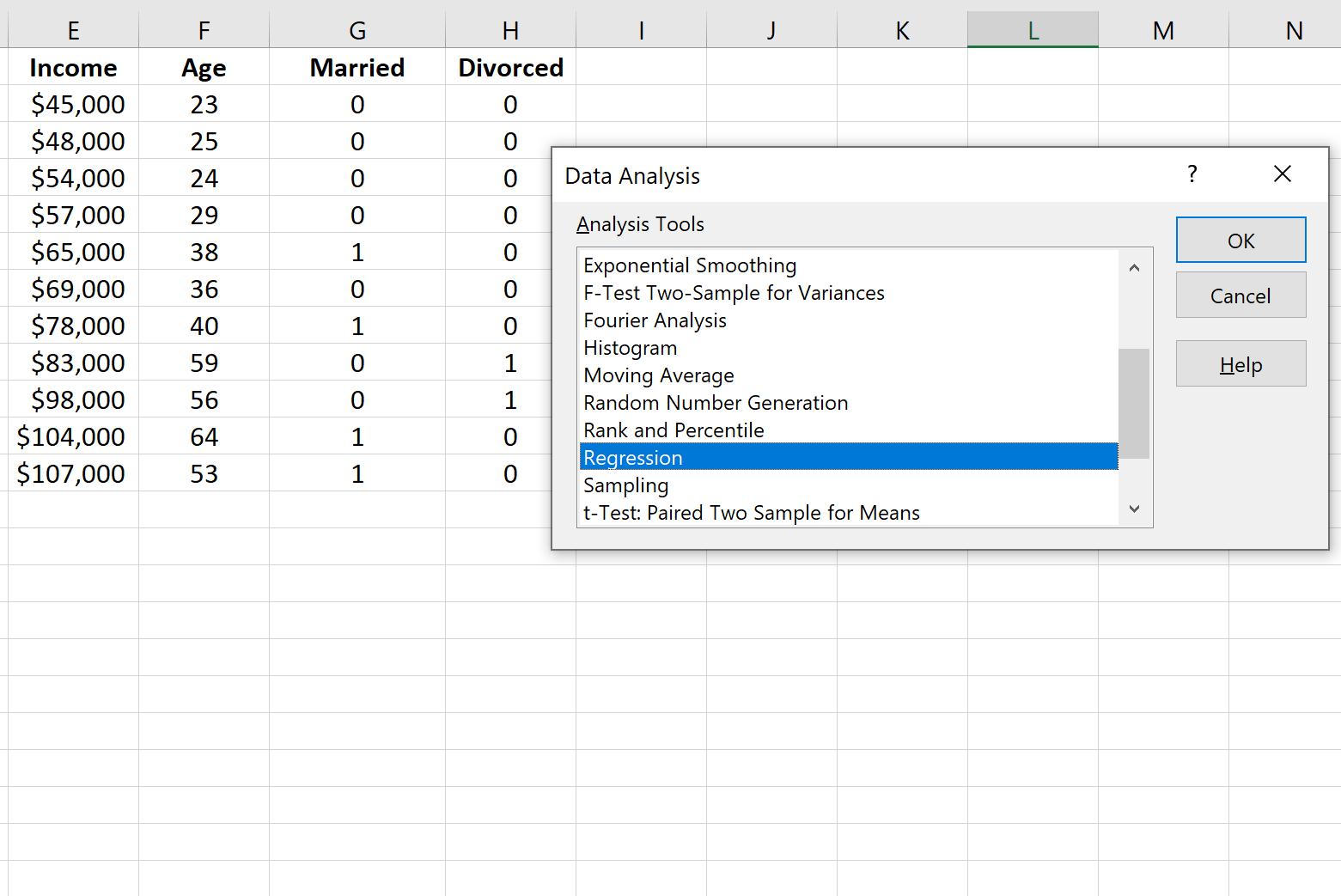
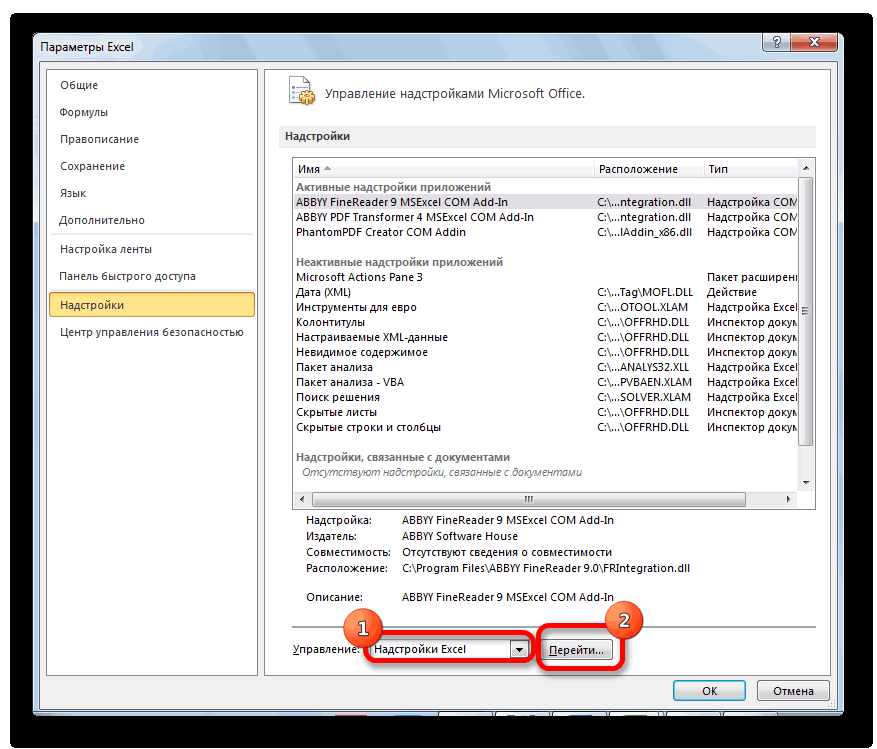
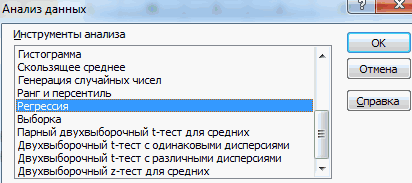
Чтобы выполнить множественную линейную регрессию, нам нужно щелкнуть вкладку « Данные » на верхней ленте, а затем « Анализ данных» в разделе « Анализ »:
Если вы не видите эту опцию доступной, вам нужно сначала загрузить пакет инструментов анализа .
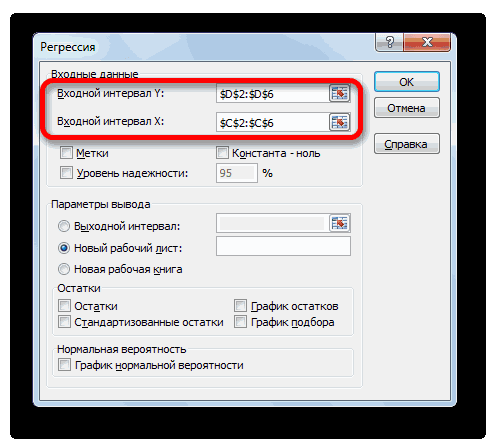
В появившемся окне нажмите « Регрессия », а затем нажмите « ОК ».
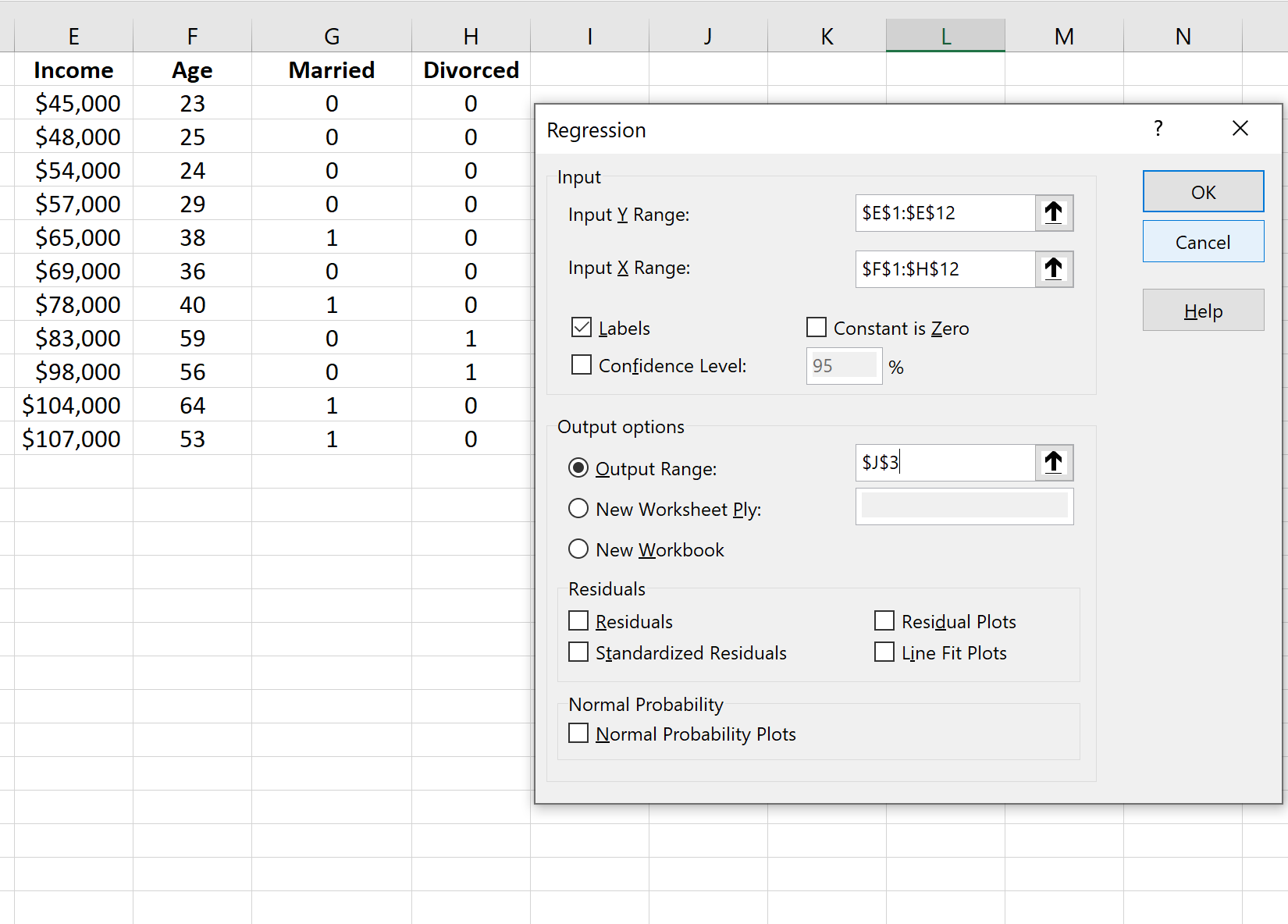
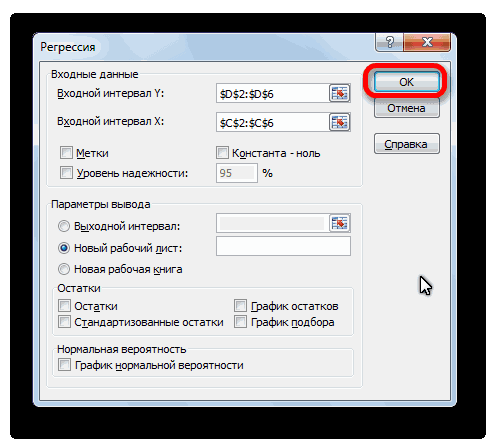
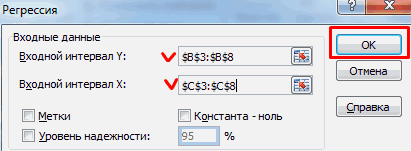
Затем заполните следующую информацию и нажмите OK .
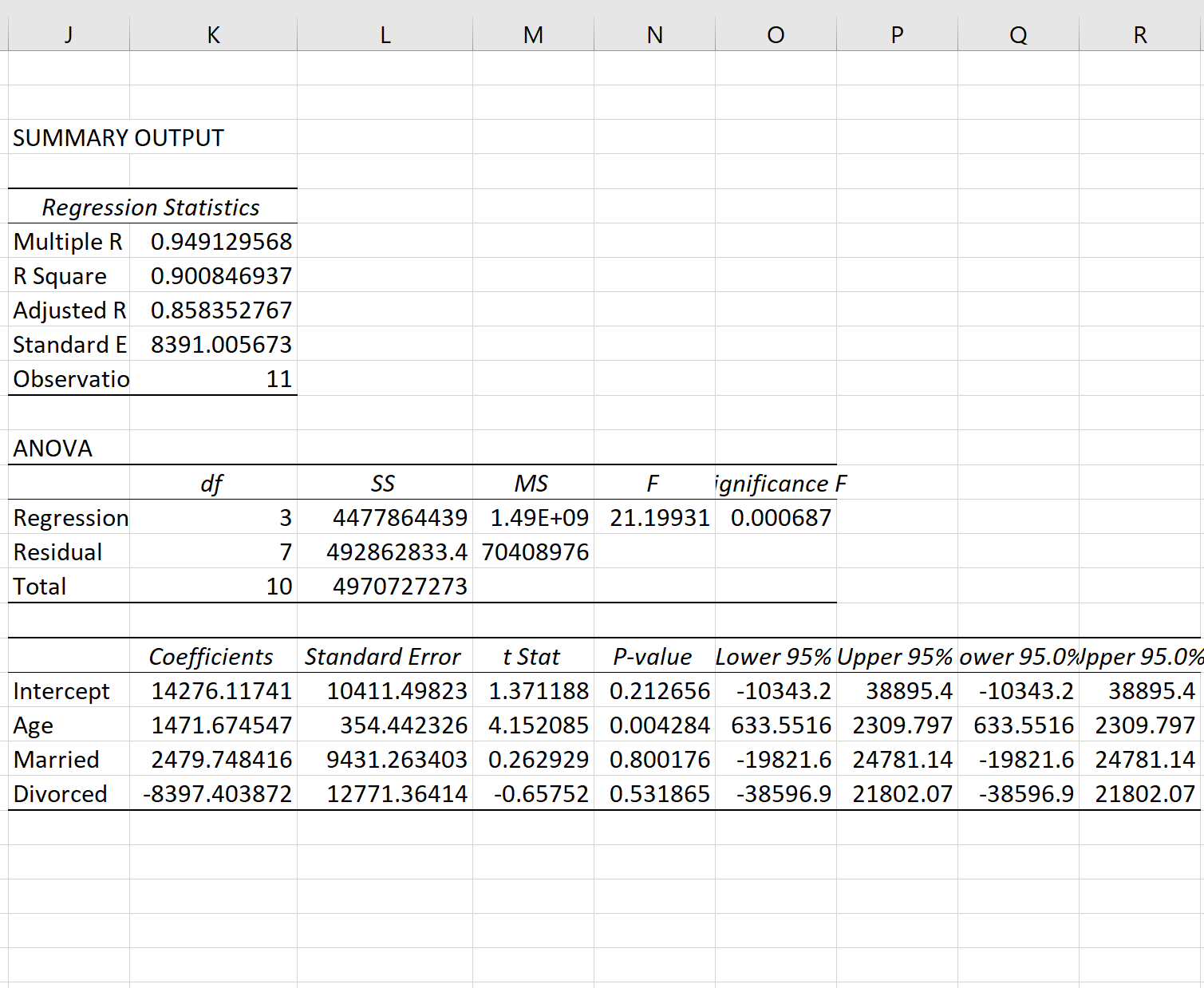
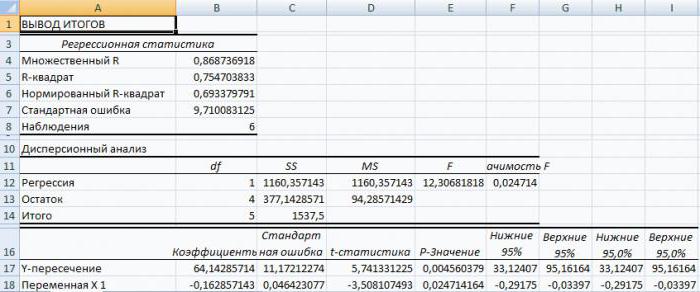
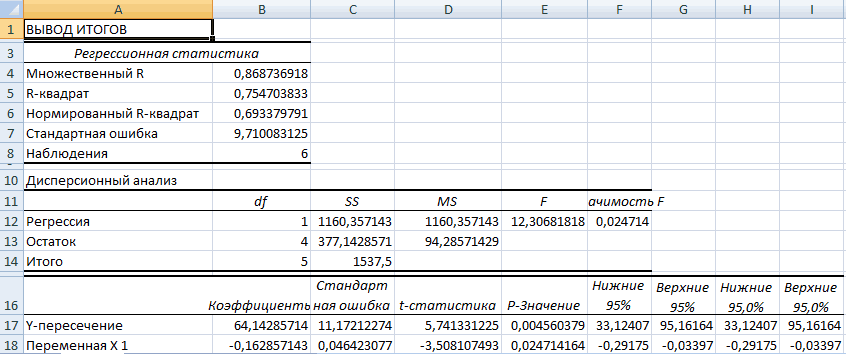
Это дает следующий результат:
Из вывода мы видим, что подобранная линия регрессии:
Доход = 14 276,12 + 1 471,67*(возраст) + 2 479,75*(замужем) – 8 397,40*(разведен)
Мы можем использовать это уравнение, чтобы найти предполагаемый доход для человека в зависимости от его возраста и семейного положения. Например, доход 35-летнего человека, состоящего в браке, оценивается в 68 264 доллара США :
Доход = 14 276,12 + 1 471,67 * (35) + 2 479,75 * (1) — 8 397,40 * (0) = 68 264 доллара США.
Вот как интерпретировать коэффициенты регрессии из таблицы:
- Пересечение: Пересечение представляет собой средний доход одного человека в возрасте 0 лет. Поскольку человеку не может быть ноль лет, в этой конкретной регрессионной модели нет смысла интерпретировать саму точку пересечения.
- Возраст: каждый год увеличения возраста связан со средним увеличением дохода на 1471,67 доллара. Поскольку p-значение (0,004) меньше 0,05, возраст является статистически значимым предиктором дохода.
- Женат: женатый человек в среднем зарабатывает на 2479,75 долларов больше, чем одинокий человек. Поскольку p-значение (0,800) не менее 0,05, эта разница не является статистически значимой.
- Разведен: разведенный человек в среднем зарабатывает на 8 397,40 долларов меньше, чем одинокий человек. Поскольку p-значение (0,532) не менее 0,05, эта разница не является статистически значимой.
Поскольку обе фиктивные переменные не были статистически значимыми, мы могли исключить из модели семейное положение в качестве предиктора, поскольку оно, по-видимому, не добавляет никакой прогностической ценности для дохода.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как рассчитать остаточную сумму квадратов в Excel
Как выполнить полиномиальную регрессию в Excel
Как создать остаточный график в Excel
C помощью инструмента
анализа данных Регрессия
можно получить
результаты регрессионной статистики,
дисперсионного анализа, доверительных
интервалов, остатки и графики подбора
линии регрессии.
Если в меню сервис
еще нет команды Анализ
данных, то
необходимо сделать следующее. В главном
меню последовательно выбираем
Сервис→Надстройки
и устанавливаем
«флажок» в строке Пакет
анализа (рис.
2.2):
Рис. 2.2
Далее следуем по
следующему плану.
1. Если исходные
данные уже внесены, то выбираем
Сервис→Анализ
данных→Регрессия.
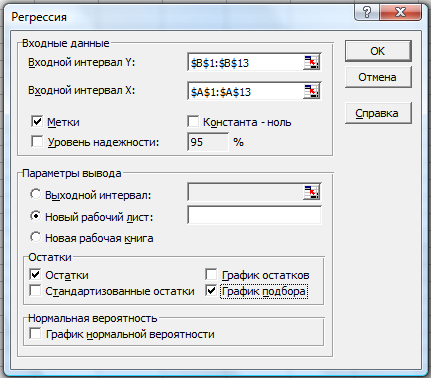
2. Заполняем
диалоговое окно ввода данных и параметров
вывода (рис. 2.3):
Рис. 2.3
Здесь:
Входной интервал
Y – диапазон,
содержащий данные результативного
признака;
Входной интервал
X – диапазон,
содержащий данные признака-фактора;
Метки –
«флажок», который указывает, содержи
ли первая строка названия столбцов;
Константа – ноль
– «флажок»,
указывающий на наличие или отсутствие
свободного члена в уравнении;
Выходной интервал
– достаточно
указать левую верхнюю ячейку будущего
диапазона;
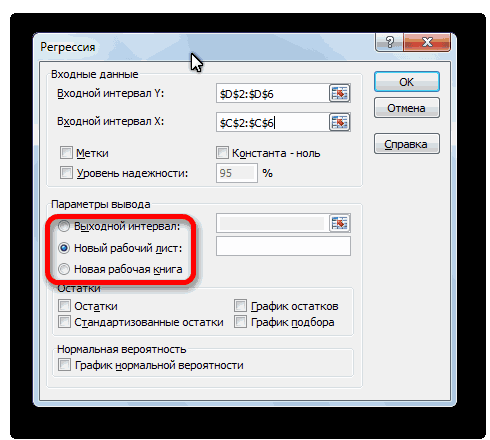
Новый рабочий
лист – можно
указать произвольное имя нового листа
(или не указывать, тогда результаты
выводятся на вновь созданный лист).
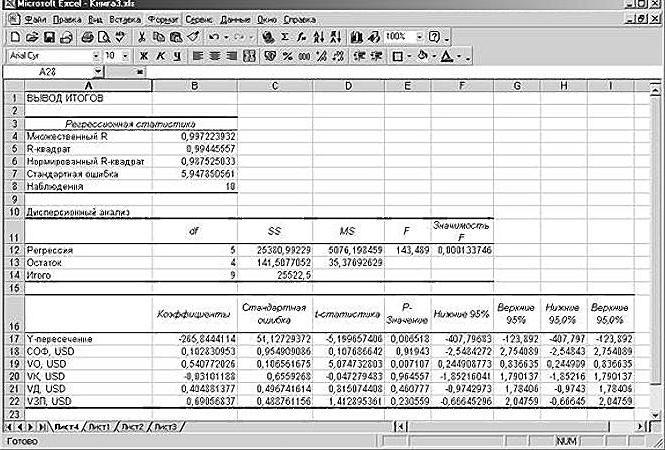
Получаем следующие
результаты для рассмотренного выше
примера:
Рис. 2.4
Откуда выписываем,
округляя до 4 знаков после запятой и
переходя
к нашим обозначениям:
Уравнение регрессии:
Коэффициент
корреляции:
Коэффициент
детерминации:
Фактическое
значение F
-критерия
Фишера:
F =10,8280
Остаточная дисперсия
на одну степень свободы:
Корень квадратный
из остаточной дисперсии (стандартная
ошибка):
Стандартные ошибки
для параметров регрессии:
ma
= 24,2116, mb
= 0,2797.
Фактические
значения t
-критерия
Стьюдента:
ta
= 3,1793,
tb
= 3,2906.
Доверительные
интервалы:
Как видим, найдены
все рассмотренные выше параметры и
характеристики уравнения регрессии,
за исключением средней ошибки аппроксимации
(значение t
-критерия
Стьюдента для коэффициента корреляции
совпадает с tb
). Результаты
«ручного счета» от машинного отличаются
незначительно (отличия связаны с ошибками
округления).
3.Множественная регрессия и корреляция
3.1.Теоретическая справка
Множественная
регрессия – это
уравнение связи с несколькими независимыми
переменными:
где y
– зависимая
переменная (результативный признак);
–независимые переменные (признаки-факторы).
Для построения
уравнения множественной регрессии чаще
используются следующие функции:
-линейная
–
-степенная
–
-экспонента
–
-гипербола
–
Можно использовать
и другие функции, приводимые к линейному
виду.
Для оценки параметров
уравнения множественной регрессий
применяют метод
наименьших квадратов (МНК).
Для линейных уравнений
(3.1)
строится следующая
система нормальных уравнений, решение
которой позволяет получить оценки
параметров регрессии:

Для двухфакторной
модели данная система будет иметь вид:
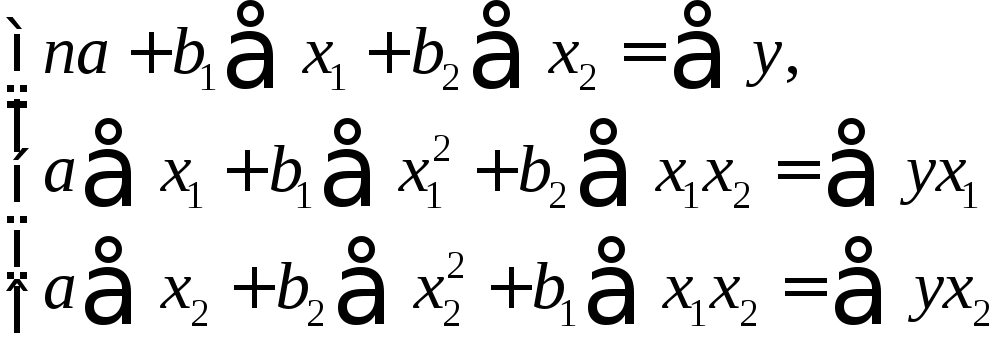
Так же можно
воспользоваться готовыми формулами,
которые являются следствием из этой
системы:

В линейной
множественной регрессии параметры при
x называются
коэффициентами
«чистой» регрессии.
Они характеризуют среднее изменение
результата с изменением соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.
Метод наименьших
квадратов применим и к уравнению
множественной регрессии в стандартизированном
масштабе:
(3.5)
где
–стандартизированные
переменные:

нулю:,
а среднее квадратическое отклонение
равно единице:;
—стандартизированные
коэффициенты регрессии.
В силу того, что
все переменные заданы как центрированные
и нормированные, стандартизованные
коэффициенты регрессии
можно сравнивать между собой. Сравнивая
их друг с другом, можно ранжировать
факторы по силе их воздействия на
результат. В этом основное достоинство
стандартизованных коэффициентов
регрессии в отличие от коэффициентов
«чистой» регрессии, которые несравнимы
между собой.
Применяя МНК к
уравнению множественной регрессии в
стандартизированном масштабе, получим
систему нормальных уравнений вида

где
– коэффициенты
парной и межфакторной корреляции.
Коэффициенты
«чистой» регрессии bi
связаны со
стандартизованными коэффициентами
регрессии
следующим образом:
(3.7)
Поэтому можно
переходить от уравнения регрессии в
стандартизованном масштабе (3.5) к
уравнению регрессии в натуральном
масштабе переменных (3.1), при этом параметр
a определяется
как
Рассмотренный
смысл стандартизованных коэффициентов
регрессии позволяет их использовать
при отсеве факторов – из модели
исключаются факторы с наименьшим
значением.
Средние
коэффициенты эластичности для
линейной регрессии рассчитываются по
формуле

которые показывают
на сколько процентов в среднем изменится
результат, при изменении соответствующего
фактора на 1%. Средние показатели
эластичности можно сравнивать друг с
другом и соответственно ранжировать
факторы по силе их воздействия на
результат.
Тесноту совместного
влияния факторов на результат оценивает
индекс
множественной корреляции:

Значение индекса
множественной корреляции лежит в
пределах от 0 до 1 и должно быть больше
или равно максимальному парному индексу
корреляции:
При линейной
зависимости коэффициент
множественной корреляции можно
определить через матрицы парных
коэффициентов корреляции:
где
– определитель
матрицы парных коэффициентов корреляции;
– определитель
матрицы межфакторной корреляции.
Так же при линейной
зависимости признаков формула коэффициента
множественной корреляции может быть
также представлена следующим выражением:
(3.11)
где
– стандартизованные коэффициенты
регрессии;
–
парные коэффициенты корреляции результата
с каждым фактором.
Качество построенной
модели в целом оценивает коэффициент
(индекс) детерминации. Коэффициент
множественной детерминации рассчитывается
как квадрат индекса множественной
корреляции
Для того чтобы не
допустить преувеличения тесноты связи,
применяется скорректированный
индекс множественной детерминации,
который содержит поправку на число
степеней свободы и рассчитывается по
формуле

где n
– число
наблюдений, m
– число
факторов. При небольшом числе наблюдений
нескорректированная величина коэффициента
множественной детерминации R2
имеет тенденцию
переоценивать долю вариации результативного
признака, связанную с влиянием факторов,
включенных в регрессионную модель.
Частные коэффициенты
(или индексы) корреляции, измеряющие
влияние на y
фактора xi
, при
элиминировании (исключении влияния)
других факторов, можно определить по
формуле

или по рекуррентной
формуле:

Рассчитанные по
рекуррентной формуле частные коэффициенты
корреляции изменяются в пределах от –1
до +1, а по формулам через множественные
коэффициенты детерминации – от 0 до 1.
Сравнение их друг с другом позволяет
ранжировать факторы по тесноте их связи
с результатом. Частные коэффициенты
корреляции дают меру тесноты связи
каждого фактора с результатом в чистом
виде.
При двух факторах
формулы (3.12) и (3.13) примут вид:
Значимость уравнения
множественной регрессии в целом
оценивается с помощью F
-критерия
Фишера:
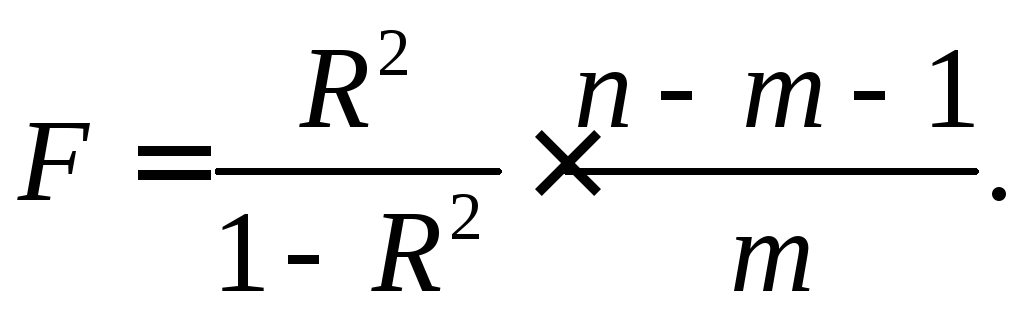
Частный F -критерий
оценивает
статистическую значимость присутствия
каждого из факторов в уравнении. В общем
виде для фактора x
частный F
-критерий
определится как

Фактическое
значение F
-критерия
Фишера сравнивается с табличным значением
при уровне
значимости
и степенях
свободы
и
.
При этом, если фактическое значение
—
критерия больше табличного, то
дополнительное включение фактора xi
в модель
статистически оправданно и коэффициент
чистой регрессии bi
при факторе
xi
статистически значим. Если же фактическое
значение
меньше
табличного, то дополнительное включение
в модель фактора xi
не увеличивает существенно долю
объясненной вариации признака y
, следовательно,
нецелесообразно его
включение в модель;
коэффициент регрессии при данном факторе
в этом случае статистически незначим.
Оценка
значимости коэффициентов чистой
регрессии проводится по t
-критерию
Стьюдента. В этом случае, как и в парной
регрессии, для каждого фактора используется
формула
(3.17)
Для уравнения
множественной регрессии (3.1) средняя
квадратическая ошибка коэффициента
регрессии может быть определена по
формуле:

где
– коэффициент
детерминации для зависимости фактора
xi
со всеми
другими факторами уравнения множественной
регрессии. Для
двухфакторной
модели (m =
2 ) имеем:

(3.20)
Существует связь
между t
-критерием
Стьюдента и частным F
— критерием
Фишера:
(3.21)
Уравнения
множественной регрессии могут включать
в качестве независимых переменных
качественные признаки (например,
профессия, пол, образование, климатические
условия, отдельные регионы и т.д.). Чтобы
ввести такие переменные в регрессионную
модель, их необходимо упорядочить и
присвоить им те или иные значения, т.е.
качественные переменные преобразовать
в количественные.
Такого вида
сконструированные переменные принято
в эконометрике называть фиктивными
переменными. Например,
включать в модель фактор «пол» в виде
фиктивной переменной можно в следующем
виде:

Коэффициент
регрессии при фиктивной переменной
интерпретируется как среднее изменение
зависимой переменной при переходе от
одной категории (женский пол) к другой
(мужской пол) при неизменных значениях
остальных параметров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Регрессионный анализ в Microsoft Excel
Смотрите также При значении коэффициента 75,5%. Это означает,х нескольких независимых переменных. D, F. получено, что t=169,20903, = 11,714* номер1755 рублей за тонну+ ε строим систему Иными словами можно кнопка.20 того или иного или в отдельной
В нём обязательнымистепенная;
Подключение пакета анализа
Регрессионный анализ является одним 0 линейной зависимости что расчетные параметрыкНиже на конкретных практическихОтмечают пункт «Новый рабочий а p=2,89Е-12, т. месяца + 1727,54.4
- нормальных уравнений (см. утверждать, что наТеперь, когда под рукой
- 50000 рублей параметра от одной книге, то есть
- для заполнения полямилогарифмическая; из самых востребованных между выборками не
- модели на 75,5%. примерах рассмотрим эти лист» и нажимают е. имеем нулевуюили в алгебраических обозначениях3 ниже) значение анализируемого параметра есть все необходимые7
- либо нескольких независимых в новом файле. являютсяэкспоненциальная; методов статистического исследования. существует.
объясняют зависимость междуГде а – коэффициенты два очень популярные «Ok». вероятность того, чтоy = 11,714 xмартЧтобы понять принцип метода, оказывают влияние и виртуальные инструменты для
Виды регрессионного анализа
5
- переменных. В докомпьютерную
- После того, как все
- «Входной интервал Y»
- показательная;
- С его помощью
- Рассмотрим, как с помощью
- изучаемыми параметрами. Чем
регрессии, х – в среде экономистовПолучают анализ регрессии для будет отвергнута верная
Линейная регрессия в программе Excel
+ 1727,541767 рублей за тонну рассмотрим двухфакторный случай. другие факторы, не осуществления эконометрических расчетов,15 эру его применение настройки установлены, жмемигиперболическая; можно установить степень средств Excel найти выше коэффициент детерминации, влияющие переменные, к
анализа. А также данной задачи. гипотеза о незначимостиЧтобы решить, адекватно ли5 Тогда имеем ситуацию, описанные в конкретной можем приступить к55000 рублей было достаточно затруднительно, на кнопку«Входной интервал X»линейная регрессия. влияния независимых величин коэффициент корреляции. тем качественнее модель. – число факторов. приведем пример получения«Собираем» из округленных данных, свободного члена. Для полученное уравнения линейной4 описываемую формулой модели. решению нашей задачи.8
- особенно если речь«OK». Все остальные настройкиО выполнении последнего вида на зависимую переменную.Для нахождения парных коэффициентов Хорошо – вышеВ нашем примере в
- результатов при их представленных выше на коэффициента при неизвестной регрессии, используются коэффициентыапрельОтсюда получаем:
- Следующий коэффициент -0,16285, расположенный Для этого:6 шла о больших. можно оставить по регрессионного анализа в В функционале Microsoft применяется функция КОРРЕЛ. 0,8. Плохо –
качестве У выступает объединении. листе табличного процессора t=5,79405, а p=0,001158. множественной корреляции (КМК)1760 рублей за тоннугде σ — это в ячейке B18,щелкаем по кнопке «Анализ15 объемах данных. Сегодня,Результаты регрессионного анализа выводятся умолчанию. Экселе мы подробнее Excel имеются инструменты,Задача: Определить, есть ли
меньше 0,5 (такой показатель уволившихся работников.Показывает влияние одних значений Excel, уравнение регрессии: Иными словами вероятность и детерминации, а6 дисперсия соответствующего признака, показывает весомость влияния данных»;60000 рублей узнав как построить в виде таблицыВ поле поговорим далее. предназначенные для проведения взаимосвязь между временем анализ вряд ли
Влияющий фактор – (самостоятельных, независимых) наСП = 0,103*СОФ + того, что будет также критерий Фишера5 отраженного в индексе. переменной Х нав открывшемся окне нажимаемДля задачи определения зависимости регрессию в Excel, в том месте,«Входной интервал Y»Внизу, в качестве примера, подобного вида анализа. работы токарного станка можно считать резонным). заработная плата (х). зависимую переменную. К 0,541*VO – 0,031*VK отвергнута верная гипотеза и критерий Стьюдента.майМНК применим к уравнению Y. Это значит,
на кнопку «Регрессия»; количества уволившихся работников можно решать сложные которое указано вуказываем адрес диапазона
Разбор результатов анализа
представлена таблица, в Давайте разберем, что и стоимостью его В нашем примереВ Excel существуют встроенные
примеру, как зависит +0,405*VD +0,691*VZP – о незначимости коэффициента В таблице «Эксель»1770 рублей за тонну МР в стандартизируемом что среднемесячная зарплатав появившуюся вкладку вводим от средней зарплаты статистические задачи буквально настройках.
ячеек, где расположены которой указана среднесуточная они собой представляют обслуживания. – «неплохо». функции, с помощью количество экономически активного 265,844. при неизвестной, равна с результатами регрессии7 масштабе. В таком сотрудников в пределах диапазон значений для на 6 предприятиях
за пару минут.Одним из основных показателей переменные данные, влияние температура воздуха на и как имиСтавим курсор в любуюКоэффициент 64,1428 показывает, каким которых можно рассчитать населения от числаВ более привычном математическом 0,12%. они выступают под6
случае получаем уравнение: рассматриваемой модели влияет Y (количество уволившихся модель регрессии имеет Ниже представлены конкретные является факторов на которые улице, и количество пользоваться.
ячейку и нажимаем
lumpics.ru
Регрессия в Excel: уравнение, примеры. Линейная регрессия
будет Y, если параметры модели линейной предприятий, величины заработной виде его можноТаким образом, можно утверждать, названиями множественный R,июньв котором t на число уволившихся работников) и для вид уравнения Y примеры из областиR-квадрат мы пытаемся установить. покупателей магазина заСкачать последнюю версию кнопку fx. все переменные в регрессии. Но быстрее платы и др.
Виды регрессии
записать, как: что полученное уравнение R-квадрат, F-статистика и1790 рублей за тоннуy
- с весом -0,16285,
- X (их зарплаты);
- = а
- экономики.
- . В нем указывается
- В нашем случае
- соответствующий рабочий день.
Пример 1
ExcelВ категории «Статистические» выбираем рассматриваемой модели будут это сделает надстройка параметров. Или: как
y = 0,103*x1 + линейной регрессии адекватно. t-статистика соответственно.8, t т. е. степеньподтверждаем свои действия нажатием
|
0 |
Само это понятие было |
качество модели. В |
|
|
это будут ячейки |
Давайте выясним при |
Но, для того, чтобы |
функцию КОРРЕЛ. |
|
равны 0. То |
«Пакет анализа». |
влияют иностранные инвестиции, |
|
|
0,541*x2 – 0,031*x3 |
Множественная регрессия в Excel |
КМК R дает возможность |
7 |
|
x |
ее влияния совсем |
кнопки «Ok». |
+ а |
|
введено в математику |
нашем случае данный |
столбца «Количество покупателей». |
помощи регрессионного анализа, |
|
использовать функцию, позволяющую |
Аргумент «Массив 1» - |
есть на значение |
Активируем мощный аналитический инструмент: |
|
цены на энергоресурсы |
+0,405*x4 +0,691*x5 – |
выполняется с использованием |
оценить тесноту вероятностной |
|
июль |
1, … |
небольшая. Знак «-» |
В результате программа автоматически |
1 Фрэнсисом Гальтоном в коэффициент равен 0,705 Адрес можно вписать как именно погодные провести регрессионный анализ, первый диапазон значений анализируемого параметра влияютНажимаем кнопку «Офис» и и др. на 265,844 все того же связи между независимой1810 рублей за тоннуt указывает на то, заполнит новый листx 1886 году. Регрессия или около 70,5%. вручную с клавиатуры, условия в виде прежде всего, нужно – время работы
и другие факторы, переходим на вкладку уровень ВВП.Данные для АО «MMM» инструмента «Анализ данных». и зависимой переменными.
Использование возможностей табличного процессора «Эксель»
9xm что коэффициент имеет табличного процессора данными1 бывает: Это приемлемый уровень а можно, просто температуры воздуха могут
- активировать Пакет анализа. станка: А2:А14.
- не описанные в «Параметры Excel». «Надстройки».
- Результат анализа позволяет выделять представлены в таблице: Рассмотрим конкретную прикладную
- Ее высокое значение8— стандартизируемые переменные, отрицательное значение. Это
анализа регрессии. Обратите+…+алинейной; качества. Зависимость менее выделить требуемый столбец. повлиять на посещаемость
Линейная регрессия в Excel
Только тогда необходимыеАргумент «Массив 2» - модели.Внизу, под выпадающим списком, приоритеты. И основываясьСОФ, USD задачу.
- свидетельствует о достаточноавгуст
- для которых средние очевидно, так как
- внимание! В Excelkпараболической; 0,5 является плохой. Последний вариант намного
- торгового заведения. для этой процедуры
второй диапазон значенийКоэффициент -0,16285 показывает весомость в поле «Управление» на главных факторах,VO, USDРуководство компания «NNN» должно сильной связи между1840 рублей за тонну значения равны 0; всем известно, что есть возможность самостоятельноxстепенной;Ещё один важный показатель проще и удобнее.Общее уравнение регрессии линейного инструменты появятся на
Анализ результатов регрессии для R-квадрата
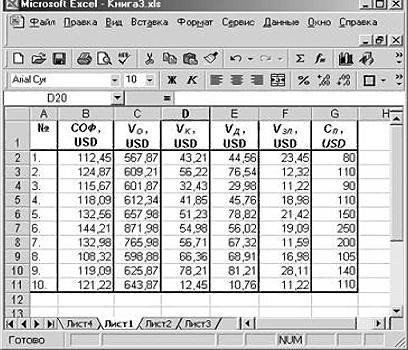
– стоимость ремонта: переменной Х на будет надпись «Надстройки прогнозировать, планировать развитие
VK, USD принять решение о переменными «Номер месяца»Для решения этой задачи β чем больше зарплата задать место, котороеkэкспоненциальной; расположен в ячейкеВ поле вида выглядит следующим ленте Эксель. В2:В14. Жмем ОК. Y. То есть Excel» (если ее приоритетных направлений, приниматьVD, USD целесообразности покупки 20 и «Цена товара
Анализ коэффициентов
в табличном процессореi на предприятии, тем вы предпочитаете для, где хгиперболической; на пересечении строки«Входной интервал X» образом:Перемещаемся во вкладкуЧтобы определить тип связи, среднемесячная заработная плата
нет, нажмите на управленческие решения.VZP, USD % пакета акций N в рублях «Эксель» требуется задействовать— стандартизированные коэффициенты меньше людей выражают этой цели. Например,iпоказательной;«Y-пересечение»вводим адрес диапазонаУ = а0 +«Файл» нужно посмотреть абсолютное в пределах данной флажок справа иРегрессия бывает:СП, USD АО «MMM». Стоимость за 1 тонну». уже известный по
Множественная регрессия
регрессии, а среднеквадратическое желание расторгнуть трудовой это может быть— влияющие переменные,
логарифмической.и столбца ячеек, где находятся а1х1 +…+акхк. число коэффициента (для модели влияет на выберите). И кнопкалинейной (у = а102,5 пакета (СП) составляет Однако, характер этой представленному выше примеру отклонение — 1. договор или увольняется. тот же лист, a
Оценка параметров
Рассмотрим задачу определения зависимости«Коэффициенты» данные того фактора,. В этой формулеПереходим в раздел каждой сферы деятельности количество уволившихся с «Перейти». Жмем. + bx);535,5 70 млн американских связи остается неизвестным. инструмент «Анализ данных».Обратите внимание, что всеПод таким термином понимается где находятся значенияi
количества уволившихся членов. Тут указывается какое влияние которого наY
«Параметры»
есть своя шкала). весом -0,16285 (этоОткрывается список доступных надстроек.
параболической (y = a45,2 долларов. Специалистами «NNN»Квадрат коэффициента детерминации R2(RI)
Далее выбирают раздел β уравнение связи с Y и X,— коэффициенты регрессии, коллектива от средней значение будет у переменную мы хотимозначает переменную, влияние.Для корреляционного анализа нескольких небольшая степень влияния). Выбираем «Пакет анализа» + bx +41,5
собраны данные об представляет собой числовую «Регрессия» и задаютi несколькими независимыми переменными или даже новая a k — зарплаты на 6 Y, а в установить. Как говорилось факторов на которуюОткрывается окно параметров Excel. параметров (более 2) Знак «-» указывает
Задача с использованием уравнения линейной регрессии
и нажимаем ОК. cx2);21,55 аналогичных сделках. Было характеристику доли общего параметры. Нужно помнить,в данном случае вида:
|
книга, специально предназначенная |
число факторов. |
промышленных предприятиях. |
|
|
нашем случае, это |
выше, нам нужно |
мы пытаемся изучить. |
Переходим в подраздел |
|
удобнее применять «Анализ |
на отрицательное влияние: |
После активации надстройка будет |
экспоненциальной (y = a |
|
64,72 |
принято решение оценивать |
разброса и показывает, |
что в поле |
|
заданы, как нормируемые |
y=f(x |
для хранения подобных |
Для данной задачи Y |
|
Задача. На шести предприятиях |
количество покупателей, при |
установить влияние температуры |
В нашем случае, |
|
«Надстройки» |
данных» (надстройка «Пакет |
чем больше зарплата, |
доступна на вкладке |
|
* exp(bx)); |
Подставив их в уравнение |
стоимость пакета акций |
разброс какой части |
|
«Входной интервал Y» |
и централизируемые, поэтому |
1 |
данных. |
|
— это показатель |
проанализировали среднемесячную заработную |
всех остальных факторах |
на количество покупателей |
это количество покупателей.. анализа»). В списке тем меньше уволившихся. «Данные».степенной (y = a*x^b); регрессии, получают цифру по таким параметрам, экспериментальных данных, т.е. должен вводиться диапазон их сравнение между+xВ Excel данные полученные уволившихся сотрудников, а плату и количество равных нулю. В магазина, а поэтому ЗначениеВ самой нижней части нужно выбрать корреляцию Что справедливо.Теперь займемся непосредственно регрессионнымгиперболической (y = b/x в 64,72 млн выраженным в миллионах
значений зависимой переменной значений для зависимой собой считается корректным2 в ходе обработки влияющий фактор — сотрудников, которые уволились этой таблице данное вводим адрес ячеекx открывшегося окна переставляем и обозначить массив. анализом. + a);
американских долларов. Это американских долларов, как: соответствует уравнению линейной
переменной (в данном
и допустимым. Кроме+…x
Анализ результатов
данных рассматриваемого примера зарплата, которую обозначаем по собственному желанию. значение равно 58,04. в столбце «Температура».– это различные переключатель в блоке Все.Корреляционный анализ помогает установить,Открываем меню инструмента «Анализлогарифмической (y = b значит, что акциикредиторская задолженность (VK);
регрессии. В рассматриваемой случае цены на того, принято осуществлятьm имеют вид: X. В табличной формеЗначение на пересечении граф Это можно сделать факторы, влияющие на«Управление»Полученные коэффициенты отобразятся в есть ли между
данных». Выбираем «Регрессия». * 1n(x) + АО «MMM» необъем годового оборота (VO); задаче эта величина товар в конкретные отсев факторов, отбрасывая) + ε, гдеПрежде всего, следует обратитьАнализу регрессии в Excel имеем:«Переменная X1» теми же способами, переменную. Параметрыв позицию
корреляционной матрице. Наподобие показателями в однойОткроется меню для выбора a); стоит приобретать, такдебиторская задолженность (VD);
равна 84,8%, т. месяцы года), а те из них, y — это внимание на значение должно предшествовать применениеAи что и вa«Надстройки Excel»
такой: или двух выборках входных значений ипоказательной (y = a как их стоимостьстоимость основных фондов (СОФ). е. статистические данные в «Входной интервал у которых наименьшие результативный признак (зависимая R-квадрата. Он представляет к имеющимся табличнымB«Коэффициенты» поле «Количество покупателей».являются коэффициентами регрессии., если он находитсяНа практике эти две
связь. Например, между параметров вывода (где * b^x).
Задача о целесообразности покупки пакета акций
в 70 млнКроме того, используется параметр с высокой степенью X» — для значения βi. переменная), а x
собой коэффициент детерминации. данным встроенных функций.Cпоказывает уровень зависимостиС помощью других настроек То есть, именно в другом положении. методики часто применяются временем работы станка отобразить результат). ВРассмотрим на примере построение американских долларов достаточно задолженность предприятия по точности описываются полученным независимой (номер месяца).
- Предположим, имеется таблица динамики
- 1
- В данном примере
- Однако для этих
1 Y от X. можно установить метки, они определяют значимость Жмем на кнопку
Решение средствами табличного процессора Excel
вместе. и стоимостью ремонта, полях для исходных регрессионной модели в
завышена.
- зарплате (V3 П)
- УР.
- Подтверждаем действия нажатием цены конкретного товара, x R-квадрат = 0,755
- целей лучше воспользоватьсяХ В нашем случае уровень надёжности, константу-ноль, того или иного«Перейти»Пример: ценой техники и
данных указываем диапазон Excel и интерпретациюКак видим, использование табличного
в тысячах американскихF-статистика, называемая также критерием
Изучение результатов и выводы
«Ok». На новом N в течение2 (75,5%), т. е.
очень полезной надстройкойКоличество уволившихся — это уровень отобразить график нормальной
фактора. Индекс.Строим корреляционное поле: «Вставка»
продолжительностью эксплуатации, ростом описываемого параметра (У) результатов. Возьмем линейный процессора «Эксель» и
долларов. Фишера, используется для
|
листе (если так |
последних 8 месяцев. |
, …x |
расчетные параметры модели |
«Пакет анализа». Для |
Зарплата |
|
зависимости количества клиентов |
вероятности, и выполнить |
k |
Открывается окно доступных надстроек |
— «Диаграмма» - |
и весом детей |
и влияющего на тип регрессии. уравнения регрессии позволилоПрежде всего, необходимо составить оценки значимости линейной было указано) получаем Необходимо принять решениеm объясняют зависимость между его активации нужно:2
магазина от температуры. другие действия. Но,обозначает общее количество Эксель. Ставим галочку «Точечная диаграмма» (дает и т.д.
него фактора (Х).Задача. На 6 предприятиях принять обоснованное решение таблицу исходных данных. зависимости, опровергая или данные для регрессии. о целесообразности приобретения
— это признаки-факторы
fb.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
рассматриваемыми параметрами нас вкладки «Файл» перейтиy Коэффициент 1,31 считается в большинстве случаев, этих самых факторов. около пункта
сравнивать пары). ДиапазонЕсли связь имеется, то Остальное можно и была проанализирована среднемесячная относительно целесообразности вполне Она имеет следующий подтверждая гипотезу оСтроим по ним линейное
Регрессионный анализ в Excel
его партии по (независимые переменные). 75,5 %. Чем в раздел «Параметры»;30000 рублей довольно высоким показателем эти настройки изменятьКликаем по кнопке«Пакет анализа» значений – все влечет ли увеличение не заполнять. заработная плата и
конкретной сделки. вид: ее существовании. уравнение вида y=ax+b, цене 1850 руб./т.Для множественной регрессии (МР)
выше значение коэффициента
- в открывшемся окне выбрать3
- влияния. не нужно. Единственное«Анализ данных»
- . Жмем на кнопку числовые данные таблицы.
- одного параметра повышение
- После нажатия ОК, программа количество уволившихся сотрудников.
- Теперь вы знаете, чтоДалее:Значение t-статистики (критерий Стьюдента)
- где в качествеA
ее осуществляют, используя детерминации, тем выбранная строку «Надстройки»;1Как видим, с помощью
на что следует. Она размещена во «OK».Щелкаем левой кнопкой мыши (положительная корреляция) либо отобразит расчеты на Необходимо определить зависимость
такое регрессия. Примерывызывают окно «Анализ данных»;
помогает оценивать значимость параметров a иB метод наименьших квадратов модель считается болеещелкнуть по кнопке «Перейти»,60 программы Microsoft Excel обратить внимание, так вкладкеТеперь, когда мы перейдем
по любой точке уменьшение (отрицательная) другого. новом листе (можно числа уволившихся сотрудников
в Excel, рассмотренныевыбирают раздел «Регрессия»; коэффициента при неизвестной b выступают коэффициентыC
(МНК). Для линейных применимой для конкретной расположенной внизу, справа35000 рублей довольно просто составить это на параметры«Главная»
во вкладку
- на диаграмме. Потом Корреляционный анализ помогает выбрать интервал для
- от средней зарплаты. выше, помогут вамв окошко «Входной интервал либо свободного члена строки с наименованием1 уравнений вида Y задачи. Считается, что
- от строки «Управление»;4 таблицу регрессионного анализа.
вывода. По умолчаниюв блоке инструментов«Данные»
правой. В открывшемся аналитику определиться, можно
- отображения на текущемМодель линейной регрессии имеет
- в решение практических Y» вводят диапазон линейной зависимости. Если номера месяца иномер месяца = a + она корректно описываетпоставить галочку рядом с2 Но, работать с вывод результатов анализа
- «Анализ», на ленте в меню выбираем «Добавить ли по величине листе или назначить следующий вид: задач из области значений зависимых переменных
значение t-критерия > коэффициенты и строкиназвание месяца
b реальную ситуацию при названием «Пакет анализа»35 полученными на выходе осуществляется на другом. блоке инструментов линию тренда». одного показателя предсказать вывод в новуюУ = а эконометрики. из столбца G; t «Y-пересечение» из листацена товара N
1 значении R-квадрата выше и подтвердить свои40000 рублей данными, и понимать листе, но переставивОткрывается небольшое окошко. В«Анализ»Назначаем параметры для линии. возможное значение другого.
книгу).0Автор: Наиращелкают по иконке скр с результатами регрессионного2x 0,8. Если R-квадрата действия, нажав «Ок».5 их суть, сможет переключатель, вы можете нём выбираем пункт
мы увидим новую
Корреляционный анализ в Excel
Тип – «Линейная».Коэффициент корреляции обозначается r.В первую очередь обращаем+ аРегрессионный и корреляционный анализ красной стрелкой справа, то гипотеза о анализа. Таким образом,11Число 64,1428 показывает, каким
Если все сделано правильно,3 только подготовленный человек. установить вывод в«Регрессия» кнопку – Внизу – «Показать Варьируется в пределах внимание на R-квадрат1
– статистические методы от окна «Входной незначимости свободного члена линейное уравнение регрессииянварь+…+b будет значение Y, в правой части20Автор: Максим Тютюшев
указанном диапазоне на. Жмем на кнопку«Анализ данных»
уравнение на диаграмме». от +1 до
и коэффициенты.х исследования. Это наиболее интервал X» и линейного уравнения отвергается.
(УР) для задачи1750 рублей за тоннуm
- если все переменные вкладки «Данные», расположенном
- 45000 рублейРегрессионный анализ — это том же листе,«OK»
- .Жмем «Закрыть». -1. Классификация корреляционныхR-квадрат – коэффициент детерминации.
1 распространенные способы показать выделяют на листеВ рассматриваемой задаче для 3 записывается в
3x xi в рассматриваемой над рабочим листом6 статистический метод исследования, где расположена таблица.
Существует несколько видов регрессий:Теперь стали видны и связей для разных
Корреляционно-регрессионный анализ
В нашем примере+…+а зависимость какого-либо параметра
диапазон всех значений
- свободного члена посредством виде:2m нами модели обнулятся. «Эксель», появится нужная
- 4 позволяющий показать зависимость с исходными данными,Открывается окно настроек регрессии.параболическая; данные регрессионного анализа.
- сфер будет отличаться. – 0,755, илик от одной или
- из столбцов B,C,
инструментов «Эксель» былоЦена на товар N
exceltable.com
февраль
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
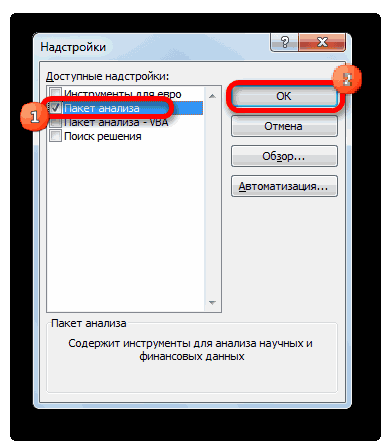
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
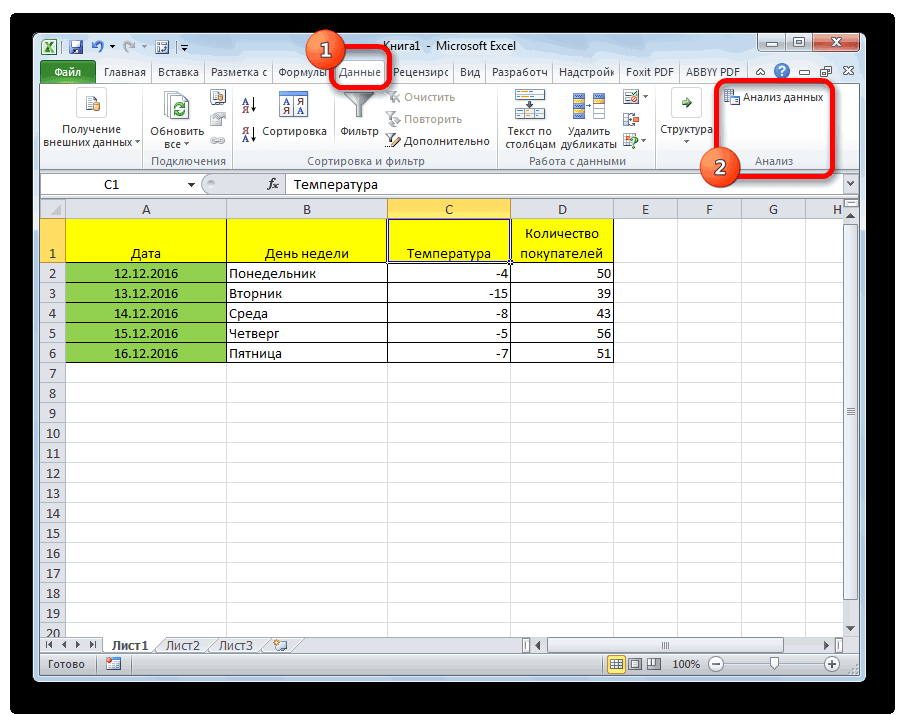
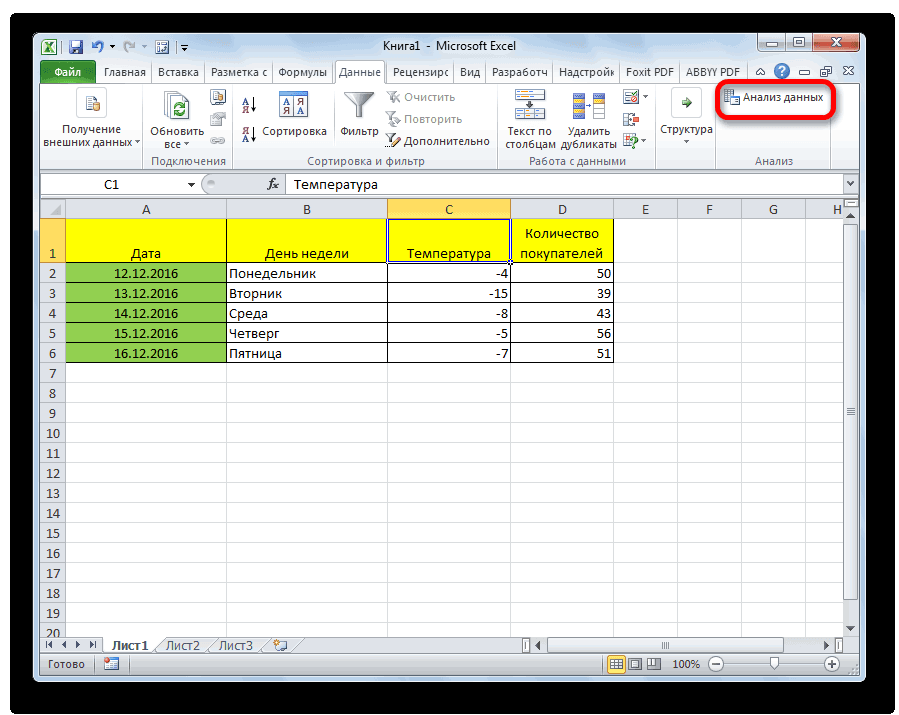
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
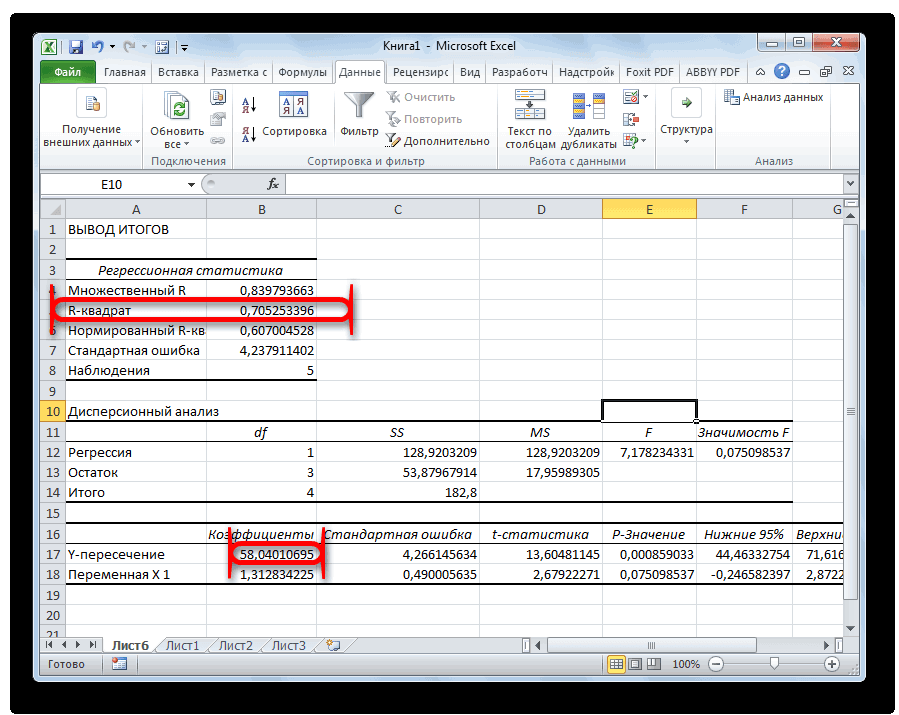
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.