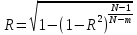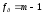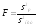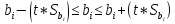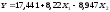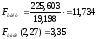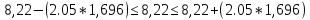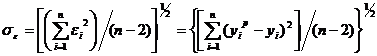Министерство
образования и науки Российской Федерации
Федеральное
агентство по образованию
Саратовский
государственный технический университет
Балаковский
институт техники, технологии и управления
Методическое
указание к выполнению лабораторной
работы
по дисциплине
“Идентификация и диагностика систем
управления”
для студентов
специальности 220201
очной и заочной
форм обучения
Одобрено
редакционно-издательским
советом
Балаковского
института техники,
технологии
и управления
Балаково 2010
Цель работы:
Освоение регрессионного анализа в
пакете EXCEL.
ОСНОВНЫЕ ПОНЯТИЯ
Задачами
регрессионного анализа являются:
установление формы зависимости между
переменными, оценка функций регрессии,
оценка неизвестных значений зависимой
переменной (прогноз).
Односторонняя
зависимость случайной зависимой
переменной Y
от одной или нескольких независимых
переменных Х
называется объясняющей
регрессией.
Такая
зависимость может возникать тогда,
когда при каждом фиксированном значении
X,
соответствующее значение Y
подвержено случайному разбросу под
воздействием неконтролируемых факторов.
Такая зависимость Y(X)
называется регрессионной.
Она может
быть представлена в виде модельного
уравнения регрессии:
(1)
где
— случайная переменная характеризующая
отклонение функции регрессии.
Линейный
регрессионный анализ
— это анализ, для которого функция f(X)
линейна относительно оцениваемых
факторов. Уравнение линейной регрессии
имеет вид:
(2)
Регрессионный
анализ включает в себя две основные
компоненты:
1. оценка вектора
коэффициентов с помощью метода наименьших
квадратов:

2. дисперсионный
анализ.
Предпосылки
регрессионный анализ:
-
чтобы количество
экспериментальных данных было больше
либо равно 30 на один вход; -
распределение
выходной величины должно быть нормальным; -
в процессе
эксперимента дисперсия выходной
величины Y
не меняется:
;
-
переменная X
изменяется с пренебрежительно малыми
ошибками, то есть является детерменированой; -
выходные переменные
Y1,
Y2,
… Yn
стохастически независимы между собой:
;
-
дискретность
проведения экспериментов во времени
берется
таким образом, чтобы последовательно
взятые значения Y1,
Y2,
… Yn
были стохастически независимы, то есть
больше времени затухания автокорреляционной
функции; -
учет динамики в
регрессионном анализе производится в
виде транспортного запаздывания,
которое определяется как время нахождения
максимума взаимно корреляционной
функции X
и Y.
На основании этих
предпосылок получают уравнение
регрессионной модели методом наименьших
квадратов.
Задача дисперсионного
анализа заключается в определении той
части экспериментальных данных, которая
описывается регрессионной моделью
(определяется коэффициент детерминации
R2
),
а также определение адекватности
регрессионной модели. Для этого
используется основное уравнение
дисперсионного анализа, которое имеет
вид:
(3)
где

сумма квадратичных отклонений
характеризует разброс значений выходной
величины Y
вокруг его среднего значения;
— остаточная
сумма отклонений используется в качестве
критерия МНК;
сумма
обусловленная регрессией.
Коэффициент
детерминации R2
определяется
соотношением суммы обусловленной
регрессией и остаточной
суммы отклонений:
(4)
Коэффициент
детерминации изменяется от 0 до 1:
При
коэффициент детерминации
а при
коэффициент детерминации

Чем ближе коэффициент детерминации к
1, тем точнее регрессионная модель.
При малых объемах
выборки используется коэффициент
множественной корреляции:
,
(5)
где N
– количество выборки; m
– количество входов.
Для оценки
адекватности регрессионной модели
используется критерий Фишера, который
определяется отношением дисперсии
обусловленной регрессией и остаточной
дисперсией:

(6)
Дисперсия,
обусловленная регрессией — среднее
значение квадратов отклонения
обусловленных регрессией определяется
выражением:
(7)
где fр
— число
степеней свободы суммы обусловленной
регрессией:

(8)
где m
– число
коэффициентов уравнения регрессии.
Остаточная дисперсия
определяется выражением:
(9)
где fост
— число
степеней свободы остаточной суммы:

(10)
где N
— число
экспериментов.
Для определения
адекватности регрессионной модели
сравнивают F-отношение,
рассчитанное по выражению (6), со значением
критерия Фишера выбранного из таблиц
для принятого уровня значимости
и числа степеней свободы сравниваемых
дисперсий


Если

то при соответствующем уровне значимости
регрессионная модель не адекватна.
Если

то при соответствующем уровне значимости
регрессионная модель адекватна.
Результаты
дисперсионного анализа сводятся в
таблицу 1.
Таблица
1.
Дисперсионный
анализ
|
SS |
f |
MS |
F |
P— |
F |
|
|
регрессия |
|
|
|
|
||
|
остатки |
|
|
|
|||
|
Итого |
|
|
Интерпретация
результатов:
SS
— сумма квадратов; f
— число
степеней свободы; MS
— средний квадрат отклонений (дисперсия);
F—
расчетное значение отношения Фишера;
P—уровень
значимости для вычисленного значения
F;
Fкрит
— табличное значение отношения Фишера.
Если регрессионная
модель адекватна, определяют значимость
коэффициентов регрессии. Для проверки
значимости анализируется отношение
коэффициента регрессии и его
среднеквадратичного отклонения. Это
отношение является распределением
Стьюдента, то есть для определения
значимости используем t
– критерий:
(11)
где

,

значение коэффициента и его
среднеквадратичное отклонение.
Для определения
значимости коэффициента сравнивают
расчетное и табличное значение t
– критерия. Табличное значение t
– критерия определяется степенью
свободы

значением заданной вероятности Р
: tтаб.
(
Р).
Если tрас.>tтаб.,
то коэффициент bi
является
значимым.
Доверительный
интервал определяется по формуле:
.
(12)
Если коэффициент
регрессии незначим, то соответствующий
ему входной фактор несущественно влияет
на выходную величину и его можно исключить
из регрессионной модели.
ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ
-
Исходные данные
взять в таблицах(2,3) согласно варианту
(по номеру студента в журнале). -
Ввести исходные
данные в таблицу в пакете Excel. -
Подготовить два
столбца для ввода расчетных значений
Y
и остатков. -
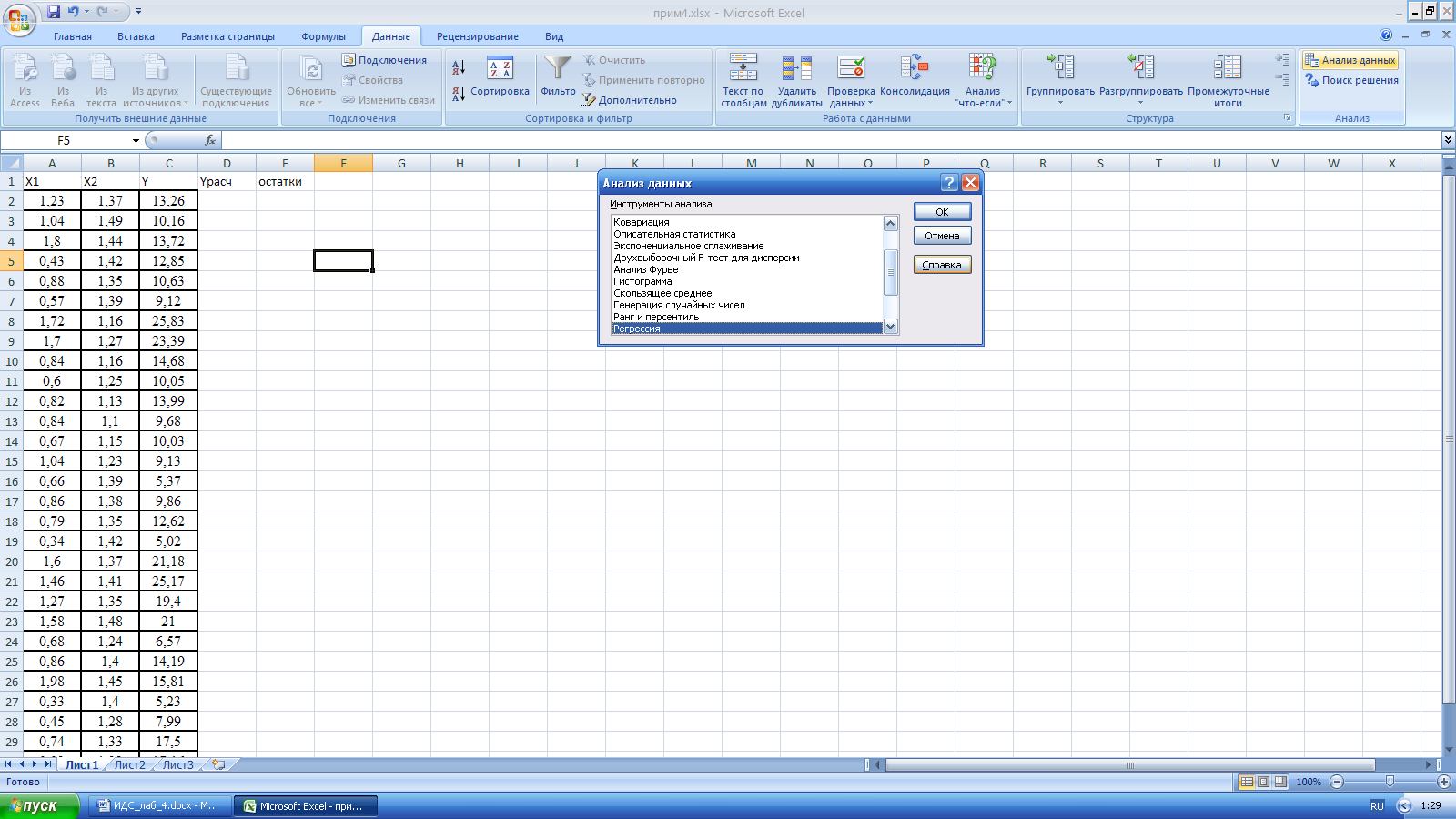
Вызвать программу
«Регрессия»: Данные/ Анализ данных/
Регрессия. Диалоговое окно «Анализ
данных» представлено на рисунке 1.
Рис. 1. Диалоговое окно «Анализ данных».
-
Ввести в диалоговое
окно «Регрессия» адреса исходных
данных:
-
входной интервал
Y,
входной интервал X
(3 столбца), -
установить уровень
надежности 95%, -
в опции «Выходной
интервал, указать левую верхнюю ячейку
места вывода данных регрессионного
анализа (первую ячейку на 2-странице
рабочего листа), -
включить опции
«Остатки» и «График остатков», -
нажать кнопку ОК
для запуска регрессионного анализа.
Диалоговое окно «Регрессия» представлено
на рисунке 2.
Рис. 2. Диалоговое окно
«Регрессия».
-
Excel выведет четыре
таблицы и два графика зависимости
остатков от переменных Х1
и Х2. -
Построить графики
для Yэксп,
Yрасч
и график ошибки прогноза (остатка). -
По полученным
графикам оценить правильность модели
по входам Х1,
Х2. -
Рассчитать
коэффициент множественной корреляции,
расчетные значения t-критериев,
доверительные интервалы коэффициентов
регрессии по выражениям (5,11,12). -
Сделать выводы
по результатам регрессионного анализа. -
Подготовить отчет
по работе.
ПРИМЕР ВЫПОЛНЕНИЯ
РАБОТЫ
Результаты
регрессионного анализа представлены
на рисунке 3.
Графики зависимости
остатков от переменных Х1
и Х2 представлены
на рисунке 4.
Графики расчетной
и экспериментальной выходной величины,
и график ошибки прогноза представлены
на рисунке 5.
Рис. 3. Пример регрессионного анализа в
пакете EXCEL
Рис.4 . Графики остатков переменных Х1,
Х2
Рис. 5. Графики Yэксп,
Yрасч и
ошибки прогноза (остатки).
По результатам
регрессионного анализа можно сказать:
-
Уравнение регрессии
полученное с помощью Excel,
имеет вид:
-
Коэффициент
детерминации:
Вариация результата
на 46,5% объясняется вариацией факторов.
-
Коэффициент
множественной корреляции:
-
Проверка на
адекватность модели. Анализ выполняется
при сравнении фактического и табличного
значения F-критерия
Фишера.
Фактическое
значение F-критерия Фишера
превышает табличное
— модель адекватна.
-
Проверка значимости
коэффициента b0.
Расчетное значение
t-критерия
для коэффициента
b0:
Табличное значение
t-критерия
tтаб.
(29, 0.975)=2.05
-
Доверительный
интервал коэффициента b0:
-
Проверка значимости
коэффициента b1.
Расчетное значение
t-критерия
для коэффициента
b1:
tрас.>tтаб.,
коэффициент b1
является значимым
-
Доверительный
интервал
коэффициента
b1:
-
Проверка значимости
для коэффициентаb2.
Расчетное значение
t-критерия
для коэффициента
b2:
tрас.<tтаб.,
коэффициент b2
является не значимым, значит фактор X
2 незначительно влияет на выходную
величину Y,
и его можно исключить из уравнения
регрессии.
-
На основании
анализа значимости коэффициентов
уравнение регрессии примет вид:
Соседние файлы в папке LR-3
- #
- #
17.02.201457.34 Кб36Копия Xl0000004.xls
- #
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Регрессионный анализ: в пакете Statistica и MS Exel
Кафедра
«Информатика и программное обеспечение»
Курсовая
работа по компьютерному моделированию
«Регрессионный
анализ: в пакете STATISTICA и MS Exel»
Выполнила
студентка группы 09-СЦ
Петрякова
Екатерина
Проверил доц.
каф. «ИиПО»
Брянск 2012
г.
Введение
В условиях рыночной конкуренции процесс подготовки и
принятия решений менеджерами компаний должен включать тщательный анализ
имеющихся данных, базирующийся на методах математической статистики. В этой
связи существенную помощь в получении необходимой информации могут оказать
современные информационные технологии интеллектуального и статистического
анализа данных. Оценка кредитных и страховых рисков, прогнозирование тенденций
на финансовых рынках, оценка объектов недвижимости, построение профилей
потенциальных покупателей определенного товара, анализ продуктовой корзины и
так далее.
Системы интеллектуального анализа предназначены для
автоматизированного поиска ранее неизвестных закономерностей в имеющихся в
распоряжении менеджера данных с последующим использованием полученной
информации для подготовки решений. Помимо статистических методов базовыми
инструментами анализа в таких системах являются нейронные сети, деревья решений
и индукция правил. Однако несмотря на то, что в последние годы рынок
программных продуктов этого типа активно развивается, они все еще недоступны по
цене предприятиям среднего и малого бизнеса. В то же время компаниям такого
размера, как правило, не требуется столь мощный аналитический инструментарий,
предлагаемый этими системами.
Более доступными средствами анализа данных на
сегодняшний день являются статистические программные продукты (СПП). В мировой
практике компьютерные системы статистического анализа и обработки данных широко
применяются как в исследовательской работе в области экономики, так и в
практической деятельности аналитических, маркетинговых и плановых отделов
банков, страховых компаний, производственных и торговых фирм. В последние годы
заметно возрос спрос на СПП и в нашей стране.
СПП позволяют решить широкий спектр задач
«разведочного» анализа данных, статистического исследования зависимостей,
планирования экспериментов, анализа временных рядов, анализа данных нечисловой
природы и т.д. Настоящие методические разработки посвящены вопросам
корреляционно-регрессионного анализа статистических связей с использованием
одного из самых популярных в России статистических программных продуктов —
пакета STATISTICA, функционирующего в среде Window
Общее описание программы Statistica
Пакет STATISTICA разработан фирмой StatSoft (США). Первоначально он
входил в качестве модуля в состав самых популярных в то время электронных
таблиц Lotus 1-2-3. Как самостоятельный продукт пакет впервые заявил о себе в
1991 г. Последняя версия продукта совместима с Windows Vista, в ней поддерживаются графический интерфейс
пользователя и динамический обмен данными. Благодаря этому пакет может работать
в сочетании с другими Windows-приложениями. В последние версии включен также
язык программирования Statistica-BASIC, позволяющий расширять возможности
пакета в соответствии с потребностями пользователя.
Системные требования. Платформа Macintosh или Windows, процессор 386 и
выше, 4 Мбайт ОЗУ (рекомендуется 8 Мбайт), дисковое пространство — 18 Мбайт.
Возможности. STATISTICA позволяет проводить исчерпывающий, всесторонний
анализ данных, представлять результаты анализа в виде таблиц и графиков,
автоматически создавать отчеты о проделанной работе. С помощью удобной системы
подсказок можно обучаться не только работе с самим пакетом, но и современным
методам статистического анализа.
Файлы данных. Данные в системе STATISTICA организованы в виде электронных
таблиц, как в привычной для пользователей программе Excel. Файл содержит
наблюдения и переменные (см. рис.1.1). Наблюдения можно рассматривать как
эквивалент записей в базах данных (или строк электронной таблицы), а переменные
— как эквивалент полей (столбцов электронной таблицы). Каждое наблюдение
состоит из набора значений переменной.
В пакете STATISTICA все операции, включая копирование, перетаскивание и
автоматическое заполнение ячеек, производятся так же, как в популярных
электронных таблицах. При нажатии правой кнопки мыши появляется всплывающее
меню, где точно так же предлагается перечень операций, которые можно выполнить
над выделенным объектом.
Общее число переменных в стандартном файле STATISTICA может быть до 4092,
количество наблюдений ограничено лишь объемом жесткого диска. В системе имеется
также менеджер мегафайлов (доступный из модуля Управление данными), который
позволяет работать с очень большими файлами, содержащими до 32000 переменных.
Система STATISTICA предоставляет всесторонние возможности по импорту и
экспорту данных, в том числе и из таблиц Excel.
Архитектура и интерфейс системы. Система STATISTICA состоит из отдельных
модулей, каждый из которых является полноценным Windows-приложением. Система
постоянно обновляется, в нее вводятся новые модули и вычислительные процедуры.
Быстро переключаться из одного модуля в другой можно: а) щелкая мышью на
значках модулей на рабочем столе; б) активизируя соответствующее окно
приложения (если оно уже было открыто) или в) выбирая модули в диалоговом окне
Переключатель модулей, причем эту операцию можно настроить так, чтобы было
удобно обращаться к модулям, которые используются чаще всего.
Интерфейс системы может быть настроен на конкретный пользовательский
проект: можно задать отображение стольких диалоговых окон, таблиц результатов,
графиков, сколько в данном случае необходимо.
Методы анализа. Система включает следующие модули: Основные статистики и
таблицы. Исчерпывающий набор описательных статистик, таблицы сопряженности,
таблицы флагов и заголовков, кросстабуляция многомерных откликов и многомерных
дихотомий, вычисление корреляционных матриц, обработка пропущенных данных,
t-критерии для зависимых и независимых выборок, критерии однородности
дисперсии, однофакторный дисперсионный анализ.
Непараметрическая статистика. Непараметрические критерии, ранговые
корреляции, подгонка распределений.
Множественная регрессия. Пошаговая регрессия с включением и исключением
предикторов, нелинейная регрессия, ридж-регрессия, построение прогнозов,
всесторонний анализ остатков, вычисление прогнозов и доверительных интервалов
для прогнозируемых значений (можно анализировать очень большие модели, до 500
переменных).
Нелинейное оценивание. Подгонка любой задаваемой пользователем функции,
задаваемая пользователем функция потерь, разрывная регрессия.
Временные ряды и прогнозирование. Широкий выбор моделей анализа временных
рядов, включая модели АРПСС — авторегрессии и проинтегрированного скользящего
среднего, модели с интервенцией, анализ распределенных лагов, спектральный
анализ чрезвычайно длинных временных рядов, преобразования рядов, включая
быстрое преобразование Фурье и многие другие процедуры углубленного анализа.
Кластерный анализ. Широкий набор процедур кластерного анализа, включая
иерархическое объединение, двухвходовое объединение, метод к-средних; алгоритмы
оптимизированы для анализа очень больших проектов, например, методом к-средних
можно анализировать 400000 наблюдений с 10 переменными.
Факторный анализ. Процедуры факторного анализа и анализа главных
компонент, ортогональные и косоугольные факторы, иерархический анализ
косоугольных факторов и др.
Канонический анализ. Вычисление канонических переменных и канонических
корней.
Многомерное шкалирование. Анализ расстояний, матриц сходств и различия,
диаграмма Шепарда и др.
Деревья классификации. Современные методы построения деревьев
классификации с категориальными и порядковыми предикторами и различными
функциями потерь.
Анализ соответствий. Современные методы анализа таблиц сопряженности.
Структурное моделирование. Построение структурных моделей, продвинутый
факторный анализ.
Надежность и позиционный анализ. Методы построения вопросников, оценка
надежности позиций и др.
Дискриминантный анализ. Процедуры всестороннего дискриминантного анализа,
разнообразные статистики и графическое представление результатов.
Логлинейный анализ. Всесторонний анализ многовходовых таблиц
сопряженности, автоматическое построение лучшей модели.
Анализ выживаемости. Анализ таблиц жизни, оценки Каплана-Мейера,
регрессионные модели: Кокса, логнормальная, экспоненциальная, зависящие от
времени ковариаты, разнообразные статистики и критерии.
Дисперсионный анализ. Полный набор методов одномерного и многомерного
дисперсионного анализа, фиксированные и переменные ковариаты, апостериорные
критерии, контрасты, проверка предположений дисперсионного анализа, планы с
повторными измерениями, иерархически вложенные планы, планы с пропущенными
ячейками и многое другое.
Компоненты дисперсии. Смешанные модели дисперсионного анализа, оценка
компонент дисперсии.
Графические возможности. STATISTICA обладает огромными возможностями для
построения графиков непосредственно из таблиц исходных данных и таблиц
результатов, причем графика и анализ данных тесно интегрированы. Например, если
после вычисления корреляционной матрицы у пользователя возникает потребность в
графическом представлении корреляционной зависимости, то достаточно поместить
курсор на соответствующий коэффициент корреляции, нажать правую кнопку мыши и в
появившемся меню выбрать пункт Быстрые статистические графики, а затем одну из
диаграмм рассеяния (см. рис. 1.3). На экране появится требуемый график. В
разных модулях системы имеются свои специальные графики, учитывающие
особенности получаемых в них результатов.
Один из способов построения графиков в системе STATISTICA — использовать
окно Галерея графиков.
Регрессионный
анализ в STATISTICA <#»600910.files/image005.gif»>
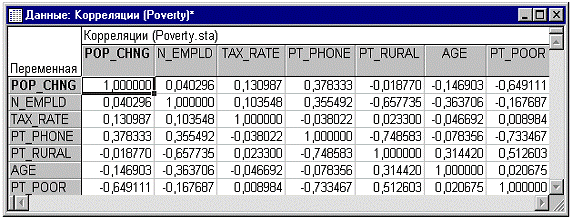
Цель исследования. Мы проанализируем корреляты
бедности (т.е. предикторы, «сильно» коррелирующие с процентом семей,
живущих за чертой бедности). Таким образом, будем рассматривать переменную 3
(Pt_Poor), как зависимую или критериальную переменную, а все остальные
переменные — в качестве независимых переменных или предикторов.
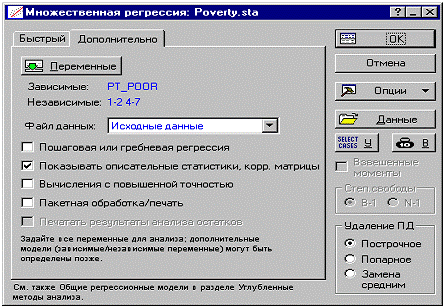
Начальный анализ. Когда вы выбираете команду
Множественной регрессии с помощью меню Анализ, открывается стартовая панель
модуля Множественная регрессия. Вы можете задать регрессионное уравнение
щелчком мыши по кнопке Переменные во вкладке Быстрый стартовой панели модуля
Множественная регрессия. В появившемся окне Выбора переменных выберите Pt_Poor
в качестве зависимой переменной, а все остальные переменные набора данных — в
качестве независимых. Во вкладке Дополнительно отметьте также опции Показывать
описательные статистики, корр. матрицы.
Теперь нажмите OK этого диалогового окна, после чего
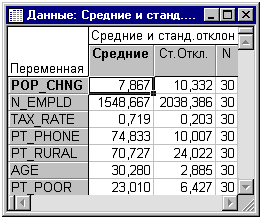
откроется диалоговое окно Просмотр описательных статистик. Здесь вы можете
просмотреть средние и стандартные отклонения, корреляции и ковариации между
переменными. Отметим, что это диалоговое окно доступно практически из всех
последующих окон модуля Множественная регрессия, так что вы всегда сможете
вернуться назад, чтобы посмотреть на описательные статистики определенных
переменных.
Распределение переменных. Сначала изучим распределение
зависимой переменной Pt_Poor по округам. Нажмите Средние и стд.отклонения для
показа таблицы результатов.
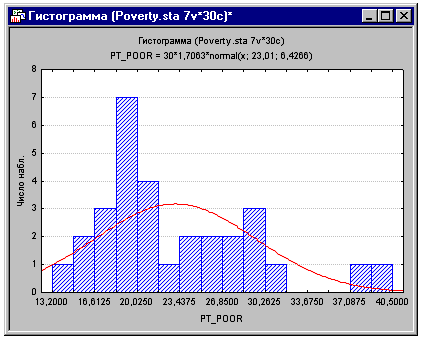
Выберите Гистограммы в меню Графика, чтобы построить
гистограмму для переменной Pt_Poor (во вкладке Дополнительно диалогового окна
2М Гистограммы установите опцию Число категорий в строке Категории равной 16).
Как видно ниже, распределение этой переменной чем-то отличается от нормального
распределения. Коэффициенты корреляции могут оказаться существенно завышенными
или заниженными при наличии в выборке существенных выбросов. Однако, хотя два округа
(две самые правые колонки) имеют более высокий процент семей, проживающих за
чертой бедности, чем это можно было бы ожидать в соответствии с нормальным
распределением, они все еще, как нам кажется, находятся «в рамках
допустимого».
Это решение является в определенной степени
субъективным; эмпирическое правило состоит в том, что беспокойство требуется
проявлять только тогда, когда наблюдение (или наблюдения) лежат вне интервала,
заданного средним значением ± 3 стандартных отклонения. В этом случае будет
разумно повторить критическую (с точки зрения влияния выбросов) часть анализа с
выбросами и без них, с тем, чтобы удостовериться в отсутствии их влияния на
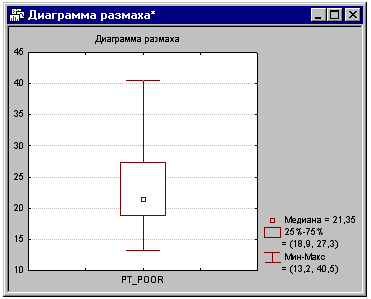
характер взаимных корреляций. Вы также можете просмотреть распределение этой
переменной, щелкнув мышкой на кнопке Диаграмма размаха во вкладке Дополнительно
диалогового окна Просмотр описательных статистик, выбрав переменную Pt_Poor.
Далее, выберите опцию Медиана/квартили/размах в диалоговом окне Диаграммы размаха
и нажмите кнопку OK.
(Заметим, что определенный метод вычисления медианы и
квартилей может быть выбран для всей «системы» в диалоговом окне
Параметры в меню Сервис.)
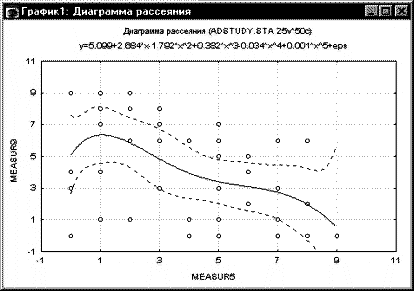
Диаграммы рассеяния. Если имеются априорные гипотезы о
связи между определенными переменными, на этом этапе может оказаться полезным
вывести соответствующую диаграмму рассеяния. Например, посмотрим на связь между
изменением популяции и процентом семей, проживающих за чертой бедности. Было бы
естественно ожидать, что бедность приводит к миграции населения; таким образом,
должна наблюдаться отрицательная корреляция между процентом семей, проживающих
за чертой бедности, и изменением популяции.
Возвратимся к диалоговому окну Просмотр описательных
статистик и щелкнем мышкой по кнопке Корреляции во вкладке Быстрый для
отображения таблицы результатов с корреляционной матрицей.
Корреляции между переменными могут быть отображены
также и на матричной диаграмме рассеяния. Матричная диаграмма рассеяния для
выбранных переменных может быть получена щелчком мыши по кнопке Матричный
график корреляций во вкладке Дополнительно диалогового окна Просмотр
описательных статистик и последующим выбором интересующих переменных.
Задание множественной регрессии. Для выполнения
регрессионного анализа от вас требуется только щелкнуть по кнопке OK в
диалоговом окне Просмотр описательных статистик и перейти в окно Результаты
множественной регрессии. Стандартный регрессионный анализ (со свободным членом)
будет выполнен автоматически.
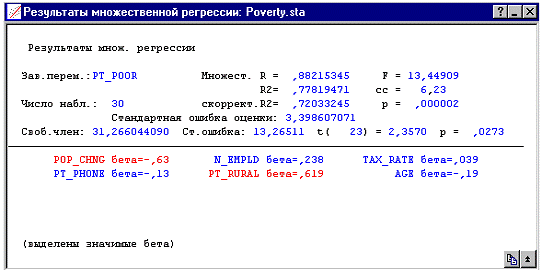
Просмотр результатов. Ниже изображено диалоговое окно
Результаты множественной регрессии. Общее уравнение множественной регрессии
высоко значимо. Таким образом, зная значения независимых переменных, можно
«предсказать» предиктор, связанный с бедностью, лучше, чем угадывая
его чисто случайно.
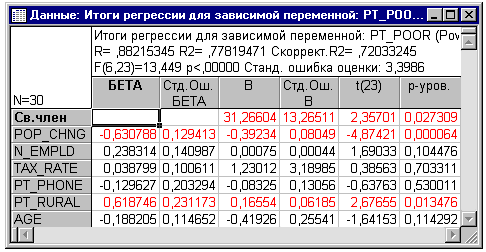
Регрессионные коэффициенты. Чтобы узнать, какие из
независимых переменных дают больший вклад в предсказание предиктора, связанного
с бедностью, изучим регрессионные (или B) коэффициенты. Щелкните мышкой по
кнопке Итоговая таблица регрессии во вкладке Быстрый диалогового окна
Результаты множественной регрессии для вывода таблицы результатов с этими
коэффициентами.
Таким образом, величина этих Бета-коэффициентов
позволяет сравнивать относительный вклад каждой независимой переменной в
предсказание зависимой переменной. Как видно из таблицы результатов,
изображенной выше, переменные Pop_Chng, Pt_Rural и N_Empld являются наиболее
важными предикторами для бедности; из них только первые два статистически
значимы. Регрессионный коэффициент для Pop_Chng отрицателен; т.е. чем меньше
прирост популяция, тем большее число семей живут ниже уровня бедности в
соответствующем округе. Вклад в регрессию для Pt_Rural положителен; т.е. чем
больше процент сельского населения, тем выше уровень бедности.
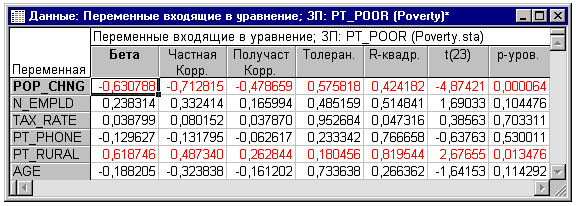
Частные корреляции. Другой путь изучения вкладов
каждой независимой переменной в предсказание зависимой переменной состоит в
вычислении частных и получастных корреляций (щелкните на кнопке Частные
корреляции во вкладке Дополнительно диалогового окна Результаты множественной
регрессии). Частные корреляции являются корреляциями между соответствующей
независимой переменной и зависимой переменной, скорректированными относительно
других переменных. Таким образом, это корреляция между остатками после
корректировки относительно независимых переменных. Частная корреляция
представляет самостоятельный вклад соответствующей независимой переменной в
предсказание зависимой переменной.
Получастные корреляция являются корреляциями между
соответствующей независимой переменной, скорректированной относительно других
переменных, и исходной (нескорректированной) зависимой переменной. Таким
образом, получастная корреляция является корреляцией соответствующей
независимой переменной после корректировки относительно других переменных, и
нескорректированными исходными значениями зависимой переменной. Иначе говоря,
квадрат получастной корреляции является показателем процента Общей дисперсии,
самостоятельно объясняемой соответствующей независимой переменной, в то время
как квадрат частной корреляции является показателем процента остаточной
дисперсии, учитываемой после корректировки зависимой переменной относительно
независимых переменных.
В этом примере частные и получастные корреляции имеют
близкие значения. Однако иногда их величины могут различаться значительно
(получастная корреляция всегда меньше). Если получастная корреляция очень мала,
в то время как частная корреляция относительно велика, то соответствующая
переменная может иметь самостоятельную «часть» в объяснении
изменчивости зависимой переменной (т.е. «часть», которая не объясняется
другими переменными). Однако в смысле практической значимости, эта часть может
быть мала, и представлять только небольшую долю от общей изменчивости.
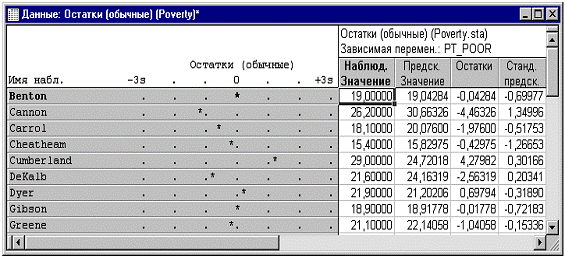
Анализ остатков. После подбора уравнения регрессии
всегда полезно изучить полученные предсказанные значения и остатки. Например,
экстремальные выбросы могут существенно сместить результаты и привести к
ошибочным заключениям. Во вкладке Остатки/предложения/наблюдаемые нажмите
кнопку Анализ остатков для перехода в соответствующее диалоговое окно.
Построчный график остатков. Эта опция диалогового окна
предоставляет вам возможность выбрать один из возможных типов остатков для
построения построчного графика. Обычно, следует изучить характер исходных
(нестандартизованных) или стандартизованных остатков для идентификации
экстремальных наблюдений. В нашем примере, выберите вкладку Остатки и нажмите
кнопку Построчные графики остатков; по умолчанию будет построен график исходных
остатков; однако, вы можете изменить тип остатков в соответствующем поле.
Масштаб, используемый в построчном графике в самой
левой колонке, задается в терминах сигмы, т.е. стандартного отклонения
остатков. Если один или несколько наблюдений попадают за границы ± 3 * сигма,
то, вероятно, следует исключить соответствующие наблюдения (это легко
достигается с помощью условий отбора) и выполнить анализ снова, чтобы убедиться
в отсутствии смещения ключевых результатов, вызванного этими выбросами в
данных.
Построчный график выбросов. Быстрый способ идентификации
выбросов состоит в использовании опции График выбросов во вкладке Выбросы. Вы
можете выбрать просмотр всех стандартных остатков, выпадающих за границы ± 2-5
сигма, или просмотр 100 наиболее выделяющихся наблюдений, выбранных в поле Тип
выброса во вкладке Выбросы. При использовании опции Стандартный остаток
(>2*сигма) в нашем примере какие-либо выбросы не заметны.
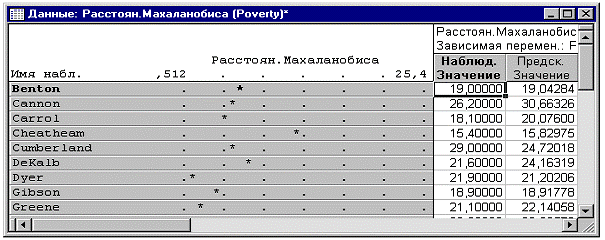
Расстояния Махаланобиса. Большинство учебников по
статистике отводят определенное место для обсуждения темы выбросов и остатков
для зависимой переменной. Однако роль выбросов для набора независимых
переменных часто упускается из виду. Со стороны независимых переменных, имеется
список переменных, участвующий с различными весами (регрессионные коэффициенты)
в предсказании зависимой переменной. Независимые переменные можно представить
себе в виде точек некоторого многомерного пространства, в котором может
располагаться каждое наблюдение. Например, если вы имеете две независимые
переменные с равными регрессионными коэффициентами, то можно построить диаграмму
рассеяния этих двух переменных и расположить каждое наблюдение на этом графике.
Вы можете затем нарисовать точку средних значений обоих переменных и вычислить
расстояния от каждого наблюдения до этого среднего (называемого теперь
центроидом) в этом двумерном пространстве; в этом состоит концептуальная идея,
стоящая за вычислением расстояний Махаланобиса. Теперь посмотрим на эти
расстояния, отсортированные по величине, с целью идентификации экстремальных
наблюдений по независимым переменным. В поле Тип выбросов отметьте опцию
расстояний Махаланобиса и нажмите кнопку Построчный график выбросов. Полученный
график показывает расстояния Махаланобиса, отсортированные в порядке убывания.
Отметим, что округ Shelby оказывается в чем-то
выделяющимся по сравнению с другими округами на графике. Если посмотреть на
исходные данные, можно обнаружить, что в действительности округ Shelby —
значительно больший по размеру округ с большим числом людей, занятых сельским
хозяйством (переменная N_Empld), и намного более весомой популяцией
афроамериканцев. Вероятно, было бы разумно выражать эти числа в процентах, а не
в абсолютных значениях, в этом случае расстояние Махаланобиса округа Shelby от
других округов в данном примере не было бы столь велико. Однако мы получили,
что округ Shelby оказывается явным выбросом.
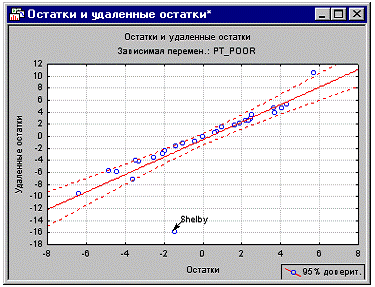
Удаленные остатки. Другой очень важной статистикой,
позволяющей оценить масштаб проблемы выбросов, являются удаленные остатки. Они
определяются как стандартизованные остатки для соответствующих наблюдений,
которые получились бы при исключении соответствующих наблюдений из анализа.
Напомним, что процедура множественной регрессии подбирает прямую линию для
выражения взаимосвязи между зависимой и независимыми переменными. Если одно из
наблюдений является очевидным выбросом (как округ Shelby в этих данных), то
линия регрессии стремиться «приблизится» к этому выбросу, с тем чтобы
учесть его, насколько это возможно. В результате, при исключении
соответствующего наблюдения, возникнет совершенно другая линия регрессии (и
B-коэффициенты). Поэтому, если удаленный остаток сильно отличается от
стандартизованного остатка, у вас есть основания полагать, что результаты
регрессионного анализа существенно смещены соответствующим наблюдением. В данном
примере удаленный остаток для округа Shelby является выбросом, который
существенно влияет на анализ. Вы можете построить диаграмму рассеяния остатков
относительно удаленных остатков с помощью опции Остатки и удал. остатки во
вкладке Диаграммы рассеяния. Ниже на диаграмме рассеяния явно заметен выброс.
предоставляет интерактивное средство для удаления
выбросов (Кисть на панели инструментов для графики;). Позволяющее
экспериментировать с удалением выбросов и позволяющее сразу же увидеть их
влияние на линию регрессии. Когда это средство активизировано, курсор меняется
на крестик и рядом с графиком высвечивается диалоговое окно Закрашивание. Вы
можете (временно) интерактивно исключать отдельные точки данных из графика,
отметив (1) опцию Автообновление и (2) поле Выключить из блока Операция; а
затем щелкнув мышкой на точке, которую нужно удалить, совместив ее с крестиком
курсора.
Отметим, что удаленные точки можно
«возвратить», щелкнув по кнопке Отменить все в диалоговом окне
Закрашивание.
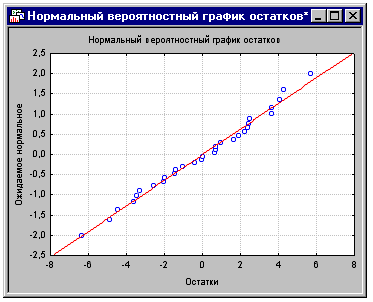
Нормальные вероятностные графики. Из окна Анализ
остатков пользователь получает большому количеству дополнительных графиков.
Большинство этих графиков более или менее просто интерпретируются. Тем не
менее, здесь мы дадим интерпретацию нормального вероятностного графика,
поскольку он наиболее часто используется при анализе справедливости
предположений регрессии.
Как было замечено ранее, множественная линейная
регрессия предполагает линейную связь между переменными в уравнении, и
нормальным распределением остатков. Если эти предположения нарушаются,
окончательные заключения могут оказаться неточными. Нормальный вероятностный
график остатков наглядно показывает наличие или отсутствие больших отклонений
от высказанных предположений. Нажмите кнопку Нормальный во вкладке
Вероятностные графики для построения этого графика.
Этот график строится следующим образом. Сначала
остатки регрессии ранжируются. Для этих упорядоченных остатков вычисляются
z-значения (т.е. стандартные значения нормального распределения), исходя из
предположения, что данные имеют нормальное распределение. Эти z-значения
откладываются по оси Y на графике.
Если наблюдаемые остатки (отложенные по оси X)
нормально распределены, то все значения будут располагаться на графике вблизи
прямой линии; на данном графике все точки лежат очень близко к прямой линии.
Если остатки не распределены нормально, то они будут отклоняться от линии. На
этом графике также могут стать заметны выбросы.
Если имеющаяся модель плохо согласуется с данными, и
данные на графике, похоже, образуют некоторую структуру (например, облако
наблюдений принимает S-образную форму) около линии регрессии, то, возможно,
будет полезным применение некоторого преобразования зависимой переменной
(например, логарифмирование с целью «поджать» хвост распределения, и
т.п.; см. также краткое обсуждение преобразований Бокса-Кокса и Бокса-Тидвелла
в разделе Примечания и техническая информация). Однако слишком часто
исследователи просто принимают свои данные, не пытаясь присмотреться к их
структуре или проверить их на соответствие своим предположениям, что приводит к
ошибочным заключениям. По этой причине одной из основных задач, стоявшей перед
разработчиками пользовательского интерфейса модуля Множественной регрессии было
максимально возможное упрощение (графического) анализа остатков.
Многомерный анализ в SPSS
Многомерный дисперсионный анализ применяется тогда, когда в одном
дисперсионном анализе необходимо одновременно исследовать влияние факторов и
возможных ковариации (независимых переменных) на несколько зависимых
переменных. Такой многомерный дисперсионный анализ следует предпочесть
одномерному тогда (и только тогда), когда зависимые переменные не являются
независимыми друг от друга, а наоборот коррелируют между собой.
Если Вы откроете данные из исследования гипертонии (файл hyper.sav) и
рассчитаете корреляции между исходными значениями систолического и
диастолического давлений, то вы заметите, что эти переменные, хотя и не сильно,
но всегда значимо коррелируют между собой.
Если Вы хотите узнать, значимо ли отличаются перечисленные переменные для
четырёх заданных возрастных групп (переменная ak), то вместо четырёх отдельных
одномерных однофакторных дисперсионных анализов Вы должны провести один
многомерный однофакторный анализ.
· Откройте
файл hyper.sav <#»600910.files/image019.gif»>
Рис.: Диалоговое окно Multivariate (Многомерная)
Появятся довольно обширные результаты расчёта. Важным для нас является в
первую очередь глобальный многомерный тест на предмет выявления значимых
различий «где-нибудь» между возрастными группами:. Exact statistic
(Точная статистика). The statistic is an upper bound on F that yields a lower
bound on the significance level (Статистической характеристикой является верхний
придел значения F-распределе-ния, который указывает на нижний предел уровня
значимости).
с Design: Intercept+AK (Компоновка: Отрезок + АК)
Multivariate Tests c (Многомерные тесты)
|
Effect (Эффект ) |
Value (Значение) |
F |
Hypo-thesis df (Гипотеза df) |
Error df (Ошибка df) |
Sig. (Значимость) |
|
|
Inte-rcept Отре-зок) |
Pillai’s Trace (След Пиллая) |
,996 |
9252, 061а |
4,000 |
167,000 |
,000 |
|
Wilks’ Lambda (Лямбда Уилкса) |
,004 |
9252,061 а |
4,000 |
167,000 |
,000 |
|
|
Hotelling’s Trace (След Хоттелинга) |
221,606 |
9252, 061а |
4,000 |
167,000 |
,000 |
|
|
Roy’s Largest Root ‘Максимальный характеристический корень |
221,606 |
9252,061 а |
4,000 |
167,000 |
,000 |
|
|
АК |
Dillai’s Trace (След Пиллая) |
,178 |
2,661 |
12,00ol |
507,00o’ |
|
|
Wilks’ Lambda (Лямбда Уилкса) |
,827 |
2,740 |
12,000 |
442,132 |
,001 |
|
|
Hotelling’s Trace (След Хоттелинга) |
,203 |
,805 |
12,000 |
197,000 |
,001 |
|
|
Roy’s Largest Root (Макси-мальный характеристический корень |
,169 |
7,159Ь |
4,000 |
167,000 |
,000 |
Здесь производится расчёт величин, традиционных для общей линейной
модели. Основываясь на критерии «След Пиллая» («Pillai’s
Trace»), следует отклонить нулевую гипотезу о том, что между четырьмя
возрастными группами не наблюдается различий ни для одной из зависимых
переменных (значение р = 0,002).
Для проверки, какие из четырёх зависимых переменных в чем-то различаются
между собой, были проведены одномерные тесты. Результаты этих тестов полностью
соответствуют результатам отдельного одномерного дисперсионного анализа для
каждой зависимой переменной.
Отметим то, что для систолического и диастолического давлений, уровней
холестерина и сахара в крови получаются следующие значения вероятности ошибки
р: 0,153, 0,002, 0,267 и 0,688 соответственно. Причиной суммарной значимости,
поучающейся в результате многомерного теста, являются прежде всего значимые
различия для диастолического давления.
Для опытных статистиков, хорошо знакомых с тонкостями многомерных
методов, SPSS может предложить избыточное количество разнообразных возможностей
в области дисперсионного анализа.
В первую очередь можно использовать разнообразные возможности процедуры
MANOVA, доступной отныне только через командный синтаксис. Эта процедура
позволяет проводить простой и множественный регрессионный анализ,
дискриминантный анализ, канонический анализ, анализ главных компонентов и др.
Однако сложность работы с заданием параметров может составить некоторые
затруднения для менее опытных пользователей.
Классификация переменных
. Несколько количественных независимых и одна количественных зависимая
переменные

) сделать
прогноз(при) или сделать вывод о невозможности прогнозирования с
помощью найденной регрессионной зависимости. При этом не рекомендуется
использовать модель регрессии для тех значений независимого параметра X,
которые не принадлежат интервалу, заданному в исходных данных.
Режим работы «Регрессия» служит для расчета параметров
уравнения линейной регрессии и проверки его адекватности исследуемому процессу.
Для решения задачи регрессионного анализа в MS Excel выбираем в меню
Сервис/команду Анализ данных и инструмент анализа «Регрессия».
В появившемся диалоговом окне задаем следующие параметры:
1. Входной интервал Y — это диапазон данных по результативному
признаку. Он должен состоять из одного столбца.
2. Входной интервал X — это диапазон ячеек, содержащих значения
факторов (независимых переменных). Число входных диапазонов (столбцов) должно
быть не больше 16.
. Флажок Метки, устанавливается в том случае, если в первой строке
диапазона стоит заголовок.
. Флажок Уровень надежности активизируется, если в поле,
находящееся рядом с ним необходимо ввести уровень надежности, отличный от
установленного по умолчанию. Используется для проверки значимости коэффициента
детерминации R2 и коэффициентов регрессии.
. Константа ноль. Данный флажок необходимо установить, если линия
регрессии должна пройти через начало координат (а0=0).
. Выходной интервал/ Новый рабочий лист/ Новая рабочая книга —
указать адрес верхней левой ячейки выходного диапазона.
. Флажки в группе Остатки устанавливаются, если необходимо
включить в выходной диапазон соответствующие столбцы или графики.
. Флажок График нормальной вероятности необходимо сделать
активным, если требуется вывести на лист точечный график зависимости
наблюдаемых значений Y от
автоматически формируемых интервалов перцентилей.
После нажатия кнопки ОК в выходном диапазоне получаем отчет.
Задача:
Требуется построить регрессионную линейную модель для исходных данных,
построенных в таблице 1, и сделать прогноз для х*.
Некоторая
фирма занимается поставками различных грузов на короткие расстояния внутри
города. Оценить стоимость таких услуг, зависящую от затрачиваемого на поставку
времени. В качестве наиболее важного фактора, влияющего на время поставки,
выбрано пройденное расстояние. Были собраны исходные данные о поставках
(таблица 1).
Таблица 1 :Исходные данные
|
X |
1 |
2 |
3 |
4 |
X*=3,6 |
|
Y |
13 |
9 |
8 |
7 |
— |
Определим характер зависимости между расстоянием и затраченным временем,
используя мастер диаграмм MS Excel, проанализируем применимость метода
наименьших квадратов, построим уравнение регрессии, используя МНК,
проанализируйте силу регрессионной связи. Провем регрессионный анализ, используя
режим работы «Регрессия» в MS Excel и сравним с
результатами, полученными ранее. Сделаем прогноз времени поездки на 2 мили.
Посчитаем и построим графически меру ошибки регрессионной модели используя
табличный процессор Excel.
Решение задачи:
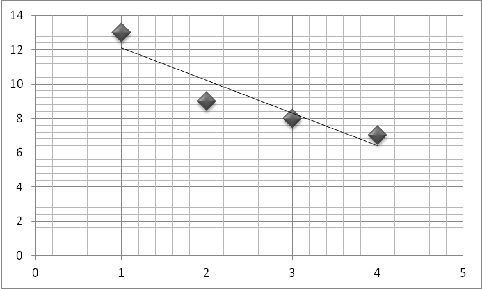
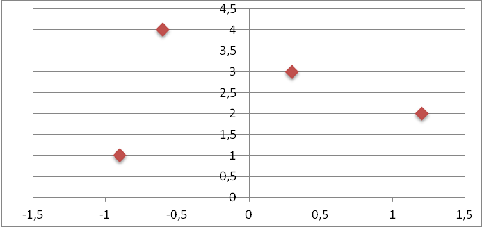
На графике строим исходные данные по четырем поездкам.
Рис.1: График исходных данных и предполагаемая линия регрессии
Помимо расстояния на время поставки влияют пробки на дорогах, время
суток, дорожные работы, погода, квалификация водителя, вид транспорта.
Построенные точки не находятся точно на линии, что обусловлено описанными выше
факторами. Но эти точки собраны вокруг прямой линии, поэтому можно предположить
линейную связь между параметрами. Все исходные точки равномерно распределены
вдоль предполагаемой прямой линии, что позволяет применить метод наименьших
квадратов.
Вычислим суммы, необходимые для расчета коэффициентов уравнения линейной
регрессии и коэффициента детерминации R2 с помощью
вспомогательной таблицы (таблица 2).
|
|
||||||
|
1 |
13 |
1 |
13 |
12,1 |
8,1225 |
14,0625 |
|
2 |
9 |
4 |
10,2 |
0,9025 |
0,0625 |
|
|
3 |
8 |
9 |
24 |
8,3 |
0,9025 |
1,5625 |
|
4 |
7 |
16 |
28 |
6,4 |
8,1225 |
5,0625 |
|
∑=10 |
∑=37 |
∑=30 |
∑=83 |
— |
18,05 |
20,75 |
Таблица 2: Расчет коэффициентов уравнения.
Вычислим коэффициенты линейной регрессии по формулам (1) и (2):
(1)
(2)
Таким
образом, искомая регрессионная зависимость имеет вид:
Наклон
линии регрессии минут на
милю — это количество минут, приходящееся на одну милю расстояния. Координата
точки пересечения прямой с осью Y минут —
это время, которое не зависит от пройденного расстояния, а обуславливается
всеми остальными возможными факторами, явно не учтенными при анализе.
Вычислим
коэффициент детерминации:
R²== 0,86988
или 86,98%
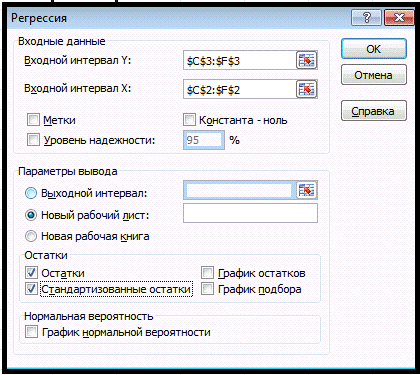
Проведем регрессионный анализ с использованием режима Регрессия MSExcel. Значения параметров, установленных
в одноименном диалоговом окне, представлены на рис.2.
Рис.2: Регрессионный анализ
Сгенерируются результаты по регрессионной статистике, представленные в
таблице 3.
Таблица 3: Регрессионная статистика
Рассмотрим представленную в таблице 3 регрессионную статистику.
Величина R-квадрат, называемая также мерой определенности, характеризует
качество полученной регрессионной прямой. Это качество выражается степенью
соответствия между исходными данными и регрессионной моделью (расчетными
данными). Мера определенности всегда находится в пределах интервала [0;1]. В
нашем примере мера определенности равна 0,86988, что говорит об очень хорошей
подгонке регрессионной прямой к исходным данным и совпадает с коэффициентом
детерминации R2, вычисленным по формуле.
Таким
образом, линейная модель объясняет 86,98% вариации времени доставки, что
означает не правильность выбора фактора (расстояния). Объясняется вариации времени поездки, которые обусловлены
остальными факторами, влияющими на время поставки, но не включенными в линейную
модель регрессии.
Множественный
R- коэффициент множественной корреляции R — выражает степень зависимости
независимых переменных (X) и зависимой переменной (Y) и равен квадратному корню
из коэффициента детерминации, эта величина принимает значения в интервале от
нуля до единицы.
Теперь рассмотрим среднюю часть расчетов, представленную в таблице
4(приведена в сокращенном варианте). Здесь даны коэффициент регрессии а1
(-1,9) и смещение по оси ординат, т.е. константа a0 (14).
Таблица 3:Коэффициенты регрессии
Исходя из расчетов, можем записать уравнение регрессии таким образом
Видим,
что это уравнение совпадает с уравнением, полученным нами при расчете по МНК
вручную с точностью до ошибки округления.
Направление
связи между переменными определяется на основании знаков (отрицательный или
положительный) коэффициента регрессии (коэффициента а1). В нашем
случае знак коэффициента регрессии положительный, следовательно, связь также
является положительной.
Далее
проверим значимость коэффициентов регрессии: а0 и а1.Сравнивая
попарно значения столбцов Коэффициенты и Стандартная ошибка в таблице 4, видим,
что абсолютные значения коэффициентов больше чем их стандартные ошибки. К тому
же эти коэффициенты являются значимыми, о чем можно судить по значениям
показателя Р-значение в таблице 4, которые больше заданного уровня значимости α=0,05.
Таблица 4: Вывод остатка
При помощи этой части отчета мы можем видеть отклонения каждой точки от
построенной линии регрессии. Наибольшее абсолютное значение остатка в нашем
случае -1,2649, наименьшее -0,6324.Для лучшей интерпретации этих данных
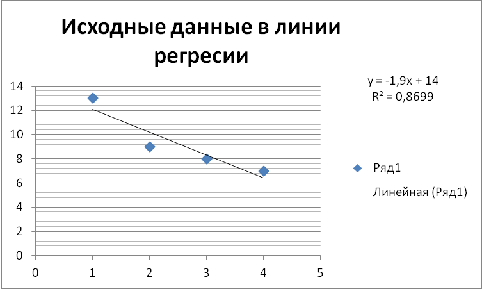
воспользуемся графиком исходных данных и построенной линией регрессии,
представленными на рис. 3. Как видим, линия регрессии хорошо
«подогнана» под значения исходных данных.
Рис.3 Исходные данные и линия регрессии
Приблизительным, но самым простым и наглядным способом проверки
удовлетворительности регрессионной модели является графическое представление
отклонений.
Рис. 4. График отклонений
Отложим
отклонения по оси Y, для каждого значения
(рис.4).
Если регрессионная модель близка к реальной зависимости, то отклонения будут
носить случайный характер и их сумма будет равна нулю.
В
рассмотренном примере
Обычно мерой ошибки регрессионной модели служит среднее квадратическое
отклонение
Решим задачу прогнозирования.
Поскольку коэффициент детерминации R2 имеет достаточно высокое значение и расстояние 3,6 мили, для
которого надо сделать прогноз, находится в пределах диапазона исходных данных
(таблица 1), то мы можем использовать полученное уравнение линейной регрессии
для прогнозирования
минут.
При прогнозах на расстояния, не входящие в диапазон исходных данных,
нельзя гарантировать справедливость полученной модели.
Это объясняется тем, что связь между временем и расстоянием может
изменяться по мере увеличения расстояния.
Таким образом, в результате регрессионного анализа в пакете MS Exel,мы:
· построено уравнение регрессии;
· установлена форма зависимости и направление связи между
переменными — положительная линейная регрессия, которая выражается в
равномерном росте функции;
· установлено направление связи между переменными;
· оценено качество полученной регрессионной прямой;
· рассмотрено отклонения расчетных данных от данных исходного
набора;
· предсказано будущее значение зависимой переменной.
Список литературы
1). Кендалл М. Д ж., Стьюарт А., Статистические выводы и связи, пер. с
англ., М., 1973;
). Смирнов Н. В., Дунин — Барковский Н. В., Курс теории вероятностей и
математической статистики для технических приложений, 3 изд., М., 1969;
). Айвазян С. А., Статистическое исследование зависимостей, М., 1968;
). Р а о С. Р., Линейные статистические методы и их применения, пер. с
англ., М., 1968;
). Дрейпер Н., С м и т Г., Прикладной регрессионный анализ, пер. с англ.,
М., 1973. А. В. Прохоров.
6). Afifi, A., V.
Clark, and S. May (2003). Computer-Aided Multivariate Analysis. 4th ed. New
York: CRC Press. ISBN 1584883081
<http://ru.wikipedia.org/wiki/%D0%A1%D0%BB%D1%83%D0%B6%D0%B5%D0%B1%D0%BD%D0%B0%D1%8F:%D0%98%D1%81%D1%82%D0%BE%D1%87%D0%BD%D0%B8%D0%BA%D0%B8_%D0%BA%D0%BD%D0%B8%D0%B3/1584883081>.
). Sá Joaquim Applied Statistics Using Spss,
Statistica, Matlab and R. — Berlin: Springer, 2007. — ISBN 3540719717
<http://ru.wikipedia.org/wiki/%D0%A1%D0%BB%D1%83%D0%B6%D0%B5%D0%B1%D0%BD%D0%B0%D1%8F:%D0%98%D1%81%D1%82%D0%BE%D1%87%D0%BD%D0%B8%D0%BA%D0%B8_%D0%BA%D0%BD%D0%B8%D0%B3/3540719717>
8). Страница компании StatSoft Russia
). Страница компании StatSoft Inc.
).
<http://www.unn.ru/fsn/k2/courses/borisova/12.htm>
).
<http://statsoft.ru/_Rainbow/documents/DataMiner2011.pdf>
). «Многомерный
статистический анализ в экономических задачах. Компьютерное моделирование в
SPSS», Вузовский учебник <http://www.ozon.ru/context/detail/id/1451961/>,
2009 г.
- Выдержка
- Другие работы
- Помощь в написании
Технология решения задач корреляционного и регрессионного анализа с применением Microsoft Excel (реферат, курсовая, диплом, контрольная)
Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии). Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Пакет анализа — это надстройка, которая предоставляет широкие возможности для проведения статистического анализа маркетинговых исследований.
Для установки средств Пакета анализа необходимо выполнить следующие действия:
- 1) выбрать команду Сервис — Надстройки;
- 2) в диалоговом окне Надстройки установить флажок Пакет анализа;
- 3) щелкнуть по кнопке ОК (рис. 6.5).
Рис. 6.5. Диалоговое окно Надстройки
Рассмотрим построение однофакторной линейной регрессионной модели связи изучаемых признаков на примере рынка образовательных услуг (табл. 6.17), т. е. определим взаимосвязь престижности специальности и количества студентов, желающих поступить на эту специальность.
Таблица 6.17
Исходные данные
|
Престижность специальности х, баллы. |
Количество студентов, выбирающих специальность у, чел. |
|
?15. |
?80. |
Регрессионный анализ заключается в определении аналитического выражения между факторным (x) и результативным (у) признаками. В результате работы инструмента Регрессия производится расчет параметров a0 и а1 уравнения линейной регрессии у = а() + а1х и проверка его адекватности исследуемым фактическим данным. В Microsoft Excel необходимо перенести данные табл. 6.17, далее запустить инструмент Регрессия.
1. Выбрать Сервис — Анализ данных — Регрессия — ОК. Появится окно Регрессия (рис. 6.6). 2.
Рис. 6.6. Окно Регрессия
- 2. Установить входной интервал Y — диапазон ячеек таблицы со значениями признака Y (В3:В7).
- 3. Входной интервал X — диапазон ячеек таблицы со значениями X (А3:А7).
- 4. Метки — не активизировать.
- 5. Уровень надежности — 95%.
- 6. Константа — ноль — не активизировать.
- 7. Выходной интервал — ячейка с параметрами А9.
- 8. Новый рабочий лист / Новая рабочая книга — не активизировать.
- 9. График остатков — не активизировать.
- 10. График подбора — активизировать.
- 11. График нормальной вероятности — не активизировать (рис. 6.7). Нажать О К.
Рис. 6.7. Окно Регрессия с заданными параметрами.
В результате указанных действий осуществляется вывод в заданный диапазон рабочего листа выходных данных (табл. 6.18— 6.20) и одного графика (рис. 6.8).
Таблица 6.18
Вывод итогов
|
Регрессионная статистика. |
Значение. |
|
Множественный R |
0,912 292. |
|
R-квадрат. |
0,832 277. |
|
Нормированный R-квадрат. |
0,776 369. |
|
Стандартная ошибка. |
6,228 965. |
|
Наблюдения. |
Таблица 6.19
Дисперсионный анализ
|
Показатель. |
SS |
MS |
F |
Значимость F |
||||
|
Регрессия. |
577,6. |
577,6. |
14,8866. |
0,30 768. |
||||
|
Остаток. |
116,4. |
38,8. |
; |
; |
||||
|
Итого. |
; |
; |
; |
|||||
|
Показатель. |
Коэффициент. |
Стандартная ошибка. |
t-статистика. |
Р-значение. |
Нижние. 95%. |
Верхние. 95%. |
Нижние. 95,0%. |
Верхние. 95,0%. |
|
Y-пересечен не. |
— 6,8. |
6,532 993. |
— 1,4 087. |
0,374 445. |
— 27,5909. |
13,99 092. |
— 27,5909. |
13,99 092. |
|
Переменная X1. |
7,6. |
1,969 772. |
3,858 315. |
0,30 768. |
1,331 302. |
13,8687. |
1,331 302. |
13,8687. |
Таблица 6.20
Вывод остатка
|
Наблюдение. |
Предсказанное Y |
Остаток. |
|
0,8. |
3,2. |
|
|
8,4. |
0,6. |
|
|
— 4. |
||
|
23,6. |
— 6,6. |
|
|
31,2. |
6,8. |
Рис. 6.8. Переменная Х1. График подбора.
Интерпретация параметров инструмента Регрессия такова:
- • множественный R — линейный коэффициент корреляции (r);
- • R-квадрат — коэффициент детерминации (R2);
- • стандартная ошибка — среднее квадратическое отклонение расчетных значений от фактических (??);
- • наблюдения — число наблюдений (п);
- • Df — число степеней свободы;
- • SS — сумма квадратов;
- • F — критерий Фишера;
- • MS — дисперсия факторная и остаточная (
);
- • ?-пересечение — свободный член регрессии (a0);
- • переменная Х1 — коэффициент регрессии (а1);
- • коэффициенты — значения коэффициентов уравнения регрессии;
- — нижние 95% и верхние 95% — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии, рассчитанные для уравнения надежности Р = 0,95;
- — нижние 68,3% и верхние 68,3% — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии, рассчитанные для уравнения надежности Р = 0,683;
- • пересеченное? — расчетные значения результативного признака (yi);
- • остатки — отклонение расчетных значений от фактических (yi — yфi).
- 4. Технология прогноза объема продаж с помощью Мастера функций. Прогнозирование в маркетинге является важнейшим элементом системы планово-экономических расчетов. В Microsoft Excel есть несколько стандартных функций, позволяющих решать задачи прогнозирования.
Вызов функции ТЕНДЕНЦИЯ для прогноза объема продаж на некоторый товар по временному ряду показан на рис. 6.9. В ячейках В4: В8 находятся данные об объеме продаж за прошедшие пять лет. В ячейку В10 будет возвращено прогнозное значение объема продаж. Для открытия диалога Мастер функций нажата кнопка fx на панели управления. Функция ТЕНДЕНЦИЯ расположена в категории Статистические (левое окно диалога). Для того чтобы вызвать функцию ТЕНДЕНЦИЯ, нужно щелкнуть мышью (левой клавишей) по названию функции в правом окне и нажать кнопку ОК.
Рис. 6.9. Вызов функции ТЕНДЕНЦИЯ.
Заполнение диалога функции ТЕНДЕНЦИЯ показано в табл. 6.21 и на рис. 6.10.
Таблица 6.21
Окно диалога функции ТЕНДЕНЦИЯ
|
Значение. |
Формула. |
|
Изв_знач_Y. |
В4:В8. |
|
Изв_знач_Х. |
Л4:Л8. |
|
Нов_знач_Х. |
А10. |
|
Константа. |
Заполнять не нужно. |
Рис. 6.10. Диалог функции ТЕНДЕНЦИЯ.
Функция ТЕНДЕНЦИЯ строит прогноз на основе модели.
где у — прогнозируемая переменная (в данном случае объем продаж); а, b — параметры; х — независимая переменная (в данном случае время).
Известные значения х — это пять предплановых лет, пронумерованных от 1 до 5. Известные значения у — объемы продаж в эти годы. Новое значение х — это номер планового года, в данном случае 6.
После ввода формул в окна диалога нужно нажать кнопку ОК. Результат вычислений показан на рис. 6.11.
Рис. 6.11. Прогноз объема продаж.
Показать весь текст
Заполнить форму текущей работой



 ;
; ;
; берется
берется