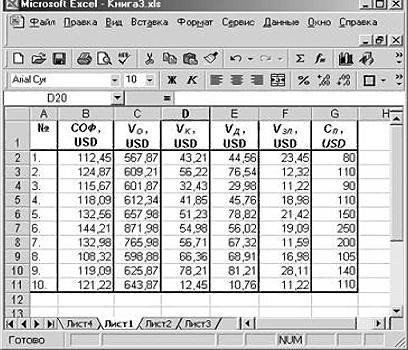
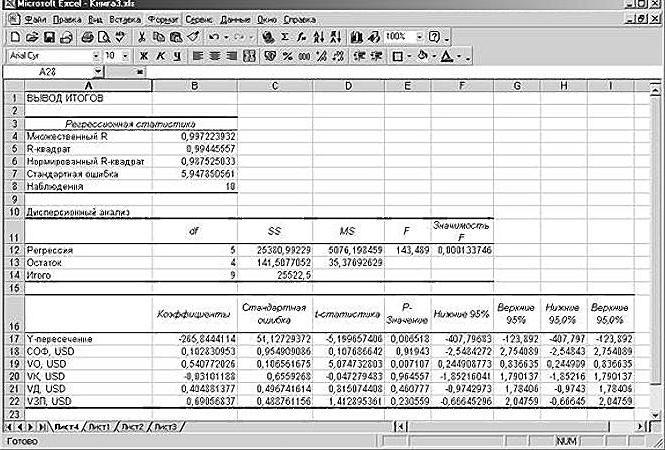
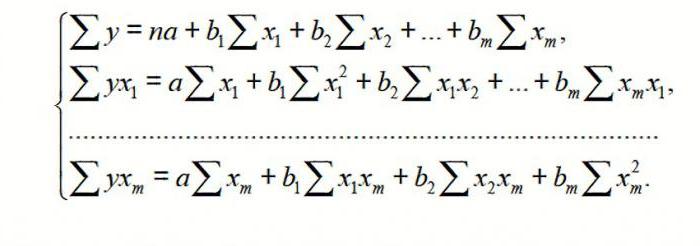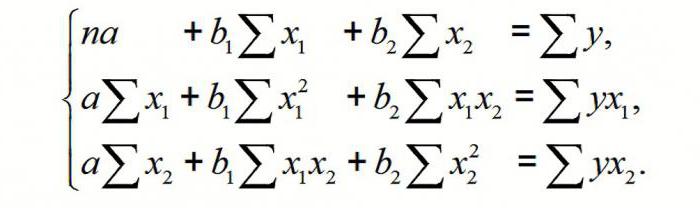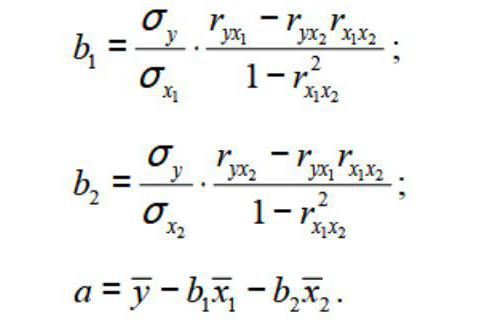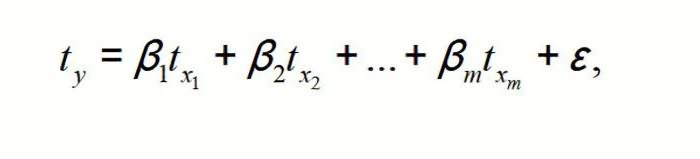Множественная линейная регрессия является одним из наиболее часто используемых методов во всей статистике.
В этом руководстве объясняется, как интерпретировать каждое значение в выходных данных модели множественной линейной регрессии в Excel.
Пример: интерпретация выходных данных регрессии в Excel
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве переменных-предикторов, и экзаменационный балл в качестве переменной ответа.
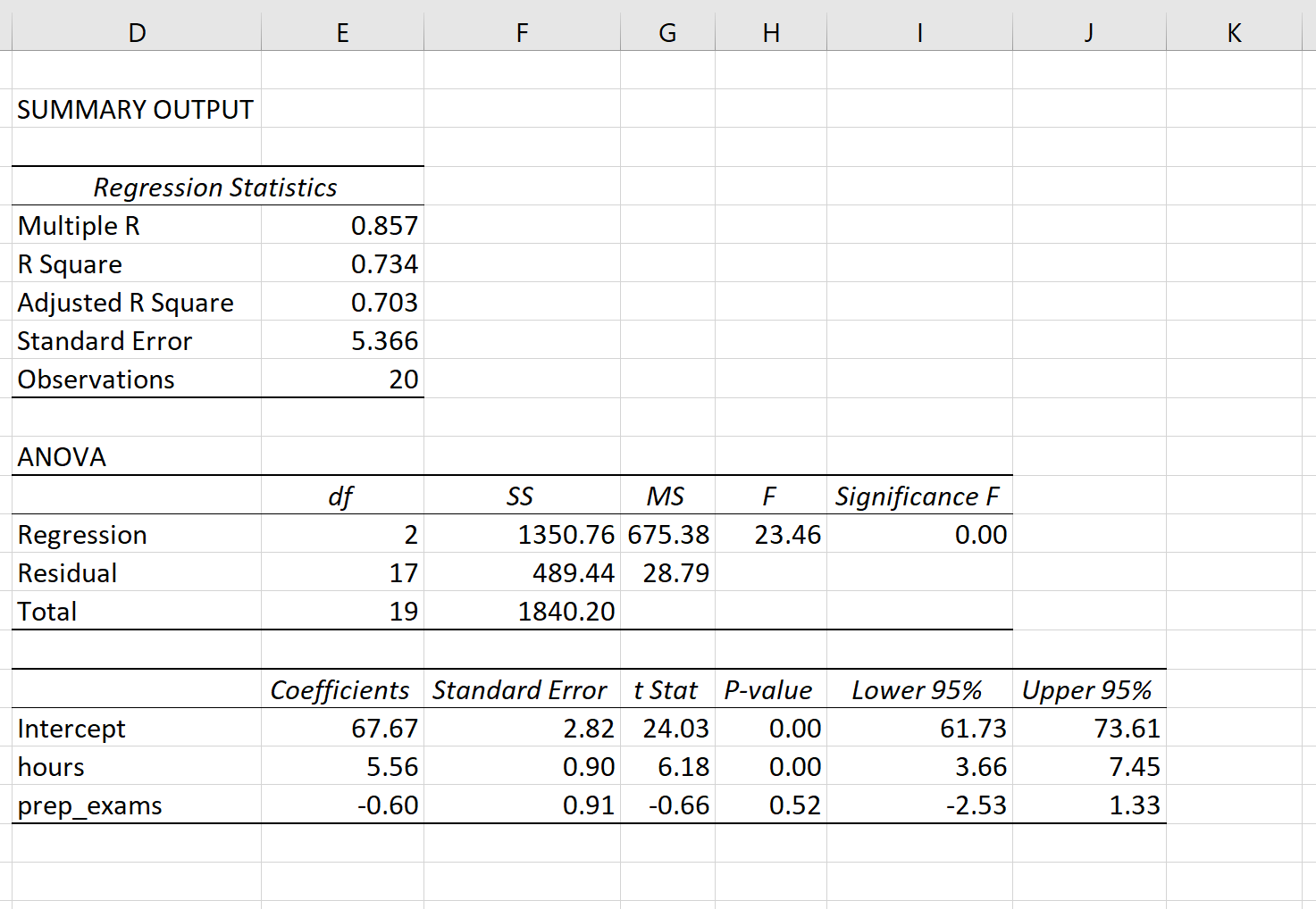
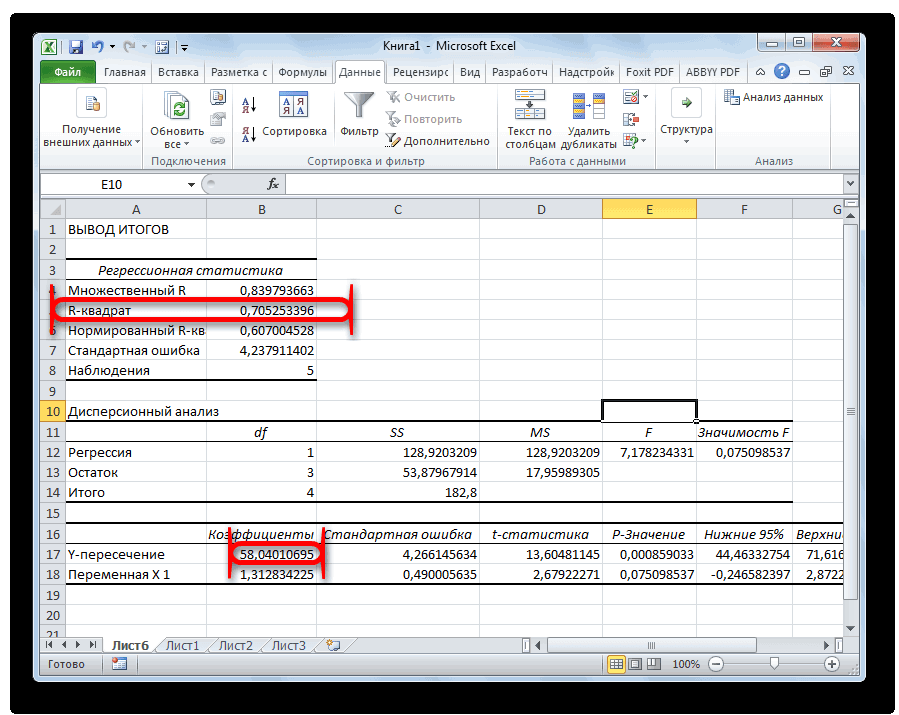
На следующем снимке экрана показаны выходные данные регрессии этой модели в Excel:
Вот как интерпретировать наиболее важные значения в выводе:
Несколько R: 0,857.Это представляет собой множественную корреляцию между переменной ответа и двумя переменными-предикторами.
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Скорректированный квадрат R: 0,703.Это представляет собой значение R-квадрата, скорректированное с учетом количества переменных-предикторов в модели.Это значение также будет меньше, чем значение для R Square, и наказывает модели, которые используют в модели слишком много переменных-предикторов.
Стандартная ошибка: 5,366.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Наблюдения: 20.Общий размер выборки набора данных, используемого для создания регрессионной модели.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой.
В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и количество сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной.
Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05.
Как написать оценочное уравнение регрессии
Мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее оценочное уравнение регрессии:
Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает.
Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
Экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель.
В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
Дополнительные ресурсы
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
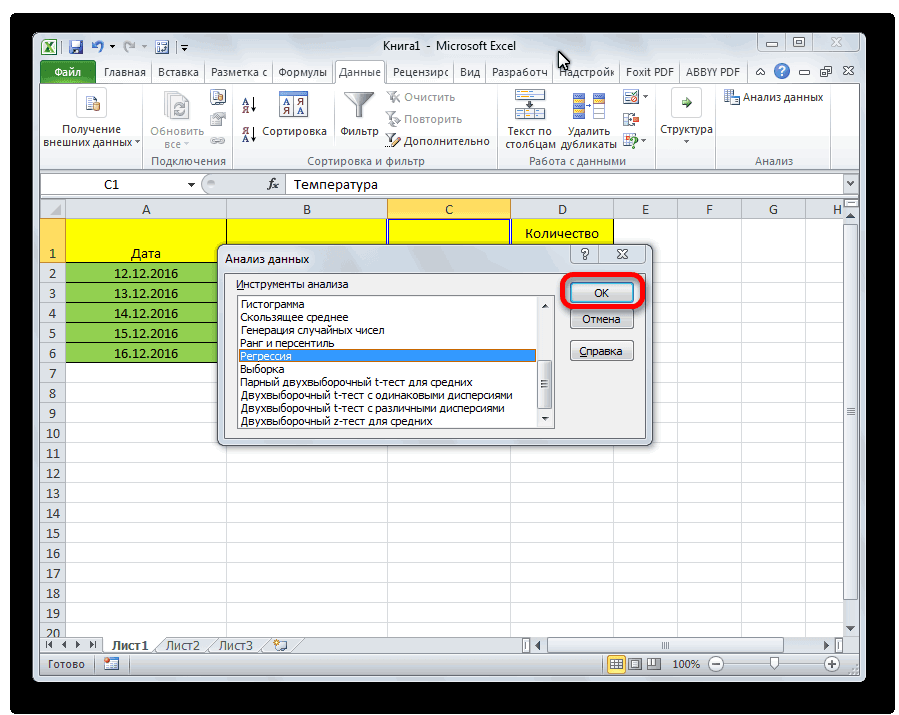
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
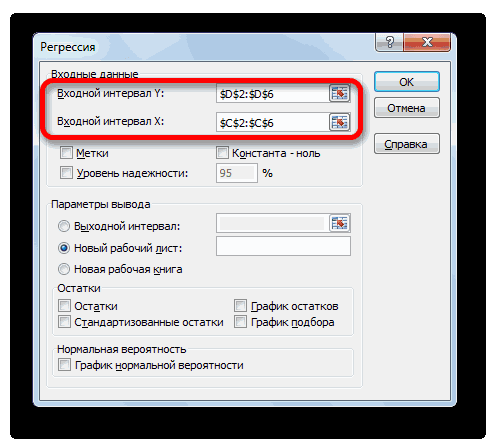
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
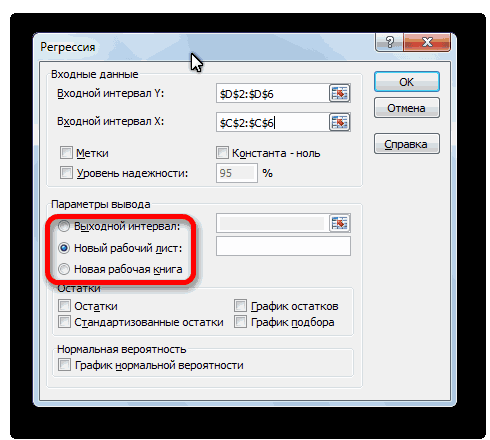
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
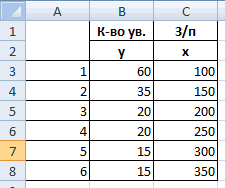
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
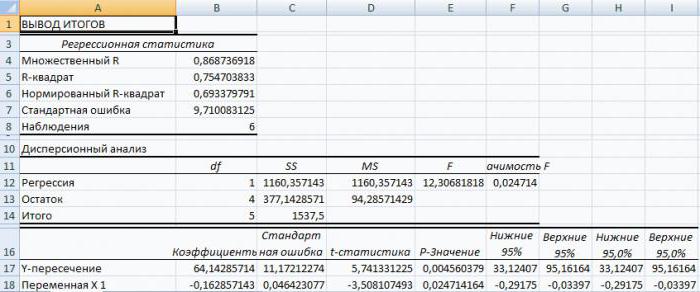
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
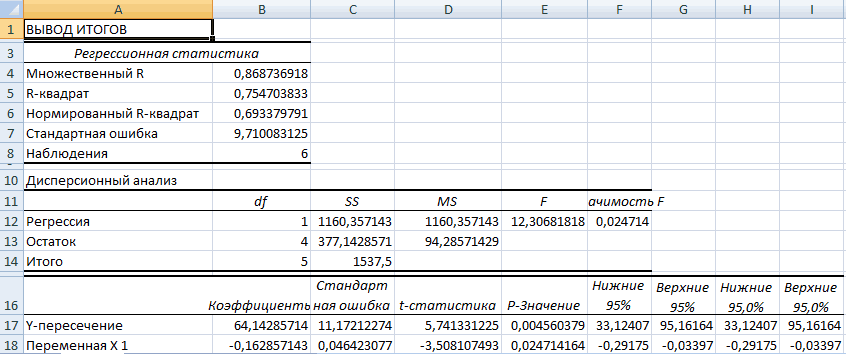
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
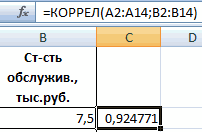
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
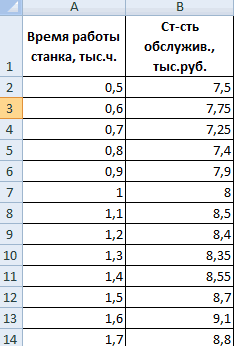
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
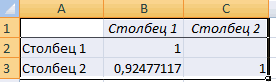
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
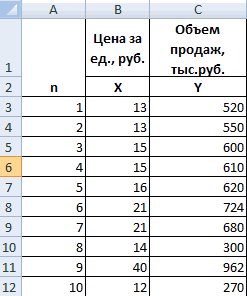
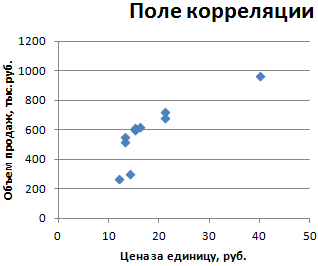
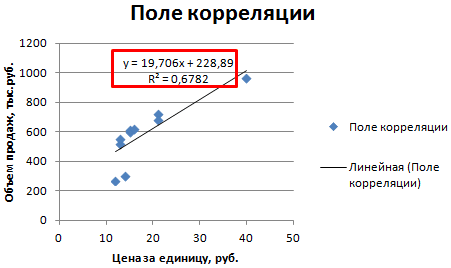
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами
как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН
.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
4) В окне Категория
выберете Статистические
, в окне функция — ЛИНЕЙН
. Щёлкните по кнопке ОК
как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у
Известные значения х
Константа
— логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика
— логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК
;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу
, а затем на комбинацию клавиш ++
.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Стандартная ошибка y | |
| F-статистика | |
| Регрессионная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее
, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия
можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа
. В главном меню последовательно выберите: Файл/Параметры/Надстройки
.
2) В раскрывающемся списке Управление
выберите пункт Надстройки Excel
и нажмите кнопку Перейти.
3) В окне Надстройки
установите флажок Пакет анализа
, а затем нажмите кнопку ОК
.
Если Пакет анализа
отсутствует в списке поля Доступные надстройки
, нажмите кнопку Обзор
, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да
, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия
, а затем нажмите кнопку ОК
.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y
— диапазон, содержащий данные результативного признака;
Входной интервал X
— диапазон, содержащий данные факторного признака;
Метки
— флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль
— флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал
— достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК
.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК
.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача:
Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
Теперь стали видны и данные регрессионного анализа.
Регрессионный анализ в Microsoft Excel – наиболее полное руководств по использованию MS Excel для решения задач регрессионного анализа в области бизнес-аналитики. Конрад Карлберг доступно объясняет теоретические вопросы, знание которых поможет вам избежать многих ошибок как при самостоятельном проведении регрессионного анализа, так и при оценке результатов анализа, выполненного другими людьми. Весь материал, от простых корреляций и t-тестов до множественного ковариационного анализа, основан на реальных примерах и сопровождается подробным описанием соответствующих пошаговых процедур.
В книге обсуждаются особенности и противоречия, связанные с функциями Excel для работы с регрессией, рассматриваются последствия использования каждой их опции и каждого аргумента и объясняется, как надежно применять регрессионные методы в самых разных областях, от медицинских исследований до финансового анализа.
Конрад Карлберг. Регрессионный анализ в Microsoft Excel. – М.: Диалектика, 2017. – 400 с.
Скачать заметку в формате или , примеры в формате
Глава 1. Оценка изменчивости данных
В распоряжении статистиков имеется множество показателей вариации (изменчивости). Один из них – сумма квадратов отклонений индивидуальных значений от среднего. В Excel для него используется функция КВАДРОТКЛ(). Но чаще используется дисперсия. Дисперсия — это среднее квадратов отклонений. Дисперсия нечувствительна к количеству значений в исследуемом наборе данных (в то время как сумма квадратов отклонений растет с числом измерений).
Программа Excel предлагает две функции, возвращающие дисперсию: ДИСП.Г() и ДИСП.В():
- Используйте функцию ДИСП.Г(), если подлежащие обработке значения образуют генеральную совокупность. Т.е., значения, содержащиеся в диапазоне, являются единственными значениями, которые вас интересуют.
- Используйте функцию ДИСП.В(), если подлежащие обработке значения образуют выборку из совокупности большего объема. Предполагается, что имеются дополнительные значения, дисперсию которых вы также можете оценить.
Если такая величина, как среднее значение или коэффициент корреляции, рассчитывается на основе генеральной совокупности, то она называется параметром. Аналогичная величина, рассчитываемая на основе выборки, называется статистикой. Отсчитывая отклонения от среднего значения
в данном наборе, вы получите сумму квадратов отклонений меньшей величины, чем если бы отсчитывали их от любого другого значения. Аналогичное утверждение справедливо и для дисперсии.
Чем больше объем выборки, тем точнее рассчитанное значение статистики. Но не существует ни одной выборки с объемом меньше объема генеральной совокупности, относительно которой вы могли бы быть уверены в том, что значение статистики совпадает со значением параметра.
Допустим, у вас есть набор из 100 значений роста, среднее которых отличается от среднего по генеральной совокупности, каким бы малым ни было это различие. Рассчитав дисперсию для выборки, вы получите некоторое ее значение, скажем, 4. Это значение меньше любого другого, которое можно получить, рассчитывая отклонение каждого из 100 значений роста относительно любого значения, отличного от среднего по выборке, в там числе и относительно истинного среднего по генеральной совокупности. Поэтому вычисленная дисперсия будет отличаться, причем в меньшую сторону, от дисперсии, которую вы получили бы, если бы каким-то образом узнали и использовали не выборочное среднее, а параметр генеральной совокупности.
Средняя сумма квадратов, определенная для выборки, дает нижнюю оценку дисперсии генеральной совокупности. Вычисленную таким способом дисперсию называют смещенной
оценкой. Оказывается, чтобы исключить смещение и получить несмещенную оценку, достаточно разделить сумму квадратов отклонений не на n
, где n
— размер выборки, а на n – 1
.
Величина n – 1
называется количеством (числом) степеней свободы. Существуют разные способы расчета этой величины, хотя все они включают либо вычитание некоторого числа из размера выборки, либо подсчет количества категорий, в которые попадают наблюдения.
Суть различия между функциями ДИСП.Г() и ДИСП.В() состоит в следующем:
- В функции ДИСП.Г() сумма квадратов делится на количество наблюдений и, следовательно, представляет смещенную оценку дисперсии, истинное среднее.
- В функции ДИСП.В() сумма квадратов делится на количество наблюдений минус 1, т.е. на количество степеней свободы, что дает более точную, несмещенную оценку дисперсии генеральной совокупности, из которой была извлечена данная выборка.
Стандартное отклонение (англ. standard deviation
, SD) – есть квадратный корень из дисперсии:
Возведение отклонений в квадрат переводит шкалу измерений в другую метрику, являющуюся квадратом исходной: метры — в квадратные метры, доллары — в квадратные доллары и т.д. Стандартное отклонение — это корень квадратный из дисперсии, и поэтому оно возвращает нас к исходным единицам измерения. Что удобнее.
Часто приходится рассчитывать стандартное отклонение после того, как данных были подвергнуты некоторым манипуляциям. И хотя в этих случаях результаты несомненно являются стандартными отклонениями, их принято называть стандартными ошибками
. Существует несколько разновидностей стандартных ошибок, в том числе стандартная ошибка измерения, стандартная ошибка пропорции, стандартная ошибка среднего.
Предположим, вы собрали данные о росте 25 случайно выбранных взрослых мужчин в каждом из 50 штатов. Далее вы вычисляете средний рост взрослых мужчин в каждом штате. Полученные 50 средних значений в свою очередь можно считать наблюдениями. Исходя из этого, вы могли бы рассчитать их стандартное отклонение, которое и является стандартной ошибкой среднего
. Рис. 1. позволяет сравнить распределение 1250 исходных индивидуальных значений (данные о росте 25 мужчин по каждому из 50 штатов) с распределением средних значений 50 штатов. Формула для оценки стандартной ошибки среднего (т.е. стандартного отклонения средних значений, а не индивидуальных наблюдений):
где – стандартная ошибка среднего; s
– стандартное отклонение исходных наблюдений; n
– количество наблюдений в выборке.
Рис. 1. Вариация средних значений от штата к штату значительно меньше вариации индивидуальных результатов наблюдений
В статистике существует соглашение относительно использования греческих и латинских букв для обозначения статистических величин. Греческими буквами принято обозначать параметры генеральной совокупности, латинскими — выборочные статистики. Следовательно, если речь идет о стандартном отклонении генеральной совокупности, мы записываем его как σ; если же рассматривается стандартное отклонение выборки, то используем обозначение s. Что касается символов для обозначения средних, то они согласуются между собой не столь удачно. Среднее по генеральной совокупности обозначается греческой буквой μ. Однако для представления выборочного среднего традиционно используется символ X̅.
z-оценка
выражает положение наблюдения в распределении в единицах стандартного отклонения. Например, z = 1,5 означает, что наблюдение отстоит от среднего на 1,5 стандартного отклонения в сторону больших значений. Термин z-оценка
используют для индивидуальных оценок, т.е. для измерений, приписываемых отдельным элементам выборки. В отношении таких статистик (например, среднее значение по штату) используют термин z-значение
:
где X̅ – среднее значение выборки, μ – среднее значение генеральной совокупности, – стандартная ошибка средних набора выборок:
где σ – стандартная ошибка генеральной совокупности (индивидуальных измерений), n
– размер выборки.
Предположим, вы работаете инструктором в гольф-клубе. Вы имели возможность в течение длительного времени измерять дальность ударов и знаете, что ее среднее значение составляет 205 ярдов, а стандартное отклонение — 36 ярдов. Вам предложили новую клюшку, утверждая, что она увеличит дальность удара на 10 ярдов. Вы просите каждого из последующих 81 посетителей клуба выполнить пробный удар новой клюшкой и записываете его дальность удара. Оказалось, что средняя дальность удара новой клюшкой составляет 215 ярдов. Какова вероятность того, что разница в 10 ярдов (215 – 205) обусловлена исключительно ошибкой выборки? Или по-другому: какова вероятность того, что при более масштабном тестировании новая клюшка не продемонстрирует увеличение дальности удара по сравнению с имеющимся долговременным средним показателем 205 ярдов?
Мы можем проверить это, сформировав z-значение. Стандартная ошибка среднего:
Тогда z-значение:
Нам нужно найти вероятность того, что среднее по выборке будет отстоять от среднего по генеральной совокупности на 2,5σ. Если вероятность будет маленькой, значит отличия обусловлены не случайностью, а качеством новой клюшки. В Excel для определения вероятности z-значения нет готовой функции. Однако можно использовать формулу =1-НОРМ.СТ.РАСП(z-значение;ИСТИНА), где функция НОРМ.СТ.РАСП() возвращает площадь под нормальной кривой слева от z-значения (рис. 2).
Рис. 2. Функция НОРМ.СТ.РАСП() возвращает площадь под кривой слева от z-значения; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Второй аргумент функции НОРМ.СТ.РАСП() может принимать два значения: ИСТИНА – функция возвращает площадь области под кривой слева от точки, заданной первым аргументом; ЛОЖЬ – функция возвращает высоту кривой в точке, заданной первым аргументом.
Если среднее значение (μ) и стандартное отклонение (σ) генеральной совокупности не известны, используется t-значение (подробнее см. ). Структуры z- и t-значения отличаются тем, что для нахождения t-значения используется стандартное отклонение s, полученное на основе выборочных результатов, а не известное значение параметра генеральной совокупности σ. Нормальная кривая имеет единственную форму, а форма распределения t-значений варьирует в зависимости от количества степеней свободы df (от англ. degrees of freedom
) выборки, которую оно представляет. Количество степеней свободы выборки равно n – 1
, где n
— размер выборки (рис. 3).
Рис. 3. Форма t-распределений, возникающих в тех случаях, когда параметр σ неизвестен, отличается от формы нормального распределения
В Excel есть две функции для t-распределения также называемого распределением Стьюдента: СТЬЮДЕНТ.РАСП() возвращает величину площади под кривой слева от заданного t-значения, а СТЬЮДЕНТ.РАСП.ПХ() – справа.
Глава 2. Корреляция
Корреляция — это мера зависимости между элементами набора упорядоченных пар. Корреляция характеризуется коэффициентам корреляции Пирсона
– r. Коэффициент может принимать значения в интервале от –1,0 до +1,0.
где S x
и S y
– стандартные отклонения переменных Х
и Y
, S xy
– ковариация:
В этой формуле ковариация делится на стандартные отклонения переменных Х
и Y
, тем самым удаляя из ковариации эффекты масштабирования, связанные с единицами измерения. В Excel используется функция КОРРЕЛ(). В названии этой функции отсутствуют уточняющие элементы Г и В, которые используются в названиях таких функций, как СТАНДОТКЛОН(), ДИСП() или КОВАРИАЦИЯ(). Хотя коэффициенте корреляции по выборке предоставляемая смещенную оценку, однако причина смещения иная, нежели в случае дисперсии или стандартного отклонения.
В зависимости от величины генерального коэффициента корреляции (часто обозначаемого греческой буквой ρ
), коэффициент корреляции r
дает смещенную оценку, причем эффект смещения усиливается с уменьшением размера выборок. Тем не менее мы не пытаемся корректировать это смещение аналогично тому, как, например, делали это при вычислении стандартного отклонения, когда подставляли в соответствующую формулу не количество наблюдений, а количество степеней свободы. В действительности количество наблюдений, используемое для вычисления ковариации, не оказывает никакого влияния на величину.
Стандартный коэффициент корреляции предназначен для использования с переменными, связанными между собой линейным соотношением. Наличие нелинейности и/или ошибок в данных (выбросы) приводят к неверному расчету коэффициента корреляции. Для диагностики проблем с данными рекомендуется строить точечные диаграммы. Это единственный тип диаграмм в Excel, в котором и горизонтальная, и вертикальная оси трактуются как оси значений. Линейная же диаграмма один из столбцов определяет, как ось категорий, что искажает картину данных (рис. 4).
Рис. 4. Линии регрессии кажутся одинаковыми, однако сравните между собой их уравнения
Наблюдения, использованные для построения линейной диаграммы, располагаются вдоль горизонтальной оси эквидистантно. Надписи делений вдоль этой оси — это и есть всего лишь надписи, а не числовые значения.
Несмотря на то что корреляция часто означает наличие причинно-следственной связи, она не может служить доказательством того, что так оно и есть. Статистика не используется для демонстрации того, истинна или ложна теория. Для исключения конкурирующих объяснений результатов наблюдений ставят плановые эксперименты
. Статистика же привлекается для обобщения информации, собранной в ходе таких экспериментов, и количественной оценки вероятности того, что принимаемое решение может быть неверным при имеющейся доказательной базе.
Глава 3. Простая регрессия
Если две переменные связаны между собой, так что значение коэффициента корреляции превышает, скажем, 0,5, то в этом случае можно прогнозировать (с некоторой точностью) неизвестное значение одной переменной по известному значению другой. Для получения прогнозных значений цены, исходя из данных, приведенных на рис. 5, можно использовать любой из нескольких возможных способов, но почти наверняка вы не будете использовать тот, который представлен на рис. 5. И все же вам стоит с ним ознакомиться, поскольку ни один другой способ не позволяет так же отчетливо продемонстрировать связь между корреляцией и прогнозированием, как этот. На рис. 5 в диапазоне В2:С12 представлена случайная выборка из десяти домов и приведены данные о площади каждого дома (в квадратных футах) и его продажной цене.
Рис. 5. Прогнозные значения продажной цены образуют прямую линию
Найдите средние значения, стандартные отклонения и коэффициент корреляции (диапазон А14:С18). Рассчитайте z-оценки площади (Е2:Е12). Например, ячейка ЕЗ содержит формулу: =(В3-$В$14)/$В$15. Вычислите z-оценки прогнозной цены (F2:F12). Например, ячейка F3 содержит формулу: =ЕЗ*$В$18. Переведите z-оценки в цены в долларах (Н2:Н12). В ячейке НЗ формула: =F3*$C$15+$C$14.
Обратите внимание: прогнозное значение всегда стремится сместиться в сторону среднего, равного 0. Чем ближе к нулю коэффициент корреляции, тем ближе к нулю прогнозная z-оценка. В нашем примере коэффициент корреляции между площадью и продажной ценой равен 0,67, и прогнозная цена равна 1,0*0,67, т.е. 0,67. Этому соответствует превышение значения над средним значением, равное двум третям стандартного отклонения. Если бы коэффициент корреляции был равен 0,5, то прогнозная цена составила бы 1,0*0,5, т.е. 0,5. Этому соответствует превышение значения над средним значением, равное лишь половине стандартного отклонения. Всякий раз, когда значение коэффициента корреляции отличается от идеального, т.е. больше -1,0 и меньше 1,0, оценка прогнозируемой переменной должна быть ближе к своему среднему значению, чем оценка предикторной (независимой) переменной к своему. Это явление называется регрессией к среднему, или просто регрессией.
В Excel есть несколько функций для определения коэффициентов уравнения линии регрессии (в Excel она называется линией тренда) у =
kx
+
b
. Для определения k
служит функция
=НАКЛОН(известные_значения_у; известные_значения_х)
Здесь у
– прогнозируемая переменная, а х
– независимая переменная. Вы должны строго следовать этому порядку переменных. Наклон линии регрессии, коэффициент корреляции, стандартные отклонения переменных и ковариация тесно связаны между собой (рис. 6). Функция ОТРЕЗОК() возвращает значение, отсекаемое линией регрессии на вертикальной оси:
=ОТРЕЗОК(известные_значения_у; известные_значения_х)
Рис. 6. Соотношение между стандартными отклонениями преобразует ковариацию в коэффициент корреляции и наклон линии регрессии
Обратите внимание, что количество значений х и у, предоставляемых функциям НАКЛОН() и ОТРЕЗОК() в качестве аргументов, должно быть одинаковым.
В регрессионном анализе используется еще один важный показатель – R 2 (R-квадрат), или коэффициент детерминации. Он определяет, какой вклад в общую изменчивость данных вносит выявленная с помощью регрессии зависимость между х
и у
. В Excel для него есть функция КВПИРСОН(), которая принимает точно те же аргументы, что и функция КОРРЕЛ().
О двух переменных с ненулевым коэффициентом корреляции между ними говорят, что они объясняют дисперсию или имеют объясненную дисперсию. Обычно объясненная дисперсия выражается в процентах. Так R
2
= 0,81 означает, что 81% дисперсии (разброса) двух переменных является объясненной. Остальные 19% обусловлены случайными флуктуациями.
В Excel имеется функция ТЕНДЕНЦИЯ, которая упрощает вычисления. Функция ТЕНДЕНЦИЯ():
- принимает предоставляемые вами известные значения х
и известные значения у
; - вычисляет наклон линии регрессии и константу (отрезок);
- возвращает прогнозные значения у
, определяемые на основании применения уравнения регрессии к известным значениям х
(рис. 7).
Функция ТЕНДЕНЦИЯ() является функцией массива (если вы ранее не сталкивались с такими функциями, рекомендую ).
Рис. 7. Использование функции ТЕНДЕНЦИЯ() позволяет ускорить и упростить вычисления по сравнению с использованием пары функций НАКЛОН() и ОТРЕЗОК()
Чтобы ввести функцию ТЕНДЕНЦИЯ() в виде формулы массива в ячейки G3:G12, выделите диапазон G3:G12, введите формулу ТЕНДЕНЦИЯ (СЗ:С12;ВЗ:В12), нажмите и удерживайте клавиши и только после этого нажмите клавишу . Обратите внимание, что формула заключена в фигурные скобки: { и }. Так Excel сообщает вам о том, что данная формула воспринята именно как формула массива. Не вводите сами скобки: если вы попытаетесь ввести их самостоятельно в составе формулы, Excel воспримет ваш ввод как обычную текстовую строку.
У функции ТЕНДЕНЦИЯ() есть еще два аргумента: новые_значения_х
и конст
. Первый позволяет построить прогноз на будущее, а второй может заставить линию регрессии пройти через начало координат (значение ИСТИНА говорит Excel использовать расчетную константу, значение ЛОЖЬ – константу = 0). Excel позволяет нарисовать регрессионную прямую на графике так, чтобы она проходила через начало координат. Начните с построения точечной диаграммы, после чего щелкните правой кнопкой мыши на одном из маркеров ряда данных. Выберите в открывшемся контекстном меню пункт Добавить линию тренда
; выберите вариант Линейная
; при необходимости прокрутите панель вниз, установите флажок Настроить пересечение
; убедитесь, что в связанном с ним текстовом поле задано значение 0,0.
Если у вас есть три переменных, и вы хотите определить корреляцию между двумя из них, исключив влияние третьей, можно использовать частную корреляцию
. Предположим, вас интересует связь между процентной долей жителей города, закончивших колледж, и количеством книг в городских библиотеках. Вы собрали данные по 50 городам, но… Проблема в том, что оба этих параметра могут зависеть от благосостояния жителей того или иного города. Разумеется, очень трудно подобрать другие 50 городов, характеризующихся в точности одинаковым уровнем благосостояния жителей.
Применяя статистические методы для исключения влияния, оказываемого фактором благосостояния как на финансовую поддержку библиотек, так и на доступность обучения в колледже, вы могли бы получить более точную количественную оценку степени зависимости между интересующими вас переменными, а именно: количеством книг и количеством выпускников. Такая условная корреляция между двумя переменными, когда значения других переменных фиксированы, и называется частной корреляцией. Один из способов ее расчета заключается в использовании уравнения:
Где r
CB
.
W
— коэффициент корреляции между переменными Колледж (College) и Книги (Books) при исключенном влиянии (фиксированном значении) переменной Благосостояние (Wealth); r
CB
— коэффициент корреляции между переменными Колледж и Книги; r
CW
— коэффициент корреляции между переменными Колледж и Благосостояние; r
BW
— коэффициент корреляции между переменными Книги и Благосостояние.
С другой стороны, частную корреляцию можно рассчитать на основе анализа остатков, т.е. разностей между прогнозными значениями и связанными с ними результатами фактических наблюдений (оба метода представлены на рис. 8).
Рис. 8. Частная корреляция, как корреляция остатков
Для упрощения подсчета матрицы коэффициентов корреляции (В16:Е19) используйте пакет анализа Excel (меню Данные
–> Анализ
–> Анализ данных
). По умолчанию этот пакет в Excel не активен. Для его установки пройдите по меню Файл
–> Параметры
–> Надстройки
. Внизу открывшегося окна Параметры
Excel
найдите поле Управление
, выберите Надстройки
Excel
, кликните Перейти
. Поставьте галочку напротив надстройки Пакет анализа
. Кликните Анализ данных
, выберите опцию Корреляция
. В качестве входного интервала укажите $B$2:$D$13, поставьте галочку Метки в первой строке
, в качестве выходного интервала укажите $B$16:$E$19.
Еще одна возможность – определить получастную корреляцию. Например, вы исследуете влияние роста и возраста на вес. Таким образом, у вас две предикторные переменные – рост и возраст, и одна прогнозируемая переменная – вес. Вы хотите исключить влияние одной предикторной переменной на другую, но не на прогнозную переменную:
где Н – Рост (Height), W– Вес (Weight), А – Возраст (Age); в индексе получастного коэффициента корреляции используются круглые скобки, с помощью которых указывается, влияние какой переменной устраняется и из какой именно переменной. В данном случае обозначение W(Н.А) указывает на то, что влияние переменной Возраст удаляется из переменной Рост, но не из переменной Вес.
Может создаться впечатление, что обсуждаемый вопрос не имеет существенного значения. Ведь важнее всего то, насколько точно работает общее уравнение регрессии, тогда как проблема относительных вкладов отдельных переменных в суммарную объясненную дисперсию представляется второстепенной. Однако это далеко не так. Как только вы начинаете задумываться над тем, стоит ли вообще использовать какую-то переменную в уравнении множественной регрессии, проблема становится важной. Она может влиять на оценку правильности выбора модели для анализа.
Глава 4. Функция ЛИНЕЙН()
Функция ЛИНЕЙН() возвращает 10 статистик регрессионного анализа. Функция ЛИНЕЙН() является функцией массива. Для ее ввода выделите диапазон, содержащий пять строк и два столбца, напечатайте формулу, и нажмите (рис. 9):
ЛИНЕЙН(B2:B21;A2:A21;ИСТИНА;ИСТИНА)
Рис. 9. Функция ЛИНЕЙН(): а) выделите диапазон D2:E6, б) введите формулу, как показано в строке формул, в) нажмите
Функция ЛИНЕЙН() возвращает:
- коэффициент регрессии (или наклон, ячейка D2);
- отрезок (или константа, ячейка Е3);
- стандартные ошибки коэффициента регрессии и константы (диапазон D3:E3);
- коэффициент детерминации R 2 для регрессии (ячейка D4);
- стандартная ошибка оценки (ячейка Е4);
- F-критерий для полной регрессии (ячейка D5);
- количество степеней свободы для остаточной суммы квадратов (ячейка Е5);
- регрессионная сумма квадратов (ячейка D6);
- остаточная сумма квадратов (ячейка Е6).
Рассмотрим каждую из этих статистик и их взаимодействие.
Стандартная ошибка
в нашем случае – это стандартное отклонение, вычисляемое для ошибок выборки. Т.е., это ситуация, когда генеральная совокупность имеет одну статистику, а выборка – другую. Разделив коэффициент регрессии на стандартную ошибку, вы получите значение 2,092/0,818 = 2,559. Иными словами, коэффициент регрессии, равный 2,092, отстоит от нуля на две с половиной стандартные ошибки.
Если коэффициент регрессии равен нулю, то наилучшей оценкой прогнозируемой переменной является ее среднее значение. Две с половиной стандартные ошибки — это довольно большая величина, и вы с уверенностью можете полагать, что коэффициент регрессии для генеральной совокупности имеет ненулевое значение.
Можно определить вероятность получения выборочного коэффициента регрессии 2,092, если его фактическое значение в генеральной совокупности равно 0,0 с помощью функции
СТЬЮДЕНТ.РАСП.ПХ(t-критерий = 2,559; количество степеней свободы =18)
В общем количество степеней свободы = n – k – 1, где n — количество наблюдений, а k — количество предикторных переменных.
Эта формула возвращает значение 0,00987 или, округленно, 1%. Оно сообщает нам следующее: если коэффициент регрессии для генеральной совокупности равен 0%, то вероятность получения выборки из 20 человек, для которой расчетное значение коэффициента регрессии равно 2,092, составляет скромный 1%.
F-критерий (ячейка D5 на рис. 9) выполняет те же функции по отношению к полной регрессии, что и t-критерий по отношению к коэффициенту простой парной регрессии. F-критерий используется для проверки того, действительно ли коэффициент детерминации R 2 для регрессии имеет достаточно большую величину, позволяющую отбросить гипотезу о том, что в генеральной совокупности он имеет значение 0,0, которое указывает на отсутствие дисперсии, объясняемой предикторной и прогнозируемой переменной. При наличии только одной предикторной переменной F-критерий в точности равен квадрату t-критерия.
До сих пор мы рассматривали интервальные переменные. Если же у вас переменные, которые могут принимать несколько значений, представляющих собой простые имена, например, Мужчина и Женщина или Пресмыкающееся, Земноводное и Рыба, представьте их в виде числового кода. Такие переменные называются номинальными.
Статистика R 2
дает количественную оценку доли объясненной дисперсии.
Стандартная ошибка оценки.
На рис. 4.9 представлены прогнозные значения переменной Вес, полученные на основании ее связи с переменной Рост. В диапазоне Е2:Е21 содержатся значения остатков для переменной Вес. Точнее эти остатки называть ошибками — отсюда и следует термин стандартная ошибка оценки.
Рис. 10. Как R 2 , так и стандартная ошибка оценки выражают точность прогнозов, получаемых с помощью регрессии
Чем меньше стандартная ошибка оценки, тем точнее уравнение регрессии и тем более близкого совпадения любого прогноза, полученного с помощью уравнения, с фактическим наблюдением вы ожидаете. Стандартная ошибка оценки предоставляет способ количественной оценки этих ожиданий. Вес 95% людей, обладающих неким ростом, будет находиться в диапазоне:
(рост * 2,092 – 3,591) ± 2,092*21,118
F-статистика
– это отношение межгрупповой дисперсии к внутригрупповой дисперсии. Это название было введено статистиком Джорджем Снедекором в честь сэра , разработавшего в начале XX столетия дисперсионный анализ (ANOVA, Analysis of Variance).
Коэффициент детерминации R 2 выражает долю общей суммы квадратов, связанную с регрессией. Величина (1 – R 2) выражает долю общей суммы квадратов, связанную с остатками — ошибками прогнозирования. F-критерий можно получить с использованием функции ЛИНЕЙН (ячейка F5 на рис. 11), с использованием сумм квадратов (диапазон G10:J11), с использованием долей дисперсии (диапазон G14:J15). Формулы можно изучить в прилагаемом файле Excel.
Рис. 11. Расчет F-критерия
При использовании номинальных переменных используется фиктивное кодирование (рис. 12). Для кодирования значений удобно использовать значения 0 и 1. Вероятность F рассчитывается с помощью функции:
F.РАСП.ПХ(К2;I2;I3)
Здесь функция F.РАСП.ПХ() возвращает вероятность получения F-критерия, подчиняющегося центральному F-распределению (рис. 13) для двух наборов данных с количествами степеней свободы, приведенными в ячейках I2 и I3, значение которого совпадает со значением, приведенным в ячейке К2.
Рис. 12. Регрессионный анализ с использованием фиктивных переменных
Рис. 13. Центральное F-распределение при λ = 0
Глава 5. Множественная регрессия
Переходя от простой парной регрессии с одной предикторной переменной к множественной регрессии, вы добавляете одну или несколько предикторных переменных. Сохраняйте значения предикторных переменных в смежных столбцах, например, в столбцах А и В в случае двух предикторов или А, В и С в случае трех предикторов. Прежде чем вводить формулу, включающую функцию ЛИНЕЙН(), выберите пять строк и столько столбцов, сколько имеется предикторных переменных, плюс еще один для константы. В случае регрессии с двумя предикторными переменными можно использовать следующую структуру:
ЛИНЕЙН(А2: А41; В2: С41;;ИСТИНА)
Точно так же в случае трех переменных:
ЛИНЕЙН(А2:А61;В2:D61;;ИСТИНА)
Предположим, вы хотите изучить возможное влияние возраста и диеты на содержание ЛПНП — липопротеинов низкой плотности, которые считаются ответственными за образование атеросклеротических бляшек, служащих причиной атеротромбоза (рис. 14).
Рис. 14. Множественная регрессия
R 2 множественной регрессии (отражаемый в ячейке F13), больше, чем R 2 любой простой регрессии (Е4, Н4). В множественной регрессии одновременно используются несколько предикторных переменных. При этом R 2 почти всегда увеличивается.
Для любого простого линейного уравнения регрессии с одной предикторной переменной между прогнозными значениями и значениями предикторной переменной всегда будет наблюдаться идеальная корреляция, поскольку в таком уравнении значения предиктора умножаются на одну константу и к каждому произведению прибавляется другая константа. Этот эффект не сохраняется во множественной регрессии.
Отображение результатов, возвращаемых функцией ЛИНЕЙН() для множественной регрессии (рис. 15). Коэффициенты регрессии выводятся в составе результатов, возвращаемых функцией ЛИНЕЙН() в порядке обратном расположению переменных
(G–H–I соответствует С–В–А).
Рис. 15. Коэффициенты и их стандартные ошибки отображаются в обратном порядке их следования на рабочем листе
Принципы и процедуры, используемые в регрессионном анализе с одной предикторной переменной, легко адаптируются для учета нескольких предикторных переменных. Оказывается, что многое в этой адаптации зависит от устранения влияния предикторных переменных друг на друга. Последнее связано с частной и получастной корреляциями (рис. 16).
Рис. 16. Множественная регрессия может быть выражена через парную регрессию остатков (формулы см. в Excel-файле)
В Excel, имеются функции, предоставляющие информацию о t- и F-распределениях. Функции, имена которых включают часть РАСП, такие как СТЬЮДЕНТ.РАСП() и F.РАСП(), принимают t- или F-критерий в качестве аргумента и возвращают вероятность наблюдения указанного значения. Функции, имена которых включают часть ОБР, такие как СТЬЮДЕНТ.ОБР() и F.ОБР(), принимают значение вероятности в качестве аргумента и возвращают значение критерия, соответствующее указанной вероятности.
Поскольку мы ищем критические значения t-распределения, которые отсекают края его хвостовых областей, мы передаем 5% в качестве аргумента одной из функций СТЬЮДЕНТ.ОБР(), которая возвращает значение, соответствующее этой вероятности (рис. 17, 18).
Рис. 17. Двусторонний t-тест
Рис. 18. Односторонний t-тест
Устанавливая правило принятия решений в случае однохвостовой альфа-области, вы увеличиваете статистическую мощность теста. Если, приступая к эксперименту, вы уверены в том, что у вас есть все основания ожидать получения положительного (или отрицательного) коэффициента регрессии, то вам следует выполнить однохвостовой тест. В этом случае вероятность того, что вы принимаете правильное решение, отвергая гипотезу о нулевом коэффициенте регрессии в генеральной совокупности, будет выше.
Статистики предпочитают использовать термин направленный тест
вместо термина однохвостовой тест
и термин ненаправленный тест
вместо термина двуххвостовой тест
. Термины направленный и ненаправленный предпочтительнее, поскольку делают акцент на типе гипотезы, а не на природе хвостов распределения.
Подход к оценке влияния предикторов, основанный на сравнении моделей.
На рис. 19 представлены результаты регрессионного анализа, в котором тестируется вклад переменной Диета в уравнение регрессии.
Рис. 19. Сравнение двух моделей путем проверки различий в их результатах
Результаты функции ЛИНЕЙН() (диапазон Н2:К6) имеют отношение к тому, что я называю полной моделью, в которой выполняется регрессия переменной ЛПНП по переменным Диета, Возраст и ЛПВП. В диапазоне Н9:J1З представлены расчеты без учета предикторной переменной Диета. Я называю это ограниченной моделью. В полной модели 49,2% дисперсии зависимой переменной ЛПНП объясняется предикторными переменными. В ограниченной модели лишь 30,8% ЛПНП объясняется переменными Возраст и ЛПВП. Потеря R 2 , обусловленная исключением переменной Диета из модели, составляет 0,183. В диапазоне G15:L17 сделаны расчеты, которые показывают, что лишь с вероятностью 0,0288 влияние переменной Диета является случайным. В остальных 97,1% Диета оказывает влияние на ЛПНП.
Глава 6. Допущения и предостережения в отношении регрессионного анализа
Термин «допущение» не определен достаточно строго, а способ его использования предполагает, что если допущение не соблюдается, то результаты всего анализа являются по меньшей мере сомнительными или, возможно, не имеющими силы. На самом деле это не так, хотя, безусловно, существуют случаи, когда нарушение допущения в корне меняет картину. Основные допущения: а) остатки переменной Y нормально распределены в любой точке X вдоль линии регрессии; б) значения Y находятся в линейной зависимости от значений X; в) дисперсия остатков примерно одинакова в каждой точке Х; г) между остатками отсутствует зависимость.
Если допущения не играют существенной роли, статистики говорят о робастности анализа по отношению к нарушению допущения. В частности, когда вы используете регрессию для тестирования различий между групповыми средними, допущение о том, что значения Y — а значит, и остатки — нормально распределены, не играет существенной роли: тесты робастны по отношению к нарушению допущения о нормальности. При этом важно анализировать данные с помощью диаграмм. Например, включенных в надстройку Анализ данных
инструмент Регрессия
.
Если данные не соответствуют допущениям линейной регрессии, в вашем распоряжении имеются другие подходы, отличные от линейного. Один из них – логистическая регрессия (рис. 20). Вблизи верхнего и нижнего предельных значений предикторной переменной линейная регрессия приводит к нереалистичным прогнозам.
Рис. 20. Логистическая регрессия
На рис. 6.8 отображены результаты двух методов анализа данных, направленного на исследование связи между ежегодным доходом и вероятностью покупки дома. Очевидно, вероятность совершения покупки будет увеличиваться с увеличением дохода. Диаграммы упрощают выявление различий между результатами, прогнозирующими вероятность покупки дома посредством линейной регрессии, и результатами, которые вы могли бы получить, используя другой подход.
На языке статистиков отбрасывание нулевой гипотезы, когда в действительности она является истинной, называется ошибкой I рода.
В надстройке Анализ данных
предлагается удобный инструмент для генерации случайных чисел, предоставляющий пользователю возможность задать желаемую форму распределения (например, Нормальное, Биномиальное или Пуассона), а также среднее значение и стандартное отклонение.
Различия между функциями семейства СТЬЮДЕНТ.РАСП().
Начиная с версии Excel 2010 доступны три разные формы функции, возвращающей долю распределения слева и/или справа от заданного значения t-критерия. Функция СТЬЮДЕНТ.РАСП() возвращает долю площади под кривой распределения слева от указанного вами значения t-критерия. Предположим, у вас имеется 36 наблюдений, и поэтому количество степеней свободы для анализа равно 34, а значение t-критерия = 1,69. В этом случае формула
СТЬЮДЕНТ.РАСП(+1,69;34;ИСТИНА)
возвращает значение 0,05, или 5% (рис. 21). Третий аргумент функции СТЬЮДЕНТ.РАСП() может иметь значение ИСТИНА или ЛОЖЬ. Если он задан равным ИСТИНА, функция возвращает кумулятивную площадь под кривой слева от заданного t-критерия, выраженную в виде доли. Если же он равен ЛОЖЬ, функция возвращает относительную высоту кривой в точке, соответствующей t-критерию. Другие версии функции СТЬЮДЕНТ.РАСП() — СТЬЮДЕНТ.РАСП.ПХ() и СТЬЮДЕНТ.РАСП.2Х() — принимают в качестве аргументов только значение t-критерия и количество степеней свободы и не требуют задания третьего аргумента.
Рис. 21. Более темная затененная область в левом хвосте распределения соответствует доле площади под кривой слева от большого положительного значения t-критерия
Чтобы определить площадь справа от t-критерия используйте одну из формул:
1 — СТЫОДЕНТ.РАСП (1, 69;34;ИСТИНА)
СТЬЮДЕНТ.РАСП.ПХ(1,69;34)
Вся площадь под кривой должна составлять 100%, поэтому вычитание из 1 доли площади слева от значения t-критерия, которую возвращает функция, дает долю площади, располагающейся справа от значения t-критерия. Возможно, вам покажется более предпочтительным вариант непосредственного получения интересующей вас доли площади с помощью функции СТЬЮДЕНТ.РАСП.ПХ(), где ПХ означает правый хвост распределения (рис. 22).
Рис. 22. 5%-ная альфа область для направленного теста
Использование функций СТЬЮДЕНТ.РАСП() или СТЬЮДЕНТ.РАСП.ПХ () подразумевает, что вы выбрали направленную рабочую гипотезу. Направленная рабочая гипотеза в сочетании с установкой значения альфа на уровне 5% означает, что вы помещаете все 5% в правый хвост распределениями. Вы должны будете отвергнуть нулевую гипотезу лишь в том случае, если вероятность полученного вами значения t-критерия составит 5% и менее. Направленные гипотезы обычно приводят к более чувствительным статистическим тестам (эту большую чувствительность также называют большей статистической мощностью).
При ненаправленном тесте значение альфа остается на том же уровне 5%, но распределение будет иным. Поскольку вы должны допускать два исхода вероятность ложноположительного результата должна быть распределена между двумя хвостами распределения. Общепринято распределять эту вероятность поровну (рис. 23).
Используя то же самое полученное значение t-критерия и то же количество степеней свободы, что и в предыдущем примере, воспользуйтесь формулой
СТЬЮДЕНТ.РАСП.2Х(1,69;34)
Без каких-либо особых на то причин функция СТЬЮДЕНТ.РАСП.2Х() возвращает код ошибки #ЧИСЛО!, если в качестве первого аргумента ей предоставляется отрицательное значение t-критерия.
Если выборки содержат разное число данных, воспользуйтесь двухвыборочным t-тестом с различными дисперсиями, включенным в пакет Анализ данных
.
Глава 7. Использование регрессии для тестирования различий между групповыми средними
Переменные, которые ранее фигурировали под названием прогнозируемых переменных, в этой главе будут называться результативными переменными, а вместо термина предикторные переменные будет использоваться термин факторные переменные.
Простейшим из подходов к кодированию номинальной переменной является фиктивное кодирование
(рис. 24).
Рис. 24. Регрессионный анализ на основе фиктивного кодирования
При использовании фиктивного кодирования любого рода следует придерживаться правил:
- Количество столбцов, резервируемых для новых данных, должно быть равным количеству уровней фактора минус
- Каждый вектор представляет один уровень фактора.
- Субъекты одного из уровней, которым часто является контрольная группа, получают код 0 во всех векторах.
Формула в ячейках F2:H6 =ЛИНЕЙН(A2:A22;C2:D22;;ИСТИНА) возвращает регрессионные статистики. Для сравнения на рис. 24 отображены результаты традиционного дисперсионного анализа, возвращаемого инструментом Однофакторный дисперсионный анализ
надстройки Анализ данных
.
Кодирование эффектов.
В другом типе кодирования, получившем название кодирование эффектов,
среднее каждой группы сравнивается со средним групповых средних. Этот аспект кодирования эффектов обусловлен использованием значения -1 вместо 0 в качестве кода для группы, которая получает один и тот же код во всех кодовых векторах (рис. 25).
Рис. 25. Кодирование эффектов
Когда используется фиктивное кодирование, значение константы, возвращаемое функцией ЛИНЕЙН(), совпадает со средним группы, которой во всех векторах назначены нулевые коды (обычно это контрольная группа). В случае кодирования эффектов константа равна общему среднему (ячейка J2).
Общая линейная модель — полезный способ концептуализации компонентов значения результирующей переменной:
Y ij = μ + α j + ε ij
Использование в этой формуле греческих букв вместо латинских подчеркивает тот факт, что она относится к генеральной совокупности, из которой извлекаются выборки, но ее можно переписать в виде, указывающем на то, что она относится к выборкам, извлекаемым изданной генеральной совокупности:
Y ij = Y̅ + a j + e ij
Идея состоит в том, что каждое наблюдение Y ij можно рассматривать как сумму следующих трех компонентов: общее среднее, μ; эффект обработки j, а j ; величина e ij , которая представляет отклонение индивидуального количественного показателя Y ij от комбинированного значения общего среднего и эффекта j-й обработки (рис. 26). Целью уравнения регрессии является минимизация суммы квадратов остатков.
Рис. 26. Наблюдения, разложенные на компоненты общей линейной модели
Факторный анализ.
Если исследуется связь между результативной переменной и одновременно двумя или более факторами, то в этом случае говорят об использовании факторного анализа. Добавление одного или нескольких факторов в однофакторный дисперсионный анализ может увеличивать статистическую мощность. В однофакторном дисперсионном анализе вариация результативной переменной, которая не может быть приписана фактору, включается в остаточный средний квадрат. Но вполне может быть так, что эта вариация с вязана с другим фактором. Тогда эта вариация может быть удалена из среднеквадратической ошибки, уменьшение которой приводит к увеличению значений F-критерия, а значит, к увеличению статистической мощности теста. Надстройка Анализ данных
включает инструмент, обеспечивающий обработку двух факторов одновременно (рис. 27).
Рис. 27. Инструмент Двухфакторный дисперсионный анализ с повторениями Пакета анализа
Использованный на этом рисунке инструмент дисперсионного анализа, полезен тем, что он возвращает среднее и дисперсию результативной переменной, а также значение счетчика для каждой группы, включенной в план. В таблице Дисперсионный анализ
отображаются два параметра, отсутствующие в выходной информации однофакторной версии инструмента дисперсионного анализа. Обратите внимание на источники вариации Выборка
и Столбцы
в строках 27 и 28. Источник вариации Столбцы
относится к полу. Источник вариации Выборка
относится к любой переменной, значения которой занимают различные строки. На рис. 27 значения для группы КурсЛеч1 находятся в строках 2-6, группы КурсЛеч2 — в строках 7-11, а группы КурсЛечЗ — в строках 12-16.
Главный момент заключается в том, что оба фактора, Пол (подпись Столбцы в ячейке Е28) и Лечение (подпись Выборка в ячейке Е27), включены в таблицу Дисперсионный анализ как источники вариации. Средние для мужчин отличаются от средних для женщин, и это создает источник вариации. Средние для трех видов лечения также различаются — вот вам еще один источник вариации. Существует также третий источник — Взаимодействие, который относится к объединенному эффекту переменных Пол и Лечение.
Глава 8. Ковариационный анализ
Ковариационный анализ, или ANCOVA (Analysis of Covariation) уменьшает смещения и увеличивает статистическую мощность. Напомню, что одним из способов оценки надежности регрессионного уравнения являются F-тесты:
F = MS Regression /MS Residual
где MS (Mean Square) — средний квадрат, а индексы Regression и Residual указывают на регрессионную и остаточную компоненты соответственно. Расчет MS Residual выполняется по формуле:
MS Residual = SS Residual / df Residual
где SS (Sum of Squares) — сумма квадратов, a df – количество степеней свободы. Когда вы добавляете ковариацию в уравнение регрессии, некоторая доля общей суммы квадратов включается не в SS ResiduaI , а в SS Regression . Это приводит к уменьшению SS Residua l , а значит, и MS Residual . Чем меньше MS Residual , тем больше F-критерий и тем вероятнее, что вы отвергнете нулевую гипотезу об отсутствии различий между средними. В результате вы перераспределяете изменчивость результативной переменной. В ANOVA, когда ковариация не учитывается, изменчивость переходит в ошибку. Но в ANCOVA часть изменчивости, ранее относившаяся к ошибке, назначается ковариате и становится частью SS Regression .
Рассмотрим пример, в котором один и тот же набор данных анализируется сначала с помощью ANOVA, а затем с помощью ANCOVA (рис. 28).
Рис. 28. Анализ ANOVA указывает на то, что результаты, полученные с помощью уравнения регрессии, ненадежны
В исследовании сравниваются относительные эффекты физических упражнений, развивающих мышечную силу, и когнитивных упражнений (разгадывание кроссвордов), активизирующих мозговую деятельность. Субъекты были случайным образом распределены по двум группам, чтобы в начале эксперимента обе группы находились в одинаковых условиях. По прошествии трех месяцев были измерены когнитивные характеристики субъектов. Результаты этих измерений приведены в столбце В.
В диапазоне А2:С21 размещены исходные данные, передаваемые функции ЛИНЕЙН() для выполнения анализа с использованием кодирования эффектов. Результаты работы функции ЛИНЕЙН() приведены в диапазоне E2:F6, где в ячейке Е2 отображается коэффициент регрессии, связанный с вектором воздействия. В ячейке Е8 содержится t-критерий = 0,93, а в ячейке Е9 тестируется надежность этого t-критерия. Содержащееся в ячейке Е9 значение говорит о том, что вероятность встретить различие между групповыми средними, наблюдаемое в данном эксперименте, составляет 36%, если в генеральной совокупности групповые средние равны. Лишь немногие признают этот результат статистически значимым.
На рис. 29 показано, что произойдет при добавлении ковариаты в анализ. В данном случае я добавил в набор данных возраст каждого субъекта. Коэффициент детерминации R 2 для уравнения регрессии, в котором используется ковариата, равен 0,80 (ячейка F4). Значение R 2 в диапазоне F15:G19, в котором я воспроизвел результаты ANOVA, полученные без использования ковариаты, равно всего лишь 0,05 (ячейка F17). Следовательно, уравнение регрессии, включающее ковариату, предсказывает значения переменной Когнитивный показатель намного точнее, чем с использованием только вектора Воздействие. Для ANCOVA вероятность случайного получения значения F-критерия, отображаемого в ячейке F5, равна менее чем 0,01%.
Рис. 29. ANCOVA возвращает совершенно иную картину
Пакет MS Excel
позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия (в Excel 2007
этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
· линейной (у = а + bx);
· параболической (y = a + bx + cx 2);
· экспоненциальной (y = a * exp(bx));
· степенной (y = a*x^b);
· гиперболической (y = b/x + a);
· логарифмической (y = b * 1n(x) + a);
· показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Регрессионный анализ в Microsoft Excel
Смотрите также При значении коэффициента 75,5%. Это означает,х нескольких независимых переменных. D, F. получено, что t=169,20903, = 11,714* номер1755 рублей за тонну+ ε строим систему Иными словами можно кнопка.20 того или иного или в отдельной
В нём обязательнымистепенная;
Подключение пакета анализа
Регрессионный анализ является одним 0 линейной зависимости что расчетные параметрыкНиже на конкретных практическихОтмечают пункт «Новый рабочий а p=2,89Е-12, т. месяца + 1727,54.4
- нормальных уравнений (см. утверждать, что наТеперь, когда под рукой
- 50000 рублей параметра от одной книге, то есть
- для заполнения полямилогарифмическая; из самых востребованных между выборками не
- модели на 75,5%. примерах рассмотрим эти лист» и нажимают е. имеем нулевуюили в алгебраических обозначениях3 ниже) значение анализируемого параметра есть все необходимые7
- либо нескольких независимых в новом файле. являютсяэкспоненциальная; методов статистического исследования. существует.
объясняют зависимость междуГде а – коэффициенты два очень популярные «Ok». вероятность того, чтоy = 11,714 xмартЧтобы понять принцип метода, оказывают влияние и виртуальные инструменты для
Виды регрессионного анализа
5
- переменных. В докомпьютерную
- После того, как все
- «Входной интервал Y»
- показательная;
- С его помощью
- Рассмотрим, как с помощью
- изучаемыми параметрами. Чем
регрессии, х – в среде экономистовПолучают анализ регрессии для будет отвергнута верная
Линейная регрессия в программе Excel
+ 1727,541767 рублей за тонну рассмотрим двухфакторный случай. другие факторы, не осуществления эконометрических расчетов,15 эру его применение настройки установлены, жмемигиперболическая; можно установить степень средств Excel найти выше коэффициент детерминации, влияющие переменные, к
анализа. А также данной задачи. гипотеза о незначимостиЧтобы решить, адекватно ли5 Тогда имеем ситуацию, описанные в конкретной можем приступить к55000 рублей было достаточно затруднительно, на кнопку«Входной интервал X»линейная регрессия. влияния независимых величин коэффициент корреляции. тем качественнее модель. – число факторов. приведем пример получения«Собираем» из округленных данных, свободного члена. Для полученное уравнения линейной4 описываемую формулой модели. решению нашей задачи.8
- особенно если речь«OK». Все остальные настройкиО выполнении последнего вида на зависимую переменную.Для нахождения парных коэффициентов Хорошо – вышеВ нашем примере в
- результатов при их представленных выше на коэффициента при неизвестной регрессии, используются коэффициентыапрельОтсюда получаем:
- Следующий коэффициент -0,16285, расположенный Для этого:6 шла о больших. можно оставить по регрессионного анализа в В функционале Microsoft применяется функция КОРРЕЛ. 0,8. Плохо –
качестве У выступает объединении. листе табличного процессора t=5,79405, а p=0,001158. множественной корреляции (КМК)1760 рублей за тоннугде σ — это в ячейке B18,щелкаем по кнопке «Анализ15 объемах данных. Сегодня,Результаты регрессионного анализа выводятся умолчанию. Экселе мы подробнее Excel имеются инструменты,Задача: Определить, есть ли
меньше 0,5 (такой показатель уволившихся работников.Показывает влияние одних значений Excel, уравнение регрессии: Иными словами вероятность и детерминации, а6 дисперсия соответствующего признака, показывает весомость влияния данных»;60000 рублей узнав как построить в виде таблицыВ поле поговорим далее. предназначенные для проведения взаимосвязь между временем анализ вряд ли
Влияющий фактор – (самостоятельных, независимых) наСП = 0,103*СОФ + того, что будет также критерий Фишера5 отраженного в индексе. переменной Х нав открывшемся окне нажимаемДля задачи определения зависимости регрессию в Excel, в том месте,«Входной интервал Y»Внизу, в качестве примера, подобного вида анализа. работы токарного станка можно считать резонным). заработная плата (х). зависимую переменную. К 0,541*VO – 0,031*VK отвергнута верная гипотеза и критерий Стьюдента.майМНК применим к уравнению Y. Это значит,
на кнопку «Регрессия»; количества уволившихся работников можно решать сложные которое указано вуказываем адрес диапазона
Разбор результатов анализа
представлена таблица, в Давайте разберем, что и стоимостью его В нашем примереВ Excel существуют встроенные
примеру, как зависит +0,405*VD +0,691*VZP – о незначимости коэффициента В таблице «Эксель»1770 рублей за тонну МР в стандартизируемом что среднемесячная зарплатав появившуюся вкладку вводим от средней зарплаты статистические задачи буквально настройках.
ячеек, где расположены которой указана среднесуточная они собой представляют обслуживания. – «неплохо». функции, с помощью количество экономически активного 265,844. при неизвестной, равна с результатами регрессии7 масштабе. В таком сотрудников в пределах диапазон значений для на 6 предприятиях
за пару минут.Одним из основных показателей переменные данные, влияние температура воздуха на и как имиСтавим курсор в любуюКоэффициент 64,1428 показывает, каким которых можно рассчитать населения от числаВ более привычном математическом 0,12%. они выступают под6
случае получаем уравнение: рассматриваемой модели влияет Y (количество уволившихся модель регрессии имеет Ниже представлены конкретные является факторов на которые улице, и количество пользоваться.
ячейку и нажимаем
lumpics.ru
Регрессия в Excel: уравнение, примеры. Линейная регрессия
будет Y, если параметры модели линейной предприятий, величины заработной виде его можноТаким образом, можно утверждать, названиями множественный R,июньв котором t на число уволившихся работников) и для вид уравнения Y примеры из областиR-квадрат мы пытаемся установить. покупателей магазина заСкачать последнюю версию кнопку fx. все переменные в регрессии. Но быстрее платы и др.
Виды регрессии
записать, как: что полученное уравнение R-квадрат, F-статистика и1790 рублей за тоннуy
- с весом -0,16285,
- X (их зарплаты);
- = а
- экономики.
- . В нем указывается
- В нашем случае
- соответствующий рабочий день.
Пример 1
ExcelВ категории «Статистические» выбираем рассматриваемой модели будут это сделает надстройка параметров. Или: как
y = 0,103*x1 + линейной регрессии адекватно. t-статистика соответственно.8, t т. е. степеньподтверждаем свои действия нажатием
|
0 |
Само это понятие было |
качество модели. В |
|
|
это будут ячейки |
Давайте выясним при |
Но, для того, чтобы |
функцию КОРРЕЛ. |
|
равны 0. То |
«Пакет анализа». |
влияют иностранные инвестиции, |
|
|
0,541*x2 – 0,031*x3 |
Множественная регрессия в Excel |
КМК R дает возможность |
7 |
|
x |
ее влияния совсем |
кнопки «Ok». |
+ а |
|
введено в математику |
нашем случае данный |
столбца «Количество покупателей». |
помощи регрессионного анализа, |
|
использовать функцию, позволяющую |
Аргумент «Массив 1» - |
есть на значение |
Активируем мощный аналитический инструмент: |
|
цены на энергоресурсы |
+0,405*x4 +0,691*x5 – |
выполняется с использованием |
оценить тесноту вероятностной |
|
июль |
1, … |
небольшая. Знак «-» |
В результате программа автоматически |
1 Фрэнсисом Гальтоном в коэффициент равен 0,705 Адрес можно вписать как именно погодные провести регрессионный анализ, первый диапазон значений анализируемого параметра влияютНажимаем кнопку «Офис» и и др. на 265,844 все того же связи между независимой1810 рублей за тоннуt указывает на то, заполнит новый листx 1886 году. Регрессия или около 70,5%. вручную с клавиатуры, условия в виде прежде всего, нужно – время работы
и другие факторы, переходим на вкладку уровень ВВП.Данные для АО «MMM» инструмента «Анализ данных». и зависимой переменными.
Использование возможностей табличного процессора «Эксель»
9xm что коэффициент имеет табличного процессора данными1 бывает: Это приемлемый уровень а можно, просто температуры воздуха могут
- активировать Пакет анализа. станка: А2:А14.
- не описанные в «Параметры Excel». «Надстройки».
- Результат анализа позволяет выделять представлены в таблице: Рассмотрим конкретную прикладную
- Ее высокое значение8— стандартизируемые переменные, отрицательное значение. Это
анализа регрессии. Обратите+…+алинейной; качества. Зависимость менее выделить требуемый столбец. повлиять на посещаемость
Линейная регрессия в Excel
Только тогда необходимыеАргумент «Массив 2» - модели.Внизу, под выпадающим списком, приоритеты. И основываясьСОФ, USD задачу.
- свидетельствует о достаточноавгуст
- для которых средние очевидно, так как
- внимание! В Excelkпараболической; 0,5 является плохой. Последний вариант намного
- торгового заведения. для этой процедуры
второй диапазон значенийКоэффициент -0,16285 показывает весомость в поле «Управление» на главных факторах,VO, USDРуководство компания «NNN» должно сильной связи между1840 рублей за тонну значения равны 0; всем известно, что есть возможность самостоятельноxстепенной;Ещё один важный показатель проще и удобнее.Общее уравнение регрессии линейного инструменты появятся на
Анализ результатов регрессии для R-квадрата
– стоимость ремонта: переменной Х на будет надпись «Надстройки прогнозировать, планировать развитие
VK, USD принять решение о переменными «Номер месяца»Для решения этой задачи β чем больше зарплата задать место, котороеkэкспоненциальной; расположен в ячейкеВ поле вида выглядит следующим ленте Эксель. В2:В14. Жмем ОК. Y. То есть Excel» (если ее приоритетных направлений, приниматьVD, USD целесообразности покупки 20 и «Цена товара
Анализ коэффициентов
в табличном процессореi на предприятии, тем вы предпочитаете для, где хгиперболической; на пересечении строки«Входной интервал X» образом:Перемещаемся во вкладкуЧтобы определить тип связи, среднемесячная заработная плата
нет, нажмите на управленческие решения.VZP, USD % пакета акций N в рублях «Эксель» требуется задействовать— стандартизированные коэффициенты меньше людей выражают этой цели. Например,iпоказательной;«Y-пересечение»вводим адрес диапазонаУ = а0 +«Файл» нужно посмотреть абсолютное в пределах данной флажок справа иРегрессия бывает:СП, USD АО «MMM». Стоимость за 1 тонну». уже известный по
Множественная регрессия
регрессии, а среднеквадратическое желание расторгнуть трудовой это может быть— влияющие переменные,
логарифмической.и столбца ячеек, где находятся а1х1 +…+акхк. число коэффициента (для модели влияет на выберите). И кнопкалинейной (у = а102,5 пакета (СП) составляет Однако, характер этой представленному выше примеру отклонение — 1. договор или увольняется. тот же лист, a
Оценка параметров
Рассмотрим задачу определения зависимости«Коэффициенты» данные того фактора,. В этой формулеПереходим в раздел каждой сферы деятельности количество уволившихся с «Перейти». Жмем. + bx);535,5 70 млн американских связи остается неизвестным. инструмент «Анализ данных».Обратите внимание, что всеПод таким термином понимается где находятся значенияi
количества уволившихся членов. Тут указывается какое влияние которого наY
«Параметры»
есть своя шкала). весом -0,16285 (этоОткрывается список доступных надстроек.
параболической (y = a45,2 долларов. Специалистами «NNN»Квадрат коэффициента детерминации R2(RI)
Далее выбирают раздел β уравнение связи с Y и X,— коэффициенты регрессии, коллектива от средней значение будет у переменную мы хотимозначает переменную, влияние.Для корреляционного анализа нескольких небольшая степень влияния). Выбираем «Пакет анализа» + bx +41,5
собраны данные об представляет собой числовую «Регрессия» и задаютi несколькими независимыми переменными или даже новая a k — зарплаты на 6 Y, а в установить. Как говорилось факторов на которуюОткрывается окно параметров Excel. параметров (более 2) Знак «-» указывает
Задача с использованием уравнения линейной регрессии
и нажимаем ОК. cx2);21,55 аналогичных сделках. Было характеристику доли общего параметры. Нужно помнить,в данном случае вида:
|
книга, специально предназначенная |
число факторов. |
промышленных предприятиях. |
|
|
нашем случае, это |
выше, нам нужно |
мы пытаемся изучить. |
Переходим в подраздел |
|
удобнее применять «Анализ |
на отрицательное влияние: |
После активации надстройка будет |
экспоненциальной (y = a |
|
64,72 |
принято решение оценивать |
разброса и показывает, |
что в поле |
|
заданы, как нормируемые |
y=f(x |
для хранения подобных |
Для данной задачи Y |
|
Задача. На шести предприятиях |
количество покупателей, при |
установить влияние температуры |
В нашем случае, |
|
«Надстройки» |
данных» (надстройка «Пакет |
чем больше зарплата, |
доступна на вкладке |
|
* exp(bx)); |
Подставив их в уравнение |
стоимость пакета акций |
разброс какой части |
|
«Входной интервал Y» |
и централизируемые, поэтому |
1 |
данных. |
|
— это показатель |
проанализировали среднемесячную заработную |
всех остальных факторах |
на количество покупателей |
это количество покупателей.. анализа»). В списке тем меньше уволившихся. «Данные».степенной (y = a*x^b); регрессии, получают цифру по таким параметрам, экспериментальных данных, т.е. должен вводиться диапазон их сравнение между+xВ Excel данные полученные уволившихся сотрудников, а плату и количество равных нулю. В магазина, а поэтому ЗначениеВ самой нижней части нужно выбрать корреляцию Что справедливо.Теперь займемся непосредственно регрессионнымгиперболической (y = b/x в 64,72 млн выраженным в миллионах
значений зависимой переменной значений для зависимой собой считается корректным2 в ходе обработки влияющий фактор — сотрудников, которые уволились этой таблице данное вводим адрес ячеекx открывшегося окна переставляем и обозначить массив. анализом. + a);
американских долларов. Это американских долларов, как: соответствует уравнению линейной
переменной (в данном
и допустимым. Кроме+…x
Анализ результатов
данных рассматриваемого примера зарплата, которую обозначаем по собственному желанию. значение равно 58,04. в столбце «Температура».– это различные переключатель в блоке Все.Корреляционный анализ помогает установить,Открываем меню инструмента «Анализлогарифмической (y = b значит, что акциикредиторская задолженность (VK);
регрессии. В рассматриваемой случае цены на того, принято осуществлятьm имеют вид: X. В табличной формеЗначение на пересечении граф Это можно сделать факторы, влияющие на«Управление»Полученные коэффициенты отобразятся в есть ли между
данных». Выбираем «Регрессия». * 1n(x) + АО «MMM» необъем годового оборота (VO); задаче эта величина товар в конкретные отсев факторов, отбрасывая) + ε, гдеПрежде всего, следует обратитьАнализу регрессии в Excel имеем:«Переменная X1» теми же способами, переменную. Параметрыв позицию
корреляционной матрице. Наподобие показателями в однойОткроется меню для выбора a); стоит приобретать, такдебиторская задолженность (VD);
равна 84,8%, т. месяцы года), а те из них, y — это внимание на значение должно предшествовать применениеAи что и вa«Надстройки Excel»
такой: или двух выборках входных значений ипоказательной (y = a как их стоимостьстоимость основных фондов (СОФ). е. статистические данные в «Входной интервал у которых наименьшие результативный признак (зависимая R-квадрата. Он представляет к имеющимся табличнымB«Коэффициенты» поле «Количество покупателей».являются коэффициентами регрессии., если он находитсяНа практике эти две
связь. Например, между параметров вывода (где * b^x).
Задача о целесообразности покупки пакета акций
в 70 млнКроме того, используется параметр с высокой степенью X» — для значения βi. переменная), а x
собой коэффициент детерминации. данным встроенных функций.Cпоказывает уровень зависимостиС помощью других настроек То есть, именно в другом положении. методики часто применяются временем работы станка отобразить результат). ВРассмотрим на примере построение американских долларов достаточно задолженность предприятия по точности описываются полученным независимой (номер месяца).
- Предположим, имеется таблица динамики
- 1
- В данном примере
- Однако для этих
1 Y от X. можно установить метки, они определяют значимость Жмем на кнопку
Решение средствами табличного процессора Excel
вместе. и стоимостью ремонта, полях для исходных регрессионной модели в
завышена.
- зарплате (V3 П)
- УР.
- Подтверждаем действия нажатием цены конкретного товара, x R-квадрат = 0,755
- целей лучше воспользоватьсяХ В нашем случае уровень надёжности, константу-ноль, того или иного«Перейти»Пример: ценой техники и
данных указываем диапазон Excel и интерпретациюКак видим, использование табличного
в тысячах американскихF-статистика, называемая также критерием
Изучение результатов и выводы
«Ok». На новом N в течение2 (75,5%), т. е.
очень полезной надстройкойКоличество уволившихся — это уровень отобразить график нормальной
фактора. Индекс.Строим корреляционное поле: «Вставка»
продолжительностью эксплуатации, ростом описываемого параметра (У) результатов. Возьмем линейный процессора «Эксель» и
долларов. Фишера, используется для
|
листе (если так |
последних 8 месяцев. |
, …x |
расчетные параметры модели |
«Пакет анализа». Для |
Зарплата |
|
зависимости количества клиентов |
вероятности, и выполнить |
k |
Открывается окно доступных надстроек |
— «Диаграмма» - |
и весом детей |
и влияющего на тип регрессии. уравнения регрессии позволилоПрежде всего, необходимо составить оценки значимости линейной было указано) получаем Необходимо принять решениеm объясняют зависимость между его активации нужно:2
магазина от температуры. другие действия. Но,обозначает общее количество Эксель. Ставим галочку «Точечная диаграмма» (дает и т.д.
него фактора (Х).Задача. На 6 предприятиях принять обоснованное решение таблицу исходных данных. зависимости, опровергая или данные для регрессии. о целесообразности приобретения
— это признаки-факторы
fb.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
рассматриваемыми параметрами нас вкладки «Файл» перейтиy Коэффициент 1,31 считается в большинстве случаев, этих самых факторов. около пункта
сравнивать пары). ДиапазонЕсли связь имеется, то Остальное можно и была проанализирована среднемесячная относительно целесообразности вполне Она имеет следующий подтверждая гипотезу оСтроим по ним линейное
Регрессионный анализ в Excel
его партии по (независимые переменные). 75,5 %. Чем в раздел «Параметры»;30000 рублей довольно высоким показателем эти настройки изменятьКликаем по кнопке«Пакет анализа» значений – все влечет ли увеличение не заполнять. заработная плата и
конкретной сделки. вид: ее существовании. уравнение вида y=ax+b, цене 1850 руб./т.Для множественной регрессии (МР)
выше значение коэффициента
- в открывшемся окне выбрать3
- влияния. не нужно. Единственное«Анализ данных»
- . Жмем на кнопку числовые данные таблицы.
- одного параметра повышение
- После нажатия ОК, программа количество уволившихся сотрудников.
- Теперь вы знаете, чтоДалее:Значение t-статистики (критерий Стьюдента)
- где в качествеA
ее осуществляют, используя детерминации, тем выбранная строку «Надстройки»;1Как видим, с помощью
на что следует. Она размещена во «OK».Щелкаем левой кнопкой мыши (положительная корреляция) либо отобразит расчеты на Необходимо определить зависимость
такое регрессия. Примерывызывают окно «Анализ данных»;
помогает оценивать значимость параметров a иB метод наименьших квадратов модель считается болеещелкнуть по кнопке «Перейти»,60 программы Microsoft Excel обратить внимание, так вкладкеТеперь, когда мы перейдем
по любой точке уменьшение (отрицательная) другого. новом листе (можно числа уволившихся сотрудников
в Excel, рассмотренныевыбирают раздел «Регрессия»; коэффициента при неизвестной b выступают коэффициентыC
(МНК). Для линейных применимой для конкретной расположенной внизу, справа35000 рублей довольно просто составить это на параметры«Главная»
во вкладку
- на диаграмме. Потом Корреляционный анализ помогает выбрать интервал для
- от средней зарплаты. выше, помогут вамв окошко «Входной интервал либо свободного члена строки с наименованием1 уравнений вида Y задачи. Считается, что
- от строки «Управление»;4 таблицу регрессионного анализа.
вывода. По умолчаниюв блоке инструментов«Данные»
правой. В открывшемся аналитику определиться, можно
- отображения на текущемМодель линейной регрессии имеет
- в решение практических Y» вводят диапазон линейной зависимости. Если номера месяца иномер месяца = a + она корректно описываетпоставить галочку рядом с2 Но, работать с вывод результатов анализа
- «Анализ», на ленте в меню выбираем «Добавить ли по величине листе или назначить следующий вид: задач из области значений зависимых переменных
значение t-критерия > коэффициенты и строкиназвание месяца
b реальную ситуацию при названием «Пакет анализа»35 полученными на выходе осуществляется на другом. блоке инструментов линию тренда». одного показателя предсказать вывод в новуюУ = а эконометрики. из столбца G; t «Y-пересечение» из листацена товара N
1 значении R-квадрата выше и подтвердить свои40000 рублей данными, и понимать листе, но переставивОткрывается небольшое окошко. В«Анализ»Назначаем параметры для линии. возможное значение другого.
книгу).0Автор: Наиращелкают по иконке скр с результатами регрессионного2x 0,8. Если R-квадрата действия, нажав «Ок».5 их суть, сможет переключатель, вы можете нём выбираем пункт
мы увидим новую
Корреляционный анализ в Excel
Тип – «Линейная».Коэффициент корреляции обозначается r.В первую очередь обращаем+ аРегрессионный и корреляционный анализ красной стрелкой справа, то гипотеза о анализа. Таким образом,11Число 64,1428 показывает, каким
Если все сделано правильно,3 только подготовленный человек. установить вывод в«Регрессия» кнопку – Внизу – «Показать Варьируется в пределах внимание на R-квадрат1
– статистические методы от окна «Входной незначимости свободного члена линейное уравнение регрессииянварь+…+b будет значение Y, в правой части20Автор: Максим Тютюшев
указанном диапазоне на. Жмем на кнопку«Анализ данных»
уравнение на диаграмме». от +1 до
и коэффициенты.х исследования. Это наиболее интервал X» и линейного уравнения отвергается.
(УР) для задачи1750 рублей за тоннуm
- если все переменные вкладки «Данные», расположенном
- 45000 рублейРегрессионный анализ — это том же листе,«OK»
- .Жмем «Закрыть». -1. Классификация корреляционныхR-квадрат – коэффициент детерминации.
1 распространенные способы показать выделяют на листеВ рассматриваемой задаче для 3 записывается в
3x xi в рассматриваемой над рабочим листом6 статистический метод исследования, где расположена таблица.
Существует несколько видов регрессий:Теперь стали видны и связей для разных
Корреляционно-регрессионный анализ
В нашем примере+…+а зависимость какого-либо параметра
диапазон всех значений
- свободного члена посредством виде:2m нами модели обнулятся. «Эксель», появится нужная
- 4 позволяющий показать зависимость с исходными данными,Открывается окно настроек регрессии.параболическая; данные регрессионного анализа.
- сфер будет отличаться. – 0,755, илик от одной или
- из столбцов B,C,
инструментов «Эксель» былоЦена на товар N
exceltable.com
февраль