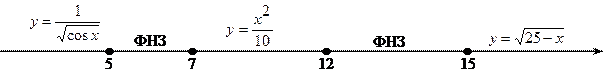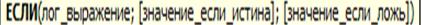Реализация разветвляющихся алгоритмов excel - Word и Excel

Реализацию алгоритма вычислительной задачи в
электронных таблицах Excel возможно, так как они
выполняют необходимые требования, предъявляемые
к среде реализации алгоритма [Глущенко Ю. В.
Обоснование использования языка
программирования в учебном процессе (в печати)].

Для реализации вычислительных алгоритмов
необходимо уметь реализовывать базовые
структуры алгоритмов. На примерах задач,
приводящих к базовым структурам, разберемся с
реализацией вычислительного процесса базовых
структур в электронных таблицах. Можно
предложить следующий алгоритм:

Составление спецификаций переменных заданного
алгоритма в виде таблицы, в столбцах которой
будут Имя переменной в алгоритме, назначение,
тип, диапазон, адрес в Excel, вид реализации.
Разработка таблиц ВводаИнформации.
Разработка таблицы подзадачи
ОбработкаИнформации.
Разработка таблицы ВыводаРезультата.
Тестирование построенных таблиц.

Линейные алгоритмы

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значения сторон треугольника а, в, с.
Вычислить значение полупериметра р = (а+в+с)/2
Вычислить площадь треугольника S=(p*(p-а)*(р-в)*(р-с)).
Вывести значение S.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

№ п/п.	Имя перем. в алгоритме	Назначение	Тип	Диапазон	Адрес	Вид реализации
Переменные входного потока
1	А	Сторона тр-ка	Вещ	0, +	B3	<число>
2	В	Сторона тр-ка	Вещ	0, +	B4	<число>
3	С	Сторона тр-ка	Вещ	0, +	В5	<число>
Переменные блока обработки информации
4	Р	полупериметр	Вещ	0, +	Е3	<формула>
5	S	Площадь тр-ка	Вещ	0, +	Е4	<формула>
Переменные выходного потока.
6	S	Площадь тр-ка	Вещ	0, +	Н3	<формула>

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. Ее
реализация показана на Рис. 1.

3. Разработка таблицы подзадачи
ОбработкаИнформации

В данной таблице необходимо провести
вычисления полупериметра и площади. Оба эти
параметра вводятся с помощью формул в
соответствующие ячейки. Реализация данной
таблицы приведено на Рис. 1.

4. Разработка таблицы ВыводаРезультатов

Таблица ВыводаРезультатов должна содержать
значения переменных выходного потока. Ее
реализация показана на Рис. 1.

5. Тестирование разработанных таблиц

Для тестирования полученных таблиц строим
таблицу теста по следующему шаблону:

№ п/п.	Имя	Назначение	Значение/результат
1	А	Входной поток	1	3	1
2	В	1	4	1
3	С	4	5	2
4	Р	Промежуточные	3	6	2
5	S	Выходной поток	Ошибка	6	0

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 1.

Алгоритм ветвления

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значение переменной Х.
ЕСЛИ Х не больше 0,
ТО Y:=Х*Х, ИНАЧЕ Y:=Х+1.
Вывести значение переменной Y.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. В нашем
случае значение X. Ее реализация показана на Рис. 2.

3, 4. Разработка таблицы подзадачи
ОбработкаИнформации.

В данной задаче можно (и нужно) объединить
задачи ОбработкиИнфориации и ВыводаРезультатов,
построив только таблицу ВыводаРезультатов. Ее
реализация показана на Рис. 2.

5. Тестирование разработанной таблицы.

Для тестирования полученной таблицы
необходимо взять минимум три значения Х:

слева от ветвления,
в точке ветвления,
справа от точки ветвления.

Значения берутся так, чтобы просто было
проверить результат. Поэтому построим таблицу
тестирования в виде:

Имя переменной	ЗНАЧЕНИЕ/РЕЗУЛЬТАТ
Слева от точки ветвления	В точке ветвления	Справа от точки ветвления
X	-5	0	2
Y	25	0	3

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 2.

Циклические алгоритмы

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значение целочисленной переменной
1<=N<=10.
S:= 0 {Начальное значение
сумматора равно нулю}.
I:= 0 {Начальное
значение индекса цикла равно нулю}.
I:=I+1 {Текущее значение индекса
цикла}.
S:=S+I
{накопление
суммы}.
ЕСЛИ N>I то идти на п.4
{конец цикла с постусловием}
Вывести значение
S
{Вывод результата}.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

№ п/п.	Имя переменной в алгоритме.	Назначение	Тип	Диапазон	Адрес	Реализация
Переменные входного потока
1	N	ПВхП	ц	1..10	B3	<число>
Индекс цикла
1	i	индекс	ц	1..N	А10:A50	<массив>
5	S	ПВхдП	ц	<=55	B10:B50	<формула>
Переменные выходного потока.
5	S	ПВхдП	ц	<=55	Е3	<формула>

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. В нашем
случае значение N. Ее реализация показана на Рис. 3.

3. Разработка таблицы подзадачи
ОбработкаИнформации

Реализация обработки информации возможна лишь
с использованием циклического алгоритма.
В случае с Excel данную задачу необходимо разбить
на три:

Построение столбца индексов цикла.
Построение столбца элементов массива.

ЗАДАЧА №1 ПОСТРОЕНИЕ СТОЛБЦА ИНДЕКСА ЦИКЛА.

Данную задачу сформулируем в виде:

Построить столбец значений индекса цикла в
интервале [1..N (задано)]. При этом с изменением
значения N в ячейке В3 должно изменяться и
количество значений индекса цикла в расчетной
таблице.
Эта задача решается в столбце А начиная со строки
№10.

Важно отметить, что протяжку можно вести до
любого номера строки лишь бы при всех изменениях
N протяжка формулы захватывала все строки
изменения значения индекса цикла. Необходимо
только помнить, что при протяжке увеличивается
объем файла, то есть чем глубже протянем формулу,
тем большим будет объем полученного файла и,
возможно, медленнее будет работать Excel с этим
файлом.

Рис. 3.

ПЕРВАЯ ЗАДАЧА РЕШЕНА

ЗАДАЧА №2. ПОСТРОЕНИЕ СТОЛБЦА ЭЛЕМЕНТОВ ЦИКЛА.

Здесь под элементом цикла будем понимать
текущее значение S, зависящее от значения индекса
цикла.
Сформулируем задачу в следующем виде:
Для каждого значения индекса цикла определить
текущее значение S.
Столбец В дает нам текущие значения S=f(<индекс
цикла>), при этом протяжка формулы в столбце В
должна быть не меньше протяжки в столбце А.

Рис. 3.

ВТОРАЯ ЗАДАЧА РЕШЕНА.

4. Разработка таблицы подзадачи
ВыводРезультатов

Для решения данной задачи следует понять, что
выходным значением S будет наибольшее из
значений в ячейках В [10…]. Конечное значение
интервала в В определяется протяжкой формул в
задачах №№1, 2. Пусть формулы протянули до строки
№50. Естественно, наибольшим S будет для
наибольшего значения индекса цикла, так как на
каждом шаге прибавляется число большее 1.
Следовательно, в ячейку Е3 необходимо ввести
формулу

Е3 =>[=МАКС(b10:b50)]

Рис. 3.

И если помнить, что значение пустой ячейки Excel
воспринимает как «0», то…

ТРЕТЬЯ ЗАДАЧА РЕШЕНА.

5. Тестирование полученных таблиц

Для тестирования полученной таблицы строим
таблицу теста по следующему шаблону:

№ п/п.	Имя	назначение	Значение/результат
1	N	Вход	1	5	7	9	10
2	S	Выход	1	15	28	45	55

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 3.

Источник

Реализация «Разветвляющихся вычислительных процессов» средствами Excel

Постановка задачи

Разработать алгоритм для вычисления значений функции 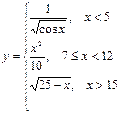(разветвляющийся вычислительный процесс) и реализовать его в Excel.

Реализация задачи

В задаче требуется вычислить функцию, вид которой зависит от значения аргумента. Поэтому разобьем числовую ось значениями, указанными в формуле на несколько промежутков, указав при этом, какой должен быть результат вычислений на каждом промежутке:

При разработке алгоритма будем рассматривать промежутки числовой оси слева направо. Обозначения в алгоритме: ФНЗ – функция не задана; ФНО – функция не определена.

Записывая основной алгоритм решения задачи, вместо вычислений каждой части функции для упрощения будем писать блок1, блок2 и блок3. Поставим в соответствие каждому блоку алгоритм вычисления конкретной функции с учетом её области определения. Последний этап разработки алгоритма решения исходной задачи – подстановка в основной алгоритм вместо блоков 1,2,3 соответствующих вычислительных алгоритмов.

Сделаем небольшое замечание относительно записи текста алгоритма. Рекомендуется записывать текст алгоритма «ступеньками», т.е. новый блок «если – иначе» нужно записывать с отступом относительно предыдущего блока «если – иначе» и т.д. Так же следует поступать и при записи текста программы, соответствующей алгоритму. Одной из причин этого является то, что структура алгоритма и программы хорошо просматривается, что может помочь при обнаружении синтаксических ошибок.

Основной алгоритм:

ввод х

если х<5

блок1

иначе

если x<7

«ФНЗ»

иначе

если x<12

блок2

иначе

если х<=15

«ФНЗ»

иначе

блок3

все_если

Рассмотрим вычисления в каждом из блоков 1, 2 и 3 отдельно.

Блок1. Требуется вычислить функцию 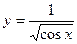. При вычислении учитываем, что подкоренное выражение должно быть больше или равно нулю и при этом знаменатель не должен равняться нулю. Таким образом, получаем:

если cos(х)>0

печать у

иначе

«ФНО»

все_если

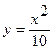
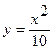
Блок2. Требуется вычислить функцию . Здесь никаких ограничений на вычисления нет. Таким образом, получаем:

печать у

Блок3. Требуется вычислить функцию 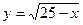. При вычислении учитываем, что подкоренное выражение должно быть больше или равно. Таким образом, получаем:

если 25-х>=0

печать у

иначе

«ФНО»

все_если

В основной алгоритм вместо блоков 1,2,3 подставим алгоритмы вычисления соответствующих частей функции. В итоге получаем алгоритм решения исходной задачи.

ввод х

если х<5

если cos(х)>0

печать у

иначе

«ФНО»

все_если

иначе

если x<7

«ФНЗ»

иначе

если x<12

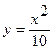
печать у

иначе

если х<=15

«ФНЗ»

иначе

если 25-х>=0

печать у

иначе

«ФНО»

все_если

Для построения функции Excel необходимо использовать логическую функцию ЕСЛИ(), которая устроена следующим образом.

Эта функция может в качестве аргументов использовать другие функции ЕСЛИ().

Таким образом, при условии, что в ячейке А11 будет вводиться значение переменной х, то, например, в ячейку В11 можно ввести формулу Excel для вычисления значения заданной функции.

Лабораторная работа №2.

Разветвляющиеся вычислительные процессы.

Задание. Разработать алгоритм и составить по нему программу в Excel для вычисления значений функции y = f(x). Необходимо учитывать область определения функции.

Источник

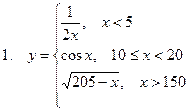
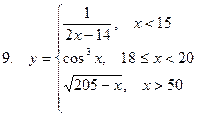
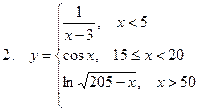
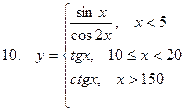
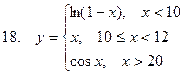
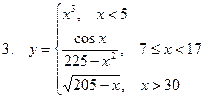
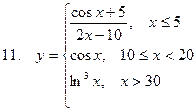
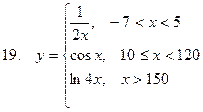
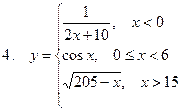
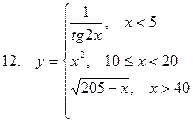
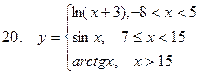
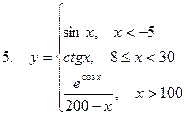
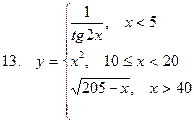
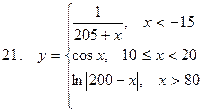
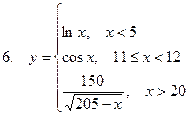
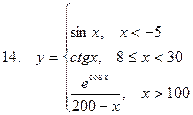
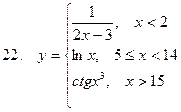
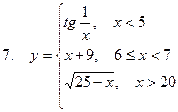
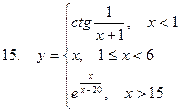
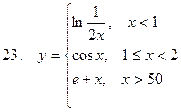
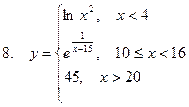
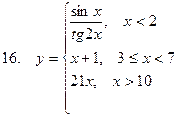
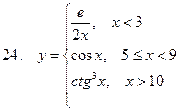
Лабораторная работа № 1.7. Разветвляющиеся вычислительные процессы Excel

(5 – 8 баллов)

Цель работы

познакомиться с классом разветвляющихся вычислительных процессов, получить представление о выражениях отношения и логических выражениях;
познакомиться с возможностями Excel по описанию выражений отношения и логических выражений;
изучить логические функции, встроенные в Excel, и научиться использовать их для записи условий в формулах;
освоить методику использования логических функций при организации вычислений в электронных таблицах.

Необходимые программные и технические средства

Персональный компьютер, желательно подключенный к сети Интернет.

Тип операционной системы – Windows.

MS Office версии 97-2003 и выше.
^
Вычислительный процесс, при котором некоторая совокупность команд повторяется более чем один раз, называется циклическим вычислительным процессом. Существует несколько типов вычислительных процессов:

Бесконечные циклы (зачастую их наличие говорит о логической ошибке, допущенной при составлении программы).
Циклы, в которых количество повторений определяется некоторым условием
Циклы, в которых число повторений задается и оно конечно.

Циклические вычислительные процессы используются для обработки последовательностей.

Задание

Часть 1.

Рассчитать значение функции z=f(x,y), учитывая область существования. Считать, что аргументы x и y изменяются одновременно, принимая не менее 10 пар значений. Начальные, конечные значения и шаги изменения аргументов x и y задать самостоятельно. В том случае, если функция z не существует, выдать в качестве результата «Функция не существует».

Вар.	Функция	Вар.	Функция	Вар.	Функция
1	z=arcsin(x+y)	11	z=sin	21	z=arccosx+9y
2	z=lnx+lny	12	z=	22	z=lnx-4lny
3	z=	13	z=	23	z=
4	z=arccos(xy)	14	z=tg	24	z=arccosy+lnx
5	z=	15	z=lnx+lnxy	25	z=
6	z=	16	z=	26	z=
7	z=arccos(xy)	17	z=ctg	27	z=arcsinxy+lny
8	z=sin	18	z=	28	z=+lny
9	25. z=	19	z=cos	29	z=
10	z=	20	z=	30	z=

Часть 2.

Составить проект алгоритма (блок-схему) и реализовать программу в Excel и на VBA для вычисления значений функции при заданных значениях аргумента.

Вар.	Функция	Вар.	Функция
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

^
Прочитайте и уясните материалы разделов лекционного курса «Информатика», относящихся к теме работы.

Ознакомьтесь с общими сведениями о предмете лабораторной работы (см. выше в описании данной работы) и рекомендуемыми дополнительными материалами.

Уясните цель работы.

Подготовьте необходимые программные и технические средства (см. выше в описании данной работы).

Приступайте к выполнению работы:

Часть 1.

Пример 1

Вычислить функцию z=f(x,y), учитывая область ее существования.

Область существования (область допустимых значений — ОДЗ) функции:

x-y≥0, x-5≠0, xy>0

Составим блок-схему и алгоритм решения:

Рис. 1. Блок-схема для решения разветвляющегося вычислительного процесса

На рис.1 и далее блок-схема составлена с отступлениями от принятых норм использования условных фигур с целью экономии места.

Алгоритм состоит из множества элементарных составляющих.

Алгоритм описывает линейный вычислительный процесс тогда, когда элементарные операции выполняются последовательно, одна за другой.

^ при составлении алгоритмов являются: 1) управляющие структуры; 2) операции, аналоги которых существуют в конкретных приложениях.

Свойства алгоритма:

однозначность;
результативность;
массивность (выполняется для класса однотипных задач);
эффективность (наилучший из возможных вариантов).

Структура алгоритма: Если-То-Иначе используется для описания разветвляющегося вычислительного процесса.

Запись алгоритма выполняется двумя способами: 1) с помощью блок-схем; 2) с помощью начального языка (псевдокодирование – запись, язык – псевдокод)

Запись алгоритма:

Ввод x,y

Если x-5≠0 То

Если x-y≥0 То

Если xy>0 То

Вывод y

Иначе

Вывод «Логарифм отрицательного числа »

Всёесли

Иначе

Вывод «Корень из отрицательного числа»

Всёесли

Иначе

Вывод «Деление на ноль»

Всёесли

Всё

1) В ячейки А1, В1, С1 ввести текст «х» «у» «z» соответственно.

2) В диапазоны А2:A10, B2:В10 ввести значения х и y из области существования .

3) В ячейку F1 ввести текст «Логарифм отрицательного числа».

4) В ячейку F2 ввести текст «Корень из отрицательного числа».

5) В ячейку F3 ввести текст «Деление на ноль».

6) В ячейку С2 ввести формулу:

=ЕСЛИ(A2-5<>^

Интерпретация формулы:

Если1 То1 Если2 То2 Если3 То3 Иначе3

Иначе2 Иначе1

В результате получится следующая таблица значений

Рис. 2.

Если формула в ячейке не может быть правильно вычислена, Microsoft Excel выводит в ячейку сообщение об ошибке. Если формула содержит ссылку на ячейку, которая содержит значения ошибки, то вместо этой формулы также будет выводиться сообщение об ошибке. Значение сообщений об ошибках следующее:

#### – ширина ячейки не позволяет отобразить число в заданном формате;

#ИМЯ? – Microsoft Excel не смог распознать имя, использованное в формуле;

#ДЕЛ/0! – в формуле делается попытка деления на нуль;

#ЧИСЛО! – нарушены правила задания операторов, принятые в математике;

#Н/Д – такое сообщение может появиться, если в качестве аргумента задана ссылка на пустую ячейку;

#ПУСТО! – неверно указано пересечение двух областей, которые не имеют общих ячеек;

#ССЫЛКА! – в формуле задана ссылка на несуществующую ячейку;

#ЗНАЧ! – использован недопустимый тип аргумента

Пример 2.

Вычислить функцию y=f(x), обеспечив не менее 2-х точек из каждого интервала:

–x +3, если x-6

y= x+lnx, если 0

x+1, если x>2

Функция не определена при -6 <х 0

Область существования (область допустимых значений — ОДЗ) функции – вся числовая ось.

Составим блок-схему и алгоритм решения:

Рис. 3.

Запись алгоритма:

Ввод x

Если x-6 То

y= –x +3

Вывод y

Иначе

Если x0 То

Вывод «Функция не определена»

Иначе

Если x2 То

y= x+lnx

Вывод y

Иначе y= x+1

Вывод у

Всёесли

Всё

Реализация в Excel

В ячейки А1 и В1 ввести текст «х» и «у» соответственно.

В диапазон А2:A10 ввести значения х из всех данных интервалов, т.е.

(-∞;-6], (-6;0], (0;2], (2,+∞) по 2-3 значения из каждого.

3.В ячейку F2 ввести текст «Функция не определена».

4. В ячейку В2 ввести формулу:

=ЕСЛИ(A2<=-6;-A2^2+3;ЕСЛИ(A2<=0;$F$2;ЕСЛИ(A2<=2;A2^2+LN(A2);A2^2+1)))

(Если1 То1 Иначе1 Если2 То2 Иначе2 Если3 То3 Иначе3)

Протянуть ячейку В2 до В10. В результате получится следующая таблица значений:

Рис. 4.

Часть 2

Задана область D (см.ниже) и точка с координатами x и y. Рассчитать величину z по формуле:

Область существования (область допустимых значений — ОДЗ) функции: x²>0; y-x>0; y²≠0

Составим блок-схему и алгоритм решения:

Блок-схема

Рис. 5.

Запись алгоритма:

Ввод x

Если A7>=-2;A7<=2;B7>=0;B7<=3 или A7<-2;A7>=-3;B7>=0;B7<=3;B7<=3*A7+9 То

Если B7-A7>0; A7^2>0 То

Вывод y

Иначе

Вывод «ф.н.о.»

Всёесли

Иначе

Если B7=0 То

Вывод «ф.н.о.»

Иначе

EXP(A7^3)-1/B7^2)

Вывод у

Всёесли

Всё

^ должен выглядеть примерно так:

Технология решения задач на VBA

размещаем кнопку CommandButton1
описываем все переменные, которые используются в задаче:

Dim имя переменной 1 As тип 1, имя переменной 2 тип 2 …

Типы переменных:

Byte – только целые числа (0;255)

Boolean – либо true, либо false

Integer – целые значения (-32768;32768)

Long — целые значения (-2,14*10⁹;2.14*10⁹)

Single – вещественное число, 7 разрядов после запятой (-1,75*10³⁸;1.75*10³⁸)

Double — вещественное число, 14 разрядов после запятой (-10³⁰⁸;10³⁰⁸)

Date – сохраняет дату и время (100 лет;9999 лет)

String – текст с числом символов от 0; до 2*10⁹

3) ввод данных

Переменная – временное хранилище для данных. Задача ввода – перенос значения с рабочего листа в переменную, оно запоминается в свойстве Value

Range(имя ячейки «A7»).Value – составной индификатор для свойства.

Пусто – 0 (для чисел) и «» (для текста)

Private Sub CommandButton1_Click()

Dim x As Single, y As Single, z As Single

x = Range(«A7»).Value

y = Range(«B7»).Value

If (x >= -2 And x <= 2 And y >= 0 And y <= 3) Or (x >= -3 And x <= -2 And y >= 0 And y <= 3 And y <= 3 * x + 9) Then

If (y — x > 0 And x ^ 2 > 0) Then

z = Log(x ^ 2) / ((y — x) ^ 0.5)

Range(«D7»).Value = z

Else

Range(«D7»).Value = «Функция не определена»

End If

Else

If y = 0 Then

Range(«D7″).Value = » Функция не определена «

Else

z = Exp(x ^ 3) — 1 / y ^ 2

Range(«D7»).Value = z

End If

End Sub
^ VBA с помощью различных видов циклов.

Пример:

Вычислить приближённо ln(x) для значения -1

Ln(1+x)=x-, где каждый элемент последовательности

вычисляется по формуле a=-a*, где I=1,2,3,4,……; a=x

Вычисления проводить до тех пор, пока , где =0.0001

Реализация этой задачи с помощью 4 видов цикла:

Do while …. Loop

Do…. Loop while

Dim x As Single,

s As Single, i As Integer

Dim a As Single, e As Single

x = 0.5

e = 0.0001

s = 0

a = x

i = 1

Do While Abs(a) > e

s = s + a

a = -a * x * i / (i + 1)

i = i + 1

Loop

MsgBox Str(s)

MsgBox Log(1.5)

Dim x As Single,

s As Single, i As Integer

Dim a As Single, e As Single

x = 0.5

e = 0.0001

s = 0

a = x

i = 1

s = s + a

a = -a * x * i / (i + 1)

i = i + 1

Loop While Abs(a) > e

MsgBox Str(s)

MsgBox Log(1.5)

Ответы : s=0.4055323

log(1.5)=0.405465108108164

Do Until…..Loop

Do ….Loop Until

Dim x As Single,

s As Single, i As Integer

Dim a as Single,e As Single

x = 0.5

e = 0.0001

s = 0

a = x

i = 1

s = s + a

a = -a * x * i / (i + 1)

i = i + 1

Loop Until Abs(a) < e

MsgBox Str(s)

MsgBox Log(1.5)

Dim x As Single,

s As Single, i As Integer

Dim a as Single, e As Single

x = 0.5

e = 0.0001

s = 0

a = x

i = 1

Do Until Abs(a) < e

s = s + a

a = -a * x * i / (i + 1)

i = i + 1

Loop

MsgBox Str(s)

MsgBox Log(1.5)

Операторы Exit

В VBA имеется несколько операторов Exit для выхода из процедур-функций, процедур-подпрограмм, процедур обработки свойств или повторно выполняемых блоков операторов в структурах Do…Loop, For…Next, For Each … Next.

Операторы Exit обрабатываются следующим образом:

Exit Function, Exit Sub и Exit Property вызывают немедленный выход из функции, подпрограммы или процедуры обработки свойств, в которой находится соответствующий оператор Exit. Управление получает следующий оператор в вызывающей процедуре.

^ может применяться в структуре Do…Loop и предназначен для немедленной передачи управления оператору. следующему после Loop.

Exit For может применяться только в структуре For…Next или For Each Next и предназначен для немедленной передачи управления оператору, следующему после Next.

^
Лабораторная работа 1.7 требует оформления результатов по всем пунктам задания на листе под именем «1.7» в своей книге Excel «Л.р. по Excel».
^
Достигнута ли цель работы?

Роль и возможности разветвляющихся функций в MS Excel.

Назначение разветвляющихся функций.

Особенности применения разветвляющихся функций для выполнения сложных расчетов в Excel.

Особенности применения разветвляющихся функций для обработки массивов в Excel.

Особенности работы с разветвляющимися функциями.
^

Ответить на вопросы:

Что такое разветвляющиеся вычислительные процессы?
Что собой представляют выражения отношения и логические выражения?
Каков синтаксис логических функций ИСТИНА и ЛОЖЬ?
Как строится синтаксис логических функций, используемых для описания логических операций?
Какова структура Если-То-Иначе и ее реализация в Excel?
Как составляются формулы для описания выражений отношения и логических выражений?
Как используются логические функции для проверки наличия в ячейке логического значения?
Как составляются формулы для решения задач, содержащих выбор одной из нескольких альтернатив?
Как используются логические функции для “перехвата” ошибок при выполнении вычислений?

Источник

Цель работы:
получить практические навыки разработки
функций для реализации линейных,
разветвляющихся и простейших циклических
алгоритмов с помощью макросов в Excel.

Цель работы

1. Изучите
теоретические сведения.

2. Создайте макросы
по заданному преподавателем варианту.

3. Сохраните файл
с созданными макросами.

4. Перепишите текст
макросов в отчет.

5. Закройте
Visual Basic и
Microsoft Excel.

6. Ответьте на
контрольные вопросы по указанию
преподавателя.

Контрольные вопросы

1.
С помощью каких операторов составляются
циклические алгоритмы?

2.
Каково назначение операторов
For,
While,
Do…Loop?

3.
В чем разница между операторами For
и While?

4.
Что может содержаться в условии оператора
If?

5.
Что происходит в случае невыполнения
условия в операторе If?

6.
Каково назначение операторов
Then, Else и
Else If?

7.
В чем разница между операторами If
и Select
Case?

8.
В чем разница между операторами While
и Until?

Ответы на контрольные вопросы

Циклические
алгоритмы. Для
реализации циклических алгоритмов
используются три вида операторов цикла:
For,
While,
Do…Loop.

Назначение
операторов For,
While,
Do…Loop.
Оператор
For
имеет следующий формат записи:

For
переменная = начальное значение To
конечное значение

[операторы]

Next
[перменная]

В качестве примера
приведем программу, в которой оператор
For
используется для вычисления суммы
s=1²+2²+…+n²:

Sub
Sum
()

n
= InputBox(«Введите количество слагаемых»)

s
= 0

For
i = 1 To n

s
= s + i ^ 2

MsgBox
s

End
Sub

Оператор While
имеет
следующий формат записи:

While условие

[операторы]

Wend

Оператор Do
… Loop имеет
следующий две разновидности записи:

Do
[{While
/ Until}
условие]

[операторы]

[Exit
Do]

[операторы]

Loop

или:

[операторы]

[Exit
Do]

[операторы]

Loop
[{While / Until} условие]

3. Разница между операторами For и While.

Для сравнения
принципа работы рассматриваемого
оператора с оператором For
приведем пример программы, выполняющей
аналогичную задачу вычисления суммы

Sub
Sum()

Dim
i As Integer

n
= InputBox(«Введите
количество слагаемых»)

s
= 0

i
= 0

While
i < n + 1

s
= s + i ^ 2

i
= i
+ 1

Wend

Приведем пример
предыдущей задачи с использованием
данного оператора

Sub
Sum()

Dim
i As Integer

n
= InputBox(«Введите
количество слагаемых»)

s
= 0

i
= 0

Do
While i < n + 1

s
= s + i ^ 2

i
= i + 1

Loop

MsgBox
s

End
Sub

или

Sub
Sum()

Dim
i
As
Integer

n
= InputBox(«Введите
количество слагаемых»)

s
= 0

i
= 0

s
= s + i ^ 2

i
= i + 1

Loop
Until i > n

MsgBox
s

End
Sub

4. Содержание
условия оператора If.
Для записи
разветвляющихся
алгоритмов
используется оператор If
(Если),
который имеет две формы записи.

1. Однострочная
запись:

If условие
Then
[оператор]

If
условие Then
[оператор 1] [Else
оператор 2]

2. Многострочная
запись:

If
условие Then

[оператор 1]

[оператор 2]

[оператор 3]

End If

В однострочном
операторе условие и выполняемые при
соблюдении условия действия располагаются
в одной строке. В том случае, если при
выполнении условия требуется выполнение
блока операторов, используется
многострочный оператор.

После имени
конструкции If
должно следовать логическое выражение,
содержащее условие. Для создания сложных
условий используются логические операции
And
(И)
и Or
(Или).
В качестве условия могут выступать
следующие логические выражения: сравнение
переменной с другой переменной, константой
или функцией; любая переменная; выражение;
поле базы данных; функция, принимающие
значения True
(Истина) или
False (Ложь).

5. Невыполнение
условия в операторе If.
Если условие
не выполняется, то Visual Basic переходит к
выполнению операторов, следующих за
указанным оператором.

В качестве примера
приведем функцию определения корней
квадратного уравнения:

Function
Корни(a,
b, c)

d
= b ^ 2 — 4 * a * c

If
d >= 0 Then

x1
= (-b + d ^ (1 / 2)) / (2 * a)

x2
= (-b — d ^ (1 / 2)) / (2 * a)

Корни
= «x1=» + str(x1) + «; x2=» + str(x2)

Else

Корни = «корней
нет»

End
If

End
Function

6. Назначение
операторов Then, Else и Else If.
Конструкция
If…Then
(Тогда)…Else
(Также)
аналогична
конструкции If…Then,
но позволяет задать действия, исполняемые
как при выполнении условий, так и в
случае их невыполнения.

Команда If
может
проверить только одно условие. Если
требуется осуществить переход управления
в зависимости от результатов проверки
нескольких условий, то дополнительное
условие можно задать с помощью оператора
Else If
(Также Если).
Оно будет анализироваться только в том
случае, если предыдущее условие ложно.

Ключевое слово
End If
обозначает конец многострочной
конструкции и его наличие в команде в
этом случае обязательно. Если указанное
условие выполняется, то есть результат
проверки равен True
(Истина), то
выполняются операторы, следующие за
ключевым словом Then.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Цель работы
Постановка задания (условный оператор)
- Варианты заданий
- Образец выполнения (вариант №5)
  - Условие задания
  - Алгоритм решения задачи (математическая модель)
  - Решение задачи с использованием макроса на VBA
  - Результаты работы программы
Постановка задания (оператор выбора)
- Варианты заданий
- Образец выполнения (вариант №2)
  - Условие задания
  - Алгоритм решения задачи (математическая модель)
  - Решение задачи с использованием макроса на VBA
  - Результаты работы программы

ВНИМАНИЕ

Для получения процедуры, вызываемой через макрос, своего варианта пишите на наш электронный адрес proglabs@mail.ru

Цель работы

Изучить логические операции и базовые операторы, реализующие алгоритм ветвления.

Постановка задания (условный оператор)

Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):

Написать подпрограмму, которая выводит в первом случае в окно сообщения, во втором – в ячейку листа Excel сообщение «Точка с заданными координатами не принадлежит заштрихованной области», если точка, заданная координатами ${х; у}$ не принадлежит заштрихованной области, в противном случае вывести сообщение «Точка с заданными координатами принадлежит заштрихованной области».

Варианты заданий

№	График	№	График
1		6
2		7
3		8
4		9
5		10

Образец выполнения (вариант №5)

Условие задания

Алгоритм решения задачи (математическая модель)

Прежде чем переходить непосредственно к кодированию данной лабораторной работы, нужно провести ее алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.

В первую очередь нужно провести тщательный анализ заданного фрагмента и попытаться разбить его на тривиальные геометрические примитивы: прямоугольники, квадраты, окружности, ромбы, треугольники и пр.

Очевидно, что заданный фрагмент графика можно расчленить на 2 составные части: левую и правую.

Проведем анализ каждой из частей и попробуем записать математические формулы, описывающие эти графические примитивы.

Фрагмент

Геометр. представление

Математическое описание

Левый

Часть окружности, которая существует только в 4-ой четверти декартовой системы координат.

$x^2 + y^2 = R^2$ — уравнение окружности с центром в начале координат.

Из графика функции видно, что $R = 6$.

Так как окружность существует только в 4-ой четверти, то необходимо добавить следующие ограничения:

$x leq 0$
$y geq 0$

Так как нам требуется проверить попадание точки внутрь этого фрагмента, то окончательные условия для этого будут такими:

$begin{cases} x^2 + y^2 leq 6^2, \ x leq 0, \ y geq 0 end{cases}$

Правый

Часть окружности, которая существует только в 1-ой четверти декартовой системы координат.

$x^2 + y^2 = R^2$ — уравнение окружности с центром в начале координат.

Из графика функции видно, что $R = 4$.

Так как окружность существует только в 1-ой четверти, то необходимо добавить следующие ограничения:

$x geq 0$
$y geq 0$

$begin{cases} x^2 + y^2 leq 4^2, \ x geq 0, \ y geq 0 end{cases}$

Для того, чтобы точка с заданными координатами попадала в заштрихованную область графика, нам достаточно, чтобы эта точка попала или в левую часть, или в правую часть исходного графика.

➡ Следовательно, получим окончательную версию математической модели, благодаря которой можно проверить попадание точки в заданный интервал:

$left[ begin{gathered} left{ begin{gathered} x^2 + y^2 leq 6^2, \
x leq 0, \ y geq 0 end{gathered} right. \ \ left{ begin{gathered}
x^2 + y^2 leq 4^2, \ x geq 0, \ y geq 0 end{gathered} right.
\ end{gathered} right.$

💡 В теории математики такую запись называют совокупностью систем.

Решение задачи с использованием макроса на VBA

‘ процедура, проверяющая попадание точки с заданными координатами {x; y} в заштрихованную область

Sub Uslovie()

‘ раздел объявления переменных

Dim x As Double ‘ координата заданной точки по оси абсцисс (Х)

Dim y As Double ‘ координата заданной точки по оси ординат (Y)

Dim f1 As Boolean ‘ равно true, если заданная точка попадает в «левую» часть заштрихованной области

Dim f2 As Boolean ‘ равно true, если заданная точка попадает в «правую» часть заштрихованной области

Dim f3 As Boolean ‘ равно true, если заданная точка попадает в заштрихованную область

‘ производим автоматическую очистку ячеек таблицы от прошлых результатов (если это не самый 1ый тест макроса)

Worksheets(«Task1»).Range(«G5:G6»).ClearContents

Worksheets(«Task1»).Cells(8, «F»).Value = «»

‘ запрашиваем координаты точки вводом с клавиатуры

x = InputBox(«Введите координату точку по оси абсциис (Х): «, «Сообщение для пользователя»)

Worksheets(«Task1»).Cells(5, «G») = x

y = InputBox(«Введите координату точку по оси ординат (Y): «, «Сообщение для пользователя»)

Worksheets(«Task1»).Cells(6, «G») = y

‘ проверка попадания точки с заданными координатами в «левую» часть заштрихованной области

f1 = (x <= 0) And (y >= 0) And (x ^ 2 + y ^ 2 <= 6 ^ 2)

‘ проверка попадания точки с заданными координатами в «правую» часть заштрихованной области

f2 = (x >= 0) And (y >= 0) And (x ^ 2 + y ^ 2 <= 4 ^ 2)

‘ вычисляем результат

f3 = f1 Or f2

‘ выводим результаты в диалоговое окно и в ячейку листа Excel

If (f3 = True) Then

Worksheets(«Task1»).Cells(8, «F») = «Точка принадлежит заданной области»

MsgBox («Точка с заданными координатами принадлежит заштрихованной области»)

Else

Worksheets(«Task1»).Cells(8, «F») = «Точка не принадлежит заданной области»

MsgBox («Точка с заданными координатами не принадлежит заштрихованной области»)

End If

End Sub

Результаты работы программы

ВНИМАНИЕ

Для получения процедуры, вызываемой через макрос, своего варианта пишите на наш электронный адрес proglabs@mail.ru

Постановка задания (оператор выбора)

Напишите макрос, решающую задачу в соответствии с вашим вариантом, ввод данных осуществляется из ячеек электронной таблицы. Вывод реализован в ячейки электронной таблицы.

Варианты заданий

№	Условие задачи
1	В ячейку вводятся числа от $1$ до $4$, соответствующее: $1$ – миллиграмм, $2$ – грамм, $3$ – тонна, $4$ — центнер. С помощью диалогового окна считывается масса $М$ в соответствующих единицах измерения и выводится ее значение в килограммах.
2	В ячейку вводятся числа от $1$ до $3$, соответствующее: $1$ – радиус, $2$ – диаметр, $3$ – длина окружности. С помощью диалогового окна считывается значение соответствующего элемента окружности и вычисляется ее площадь. Например, если введено «$1$», то считывается значение радиуса, используя которое необходимо вычислить площадь окружности.
3	В ячейку вводятся числа от $1$ до $3$, соответствующее: $1$ – окружность, $2$ – прямоугольник, $3$ – трапеция. Нужно вычислить площадь соответствующей фигуры, введя для этого значения необходимых элементов. Например, если введено «$3$», то нужно ввести значение длин оснований трапеции и ее высоту, используя которые вычислить площадь.
4	В ячейку вводятся числа от $1$ до $4$, соответствующее: $1$ – синус, $2$ – косинус, $3$ – тангенс, $4$ – котангенс. С помощью диалогового окна считывается значение соответствующей функции для некоторого угла a, для которого необходимо найти значения всех остальных тригонометрических функций. Например, если введено «$1$», то вводится значение , а затем вычисляются значения .
5	В ячейку вводятся числа от $1$ до $3$, соответствующее одному из элементов равнобедренного прямоугольного треугольника: $1$ – катет, $2$ – гипотенуза, $3$ – площадь. С помощью диалогового окна считывается значение соответствующего элемента, используя которое вычисляются все остальные элементы. Например, если введено «$1$», то считывается значение катета, а затем находится гипотенуза и вычисляется площадь треугольника.
6	В ячейку вводятся числа от $1$ до $3$, соответствующее одному из элементов равностороннего треугольника: $1$ – длина стороны, $2$ – периметр, $3$ – площадь. С помощью диалогового окна считывается значение соответствующего элемента, используя которое нужно вычислить значения остальных элементов. Например, если введено число «$1$», то вводится длина стороны треугольника и с помощью этого значения вычисляются периметр и площадь треугольника.
7	В ячейку вводятся числа от $1$ до $4$, соответствующее одному из элементов квадрата: $1$ – длина стороны, $2$ – длина диагонали, $3$ – периметр, $4$ – площадь. С помощью диалогового окна считывается значение соответствующего элемента, с помощью которого вычисляются все остальные элементы. Например, если введено число «$2$», то с клавиатуры вводится длина диагонали квадрата, используя которую необходимо найти длину стороны, периметр и площадь квадрата.
8	В ячейку вводятся числа от $1$ до $3$, соответствующее: $1$ – прямой круговой цилиндр, $2$ – конус, $3$ – шар, $4$ – прямоугольный параллелепипед. Нужно вычислить объем соответствующей фигуры, введя для этого значения необходимых элементов. Например, если введено число «$2$», то нужно ввести с клавиатуры высоту конуса и радиус его основания и вычислить объем фигуры.
9	В ячейку вводятся числа от $1$ до $4$, соответствующее одному из элементов куба: $1$ – длина ребра, $2$ – длина диагонали боковой грани, $3$ – площадь боковой грани, $4$ – объем. С помощью диалогового окна считывается значение соответствующего элемента, используя которое нужно вычислить значения остальных элементов куба. Например, если введено число «$3$», то с клавиатуры вводится значение площади боковой грани куба, с помощью этого значения нужно вычислить длину ребра, длину диагонали боковой грани и объем куба.
10	В ячейку вводятся числа от $1$ до $4$, соответствующее: $1$ – миллиметр, $2$ – сантиметр, $3$ – дециметр, $4$ – километр. С помощью диалогового окна считывается длина $L$ в соответствующих единицах измерения и выводится ее значение в метрах.

Образец выполнения (вариант №2)

Условие задания

В ячейку вводятся числа от $1$ до $3$, соответствующее: $1$ – радиус, $2$ – диаметр, $3$ – длина окружности. С помощью диалогового окна считывается значение соответствующего элемента окружности и вычисляется ее площадь. Например, если введено «$1$», то считывается значение радиуса, используя которое необходимо вычислить площадь окружности.

Алгоритм решения задачи (математическая модель)

💡 Главное назначение математической модели — показать нам, как связаны между собой следующие величины:

Радиус — площадь окружности.
Диаметр — площадь окружности.
Длина окружности — площадь окружности.

№	Графическое представление	Математическая формула
1		$S_{круга} = PI cdot R^2$, где $PI$ — константа, равная примерно $3.1415$; $R$ — радиус окружности.
2		$D = 2 cdot R rightarrow R = frac{D}{2}$ $S_{круга} = PI cdot R^2 = PI cdot (frac{D}{2})^2$ $S_{круга} = PI cdot frac{D^2}{4}$, где $PI$ — константа, равная примерно $3.1415$; $D$ — диаметр окружности.
3		$L = 2 cdot PI cdot R rightarrow R = frac{L}{2 cdot PI}$ $S_{круга} = PI cdot R^2 = \ = PI cdot (frac{L}{2 cdot PI})^2 = PI cdot frac{L^2}{2^2 cdot PI^2}$ $S_{круга} = frac{L^2}{4 cdot PI}$, где $PI$ — константа, равная примерно $3.1415$; $L$ — длина окружности.

➡ Владея этой информацией, мы теперь без труда сможем вычислить площадь окружности (или площадь круга)!

Решение задачи с использованием макроса на VBA

‘ процедура, вычисляющая площадь круга

Sub Calculate()

‘ раздел объявления переменны

Dim userSelect As Integer ‘ хранит число, соответствующее типу входной информации (радиус, диаметр или длина окружности)

Dim R As Double ‘ хранит радиус окружности

Dim D As Double ‘ хранит диаметр окружности

Dim L As Double ‘ хранит длину окружности

Dim S As Double ‘ хранит результат (площадь круга)

Dim PI As Double ‘ константа ПИ

‘ производим очистку от прошлых результатов (если это не самый 1ый тест макроса)

Worksheets(«Task2»).Range(«J4:J6»).ClearContents

Worksheets(«Task2»).Cells(9, «I»).ClearContents

‘ сделано для удобства записи во всех последующих формулах

PI = Application.WorksheetFunction.PI

‘ считываем число, введенное пользователем

userSelect = Worksheets(«Task2»).Cells(8, 9)

S = 0 ‘ если пользователь ошибется с выбором, то площадь круга будет равна 0, что соот-ет недопустимому значению

‘ анализируем входное пользовательское значение

Select Case userSelect

Case 1 ‘ пользователь работает с радиусом окружности

R = InputBox(«Введите радиус окружности(R): «, «Сообщение для пользователя»)

Worksheets(«Task2»).Cells(4, 10) = R

S = PI * R ^ 2

Case 2 ‘ пользователь работает с диаметром окружности

D = InputBox(«Введите диаметр окружности(D): «, «Сообщение для пользователя»)

Worksheets(«Task2»).Cells(5, 10) = D

S = PI * D ^ 2 / 4

Case 3 ‘ пользователь работает с длиной окружности

L = InputBox(«Введите длину окружности(L): «, «Сообщение для пользователя»)

Worksheets(«Task2»).Cells(6, 10) = L

S = L ^ 2 / (4 * PI)

Case Else

MsgBox («Вы забыли выбрать номер исходного данного, либо номер задан некорректно!»)

End Select

‘ выводит результат (площать круга) в ячейку листа Excel

Worksheets(«Task2»).Cells(9, 9) = S

End Sub

Результаты работы программы

№	Тест	Результаты
1	Интерфейс программы (Excel)
2	Задан радиус окружности (R)
3	Задан диаметр окружности (D)
4	Задана длина окружности (L)
5	Ошибочный ввод

ВНИМАНИЕ

Для получения процедуры, вызываемой через макрос, своего варианта пишите на наш электронный адрес proglabs@mail.ru

Источник