Реализация метода моделирования в ms excel

Автор статьи

Дмитрий Михайлович Беляев

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Определение 1

Моделирование — это изучение какого-либо явления, процесса или системы объектов посредством формирования и исследования их моделей.

Введение

В системах, связанных с экономикой, руководящим работникам необходимо постоянно принимать решения следующих категорий:

  1. Стратегические решения.
  2. Тактические решения.
  3. Оперативные решения.

Если принимаемые решения обладают низким интеллектуальным уровнем, то простота представления реальных ситуаций обычно ведёт к неточностям при выработке прогнозов, а, кроме того, к убыткам и добавочным финансовым потерям. Чтобы избежать возникновения подобных ситуаций и обеспечить устойчивое экономическое положение, существуют разнообразные системы поддержки выработки решений, усовершенствование которых превращается в наиболее актуальную проблему при наличии жёсткой конкуренции.

Логотип iqutor

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Существенным условием для таких программ считается возможность имитации вырабатываемых решений, апробации вероятных коррекций в экономической системе, появляющихся в результате влияния разных факторов, то есть нахождение ответа на вопрос типа, «что случится, если…». Это позволит существенно сократить риски от осуществления решений и сэкономить ресурсы, чтобы достичь поставленной цели.

Такие возможности предоставляют имитационные модели, которые обладают следующим набором качеств:

  1. Возможность регулировать уровень сложности модели.
  2. Присутствие случайных факторов.
  3. Возможность описать процесс, развивающийся по времени.
  4. Обязательное использование электронной вычислительной машины.

Имитационные модели предназначаются для того, чтобы оценить варианты намечаемых коррекций, обладать игровой формой для обучения работников, визуально отобразить работу исследуемого объекта во времени и так далее. Реализовать модели можно при помощи универсальных языков программирования, к примеру,Pascal, Basic, пакетов прикладных программ, таких как,Excel, MathCAD, и так далее. Выбор конкретного метода моделирования определяется сложностью задачи, наличием необходимых ресурсов и так далее.

«Моделирование в Excel» 👇

Однако имитационное моделирование применяется экономистами и другими специалистами только в малом проценте случаев, в которых можно было бы при помощи моделей поиметь важную для выработки решений информацию.Причина этого явления кроется в отсутствии инструкций по проведению имитационного моделирования при помощи общеизвестного и доступного инструментария, а именно, пакетов прикладного программного обеспечения, такого как Excel и MathCAD, которые могут обеспечить простую платформу для моделирования.Поэтому примеры формирования имитационных моделей при помощи, например, приложения Excel, помогают их широкому распространению в кругу работников, не владеющих языками моделирования и методиками, имеющимися в средах моделирования.

Электронные таблицы Excel как инструмент формирования имитационных моделей

Имитационное моделирование при помощи табличного процессора является отдельным направлением, имеющем свои особенности. Применение таких систем позволяет лучше понять происходящие процессы, в сравнении с использованием специализированных программ, обладающих высокой стоимостью и требующих много времени для их освоения, а также не позволяющих увидеть применяемые механизмы. Например, специалисты полагают, что имитация при помощи таблиц Excel позволяет лучше представить работу систем массового обслуживания, чем даже теория очередей, а также помогает в развитии интуиции, предоставляет даже не знающим программирования пользователям опыт формирования разных моделей. Специалисты предлагают следующие этапы обучения моделированию в Excel:

  1. Базовые понятия.
  2. Введение в теорию вероятности и статистику.
  3. Процесс имитационного моделирования в ручном режиме.
  4. Имитационное моделирование при помощи электронных таблиц.
  5. Генерирование случайных чисел.
  6. Осуществление анализа исходных данных.
  7. Осуществление анализа итогов моделирования.

При формировании моделей в Excelприменяются следующие главные подходы к осуществлению имитации:

  1. Подход, который ориентирован на события.
  2. Подход, имеющий ориентацию на процессы.
  3. Подход, направленный на сканирование активностей.

Первый подход служит для описания изменений в системе, которые происходят при совершении любого случайного события, например, получение заявки, завершение обслуживания. При его формировании при помощи электронных таблиц обычно применяется одна строчка для каждого события.

Если используется подход, ориентированный на процесс, то выполняется моделирование очерёдности событий для каждой заявки, и чтобы его реализовать, применяется одна строчка для каждого требования (используется при моделировании систем массового обслуживания).

Сканирование активностей состоит в описании действий, возникающих в системе за фиксированный временной интервал (день, неделя, месяц, год), и при его осуществлении, как правило, применяется одна строчка для каждого отрезка времени. К примеру, это может быть моделирование системы управления запасами.

Использование программного пакета MSExcelобладает следующими преимуществами:

  1. В составе пакета Excelесть значительное число встроенных функций из области математики, статистики и других областей, включая возможность генерации случайных значений.
  2. Excelдаёт возможность сохранять информацию и иметь к ней доступ.
  3. Программный пакетExcelпозволяет строить графики и диаграммы.
  4. Программный пакет Excel обладает встроенным языкомVBA (VisualBasicforApplication).
  5. Программный пакет Excelшироко распространён среди специалистов, то есть имеется на компьютере практически у всех.
  6. Наличие возможности экспорта информационных данных в иные программные приложения.

Помимо этих достоинств, возможен просмотр любой формулы, занесённой в ячейку таблицы, что увеличивает уровень доверия к итогам моделирования.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Сборник заданий по разделу:

ОМПЬЮТЕРНОЕ

МОДЕЛИРОВАНИЕ В MS EXCEL

Иванов Иван

Для всех специальностей СПО

Разработала:

преподаватель

Белева Людмила Федоровна

Сыктывкар,2016 год

Пояснительная записка:

Учебно-методическое пособие предназначено для студентов всех специальностей и может быть использовано, в управлении образовательным процессом как одно из дидактических средств обучения.

Изучение содержания данного учебно-методического пособия обеспечит возможность студенту научиться строить и исследовать модели с помощью ЭВМ, применять и использовать электронные таблицы для решения данной категории  задач.

МАТЕМАТИЧЕСКИЙ АППАРАТ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ

Событие, которое может произойти, а может и не произойти, называют случайным событием. Например, поражение мишени или промах при выстреле – случайные события. Выигрыш команды во встрече с соперником, проигрыш или ничейный результат – это тоже примеры случайных событий.

Вообще, пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло или нет интересующее нас событие А. Число m называют частотой события А, а отношение m/n – относительной частотой, где n – общее число испытаний.

Задача 1.

Определить относительную частоту выпадения орла.

Для этого: введите формулы в расчетные ячейки.

Формула

Комментарий

Результаты

А1

=ЦЕЛОЕ (СЛЧИС()+0,5)

Выпадение орла или решки

0 или 1

A2

Копируем формулу

А3

до

A4

A5

500

A6

….

строки

А500

включительно

А501

=СЧЕТЕСЛИ(А1:А500;1)

Число выпадений орла

234

А502

=СЧЕТ(А1:А500)

Число бросков

500

А503

= А501/ А502*100

Относительная частота

0,49

Вообще, результаты наблюдений и опытов показывают, что при большом числе испытаний, проводимых в одних и тех же условиях, относительная частота принимает достаточно устойчивое значение.

Такое определение называют статистическим определением вероятности.

Задача 2. Бросание кубика

Найдите статистическую вероятность для каждого значения выпадения очков 1,2,3,4,5,6.

Для этого: введите формулы в расчетные ячейки.

A

B

C

D

1

=ЦЕЛОЕ(СЛЧИС()*6+1

1

{=ЧАСТОТА(A1:A500;B1:B6)}

=С1/500*100

2

Копируем формулу

2

3

до

3

4

500

4

5

строки

5

6

включительно

6

….

500

Дополнение: рассмотрим событие В, которое означает выпадение числа очков, кратного 3. Это событие происходит при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков. Эти исходы называют благоприятными исходами для события В. При бросании кубика из 6 равновозможных исходов испытания благоприятными для события В являются лишь два исхода. Отношение числа благоприятных исходов к числу всех равновозможных исходов равно 2/6. Это отношение называют вероятностью события В и пишут Р(В)=2/6=1/3.

Вероятностью события называют отношение числа благоприятных для него исходов испытания к числу всех равновозможных исходов.

В рассмотренном примере посмотрим назначения ячеек D3 и D6, их сумма 32,6 колеблется около 33%. Таким образом, классическое и статистическое определение вероятности совпадают с определенной степенью точности.

Задача 3.

Проверить, что вероятность выпадения оба раза решки равна 0,25.

Решение.

Для этого: введите формулы в расчетные ячейки.

A

B

C

D

E

F

1

=ЦЕЛОЕ(СЛЧИС()+0,5)

=ЦЕЛОЕ(СЛЧИС()+0,5)

=A1+B1

0

{=ЧАСТОТА

(C1:C50;D1:B3)}

=E1/50*100

2

Копируем формулу

1

3

до

2

4

50

5

строки

6

включительно

…

Задача 4.

Из 25 экзаменационных билетов по геометрии ученик успел приготовить 11 первых 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?

Решение.

Общее число равновозможных исходов при выборе билетов на экзамене 25. Пусть М – событие, заключающееся в том, что ученику достанется на экзамене билет, к которому он не подготовился. Число благоприятных для М исходов (но не для ученика) равно 25-(11+8). Значит Р (М) =6/26=0,24. Проверим это. Для этого: введите формулы в расчетные ячейки.

A

B

C

D

1

=ЦЕЛОЕ (СЛЧИС()*25+1)

=ЕСЛИ(A911;1;0)

=ЕСЛИ(A1

=B1+C1

2

Копируем формулу

Копируем формулу

Копируем формулу

Копируем формулу

3

до

4

49

5

строки

…

включительно

49

Число неудачных билетов

=СЧЁТЕСЛИ(D1:D49;2)

50

Число всех билетов

=СЧЁТ(D1:D49)

52

Относительная

вероятность в %

=D50/D51*100

Задача 5.

Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередной попытке в сумме выпадает 8 очков, то выигрывает Антон, а если в сумме выпадает 7 оков, то выигрывает Игорь. Является ли такая игра справедливой?

Решение.

При бросании кубиков на белом кубике может выпасть 1,2,3,4,5 или 6 очков.

Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов числа очков, выпавших на черном кубике. Все равновозможные исходы этого испытания приведены в таблице:

(1,1)

(2,1)

(3,1)

(4,1)

(5,1)

(6,1)

(1,2)

(2,2)

(3,2)

(4,2)

(5,2)

(6,2)

(1,3)

(2,3)

(3,3)

(4,3)

(5,3)

(6,3)

(1,4)

(2,4)

(3,4)

(4,4)

(5,4)

(6,4)

(1,5)

(2,5)

(3,5)

(4,5)

(5,5)

(6,5)

(1,6)

(2,6)

(3,6)

(4,6)

(5,6)

(6,6)

В каждой паре на первом месте записано число очков, выпавших на белом кубике, на втором – число очков на черном кубике. Общее число равновозможных исходов равно 36. Пусть событие А означает, что при бросании кубиков в сумме выпало 8 очков, а событие В означает, что в сумме выпало 7 очков. Для события А благоприятными являются следующие 5 исходов:(2;6), (3,5), (4;4), (5,3), (6;2). Для события В благоприятными являются следующие 6 исходов:(1;6), (2,5), (3,4), (4;3), (5,2), (6;1). Отсюда: Р (А)=5/36 Р(В)=6/36.Поэтому делаем вывод шансов выиграть у Игоря больше, чем у Антона. Значит, такая игра не является справедливой.

Проверим это. Для этого: введите формулы в расчетные ячейки.

A

B

C

D

E

F

1

=ЦЕЛОЕ(СЛЧИС()*6+1)

=ЦЕЛОЕ(СЛЧИС()*6+1)

=A1+B1

1

{=ЧАСТОТА(C1:C100;D1:D12)}

=Е1/100*100

2

Копируем формулу

Копируем формулу

2

3

до

до

3

4

100

100

4

5

строки

строки

5

…

6

…

12

100

Задача 6.

На карточках написаны натуральные числа от 1 до 10 включительно, после чего карточки перевернули и перемешали. Затем наугад открыли одну карточку. Какова вероятность того, что на ней будет написано простое число или число, большее 7?

Решение.

Пусть событие А означает, что на каточке написано простое число, а событие В означает число, большее 7. Для события А благоприятными являются 4 исхода 10 равновозможных(появление одного из чисел 2,3,5,7), то есть вероятность события А равна 0,4.

Для события В благоприятными являются 3 исхода из 10 равновозможных(появление чисел 8,9,10), то есть вероятность события В равна 0,3.

Нас интересует событие С, когда на карточке написано простое число или число, большее 7. Событие С наступает тогда, когда наступает одно из событий А или В. Очевидно, что эти события являются несовместимыми. Значит, вероятность события С равна сумме вероятностей событий А и В, то есть: Р(С)= Р(А) + Р(В)=0,4+0,3=0,7.

Проверим это. Для этого: введите формулы в расчетные ячейки.

A

B

C

D

E

F

G

H

1

2

3

5

7

7

2

1

=ЦЕЛОЕ(СЛЧИС()*10+1)

=ЕСЛИ(B2=C$1;1;0)

=ЕСЛИ(B2=D$1;1;0)

=ЕСЛИ(B2=Е$1;1;0

=ЕСЛИ(B2= F$1;1;0)

=ЕСЛИ(B27;1;0)

=СУММ(C2:G2)

3

2

Копируем формулу

4

до

5

97

…

98

=СЧЁТЕСЛИ

(H2:H97;»0″)

99

=Н98/97

Задача 7.

В результате многократных наблюдений установили, что вероятность попадания в мишень одного стрелка равна 0,9, а другого – 0,8. Каждый из стрелков сделал по одному выстрелу по мишени. Какова вероятность того, что мишень будет поражена?

Решение.

Рассмотрим такие события: А – первый стрелок попал в мишень; В – второй стрелок попал в мишень; С – мишень поражена. События А и В независимые. Однако воспользоваться в этом случае умножением вероятностей нельзя, так как событие С наступает не только, тогда, когда оба стрелка попали в мишень, но и тогда, когда в мишень попал хотя бы один из них.

Поступим иначе. Рассмотрим события Ā, B, С, противоположные соответственно событиям А, В, С. События Ā, B являются независимыми, так как промах при выстреле по мишени первого стрелка ( событие Ā) не зависит от промаха второго стрелка( событие B). Событие С означает совместное появление событий Ā,B. Поэтому Р(С)= Р(Ā) • Р(B).

Из свойств вероятностей противоположных событий вытекает, что Р(Ā)=1-0,9=0,1;

Р(B)=1-0,8=0,2; Отсюда получаем Р(С)= Р(Ā) •Р(B)=0,1•0,2=0,02. Так как события С и С противоположные, то теперь несложно найти вероятность события С: Р(С)= 1-Р(С)=1-0,02=0,98. Значит, вероятность того, что мишень будет поражена, равна 0,98.

Проверим это на компьютере. Для этого: введите формулы в расчетные ячейки.

A

B

C

D

E

F

1

1

=СЛЧИС()

=СЛЧИС()

=ЕСЛИ(B10,1;1;0)

=ЕСЛИ(C10,2;1;0)

=C1+D1

2

2

заполнить

заполнить

заполнить

заполнить

заполнить

3

3

4

4

5

5

6

6

7

7

…

97

98

98

=СЧЁТЕСЛИ(F1:F97;»0″)

99

99

=F98/A97

Задания для самостоятельного выполнения:

  1. На карточках написали цифры 1,2,3, после чего карточки перевернули и перемешали. Затем последовательно открыли карточки и положили в ряд. Какова вероятность того, что получится трехзначное число, большее 300?

  2. Для экзамена подготовили билеты с номерами от 1 до 25. Какова вероятность того,

что взятый наугад учеником билет имеет:

а) однозначный номер;

б) двухзначный номер?

  1. Многократные испытания показали, что для некоторого стрелка вероятность выбить при стрельбе 10 очков равна 0,1, а вероятность выбить 9 очков равна 0,3. Чему равна для этого стрелка вероятность выбить не менее 9 очков?

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ

Случай является неотъемлемой частью нашей жизни. Если случай помог нам в чем-то, мы говорим — повезло, если оказался не в нашу пользу, мы сокрушаемся — что за судьба! Многие ученые посвятили свой талант изучению закономерностей случайных событий. Знание законов случайностей может быть полезным в разных сферах: от определения вероятности некоторого события, например выигрыша в лотерею, до использования статистических закономерностей в научных опытах. Ниже будут смоделированы ситуации, которые в теории вероятности получили название «случайных блужданий».

ЗАДАЧА. Бросание монеты

I ЭТАП. ПОСТАНОВКА ЗАДАЧИ

Описание задачи

У вас есть 10 монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою судьбу. Суть игры проста. Играя с маклером, вы делаете ставку и бросаете монету. Если выпадет «орел», маклер выдает вам сумму вашей ставки, в противном случае — вы ему отдаете эту сумму. Ставка может быть любой: от 1 до 10 монет. Удвоение начального капитала или банкротство приводит к незамедлительному прекращению этого сеанса игры и расчету. Игра может продолжиться по вашему усмотрению. 

Цель моделирования

Моделируя возможные игровые ситуации, в частности, варьируя ставки в данной игре, выяснить, какая тактика чаще приводит к результату (положительному или отрицательному).

Предупредить потенциальных игроков о степени риска и невозможности обогащения за счет азартных игр. 

Формализация задачи

Уточняющий вопрос

Что моделируется?

Каков характер процесса?

Чем определяется выигрыш/проигрыш?

Какие объекты участвуют?

Чем характеризуется игрок?

Чем характеризуется монета?

Какую роль выполняет маклер?

Ответ

Процесс игры

Случайный

Монетой: орел/решка

Игрок, маклер и монета

Начальным капиталом Кнач

Ставкой СТ

Текущей наличностью Ктек

II ЭТАП. РАЗРАБОТКА МОДЕЛИ

Информационная модель

Здесь моделируется игра. Игра — это процесс, в котором участвуют три объекта: игрок, маклер и случай, который в данной игре представлен монетой. Маклер определяет проигрыш или выигрыш игрока, выплачивает выигрыш.

Математическая модель процесса складывается из следующих рассуждений.

Имитировать результат падения монеты можно с помощью функции СЛЧИС(). Эта функция выдает случайные числа х в диапазоне 0 ≤ х ˂ 1. Поскольку вероятность выпадения той или иной стороны «половина на половину», то, если СЛЧИС() ˂ 0,5, то результат «орел» (1), в противном случае — «решка» (0).

Формула падения монеты при броске имеет следующий вид:

Бросок = ЕСЛИ(СЛЧИС() ˂ 0,5; 1; 0).

Объект

Параметры

Действия

Название

Значение

Игрок

Начальным капиталом Кнач

Ставкой СТ

Текущей наличностью Ктек

Исходные данные

Исходные данные

Расчетные данные

Выбор ставки

Вычисление наличности

Продолжение игры

Маклер

Бросок

Выигрыш

Проигрыш

Расчетные данные

Расчетные данные

Расчетные данные

Выплата проигранного

Прекращение игры по банкротству

Монета

Вероятность угадывания результата

Положение «орел/решка»

Константа

Расчетные данные

Подбрасывание монет

Определение результата падения

Формула изменения наличности игрока:

Наличность = ЕСЛИ (Бросок=1; Наличность+Ставка; Наличность-Ставка)

Формула определения выигрыша:

Выигрыш = ЕСЛИ(Наличность ˂ 2*Нач.Капитал;»-«; «банк») здесь выдается сообщение «банк» при увеличении наличности вдвое или больше, что является условием прекращения игры.

Функция определения проигрыша:

Проигрыш = ЕСЛИ (Наличность ˃ 0; «банкрот») здесь выдается сообщение «банкрот» по окончании наличности, что также является условием прекращения игры. 

Компьютерная модель

Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области: исходные данные;  расчетные данные (результаты); статистика по экспериментам.

В ячейку А7 вводится формулу:=ЕСЛИ(СЛЧИС()

В ячейку В7 вводится формулу:=ЕСЛИ(A7=1;$B$4+$D$4;$B$4-$D$4)

В ячейку C7 вводится формулу:=ЕСЛИ(B7B$4;”-“;”банк”)

В ячейку D7 вводится формулу:=ЕСЛИ(B70;”-“;”банкрот”)

В ячейку B8 вводится формулу:=ЕСЛИ(A8=1;B7+$D$4;B7-$D$4)

Ввести в таблицу исходные данные.

A

B

C

D

1

БРОСАНИЕ МОНЕТЫ

2

3

Исходные данные

4

Начальный капитал

10

ставка

1

5

Результаты

6

Бросок

Наличность

Выиграш

Проигрыш

7

Формула 1

Формула 2

Формула 3

Формула 4

8

…

Статистика по экспериментам

…

Ставка

№ сеанса

Количество бросков до результата

Результат

…

III ЭТАП. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ

План эксперимента

Тестирование

Проверить правильность ввода формул.

Эксперимент 1

Исследовать выпадение «орла» и «решки» в течение сеанса игры.

Эксперимент 2

Собрать статистические данные о выигрыше и проигрыше в течение нескольких сеансов игры с различными значениями ставок и исследовать их. 

Проведение исследования

Тестирование

Введите в таблицу контрольные исходные данные и расчетные формулы в первую строку. Результаты сравнить с приведенными в таблице.

IV ЭТАП. АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ

На основе области «Статистика» сделать выводы по поводу ставки в одну монету; других ставок. Выбрать и обосновать собственную тактику игры (ставку). 

Задания для самостоятельного выполнения:

Задача 1. Игра в рулетку

Казино процветает из-за того, что у владельца всегда есть некоторое преимущество перед игроком. Например, в одном из вариантов рулетки колесо имеет 38 лунок: 36 пронумерованы и разбиты на черный и красный цвет, а две оставшиеся имеют № 0 и 00 и выкрашены зеленым. Игрок, ставя на красное или черное, имеет на выигрыш 18 шансов из 38, а на то, что он проиграет, — 20 шансов из 38. Пусть у вас имеется некоторый начальный капитал, который вы хотите удвоить. Постройте компьютерную модель ситуации.

Задача 2. Игра в кости

Два игрока бросают по две игровые кости. Сумма очков, выпавших на двух игровых костях, накапливается. Игра прекращается, когда один из игроков достигает суммы 101.

Игра повторяется до трех побед. 

Задача 3. Лотерея «Спортлото»

Смоделируйте серию игр в 5 из 36. Изберите следующую тактику игры:

  • зачеркивать в билетах одну и ту же комбинацию из «счастливых билетов»

  • бросать кубик и из количества точек на верхней грани составлять набор чисел.

Задача 4. Очередь

За два часа обеденного перерыва 40 человек встали в очередь за билетами.

Кассирша обслуживает одного клиента в среднем одну минуту. Каждый клиент «мучает» вопросами кассиршу до пяти минут(случайным образом). Построить модель ситуации и исследовать ее. Ответьте на вопросы:

  • Хватит ли на обслуживание всех клиентов 2 часов?

  • Если не хватит, то, сколько будет обслужено?

  • Как влияет время расспросов на время обслуживания очереди?

ИГРАЛЬНАЯ КОСТЬ. ИМИТАЦИЯ БРОСАНИЯ ИГРАЛЬНОЙ КОСТИ (VBA)

Microsoft Excel имеет встроенный язык программирования — Visual Basic for Аpplications (VBA). Этот язык позволяет создавать приложения, выполняемые в среде Microsoft Office. Редактор Visual Basic for Application позволяет существенно расширить возможности Excel.

С помощью VBA можно легко и быстро создавать различные приложения, даже не являясь специалистом в области программирования. Редактор Visual Basic for Application имеет графическую инструментальную среду, позволяющую создавать экранные формы и управляющие элементы. С его помощью можно создавать свои собственные функции для Excel, вызываемые мастером функций, разрабатывать макросы, создавать собственные меню и многое другое.

ЗАДАЧА. Снова бросаем игральный кубик

Разработайте программу, которая будет имитировать многократное бросание одной игральной кости, а также определять и показывать количество выпадений на кубике того или иного числа. Программа должна делать ставки, позволять начинать бросание кости, останавливать его в любой момент и переустанавливать результаты подсчета.

Игральную кость можно рассматривать как генератор случайных чисел в целочисленном интервале [1..N] с одинаковой вероятностью выпадения всех чисел интервала.

Создание интерфейса

П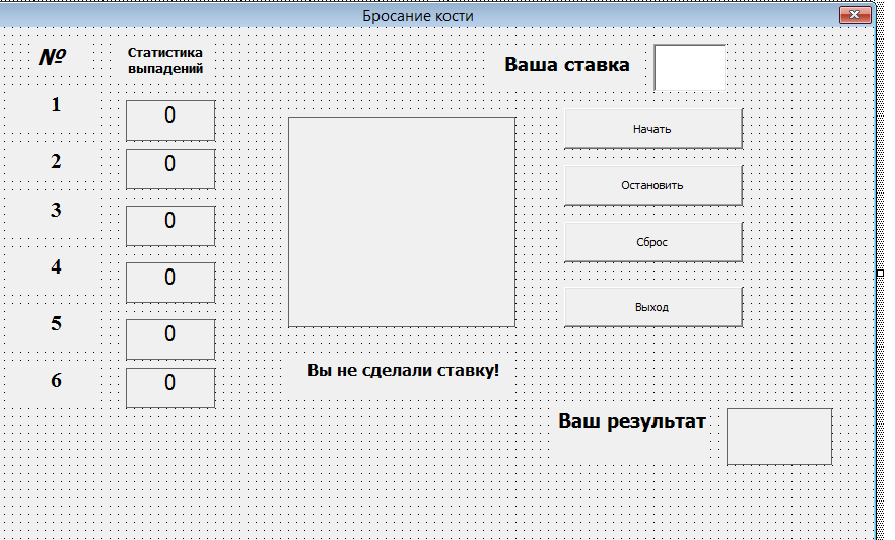еред началом работы над программой в VBA, вам нужно воспользоваться графическим редактором Paint или другим, чтобы создать изображения игральной кости. Вам понадобятся шесть отдельных bmp-файлов, каждый из которых будет картинкой одной из граней кубика (кости).

Запустите VBA, начните новый проект и разместите на форме элемент управления Image, 18 надписей и четыре кнопки.

Н

Рисунок 1.

азначение каждого элемента управления: (см. рисунок 1)

  • элемент управления Image — для графического представления игральной кости (одной ее грани);

  • надписи — для показа количества выпадений того или иного числа и для подписей к ним;

  • кнопки:

Выход — для завершения программы по щелчку на ней;

Начать — чтобы начать бросание по щелчку на кнопке;

Остановить — чтобы остановить бросание по щелчку на ней;

Сброс — чтобы обнулить счет по щелчку на кнопке.

В этой программе присутствует повторяющийся процесс (бросание кости и вывод результата) через регулярные интервалы времени функция — timer.

Код:

Private Sub atimer()

Dim Kost, a, d, stavka As Integer

stavka = CDbl(TextBox2.Text)

PauseTime = 1

Start = timer

Do While timer

DoEvents

Randomize

kost = Int(Rnd * 6) + 1

Select Case kost

Case 1

Image1.Picture = LoadPicture(«C:UsersDesktopkosti1.bmp»)

Label1.Caption = Label1.Caption + 1

Case 2

Image1.Picture = LoadPicture(«C:UsersDesktopkosti2.bmp»)

Label2.Caption = Label2.Caption + 1

Case 3

Image1.Picture = LoadPicture(«C:UsersDesktopkosti3.bmp»)

L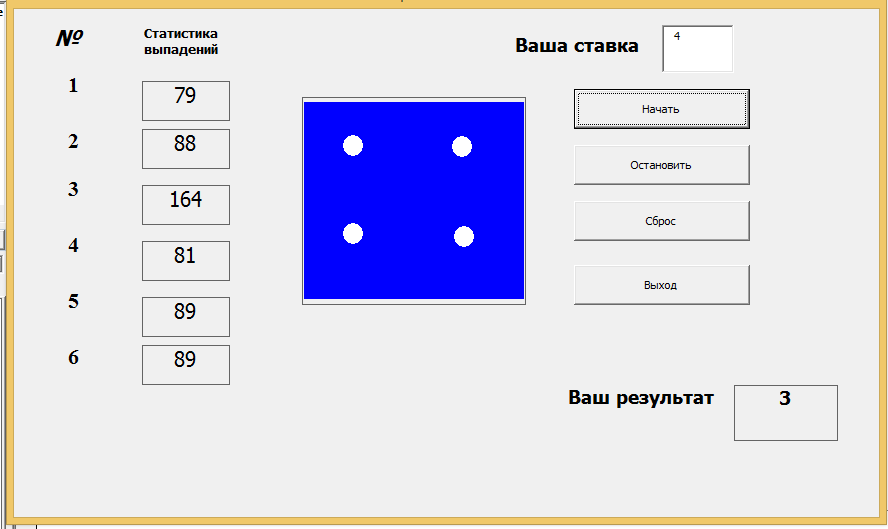abel3.Caption = Label3.Caption + 1

Label3.Caption = Label3.Caption + 1

Case 4

Image1.Picture = LoadPicture(«C:UsersDesktopkosti4.bmp»)

Label4.Caption = Label4.Caption + 1

Case 5

Image1.Picture = LoadPicture(«C:UsersDesktopkosti5.bmp»)

Label5.Caption = Label2.Caption + 1

C

Рисунок 2.

ase 6

Image1.Picture = LoadPicture(«C:UsersDesktopkosti6.bmp»)

Label6.Caption = Label6.Caption + 1

End Select

Loop

If stavka = kost Then

Label15.Caption = Label15.Caption + 3

Else

Label15.Caption = Label15.Caption — 2

End If

End Sub

Private Sub CommandButton1_Click()

stavka = CDbl(TextBox2.Text)

Label18.Visible = False

If stavka 0 Then

atimer

Else

Label18.Visible = True

Label18.Caption = «Вы не сделали ставку !!!»

End If

End Sub

Private Sub CommandButton2_Click()

PauseTime = 0

End Sub

Private Sub CommandButton3_Click()

Label1.Caption = «0»

Label2.Caption = «0»

Label3.Caption = «0»

Label4.Caption = «0»

Label5.Caption = «0»

Label6.Caption = «0»

Label15.Caption = «0»

TextBox2.Text = » «

End Sub

Private Sub CommandButton4_Click()

UserForm1.Hide

End Sub

Заключение:

Тема работы со случайными числами является очень актуальной, так как случайные числанаходят своё применение в приложениях различных типов и имеет большое практическое значение. Не одна задача современного программирования (в криптографии) не обходится без решения вопроса генерирования случайных данных.

Задания для самостоятельного выполнения:

Задача 1. Эксперимент состоит в подсчете числа бросаний двух костей до выпадения двух шестерок. Требуется найти среднее число бросаний, необходимых для получения двух шестерок. (Проводится N экспериментов).

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ

Задача 1. Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 у. е. Необходимо определить, какими должны быть оклады сотрудников больницы.

Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во сколько-то раз или на сколько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: , где С – оклад санитарки; Аi и Bi – коэффициенты, которые для каждой должности определяются следующим образом:

– медсестра получает в 1,5 раза больше санитарки (; );

– врач – в 3 раза больше санитарки (;);

– заведующий отделением – на 30 у. е. больше, чем врач (; );

– заведующий аптекой – в 2 раза больше санитарки (; );

– заведующий хозяйством – на 40 у.е. больше медсестры (; );

– главный врач – в 4 раза больше санитарки (; );

– заведующий больницей – на 20 у.е. больше главного врача (; ).

Зная количество человек на каждой должности, нашу модель можно записать как уравнение:

где N1 – число санитарок, N2 – число медсестер и т. д.

В этом уравнении нам известны А1…А8, В1…В8 и N1…N8, а С неизвестно.

Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С. Решим его.

– Заполните таблицу в соответствии с образцом:

A

B

C

D

E

F

G

1

Должность

Коэф.

А

Коэф.

В

Зарплата

сотрудника

Кол-во

сотрудников

Суммарная

зарплата

Зарплата

санитарки

2

Санитарка

1

0

=B2*$G$2+C2

6

=D2*E2

150

3

Медсестра

1,5

0

8

4

Врач

3

0

10

5

Зав.отделением

3

30

3

6

Зав. аптекой

2

0

1

7

Завхоз

1,5

40

1

8

Главврач

4

0

1

9

Зав. больницей

4

20

1

10

Итого

=СУММ(F2:F9)

В ячейке F10 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже:

A

B

C

D

E

F

G

1

Должность

Коэф.

А

Коэф.

В

Зарплата

сотрудника

Кол-во

сотрудников

Суммарная

зарплата

Зарплата санитарки

2

Санитарка

1

0

150

6

900

150

3

Медсестра

1,5

0

225

8

1800

4

Врач

3

0

450

10

4500

5

Зав.отделением

3

30

480

3

1440

6

Зав. аптекой

2

0

300

1

300

7

Завхоз

1,5

40

265

1

265

8

Главврач

4

0

600

1

600

9

Зав. больницей

4

20

620

1

620

10

10425

Как видите, взяв оклад санитарки за 150, мы превысили месячный фонд зарплаты.

Определите оклад санитарки так, чтобы расчетный фонд был равен заданному.

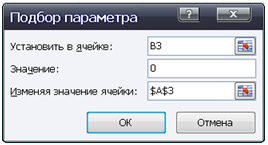
Для этого:

– активизируйте команду Подбор параметра;

– в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F10, содержащую формулу;

– в поле «Значение» наберите искомый результат 10000.

– В поле «Изменяя значение ячейки» введите ссылку на изменяемую ячейку G2 и щелкните кнопкой ОК. Таблица будет выглядеть следующим образом:

A

B

C

D

E

F

G

1

Должность

Коэф.

А

Коэф.

В

Зарплата

сотрудника

Кол-во

сотрудников

Суммарная

зарплата

Зарплата санитарки

2

Санитарка

1

0

143,80

6

862,77

143,79

3

Медсестра

1,5

0

215,69

8

1 725,55

4

Врач

3

0

431,39

10

4 313,87

5

Зав. отделением

3

30

461,39

3

1 384,16

6

Зав. аптекой

2

0

287,59

1

287,59

7

Завхоз

1,5

40

255,69

1

255,69

Главврач

4

0

575,18

1

575,18

Зав. больницей

4

20

595,18

1

595,18



Итого

10 000,00

Задача об использовании сырья

Что такое линейное программирование

Многие экономические процессы описываются математическими моделями, в которых требуется найти такие значения переменных параметров, при которых достигается максимальное или минимальное значение линейной функции от этих переменных, при различных ограничениях, задаваемых линейными управлениями или неравенствами. Искомые переменные, называются контролируемыми факторами, функция – целевой функцией. Задачи такого типа называются задачами линейного программирования.

Модели линейного программирования в экономике и управлении используются как инструмент оптимизации при планировании производства, составление планов перевозов и т.д.

Постановка задачи

Предприятие выпускает курс n видов продукции, которые обозначим: P1, P2,…, Pn. Для этого используется m вида сырья: S1, S2, … , Sm, запасы которого равны соответственно b1, b2, … , bm. Известно, что расход i-го вида сырья для производства единицы j-го вида продукции Pj равен aij. От реализации единицы j-го вида продукции Pj предприятие получает доход, равный Cj. Требуется составить такой план производства каждого вида продукции, чтобы при имеющихся запасах сырья обеспечить предприятию максимальный суммарный доход.

Математическая модель

Построение математической модели осуществляется в три этапа:

  1. Определение переменных, для которых будет составляться математическая модель.

  2. Формирование целевой функции.

  3. Формирование системы ограничений.

Составим план производства для ателье, занимающегося пошивом туристического снаряжения – палаток. Для пошива используется три вида материалов (сырья): водоотталкивающая ткань, утеплитель, москитная сетка. Представим данные с двумя видами продукции (палатки двух моделей) и тремя видами материалов (водоотталкивающая ткань, утеплитель, москитная сетка) в виде таблицы.

Материалы(Si)

Запасы материалов (bi), м

Расход материалов на продукцию Pj, м

Палатка (модель 1)

Палатка (модель 2)

Водооттал. ткань

105

7

4

Утеплитель

68

3

5

Москитная сетка

66

1

6

Удельный доход от реализации (Сj)

5

6

Ячейки, выделенные фоном, содержат значения расхода каждого вида сырья (материалов) на производство единицы каждого вида продукции. Это и есть матрица aij. Такой расход сырья называется удельным. Обозначим план пошива палаток модели 1 через X (шт.), а план пошива палат моделей палаток модели 2 через Y (шт.). При таком плане расход материалов, например водоотталкивающей ткани, составит 7 X + 4 Y метров. Поскольку расход материала не может превышать имеющиеся запасы, получаем ограничения по расходу водоотталкивающей ткани 7 X + 4 Y  105. Аналогические рассуждения приводят к ограничениям и по другим видам материалов. Кроме того, значения X и Y не могут быть отрицательными. Сформулированные условия запишем в виде системы неравенств, которым должны удовлетворять неизвестные X и Y:

Доход от реализации одной палатки модели 1 равен 5 единицам стоимости (например, 5 тыс. руб.), а доход от реализации палатки модели 2 — 6 единицам стоимости тогда суммарный доход предприятия от реализации всей произведенной продукции определится формулой: Z =5 X + 6 Y. Следовательно, Z есть функция от X и Y. Z(X, Y) является целевой функцией, поскольку целью производства является получение максимального дохода.

Таким образом, математическая формулировка задачи звучит так: требуется найти такое решение системы линейных неравенств (1)-(5),при котором целевая функция Z(X, Y) принимает максимальное значение.

Решение с помощью электронных таблиц

П

Таблица 1.

одготовим данные, как это показано в таб.1. В ячейках В2 и В3 будет получено решение, т.е. найдены объемы производства каждого вида продукции, при которых суммарных доход, вычисляемый в ячейках В17, принимает максимальное значение. Диапазон ячеек В13:В15 содержит формулы, с помощью которых задаются левые части неравенств (1)-(2), ограничивающих расход сырья. Диапазон ячеек D13:D15 содержит запасы материалов.

A

B

C

D

1

Объем производства

2

Палатки (модель 1)

3

Палатки (модель 2)

4

5

6

Материалы

Запасы материалов

Палатки (модель 1)

Палатки (модель 2)

7

Водооттал. ткань

105

7

4

8

Утеплитель

68

3

5

9

Москитная сетка

66

1

6

10

Удельный доход от реализации

5

6

11

12

Ограничения

13

=C7*$B$2+D7*$B$3

105

14

=C8*$B$2+D8*$B$3

68

15

=C9*$B$2+D9*$B$3

66

16

17

Суммарный доход

=C10*B2+D10*B3

Установим курсор в ячейку В17, в которой должно быть вычислено значение целевой функции, и выполним команду Поиск решения. В открывшемся окне необходимо произвести установки, показанные на рис. 1.

Д

Рисунок 1.

ля этого выполняются следующие действия:

В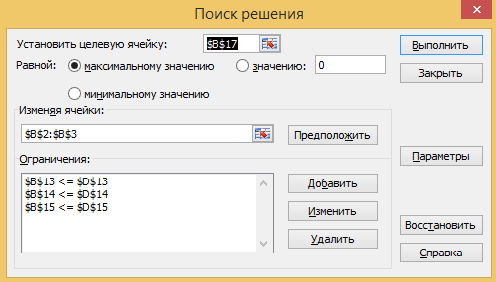 поле Установить целевую ячейку вводится адрес ячейки В17.

  • Для поля Равной выбирается параметр максимальному значению.

  • В поле Изменяя ячейки вводится диапазон ячеек с неизвестными В2:В3.

  • Щелчком на кнопке Добавить вызывается окно Добавить ограничение.

  • Для ввода первого ограничения в поле Ссылка на ячейку указывается адрес ячейки В13, а в поле Ограничение – адрес ячейки D13. Между ними выбирается знак отношения  и нажимается кнопка Добавить. Аналогично добавляются два оставшихся ограничения.

  • Щелчком на кнопке параметры вызывается окно Параметры поиска решения (рис. 2), в котором необходимо отметить, что ищутся неотрицательные значения X и Y и используется линейная модель. Это означает то, что целевая функция линейно зависит от переменных X и Y.

Неотрицательные решения системы линейных неравенств, при которых целевая функция (суммарный доход) принимает максимальное значение, табличный процессор Microsoft Excel находит приближенно, используя итерационный метод поиска, который называется методом Ньютона. Поэтому в качестве параметров указывается предельное число итераций и относительная погрешность. С такого рода параметрами мы встречались при решении задачи теплопроводности методов итераций.

Рисунок 2.

П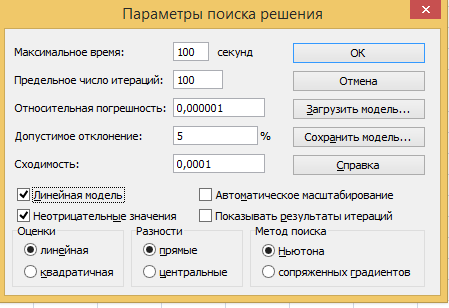осле того как все установки сделаны, следует нажать кнопку Выполнить.

В результате в ячейках В2 и В3 будет получено решение – объем производства палаток первой и второй моделей (таб.2), а в ячейке В17 – максимальный доход, полученный от реализации такого объема продукции. Как исследовало ожидать, полученные значения совпадают с результатами графического метода решения задачи: X = 11, Y = 7, Z = 97.

Таблица 2. Результаты решение задачи

A

B

C

D

1

Объем производства

2

Палатки (модель 1)

11

3

Палатки (модель 2)

7

4

5

6

Материалы

Запасы материалов

Палатки (модель 1)

Палатки (модель 2)

7

Водооттал. ткань

105

7

4

8

Утеплитель

68

3

5

9

Москитная сетка

66

1

6

10

Удельный доход от реализации

5

6

11

12

Ограничения

13

105

105

14

68

68

15

53

66

16

17

Суммарный доход

97

Задания для самостоятельного выполнения:

Задача 1.

Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у. е., «В» – 10 у. е., «С» – 16 у. е.

Конфеты можно производить в любых количествах, но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Какао

18

15

12

360

Сахар

6

4

8

192

Наполнитель

5

3

3

180

Прибыль

9

10

16

Задача 2.

Ваше предприятие выпускает изделия 1, изделия 2, изделия 3, используя общий склад комплектующих. Каждое изделие состоит из деталей, имеющихся на складе. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Прибыль, получаемая от каждого изделия, равна соответственно 47,32; 31,55; 22,08. Число деталей, идущих на каждое изделие, указано в таблице.

Наличие на складе

Изделие 1

Изделие 2

Изделие 3

Деталь 1

450

1

1

0

Деталь 2

250

1

0

0

Деталь 3

800

2

2

1

Деталь 4

450

1

1

0

Деталь 5

600

2

1

1

Задача 3.

В ресторане готовятся фирменные блюда трех видов (блюдо А, блюдо В и блюдо С) с использованием при приготовлении ингредиентов трех видов (ин­гредиент 1, ингредиент 2 и ингредиент 3). Расход ингредиентов в граммах на блю­до задается следующей таблицей:

Вид ингредиента

Блюдо А

Блюдо В

Блюдо C

Ингредиент 1

20

50

10

Ингредиент 2

20

0

40

Ингредиент 3

20

10

10

Стоимость приготовления блюд одинакова (100 руб.).

Ежедневно в ресторан поступает 5 кг ингредиента 1 и по 4 кг ингредиентов видов 2 и 3. Каково оптимальное соотношение дневного производства блюд различного вида, если производственные мощности ресторана позволяют использовать весь запас поступивших продуктов?

Задача 4.

Пошивочная мастерская планирует выпуск двух видов костюмов: мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм — 3,5 м шерсти, 0,5 м лавсана и 1 челове­ко-день трудозатрат. Всего имеется 350 м шерсти и 240 м лавсана, 150 человеко-дней трудозатрат. Предусматривается выпуск не менее 110 костюмов, причем, необходимо обеспечить прибыль не менее 1400 руб. Определите оптимальное количество костюмов каждого вида, если прибыль от реализации женского костюма составляет 10 руб., а мужского — 20 руб.

ПОСТРОЕНИЕ И ИССЛЕДОВАНИЕ ОПТИМИЗАЦИОННОЙ МОДЕЛИ НА VBA

Задача 1.

В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и В тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.

Тип заготовки Способы раскроя
1-й

2-й

3-й

А

10

3

8

В

3

6

4

Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок типа А и 300 заготовок типа В.

Формальная модель:

Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:

X1— количество листов, раскроенное способом 1;

X2— количество листов, раскроенное способом 2;

X3— количество листов, раскроенное способом 3.

Ограничения:

Определяются значениями требуемых количеств заготовок типа А и В:

10X1+3X2+8X3=500 и 3X1+6X2+4X3=300

Кроме того, количества листов не могут быть отрицательными: X10, X20, X30 и дробными X1, X2, X3 – целые.

Создание интерфейса:

Запустите V BA, начните новый проект и разместите на форме 8 надписей; одну кнопку.

P

Рисунок 1.

rivate Sub CommandButton1_Click()

Dim x1, x2, x3, F As Integer

F = 300

For x1 = 0 To 100

For x2 = 0 To 100

For x3 = 0 To 100

If (10 * x1 + 3 * x2 + 8 * x3 = 500) And (3 * x1 + 6 * x2 + 4 * x3 = 300) Then

If x1 + x2 + x3

F = x1 + x2 + x3

Label1.Caption = x1

Label2.Caption = x2

Label3.Caption = x3

Label4.Caption = F

End If

End If

Next x3

Next x2

Next x1

End Sub

Задания для самостоятельного выполнения:

Задача 1.

Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используется два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известные расходы А и В на 1 т красок:

Ингредиенты

Расход ингредиентов, т.ингр./т.краски

Запас, т.ингр./сут

Краска 1-го вида

Краска 2-го вида

А

1

2

6

В

2

1

8

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, спрос на краску 2-го вида не превышает 2 т /сут. Оптовые цены 1 т красок равны: 3 т. руб. для краски 1-го вида и 2 т. руб. для краски 2-го вида. Найти какое количество краски каждого вида необходимо производить, чтобы доход от реализации продукции был максимальным.

Задача 2.

Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используется два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известные расходы А и В на 1 т красок:

Ингредиенты

Расход ингредиентов, т.ингр./т.краски

Запас, т.ингр./сут

Краска 1-го вида

Краска 2-го вида

А

1

2

6

В

2

1

8

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более чем на 1 т. Кроме того, спрос на краску 2-го вида не превышает 2 т /сут. Оптовые цены 1 т красок равны: 3 т. руб. для краски 1-го вида и 2 т. руб. для краски 2-го вида. Найти какое количество краски каждого вида необходимо производить, чтобы доход от реализации продукции был максимальным.

Транспортная задача

Рассмотрим еще одну типовую задачу линейного программирования.

Постановка задачи

Транспортной задачей называют составления плана перевозок от поставщиков к потребителям с помощью некоторых транспортных средств. Составленный план должен обеспечивать выполнение таких условий, как:

  • Полное удовлетворение спроса потребителей;

  • Вывоз всей продукции от поставщика;

  • Минимизация транспортных затрат.

Математическая модель

Рассмотрим простейший вариант транспортной задачи. В т пунктах отправления (складах) А1, А2, …, Ат находится однородный груз в количестве а1, а2, …, ат единиц соответственно. Потребность в этом грузе в п пунктах назначения (магазинах) В1, В2, …, Вп составляет b1, b2, …, bn соответственно. Будем считать, что сумма запасов на складах равна суммарным потребностям в магазинах, т.е. = . Такая модель называется замкнутой.

Обозначим через Сij удельные затраты, т.е. затраты на перевозку единицы груза из i—го пункта в j-й пункт назначения, а через Xij – неизвестный объем груза, который надор перевезти из j— го пункта отправления в j-й пункт назначения.

Перевозку груза надо организовать таким образом, чтобы суммарные затраты на перевозки были минимальными. Суммарные затраты на перевозки Z определяются следующим образом: необходимо просуммировать все объемы перевозок груза, умноженные на соответствующие удельные затраты, т.е. Z=. Суммарные затраты являются целевой функцией.

Искомыми величинами являются объемы Xij перевозок груза, отправляемые каждым поставщиком каждому потребителю при выполнении указанных условий.

Рассмотрим транспортную задачу на примере четырех складов и четырех магазинов.

Задача. Известно, что на складах имеется запас муки в количестве 45, 100, 20, 75 мешков. А магазины имеют потребность в этом товаре в количестве 30, 80, 95, 35 мешков.

Магазин № 1

Магазин №2

Магазин №3

Магазин №4

b1 = 30

b2 = 80

b3 = 95

b4 = 35

Склад № 1

a1 = 45

6

3

7

10

Склад № 2

a2 = 100

10

4

12

10

Склад № 3

a3 = 20

5

9

8

11

Склад № 4

a4 = 75

4

2

4

8

Ячейки, выделенные фоном, содержат удельные стоимости перевозок Cij. Например, стоимость перевозки единицы груза (мешка) со склада № 3 в магазин № 4 составляет 11 денежных единиц. Проверим замкнутость модели. Для этого просуммируем все запасы муки на складах: 45 + 100 + 20 + 75 = 240. Найдем суммарные потребности магазинов в муке: 30 + 80 + 95 + 35 = 240. Таким образом, модель является замкнутой, т. е. потребность магазинов в муке равна запасу на складах.

Весь груз со складов должен быть вывезен. Этот факт для i-го склада можно отразить следующим образом: Xi1 + Xi2 + Xi3 + Xi4 = ai. Весь груз в магазины должен быть ввезен. Для j-го магазина будет справедливо следующее: X1j + X2j + X3j + X4j = bj.

Таким образом, удовлетворению спроса магазинов отвечает выполнение системы уравнений:

Вывоз всего груза со складов достигается при выполнении системы уравнений:

Получается общая система из 8 уравнений с 16 неизвестными, которая имеет, вообще говоря, бесконечное множество решений. Среди этих решений интерес представляют неотрицательные решения, при которых суммарные затраты по всем маршрутам будут минимальны, т. е. целевая функция может быть представлена следующим образом:

Z = C11 X11 + … + C14X14 + C21 · X 21 + … + С24 · X24 + C31 · X31 +…+ C34 · X34 +C41 · X41 +…+ C44 · X44.

Решение с помощью электронных таблиц

Р

Таблица 1.

ассмотрим решение задачи на примере табличного процессора Microsoft Excel.

Представим данные в виде, показанном в таблице 1.

A

B

C

D

E

F

G

1

Матрица перевозок

2

Магазин 1

Магазин 2

Магазин 3

Магазин 4

3

Склад № 1

=сумм

4

Склад № 2

=сумм

5

Склад № 3

=сумм

6

Склад № 4

=сумм

7

=сумм

=сумм

=сумм

=сумм

8

9

10

11

bj

30

80

95

35

12

ai

Магазин 1

Магазин 2

Магазин 3

Магазин 4

13

45

Склад № 1

6

3

7

10

14

100

Склад № 2

10

4

12

10

15

20

Склад № 3

5

9

8

11

16

75

Склад № 4

4

2

4

8

17

18

19

Сумм. затраты:

=СУММПРОИЗВЕД(С3:F16;C13:F16)

Исходными данными являются удельные затраты на перевозки (диапазон ячеек C13:F16), запасы муки на складах (диапазон ячеек A13:A16), потребности магазинов в муке ( диапазон ячеек С11:F11).

Диапазон ячеек C3:F6 предназначен для получения искомого решения-объемов перевозок груза. Суммируя объемы перевозок в каждой строке, задаем левые части уравнений-ограничений, обеспечивающий вывоз всего груза с каждого склада. Суммированием объемов перевозок по столбцам задаются левые части уравнений-огранечений, удовлетворяющих спрос каждого магазина в муке. Формула =СУММПРОИЗВ (С3:F6; C13:F16), вычисляющая целевую функцию(суммарные затраты) Z, размещена в ячейке С19. Встроенная функция СУММПРОИЗВ суммирует произведения, полученные построчным перемножением содерживого ячеек из диапозонов С3:F6; C13:F16.

Например, СУММПРОИЗВ (А1:В2;А3:B4) =A1*A3+B1*B3+A2*A4+B2*B4.

Рисунок 1.

Установите курсор в ячейку С19, в которой должно быть выполнено значение целевой функции.

Выполним команду Поиск решения.

В открышевшемся окне необходимо провести установки, показанные на рис.1.

В

Таблица 2.

результате будет найдено решение, представленное в таблице 2.

A

B

C

D

E

F

G

1

Матрица перевозок

2

Магазин 1

Магазин 2

Магазин 3

Магазин 4

3

Склад № 1

0

10

35

0

45

4

Склад № 2

30

70

0

0

100

5

Склад № 3

0

0

20

0

20

6

Склад № 4

0

0

40

35

75

7

30

80

95

35

8

9

10

11

bj

30

80

95

35

12

ai

Магазин 1

Магазин 2

Магазин 3

Магазин 4

13

45

Склад № 1

6

3

7

10

14

100

Склад № 2

10

4

12

10

15

20

Склад № 3

5

9

8

11

16

75

Склад № 4

4

2

4

8

17

18

19

Сумм.затраты:

1455

Искомые объемы перевозок представлены в ячейках C3:F6. Со склада №1 мука будет отправлена в магазины №2 и 3 в объемах 10 и 35 мешков соответсвенно, со склада №2 – в магазины №1 и 2 в объемах 30 и 70 мешков, со склада №3 — в магазин №3 в объеме 20 мешков, со склада №4 в магазины №3 и 4 в объемах 40 и 35 мешков. Минимальные затраты на перевозки составляют 1455 денежных единиц.

Задания для самостоятельного выполнения:

Задача 1. Найти оптимальный объем перевозок товаров с 3 заводов на 5 региональных складов. То есть минимизировать затраты на перевозку грузов от заводов-производителей на торговые склады.

Производительность каждого завода и затраты на перевозку от завода на каждый склад приведены в таблице:

Заводы

Поставки

Затраты

склад 1

склад 2

склад 3

склад 4

склад 5

Завод 1

310

10

8

6

5

4

Завод 2

260

6

5

4

3

6

Завод 3

280

3

4

5

5

9

Технология работы:

– Заполните таблицу в соответствии с образцом:

A

B

C

D

E

F

G

1

Заводы

Всего

склад 1

склад 2

склад 3

склад 4

склад 5

2

Завод 1

=СУММ (С2:G2)

1

1

1

1

1

3

Завод 2

Заполнить вниз

1

1

1

1

1

4

Завод 3

1

1

1

1

1

5

Допустим, что от каждого завода на каждый склад перевозится ед.продукции

6

Итого

=СУММ (С2;С4)

7

8

Потреб. складов

180

80

200

160

220

9

Заводы

Поставки

Затраты

10

Завод 1

310

10

8

6

5

4

11

Завод 2

260

6

5

4

3

6

12

Завод 3

280

3

4

5

5

9

13

14

Перевозка

=СУММ (С14:G14)

=С2*С10+С3*С11+С4*С12

Количество перевезенных грузов не может превышать производственных возможностей заводов. Количество доставляемых грузов не должно быть меньше потребностей складов. То есть производство должно быть не меньше потребностей. Число перевозок не может быть отрицательным.

Задача 2.

Авиакомпания по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно.

Эксплуатация 1 самолета первого типа обойдется 5000$, а второго 9000$. Сколько надо использовать самолетов каждого типа, если для формирования экипажей имеется не более 60 человек.

МОДЕЛИРОВАНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Задача. Для снабжения населенных пунктов, расположенных в труднодоступной местности, требуется разместить железнодорожную станцию и аэродром таким образом, чтобы суммарное расстояние (и, соответственно, стоимость) воздушных перевозок от станции и от аэродрома к населенным пунктам было оптимальным.

Координаты населенных пунктов приведены в табл. 1.

Таблица 1

Номера населенных пунктов

Координаты населенных пунктов

Х

У

1

2,0

8,0

2

10,0

9,0

3

1,0

2,0

4

4,0

9,0

5

9,0

5,0

Решение.

Из условия задачи следует, что надо найти оптимальное, с точки зрения экономии затрат на воздушные перевозки, местоположение двух объектов: аэродрома и железнодорожной станции. Такое возможно, если суммарная протяженность воздушных трасс между всеми объектами будет минимальной. Как известно, кратчайшее расстояние между двумя точками определяется отрезком, соединяющим эти точки.

Для решения задачи введем обозначения (табл. 2).

Таблица 2

Объект

Координата Х

Координата У

Населенный пункт №1

Х1

У1

Населенный пункт №2

Х2

У2

Населенный пункт №3

Х3

У3

Населенный пункт №4

Х4

У4

Населенный пункт №5

Х5

У5

Аэродром

ХА

УА

Железнодорожная станция

ХС

УС

Минимальное расстояние от железнодорожной станции до i-го населенного пункта (i = 1, …, 5) через аэропорт можно определить следующим образом:

Решение с помощью электронных таблиц

В соответствующие ячейки Табл. 3 введите расчетные формулы.

Таблица 3

№

Адрес ячейки

Содержимое ячейки (формула)

1

Е5

=КОРЕНЬ(($B$12-B5)^2+($C$12-C5)^2)

2

E6—E9

Скопировать формулу из Е5 в E6—E9

3

В16

=КОРЕНЬ((B14-B12)^2+(C14-C12)^2)+СУММ(Е5:Е9)

Компьютерная модель

A

B

C

D

E

1

Моделирование расположения аэродрома и железнодорожной станции

2

Расположение населенных пунктов

3

Объект, населенный пункт

Координата

Расстояние между

Аэродромом и населенными пунктами

x

y

4

5

Населенный пункт №1

2,0

8,0

6

Населенный пункт №2

10,0

9,0

7

Населенный пункт №3

1,0

2,0

8

Населенный пункт №4

4,0

9,0

9

Населенный пункт №5

9,0

5,0

10

11

Оптимальные координаты объектов (аэродрома и железнодорожных станций)

12

Аэродром

13

Железнодорожная станция

14

15

16

Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов

Эксперимент № 1

  • Применяя надстройку Excel «Поиск решения» ( Поиск решения), назначьте в качестве целевой ячейки В16 и установите переключатель Равной: равным минимальному значению.

  • Укажите в качестве изменяемых ячеек ячейки $B$12:$C$12; $B$14:$C$14 (координаты аэродрома и станции). Ограничения не вводите.

Щелкните по кнопке Выполнить. Фрагмент рабочего листа

A

B

C

D

E

1

Моделирование расположения аэродрома и железнодорожной станции

2

Расположение населенных пунктов

3

Объект, населенный пункт

Координата

Расстояние между

Аэродромом и населенными пунктами

x

y

4

5

Населенный пункт №1

2,0

8,0

2,5

6

Населенный пункт №2

10,0

9,0

5,7

7

Населенный пункт №3

1,0

2,0

6,6

8

Населенный пункт №4

4,0

9,0

1,5

9

Населенный пункт №5

9,0

5,0

5,2

10

11

Оптимальные координаты объектов (аэродрома и железнодорожных станций)

12

Аэродром

4,5

7,6

13

14

Железнодорожная станция

4,5

7,6

15

16

Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов

21,5

  • Постройте диаграмму, выберите тип Точечная.

  • Проанализируйте результат.

На основе полученных данных моделирования можно сделать следующий вывод: моделирование, проводимое в условиях, когда ограничения не заданы, приводит к совпадению координат расположения железнодорожной станции и аэродрома. Это вытекает и из простого анализа расчетной формулы. Минимальное расстояние будет, когда координаты объектов совпадут. В реальных условиях такие объекты располагаются на безопасном расстоянии друг от друга, кроме того, есть и некоторые технические критерии обеспечения нормальных условий функционирования объектов.

Эксперимент № 2

Усложним задачу. Введем ограничения. Предположим, что в указанном районе есть озеро и проходит железная дорога. Координаты ограничивающие местоположение аэродрома и станции, приведены в табл. 4

Таблица 4

Объект

Координата Х

Координата У

Озеро

≥ 0 и ≤4

≥ 3 и ≤ 6

Железная дорога

≥ 6

=1

Рисунок 1.

  • Установите курсор в ячейку В16.

  • Введите условия ограничения на расположение аэродрома и станции. В частности, примите во внимание, что аэродром не должен находиться внутри области, чьи координаты указаны в табл. 4, а железнодорожная станция, наоборот, должна находиться на железной дороге.

  • Произведите поиск решения.

Фрагмент рабочего листа (после ввода ограничений)

A

B

C

D

E

1

Моделирование расположения аэродрома и железнодорожной станции

2

Расположение населенных пунктов

3

Объект, населенный пункт

Координата

Расстояние между

Аэродромом и населенными пунктами

x

y

4

5

Населенный пункт №1

2,0

8,0

3,8

6

Населенный пункт №2

10,0

9,0

5,8

7

Населенный пункт №3

1,0

2,0

5,9

8

Населенный пункт №4

4,0

9,0

3,2

9

Населенный пункт №5

9,0

5,0

3,9

10

11

Оптимальные координаты объектов (аэродрома и железнодорожных станций)

12

Аэродром

5,2

6,1

13

14

Железнодорожная станция

6,0

1,0

15

16

Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов

27,5

ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ

Постановка задач теории расписаний

В задачах теории расписаний рассматриваются комплексы работ, связанных общим объектом или общим исполнителем, направленные на достижение определенной цели. Модели теории расписаний позволяют найти наиболее дешевый или наиболее быстрый порядок выполнения работ.

К задачам выбора самого дешевого порядка выполнения работ относится известная задача о шлюзе. Шлюз может пропускать в порядке очереди только по одному судну. Если создается очередь, то необходимо определить такой порядок прохождения судов через шлюз, при котором будет минимален ущерб от простоя. В такой формулировке задача появилась еще в XIX веке.

При выборе наиболее быстрого по времени варианта работ минимизируется отрезок времени от начала работ до их окончания (достижения цели). Простейшей задачей такого типа является задача и двух станках. На двух станках надо обработать N деталей. Каждая из деталей обрабатывается сначала на одном станке, а затем – на втором. Время обработки каждой детали на каждом станке известно. Задача состоит в том, что необходимо определить такой порядок обработки деталей, при котором время выполнения всей работы будет минимальным. Порядок обработки, минимизируется время T, называется оптимальным.

Задача о шлюзе

Математическая модель

Через шлюз последовательно должны пройти N судов. Известно время (в часах) шлюзования каждого судна – ti и ущерб от 1 часа простоя судна — Ui денежных единиц. Здесь индекс обозначает порядковый номер судна в очереди. Например, t1 – это время шлюзования 1-го судна, t2 – время шлюзования 2-го судна, u2 – стоимость 1 часа простоя в ожидании своей очереди 2-го судна и т.д. Время простоя в очереди, например, 4-го судна, если оно ждет, пока через шлюз пройдут первые три, равно: t1 + t2 + t3 , а материальный ущерб от простоя 4-го судна равен: u4(t1 + t2 + t3).

Показатель экономической эффективности работы шлюза связан с суммарным ущербом от простоя судов в ожидании своей очереди на шлюзовании. Например, если к шлюзу подошли одновременно 4 судна и они пропускаются через шлюз в порядке их номеров, то суммарный ущерб от простоя (S) вычисляется так: S = u2 • t1 + u3(t1 + t2) + u4(t1 + t2 + t3).

В общем случае, если в очереди находятся N судов, то суммарный ущерб от простоя выражается формулой: S = .

Задача состоит в том, чтобы определить такой порядок пропускания судов через шлюз, при котором величина S будет минимальна.

Математический анализ этой задачи приводит к следующему ответу: минимум величины S достигается в том случае, если суда пропускаются в порядке убывания величины . Этот принцип можно пояснить на следующем примере. Пусть к шлюзу подошли одновременно два судна, время шлюзования которых одинаково (t1 = t2 ), но стоимость простоя разная. Тогда в первую очередь надо пропустить то судно, у которого простой стоит дороже. Если же у двух судов в очереди одинаковая стоимость простоя ( u1 = u2 ), то вперед надо пропустить то судно, у которого меньше время шлюзования.

Критерию убывания величины равносилен критерий возрастания величины . При вычислениях можно использовать как тот, так и другой критерий.

Решение в электронных таблицах

Рассмотрим пример для пяти судов, выстроившихся в очередь к шлюзу в порядке из прибытия. Данные приведены в таблице 1.

№ судна

1

2

3

4

5

Время шлюзования

45

36

28

24

72

Ущерб от простоя

5

12

7

4

3

Вычислим общий ущерб от простоя по формуле:

S= u2 • t1 + u3 •(t1 + t2) + u4 •(t1 + t2 + t3) + u5 •(t1 + t2 + t3 + t4).

Если шлюзование судов проводить в таком порядке, то ущерб от простоя не будет минимальным. В нашем случае сумма ущерба составляет 1942 денежные единицы:

S=12•45+7•(45+36)+4•(45+36+28)+3•(45+36+28+24) =1942.

Найдем оптимальный порядок (расписание) шлюзования судов, обеспечивающий минимальный ущерб от простоя.

Чтобы найти ущерб от простоя, в ячейках С6:F6 вычислим суммы вида : , а в ячейку B7 поместим формулу = СУММПРОИЗВ(C3:F3;C6:F6).

В соответствии с этой формулой вычисляется сумма произведений: C3*C6+D3*D6+E3*E6+F3*F6 Таблица 2.

A

B

C

D

E

F

1

№ судна

1

2

3

4

5

2

Время простоя

45

36

28

24

72

3

Ущерб от простоя

5

12

7

4

3

4

5

6

=B2

=C6+C2

=D6+D2

=E6+E2

7

=СУММПРОИЗВ(C3:F3;C6:F6)

В 4-ю строку таблицы впишем формулы, по которым для каждого судна сосчитается величина k= . Затем отсортируем столбцы диапазона ячеек B1:F4 в порядке возрастания значений k в 4-й строке. Указание на то, что производится сортировка столбцов, задается с помощью диалогового окна Параметры сортировки: столбцы диапозона; cортировать по – строка 4, по возрастанию.

После проведения сортировки в диапазоне ячеек B1:F1 будет содержаться порядок прохождения судов через шлюз со следующими номерами: № 2, 3, 4, 1, 5. При такой очередности общий ущерб от простоя будет минимальным и составит 1347 денежных единиц, в то время как при шлюзовании судов в порядке их прибытия общий ущерб составлял 1942 денежных единицы. Таблица 3.

A

B

C

D

E

F

1

№ судна

2

3

4

1

5

2

Время простоя

36

28

24

45

72

3

Ущерб от простоя

12

7

4

5

3

4

k

3

4

6

9

24

5

6

36

64

88

133

7

Общий ущерб

1347

ИССЛЕДОВАНИЕ МЕТОДОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ

Задача 1. Вычислить по формуле прямоугольников   с шагом . Заметим, что этот интеграл легко может быть вычислен аналитически:  

Чтобы найти приближённое значение интеграла  , нужно:

  • разделить отрезок [a, b] на n равных частей точками х0= а, х1, х2,…, х n -1, х n = b;

  • вычислить значения подынтегральной функции   в точках деления, т.е. нати  у 0 = f (x0), у 1 =f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ;

  • воспользоваться одной из приближённых формул.

Метод прямоугольников:

Простейшим приближённым методом является метод прямоугольников.

Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции АВСD  заменяется суммой площадей прямоугольников, одна сторона которых равна, а другая —

Для нахождения определённого интеграла методом прямоугольников необходимо ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в диапазоне х  [0;3 ] с заданным шагом х = 0,1.

A

B

1

Аргумент

Функция

2

0

=A2^2

3

0,1

4

0,2

5

6

7

8

9

…

32

33

= 0,1* Сумм (В3:В32)

В ячейке В33 появляется приближённое значение искомого интеграла (9,455) .

Сравнивая полученное приближённое значение с истинным значением интеграла (9), можно видеть, что ошибка приближения метода прямоугольников в данном случае равна= 0,455

Метод трапеций:

Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций.

Для нахождения определенного интеграла методом трапеций, как и в случае использования метода прмоугольников, значения подынтегральной функции f(x) должны быть введены рабочую таблицу Excel в диапазоне х  [0;3] с заданным шагом х = 0,1.

A

B

1

Аргумент

Функция

2

0

=A2^2

3

0,1

4

0,2

5

6

7

8

9

…

32

33

=0,1*((B2+B32)/2+СУММ(B2:B31))

В ячейке В34 появляется приближённое значение искомого интеграла (9,005) .

Сравнивая полученное приближённое значение с истинным значением интеграла (9), можно видеть, что ошибка приближения метода трапеций в данном случае равна= 0,005

Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников

Задача 2.  Вычислить по формуле прямоугольников   с шагом .

Решение с помощью VBA

С

Рисунок 1.

оздание интерфейса:

Код программы:

Private Sub CommandButton3_Click()

End

End Sub

Рисунок 1.

Private Sub UserForm_Initialize()

With Me.ComboBox1

.AddItem «Метод_Трапеции»

.AddItem «Метод_Прямоугольников»

End With

End Sub

Private Sub CommandButton2_Click()

Dim n As Single, a As Single, x As Single

Dim b As Single, s As Single, s1 As Single

Dim s2 As Single, z As Single, i As String

i = ComboBox1.Value

a = TextBox1.Text

b = TextBox2.Text

n = TextBox3.Text

Select Case i

Case Is = «Метод_Трапеции»

h = (b — a) / n: s = 0

x = a + h

Do While x

s = s + fun(x)

x = x + h

Loop

s = (h / 2) * (fun(a) + 2 * s + fun(b))

T

Рисунок 2.

extBox4.Text = s

Case Is = «Метод_Прямоугольников»

h = (b — a) / n: s1 = 0

x = a + h

Do While x

s1 = s1 + fun(x)

x = x + h

Loop

s1 = h * s1

TextBox5.Text = s1

End Select

End Sub

Function fun(x As Single) As Single

fun = x ^ 2

End Function

Задания для самостоятельного выполнения:

Задача 1. Методом прямоугольников и методом трапеций найти следующие интегралы:

  1. при x=0,1;

  2. при x=0,1.

Задание 2. Построить график и вычислить площадь криволинейной трапеции, ограниченной линиями y=x2sin x, y=0, x=a, x=b (ai = a+(b-a) СЛЧИС()).

Литература:

  1. Информатика и ИКТ. Профильный уровень: учебник для 11 класса. / И.Г. Семакин, Е.К. Хеннер, Л.В.Шестакова.— М.: БИНОМ, Лаборатория знаний, 2012. — 330 с.

  2. Информатика. Сборник элективных курсов. А.А.Чернов. Волгоград: Учитель, 2007г

  3. http://иванов-м.рф/informatika_11/informatika_materialy_zanytii_11_20.html

  4. Куклина И. Д. Применение электронных таблиц при изучении приближенных методов вычисления интеграла // Информатика и образование. — М. — 2010. — № 9. — С. 94 —96.

  5. Попова О. Н. Моделирование задачи оптимального управления// Информатика и образование. — М. — 2002. — № 10. — С. 78 —82.

  1. Гельман В.Я. Решение математических задач средствами Excel: Практикум. – СПб.: Питер, 2003. – 240 с.

  2. Тимофеева Н.М. Как решать задачи? / “В мир информатики” № 67 (“Информатика” № 2/2006).

2

Источник

Цели мероприятия:

1. Дидактические:

  • рассмотрение этапов информационного моделирования на примере решения
    конкретных задач;
  • закрепление навыков работы в MS Excel;
  • установление межпредметных связей: информатики и математики.

2. Развивающие:

  • развитие познавательного интереса, воображения;
  • развитие умений применять знания на практике.

3. Воспитательные:

  • расширение научного кругозора;
  • воспитание самостоятельности в работе.

Учебно-методическое обеспечение: презентация (Презентация),
ПО MS Excel, ПО MS PowerPoint, методические указания.

Оборудование: мультимедийная установка, персональные компьютеры.

Ход конференции

Преподаватель: Межпредметное значение информатики в значительной
степени проявляется именно через внедрение компьютерного моделирования в
различные научные и прикладные области: математику и физику, технику, биологию и
медицину, экономику, управление и многие другие. С помощью компьютерного
моделирования решаются многие научные и производственные задачи. Гибким
инструментом для компьютерного моделирования является MS Excel.

Возможности электронных таблиц Microsoft Excel весьма многогранны. Всем
известно, что Excel является мощным вычислительным инструментом, позволяющим
производить простые и сложные расчеты в различных областях человеческой
деятельности: математике, физике, инженерных науках, экономике, технологии. На
этом уроке мы рассмотрим использование электронных таблиц для решения
математических задач и уравнений.

Теоретическая часть

Преподаватель: Рассмотрим этапы информационного моделирования.

1. Модель задачи.

Пусть вам надо решить какую-либо задачу, и вы хотите воспользоваться для
этого помощью компьютера. С чего начать? Прежде всего, нужно разобраться, что
дано, что требуется получить, как связаны исходные данные и результаты.
Предположения, которые позволяют в море информации об изучаемом явлении или
объекте определить исходные данные, понять, что будет служить результатом и
какова связь между исходными данными и результатом, называют моделью задачи.
(Презентация. Слайд 2)

2. Понятие математической модели.

В моделировании есть два различных пути. Во-первых, это использование
натурных моделей. Но если модель должна отображать реальность в абстрактной
форме, то в таком случае всегда привлекаются средства математики, и мы имеем
дело с математической моделью.

Математическая модель выражает существенные признаки объекта или процесса
языком уравнений и других математических средств. (Презентация. Слайд 3)

Собственно говоря, в историческом аспекте сама математика обязана своим
существованием тому, что пыталась отражать, т.е. моделировать, на своем
специфическом языке закономерности окружающего мира.

Под математической моделью понимают систему математических соотношений –
формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта
или процесса. (Презентация. Слайд 3)

Математическое моделирование в наше время гораздо более всеобъемлющее, нежели
моделирование натурное. Математический аппарат для моделирования объектов и
процессов реального мира ученые использовали очень давно, но огромный толчок
математическому моделированию дало появление ЭВМ, которые сегодня помогают в
этой деятельности. Использование математического моделирования – это самый общий
метод научных исследований.

Простой пример. Представьте, что нужно определить площадь поверхности
письменного стола. Как обычно поступают в таком случае? Измеряют длину и ширину
стола, а затем перемножают полученные числа. Это фактически означает, что
реальный объект – поверхность стола – заменяется абстрактной математической
моделью – прямоугольником. Площадь этого прямоугольника и считается искомой
величиной.

Как видно, из всех свойств стола мы выделили три: форму поверхности
(прямоугольник) и длины двух сторон. Для нас не важны ни цвет стола, ни
материал, из которого он сделан, ни то, как стол используется. (Если бы мы
решали другую задачу о столе, например, сколько стоит его изготовление, то
возможно, для нас важна была бы как раз эта информация.) (Презентация. Слайд 4)

Предположив, что поверхность стола – прямоугольник, мы легко указываем
исходные данные и находим результат. Они связаны соотношение S = a * b.
(Презентация. Слайд 5)

Сделанное предположение позволило «перевести» нашу задачу на язык чисел: и
исходные данные, и результат – числа, а соотношение между ними задается
математической формулой.

Анализировать математические модели проще и быстрее, чем экспериментально
определять поведение реального объекта. Кроме того, анализ математической модели
позволяет выделить наиболее существенные свойства данного объекта (процесса), на
которые надо обратить внимание при принятии решения.

3. Этапы решения задач на компьютере.

1 этап. Постановка задачи – точная формулировка условий и целей
решения, описание наиболее существенных свойств объекта. (Презентация. Слайд 6)

2 этап. Построение математической модели – описание наиболее
существенных свойств объекта с помощью математических формул. (Презентация.
Слайд 6)

3 этап. Создание компьютерной модели – выражение математической модели
на понятном для компьютера языке. Существуют два принципиально различных пути
построения компьютерной модели:

  1. Построение алгоритма решения задачи и его кодирование на одном из языков
    программирования.
  2. Построение компьютерной модели и использованием ПО компьютера
    (приложений Windows – электронных таблиц, СУБД и пр.). (Презентация. Слайд
    7)

4 этап. Проведение компьютерного эксперимента (исследование модели) –
если компьютерная модель существует в виде программы на одном из языков
программирования, то её нужно запустить на выполнение и получить результаты;
если компьютерная модель исследуется в приложении, например, в электронных
таблицах, можно провести сортировку или поиск данных, построить диаграмму или
график и т.д. (Презентация. Слайд 8)

5 этап. Анализ полученных результатов и корректировка модели – в
случае различия результатов, полученных при исследовании модели, с измеряемыми
параметрами реальных объектов можно сделать вывод, что на предыдущих этапах
построения модели были допущены ошибки или неточности. В этом случае необходимо
провести корректировку модели, причём уточнение модели может проводиться
многократно, пока анализ результатов не покажет их соответствие изучаемому
объекту. (Презентация. Слайд 9)

Рассмотрим конкретные задачи математического моделирования. Для этого будем
использовать приложение Windows – электронные таблицы MS Excel. Для этих целей в
Excel имеется много возможностей: вычисление по формулам, построение диаграмм и
графиков, поиск решения, подбор параметра и т.д.

Практическая часть

Студент 1:

Задача 1. Необходимо покрасить краской стены кухни. Сколько
потребуется банок краски, если известно, что

  • размеры кухни 405 × 310 × 285 см;
  • 88% площади стен занимает кафельная плитка;
  • 1 банка краски предназначена для покраски площади 5 м2?
    (Презентация. Слайд 10)

Решение.

Постановка задачи.

Дано:

a = 405 см – длина комнаты,
b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м2 – площадь покраски при использовании 1 банки краски.

Найти: необходимое для покраски стен кухни количество банок краски.
(Презентация. Слайд 11)

Математическая модель.

Sстен с кафелем =2(a + b)c.
Sстен для покраски = 2(a + b)c * 0,12.

Чтобы определить, сколько потребуется банок краски, надо площадь для покраски
разделить на 5 м2, т. е. Sстен для покраски /5 и результат
округлить до целых.

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
1. Презентация. Слайд 12)
Электронная таблица в режиме отображения значений. (Приложение
2. Презентация. Слайд 13)
С помощью MS Excel мы определили, что для покраски стен кухни необходима 1 банка
краски.

Студент 2:

Задача 2. Через иллюминатор корабля требуется вытащить сундук с
драгоценностями. Удастся ли это сделать?

Решение.

Постановка задачи.

Иллюминатор корабля имеет форму круга. Будем считать, что сундук имеет форму
параллелепипеда. Чтобы вытащить сундук, необходимо, чтобы диаметр иллюминатора
был больше любой из трех диагоналей поверхности сундука. (Презентация. Слайд 14)

Математическая модель.

Пусть r – радиус иллюминатора,
a, b, c – размеры сундука,
d1, d2, d3 – диагонали боковых поверхностей сундука. (Презентация. Слайд 15)

Сундук можно вытаскивать через иллюминатор одной из трех боковых граней,
следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной
из трех диагоналей сундука, т.е. должно быть истинно хотя бы одно из условий:

ЕСЛИ((2*R>КОРЕНЬ(a^2+b^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(a^2+c^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(с^2+b^2));1;0)

(Презентация. Слайд 16)

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
3. Презентация. Слайд 17)
Электронная таблица в режиме отображения значений. (Приложение
4.Презентация. Слайд 18)

Компьютерный эксперимент.

В электронной таблице находим сумму трех условий. Если сумма равна 0, делаем
вывод «Сокровища недоступны», иначе «Сокровища доступны» (Слайд 19 Презентация).

Студент 3:

Задача 3. Решить уравнение х4-4х3-10х2+37х-14=0 (Слайд 20
Презентация).

Решение.

Необходимо построить график функции у = х4 – 4х3 – 10х2
+ 37х – 14. Точки пересечения графика с осью Х будут решениями данного
уравнения. Составляем в MS Excel таблицу значений функции. (Приложение
5. Презентация. Слайд 21)

Построим график функции (диаграмму). (Приложение 5.
Презентация. Слайд 22)

Мы видим, что график четырежды пересекает ось ОХ, значит уравнение х4
– 4х3 – 10х2 + 37х –14 = 0 имеет четыре корня.

Из таблицы и графика можно определить промежутки, в которых находятся корни
этого уравнения:

х1
[–3,5; –3], х2
[0; 0,5], х3
[2; 2,5], х4
[4,5; 5].

(Презентация. Слайд 23)

Затем с помощь анализа «что-если»/Подбор параметра можно
уточнить значения корней. Для этого следует активизировать ячейку со значением
функции у = 55,56, соответствующим значению аргумента х = -3,5, или ячейку со
значением у = -26, соответствующим х = -3, и выполнить команду Данные/группа
Работа с данными/Анализ «что-если»/Подбор параметра. Появится
одноименное диалоговое окно с тремя строками (Слайд 23 Презентация).

В первой строке указан адрес выбранного значения функции. Во второй нужно
установить курсор и занести подбираемое значение функции, указанное в правой
части данного уравнения (в нашем случае – число 0). А затем, установив курсор в
третьей строке, надо щелкнуть мышью на ячейке с соответствующим значением
аргумента, чтобы получить абсолютное значение этого адреса, затем щелкнуть ОК.

Аналогично проверяются корни из других промежутков.

Из результирующей таблицы выбираем корни уравнения. (Приложение
5. Презентация. Слайд 24)

Преподаватель: С особым вниманием следует применять этот способ для
решения уравнений, у которых графики функции не являются так называемыми
«гладкими» кривыми. Это касается, прежде всего, шага изменения аргумента при
построении графика соответствующей функции: он не должен быть слишком большим,
чтобы не пропустить значения некоторых корней.

Поясним это на примере решения уравнения.

Студент 4:

Задача 4. Решить уравнение log2(x(1 – x)) – sin(π/x) + 2 =
0, область определения которого: x принадлежит промежутку (0;1). (Презентация.
Слайд 25)

Решение.

Если построить график соответствующей функции в области ее определения с
шагом h = 0,04, то получится один результат (Приложение 6.
Презентация. Слайд 27), но если построить тот же график с меньшим шагом h =
0,01, то мы получим иной результат. (Приложение 6.
Презентация. Слайд 27) Сравнение этих графиков показывает, что в первом случае
из-за слишком большого шага «потеряны» два первых корня. Всего же
рассматриваемое уравнение имеет шесть корней, которые уточняются с помощью
Подбора параметра. (Презентация. Слайд 28)

Вывод. (Презентация. Слайд 29)

  1. С помощью электронных таблиц MS Excel можно решать математические задачи
    и уравнения.
  2. При этом отрабатываются навыки работы в электронных таблицах, а именно:
    оформление таблицы, работа с формулами, построение диаграмм.

Литература:

  1. О.К. Мясникова. Моделирование и формализация в курсе информатики. //
    Информатика и образование, №11-2003.
  2. В.П. Кудинов. Решение уравнений с помощью MS Excel. // Информатика и
    образование, №3-2004.
  3. Информатика и информационные технологии. Учебник для 10-11 классов /
    Н.Д. Угринович. – М.:Бином. Лаборатория знаний, 2003.
Источник

Практическая
работа: Поиск решения.

Большинство задач, решаемых с помощью электронной таблицы,
предполагают нахождение искомого результата по известным исходным данным. Но в
Excel есть инструменты, позволяющие решить и обратную задачу: подобрать
исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения,
который особенно удобен для решения так называемых «задач
оптимизации».

Если Вы раньше не использовали Поиск решения, то Вам
потребуется установить соответствующую надстройку.

Сделать это можно  через диалоговое
окно Параметры Excel

http://www.excelworld.ru/Author/Pelena/Solver/nadstr1.jpg

http://www.excelworld.ru/Author/Pelena/Solver/nadstr2.jpg

Начиная с версии Excel 2007 кнопка для запуска Поиска
решения появится на вкладке Данные.

http://www.excelworld.ru/Author/Pelena/Solver/knop.jpg

Задание
1. Распределение премии

Предположим, что Вы начальник
производственного отдела и Вам предстоит по-честному распределить премию в
сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным
окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности
для вычисления размера премии по окладу.

 Первым делом создаём таблицу с
исходными данными и формулами, с помощью которых должен быть получен результат.
В нашем случае результат — это суммарная величина премии. Очень важно, чтобы
целевая ячейка (С8) посредством формул была связана с искомой изменяемой
ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие
размер премии для каждого сотрудника (С2:С7).

http://www.excelworld.ru/Author/Pelena/Solver/form.jpg

Теперь запускаем Поиск решения и в открывшемся
диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых
окон в разных версиях несколько различается:

 Начиная с Excel 2010

http://www.excelworld.ru/Author/Pelena/Solver/param1.jpg

1.       Целевая
ячейка, в которой должен получиться желаемый результат. Целевая ячейка может
быть только одна

2.       Варианты
оптимизации:  максимальное возможное значение, минимальное возможное
значение или конкретное значение. Если требуется получить
конкретное значение, то его следует указать в поле ввода

3.       Изменяемых
ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно
в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное
значение

4.      

http://www.excelworld.ru/Author/Pelena/Solver/Ogran.jpg

Ограничения задаются с помощью кнопки Добавить.
Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение
формул. Именно ограничения обеспечивают получение правильного результата.
Ограничения можно задавать как для отдельных ячеек, так и для диапазонов.
Помимо всем понятных знаков =, >=, <=, при задании ограничений можно
использовать варианты цел (целое), бин (бинарное
или двоичное, т.е. 0 или 1), раз (все разные — только начиная
с версии Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть
положительным. Это ограничение можно задать по-разному: либо установить явно,
воспользовавшись кнопкой Добавить, либо поставить флажок Сделать
переменные без ограничений неотрицательными.

5.    
Кнопка, включающая итеративные вычисления с заданными параметрами.

 После нажатия кнопки Найти решение (Выполнить) Вы
уже можете видеть в таблице полученный результат. При этом на экране появляется
диалоговое окно Результаты поиска решения. 

 Начиная с Excel 2010

http://www.excelworld.ru/Author/Pelena/Solver/podtv.jpg

Если результат, который Вы видите в таблице Вас устраивает, то в
диалоговом окне Результаты поиска решения нажимаете ОК и
фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и
возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

http://www.excelworld.ru/Author/Pelena/Solver/rezultat.jpg

Важно: при любых изменениях исходных данных
для получения нового результата Поиск решения придется
запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной
прибыли)

Задание
2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных
книжных полок.

Их производство ограничено наличием сырья
(высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3
м² досок, а для изделия модели В — 4 м². Фирма может получить от своих
поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12
мин машинного времени, а для изделия модели В — 30 мин. в неделю можно
использовать 160 ч машинного времени.

Сколько изделий каждой модели следует
выпускать фирме в неделю для достижения максимальной прибыли, если
каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В —
120 руб. прибыли?

Порядок действий:

1.    
Сначала создаем таблицы с исходными данными и формулами.
Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно
автору. Например, как на рисунке

http://www.excelworld.ru/Author/Pelena/Solver/polkireshenie.jpg

2.    
Запускаем Поиск решения и в диалоговом окне
устанавливаем необходимые параметры

http://www.excelworld.ru/Author/Pelena/Solver/param_polki2.jpg

1.    
Целевая ячейка B12 содержит формулу для расчёта прибыли

2.    
Параметр оптимизации — максимум

3.    
Изменяемые ячейки B9:C9

4.    
Ограничения: найденные значения должны быть целыми,
неотрицательными; общее количество машинного времени не должно превышать 160 ч
(ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м²
(ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было
указать числа, но при использовании ссылок какие-либо изменения ограничений
можно производить прямо в таблице

5.    
Нажимаем кнопку Найти решение (Выполнить) и после
подтверждения получаем результат

http://www.excelworld.ru/Author/Pelena/Solver/polkirez.jpg

Но даже если Вы правильно создали формулы
и задали ограничения, результат может оказаться неожиданным. Например, при
решении данной задачи Вы можете увидеть такой результат:

http://www.excelworld.ru/Author/Pelena/Solver/netoch.jpg

 И это несмотря на то, что было задано ограничение целое.
В таких случаях можно попробовать настроить параметры Поиска решения.
Для этого в окне Поиск решения нажимаем кнопку Параметры и
попадаем в одноимённое диалоговое окно

http://www.excelworld.ru/Author/Pelena/Solver/tochnost.jpg

Первый из выделенных параметров отвечает
за точность вычислений. Уменьшая его, можно добиться более точного результата,
в нашем случае — целых значений. Второй из выделенных параметров (доступен,
начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться
дробные результаты при ограничении целое? Оказывается Поиск
решения это ограничение просто проигнорировал в соответствии с
установленным флажком.

Задание 3. Транспортная задача
(минимизация затрат)

На заказ строительной компании песок
перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным
площадкам). Стоимость на доставку включается в себестоимость объекта, 
поэтому строительная компания заинтересована обеспечить потребности своих
стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах;
потребности в песке стройплощадок; затраты на транспортировку между каждой
парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок
для удовлетворения нужд (откуда и куда), при которой общие затраты на
транспортировку были бы минимальными.

Пример расположения ячеек с исходными
данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

 http://www.excelworld.ru/Author/Pelena/Solver/pesok.jpg

В серых ячейках формулы суммы по строкам и
столбцам, а в целевой ячейке формула для подсчёта общих затрат на
транспортировку.

Запускаем Поиск решения и устанавливаем необходимые параметры (см.
рисунок)

http://www.excelworld.ru/Author/Pelena/Solver/param_pesok.jpg

Нажимаем Найти решение (Выполнить) и
получаем результат, изображенный ниже

http://www.excelworld.ru/Author/Pelena/Solver/pesok_resh1.jpg

Иногда транспортные задачи усложняются с
помощью дополнительных ограничений. Например, по каким-то причинам невозможно
возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно
ограничение $D$13=0. И после запуска Поиска решения получаем другой
результат

http://www.excelworld.ru/Author/Pelena/Solver/pesok_resh3.jpg

И последнее, на что следует обратить внимание, это выбор метода
решения. Если задача достаточно сложная, то для достижения результата может
потребоваться подобрать метод решения

Начиная с Excel 2010

http://www.excelworld.ru/Author/Pelena/Solver/metod.jpg

Задача для самостоятельного решения.

Крестьянин на базаре за 100 рублей купил
100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек.
Сколько быков, коров и телят купил крестьянин?

Источник

Понравилась статья? Поделить с друзьями:
  • Реализация логических функций excel
  • Реализация в excel проектов
  • Реализация билетов в цирк задание excel решение
  • Реализация билетов в цирк задание excel ответы
  • Реализация for to do в excel