Расширенный алгоритм евклида excel - Word и Excel - помощь в работе с программами

Расширенный алгоритм Евклида.

Алгоритм
Евклида
используются для нахождения по заданным
целым числам A и B их наибольшего общего
делителя С=НОД(А; B). Расширенный
алгоритм Евклида используется также
для нахождения целых чисел x, y таких,
что выполняется условие

.
Используется во многих криптографических
конструкциях, в том числе в методе RSA.

Основным
равенством, используемым для вычисления
НОД чисел А и В, является условие

НОД(А,
В) = НОД( В, A
mod B) (3)

где
A
mod B – остаток от целочисленного деления
А на В. Применяя последовательно формулу
(3), мы будем уменьшать числа А и В в этом
алгоритме, пока A
mod B не станет равным 0, тогда последнее
значение аргумента В даст искомый НОД
(А, В). Полное описание расширенного
алгоритма мы объясним на примере. Пусть
числа А и В равны 172 и 38 соответственно.
Откроем рабочий лист Excel и разметим в
первых строчках заголовки столбцов, а
под заголовками А и В поместим числа
172 и 38, как указано на рисунке.

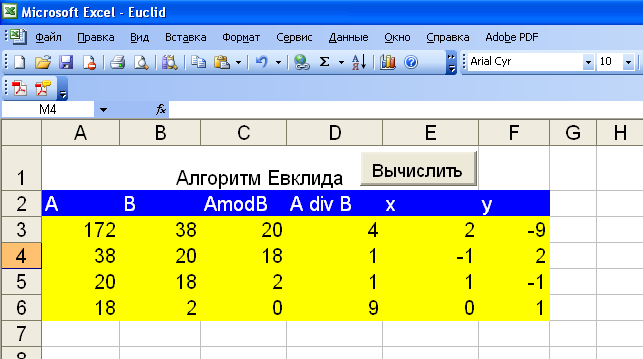
Рис.1.
Примерный вид рабочего листа Excel для
реализации расширенного алгоритма
Евклида.

В
столбце Amod B напишем формулу вычисления
остатка от целочисленного деления А на
В: =ОСТАТ(A3;B3),
а в столбце A div
B впишем формулу =ЦЕЛОЕ(A3/B3),
обозначающую операцию нахождения целой
части от деления A
на В.

В
следующей строке в столбах А и В поместим
значения 38 и 20, взятые из двух ячеек,
находящихся выше и правее (применение
формулы (3)). Значения ячеек под заголовками
Amod B и A div
B надо вычислить как в предыдущей строке.
В Excel для этого достаточно просто
скопировать и вставить вышележащие
клетки на строку ниже.

Повторяем
эти операция несколько раз, пока не
получим в столбце Amod B значение 0. Значение
В в этой строке будет равно НОД(А,В) (в
нашем примере он равен 2).

Далее
заполняем столбцы x и y в обратном порядке
снизу вверх. Поместим в столбцы x и y в
последней полученной строке значения
0 и 1. Далее в каждой следующей (вышележащей)
строке i поместим значения x_i
и y_i,
вычисленные по формулам:

где

обозначает значение из столбца A div
B, взятое из той же строки, где вычисляются
значения x и y. Используя эти формулы,
заполним столбцы x и y. В верхней строке
получим значения x и y, которые нам нужны.

Алгоритм
возведения в степень по модулю натурального
числа.

Для
выполнения шифрования по методу RSA
приходится выполнять возведение в
большую степень различных чисел, а
результат приводить по модулю числа N,
являющегося параметром метода и имеющего
длину 512 и более бит. Уже для небольших
a
и e
вычислить значение

(1)

выполняя
сначала возведение в степень, а потом
вычисляя остаток от деления

на N, становится невозможным. Между тем,
если применить алгоритм, описанный в
этом разделе, можно вычислять выражения
(1), для достаточно больших чисел a,
e,
N,
оставаясь в рамках обычных операций с
целыми числами, заложенных в компьютере.

Алгоритм
быстрого возведения в степень основывается
на идее замены прямого вычисления
возведения в степень

последовательными
операциями умножения на a и возведения
в квадрат. Для этого представим степень
e число в двоичном исчислении

(2)

где
любое t_i
для

принадлежит

,

.
Зная вектор разрядов

,
можно вычислить число e,
применяя последовательные вычисления:

(3)

Например,
если e
= 13, то в двоичном представлении e
= 1101₂
, и 13 можно представить как результат
вычисления

Последнее
число и есть e.

Используя
формулы (3), можно процедуру возведения
в степень по модулю натурального числа
N, записать в виде последовательности
итераций:

где

.
Множитель

в зависимости от

принимает либо значение a, если

,
либо 1, если

.
Результат вычислений можно свести в
таблицу

			…
			…

Пример.
Вычислить

.

Решение.
Переведем степень e=13 в двоичный вид.
Для этого заполним следующую
таблицу:

e div 2	13	6	3	1
e mod 2	1	0	1	1

Таблица
1. Перевод
десятичного числа e
к двоичному представлению.

Искомое
двоичное разложение числа e
будет во второй строке таблицы , записанное
в обратном порядке справа налево.

Далее,
составим таблицу вычисления с, заполняя
следующую таблицу:

е	1	1	0	1
с	5	11	7	10

Таблица
2. Возведение
а=5 в степень e=13 по модулю 19.

В
первой строке запишем цифры двоичное
разложения числа 13. В первую ячейку
второй строки поместим основание а=5.
Далее каждое следующее значение с
будем вычислять по формуле:

Например,

Приведем
код на Паскале вычисления функции
возведения в степень:

Function
Rise(A,B,N:Integer):Integer;

var

B2:array[1..20]
of byte;

i,C,L:integer;

Begin

C:=B;
i := 1;

While
C > 0 do

Begin

B2[i]:=
C Mod 2;

C:=
C div 2;

i:=
i + 1;

End;

L:=
i — 1;

i:=
1;

D:=
A;

While
i <L do

Begin

D:=
(D * D) Mod N;

If
B2[L-i]= 1 Then D:=(D * A) Mod N;

i
:= i + 1;

End;

Rise
:= D;

End;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
10.02.201542.64 Mб22LangLeader_Intermediate_WB.pdf
#

Источник

Алгебра. 7 класс

Конспект урока

Линейные диофантовы уравнения

Перечень рассматриваемых вопросов:

Диофантово уравнение.
Разрешимость диофантова уравнения.
Решение задач с помощью диофантова уравнения.

Диофантовым уравнением называется уравнение вида ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с, х и у – целые числа.

Если c делится на НОД(а; b), то уравнение ах + bу = с имеет решение в целых числах. Если c не делится на НОД (а; b), то уравнение ах + bу = с не имеет решений в целых числах.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Определение диофантова уравнения.

Пусть дано уравнение ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с – целые числа. Если поставлена задача найти только такие его решения (х₀; у₀), где х_0, у₀ – целые числа, то это уравнение называют линейным диофантовым уравнением.

Диофантовы уравнения связаны с именем древнегреческого математика Диофанта Александрийского. О подробностях жизни Диофанта Александрийского практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до нашей эры); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года нашей эры). Откуда можно сделать вывод, что жил он приблизительно в III веке нашей эры.

Решение диофантовых уравнений.

Решим линейное диофантово уравнение

Выразим у через х:

Из этого равенства видно, что у будет целым только тогда, когда целое число х делится на 3, т.е. х = 3х_1, где х_{1 –} некоторое целое число. Тогда у = 2 -2х₁.

Таким образом, решениями уравнения являются все пары чисел (3х_1;2 -2х₁).

Приведём некоторые частные решения этого уравнения.

Если х₁ = 0, то х = 3х_{1 =} 0, а у = 2 — 2 х₁ = 2; решением уравнения является пара (0;2).

Если х_{1 =} 1, то х = 3х_{1 =} 3, а у = 2 — 2 х₁ = 0;

решением уравнения является пара (3; 0)

Аналогично можно найти и другие частные решения, их бесконечно много.

Решение задач при помощи линейных диофантовых уравнений.

Линейные диофантовы уравнения возникают при решении некоторых задач.

У покупателя и продавца имеются монеты только по 2р. и 5р. Сможет ли покупатель заплатить за покупку стоимостью 1р.?

Если покупатель даст х монет по 2р. и у монет по 5 р., то он заплатит (2х + 5у) р. А по условию задачи это 1р. Составим уравнение:

Выразим х через у из уравнения:

Из равенства видно, что х будет целым только тогда, когда у будет нечетным числом: у = 2m + 1, где m – целое число.

Таким образом, решением уравнения являются все пары чисел (-5m – 2; 2m + 1), где m – любое целое число.

Таким образом, способов оплаты товара стоимостью 1р. Бесконечно много. Если х окажется отрицательным, то это означает, что покупатель должен получить сдачу: х монет по 2р.

Например, пара (-2; 1) является решением уравнения. Это означает, что покупатель далодну монету по 5 р. и получил сдачу 2 монеты по 2р.

Разрешимость диофантова уравнения.

Не каждое диофантово уравнение имеет решение в целых числах.

Рассмотрим на примере уравнения

3х + 6у = 2 алгоритм, с помощью которого можно определить, имеет оно решение в целых числах.

1 шаг. Надо найти наибольший общий делитель чисел 3 и 6. НОД(3; 6) = 3.

2 шаг. Определить, делится ли 2 на НОД(3; 6).

3 шаг. Если 2 делится на НОД(3; 6), то уравнение имеет решение в целых числах.

Если 2 не делится на НОД (3; 6), то уравнение не имеет решений в целых числах.

Расширенный алгоритм Евклида для решения диофантовых уравнений.

Для нахождения наибольшего общего делителя двух целых неотрицательных чисел используют алгоритм Евклида. Рассмотрим его реализацию на примере чисел 24 и 17.

Разделим большее из этих чисел на меньшее, то есть 24 на 17.

Получаем 24 : 17 = 1 (ост. 7), что можно записать в виде равенства:

Теперь разделим делитель на остаток, то есть 17 на 7, получим:

Снова разделим делитель на остаток:

Выполним деление еще раз:

Мы получили остаток, равный нулю, так как 3 делится на 1 без остатка.

В представленной последовательности действий мы получали остатки: 7, 3, 1, 0. Последний остаток, не считая 0, является наибольшим общим делителем чисел 24 и 17. То есть, НОД(24; 17) = 1.

Рассмотрим еще один пример: НОД(612; 342)?

612 = 342 ∙ 1 + 270,

342 = 270 ∙ 1 + 72,

Теперь выполним действия «в обратном направлении», то есть выразим 18 (остаток) через числа 612 и 342.

Для этого в каждой строчке последовательности Евклида выразим остатки через делимое и делитель (второй столбик таблицы):

612 = 342 ∙ 1 + 270

342 = 270 ∙ 1 + 72

270 = 612 – 342 ∙ 1

72 = 342 – 270 ∙ 1

Получаем, 18 = 72 – 54 ∙ 1 = 72 – (270 – 72 ∙ 3) = 342 – 270 ∙ 1 – (270 – (342 — 270 ∙ 1) ∙3) =

342 – ((612 – 342 ∙1) ∙ 1) – (612 – 342 ∙ 1 – (342 – (612 – 342 ∙ 1)) ∙3) = 342 – 612 + 342 – 612 + 342 + 342 ∙ 3 – 612 ∙ 3 + 342 ∙ 3 = 342 ∙ 9 – 612 ∙ 5 = 342 ∙ 9 + 612 ∙ (-5).

То есть 18 = 9 ∙ 342 + (-5) ∙ 612.

Умение выполнять действия алгоритма «в обратном направлении» понадобится нам в решении диофантовых уравнений при помощи расширенного алгоритма Евклида.

Пример: решите уравнение 24x−17y=2.

Найдем при помощи алгоритма Евклида НОД(24, 17):

Выполним действия «в обратном направлении»:

1 = 7 – 3 · 2 = 7 − (17 – 7 · 2) · 2 = 7 – 17 · 2 + 7 · 4 + 5 · 7 – 2 · 17 = 5 · (24 – 17 · 1) – 2 · 17 = 5 · 24 – 5 · 17 – 2 · 17 = 5 · 24 – 7 · 17 = 24 · 5 – 17 · 7.

24 · 5 – 17 · 7 = 1; В исходном уравнении в правой части стоит число 2. Поэтому умножим обе части уравнения на 2. Получим:

24 · 10 – 17 · 14 = 2.

То есть, x₀ = 10, y₀ = 14 – частные решения уравнения 24x −17y = 2.Если уравнение имеет одно решение в целых числах, то оно имеет бесконечное множество других решений.

Прибавим коэффициент b к значению х.

Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к х нужно вычесть другое число изу:

(-7; -10) – еще одно решение уравнения.

Значения x будут равны сумме исходного решения (х₀) и любого кратного коэффициента b. То есть х = 10 + (-17t), где t – целое число.

А значение у – равны разности у₀ и любого кратного коэффициента а. То есть у = 14 – 24t.

Ответ: (10 − 17t, 14 − 24t), t ∈ Z.

Разбор заданий тренировочного модуля.

1. Решите задачу:

Некий чиновник купил ослов и быков за 1770 талеров. За каждого осла он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько ослов и быков купил чиновник?

Пусть чиновник купил х ослов и у быков. Тогда 31х + 21у = 1770.

По смыслу задачи х и у – натуральные числа. Так как 21 и 1770 делятся на 3, то 31х делится на 3, т. е. х делится на 3: х = 3n, где n – натуральное число. Тогда 31n + 7у = 590. Откуда n =

Очевидно, что n будет целым, если 7у – 1 делится на 31.

Наименьшее натуральное у, при котором это произойдет, равно 9. При этом n = 17, х = 51. Первое решение найдено: (51; 9).

Заметим, что следующие целые n будут получаться в результате увеличения у = 9 на число, кратное 31.

При у = 9 + 21 = 40 имеем n = 10, х = 30.

При у = 40 + 9 имеем n = 3, х = 9.

При следующих значениях у значения n отрицательны. Таким образом, исходное уравнение имеет 3 решения: (51, 9), (30, 40), (9, 71).

Ответ: (51, 9), (30, 40), (9, 71).

2. Решение уравнения.

Разделите уравнения на 2 группы: уравнение имеет решение в целых числах, уравнение не имеет решений в целых числах.

1) НОД(7; 5) = 1, 2 делится на 1, следовательно, 7х – 5у = 2 имеет решение в целых числах.

2) НОД(3; 5) = 1, 10 делится на 1, следовательно, 3х + 5у = 10 имеет решение в целых числах.

3) НОД(2; 4) = 2, -1 не делится на 2, следовательно, 2х + 4у = -1 не имеет решений в целых числах.

4) НОД(3; 9) = 3, 10 не делится на 3, следовательно, 3х – 9у = 10 не имеет решений в целых числах.

5) НОД(6; 9) = 3, 2 не делится на 3, следовательно, 6х + 9у = 2 не имеет решений в целых числах.

6) НОД(2; 5) = 1, 15 делится на 1, следовательно, 2х – 5у = 15 имеет решение в целых числах.

Элективный курс Сказки Шехерезады и уравнения Диофанта Балашов 2009 Содержание

Главная > Элективный курс

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Применение алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (повторение).

Существует довольно простой прием, позволяющий находить наибольший делитель двух натуральных чисел. Этот прием называется алгоритмом Евклида. Вы с ним познакомились еще при изучении курса математики в 5 – 6 классах. Евклид, великий ученый, живший около 2000 лет назад, занимался не только геометрией, которая носит его имя. Ему принадлежит решение ряда важных задач арифметики и, в частности, тот способ нахождения наибольшего общего делителя, который мы сегодня будем использовать при изучении нового материала. А сейчас повторим суть алгоритма Евклида .

Чтобы найти наибольший общий делитель двух чисел:

1) надо большее из двух чисел разделить на меньшее;

2) потом меньшее из чисел на остаток при первом делении;

3) затем остаток при первом делении на остаток при втором делении и вести этот процесс до тех пор, пока не произойдет деление без остатка. Последний отличный от нуля остаток и есть искомый НОД двух данных чисел

Рассмотрим пример. Найти НОД (645; 381).

Разделим с остатком 645 на 381. Мы получим: 645=381·1+264.

Далее разделим с остатком 381 на 264, получим: 381=264·1+117.

Теперь разделим с остатком 264 на 117, получим: 264=117·2+30.

Продолжим процесс деления, разделим с остатком 117 на 30, получим: 117=30·3+27. Далее, 30=27·1+3. Следующий шаг – делим 27 на 3, получаем, что 27=3·9 +0, т. е. 27 делится на 3 без остатка. Значит, наибольший общий делитель чисел 27 и 3 равен 3, следовательно, и наибольший общий делитель чисел 645 и 381 равен 3, т. е. последнему отличному от нуля остатку.

Таким образом, НОД (645; 381) = 3.

Прием разыскания наибольшего общего делителя, примененный в этом примере, и представляет собой алгоритм Евклида.

2. Вывод формул для решения диофантовых уравнений с использованием алгоритма Евклида.

Прежде чем рассмотреть решение линейного уравнения с двумя неизвестными:

с использованием алгоритма Евклида, докажем утверждение о том, что наибольший общий делитель двух чисел есть последний отличный от нуля остаток в цепочке указанных в примере действий .

Чтобы доказать утверждение о наибольшем общем делителе, представим описанный процесс в виде следующей цепочки равенств: если a > b , то

·b = r 1 q 1 + r 2

r 1 = r 2 q 2 + r 3 (2)

r n – 1 = r n q n

Здесь r 1 , . . . , r n — положительные остатки, убывающие с возрастанием номера. Отсутствие остатка в последнем равенстве следует из того, что натуральные числа r n не могут убывать бесконечно, поэтому на некотором шаге остаток станет нулевым.

Обратимся к системе (2). Из первого равенства, выразив остаток r 1 через a и b , получим r 1 = a – b · q 0 . Подставляя его во второе равенство, найдём r 2 = b (1 + q 0 q 1 ) – a · q 1 . Продолжая этот процесс дальше, мы сможем выразить все остатки через a и b , в том числе и последний: r n = Aa + Bb . В результате нами доказано

что найдутся такие целые числа A и B , что d = Aa + Bb . Заметим, что коэффициенты A и B имеют разные знаки; если НОД ( a , b ) = 1 , то Aa + Bb = 1 . Как найти числа A и B , видно из алгоритма Евклида.

Перейдем теперь к решению линейного уравнения с двумя неизвестными:

Возможны два случая: либо число c делится на d = НОД( a , b ) , либо нет.

В первом случае можно разделить обе части уравнения на d и свести задачу к решению в целых числах уравнения a 1 x + b 1 y = c 1 , коэффициенты которого

a 1 = a / d и b 1 = b / d взаимно просты.

Во втором случае уравнение не имеет целочисленных решений: при любых целых x и y число ax + by делиться на d и поэтому не может равняться числу c , которое на d не делится.

Итак, мы можем ограничиться случаем, когда в уравнении (1) коэффициенты a и b взаимно просты. На основании предыдущего предложения найдутся такие целые числа х 0 и у 0 , что ax 0 + by 0 = 1 , откуда пара (сх 0 , су 0 ) удовлетворяет уравнению (1). Вместе с ней уравнению (1) удовлетворяет бесконечное множество пар ( x , у) целых чисел, которые можно найти по формулам

x = cx 0 + bt, y = cy 0 – at. (3)

Здесь t – любое целое число. Нетрудно показать, что других целочисленных решений уравнение ах + by = c не имеет. Решение, записанное в виде (3), называется общим решением уравнения (1). Подставив вместо t конкретное целое число, получим его частное решение.

Примечание . Название «лекция» как будто говорит о том, что активная роль здесь принадлежит лишь самому учителю, учащимся предоставляется пассивная роль – внимательно слушать рассказ учителя и выполнять в тетради те записи, которые учитель выполняет на классной доске. Если бы это было именно так, то данная форма обучения оказалось бы мало эффективной. Современные требования обучения математике предполагают, что даже в том случае, когда учитель является главным действующим лицом,
необходима активная деятельность самих учащихся. Поэтому лекция учителя должна пробуждать у учащихся интерес и потребность к активной умственной деятельности.

По ходу лекции следует обратиться с вопросами к учащимся . Например: Какие уравнения называются диофантовыми? Какой вид имеет линейное диофантово уравнение? Какие условия накладываются на его коэффициенты? Какой способ решения уравнения мы использовали на предыдущем занятии?

Также на занятиях, где материал изучается крупным блоком, целесообразно создание таблицы в виде конспекта изложенного учителем нового материала. Этот конспект должен стать информационно-справочной таблицей и сыграть свою
роль на занятиях тематического или итогового повторения. Сформулируем некоторые требования к его оформлению. Материал в конспекте должен быть разделен на несколько самостоятельных, логически связанных между собой блоков. В него желательно внести вспомогательные вопросы, с помощью которых готовится введение нового, узловые вопросы темы и ее практическое применение.

Таким образом, с одной стороны, в конце урока желательно иметь конспект, в котором видно главное. А с другой стороны, запись этого конспекта не должна занимать много времени. Для выполнения этих требований можно использовать заготовку для конспекта, т.е. таблицу с пропусками. В нее можно внести рисунок без подписей, частично выполненные условия теоремы, некоторые пункты алгоритмических предписаний и т.п.

Как разработать такой конспект? Учитель сначала разрабатывает конспект полностью на листе бумаге стандартного размера. На другом таком же листе он выписывает конспект-заготовку в строгом расположении текста на основном конспекте. Этот фрагментарный конспект необходимо размножить, чтобы к лекции такой конспект-заготовку имел каждый ученик. Точно такой конспект «с пропусками» учитель должен заранее написать на доске
перед началом лекции или подготовить его компьютерный вариант для использования в классе с интерактивной доской. Для проведения данной лекции был подготовлен такой
конспект-заготовка (Приложение 4).

3. Примеры решения диофантовых уравнений с использованием алгоритма Евклида.

Рассмотрим решение заданий №6 (а), №7 из Приложения 1.

Задание №6 . Решить уравнение на множестве целых чисел

НОД(7;11)=1, Найдем значение х 0 и у 0 для получения решений уравнения по формулам (3). Применим алгоритм Евклида к числам 11 и 7:

Таким образом, получаем: , следовательно х 0 = –3, у 0 =2

Запишем общее решение уравнения на множестве целых чисел согласно формулам (3):

Придавая конкретные целые значения t , можно получить частные решения уравнения. Например, при t =1, имеем x = –196, у=131.

Задача №7 . Для газификации жилого дома требуется проложить газопровод протяженностью 150 м. Имеются трубы 13 м и 9м длиной. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода.

Пусть требуется x труб по 9 м, и у труб по 13м. Составим и решим уравнение: 9х+13у=150.

НОД(9;13)=1, уравнение разрешимо во множестве целых чисел.

Найдем значение х 0 и у 0 для получения решений уравнения по формулам (3). Применим алгоритм Евклида к числам 13 и 9:

Запишем общее решение уравнения согласно формулам (3).

Так как x и y неотрицательные целые числа, то чтобы найти значение t , решим систему неравенств:

Ответ. Для прокладывания газопровода потребуется 8 труб длиной по 9м и 6 труб длиной по 13м.

4 . В домашнее задание для учащихся необходимо включить подготовку по теоретическому материалу и практические задания.

Учащиеся должны ответить на следующие вопросы.

В чем суть алгоритма Евклида?

Когда уравнение (1) разрешимо во множестве целых чисел?

По каким формулам находится общее решение диофантова уравнения первой степени с двумя переменными с использованием алгоритма Евклида? Укажите, что обозначают буквы, входящие в эти формулы.

При выполнении домашнего задания используется опорный конспект лекции, в котором выделены основные вопросы, рассмотренные на занятии, и заполнены соответственно имеющиеся пропуски (Приложение 4).

В качестве практических заданий можно предложить для решения задания №6 (б), №8 из Приложения 1. Также можно предложить составить сюжетную задачу, решение которой сводится к уравнению из №6 (б) на множестве целых неотрицательных или натуральных чисел. Найти ее решения.

Решение диофантовых уравнений с использованием алгоритма Евклида

Актуализация знаний ( проверка знания теории и выполнения практических заданий).

Решение задач с использованием алгоритма Евклида.

Постановка домашнего задания.

Оборудование: заполненные конспекты – заготовки предыдущей лекции, карточки с заданиями для фронтальной и групповой работы.

Актуализация знаний. Проведение первого этапа занятия – практикума учитель может спланировать по своему усмотрению. Необходимо организовать проверку выполнения домашнего задания, включающего как теоретические вопросы, так и практические задания.

Решение задач с использованием алгоритма Евклида .

Задания для решения выбираются по принципу: от простого к сложному. Для овладения методом решения диофантовых уравнений с использованием алгоритма Евклида можно предложить вначале решить уравнения, не связанные, с какой либо реальной ситуацией. Например, № 6 (в, г). Затем можно предложить решение текстовых задач на составление линейных диофантовых уравнений. Например, № 9, 10. Все задания указаны из Приложения 1. Задания можно выполнить в группах, а затем проверить полученные ответы. Ниже приведем решение задачи №9.

Неотъемлемой частью занятия – практикума является решение и нестандартных задач, заданий повышенной трудности. В процессе их выполнения можно использовать прием разбиения на подзадачи. К таким заданиям можно отнести и задачу № 11, которую мы далее рассмотрим.

Заметим, что в ходе решения задач, учащиеся могут опираться на заполненный опорный конспект предыдущей лекции, в котором выделен способ решения диофантовых уравнений с использованием алгоритма Евклида.

Задача №9. Транспортные организации имеют в наличие машины вместимостью 3, 5 т и 4, 5 т. Следует перевезти груз весом 53 т. Сколько машин нужно взять для одного рейса?

Пусть x машин по 3,5 т.; у машин по 4, 5 т. Составим и решим уравнение: 3,5х+4,5у=53. Перейдем к уравнению с целыми коэффициентами, например, умножим обе части уравнения на 2. Получим: 7х+9у=106.

НОД(7, 9)=1, уравнение имеет целые решения.

Так как t – принимает целые значения, то системе неравенств удовлетворяют значения t =-47 и t =-46. Получим решение диофантова уравнения в натуральных числах:

Таким образом, для одного рейса можно взять:

А) 1 машину вместимостью 3,5 т и 11 машин вместимостью 4,5 т;

В) 10 машин вместимостью 3,5 т и 4 машины вместимостью 4,5 т.

Полезно обратить внимание на то, какой из возможных вариантов будет наиболее эффективным для работы предприятия с экономической точки зрения (экономия бензина, экономия средств на оплату труда водителям и т.д.) .

Задача №11 . Школа получила 1 млн. руб. на приобретение 100 единиц учебного оборудования (на всю сумму без сдачи). Администрации школы предложили, оборудование стоимостью 3000, 8000 и 12000 руб. за единицу. Сколькими способами школа может закупить это оборудование. Укажите один из способов.

В ходе обсуждения идеи решения данной задачи, необходимо выяснить: что дано, что неизвестно в условии, как связаны между собой данные и искомые. Затем переходить к составлению математической модели задачи.

1 ) составление системы уравнений .

Пусть приобретено x единиц оборудования по 12000 руб., y единиц оборудования по 8000 руб., z единиц оборудования по
3000 руб.

Всего приобретено 100 единиц оборудования, т.е. x + y + z = 100 , причем на приобретение 100 единиц оборудования затрачено 1 млн. руб., т.е.

12000 x + 8000 y + 3000 z = 1 000 000,

12x + 8y + 3z = 1000 .

Таким образом, получаем систему двух уравнений с тремя неизвестными:

Вопрос учителя: всегда ли задача будет иметь решение? Иначе: какими
должны быть x , y , z ?

( ответ: x >0, y >0, z >0 )

2) обсуждение решения системы.

Во-первых, исключим z , путем вычитания из второго уравнения первого, умноженного на 3. Следовательно, получаем диофантово уравнение 1-ой степени с двумя неизвестными 9 x + 5 y = 700.

Во-вторых, его можно решить способом с использованием алгоритма Евклида.

3) оформление решения задачи.

Так как уже получили уравнение, которое решается известным способом, то оформление решения можно предложить выполнить учащимся дома. В результате решения получается, что приобрести оборудование библиотека может шестью способами. Укажем одно из частных решений задачи: x=65 , y=23, z=12 , т.е. школа на 1 млн. руб. может
приобрести 65 единиц оборудования по 12 тыс. руб., 23 единицы оборудования по 8 тыс. руб., 12 единиц оборудования по 3 тыс. руб.

3. Постановка домашнего задания.

В качестве домашнего задания можно преложить учащимся решить задачи № 2; №3; №5 из Приложения 1 с использованием алгоритма Евклида.

Решение диофантовых уравнений с использованием

План занятия совпадает с планом школьной лекции на указанную тему.

Понятие цепной дроби. Представление рациональных чисел в виде цепной дроби

Формулы для решения диофантовых уравнений с использованием цепной дроби

Примеры решения диофантовых уравнений с использованием цепной дроби.

Оборудование: конспект – заготовка лекции на доске и индивидуальные заготовки для каждого ученика.

Занятие № 5 по своей структуре аналогично занятию №3. В качестве примеров решения диофантовых уравнений с использованием цепной дроби, можно рассмотреть задания из Приложения 1. Заметим, что можно взять уже ранее решенные задачи и выполнить их решение новым способом.

Понятие цепной дроби. Представление рациональных чисел в виде цепной дроби

Обратимся вновь к алгоритму Евклида. Из первого равенства системы (2) вытекает, что дробь a / b можно записать в виде суммы целой части и правильной дроби: . Из второго равенства той же системы имеем. Значит,

Продолжим этот процесс до тех пор, пока не придём к знаменателю q п

В результате мы представим обыкновенную дробь a / b в следующем виде: . Эйлер назвал дробь, стоящую в правой части равенства непрерывной . Приблизительно в тоже время в Германии появился другой термин – цепная дробь . Так за этими дробями и сохранились оба названия. Ввиду громоздкости развёрнутой записи цепной дроби применяют компактную запись

a / b = [ q 0 ; q 1 , q 2 , …, q п ] .

Представить рациональное число в виде цепной дроби.

Очевидно, что любое рациональное число, и только оно записывается в виде конечной цепной дроби. Иррациональным числам соответствуют бесконечные цепные дроби.

Если при построении цепной дроби остановиться на знаменателе q k , то получиться дробь [ q 0 ; q 1 , q 2 , …, q к ] , которую называют к-й подходящей дробью для искомой и обозначают Найдем вид некоторых подходящих дробей:

Для рационального числа a / b последовательность подходящих дробей конечна, и ее последний элемент Нетрудно заметить, что имеют место следующие рекуррентные соотношения:

(4)

Формулы для решения диофантовых уравнений с использованием цепной дроби

Вернемся к уравнению: ax + by = c (1). Напомним, что в нем a и b взаимно просты. Решение этого уравнения «способом цепной дроби» завершается применением готовых формул (доказательство которых можно найти в специальных пособиях), представляющих общее решение данного уравнения

(5)

Наибольший общий делитель. Наименьшее кратное. Расширенный алгоритм Евклида. Диофантовы уравнения. Обработка строк.

1. Наибольший общий делитель. Наименьшее общее кратное. Методы вычисления, свойства.

2. Расширенный алгоритм Евклида. Описание алгоритма. Примеры.

3. Диофантовы уравнения. Решение уравнения ax + by = c в целых неотрицательных числах. Теорема о существовании решения.

4. Обработка строк. Библиотека . Длина строки. Конкатенация и копирование строк. Ввод-вывод строк при помощи функций gets и puts .

http://acm.uva.es/problemset: 10104 (Задача Евклида), 10407 (Простое деление), 10548 (Найти правильный размен), 10673 (Игра с округлением вниз и вверх), 10717 (Монетный завод).

1. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ

Определение 1.1. Наибольшим общим делителем (далее НОД) двух целых чисел a и b, одновременно не равных нулю, называется такое наибольшее целое число d, на которое a и b делятся без остатка. Этот факт обозначается так: d = НОД(a, b). Если оба числа равны нулю, то положим НОД(0, 0) = 0.

Исходя из определения, имеют место следующие равенства:

Определение 1.2. Наименьшим общим кратным (далее НОК) двух целых чисел a и b называется наименьшее общее положительное целое число, кратное как a так и b.

Основная теорема арифметики утверждает, что любое натуральное число можно представить в виде произведения простых чисел:

n = =

Из канонического разложения следует, что

НОД (a, b) =

НОК (a, b) =

Пример 1.1. Рассмотрим числа a = 24, b = 18. Разложим их на простые множители: 24 = 2 3 * 3, 18 = 2 * 3 2 . Следовательно

НОД(24, 18) = 2 min(3,1) * 3 min(1,2) = 2 1 * 3 1 = 6,

НОК(24, 18) = 2 max(3,1) * 3 max(1,2) = 2 3 * 3 2 = 8 * 9 = 72

Если НОД(a, b) = d, то a и b делятся на d. Следовательно их разница a – b также делится на d. Имеет место следующее рекурсивное соотношение для вычисления НОД, известное как алгоритм Евклида:

НОД(a, b) =

Пример 1.2. Пусть a = 32, b = 12. Тогда

НОД(32, 12) = НОД(32 – 12, 12) = НОД(20, 12) = НОД(20 – 12, 12) = НОД(8, 12) =

НОД(8, 12 – = НОД(8, 4) = НОД(8 – 4, 4) = НОД(4, 4) = НОД(4 – 4, 4) = НОД(0, 4) = 4

Приведенный метод вычисления не является оптимальным. Например, для нахождения НОД(100, 2) следует выполнить 50 операций вычитания. Для ускорения вычисления НОД операцию вычитания следует заменить операцией взятия остатка от деления:

НОД(a, b) =

Пример 1.3. Пусть a = 78, b = 14. Тогда

НОД(78, 14) = НОД(78 mod 14, 14) = НОД(8, 14) = НОД(8, 14 mod = НОД(8, 6) =

НОД(8 mod 6, 6) = НОД(2, 6) = НОД(2, 6 mod 2) = НОД(2, 0) = 2

Упростим приведенную выше рекуррентность:

НОД(a, b) =

Если a Greater Common Divisor ) вычисления НОД можно записать в виде:

int gcd(int a, int b)

return (!b) ? a : gcd(b,a % b);

Пример 1.4. Пусть a = 14, b = 78. Тогда

НОД(14, 78) = НОД(78, 14) = НОД(14, = НОД(8, 6) = НОД(6, 2) = НОД(2, 0) = 2

Бинарный алгоритм вычисления НОД имеет вид:

Теорема 1.1. Между НОД и НОК двух чисел имеет место соотношение:

Функция lcm (Lowest Common Multiple) вычисления НОК имеет вид :

int lcm(int a, int b)

return a * b / gcd(a,b);

Заметим, что при вычислении выражения a * b / gcd(a, b) может возникнуть переполнение, а при a / gcd(a, b) * b нет. Здесь подразумевается, что значения a , b и lcm (a, b) лежат в границах типа int .

Упражнение 1.1. [Вальядолид, 10407]. Простое деление. При делении числа n на d получается частное q и остаток r. При этом q – максимально возможное целое, для которого qd £ n, а r = n – qd. Для любого множества целых чисел <a₁, …, a_k> всегда существует такое d, что числа a_i mod d равны.

Вход. Каждая строка является отдельным тестом и содержит последовательность чисел a₁, …, a_k, заканчивающуюся нулем. Последний ноль не принадлежит самой последовательности. Последовательность содержит не менее 2 и не более 1000 чисел. Не все числа в последовательности равны между собой. Признаком конца входных данных является строка с одним нулем.

Выход. Для каждой входной последовательности a₁, …, a_k найти максимальное d, для которого при делении a_i на d будут получаться равные остатки.

Пример входа

Пример выхода

701 1059 1417 2312 0

14 23 17 32 122 0

14 -22 17 -31 -124 0

Упражнение 1.2. [Вальядолид, 10717]. Монетный завод. Канадский королевский завод производит столы, ножки которых составляют из куп монет. Каждый стол имеет четыре ножки, а каждая ножка должна состоять из разных типов монет. Например, одна ножка может состоять из четвертушек, другая – из десяток, третья – из одноцентовых, а четвертая – из двухцентовых монет. Имеется конечное количество типов монет. Количество монет каждого типа неограниченно. Известна толщина каждого типа монет. Необходимо определить максимально возможную высоту стола, не большую заданной величины и минимально возможную высоту стола, не меньшую заданной величины.

Вход. Состоит из нескольких тестов. Первая строка каждого теста содержит количество доступных номиналов монет n (4 £ n £ 50) и количество столов T (1 £ T £ 10), которое следует сделать. Следующие n строк характеризуют толщину монет. Далее идут T строк, описывающих желаемые высоты столов, которые следует сконструировать. Последний тест содержит n = T = 0 и не обрабатывается.

Выход. Для каждого теста вывести максимально возможную высоту стола, не большую желаемой и минимально возможную высоту стола, не меньшую желаемой.

Пример входа

Пример выхода

800 1200

2000 2000

2. РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА

Алгоритм Евклида можно расширить для нахождения по заданным a и b таких целых x и y, что ax + by = d, где d – наибольший общий делитель a и b.

Пусть для положительных целых чисел a и b (a > b) известны g = НСД(b, a mod b), а также числа x’ и y’, для которых

Поскольку a mod b = a – * b, то

g = x’ * b + y’ * (a – * b) = y’ * a + (x’ – y’ * ) * b = x * a + y * b,

где обозначено x = y’, y = x’ – y’ * .

Пусть gcdext(int a, int b, int *d, int *x, int *y) – функция, которая по входным числам a и b находит d = НСД(a, b) и такие x, y что d = a * x + b * y. Для поиска неизвестных x и y необходимо рекурсивно запустить функцию gcdext(b, a mod b, d, x, y) и пересчитать значения x и y по выше приведенной формуле. Рекурсия заканчивается, когда b = 0. При b = 0 НОД(a, 0) = a и a = a * 1 + 0 * 0, поэтому полагаем x = 1, y = 0.

Пример 2.1. Найдем решение уравнения 5x + 3y = 1. Вычисление НОД(5, 3) и нахождение соответствующих x, y произведем в таблице:

Из таблицы находим, что НОД(5, 3) = 5 * (-1) + 3 * 2 = 1, то есть x = -1, y = 2.

Упражнение 2.1. [Вальядолид, 10104]. Задача Евклида. Со времен Евклида известно, что для любых положительных a и b существуют такие целые x и y, что ax + by = d, где d – наибольший общий делитель a и b. По заданным a и b найти x, y, d.

Вход. Каждая строка содержит два числа a и b, разделенных пробелом (a, b £ 10 9 ).

Выход. Для каждого теста вывести три числа x, y, d, разделенных пробелом. Если существует несколько пар x и y, то вывести ту пару, для которой x £ y и выражение |x| + |y| минимально.

Пример входа

Пример выхода

-1 1 2

17 17

0 1 17

-1 2 1

Упражнение 2.2. [Вальядолид, 10673] Игра с округлением вниз и вверх.

Теорема. Для двух целых чисел x и k всегда существуют такие целые p и q, что

x = p + q

По заданным x и k необходимо найти хотя бы одну такую пару p и q.

Вход. Первая строка содержит количество тестов t (1 £ t £ 1000). Каждая следующая строка содержит два положительных целых числа x и k (x, k 8 ).

Выход. Для каждого теста вывести в отдельной строке два числа: p и q. Если таких пар существует несколько, то вывести одну из них. Значения p и q помещаются в 64-битовый целый тип.

Пример входа

Пример выхода

2444 6

3. ДИОФАНТОВЫ УРАВНЕНИЯ

Диофантовыми уравнениями называются уравнения вида

В этой главе рассмотрим алгоритм нахождения решения линейного диофантового уравнения с двумя неизвестными: a*x + b*y = c.

Теорема 3.1. Уравнение a*x + b*y = c имеет решения в целых числах тогда и только тогда, когда c делится на НОД( a , b ).

Теорема 3.2. Если пара ( x ₀, y ₀) является решением уравнения ax + by = c , то все множество его решений ( x , y ) описывается формулой :

Для нахождения хотя бы одного решения ( x ₀, y ₀) уравнения ax + by = c следует найти решение ( x ’, y ’ ) уравнения ax + by = d ( d – наибольший общий делитель чисел a и b ) при помощи расширенного алгоритма Евклида, после чего умножить полученное решение на k = c / d . То есть

Пример 3.1. Найти множество решений уравнения 5* x + 3* y = 7.

1. Уравнение имеет решения, так как d = НОД(5, 3) = 1, 7 делится на 1.

2. Находим решение уравнения 5* x ’ + 3* y ’ = 1 при помощи расширенного алгоритма Евклида (пример 1.2.1): ( x ’, y ’) = (-1, 2).

3. Находим решение ( x ₀, y ₀) исходного диофантового уравнения:

Согласно теореме 1.3.2. множество решений диофантового уравнения имеет вид:

Упражнение 3.1. [Вальядолид, 10548]. Найти правильный размен. В древние времена люди вместо денег обменивались товарами. В наличии имеются два типа товаров: A и B. Покупатель желает приобрести товар на сумму c > 0. Стоимости товаров A и B соответственно равны a и b. Если одно из значений a или b отрицательно, то продавец может этим товаром давать сдачу. Одновременно отрицательными a и b быть не могут. Сколькими способами покупатель может приобрести товар на сумму c, если это возможно?

Вход. Первая строка содержит количество тестов n (0 1 001). Каждая следующая строка содержит три числа a, b и c (0 31 ).

Выход. Для каждого теста вывести количество комбинаций, которыми покупатель может приобрести товар ровно на сумму c. Если приобрести товар невозможно, то вывести сообщение “Impossible”. Если число комбинаций бесконечно, то вывести “Infinitely many solutions”.

Пример входа

Пример выхода

2 3 15

Infinitely many solutions

2 –3 5

Impossible

10 36 7

4. ОБРАБОТКА СТРОК

В этом разделе мы не будем касаться класса string, а рассмотрим, как обрабатывались строки на языке Си до появления стандартной библиотеки шаблонов.

Строки представляются в памяти компьютера как массив элементов char. Первый символ строки доступен как нулевой элемент массива, второй символ – как первый и так далее. В конце строки всегда стоит символ ‘’ (нуль-символ). То есть строки в Си завершаются нулем. Такой подход позволяет снять ограничения с длины строк. Строка может быть такой длины, какой позволяет память для ее хранения. Символ ‘’ не видим в строковом выражении, но он добавляется как последний элемент при запоминании строки. Так, строка “ABC” содержит 4 символа, а не три.

Пример 4.1. Объявим две строки s и t. Строку t проинициализируем данными.

char s[10],t[10] = «This»;

Для вывода строк при помощи функции printf пользуются форматом “%s”:

Вывести строку можно и при помощи цикла посимвольно:

Цикл продолжается до тех пор, пока очередной выводимый символ не будет иметь ASCII код, равный 0.

Для работы со строками существует набор функций, объявленный в библиотеке . Рассмотрим некоторые из них.

функция

описание функции

size_t strlen(const char *string)

длина строки

char *strcpy(char *s1, const char *s2)

Копирует строку s2, включая символ ‘’, в область памяти, начинающейся с адреса s1 . Возвращает s1 .

char *strcat(char *s1, const char *s2)

Конкатенация строк s1 и s2 . Строка s2 дописывается в конец s1.

Пример 4.2. Объявим строку s и найдем ее длину.

printf(«Length of %s is %dn»,s,strlen(s));

Пример 4.3. Создадим строку t, состоящую из 10 копий “abc”.

Следующие функции позволяют читать и выводить строки из и на консоль.

функция

описание функции

char *gets(char *s)

чтение строки в символьный массив s

int puts(const char *s)

вывод строки на консоль

Пример 4.4. Прочитать текст и вывести его на консоль. Длина каждой строки не более 100.

УКАЗАНИЯ К РЕШЕНИЮ УПРАЖНЕНИЙ

Упражнение 1.1. [Вальядолид, 10407]. Простое деление. Из условия задачи следует, что

int gcd(int a, int b)

return (!b) ? a : gcd(b, a % b);

res = abs(a-b); a = b;

Упражнение 1.2. [Вальядолид, 10717]. Монетный завод. Если a, b, c, d – толщины четырех типов монет, то минимально возможная высота стола, который можно сделать, равна h = НОК(a, b, c, d). Обозначим через low максимально возможную высоту стола, не большую желаемой величины Height. Тогда low должно делиться на h и быть максимально возможным значением, не большим Height. Отсюда

low = * h

Если вычисленное low равно Height (что возможно в случае когда Height делится на h без остатка), то минимально возможная высота стола more, не меньшая Height, также равна Height. Иначе она равна low + h.

Остается перебрать все возможные четверки толщин номиналов монет и вычислить максимум среди всевозможных low и минимум среди всевозможных more.

Пример. Рассмотрим набор монет из первого теста, желаемая высота стола равна 1000. Имея 4 монеты с толщинами 50, 100, 200, 400 можно конструировать столы, высоты которых кратны НОК(50, 100, 200, 400) = 400. Искомые высоты столов, которые можно сделать, соответственно равны 800 и 1200.

Реализация. Входные тесты подобраны так, что при решении задачи следует работать с типом unsigned (32 — битовое целое, положительное). Объявим все переменные типа unsigned.

unsigned gcd(unsigned a,unsigned b)

return !a ? b : gcd(b%a,a);

Для каждой прочитанной желаемой высоты стола Height проводим выше описанный алгоритм. Обозначим через Less максимум среди всевозможных low, а через Greater – минимум среди всевозможных more. Проинициализируем их.

Перебираем все возможные четверки номиналов монет x1

Вычисляем НОК толщин монет g = НОК (coins[x1], coins[x2], coins[x3], coins[x4]).

g = coins[x1] * coins[x2] / gcd(coins[x1],coins[x2]);

g = g * coins[x3] / gcd(g,coins[x3]);

g = g * coins[x4] / gcd(g,coins[x4]);

Для каждой четверки номиналов пересчитываем значения Less и Greater.

low = Height / g * g;

if (low > Less) Less = low;

if (low != Height) low += g;

Упражнение 2.1. [Вальядолид, 10104]. Задача Евклида. Описание алгоритма приведено в разделе 2.

Реализация. Для решения задачи достаточно прочитать входные данные, вызвать функцию gcdext и напечатать результат.

void gcdext(int a,int b, int *d, int *x, int *y)

while(scanf(«%d %d»,&a,&b) == 2)

Упражнение 2.2. [Вальядолид, 10673]. Игра с округлением вниз и вверх. Если x нацело делится на k, то = = x / k. Выбрав p = 0, q = k, получим: 0 * (x / k) + k * (x / k) = x. Пусть x не делится на k. Если n = , то m = = n + 1. Поскольку НОД(n , m) = НОД(n , n + 1) = 1, то исходя из расширенного алгоритма Евклида, существуют такие целые t и u, что 1 = tn + um. Помножив равенство на x, получим x = xtn + xum, откуда p = xt, q = xu.

Пример. Для первого теста имеет место соотношение: 5 = 1 * + 1 * = 12 + 13.

Реализация. При вычислении используем 64-битовый целый тип long long. Функция gcdext выглядет так же, как и в задаче Вальядолид, 10548.

typedef long long i64;

void gcdext(i64 a,i64 b, i64 *d, i64 *x, i64 *y)

Если k = 0, то устанавливаем p = 0, q = k.

Иначе вычисляем n = и m = , запуская расширенный алгоритм Евклида. Он находит такие t и u, что 1 = tn + um. Далее находим p = xt, q = xu и выводим результат.

n = (int)floor(1.0*x/k); m = (int)ceil(1.0*x/k);

Упражнение 3.1. [Вальядолид, 10548]. Найти правильный размен. Если покупатель получит x штук товара A и y штук товара B, заплатив при этом сумму c, то получим уравнение ax + by = c. Уравнение имеет решения тогда и только тогда, когда c делится на НОД(a, b).

Если одно из значений a или b отрицательно, то уравнение ax + by = c имеет бесконечно много решений. Действительно, если (x₀, y₀) – решение, то пара (x₀ + kb, y₀ – ka) будет также решением для любого целого отрицательного k, для которого y₀ – ka ³ 0 (если b ³ 0 (если a ³ 0, y₀ – ka ³ 0. Откуда имеем следующие ограничения: k ³ , k £ . Количество решений уравнения ax + by = c, для которых x ³ 0, y ³ 0, равно – + 1.

Пример. Рассмотрим первый тест, где следует найти количество решений уравнения 2x + 3y = 15 в целых числах. Числа 2 и 3 взаимно простые, находим x’и y’, для которых 2x’ + 3y’ = 1. Из расширенного алгоритма Евклида имеем: x’ = -1, y’ = 1. Помножив их на 17, получим x₀ = 17x’ = -17, y₀ = 17y’ = 17. Имея одно решение (x₀, y₀) = (-17, 17), можно описать множество всех решений исходного уравнения согласно выше приведенной лемме: x = -17 + 3k, y = 17 – 2k. Оба значения должны быть неотрицательными, следовательно -17 + 3k ³ 0, y = 17 – 2k ³ 0. Или то же самое что 3k ³ 17, 17 ³ 2k. Откуда k ³ = 6, k £ = 8. Объединяя ограничения на k, получим: 6 £ k £ 8. То есть существует 3 варианта размена.

Для второго теста имеем уравнение 2x – 3y = 5. Одним из его решений будет x₀ = 1, y₀ = -1. Все множество решений описывается формулой: x = 1 – 3k, y = -1 – 2k. Для всех отрицательных k значения x и y будут положительными, и удовлетворять условию задачи.

Для третьего теста решений не существует, так как для любых натуральных x и y значение 10x + 36y всегда четно и не может равняться 7.

Реализация. При вычислении используем 64-битовый целый тип long long. Для простоты использования переопределим тип long long на i64.

источники:

http://gigabaza.ru/doc/68496-p3.html

http://inf5.ru/cpp_lections/lection_7.htm

Источник

Обновлено: 16.04.2023

Цель. Ознакомиться с аппаратом программирования на языке Visual Basic for Applications, примерами программ для решения простых задач. Разработать и написать в среде Excel программу выработки пар «открытый/закрытый» ключ по методу RSA. Выполнить шифрование конфиденциальных данных.

Программно-аппаратные средства. Компьютерная лаборатория, пакет Microsoft Office.

Задание на лабораторную работу

1. Изучить теоретический материал по данной лабораторной работе.

2. Ознакомиться с указаниями по программированию в на языке VBA в среде Excel.

3. Разработать программный комплекс в среде Excel генерации параметров метода RSA, шифрования/расшифровки данных.

4. Выполнить пробное шифрование/расшифровку данных, передаваемых по сети в рамках компьютерного класса. Вставить в отчет полученные данные, описать методику выполнения задания.

5. Ответить на контрольные вопросы в конце задания.

Указания к выполнению лабораторной работе.

Лабораторная работа 1 состоит из четырех частей, каждая из которых выполняется в одном и том же рабочем листе Excel.

¨ В первой части следует составить программу на языке Visual Basic для реализации расширенного алгоритма Евклида.

¨ Во второй части надо выполнить генерацию параметров метода RSA. Простые числа, необходимые для RSA, надо выбрать случайным образом, генерируя число из диапазона согласно номеру варианта. Проверить выбранные числа на простоту, используя алгоритм, указанный в вариантах работ.

¨ В третьей части надо реализовать шифрованию/расшифровку текстов, вводимых с клавиатуры.

¨ В заключительной части необходимо реализовать взлом метода RSA, считая известным открытый ключ RSA. Для разложения числа на множители использовать метод Полларда.

простоты чисел

Метод пробных делений

Односторонняя (однонаправленная) функция (one way function) — это функция f , осуществляющая отображение X ->Y , где X и Y — произвольные множества, и удовлетворяющая следующим условиям:

1. Для каждого x из области определения функции легко вычислить . Понятие «легко» обычно означает, что существует алгоритм, вычисляющий функцию f(x) за полиномиальное время от длины аргумента x.

2. Задача нахождения прообраза для произвольного y, принадлежащего области значений функции, является вычислительно сложной задачей. Последнее означает, что не существует алгоритма, вычисляющего существенно быстрее, чем алгоритм полного перебора.

Задача разложения натурального числа N на простые множители (факторизация N) явлется задачей вычисления односторонней функции: зная сомножители p и q, нетрудно вычислить их произведение N=p • q, но обратная задача нахождения делителей p и q по известному N является сложной задачей, решение которой требует значительных вычислительных ресурсов.

На вычислительной сложности решения этой задачи построен один из самых известных асимметричных методов криптографии – метод RSA. В 1977 году, когда создатели этого метода Ривест, Шамир и Адлеман объявили о новом методе криптографии, основанном на задаче факторизации, наиболее длинные числа, разложимые на множители, имели длину 40 десятичных цифр, что соответствует, примерно, 132-битовому двоичному числу (число 40 надо домножить на ). Создатели RSA предложили широкой публике расшифровать некую фразу английского языка. Для этого предварительно требовалось факторизовать 129-значное десятичное число N (длины 428 в битовом представлении), про которое было известно, что оно представимо в виде произведения двух простых сомножителей p и q, которые имели длину 65 и 64 десятичных знака.

С тех пор был достигнут значительный прогресс в этой области. Число, предложенное создателями RSA, было разложено в 1994 году с помощью нового мощного метода факторизации – метода квадратичного решета (Quadratic Sieve Factoring), разработанного Карлом Померанцем и реализованного Аткинсом, Граффом, Ленстрой и Лейлендом. В работе участвовало около 600 добровольцев, задействовано в сети около 1700 компьютеров, которые работали в течение 7 месяцев.

Параллельно с этим методом Джоном Поллардом, известным специалистом по криптографии и теории алгоритмов, был разработан еще более быстрый метод, получивший название метода решета числового поля (Generalizad Number Field Sieve — GNFS), который является наиболее быстрым методом и на сегодняшний день. Текущий рекорд, установленный немецкими исследователями, на июнь 2008 года, составляет 1000-бит. Это делает небезопасными ключи RSA длины 1024, которые являются на сегодняшний день, самыми распространенными.

Генерация пар «открытый/закрытый ключ» метода RSA.

1. Выбираются два простых числа p и q. Для нашего примера числа p и q должны находится в интервале от 100 до 200. В этом случае их произведение N=p • q будет иметь длину 10 – 12 бит. В реальных задача длина N выбирается равной 512, 768 или 1024 бита (иногда 2048 для самых ответственных задач).

2. Вычисляем их произведение N=p • q.

3. Вычисляем функцию Эйлера . Значение равно числу натуральных чисел, меньших N, взаимно простых с (т.е. числу всех k < N таких, что наибольший общий делитель НОД(N; k)=1).

4. Выбираем параметр e, входящий в открытый ключ RSA, равным произвольному числу, меньшему N, но взаимно простому с . При реальном шифровании длина e выбирается приблизительно равной L/3, где L – длина N. Можно взять e равным произвольному простому числу, меньшему N и отличному от p и q, проверив при этом условие того, что не делится на е ().

5. Находим параметр d, являющийся секретным параметром метода RSA, из условия . Для вычисления d необходимо воспользоваться расширенным алгоритмом Евклида , который описан ниже. Расширенный алгоритм Евклида по входным натуральным числам A и B находит их наибольший общий делитель C=НОД(А,В), а также числа x и y такие, что выполнено равенство . Для нахождения параметра d подставим в расширенный алгоритм Евклида входные числа и е. Их наибольший общий делитель C=НОД(,е) равен 1. Если это не так, то параметр е выбран неверно. Выполнив вычисления по алгоритму Евклиду мы найдем числа x и y такие, что . Применив операцию к обеим частям последнего равенства, получим . Значит, можно взять значение параметра d равным коэффициенту y из метода Евклида. Однако, коэффициент y может принимать как положительные, так и отрицательные значения, а параметр d обязательно должен положительным, поэтому в случае если y < 0, следует взять

Генерация параметров RSA завершена. Пара (N, e) объявляется открытым ключом, а параметры и d закрытыми параметрами (d – закрытый ключ).

Текст, который следует зашифровать, разбивается на отдельные символы (или на блоки по k бит в реальных задачах, где , L – длина N в битовом представлении). Для шифрования числа с , служащего кодом символа, выполняется операция возведения в степень по формуле

где числа N, e взяты из открытого ключа RSA.

Обратная расшифровка выполняется возведение шифра r в степень d, где d – секретный параметр RSA.

Гарантией того, что при повторном возведении в степень, будет получено исходное число, служит теорема Эйлера, которая утверждает, что для любого выполняется формула . Проверим операцию (**):

Расширенный алгоритм Евклида.

Алгоритм Евклида используются для нахождения по заданным целым числам A и B их наибольшего общего делителя С=НОД(А; B). Расширенный алгоритм Евклида используется также для нахождения целых чисел x, y таких, что выполняется условие . Используется во многих криптографических конструкциях, в том числе в методе RSA.

Основным равенством, используемым для вычисления НОД чисел А и В, является условие

НОД(А, В) = НОД( В, A mod B) (3)

где A mod B – остаток от целочисленного деления А на В. Применяя последовательно формулу (3), мы будем уменьшать числа А и В в этом алгоритме, пока A mod B не станет равным 0, тогда последнее значение аргумента В даст искомый НОД (А, В). Полное описание расширенного алгоритма мы объясним на примере. Пусть числа А и В равны 172 и 38 соответственно. Откроем рабочий лист Excel и разметим в первых строчках заголовки столбцов, а под заголовками А и В поместим числа 172 и 38, как указано на рисунке.

Рис.1. Примерный вид рабочего листа Excel для реализации расширенного алгоритма Евклида.

В столбце Amod B напишем формулу вычисления остатка от целочисленного деления А на В: =ОСТАТ(A3;B3), а в столбце A div B впишем формулу =ЦЕЛОЕ(A3/B3), обозначающую операцию нахождения целой части от деления A на В.

В следующей строке в столбах А и В поместим значения 38 и 20, взятые из двух ячеек, находящихся выше и правее (применение формулы (3)). Значения ячеек под заголовками Amod B и A div B надо вычислить как в предыдущей строке. В Excel для этого достаточно просто скопировать и вставить вышележащие клетки на строку ниже.

Повторяем эти операция несколько раз, пока не получим в столбце Amod B значение 0. Значение В в этой строке будет равно НОД(А,В) (в нашем примере он равен 2).

Далее заполняем столбцы x и y в обратном порядке снизу вверх. Поместим в столбцы x и y в последней полученной строке значения 0 и 1. Далее в каждой следующей (вышележащей) строке i поместим значения x_i и y_i , вычисленные по формулам:

где обозначает значение из столбца A div B, взятое из той же строки, где вычисляются значения x и y. Используя эти формулы, заполним столбцы x и y. В верхней строке получим значения x и y, которые нам нужны.

Алгоритм возведения в степень по модулю натурального числа.

Для выполнения шифрования по методу RSA приходится выполнять возведение в большую степень различных чисел, а результат приводить по модулю числа N, являющегося параметром метода и имеющего длину 512 и более бит. Уже для небольших a и e вычислить значение

выполняя сначала возведение в степень, а потом вычисляя остаток от деления на N, становится невозможным. Между тем, если применить алгоритм, описанный в этом разделе, можно вычислять выражения (1), для достаточно больших чисел a, e, N, оставаясь в рамках обычных операций с целыми числами, заложенных в компьютере.

Алгоритм быстрого возведения в степень основывается на идее замены прямого вычисления возведения в степень последовательными операциями умножения на a и возведения в квадрат. Для этого представим степень e число в двоичном исчислении

где любое t_i для принадлежит , . Зная вектор разрядов , можно вычислить число e , применяя последовательные вычисления:

Например, если e = 13, то в двоичном представлении e = 1101₂ , и 13 можно представить как результат вычисления , .

Последнее число и есть e .

Используя формулы (3), можно процедуру возведения в степень по модулю натурального числа N, записать в виде последовательности итераций:

где . Множитель в зависимости от принимает либо значение a, если , либо 1, если . Результат вычислений можно свести в таблицу

Алгоритм Евклида для многочленов. Алгоритм Евклида позволяет найти наибольший общий делитель двух многочленов, т.е. многочлен наибольшей степени, на который делятся без остатка оба данных многочлена.
Алгоритм основан на том факте, что для любых двух многочленов от одного переменного, f(x) и g(x), существуют такие многочлены q(x) и , называемые соответственно частное и остаток, что

при этом степень остатка меньше степени делителя, многочлена g(x), и, кроме того, по данным многочленам f(x) и g(x) частное и остаток находятся однозначно. Если в равенстве (*) остаток r(x) равен нулевому многочлену (нулю), то говорят, что многочлен f(x) делится на g(x) без остатка.
Алгоритм состоит из последовательного деления с остатком сначала первого данного многочлена, f(x), на второй, g(x):

затем, если r₃(x) ≠ 0, – второго остатка на третий:

и т.д. Поскольку на каждом этапе степень очередного остатка уменьшается, процесс не может продолжаться бесконечно, так что на некотором этапе мы обязательно придем к ситуации, когда очередной, n + 1-й остаток r_{n + 1} равен нулю:

r_n–2(x) = r_n–1(x)∙ q_n(x) + r_n(x),	(n)
r_n–1(x) = r_n(x)∙ q_n+1(x) + r_n+1(x),	(n+1)
r_n+1(x) = 0.	(n+2)

Тогда последний не равный нулю остаток r_n и будет наибольшим общим делителем исходной пары многочленов f(x) и g(x).
Действительно, если в силу равенства (n + 2) подставить 0 вместо в равенство (n + 1), затем – полученное равенство r_{n – 1}(x) = вместо r_{n – 1}(x) – в равенство (n), получится, что r_{n – 2}(x) = r_n(x)∙q_{n + 1}(x) q_n(x) + r_n(x), т.е. r_{n – 2}(x) = r_n(x)( q_{n + 1}(x) q_n(x) + 1), и т.д. В равенстве (2) после подстановки получим, что g(x) = r_n(x)∙Q(x), и, наконец, из равенства (1) – что f(x) = r_n(x)∙S(x), где Q и S – некоторые многочлены. Таким образом, r_n(x) – общий делитель двух исходных многочленов, а то, что он наибольший (т.е. наибольшей возможной степени), следует из процедуры алгоритма.
Если наибольший общий делитель двух многочленов не содержит переменную (т.е. является числом), исходные многочлены f(x) и g(x) называются взаимно-простыми.

Основным равенством, используемым для вычисления НОД чисел А и В, является условие

НОД(А, В) = НОД( В, A mod B) (3)

где A mod B – остаток от целочисленного деления А на В. Применяя последовательно формулу (3), мы будем уменьшать числа А и В в этом алгоритме, пока A mod B не станет равным 0, тогда последнее значение аргумента В даст искомый НОД (А, В). Полное описание расширенного алгоритма мы объясним на примере. Пусть числа А и В равны 172 и 38 соответственно. Откроем рабочий лист Excel и разметим в первых строчках заголовки столбцов, а под заголовками А и В поместим числа 172 и 38, как указано на рисунке.

Рис.1. Примерный вид рабочего листа Excel для реализации расширенного алгоритма Евклида.

В столбце Amod B напишем формулу вычисления остатка от целочисленного деления А на В: =ОСТАТ(A3;B3), а в столбце A div B впишем формулу =ЦЕЛОЕ(A3/B3), обозначающую операцию нахождения целой части от деления A на В.

В следующей строке в столбах А и В поместим значения 38 и 20, взятые из двух ячеек, находящихся выше и правее (применение формулы (3)). Значения ячеек под заголовками Amod B и A div B надо вычислить как в предыдущей строке. В Excel для этого достаточно просто скопировать и вставить вышележащие клетки на строку ниже.

Повторяем эти операция несколько раз, пока не получим в столбце Amod B значение 0. Значение В в этой строке будет равно НОД(А,В) (в нашем примере он равен 2).

Далее заполняем столбцы x и y в обратном порядке снизу вверх. Поместим в столбцы x и y в последней полученной строке значения 0 и 1. Далее в каждой следующей (вышележащей) строке i поместим значения x_i и y_i, вычисленные по формулам:

Алгоритм возведения в степень по модулю натурального числа.

Для выполнения шифрования по методу RSA приходится выполнять возведение в большую степень различных чисел, а результат приводить по модулю числа N, являющегося параметром метода и имеющего длину 512 и более бит. Уже для небольших a и e вычислить значение

где любое t_i для принадлежит , . Зная вектор разрядов , можно вычислить число e, применяя последовательные вычисления:

Например, если e = 13, то в двоичном представлении e = 1101₂ , и 13 можно представить как результат вычисления , .

Последнее число и есть e.

Используя формулы (3), можно процедуру возведения в степень по модулю натурального числа N, записать в виде последовательности итераций:

Рассмотренный выше метод отыскания двух чисел основывается на использовании представления этих чисел в виде произведения простых множителей. Однако на практике такой метод мало применим, так как разложение числа, как правило, неизвестно, и его отыскание (как будет показано в дальнейшем) является сложной математической задачей.

Другим, наиболее известным способом отыскания наибольшего общего делителя двух чисел является алгоритм, впервые изложенный в трудах древнегреческого математика Евклида (IV-III вв. до н.э.

Алгоритм Евклида заключается в следующем.

Пусть , гдеи мы хотим найти. Разделимнас остатком,. Если, то разделимна:,и т.д. Получим последовательность равенств с убывающими остатками:

где

Если — последний ненулевой остаток, то. , в этом случае.

Пример 5. Найти .

Таким образом.

Для практического использования приведенного алгоритма важнейшим является вопрос о времени его выполнения.

Теорема 1. При алгоритм Евклида позволяет вычислитьза время порядка.

Схема доказательства. Для доказательства данной теоремы достаточно показать, что за каждые два шага алгоритма остаток уменьшается, по крайней мере, вдвое [9]. Таким образом результат работы алгоритма достигается не позднее чем через делений чисел разрядностью, не превосходящихкаждое.

Теорема 2. Наибольший общий делитель двух чисели, где, можно представить в виде линейной комбинации этих чиселс целыми коэффициентами, за время порядка.

Схема доказательства. Для доказательства теоремы достаточно показать [8,9], что представление числа может быть найдено путем последовательного выражениячерез все более ранние остатки в алгоритме Евклида, на что будет затрачено одно умножение и одно сложение или вычитание. Поскольку количество операций реализующих сложение есть величина более низкого порядка, то получаем искомую оценку времени.

Определение 9. Два целых числа иназываются взаимно простыми, если, т.е. если они не имеют общих делителей больших 1.

Определение 10. Для любого целого положительного числа функция Эйлераопределяется как число неотрицательных целых, меньшихи взаимно простых с:

Из определения следуют следующие свойства функции Эйлера:

1. .

2. Для любого простого

Несложно показать 3, что для любого простого и некоторого

1.1.3 Расширенный метод Евклида

Рассмотрим теперь расширенный алгоритм Евклида, позволяющий наряду с наибольшим общим делителем чисел инаходить натуральные числаи, удовлетворяющие равенству. От обычного алгоритма Евклида он отличается тем, что наряду с последовательностью остатковвычисляются ещё две вспомогательные последовательностии. Расширенный алгоритм Евклида заключается в следующем. Пусть,нам необходимо найти натуральные числа и, удовлетворяющие равенству. На первом шаге положим, что.Далее будем выполнять следующую последовательность действий, до тех пор пока :

Значения и, при которых, и будут искомыми в силу следующего утверждения:

Лемма. При всех , выполнимо равенство

Доказательство. Применим индукцию по . Приравенство очевидно. Если равенства доказаны для всех значений индексов меньших, то для, пользуясь индуктивным предположением, получим

Легко видеть, что сложность данного алгоритма отличается от сложности обычного алгоритма Евклида не более, чем на константный сомножитель, и составляет , гдедлина записи чисели.

Расширенный метод Евклида может применяться для нахождения корней частного случая диофантовых уравнений .

В криптографии расширенный метод очень часто применяется для нахождения обратного значения по модулю, подробнее будет рассмотрено в разделе 2.

Упражнения для самоконтроля

Определить, сколько делителей имеет заданное число 945.

Найти степени чисел 2, 3, 4, 5 точно делящие число 23455.

Найти значение двумя способами: через разложение на простые множители и используя алгоритм Евклида.

При помощи алгоритма Евклида найти наибольший общий делитель и представить его в виде линейной комбинации с целыми коэффициентами.

Найти ииз уравнения.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Читайте также:

Easy mode что это за программа на андроид

Как сделать календарно тематическое планирование в excel

Создание скоринговой модели в ms excel

Программы для управления для андроид

Как сделать перегруз на голос в fl studio

Источник