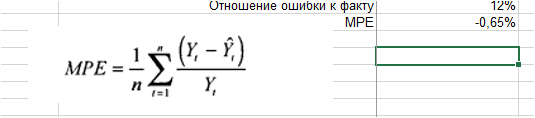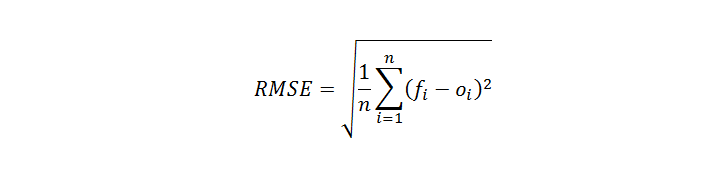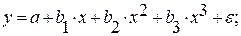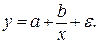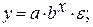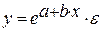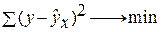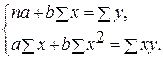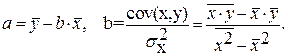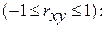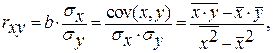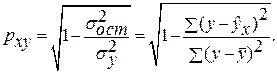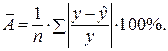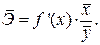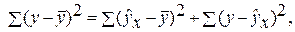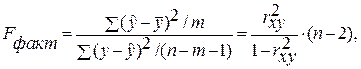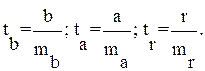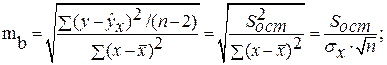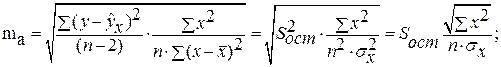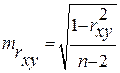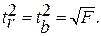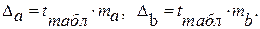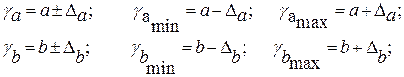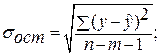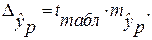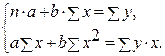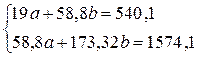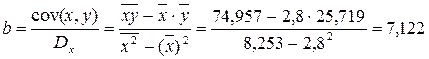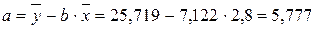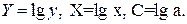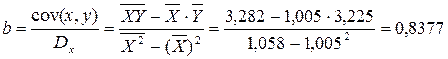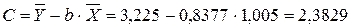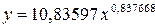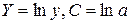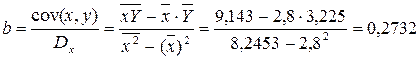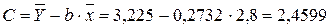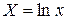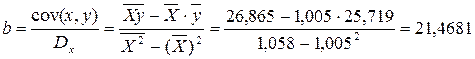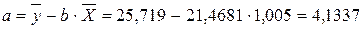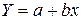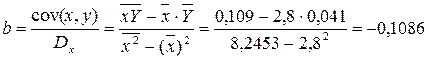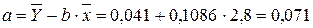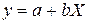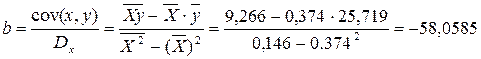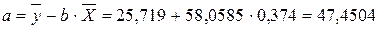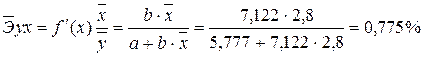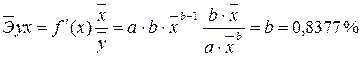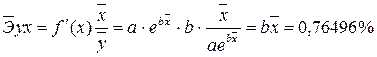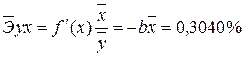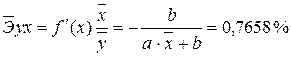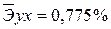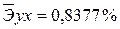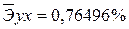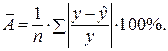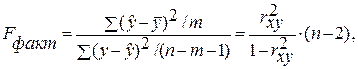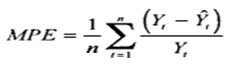
- Для чего нужна средняя процентная ошибка;
- Как она рассчитывается.
+ сможете скачать пример расчета в Excel.
MPE (mean percentage error) — средняя процентная ошибка прогноза.
MPE – средняя процентная ошибка прогноза используется в случаях, когда надо определить модель прогноза дает последовательно завышенные прогнозы или последовательно заниженные прогнозы.
Если значение больше нуля, то прогнозы последовательно занижены, т.е. в среднем меньше факта.
Если ошибка меньше нуля, то прогнозы последовательно завышены, т.е. модель делает прогноз в среднем выше факта.
Как рассчитать среднюю процентную ошибку?
- Рассчитываем ошибку для каждого значения модели;
- Делим на фактические данные ошибку в каждый момент времени.
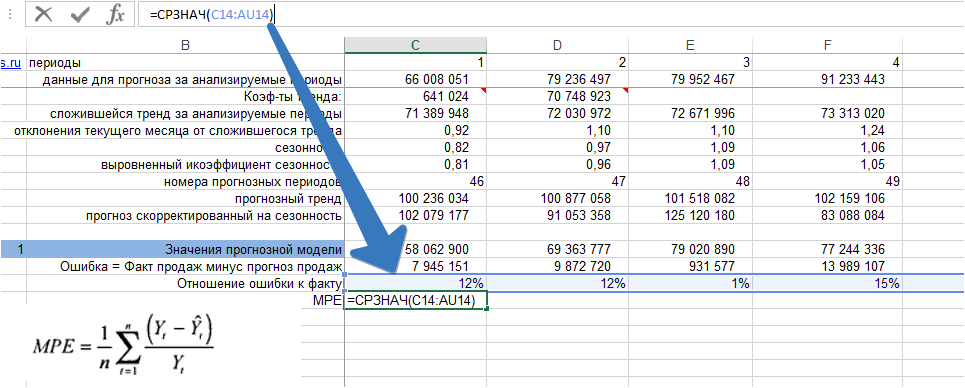
Рассчитываем среднее по пункту 2, и получает среднюю процентную ошибку — MPE:
Рассчитаем на примере прогноза объема продаж:
Скачайте файл с примером расчета ошибки MPE в Excel.
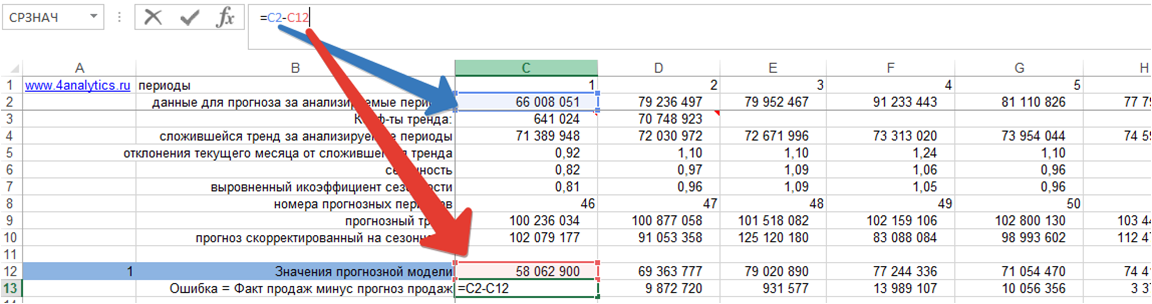
1. Ошибка = фактические продаж минус значения прогнозной модели для каждого момента времени:
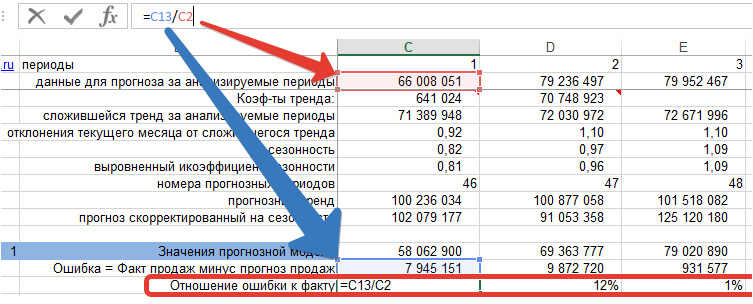
2. Делим ошибку на фактические продажи для каждого периода времени:
3. Рассчитываем среднее значение % ошибки — MPE:
Мы видим, что средняя процентная ошибка у нас получилась -0,65% — это говорит о том, что модель прогноза в среднем дает завышенные прогноза на 0,65%:
Скачайте файл с примером расчета ошибки MPE в Excel.
Из данной статьи вы узнали, для чего использовать среднюю процентную ошибку прогноза — MPE и как ее рассчитать в Excel.
Если у вас остались вопросы, пожалуйста, задавайте в комментариях, буду рад помочь!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
17 авг. 2022 г.
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является MAPE , что означает среднюю абсолютную ошибку в процентах .
Формула для расчета MAPE выглядит следующим образом:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать и легко объяснить. Например, значение MAPE, равное 11,5%, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 11,5%.
Чем ниже значение MAPE, тем лучше модель способна прогнозировать значения. Например, модель с MAPE 2% более точна, чем модель с MAPE 10%.
Как рассчитать MAPE в Excel
Чтобы рассчитать MAPE в Excel, мы можем выполнить следующие шаги:
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
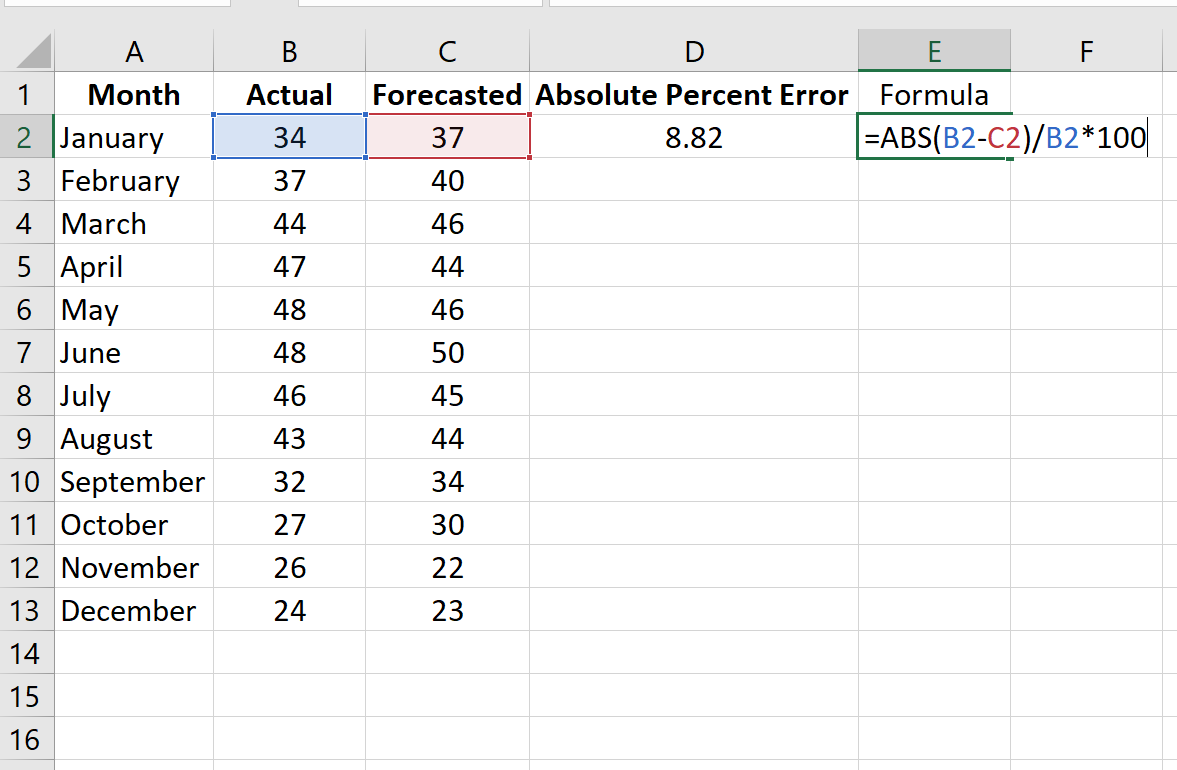
Шаг 2: Рассчитайте абсолютную процентную ошибку для каждой строки.
Напомним, что абсолютная процентная ошибка рассчитывается как: |фактический-прогноз| / |фактическое| * 100. Мы будем использовать эту формулу для расчета абсолютной процентной ошибки для каждой строки.
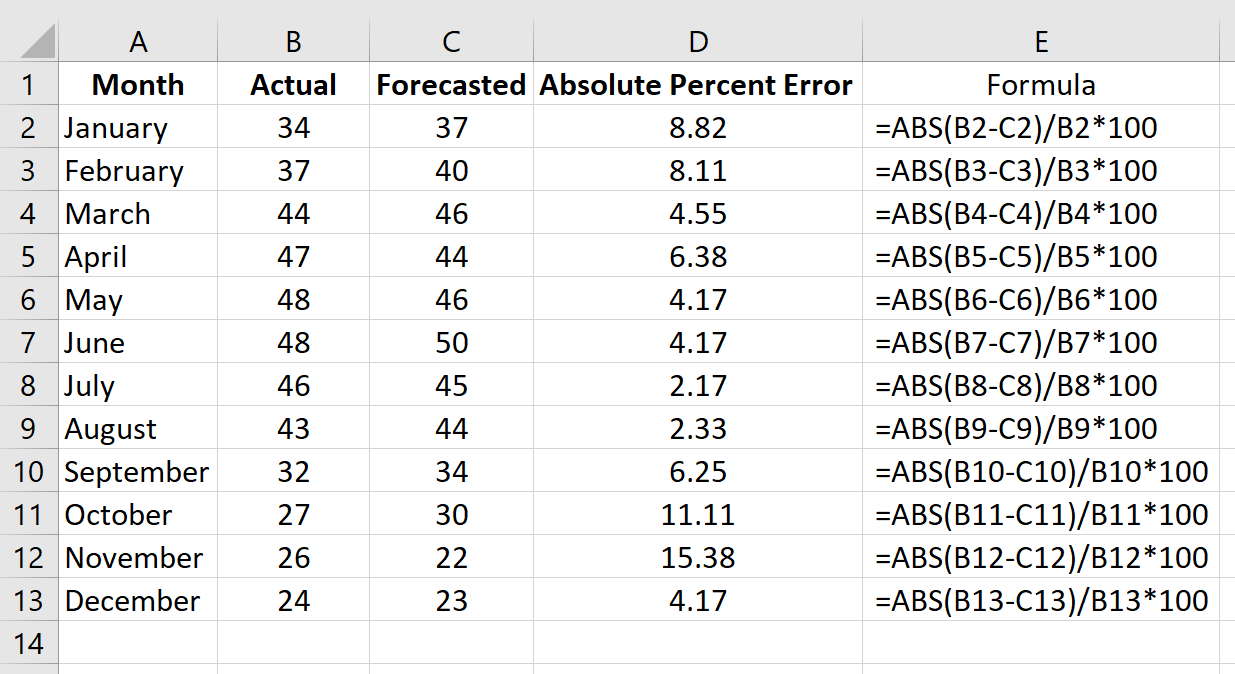
Столбец D отображает абсолютную процентную ошибку, а столбец E показывает формулу, которую мы использовали:
Повторим эту формулу для каждой строки:
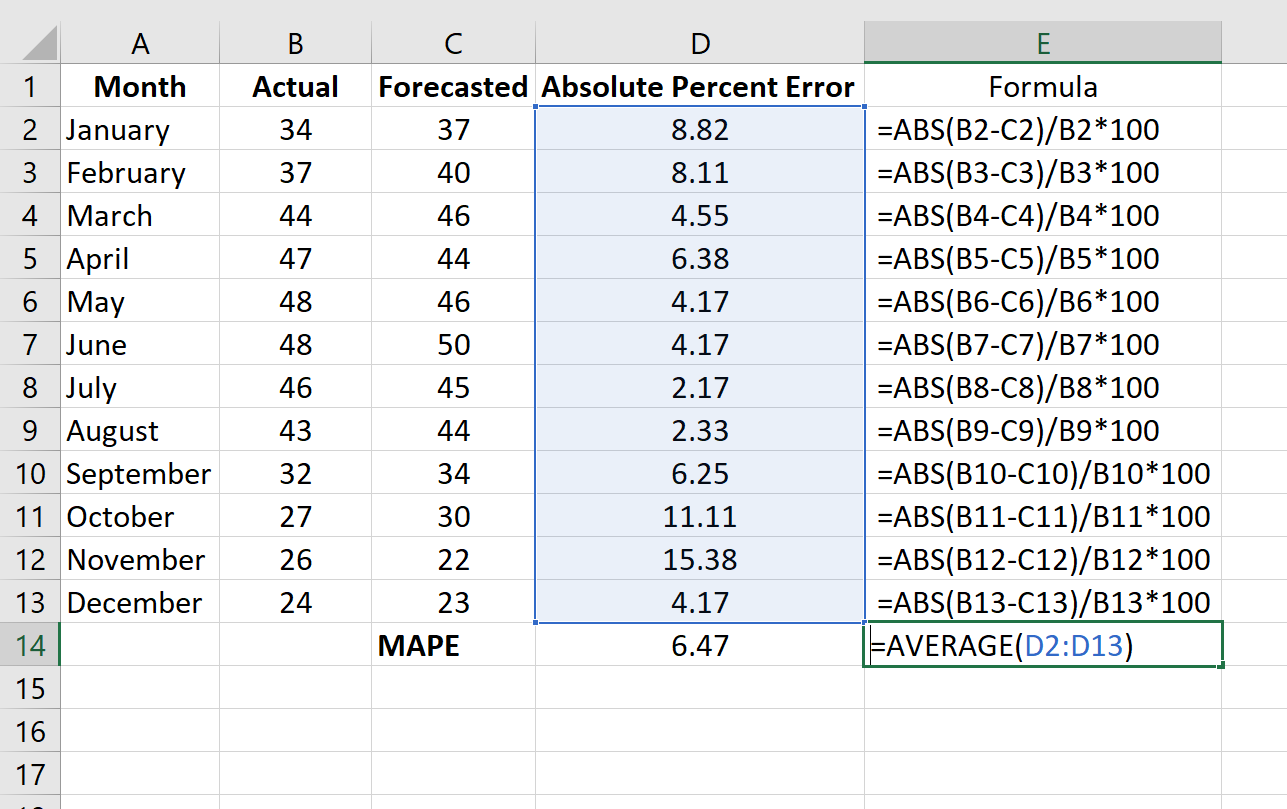
Шаг 3: Рассчитайте среднюю абсолютную ошибку в процентах.
Рассчитайте MAPE, просто найдя среднее значение в столбце D:
MAPE этой модели оказывается равным 6,47% .
Примечание по использованию MAPE
Хотя MAPE легко вычислить и легко интерпретировать, его использование имеет несколько потенциальных недостатков:
1. Поскольку формула для расчета абсолютной процентной ошибки |фактический-прогноз| / |фактическое| это означает, что он будет неопределенным, если какое-либо из фактических значений равно нулю.
2. MAPE не следует использовать с данными небольшого объема. Например, если фактический спрос на какой-либо товар равен 2, а прогноз равен 1, значение абсолютной процентной ошибки будет |2-1| / |2| = 50%, что создает впечатление, что ошибка прогноза довольно высока, несмотря на то, что прогноз отличается всего на одну единицу.
Другим распространенным способом измерения точности прогнозирования модели является MAD — среднее абсолютное отклонение. О том, как посчитать MAD в Excel, читайте здесь .
Дополнительные ресурсы
Что считается хорошей ценностью для MAPE?
Как рассчитать SMAPE в Excel
Как рассчитать MAE в Excel
Вариант 1
Задание 1. Модель парной линейной регрессии.
Имеются данные о размере среднемесячных доходов в разных группах семей
|
Номер группы |
Среднедушевой денежный доход в месяц, руб., X |
Доля оплаты труда в структуре доходов семьи, %, Y |
|
1 |
79,8 |
64,2 |
|
2 |
152,1 |
66,1 |
|
3 |
199,3 |
69,0 |
|
4 |
240,8 |
70,6 |
|
5 |
282,4 |
72,4 |
|
6 |
301,8 |
74,3 |
|
7 |
385,3 |
76,0 |
|
8 |
457,8 |
77,1 |
|
9 |
577,4 |
78,4 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы
2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.
4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.
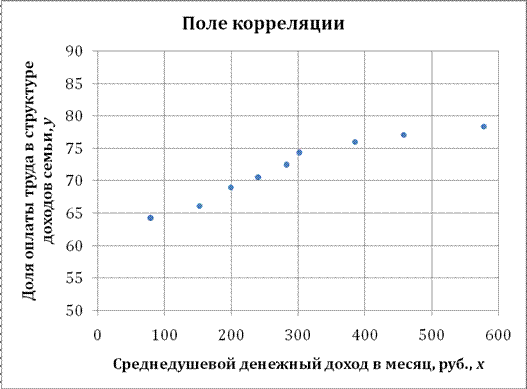
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .
Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
X×Y |
X2 |
Y2 |
|
1 |
79,8 |
64,2 |
5123,16 |
6368,04 |
4121,64 |
|
2 |
152,1 |
66,1 |
10053,81 |
23134,41 |
4369,21 |
|
3 |
199,3 |
69,0 |
13751,70 |
39720,49 |
4761,00 |
|
4 |
240,8 |
70,6 |
17000,48 |
57984,64 |
4984,36 |
|
5 |
282,4 |
72,4 |
20445,76 |
79749,76 |
5241,76 |
|
6 |
301,8 |
74,3 |
22423,74 |
91083,24 |
5520,49 |
|
7 |
385,3 |
76,0 |
29282,80 |
148456,09 |
5776,00 |
|
8 |
457,8 |
77,1 |
35296,38 |
209580,84 |
5944,41 |
|
9 |
577,4 |
78,4 |
45268,16 |
333390,76 |
6146,56 |
|
S |
2676,7 |
648,1 |
198645,99 |
989468,27 |
46865,43 |
|
Среднее |
297,41 |
72,01 |
22071,78 |
109940,92 |
5207,27 |
Вычислим коэффициент корреляции. Используем следующую формулу:
= 0,9568.
Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.
Среднюю ошибку коэффициента корреляции определим по формуле:
= 0,032.
Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.
TТабл(0,05; 7) = 2,36.
Запишем доверительный интервал для коэффициента корреляции.
Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.
Вычислим параметры уравнения регрессии.
= 0,03.
= 72,01 – 0,03×297,41 = 63,09.
Получим следующее уравнение: .
Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.
Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:
Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
|
|
|
|
1 |
79,8 |
64,2 |
65,48 |
1,6384 |
47354,1 |
|
2 |
152,1 |
66,1 |
67,65 |
2,4025 |
21115,0 |
|
3 |
199,3 |
69,0 |
69,07 |
0,0049 |
9625,6 |
|
4 |
240,8 |
70,6 |
70,31 |
0,0841 |
3204,7 |
|
5 |
282,4 |
72,4 |
71,56 |
0,7056 |
225,3 |
|
6 |
301,8 |
74,3 |
72,14 |
4,6656 |
19,3 |
|
7 |
385,3 |
76,0 |
74,65 |
1,8225 |
7724,7 |
|
8 |
457,8 |
77,1 |
76,82 |
0,0784 |
25725,0 |
|
9 |
577,4 |
78,4 |
80,41 |
4,0401 |
78394,4 |
|
S |
2676,7 |
648,1 |
648,09 |
15,4421 |
193388,1 |
Вычислим стандартные ошибки коэффициентов уравнения.


Вычислим T-статистики.
Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и
, т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.
Сделаем рисунок.
Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.
Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.
Fтабл(0,05; 1; 7) = 5,59.
Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.
Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.
XP = 297,41 × 1,11 = 330,1.
Вычислим прогнозное значение Yp с помощью уравнения регрессии.
» 73%.
Доверительный интервал прогноза имеет вид
(УP – Tкр×My, УP + Tкр×My),
Где 

Запишем доверительный интервал прогноза:
Þ
Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.
Задание 2. Модель парной нелинейной регрессии.
По территориям Центрального района известны данные за 1995 г.
|
Район |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
|
Брянская обл. |
178 |
240 |
|
Владимирская обл. |
202 |
226 |
|
Ивановская обл. |
197 |
221 |
|
Калужская обл. |
201 |
226 |
|
Костромская обл. |
189 |
220 |
|
Орловская обл. |
166 |
232 |
|
Рязанская обл. |
199 |
215 |
|
Смоленская обл. |
180 |
220 |
|
Тверская обл. |
181 |
222 |
|
Тульская обл. |
186 |
231 |
|
Ярославская обл. |
250 |
229 |
Задания:
1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной (
) парной регрессии. Сделать рисунки.
2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.
3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии
4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.
Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.
Получим следующий рисунок.
По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.
Построение полулогарифмической модели регрессии.
Уравнение логарифмической кривой: .
Обозначим:
Получим линейное уравнение регрессии:
Y = A + B×X.
Произведем линеаризацию модели путем замены . В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Xy |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
1243,63 |
26,85 |
57600 |
226,40 |
206,314 |
184,904 |
6,006 |
|
2 |
202 |
226 |
5,3083 |
1199,67 |
28,18 |
51076 |
225,17 |
0,132 |
0,694 |
0,370 |
|
3 |
197 |
221 |
5,2832 |
1167,59 |
27,91 |
48841 |
225,41 |
21,496 |
19,464 |
1,957 |
|
4 |
201 |
226 |
5,3033 |
1198,55 |
28,13 |
51076 |
225,22 |
0,132 |
0,615 |
0,348 |
|
5 |
189 |
220 |
5,2417 |
1153,18 |
27,48 |
48400 |
225,82 |
31,769 |
33,833 |
2,576 |
|
6 |
166 |
232 |
5,1120 |
1185,98 |
26,13 |
53824 |
227,08 |
40,496 |
24,172 |
2,165 |
|
7 |
199 |
215 |
5,2933 |
1138,06 |
28,02 |
46225 |
225,31 |
113,132 |
106,362 |
4,577 |
|
8 |
180 |
220 |
5,1930 |
1142,45 |
26,97 |
48400 |
226,29 |
31,769 |
39,601 |
2,781 |
|
9 |
181 |
222 |
5,1985 |
1154,07 |
27,02 |
49284 |
226,24 |
13,223 |
17,968 |
1,874 |
|
10 |
186 |
231 |
5,2257 |
1207,15 |
27,31 |
53361 |
225,97 |
28,769 |
25,273 |
2,225 |
|
11 |
250 |
229 |
5,5215 |
1264,41 |
30,49 |
52441 |
223,09 |
11,314 |
34,980 |
2,651 |
|
Итого |
2129 |
2482 |
57,862 |
13054,74 |
304,48 |
560528 |
2482,00 |
498,545 |
487,867 |
27,530 |
|
Среднее |
193,5 |
225,6 |
5,260 |
1186,79 |
27,68 |
50957,091 |
225,636 |
45,322 |
44,352 |
2,503 |
= -9,76.
= 225,6 – (-9,76)×5,26 = 276,99.
Уравнение модели имеет вид:
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Рассчитаем средний коэффициент эластичности по формуле:
= -0,04%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Построение степенной модели парной регрессии.
Уравнение степенной модели имеет вид: .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
.
Произведем линеаризацию модели путем замены и
. В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Y = ln(Y) |
XY |
X2 |
Y2 |
|
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
5,4806 |
28,3995 |
26,851 |
30,037 |
226,3 |
206,3 |
188,391 |
241,661 |
6,07 |
|
2 |
202 |
226 |
5,3083 |
5,4205 |
28,7737 |
28,178 |
29,382 |
225,1 |
0,132 |
0,835 |
71,479 |
0,406 |
|
3 |
197 |
221 |
5,2832 |
5,3982 |
28,5196 |
27,912 |
29,140 |
225,3 |
21,496 |
18,671 |
11,934 |
1,918 |
|
4 |
201 |
226 |
5,3033 |
5,4205 |
28,7467 |
28,125 |
29,382 |
225,1 |
0,132 |
0,753 |
55,570 |
0,385 |
|
5 |
189 |
220 |
5,2417 |
5,3936 |
28,2720 |
27,476 |
29,091 |
225,7 |
31,769 |
32,607 |
20,661 |
2,530 |
|
6 |
166 |
232 |
5,1120 |
5,4467 |
27,8437 |
26,132 |
29,667 |
226,9 |
40,496 |
25,675 |
758,752 |
2,233 |
|
7 |
199 |
215 |
5,2933 |
5,3706 |
28,4284 |
28,019 |
28,844 |
225,2 |
113,132 |
104,576 |
29,752 |
4,540 |
|
8 |
180 |
220 |
5,1930 |
5,3936 |
28,0089 |
26,967 |
29,091 |
226,2 |
31,769 |
38,059 |
183,479 |
2,728 |
|
9 |
181 |
222 |
5,1985 |
5,4027 |
28,0858 |
27,024 |
29,189 |
226,1 |
13,223 |
16,950 |
157,388 |
1,821 |
|
10 |
186 |
231 |
5,2257 |
5,4424 |
28,4407 |
27,308 |
29,620 |
225,9 |
28,769 |
26,413 |
56,934 |
2,275 |
|
11 |
250 |
229 |
5,5215 |
5,4337 |
30,0021 |
30,487 |
29,525 |
223,1 |
11,314 |
34,846 |
3187,116 |
2,646 |
|
Итого |
2129 |
2482 |
57,862 |
59,603 |
313,521 |
304,479 |
322,969 |
2480,927 |
498,545 |
487,777 |
4774,727 |
27,548 |
|
Среднее |
193,5 |
225,6 |
5,260 |
5,418 |
28,502 |
27,680 |
29,361 |
225,539 |
45,322 |
44,343 |
434,066 |
2,504 |
С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.
= -0,042.
= 5,418 – 0,959×5,26 = 5,637.
Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.
A = eA = e5,637 = 280,76
Получим уравнение степенной модели регрессии: .
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Для степенной модели средний коэффициент эластичности равен коэффициенту B.
= -0,042%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Сводная таблица вычислений
|
Параметры |
Модель |
|
|
Полулогарифмическая |
Степенная |
|
|
Уравнение связи |
|
|
|
Индекс корреляции |
0,1464 |
0,147 |
|
Коэффициент детерминации |
0,021 |
0,021 |
|
Средняя ошибка аппроксимации, % |
2,5 |
2,5 |
Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.
Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.
Прогнозное значение составит:
= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:
= 224,6 тыс. р.
Определим доверительный интервал прогноза для уровня значимости a = 0,05.
Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

Получаем: 
Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.
= 14,8.
Запишем доверительный интервал прогноза.
= 224,6 – 14,8 = 209,8 тыс. р.
= 224,6 + 14,8 = 239,4 тыс. р.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.
Задание 3. Моделирование временных рядов
Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.
|
Номер квартала |
Товарооборот % к предыдущему периоду |
Номер квартала |
Товарооборот % к предыдущему периоду |
|
1 |
100 |
11 |
98,8 |
|
2 |
93,9 |
12 |
101,9 |
|
3 |
96,5 |
13 |
113,1 |
|
4 |
101,8 |
14 |
98,4 |
|
5 |
107,8 |
15 |
97,3 |
|
6 |
96,3 |
16 |
112,1 |
|
7 |
95,7 |
17 |
97,6 |
|
8 |
98,2 |
18 |
93,7 |
|
9 |
104 |
19 |
114,3 |
|
10 |
99 |
20 |
108,4 |
Задания:
1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.
2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.
3. Рассчитать трендовую компоненту временного ряда и построить его график
4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.
Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.
Построим мультипликативную модель временного ряда.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.
4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений T×E.
6) Расчет абсолютных и/или относительных ошибок.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).
Таблица 2.1
|
№ месяца, T |
Товарооборот, Yi |
Итого за четыре месяца |
Скользящая средняя за четыре месяца |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
100,0 |
– |
– |
– |
– |
|
2 |
93,9 |
392 |
98 |
– |
– |
|
3 |
96,5 |
400 |
100 |
99 |
0,975 |
|
4 |
101,8 |
402 |
100,5 |
100,25 |
1,015 |
|
5 |
107,8 |
402 |
100,5 |
100,5 |
1,073 |
|
6 |
96,3 |
398 |
99,5 |
100 |
0,963 |
|
7 |
95,7 |
394 |
98,5 |
99 |
0,967 |
|
8 |
98,2 |
397 |
99,25 |
98,875 |
0,993 |
|
9 |
104,0 |
400 |
100 |
99,625 |
1,044 |
|
10 |
99,0 |
404 |
101 |
100,5 |
0,985 |
|
11 |
98,8 |
413 |
103,25 |
102,125 |
0,967 |
|
12 |
101,9 |
412 |
103 |
103,125 |
0,988 |
|
13 |
113,1 |
411 |
102,75 |
102,875 |
1,099 |
|
14 |
98,4 |
309 |
77,25 |
90 |
1,093 |
|
15 |
97,3 |
196 |
49 |
63,125 |
1,541 |
|
16 |
112,1 |
303 |
75,75 |
62,375 |
1,797 |
|
17 |
97,6 |
418 |
104,5 |
90,125 |
1,083 |
|
18 |
93,7 |
414 |
103,5 |
104 |
0,901 |
|
19 |
114,3 |
– |
– |
– |
– |
|
20 |
108,4 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 2.2
|
Показатели |
Год |
№ квартала, I |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
0,975 |
1,015 |
|
|
2 |
1,073 |
0,963 |
0,967 |
0,993 |
|
|
3 |
1,044 |
0,985 |
0,967 |
0,988 |
|
|
4 |
1,099 |
1,093 |
1,541 |
1,797 |
|
|
5 |
1,083 |
0,901 |
– |
– |
|
|
Всего за I-й квартал |
4,299 |
3,942 |
4,45 |
4,793 |
|
|
Средняя оценка сезонной компоненты для I-го квартала, |
0,860 |
0,788 |
0,890 |
0,959 |
|
|
Скорректированная сезонная компонента, |
0,984 |
0,901 |
1,018 |
1,097 |
Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.
Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки
на корректирующий коэффициент K.
Проверяем условие: равенство 4 суммы значений сезонной компоненты:
0,984 + 0,901 + 1,018 + 1,097 = 4.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.
Таблица 2.3
|
T |
Yt |
St |
|
T |
T×S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
100,0 |
0,984 |
101,6 |
100,02 |
98,42 |
1,016 |
|
2 |
93,9 |
0,901 |
104,2 |
100,19 |
90,27 |
1,040 |
|
3 |
96,5 |
1,018 |
94,8 |
100,36 |
102,17 |
0,945 |
|
4 |
101,8 |
1,097 |
92,8 |
100,53 |
110,28 |
0,923 |
|
5 |
107,8 |
0,984 |
109,6 |
100,7 |
99,09 |
1,088 |
|
6 |
96,3 |
0,901 |
106,9 |
100,87 |
90,88 |
1,060 |
|
7 |
95,7 |
1,018 |
94,0 |
101,04 |
102,86 |
0,930 |
|
8 |
98,2 |
1,097 |
89,5 |
101,21 |
111,03 |
0,884 |
|
9 |
104,0 |
0,984 |
105,7 |
101,38 |
99,76 |
1,043 |
|
10 |
99,0 |
0,901 |
109,9 |
101,55 |
91,50 |
1,082 |
|
11 |
98,8 |
1,018 |
97,1 |
101,72 |
103,55 |
0,954 |
|
12 |
101,9 |
1,097 |
92,9 |
101,89 |
111,77 |
0,912 |
|
13 |
113,1 |
0,984 |
114,9 |
102,06 |
100,43 |
1,126 |
|
14 |
98,4 |
0,901 |
109,2 |
102,23 |
92,11 |
1,068 |
|
15 |
97,3 |
1,018 |
95,6 |
102,4 |
104,24 |
0,933 |
|
16 |
112,1 |
1,097 |
102,2 |
102,57 |
112,52 |
0,996 |
|
17 |
97,6 |
0,984 |
99,2 |
102,74 |
101,10 |
0,965 |
|
18 |
93,7 |
0,901 |
104,0 |
102,91 |
92,72 |
1,011 |
|
19 |
114,3 |
1,018 |
112,3 |
103,08 |
104,94 |
1,089 |
|
20 |
108,4 |
1,097 |
98,8 |
103,25 |
113,27 |
0,957 |
|
Среднее |
101,4 |
1,0011 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.
Таблица 2.4
|
T |
|
T2 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
101,6 |
1 |
101,6 |
2,5 |
1,58 |
2,0 |
|
|
2 |
104,2 |
4 |
208,4 |
13,2 |
3,87 |
56,3 |
|
|
3 |
94,8 |
9 |
284,4 |
32,1 |
5,88 |
24,0 |
|
|
4 |
92,8 |
16 |
371,2 |
71,9 |
8,33 |
0,2 |
|
|
5 |
109,6 |
25 |
548 |
75,9 |
8,08 |
41,0 |
|
|
6 |
106,9 |
36 |
641,4 |
29,4 |
5,63 |
26,0 |
|
|
7 |
94,0 |
49 |
658 |
51,3 |
7,48 |
32,5 |
|
|
8 |
89,5 |
64 |
716 |
164,6 |
13,07 |
10,2 |
|
|
9 |
105,7 |
81 |
951,3 |
18,0 |
4,08 |
6,8 |
|
|
10 |
109,9 |
100 |
1099 |
56,3 |
7,58 |
5,8 |
|
|
11 |
97,1 |
121 |
1068,1 |
22,6 |
4,81 |
6,8 |
|
|
12 |
92,9 |
144 |
1114,8 |
97,4 |
9,69 |
0,3 |
|
|
13 |
114,9 |
169 |
1493,7 |
160,5 |
11,20 |
136,9 |
|
|
14 |
109,2 |
196 |
1528,8 |
39,6 |
6,39 |
9,0 |
|
|
15 |
95,6 |
225 |
1434 |
48,2 |
7,13 |
16,8 |
|
|
20 |
102,2 |
400 |
2044 |
0,2 |
0,37 |
114,5 |
|
|
21 |
99,2 |
441 |
2083,2 |
12,3 |
3,59 |
14,4 |
|
|
22 |
104,0 |
484 |
2288 |
1,0 |
1,05 |
59,3 |
|
|
23 |
112,3 |
529 |
2582,9 |
87,6 |
8,19 |
166,4 |
|
|
24 |
98,8 |
576 |
2371,2 |
23,7 |
4,49 |
49,0 |
|
|
Сумма |
230 |
2035,2 |
3670 |
23588 |
1008,3 |
122,49 |
778,2 |
|
Среднее |
11,5 |
101,8 |
183,5 |
1179,4 |
50,4 |
6,12 |
38,91 |
Вычислим параметры уравнения тренда.

= 99,85.
В результате получим уравнение тренда:
T = 99,85 + 0,17×T.
Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
Расчет ошибки в мультипликативной модели произведем по формуле:
Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).
Рассчитаем сумму квадратов абсолютных ошибок .
Используя 5-й столбец таблицы 2.4, получим:

Рассчитаем среднюю относительную ошибку: .
Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.
| < Предыдущая | Следующая > |
|---|
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
In simple terms, Root mean square error means how much far apart are the observed values and predicted values on average. The formula for calculating the root-mean-square error is as follows :
Where,
- n: number of samples
- f: Forecast
- o: observed values
Calculating Root Mean Square Error in Excel :
Follow the below steps to calculate the root means square error in Excel:
- Fill up the predicted values, observed values, and differences between them in the Excel sheet.
- To calculate the difference, just type the formula in one cell and then just drag that cell to the rest of the cells. The difference between the cells will be calculated automatically. Then either follow STEP 3 or STEP 4 given below :
Calculating the difference between the observed values and predicted values
- Now let us select one cell and apply the formula of root-mean-square error.
Method 1: Formula to Calculate Root Mean Square Error (RMSE)
- We could have not used the difference column at all, we can directly calculate RMS error from Predicted and Observed values Columns as follows :
Method 2: Formula to calculate Root Mean Square Error ( RMSE)
- At Last, we get the required Root Mean Square error value in the selected cell.
Root mean square error is calculated in the selected cell after applying the formula
Applications of Root Mean Square Error value in different domains :
Following are some applications of RMSE:
- It is used to predict how the atmosphere behaves and how it differs from the predicted behavior in the meteorology domain.
- It can be used to measure the average distance between two proteins that are superimposed on one other.
- It can be used to calculate the Peak Signal to Noise ratio in the field of image processing to determine the effectiveness of a method that reconstructs an image as compared to the original image.
Like Article
Save Article
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y — диапазон, содержащий данные результативного признака;
Входной интервал X — диапазон, содержащий данные факторного признака;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:


На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.

выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:

Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.

Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).
Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Средняя относительная ошибка аппроксимации
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1 , Х2 , … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у иx :

где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия: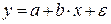
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней
•равносторонняя гипербола
Регрессии, нелинейные по оцениваемым параметрам:
• степенная 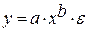
• показательная
• экспоненциальная
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических 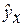
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 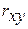
и индекс корреляции 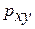
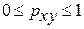
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений 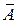
Средний коэффициент эластичности 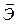
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
где 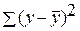
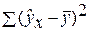
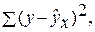
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :
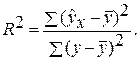
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F -критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл Fфакт , то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо .
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл tфакт , то гипотеза Но не отклоняется и признается случайная природа формирования a , b или 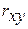
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение 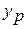
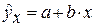
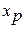
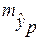
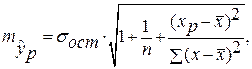
и строится доверительный интервал прогноза:
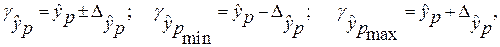
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать |
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
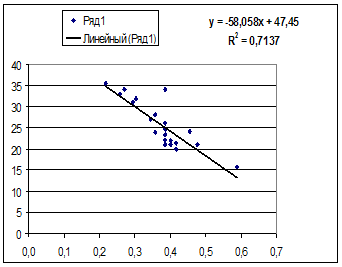
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
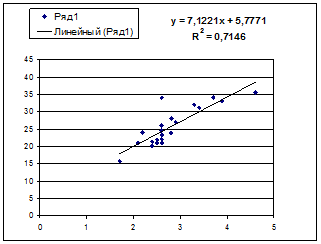
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
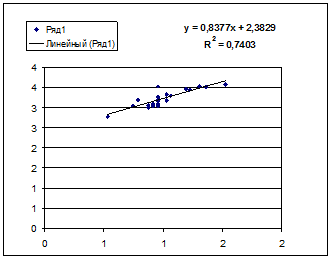
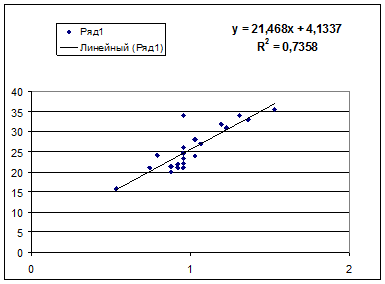
· Степенной регрессии 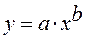
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
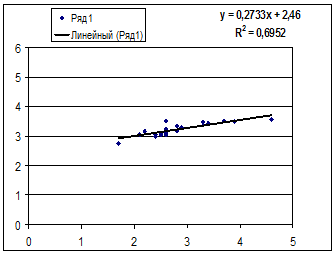
· Экспоненциальная регрессия 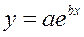
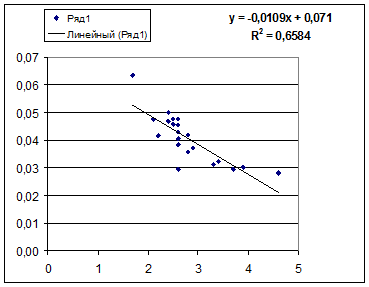
· Равносторонняя гипербола 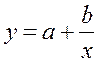
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
· Обратная гипербола 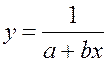
· Полулогарифмическая регрессия 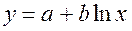
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
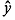
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели 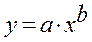
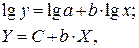
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 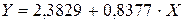
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели 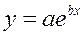
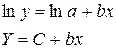
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 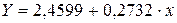
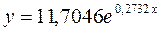
Для расчета теоретических значений y подставим в уравнение 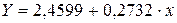
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели 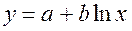
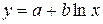
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: 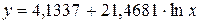
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель 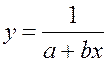
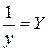
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: 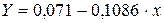
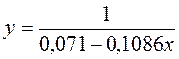
Для расчета теоретических значений y подставим в уравнение 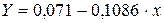
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы 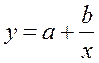
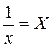
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: 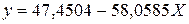
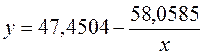
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b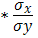
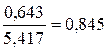
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции 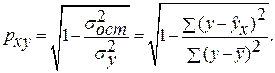
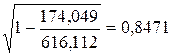
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели 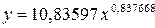
· Для уравненияэкспоненциальноймодели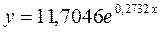
Для уравненияполулогарифмическоймодели 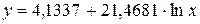
· Для уравнения обратной гиперболической модели 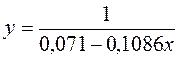
· Для уравнения равносторонней гиперболической модели 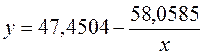
Сравнивая значения 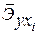
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 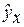
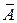
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. 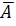
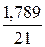
Качество построенной модели оценивается как хорошее, так как 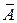
· Степенная регрессия. 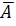
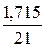
Качество построенной модели оценивается как хорошее, так как 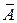
· Экспоненциальная регрессия. 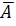
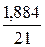
Качество построенной модели оценивается как хорошее, так как 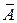
· Полулогарифмическая регрессия. 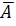
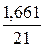
Качество построенной модели оценивается как хорошее, так как 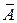
· Гиперболическая регрессия. 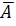
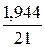
Качество построенной модели оценивается как хорошее, так как 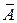
· Обратная регрессия. 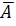
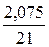
Качество построенной модели оценивается как хорошее, так как 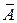
6. Рассчитаем F-критерий:
· Линейная регрессия. 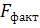
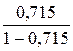
источники:
http://welom.ru/srednyaya-oshibka-approksimacii-v-excel-ocenka-kachestva-uravneniya/
http://www.bestreferat.ru/referat-268496.html
Автор: Your Mentor. Дата публикации: 15 июля 2019.
Прогнозирование продаж является важным видом деятельности практически для любого бизнеса, поскольку это влияет на все: на вашу компанию, ваших клиентов и ваших деловых партнеров. Без прогнозирования продаж вы движетесь вслепую, а ваш бизнес не будет стабильным.
Независимо от того, существует ли у вас процесс прогнозирования продаж или вы начинаете с нуля создавать новый, эта статья научит вас пошаговому систематическому процессу создания и управления эффективным прогнозом продаж. Вы узнаете, как создавать правильные процессы, выбирать правильные методы и использовать соответствующие количественные и качественные данные для создания максимально точного прогноза продаж.
Прогнозирование продаж – это навык, который вы можете использовать практически в любой области вашего бизнеса. Наличие такого навыка сделает вас более ценным, независимо от того, на какой должности вы находитесь сегодня.
Содержание статьи:
- Понимание прогноза продаж
- Подготовка к прогнозированию продаж
- Использование количественного метода прогнозирования
- Использование качественного метода прогнозирования продаж
Данный материал предназначен для профессионалов в области управления продажами, управления маркетингом или для тех, кто хочет знать, что может произойти в будущем. Возможность составлять точные прогнозы продаж делает вас ценным членом команды, включая практически любую команду, в которой вы находитесь.
Перед началом изучения данного материала у вас должно быть базовое понимание маркетинга и того, как ваша компания генерирует продажи. Мы будем использовать Microsoft Excel для количественной части этого курса. Вам не нужно быть опытным пользователем Excel, но вы должны понимать основные операции, такие как ввод формул и как копировать и вставлять эти формулы в другие ячейки. Суть в том, что вам не нужно быть специалистом по количественным показателям или мастером Excel, чтобы получить пользу от этой статьи.
Понимание прогноза продаж
Прогноз продаж – это прогноз того, какими будут ваши результаты в качестве организации сбыта продукции в конце определенного периода времени. Он используется для многих целей, но прогнозирование продаж – это гораздо больше, чем просто разработка определенного набора цифр.
Прогнозирование заключается в управлении данными, насколько неправильным является ваш прогноз, а не насколько он верный. Расстояние между фактическими результатами и ожидаемыми результатами является риском для вашего бизнеса, и этот риск может быть значительным, даже разрушительным.
Если вы ожидаете высоких результатов, но не дотягиваете до них, вы застрянете с дополнительными запасами на руках, и это будет стоить вашей компании больших денег, которые могли бы быть использованы для лучших проектов. С другой стороны, представьте, что ваши реальные результаты намного выше, чем ваш прогноз. Теперь у вас может возникнуть ситуация, когда у вас закончится продукция. У вас возникают задержки, и вы начинаете терять клиентов.
Вот почему процесс прогнозирования продаж должен информировать организацию о том, что вы ожидаете, но, главное, какие непредвиденные обстоятельства могут произойти в случае неизбежных ошибок. Конечно, время от времени вы можете получить идеальный прогноз, но не рассчитывайте на него.
У вас должен быть план для устранения ошибок. Этот план может включать безопасный резерв продукции, на случай, если клиент захочет сделать непредвиденный заказ. Или, возможно, вам понадобится команда дистрибьюторов, которая со скидкой сможет выкупить ваш резерв.
Другими словами, посмотрите на каждое последствие того, что ваш прогноз может быть слишком оптимистичным или пессимистичным, и разработайте способ смягчения этого последствия. Таким образом, ваш процесс прогнозирования помогает компании работать лучше, а также защищает компанию от неопределенности.
Прогнозирование продаж является одним из наиболее важных процессов в компании, потому что с ним связано множество отделов бизнеса. Давайте посмотрим, почему прогнозирование продаж так важно:
- Во-первых, влияние прогноза продаж на финансовое планирование бизнеса. Например, прогнозы влияют на цены акций и возможность привлечения новых инвестиций.
- Во-вторых, прогнозирование продаж влияет на то, как компания создает и управляет своим отделом продаж. Прогнозы продаж будут использоваться для определения территории продаж, установления квот для каждого торгового представителя и для измерения производительности.
- В-третьих, другие отделы компании полагаются на точные прогнозы продаж. Например, операционный отдел будет принимать важные решения на основе прогнозов продаж. Если вы производитель, вы решаете, сколько продукции производить каждый день, основываясь на тех же прогнозах.
- В-четвертых, сфера услуг, такие как розничная торговля, банковское обслуживание и общественное питание, решают, сколько сотрудников им нужно каждый день для обслуживания прогнозируемого объема клиентов.
- В-пятых, прогнозы продаж могут повлиять даже на управление людьми. Они влияют на то, как и когда вы нанимаете новых людей, и на любое увеличение или уменьшение заработной платы.
- В-шестых, если компания хочет развиваться за счет приобретения другой компании, ей потребуется точный прогноз продаж целевой компании, чтобы решить, сколько за нее заплатить.
Теперь вам должно быть очевидно, что руководители уделяют так много внимания прогнозированию продаж из-за его далекоидущих последствий. Прогнозирование продаж – это систематический процесс, включающий различные бизнес-функции. Вот почему первым шагом в этом процессе является создание правильной команды.
Так кто же должен участвовать в процессе прогнозирования продаж? Конечно, большинство компаний будут полагаться на команду управления продажами. Они ежедневно управляют торговыми представителями, у них есть много информации о ваших клиентах и конкурентах, которые могут быть использованы в прогнозировании.
Но, хотите верьте, хотите нет, но ваша команда по продажам может не подходить для прогнозирования. Дело в том, что вы можете оказаться в отрасли, где другие отделы, например, отдел маркетинга, лучше разбираются в разработке прогнозов.
Как правило, ваша межфункциональная группа по прогнозированию продаж должна включать финансовый отдел. У них есть много данных о прошлых результатах продаж и расходах в различных областях бизнеса для достижения этих результатов.
Маркетинг предоставляет важную информацию о тенденциях рынка, маркетинговой стратегии, поведении покупателей и позиционировании. Эта информация необходима вам для оценки вероятности конвертации потенциальных клиентов. Операционный отдел производит продукт или услугу и имеет в наличаи свои полезные данные и знания для более подробного прогноза.
После того как вы определили ключевых игроков в своей команде, убедитесь, что они знают о вашем графике планирования, знают свою роль, понимают ожидания, которые вы возлагаете на каждого из них при разработке хорошего прогноза продаж.
Теперь рассмотрим основные шаги прогнозирования:
- Сначала проанализируйте рынок. В какой вы категории? Насколько велик рынок, какие тенденции, а также как динамика рынка влияют на будущие результаты?
- Соберите данные. Вам нужно собирать только те данные, которые имеют отношение к прогнозу. Вы также должны учитывать данные, которые хотели бы иметь, но у вас их нет. В таком случае вы делаете предположения.
- Определитесь с техникой, которую вы будете использовать. Качественная, количественная или комбинация двух?
- Проверьте ваш прогноз. Проведите свою модель прогнозирования через прошлые циклы продаж и посмотрите, как она выполняется. Есть ли какие-то корректировки, которые необходимо внести для точной настройки прогноза?
Хорошие прогнозы не являются просто предположением. Они являются результатом дисциплинированного и многофункционального подхода.
Подготовка к прогнозированию продаж
Ваш подход к прогнозированию продаж должен соответствовать маркетинговому плану вашей компании. Сначала вам нужно определить свою рыночную нишу, т.е. пространство в котором вы конкурируете. Вы можете определить это пространство более глобально или, наоборот, более узко, но более сфокусировано.
Например, предположим, вы производите линию продуктов для чистки зубов. Вы можете определить свою нишу на очень глобальном уровне здоровья полости рта. Это говорит о том, что вы предлагаете все виды продуктов, такие как зубные щетки, зубная паста, зубная нить, отбеливание зубов и все остальное. Когда вы определяете рыночную нишу таким образом, происходят две вещи:
- Во-первых, вы предоставляете себе очень широкие возможности для рынка, решая множество специфических задач с помощью широкого спектра продуктов. Но это также означает, что вы сталкиваетесь с широким кругом конкурентов, борющихся за одних и тех же клиентов.
- Во-вторых, вы можете определить свою нишу более узко. Возможно, до определенного уровня, скажем, отбеливание зубов. Этот узкий охват означает, что вы стремитесь к меньшим возможностям на рынке, но с гораздо большей концентрацией внимания и меньшей конкуренцией.
Так что это баланс между возможностью продаж и жесткостью конкуренции, с которой вы сталкиваетесь. Вот почему для прогнозирования продаж мы рекомендуем собраться с вашим маркетинговым отделом, чтобы понять, как они определяют различные рыночные ниши, в которых вы конкурируете.
Далее, для каждой рыночной ниши вы должны понимать тенденции, которые происходят внутри нее. Есть только три направления: продажи растут, продажи снижаются или продажи не меняются. Кажется, все просто, но недостаточно знать направление тренда. Вы должны также попытаться понять причины, т.е. почему сейчас именно такой тренд. Это поможет вам составить более точный прогноз продаж.
Например, представьте, что продажи на вашем рынке растут. В таком случае лучше понять причины, чтобы не быть слишком самоуверенным. Продажи могут быть вызваны определенным трендом, который со временем прекратится. Или, возможно, клиенты или дистрибьюторы запасаются продуктами, вызывая временное увеличение продаж. Более точное прогнозирование продаж составляется тогда, когда прогнозист знает рыночную нишу и реальные причины изменений на этом рынке.
Вы можете подумать, что создали точный прогноз продаж, основанный на достоверных данных и методах прогнозирования, но на рынке, а также внутри вашей компании может многое произойти, что может повлиять на ваш прогноз.
- Во-первых, вы можете быть удивлены тем, что делает ваш конкурент. Что если они запустят отличный новый продукт, который лучше, чем ваш? Или, возможно, они снижают цену или проводят специальную акцию на свою линейку продукции? Может произойти и обратное. Что если у вашего конкурента негативный отзыв на продукт или другое неблагоприятное событие, которое выводит их продукцию с рынка? Сейчас это может показаться хорошей новостью, но вы и ваши коллеги должны скорректировать прогноз и быстро отреагировать. Если вы этого не сделаете, вы можете исчерпать запасы из-за внезапного увеличения спроса, и это может негативно повлиять на ваших постоянных клиентов.
- Во-вторых, на продажи вашей компании также могут повлиять правовые, нормативные или политические изменения. Представьте, что вы работаете в пищевой промышленности, и регулирующий орган объявляет о новом положении, которое ограничивает то, что вы можете продавать? Или представьте себе результат политических выборов, который сделает ваши товары более продаваемыми.
- Теперь, пожалуй, самая сложная вещь в прогнозировании – это изменение структуры покупательской активности. Следующее поколение потребителей может не захотеть покупать ваши товары в том виде, который пользуется спросом у нынешних постоянных клиентов, или, они будут покупать их в меньшем объеме. Здесь нужно снова корректировать ваш прогноз.
- Изменения в технологии могут также повлиять на ваш прогноз продаж. Когда такая компания, как Apple, объявляет о том, что она отказывается от 3,5-миллиметровых гнезд для наушников или использует USB-порт последнего поколения, все компании, поддерживающие эти устаревшие функции, должны пересмотреть свои прогнозы продаж.
- В вашей компании также могут происходить вещи, которые могут повлиять на ваш прогноз продаж. Ваша компания может изменить свою общую коммерческую стратегию, что может помешать или помочь продажам продуктов, которые она производит. Например, отдел маркетинга может решить провести крупную рекламную кампанию или продвигать продукцию на новые рынки.
Как только вы определите свою рыночную нишу и поймете динамику рынка, настало время сконцентрироваться на составлении прогноза продаж. Существует множество методик и пакетов программного обеспечения, поэтому вы должны определить тот, который подходит именно вам.
Методы прогнозирования продаж делятся на две большие категории. Качественный метод, основанный на данных от людей, и количественный метод, основанный на показателях числовых данных, но, честно говоря, лучшие прогнозисты полагаются на комбинацию обоих.
Вот несколько вопросов, которые вы можете задать себе при выборе метода прогнозирования:
- Насколько хорошо вы понимаете свой рынок?
- Он растет или уменьшается и почему?
- Есть ли новые потребительские, конкурентные или технологические тренды?
- Это сезонный бизнес?
Если вы не очень много знаете о своем рынке и происходящих важных изменениях, вы можете использовать качественный метод, который опирается на советы экспертов.
Количественный метод часто использует исторические данные, такие как предыдущие данные о продажах и доходах, производственные и финансовые отчеты, а также статистику посещаемости сайта. Например, анализ данных о сезонных продажах может помочь компании спланировать на следующий год производственные потребности и человеческие ресурсы на основе прошлогодних месячных или квартальных показателей.
Количественный метод также использует прогнозы, основанные на статистическом моделировании, анализе тенденций или другой информации из экспертных источников, таких как правительственные учреждения, торговые ассоциации и даже академические учреждения.
Качественное прогнозирование включает в себя сочетание количественных и качественных методов. Главное для вас – это справиться с последствиями ошибки, поэтому минимизируйте риск, выбирая лучшую технику для вашей ситуации.
Использование количественного метода прогнозирования
Прогнозирование продаж с использованием количественных методов означает, что вам необходимо иметь исторические данные о продажах. То, что вам удалось продать в прошлом, может быть очень хорошим показателем того, что вы сможете продавать в будущем. Каждый период времени, когда ваша компания продавала свои продукты и услуги, происходило множество событий, с точки зрения конкурентных действий, потребительских тенденций и даже изменений в экономике в целом.
Исторические данные, которые вы используете для прогнозирования продаж, должны быть чистыми. То есть ваши данные должны быть точны, они не искажены событиями, которые были вне вашего контроля, т.к. это маскирует истинные и фактические результаты продаж за определенный период.
Для тех методов, которыми мы собираемся поделиться, вам нужно как можно больше данных о прошлых продажах. Обратитесь в финансовый или IT-отдел, чтобы они вам помогли собрать самые точные и полные данные, которые доступны. После этого вам следует очистить эти данные от множества переменных, которые ведут к неточностям прогноза.
Для начала убедитесь, что вы понимаете периоды времени, которые ваша компания использует для регистрации продаж. Эти данные могут быть ежедневными, еженедельными, ежемесячными, ежеквартальными или даже ежегодными. Если у вас имеется такая возможность, тогда используйте ежеквартальные данные. Исследования показали, что этот период времени дает более точные результаты прогноза.
Затем нанесите данные на график о продажах и посмотрите на них визуально. Спросите себя: «Что здесь происходит?». Если вы видите дикие колебания в данных, т.е. слишком высокие продажи или слишком низкие, попробуйте выяснить, что произошло.
В ваших данных могут быть и другие искажения. Например, ваша компания может регистрировать продажи по полной прейскурантной цене, тогда как фактические денежные поступления намного меньше из-за скидок. Скидки, которые вы предлагаете от месяца к месяцу, могут существенно отличаться. Методы, о которых вы узнаете далее, могут решить проблему такого типа.
Далее, избавьтесь от данных, которые представляют период, который не отражает ваш текущий бизнес. Если вы приобретаете бизнес в результате которого заявленные продажи растут, вы можете либо проигнорировать результаты продаж до приобретения, либо использовать два отдельных набора данных для прогнозирования продаж и сложить их вместе.
Теперь перейдем непосредственно к самим методам количественного прогнозирования. Простой, но эффективный метод прогнозирования продаж – это метод, который мы называем ролловер (roll-over). Его легко использовать, потому что техника делает всю работу за вас. Нет расчетов, нет догадок.
Вот как работает прогноз ролловер. Прогноз на следующий период времени – это просто фактические результаты продаж за последний период. Другим словами, для прогнозирования продаж вы берете фактические результаты продаж за один период, например, в прошлом месяце, и делаете это же число своим прогнозом на следующий месяц.
Но как такой подход может быть точным? Как и в случае с любой другой техникой прогнозирования, эта методика будет иметь определенный уровень ошибки, но вы будете удивлены, насколько этот подход может быть очень эффективным для многих бизнес-моделей.
Если вы работаете в довольно стабильном бизнесе с небольшой сезонностью или, вообще без нее, эта техника может вам подойти. И что самое важное в данном методе – независимо от того, насколько он точен, его результаты могут служить ориентиром для сравнения с другими методами прогнозирования.
Давайте посмотрим, как рассчитать погрешность между фактическими и прогнозируемыми продажами. В столбце C вы найдете фактические результаты за 24 месяца. В столбце D вы увидите прогнозируемые результаты ролловера, которые являются фактическими результатами предыдущего месяца. Например, вы можете видеть, что прогноз ролловер на февраль такой же, как и в январе – 4398 единиц.
Теперь, чтобы определить среднюю погрешность, мы собираемся вычесть прогноз ролловер из фактических результатов. Мы будем использовать функцию абсолютного значения (=ABS), потому что нам все равно, положительная или отрицательная разница. Здесь у нас есть разница между фактическим результатом и прогнозируемым результатом за период. Мы можем перетащить эту ячейку вниз, чтобы быстро рассчитать оставшиеся погрешности по всем месяцам.
Наконец, мы хотим найти среднюю погрешность для прогноза ролловер. Мы будем использовать функцию (=СРЗНАЧ) и выделим все погрешности по всем месяцам. Получается, что округленная среднемесячная погрешность составляет 1420 единиц продукции. Это довольно хорошо, в зависимости от того, что может выдержать ваша бизнес-модель. Давайте помнить об этом числе, когда будем оценивать другие методы прогнозирования, чтобы понять, сможем ли мы его улучшить.
С помощью метода ролловер вы используете только фактические результаты продаж текущего месяца, чтобы спрогнозировать следующий. По сути, вы предполагаете, что все, что вы знаете о будущем месяце, основано только на том, что вы узнали в этом. Но это не совсем так. Если у вас есть результаты прошлых продаж в течение нескольких месяцев, у вас есть возможность учиться у каждого месяца. Это может улучшить точность вашего прогноза.
Например, что если вы взяли последние четыре месяца фактических продаж, рассчитали среднее значение и использовали это среднее в качестве прогноза на следующий месяц? Другими словами, если вы прогнозируете продажи на май, вы должны рассчитать средние фактические продажи за январь, февраль, март и апрель. Для прогноза на июнь вы снова будете использовать средние фактические продажи за предыдущие четыре месяца: февраль, март, апрель и май.
Этот метод называется прогнозом скользящего среднего. Среднее число движется от месяца к месяцу. Посмотрим, работает ли он лучше, чем наш предыдущий метод.
Мы начнем с расчета скользящей средней за май. Для этого мы сначала подведем итоги за четыре месяца, то есть с января по апрель, а затем, разделим на четыре. Скользящая средняя составляет 5 534.
Далее, мы вычисляем среднюю погрешность, вычитая скользящее среднее из фактических результатов с помощью функции абсолютного значения (=ABS). Похоже, что наша средняя погрешность составила 988 единиц.
Теперь рассчитаем среднюю погрешность за все месяцы. Мы снова перетаскиваем ячейку скользящего среднего на последний месяц и сделаем то же самое со средней погрешностью. Мы так же используем функцию =СРЗНАЧ и найдем среднюю погрешность за весь период. Она составила 1312 единиц, что уже лучше, чем 1420, которые мы получили с помощью метода ролловер.
Но что, если характер вашего бизнеса таков, что в последние месяцы квартала вы имеете наибольший объем продаж? Другими словами, в эти месяцы прослеживается наибольшая динамика на вашем рынке. Здесь вам необходимо делать упор на последние месяцы. Этот метод называется взвешенным скользящим средним.
Вот как рассчитать взвешенное скользящее среднее за май месяц:
1. Во-первых, мы используем фактические продажи за январь-апрель, как и раньше, но теперь мы хотим решить, какой вес должен иметь каждый месяц. Мы думаем, что в апреле получим 40% веса, март – 30%, февраль – 20%, а январь – 10%. Мы выбрали эти проценты произвольно, но вы можете поэкспериментировать, опираясь на вашу статистику продаж, чтобы найти то, что лучше для вас.
2. Во-вторых, вычислим взвешенное скользящее среднее в Excel. Сначала мы умножаем фактические результаты за январь на 0,1, затем добавляем фактические результаты за февраль и умножаем на 0,2, еще добавляем фактические результаты за март, умноженные на 0,3, и, наконец, добавляем фактические результаты за апрель, умноженные на 0,4. Нажимаем Enter и получаем 5 754 единиц.
3. В-третьих, когда у нас уже есть прогноз взвешенной скользящей средней, давайте посмотрим, в чем сейчас заключается погрешность, через вычитание полученного результата 5754 с фактического результата мая месяца.
4. В-четвертых, просчитаем среднюю погрешность за два года. Для этого потянем обе формулы до последнего месяца. Мы получили результат 1257, что еще лучше предыдущих результатов. Это говорит о том, что последние месяцы действительно отражают то, что происходит в нашем бизнесе.
Мы возьмем последнюю модель. В конце концов, более точный прогноз позволяет нам и нашей команде лучше управлять планами действий на случай непредвиденных обстоятельств, а именно этим и занимается прогнозирование продаж – управление рисками и возможностями нашего бизнеса.
Мы хотим показать вам еще одну методику количественного прогнозирования, потому что она популярна у опытных прогнозистов и дает очень хорошие результаты в большинстве ситуаций. Данный метод называется экспоненциальным сглаживанием (ЭС).
Вот основная идея. Используя метод взвешенного скользящего среднего, мы использовали лишь несколько предыдущих точек данных, чтобы вычислить среднее значение в качестве нашего прогноза на следующий период. Мысль здесь заключается в том, что последние месяцы обладают большим весом, с точки зрения рыночных факторов.
Что если бы был способ собрать все данные о продажах за предыдущие месяцы, но сделать это таким образом, чтобы сгладить большие максимумы и минимумы в наших данных? По сути, это устраняет то, что мы называем «шумом» наших данных.
Это легко рассчитать. Нам нужно только три показателя. Продажи за текущий период, прогноз на текущий период и весовой коэффициент для текущего периода, точно такой же, как мы использовали для взвешенной скользящей средней. Только теперь это число будет называться сглаживающим фактором.
Вот как это рассчитать. Возьмем фактические продажи за последний период, умноженные на коэффициент сглаживания. Добавьте к этому прогноз самого последнего периода, умноженный на один минус коэффициент сглаживания.
ЭС=(ФП×КС) + (ПП×(1−КС))
ФП – соответствует фактическим продажам за последний период;
КС – равно коэффициенту сглаживания, представленному в десятичной форме. Давайте использовать тот же вес из последнего примера 0,4;
ПП – соответствует прогнозу самого последнего периода. Другими словами – это результат вычисления сглаживания из предыдущего периода, т.е. ЭС предыдущего месяца.
Используя скользящую среднюю и метод ролловер, мы предполагаем, что каждый результат продаж содержит некоторое предвидение относительно будущих результатов. Теперь мы также учитываем не только прошлые фактические результаты, но и все прошлые прогнозы. Другими словами, мы предполагаем, что прошлые прогнозы тоже могут поделиться с нами о будущем прогнозе.
Рассчитаем среднее экспоненциального сглаживания в Excel. В электронной таблице Excel мы начнем со столбца J. Поскольку январь – наш первый месяц в наборе данных, мы возьмем фактические результаты за январь и предположим, что это прогноз. Итак, мы возьмем 4398 с января месяца и перенесем это же число в ячейку J3. Чтобы рассчитать прогноз на февраль, мы умножим фактические результаты предыдущего месяца на 0,4, а затем добавим прогноз предыдущего месяца, умноженный на 0,6. Опять же, эти числа выбираются произвольно, и вы можете выбрать показатели, которые больше подходят вам под бизнес-модель.
Далее, мы вычислим абсолютную погрешность, вычитая фактические результаты по прогнозу экспоненциального сглаживания.
Мы еще раз перетащим обе эти формулы до последнего месяца. Наконец, мы рассчитаем среднее значение ошибки для сравнения с другими методами прогнозирования. У нас получилась средняя погрешность равна 1229 единиц, что еще немного лучше предыдущих результатов.
Экспоненциальное сглаживание не только легко, но и отлично реагирует на новые тенденции или сезонность в вашем бизнесе. Этот метод быстро реагирует на изменения на рынке, сохраняя при этом лучший результат предвидения из всех перечисленных методик.
Использование качественного метода прогнозирования продаж
Прогнозирование продаж опирается на поведение клиентов, а именно, что клиенты будут делать или не будут делать в течение определенного периода времени, поэтому имеет смысл применить ориентированный на клиента подход к прогнозированию. Это значит смотреть на два вида данных: что вы знаете о своих клиентах и что ваши клиенты знают о себе.
Начнем с первого. Анализируя любой рынок, вы хотите сгруппировать клиентов по четырем типам:
- Клиенты, которые уже покупают у вас. На самом деле, они не только покупают у вас, они покупают исключительно у вас, и никогда у конкурентов.
- Вторая группа похожа на первую в том, что они в настоящее время покупают ваши товары и услуги. Разница в том, что эти клиенты также покупают товары у ваших конкурентов. Почему? Потому, что для некоторых категорий продуктов клиенты хотят выбора. Например, рынок одежды. Вы почти наверняка носите одежду от разных производителей. Рынок продуктов питания является еще одним примером.
- Третья группа клиентов – это те, кто покупает исключительно у ваших конкурентов, а не у вас. По крайней мере, пока.
- Четвертая группа клиентов – это те, кто не покупает ваш тип продукта у кого-либо. Они называются потребителями без категории. Эти потенциальные клиенты очень важны, потому что их приобретение дает вам новый источник дохода. Вместо того чтобы просто брать долю рынка у конкурента, получение таких клиентов помогает вам увеличить свой рынок.
Теперь вам нужно оценить потенциальное количество клиентов, которых вы могли бы привлечь для каждого из этих четырех типов.
- Сначала вы оцениваете общее количество клиентов для каждого типа.
- Затем вы делаете предположения о том, какой процент вы можете переманить на свою сторону. В прогнозировании продаж мы называем это подходом к прогнозу сверху вниз. Вы сначала оцениваете клиентов из первых групп, а затем думаете, чем вы можете привлечь остальных из последних двух категорий.
Второй ориентированный на клиента подход к прогнозированию прост: спросите своих клиентов, что они ожидают у вас заказать в ближайший период. Конечно, это зависит от вашей отрасли, но вы будете удивлены, насколько клиенты смогут и захотят рассказать вам об ожидаемых расходах на предстоящий год.
Вы можете подумать, что потенциальные клиенты не захотят тратить на это время. Тогда дайте им оптовую скидку или другой стимул, чтобы сообщить вам о своих намерениях. Даже если это не на 100% точно, это все же хорошая информация. Прогнозирование – это управление погрешностями и клиенты могут сделать многое, чтобы помочь вам.
Торговые представители и ваши дистрибьюторы обладают уникальными, близкими к рынку взглядами, что может принести дополнительную пользу в прогнозировании продаж. Вот как это можно использовать.
Во-первых, попросите своих представителей и дистрибьюторов дать вам оценку общего годового объема продаж на их территории. Затем попросите их разбить эту сумму по месяцам или кварталам. Этот шаг хорош тем, что он заставляет их распределять общее количество по меньшим периодам времени. Это заставляет их действительно задуматься об оценках, которые они вам дают.
Теперь совет. Самый большой риск, связанный с тем, чтобы спрашивать представителей и дистрибьюторов об оценках продаж заключается в том, что вряд ли они будут проводить различие между прогнозом и квотой продаж. Торговые представители предпочли бы торговую квоту ниже, чем то, что может продаться на рынке. В этом есть смысл. Кому нужна квота продаж, которая не может быть достигнута?
Это одна из основных причин, по которой вы хотите использовать комбинацию качественных и количественных методов прогнозирования. Использование нескольких методов поможет вам обнаружить эту проблему.
Когда вам дают оценки от торговых представителей и дистрибьюторов, самое важное, что вы понимаете, какие предположения они использовали для оценки. Например, каковы их предположения о новых или утерянных клиентах, новых конкурентах, ценовых изменениях, новых маркетинговых инициативах, новых продуктах и т. д.
Наконец, вы можете рассмотреть возможность использования простого математического метода, называемого анализом ожидаемых значений. Ожидаемое значение – это ожидаемый прогноз для данной территории. ОЗ рассчитывается путем умножения каждого из возможных результатов на вероятность каждого результата, а затем суммирования всех этих значений.
Как это сделать. Попросите вашего представителя или дистрибьютора предоставить вам приблизительные продажи по каждому клиенту, и вероятность их достижения. Вероятность означает, что прогноз будет достигнут от 1% до 100%.
Давайте предположим, что у представителя пять клиентов, и он предоставляет вам всю информацию. Ожидаемое значение является прогнозом, основанным приведенном выше уравнении. Таким образом, в этом уравнении вы умножаете вероятность прогноза на каждого клиента, а затем складываете все вместе.
Использование анализа ожидаемых значений, скорее всего, даст прогноз с меньшей ошибкой, чем просто запрос представителей дать общий годовой прогноз. Подход ОЗ использует их скрытые знания о том, что происходит на их территории и эти знания могут помочь вам сделать лучшие прогнозы продаж.
Для некоторых отраслей лучший способ прогнозировать продажи – использовать группу экспертов. Это люди, которые имеют широкий спектр знаний в вашей отрасли. Вы можете работать на рынке, который является сезонным или непредсказуемым из-за факторов, связанных с экономикой или политическим климатом. Именно здесь экспертная оценка может помочь уменьшить ваши ошибки в прогнозировании.
Например, давайте представим, что вы занимаетесь строительными материалами. Ваша компания производит товары для строительства новых домов, а вы продаете товары новым подрядчикам. Это прекрасный пример отрасли, на которую влияют такие экономические факторы, как доверие потребителей, процентные ставки и демографические тенденции.
Прогнозирование продаж может быть сложным и дорогостоящим, если вы ошибаетесь. Чтобы создать группу экспертов, ищите людей, которые имеют разнообразное и уникальное представление об этой отрасли. Например, вы можете включить людей, которые работают в сфере ипотеки. Вы также можете включить экспертов по недвижимости, которые отслеживают движение рынка покупки жилья. Они дают важную информацию о покупателях и строительных компаниях, которые могут помочь вам с вашим прогнозом.
Когда вы создали группу экспертов, вы должны решить, какую информацию вы хотите от них получать. Хотите ли вы, чтобы оценка строительства нового дома базировалась на национальном, региональном или вашем рынке? Хотите ли вы получать ежегодные, ежеквартальные или ежемесячные данные?
Старайтесь определить, к какой группе экспертов лучше всего обращаться. Любая группа будет иметь разные уровни знаний и опыта, что помогает нейтрализовать искажения в данных. Когда вы получите их индивидуальные прогнозы строительства новых домов в следующем году, вы обнаружите, что все они разные, иногда совсем другие.
Вот совет: главное, не индивидуальный прогноз от каждого члена группы, а то, какие предположения они сделали, чтобы сделать этот прогноз. Вам больше всего нужны их предположения, потому что именно здесь вы найдете самые важные идеи о том, как разработать свой прогноз. На основании их предположений вы сможете решить, какие из них наиболее важны, а какие следует свести к минимуму или, возможно, даже игнорировать. Возьмите важные предположения и найдите способ проверить их.
Как и все методы прогнозирования, речь идет о точности по сравнению с нашей контрольной отметкой – прогнозом по методу ролловер. Вам необходимо отслеживать, как работают эксперты, по сравнению с простым ежемесячным подходом прогнозирования и решить, смогут ли эксперты дать более надежный результат.
Заключение
Правильное прогнозирование продаж – это несложный процесс, просто он требует немного времени для получения правильных данных и применения нескольких простых методов. Чем лучше вы становитесь в этом процессе, тем больше вы помогаете своей компании расти и оставаться конкурентоспособной.