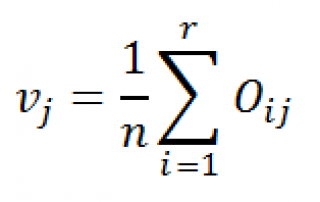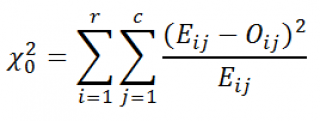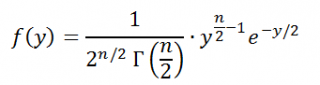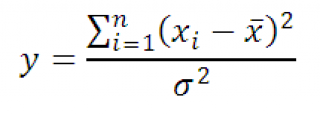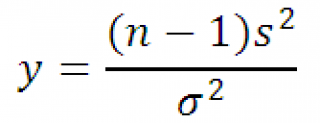Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel Web App Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ХИ2.РАСП в Microsoft Excel.
Описание
Возвращает распределение хи-квадрат.
Функция распределения хи-квадрат обычно используется для изучения вариации в процентах какой-либо величины между выборками — например, части дня, которую люди проводят у телевизора.
Синтаксис
ХИ2.РАСП(x;степени_свободы;интегральная)
Аргументы функции ХИ2.РАСП описаны ниже.
-
X — обязательный аргумент. Значение, для которого требуется вычислить распределение.
-
Степени_свободы — обязательный аргумент. Число степеней свободы.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ХИ2.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
-
Если какой-либо из аргументов не является числом, ХИ2. DIST возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если x имеет отрицательное отношение, ХИ2. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значение степени_свободы не целое, оно усекается.
-
Если deg_freedom < 1 или deg_freedom > 10^10, ХИ2. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ХИ2.РАСП(0,5;1;ИСТИНА) |
Распределение хи-квадрат для 0,5, возвращаемое как интегральная функция распределения с 1 степенью свободы. |
0,52049988 |
|
=ХИ2.РАСП(2;3;ЛОЖЬ) |
Распределение хи-квадрат для 2, возвращаемое как интегральная функция распределения с 3 степенями свободы. |
0,20755375 |
Нужна дополнительная помощь?
Рассмотрим Распределение ХИ-квадрат. С помощью функции MS EXCEL
ХИ2.РАСП()
построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение ХИ-квадрат
(
Х
2
, ХИ2,
англ.
Chi
—
squared
distribution
)
применяется в различных методах математической статистики:
-
при построении
доверительных интервалов для дисперсии
;
-
при
проверке гипотез о дисперсии нормального распределения
;
-
при
проверке гипотез с помощью критерия согласия Пирсона
(согласуются ли эмпирические данные с нашим предположением о теоретической функции распределения или нет, англ. Goodness-of-fit)
-
при
проверке гипотез с помощью критерия независимости хи-квадрат
(используется для определения связи между двумя категориальными переменными, англ. Chi-square test of association).
Определение
: Если x
1
, x
2
, …, x
n
независимые случайные величины, распределенные по
стандартному нормальному закону
N(0;1), то распределение случайной величины Y=x
1
2
+ x
2
2
+…+ x
n
2
имеет
распределение
Х
2
с n степенями свободы.
Распределение
Х
2
зависит от одного параметра, который называется
степенью свободы
(
df
,
degrees
of
freedom
). Например, при построении
доверительных интервалов для оценки дисперсии
число степеней свободы
равно df=n-1, где n – размер
выборки
.
Плотность распределения
Х
2
выражается формулой:
при y>0
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Графики функций
Распределение
Х
2
имеет несимметричную форму,
среднее значение
равно n,
дисперсия
равна 2n.
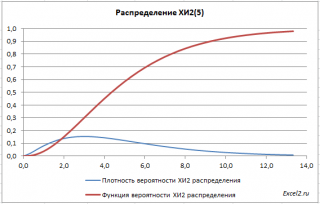
В
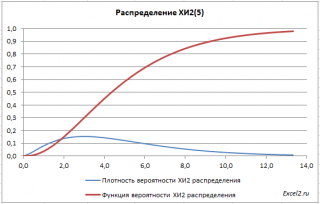
файле примера на листе График
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Полезное свойство
ХИ2-распределения
Пусть x
1
, x
2
, …, x
n
независимые случайные величины, распределенные по
нормальному закону
с одинаковыми параметрами μ и σ, а
X
cр
является
арифметическим средним
этих величин x. Тогда случайная величина
y
равная
Имеет
Х
2
-распределение
с n-1 степенью свободы. Используя определение
дисперсии выборки
вышеуказанное выражение можно переписать следующим образом:
Следовательно,
выборочное распределение
статистики y, при
выборке
из
нормального распределения
, имеет
Х
2
-распределение
с n-1 степенью свободы.
Это свойство нам потребуется при
построении доверительного интервала при оценке дисперсии распределения
. Т.к.
дисперсия
может быть только положительным числом, а
Х
2
-распределение
используется для его оценки, то
y
д.б. >0, как и указано в определении.
ХИ2-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Х
2
-распределения
имеется специальная функция
ХИ2.РАСП()
, английское название – CHISQ.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина Х, имеющая
ХИ2
—
распределение
, примет значение меньше или равное х, P{X <= x}).
Примечание
: Т.к.
ХИ2-распределение
является частным случаем
гамма распределения
, то формула
=ГАММА.РАСП(x;n/2;2;ИСТИНА)
для целого положительного n возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ИСТИНА)
или
=1-ХИ2.РАСП.ПХ(x;n)
. А формула
=ГАММА.РАСП(x;n/2;2;ЛОЖЬ)
возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ЛОЖЬ)
, т.е.
плотность вероятности
ХИ2-распределения.
Функция
ХИ2.РАСП.ПХ()
возвращает
функцию распределения
, точнее — правостороннюю вероятность, т.е. P{X > x}. Очевидно, что справедливо равенство
=ХИ2.РАСП.ПХ(x;n)+ ХИ2.РАСП(x;n;ИСТИНА)=1
т.к. первое слагаемое вычисляет вероятность P{X > x}, а второе P{X <= x}.
До MS EXCEL 2010 в EXCEL была только функция
ХИ2РАСП()
, которая позволяет вычислить правостороннюю вероятность, т.е. P{X > x}. Возможности новых функций MS EXCEL 2010
ХИ2.РАСП()
и
ХИ2.РАСП.ПХ()
перекрывают возможности этой функции. Функция
ХИ2РАСП()
оставлена в MS EXCEL 2010 для совместимости.
ХИ2.РАСП()
является единственной функцией, которая возвращает
плотность вероятности ХИ2-распределения
(третий аргумент должен быть равным ЛОЖЬ). Остальные функции возвращают
интегральную функцию распределения
, т.е. вероятность того, что случайная величина примет значение из указанного диапазона: P{X <= x}.
Вышеуказанные функции MS EXCEL приведены в
файле примера на листе Функции
.
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного
x
: P{X <= x}. Это можно сделать несколькими функциями:
= ХИ2.РАСП(x; n; ИСТИНА) =1-ХИ2.РАСП.ПХ(x; n)=1-ХИ2РАСП(x; n)
Функция
ХИ2.РАСП.ПХ()
возвращает вероятность P{X > x}, так называемую правостороннюю вероятность, поэтому, чтобы найти P{X <= x}, необходимо вычесть ее результат от 1.
Найдем вероятность, что случайная величина Х примет значение больше заданного
x
: P{X > x}. Это можно сделать несколькими функциями:
= 1-ХИ2.РАСП(x; n; ИСТИНА) =ХИ2.РАСП.ПХ(x; n)=ХИ2РАСП(x; n)
Обратная функция ХИ2-распределения
Обратная функция используется для вычисления
альфа
—
квантилей
, т.е. для вычисления значений
x
при заданной вероятности
альфа
, причем
х
должен удовлетворять выражению P{X <= x}=
альфа
.
Функция
ХИ2.ОБР()
используется для вычисления
доверительных интервалов дисперсии нормального распределения
.
Функция
ХИ2.ОБР.ПХ()
используется для вычисления
верхнего квантиля
, т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого P{X>x}=0,05. В качестве сравнения: функция
ХИ2.ОБР()
вернет такое значение случайной величины х, для которого P{X<=x}=0,05.
В MS EXCEL 2007 и ранее вместо
ХИ2.ОБР.ПХ()
использовалась функция
ХИ2ОБР()
.
Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают один и тот же результат:
=ХИ.ОБР(альфа;n) =ХИ2.ОБР.ПХ(1-альфа;n) =ХИ2ОБР(1- альфа;n)
Некоторые примеры расчетов приведены в
файле примера на листе Функции
.
Функции MS EXCEL, использующие ХИ2-распределение
В MS EXCEL имеется еще одна функция, использующая для расчетов
ХИ2-распределение
– это
ХИ2.ТЕСТ()
. Ее более ранняя версия —
ХИ2ТЕСТ()
. Подробнее об использовании этой функции см.
статью про критерий независимости хи-квадрат
.
Ниже приведено соответствие русских и английских названий функций:
ХИ2.РАСП.ПХ()
— англ. название CHISQ.DIST.RT, т.е. CHI-SQuared DISTribution Right Tail, the right-tailed Chi-square(d) distribution
ХИ2.ОБР()
— англ. название CHISQ.INV, т.е. CHI-SQuared distribution INVerse
ХИ2.ПХ.ОБР()
— англ. название CHISQ.INV.RT, т.е. CHI-SQuared distribution INVerse Right Tail
ХИ2РАСП()
— англ. название CHIDIST, функция эквивалентна CHISQ.DIST.RT
ХИ2ОБР()
— англ. название CHIINV, т.е. CHI-SQuared distribution INVerse
Оценка параметров распределения
Т.к. обычно
ХИ2-распределение
используется для целей математической статистики (вычисление
доверительных интервалов,
проверки гипотез и др.),
и практически никогда для построения моделей реальных величин, то для этого распределения обсуждение оценки параметров распределения здесь не производится.
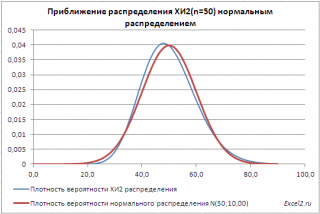
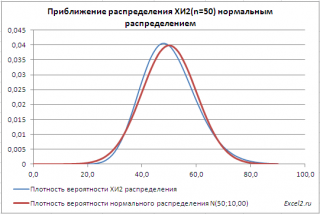
Приближение ХИ2-распределения нормальным распределением
При числе степеней свободы n>30
распределение Х
2
хорошо аппроксимируется
нормальным распределением
со
средним значением
μ=n и
дисперсией σ
=2*n (см.
файл примера лист Приближение
).
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
17 авг. 2022 г.
читать 2 мин
Хи-квадрат критерий согласия используется для определения того, следует ли категориальная переменная гипотетическому распределению.
В этом руководстве объясняется, как выполнить критерий согласия Хи-квадрат в Excel.
Пример: критерий согласия хи-квадрат в Excel
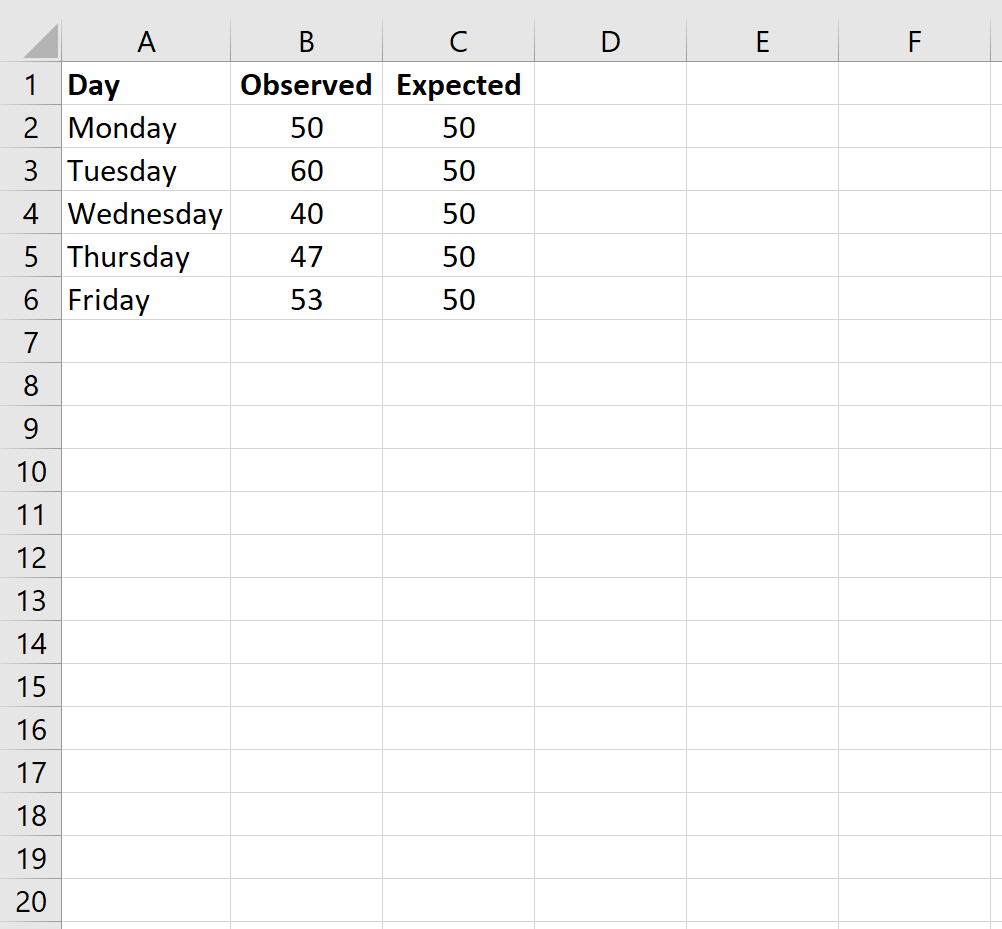
Владелец магазина утверждает, что каждый будний день в его магазин приходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, независимый исследователь записывает количество покупателей, которые заходят в магазин на определенной неделе, и обнаруживает следующее:
- Понедельник: 50 клиентов
- вторник: 60 клиентов
- Среда: 40 клиентов
- Четверг: 47 клиентов
- Пятница: 53 клиента
Мы будем использовать следующие шаги, чтобы выполнить критерий согласия Хи-квадрат, чтобы определить, согласуются ли данные с заявлением владельца магазина.
Шаг 1: Введите данные.
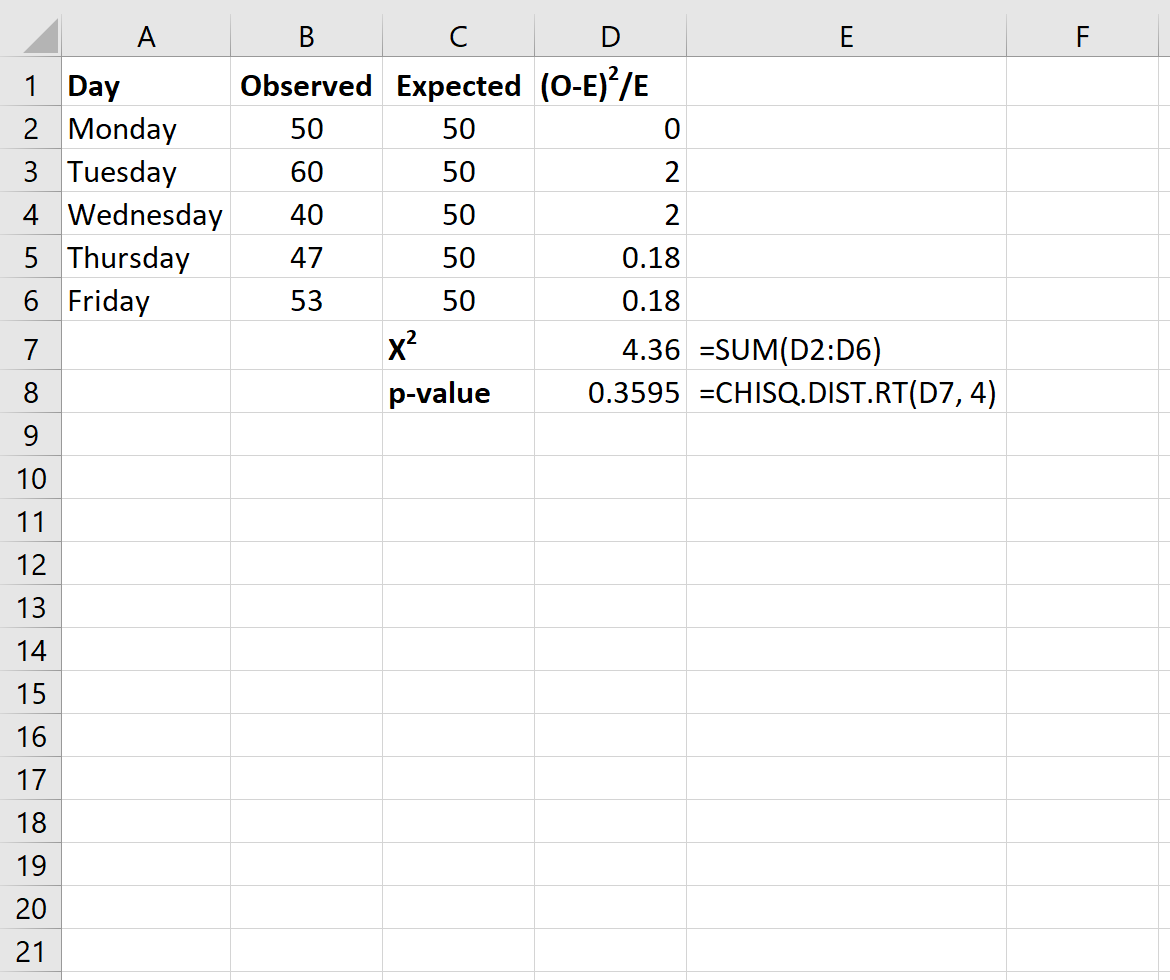
Во-первых, мы будем вводить значения данных для ожидаемого количества клиентов каждый день в одном столбце и наблюдаемое количество клиентов каждый день в другом столбце:
Примечание. Всего было 250 клиентов. Таким образом, если владелец магазина ожидает, что каждый день в магазин будет приходить такое же количество покупателей, то он ожидает 50 покупателей в день.
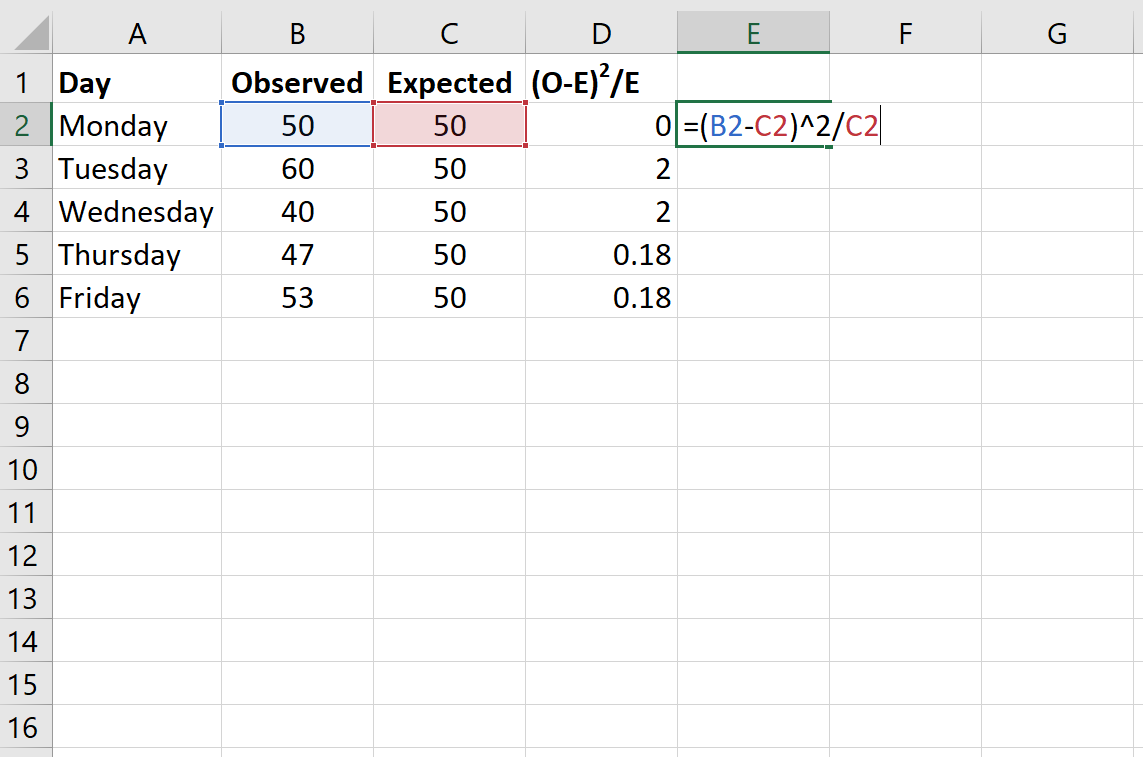
Шаг 2: Найдите разницу между наблюдаемыми и ожидаемыми значениями.
Статистика критерия хи-квадрат для теста согласия равна X 2 = Σ(OE) 2 / E
куда:
- Σ: причудливый символ, означающий «сумма».
- O: наблюдаемое значение
- E: ожидаемое значение
Следующая формула показывает, как рассчитать (OE) 2 / E для каждой строки:
Шаг 3: Рассчитайте статистику теста хи-квадрат и соответствующее значение p.
Наконец, мы рассчитаем статистику теста хи-квадрат вместе с соответствующим значением p, используя следующие формулы:
Примечание. Функция Excel ХИ.РАСП.ВР(x, степень_свободы) возвращает правостороннюю вероятность распределения хи-квадрат, связанную с тестовой статистикой x и определенными степенями свободы. Степени свободы рассчитываются как n-1. В этом случае deg_freedom = 5 – 1 = 4.
Шаг 4: Интерпретируйте результаты.
Статистика теста X 2 для теста составляет 4,36 , а соответствующее значение p равно 0,3595.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что истинное распределение покупателей отличается от распределения, о котором заявил владелец магазина.
This step-by-step tutorial explains how to plot the following Chi-Square distribution in Excel:
Step 1: Define the X Values
First, let’s define a range of x-values to use for our plot.
For this example, we’ll create a range from 0 to 20:
Step 2: Calculate the Y Values
The y values on the plot will represent the PDF values associated with the Chi-Square distribution.
We can type the following formula into cell B2 to calculate the PDF value of the Chi-Square distribution associated with an x value of 0 and a degrees of freedom value of 3:
=CHISQ.DIST(A2, $E$1, FALSE)
We can then copy and paste this formula down to every remaining cell in column B:
Step 3: Plot the Chi-Square Distribution
Next, highlight the cell range A2:B22, then click the Insert tab along the top ribbon, then click the Scatter option within the Charts group and click Scatter with Smooth Lines:
The following chart will be created:
The x-axis shows the values of a random variable that follows a Chi-Square distribution with 3 degrees of freedom and the y-axis shows the corresponding PDF values of the Chi-Square distribution.
Note that if you change the value for the degrees of freedom in cell E1, the chart will automatically update.
For example, we could change the degrees of freedom to 7:
Notice that the shape of the plot automatically changes to reflect a Chi-Square distribution with 7 degrees of freedom.
Step 4: Modify the Appearance of the Plot
Feel free to add a title, axis labels, and remove the gridlines to make the plot more aesthetically pleasing:
Additional Resources
The following tutorials explain how to plot other common distributions in Excel:
How to Plot a Bell Curve in Excel
How to Plot a Binomial Distribution in Excel
How to Plot a Poisson Distribution in Excel
Содержание
- Критерий независимости хи-квадрат в EXCEL
- Распределение ХИ-квадрат. Распределения математической статистики в EXCEL
- Графики функций
- Полезное свойство ХИ2-распределения
- ХИ2-распределение в MS EXCEL
- Примеры
- Обратная функция ХИ2-распределения
- Функции MS EXCEL, использующие ХИ2-распределение
- Оценка параметров распределения
- Приближение ХИ2-распределения нормальным распределением
Критерий независимости хи-квадрат в EXCEL
history 14 декабря 2016 г.
Критерий независимости хи-квадрат используется для определения связи между двумя категориальными переменными. Примерами пар категориальных переменных являются: Семейное положение vs. Уровень занятости респондента; Порода собак vs. Профессия хозяина, Уровень з/п vs. Специализация инженера и др. При вычислении критерия независимости проверяется гипотеза о том, что между переменными связи нет. Вычисления будем производить с помощью функции MS EXCEL 2010 ХИ2.ТЕСТ() и обычными формулами.
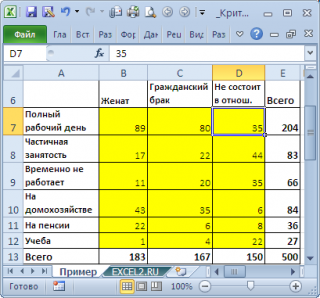
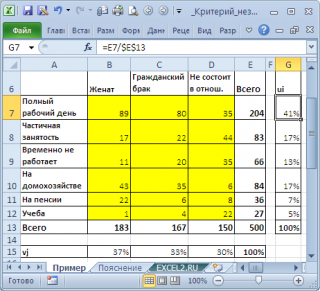
Предположим у нас есть выборка данных, представляющая результат опроса 500 человек. Людям задавалось 2 вопроса: про их семейное положение (женаты, гражданский брак, не состоят в отношениях) и их уровень занятости (полный рабочий день, частичная занятость, временно не работает, на домохозяйстве, на пенсии, учеба). Все ответы поместили в таблицу:
Данная таблица называется таблицей сопряжённости признаков (или факторной таблицей, англ. Contingency table). Элементы на пересечении строк и столбцов таблицы обычно обозначают O ij (от англ. Observed, т.е. наблюденные, фактические частоты).
Нас интересует вопрос «Влияет ли Семейное положение на Занятость?», т.е. существует ли зависимость между двумя методами классификации выборки ?
При проверке гипотез такого вида обычно принимают, что нулевая гипотеза утверждает об отсутствии зависимости способов классификации.
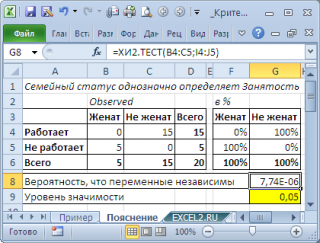
Рассмотрим предельные случаи. Примером полной зависимости двух категориальных переменных является вот такой результат опроса:
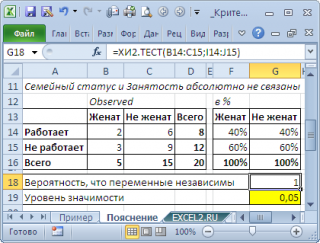
В этом случае семейное положение однозначно определяет занятость (см. файл примера лист Пояснение ). И наоборот, примером полной независимости является другой результат опроса:
Обратите внимание, что процент занятости в этом случае не зависит от семейного положения (одинаков для женатых и не женатых). Это как раз совпадает с формулировкой нулевой гипотезы . Если нулевая гипотеза справедлива, то результаты опроса должны были бы так распределиться в таблице, что процент занятых был бы одинаковым независимо от семейного положения. Используя это, вычислим результаты опроса, которые соответствуют нулевой гипотезе (см. файл примера лист Пример ).
Сначала вычислим оценку вероятности, того, что элемент выборки будет иметь определенную занятость (см. столбец u i ):
где с – количество столбцов (columns), равное количеству уровней переменной «Семейное положение».
Затем вычислим оценку вероятности, того, что элемент выборки будет иметь определенное семейное положение (см. строку v j ).
где r – количество строк (rows), равное количеству уровней переменной «Занятость».
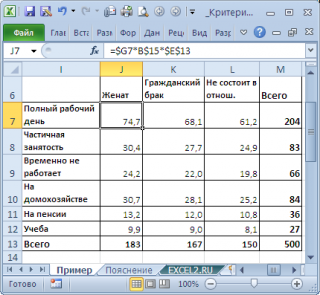
Теоретическая частота для каждой ячейки E ij (от англ. Expected, т.е. ожидаемая частота) в случае независимости переменных вычисляется по формуле: E ij =n* u i * v j
Известно, что статистика Х 2 0 при больших n имеет приблизительно ХИ2-распределение с (r-1)(c-1) степенями свободы (df – degrees of freedom):
Примечание : Вышеуказанная статистика при с=1 используется для вычисления критерия согласия Пирсона ХИ-квадрат (см. статью Проверка гипотез критерием хи-квадрат Пирсона в MS EXCEL ).
Если вычисленное на основе выборки значение этой статистики «слишком большое» (больше порогового), то нулевая гипотеза отвергается. Пороговое значение вычисляется на основании уровня значимости , например с помощью формулы =ХИ2.ОБР.ПХ(0,05; df) .
Примечание : Уровень значимости обычно принимается равным 0,1; 0,05; 0,01.
При проверке гипотезы также удобно вычислять p-значение , которое мы сравниваем с уровнем значимости . p -значение рассчитывается с использованием ХИ2-распределения с (r-1)*(c-1)=df степеней свободы.
Если вероятность, того что случайная величина имеющая ХИ2-распределение с (r-1)(c-1) степенями свободы примет значение больше вычисленной статистики Х 2 0 , т.е. P <Х 2 (r-1)*(c-1) >Х 2 0 >, меньше уровня значимости , то нулевая гипотеза отклоняется.
В MS EXCEL p-значение можно вычислить с помощью формулы =ХИ2.РАСП.ПХ(Х 2 0 ;df) , конечно, вычислив непосредственно перед этим значение статистики Х 2 0 (это сделано в файле примера ). Однако, удобнее всего воспользоваться функцией ХИ2.ТЕСТ() . В качестве аргументов этой функции указываются ссылки на диапазоны содержащие фактические (Observed) и вычисленные теоретические частоты (Expected).
Если уровень значимости > p -значения , то означает это фактические и теоретические частоты, вычисленные из предположения справедливости нулевой гипотезы , серьезно отличаются. Поэтому, нулевую гипотезу нужно отклонить.
Использование функции ХИ2.ТЕСТ() позволяет ускорить процедуру проверки гипотез , т.к. не нужно вычислять значение статистики . Теперь достаточно сравнить результат функции ХИ2.ТЕСТ() с заданным уровнем значимости .
Примечание : Функция ХИ2.ТЕСТ() , английское название CHISQ.TEST, появилась в MS EXCEL 2010. Ее более ранняя версия ХИ2ТЕСТ() , доступная в MS EXCEL 2007 имеет тот же функционал. Но, как и для ХИ2.ТЕСТ() , теоретические частоты нужно вычислить самостоятельно.
СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .
Источник
Распределение ХИ-квадрат. Распределения математической статистики в EXCEL
history 12 ноября 2016 г.
Рассмотрим Распределение ХИ-квадрат. С помощью функции MS EXCEL ХИ2.РАСП() построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение ХИ-квадрат ( Х 2 , ХИ2, англ. Chi — squared distribution ) применяется в различных методах математической статистики:
- при построении доверительных интервалов для дисперсии ;
- при проверке гипотез о дисперсии нормального распределения ;
- при проверке гипотез с помощью критерия согласия Пирсона (согласуются ли эмпирические данные с нашим предположением о теоретической функции распределения или нет, англ. Goodness-of-fit)
- при проверке гипотез с помощью критерия независимости хи-квадрат (используется для определения связи между двумя категориальными переменными, англ. Chi-square test of association).
Определение : Если x 1 , x 2 , …, x n независимые случайные величины, распределенные по стандартному нормальному закону N(0;1), то распределение случайной величины Y=x 1 2 + x 2 2 +…+ x n 2 имеет распределение Х 2 с n степенями свободы.
Распределение Х 2 зависит от одного параметра, который называется степенью свободы ( df , degrees of freedom ). Например, при построении доверительных интервалов для оценки дисперсии число степеней свободы равно df=n-1, где n – размер выборки .
Плотность распределения Х 2 выражается формулой:
Графики функций
Распределение Х 2 имеет несимметричную форму, среднее значение равно n, дисперсия равна 2n.
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Полезное свойство ХИ2-распределения
Пусть x 1 , x 2 , …, x n независимые случайные величины, распределенные по нормальному закону с одинаковыми параметрами μ и σ, а X cр является арифметическим средним этих величин x. Тогда случайная величина y равная
Имеет Х 2 -распределение с n-1 степенью свободы. Используя определение дисперсии выборки вышеуказанное выражение можно переписать следующим образом:
Следовательно, выборочное распределение статистики y, при выборке из нормального распределения , имеет Х 2 -распределение с n-1 степенью свободы.
Это свойство нам потребуется при построении доверительного интервала при оценке дисперсии распределения . Т.к. дисперсия может быть только положительным числом, а Х 2 -распределение используется для его оценки, то y д.б. >0, как и указано в определении.
ХИ2-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Х 2 -распределения имеется специальная функция ХИ2.РАСП() , английское название – CHISQ.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина Х, имеющая ХИ2 — распределение , примет значение меньше или равное х, P : Т.к. ХИ2-распределение является частным случаем гамма распределения , то формула =ГАММА.РАСП(x;n/2;2;ИСТИНА) для целого положительного n возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ИСТИНА) или =1-ХИ2.РАСП.ПХ(x;n) . А формула =ГАММА.РАСП(x;n/2;2;ЛОЖЬ) возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ЛОЖЬ) , т.е. плотность вероятности ХИ2-распределения.
Функция ХИ2.РАСП.ПХ() возвращает функцию распределения , точнее — правостороннюю вероятность, т.е. P x>. Очевидно, что справедливо равенство =ХИ2.РАСП.ПХ(x;n)+ ХИ2.РАСП(x;n;ИСТИНА)=1 т.к. первое слагаемое вычисляет вероятность P x>, а второе P x>. Возможности новых функций MS EXCEL 2010 ХИ2.РАСП() и ХИ2.РАСП.ПХ() перекрывают возможности этой функции. Функция ХИ2РАСП() оставлена в MS EXCEL 2010 для совместимости.
ХИ2.РАСП() является единственной функцией, которая возвращает плотность вероятности ХИ2-распределения (третий аргумент должен быть равным ЛОЖЬ). Остальные функции возвращают интегральную функцию распределения , т.е. вероятность того, что случайная величина примет значение из указанного диапазона: P
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного x : P x>, так называемую правостороннюю вероятность, поэтому, чтобы найти P. Это можно сделать несколькими функциями:
= 1-ХИ2.РАСП(x; n; ИСТИНА) =ХИ2.РАСП.ПХ(x; n)=ХИ2РАСП(x; n)
Обратная функция ХИ2-распределения
Обратная функция используется для вычисления альфа — квантилей , т.е. для вычисления значений x при заданной вероятности альфа , причем х должен удовлетворять выражению P доверительных интервалов дисперсии нормального распределения .
Функция ХИ2.ОБР.ПХ() используется для вычисления верхнего квантиля , т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого Px>=0,05. В качестве сравнения: функция ХИ2.ОБР() вернет такое значение случайной величины х, для которого P
Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают один и тот же результат: =ХИ.ОБР(альфа;n) =ХИ2.ОБР.ПХ(1-альфа;n) =ХИ2ОБР(1- альфа;n)
Некоторые примеры расчетов приведены в файле примера на листе Функции .
Функции MS EXCEL, использующие ХИ2-распределение
В MS EXCEL имеется еще одна функция, использующая для расчетов ХИ2-распределение – это ХИ2.ТЕСТ() . Ее более ранняя версия — ХИ2ТЕСТ() . Подробнее об использовании этой функции см. статью про критерий независимости хи-квадрат .
Ниже приведено соответствие русских и английских названий функций: ХИ2.РАСП.ПХ() — англ. название CHISQ.DIST.RT, т.е. CHI-SQuared DISTribution Right Tail, the right-tailed Chi-square(d) distribution ХИ2.ОБР() — англ. название CHISQ.INV, т.е. CHI-SQuared distribution INVerse ХИ2.ПХ.ОБР() — англ. название CHISQ.INV.RT, т.е. CHI-SQuared distribution INVerse Right Tail ХИ2РАСП() — англ. название CHIDIST, функция эквивалентна CHISQ.DIST.RT ХИ2ОБР() — англ. название CHIINV, т.е. CHI-SQuared distribution INVerse
Оценка параметров распределения
Т.к. обычно ХИ2-распределение используется для целей математической статистики (вычисление доверительных интервалов, проверки гипотез и др.), и практически никогда для построения моделей реальных величин, то для этого распределения обсуждение оценки параметров распределения здесь не производится.
Приближение ХИ2-распределения нормальным распределением
При числе степеней свободы n>30 распределение Х 2 хорошо аппроксимируется нормальным распределением со средним значением μ=n и дисперсией σ =2*n (см. файл примера лист Приближение ).
Источник