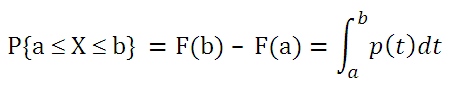Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
17 авг. 2022 г.
читать 2 мин
Распределение частоты описывает, как часто разные значения встречаются в наборе данных. Это полезный способ понять, как значения данных распределяются в наборе данных.
К счастью, легко создать и визуализировать частотное распределение в Excel, используя следующую функцию:
=ЧАСТОТА(массив_данных,массив_бинов)
куда:
- data_array : массив необработанных значений данных
- bins_array: массив верхних пределов для бинов
В следующем примере показано, как использовать эту функцию на практике.
Пример: частотное распределение в Excel
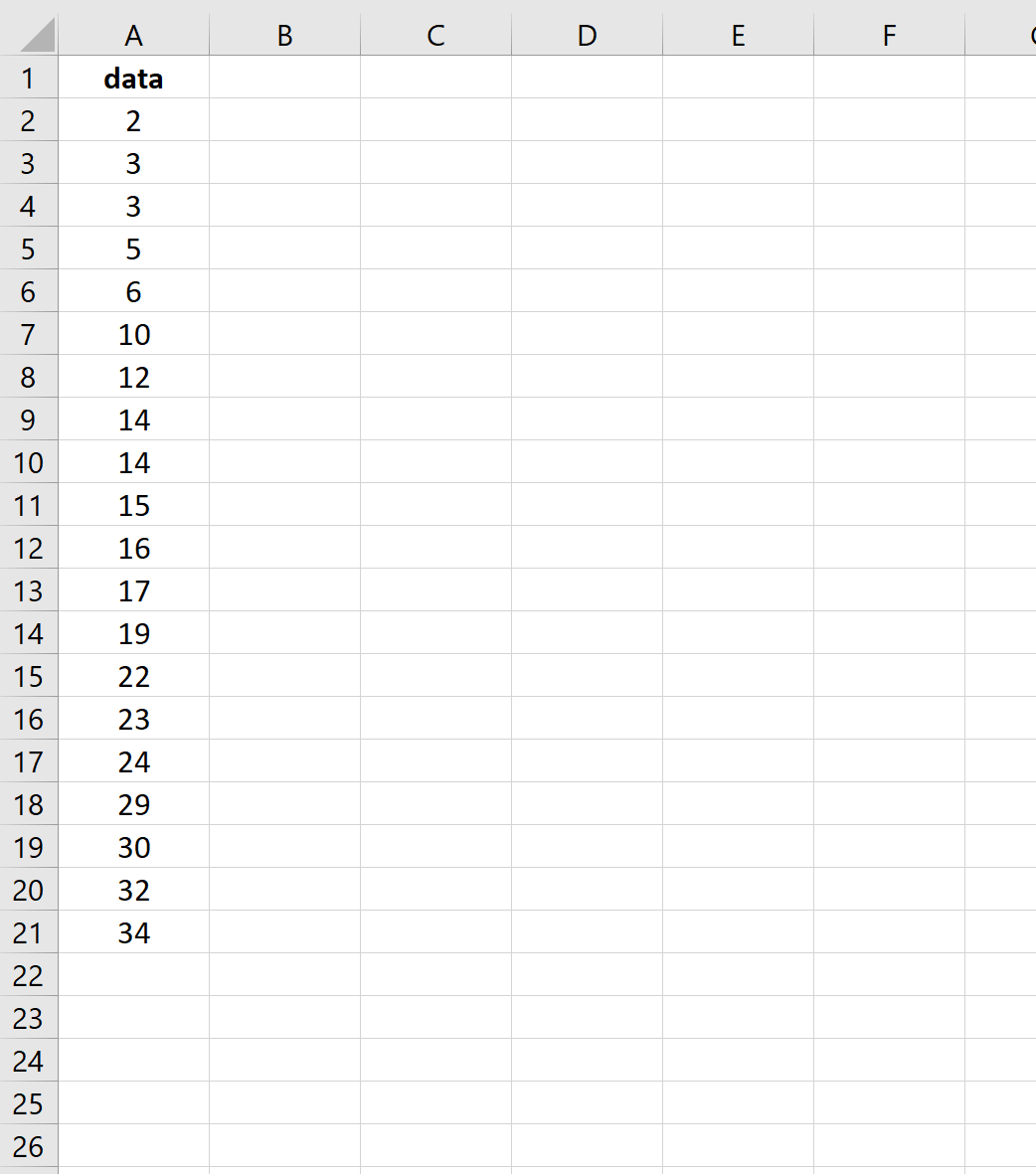
Предположим, у нас есть следующий набор данных из 20 значений в Excel:
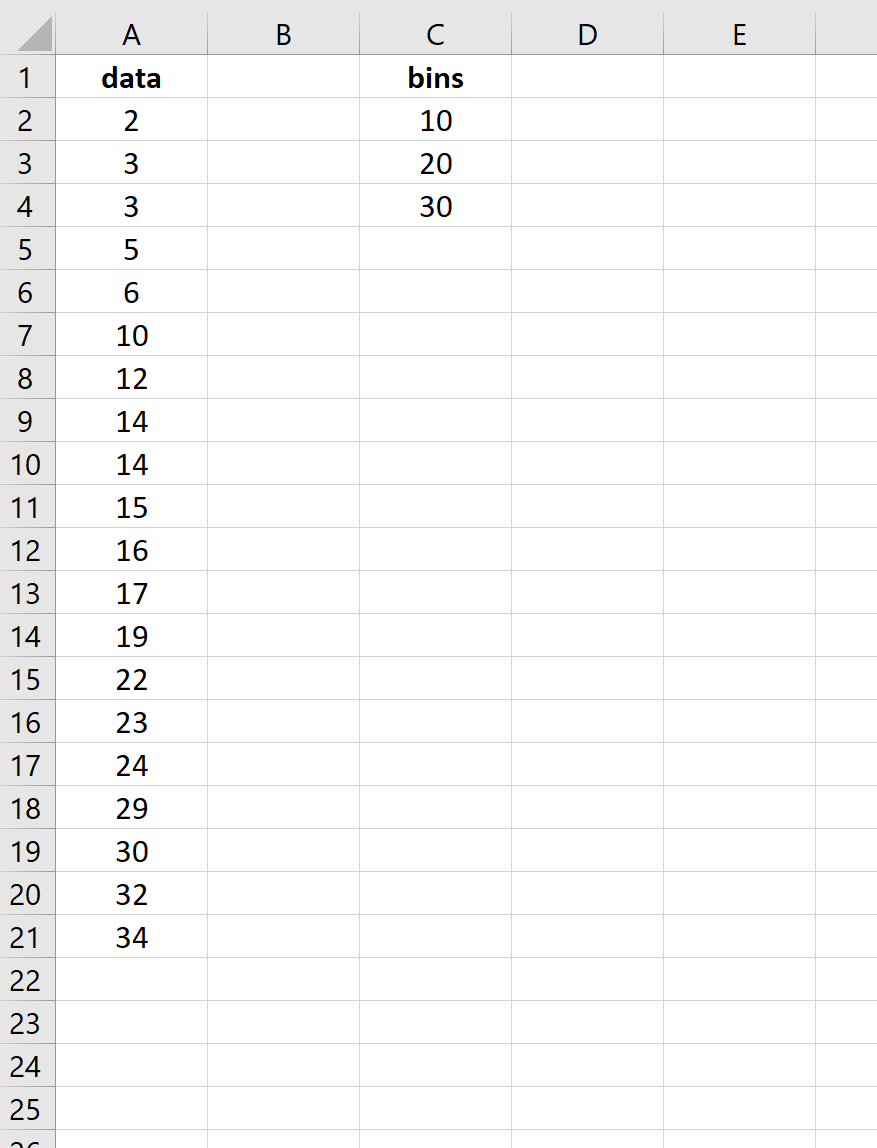
Во-первых, мы укажем Excel, какие верхние пределы мы хотели бы использовать для интервалов нашего частотного распределения. Для этого примера мы выберем 10, 20 и 30. То есть мы найдем частоты для следующих интервалов:
- от 0 до 10
- с 11 до 20
- от 21 до 30
- 30+
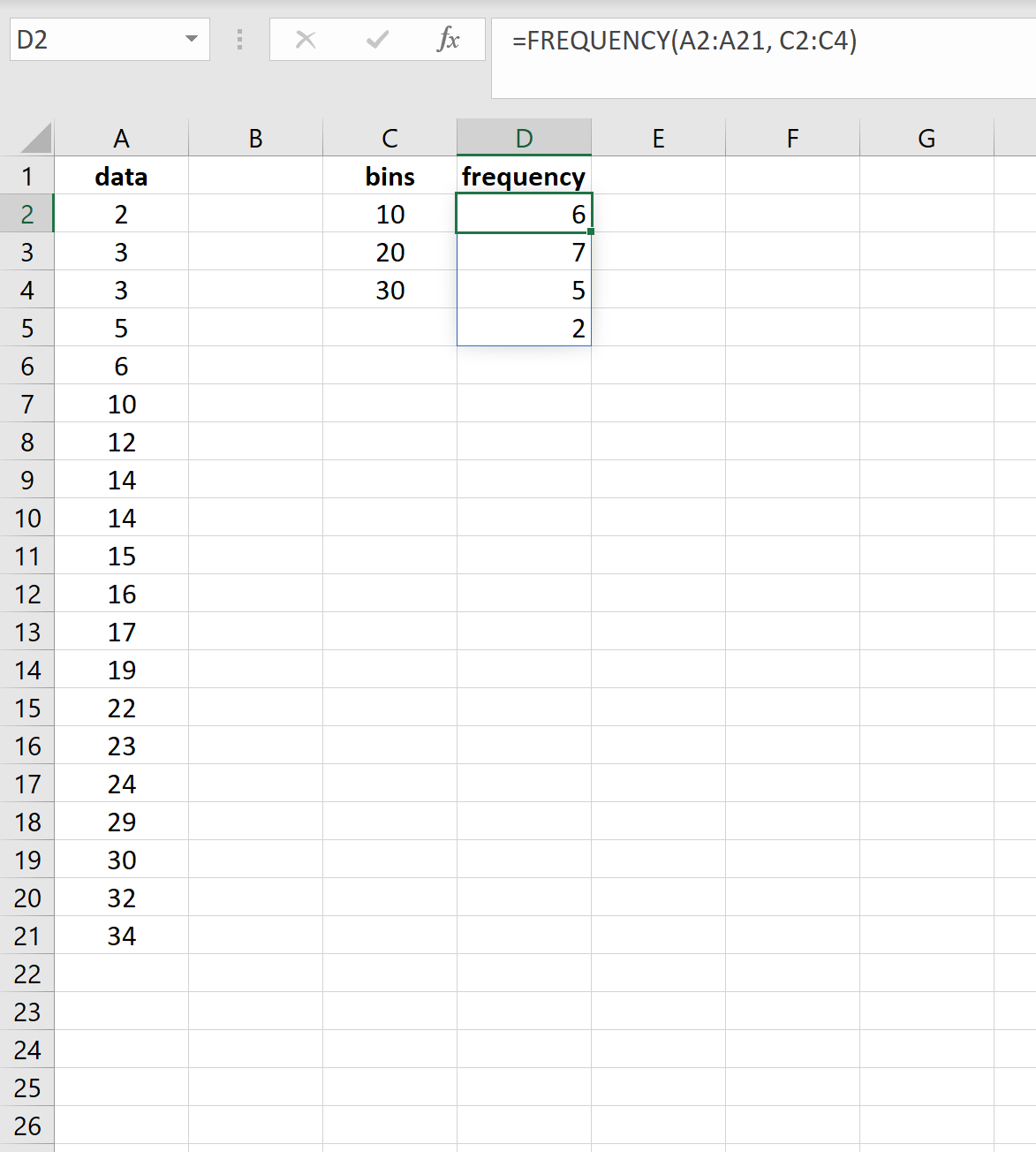
Далее мы будем использовать следующую функцию =FREQUENCY() для вычисления частот для каждого бина:
=ЧАСТОТА( A2:A21 , C2:C4 )
Вот результаты:
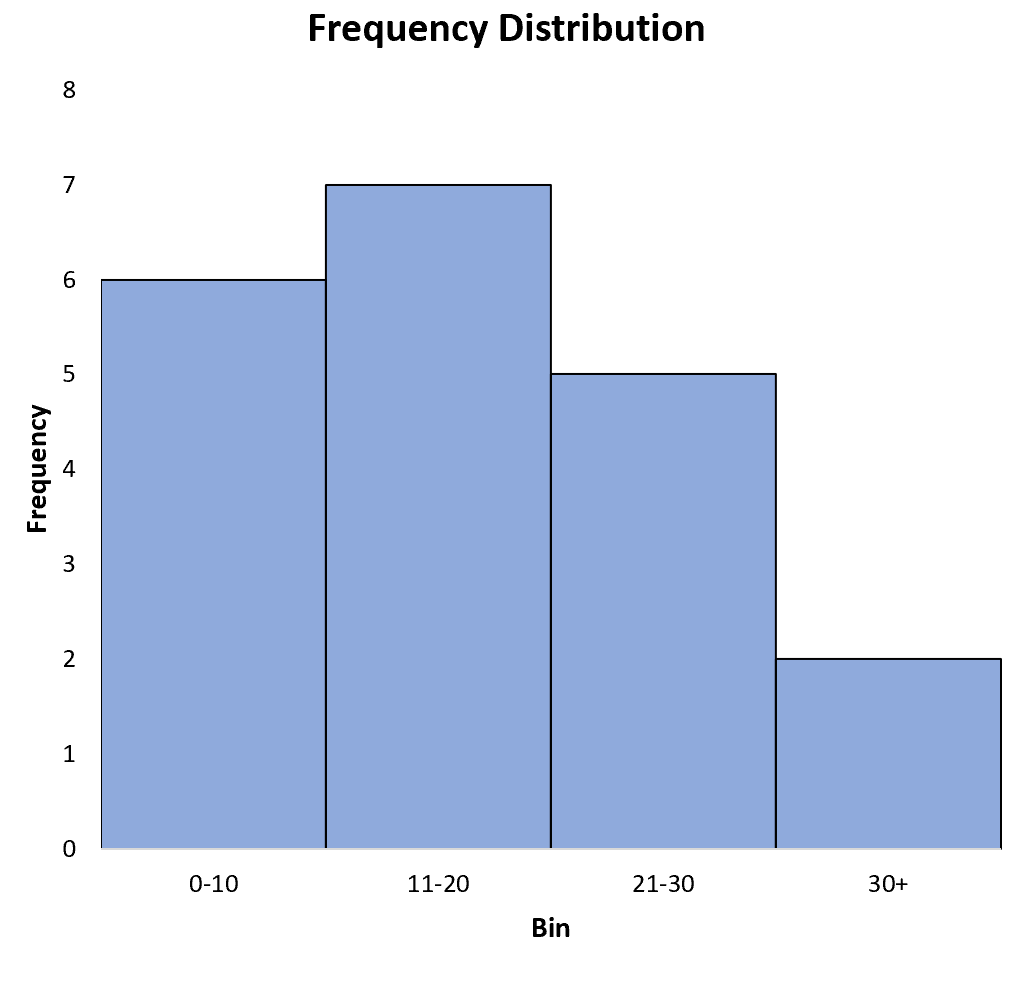
Результаты показывают, что:
- 6 значений в наборе данных находятся в диапазоне от 0 до 10.
- 7 значений в наборе данных находятся в диапазоне 11-20.
- 5 значений в наборе данных находятся в диапазоне 21-30.
- 2 значения в наборе данных больше 30.
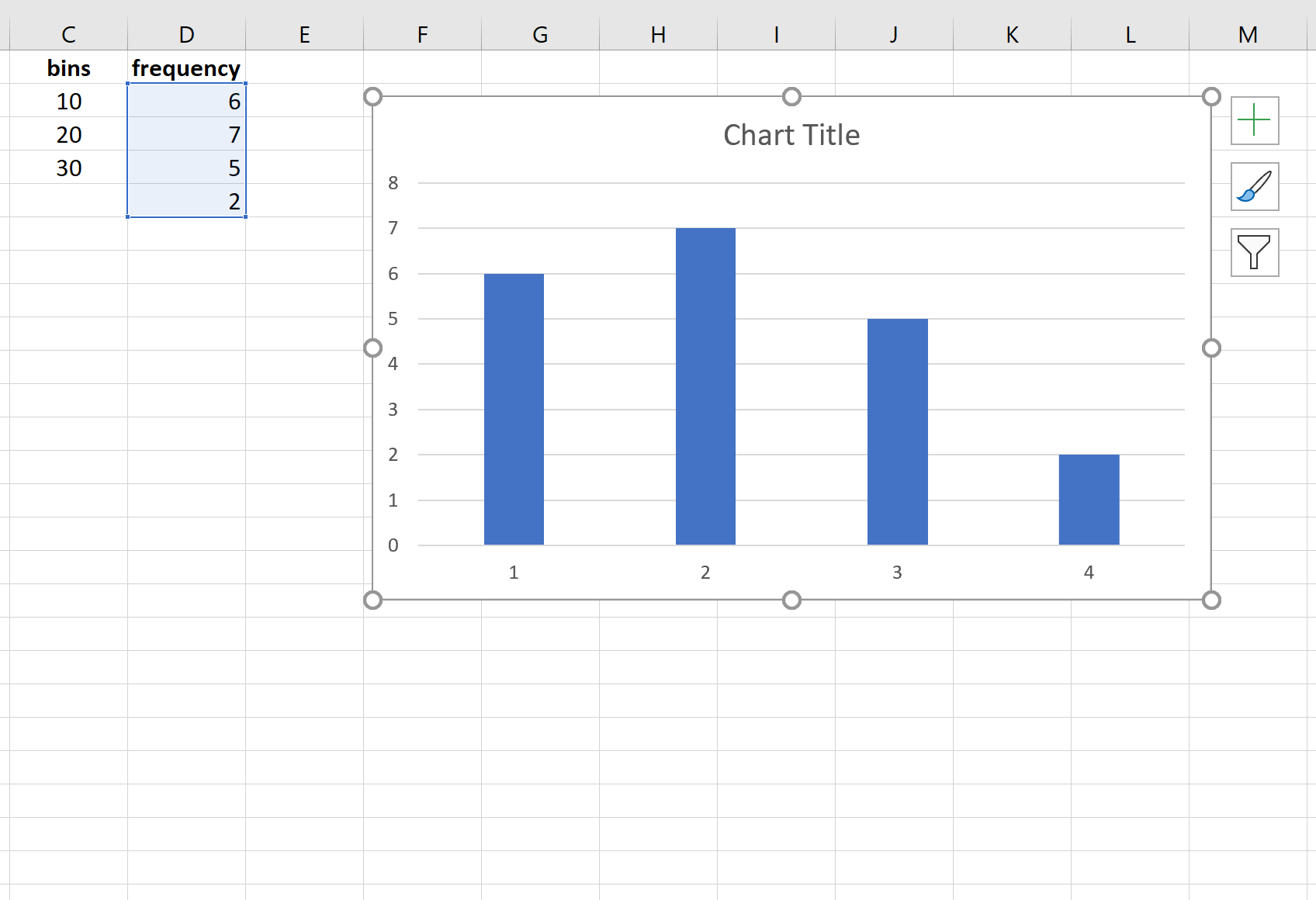
Затем мы можем использовать следующие шаги для визуализации этого частотного распределения:
- Выделите частоты в диапазоне D2:D5 .
- Нажмите на вкладку « Вставка », затем нажмите на диаграмму под названием « Двухмерный столбец » в группе « Диаграммы ».
Появится следующая диаграмма, отображающая частоты для каждого бина:
Не стесняйтесь изменять метки осей и ширину полос, чтобы сделать диаграмму более эстетичной:
Вы можете найти больше учебников по Excel здесь .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
A frequency distribution table is an organized representation of the frequency of each element in a dataset/record. It helps us to visualize data in terms of class range and the number of time each element belong to that class interval. The table usually consists of two columns, the first is the class interval and the second one is the frequency itself.
Calculate Frequency Distribution in Excel
Suppose, we want to distribute marks obtained by 40 students in a class using a frequency distribution table then a sampling frequency distribution table will look like this:
|
Marks |
Frequency |
|---|---|
|
0-20 |
5 |
|
21-40 |
7 |
|
41-60 |
13 |
|
61-80 |
9 |
|
81-100 |
6 |
In this article, we are going to see how we can calculate such a frequency distribution table inside Microsoft Excel.
Method 1: Using Pivot Table
Microsoft Excel has a powerful tool named Pivot table which helps users to analyze large amounts of data interactively by aggregating individual records of a table into different groups. A pivot table can be used to create a frequency distribution table as:
Step 1: Select the desired range of cells and then go to the Insert tab and select Pivot Table from the menu.
Step 2: A Create Pivot Table dialog box will pop up on the screen. Since we want to create the pivot table in the same worksheet. We can choose the Existing Worksheet radio check box in the dialog box and select the desired cell where we want to place the table (in the image shown below cell D1 is selected).
Step 3: A pivot table will become visible on the screen as shown in the image given below.
Step 4: From the right-hand side PivotTable Fields prompt, drag the Scores field name into the Values field and the Rows field one by one.
Step 5: We can notice the changes made in our pivot table. Now, right-click on the Sum of Scores field inside the Values section and select the Field Settings option from the menu.
Step 6: A Pivot Table Field dialog box will appear on the screen. Select the Count option from the list under the Summarise by tab and click OK.
Step 7: After hitting the OK button, we can notice the changes made to our pivot table. Now for each element, we have its frequency inside the table.
Step 8: Under the Row Labels column inside the pivot table select any record and right-click with the mouse to open a list of options. From the options menu, select the Group option.
Step 9: A dialog box named Grouping will appear on the screen. Fill out the starting and ending values in the respective fields. Since we want to divide our data into intervals of 10 hence we fill 10 in the “By” field and then click OK.
Step 10: On clicking the OK button, we can notice our data values are distributed across an interval and hence our final frequency distribution table is created.
Method 2: Using the COUNTIFS() function
We can even use the in-built COUNTIFS() function to create a frequency distribution table.
The syntax for the COUNTIFS() function is given as:
=COUNTIFS(range1,criteria1,range2,criteria2,….)
Where range1 and range2 are the cell range of the records and criteria1 and criteria2 are the logical expressions.
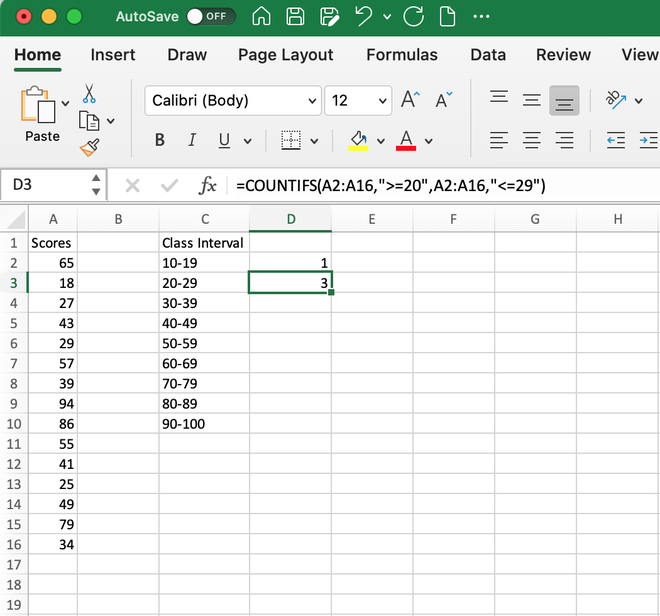
Step 1: Create a class Interval column manually assigning the appropriate values as per requirement.
Step 2: Now, click on the desired cell where you want to find out the frequency in the class interval (here, cell D2). Type the formula
=COUNTIFS(A2:A16,”>=10″,A2:A16,”<=19″)
And hit enter, it will generate the output 1 as only 18 is in the class range 10-19. Here, A2:A16 is the range as our data is stored in this cell we give A2:A16 as the range1 and range2 values, criteria1 is >=10 and criteria2 is <=19.
Step 3: Similarly, we can use the same COUNTIFS() formula for the next cells. Let’s say we want to find the count of records between the interval 20-29, then the formula will be,
=COUNTIFS(A2:A16,”>=20″,A2:A16,”<=29″)
It will generate 3 as the output as three numbers 25, 27 and 29 lie within this class interval.
Step 4: We can use the same formula for finding the values for all class intervals and our values will be shown as:
Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
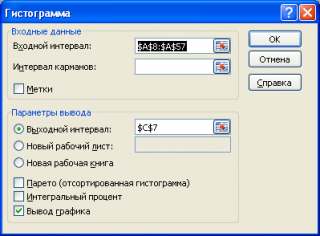
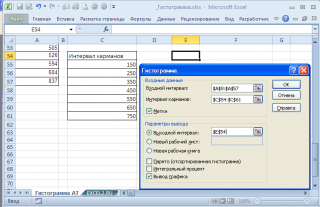
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
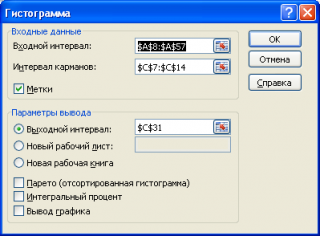
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
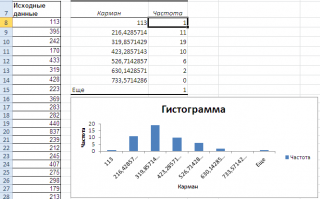
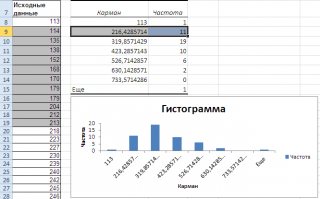
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
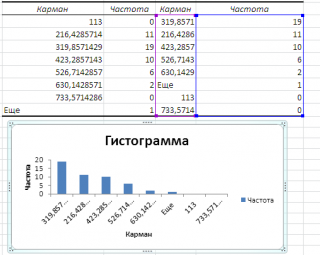
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
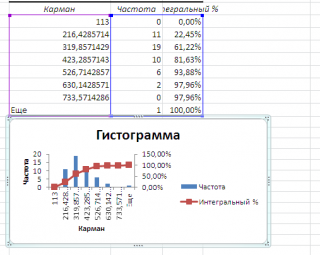
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
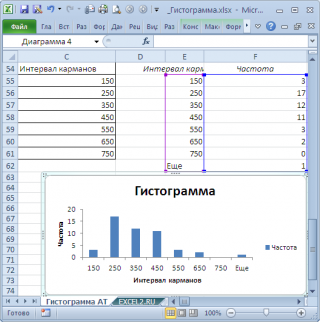
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
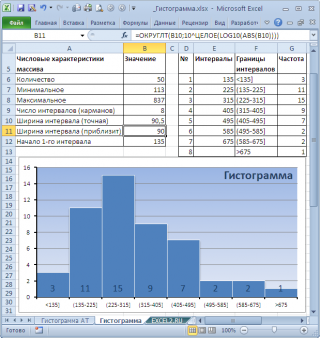
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
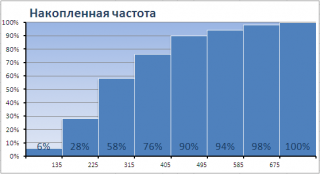
Одной из разновидностей гистограмм является
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
В
MS
Excel
есть возможность анализа формы рядов
распределения и расчета показателей
их центральной тенденции (среднего
значения, моды, медианы, экстремумов
(максимального и минимального значений)).
Для их вычисления применяются
статистические функции и инструмент
Анализ
данных.
Ряды
распределения строятся с целью изучения
состава исследуемой совокупности, ее
однородности, колеблемости значений
признаков и границ их изменения. На
основе рядов распределения рассчитываются
относительные величины структуры и
средние показатели.
Ряд
распределения
в статистике
это ряд цифровых показателей, представляющих
распределение единиц совокупности по
одному существенному признаку, значения
которого расположены в определенной
последовательности.
Ряд
распределения включает два элемента:
1. варианты
(х)
отдельные возможные значения признака;
2. частоты
или веса (f)
– это численность отдельных групп, т.е.
числа, которые показывают, сколько раз
данное значение признака встречается
в исследуемой совокупности.
Правила
построения ряда распределения аналогичны
правилам построения группировки. Но
иногда при наличии достаточно большого
количества вариантов значений признака
ряд распределения является трудно
обозримым и непосредственное рассмотрение
его не дает представления о распределении
единиц по значению признака в совокупности.
Поэтому первым шагом в упорядочении
первичного ряда является его ранжирование,
т.е. расположение всех вариантов в
возрастающем (или убывающем) порядке.
При
проведении эмпирического исследования
ряда распределения рассчитываются и
анализируются следующие группы
показателей:
• показатели
формы распределения;
• показатели
положения центра распределения;
• показатели
степени его однородности.
Для
анализа формы рядов распределения чаще
всего используют их графическое
изображение.
Для изображения рядов применяются
линейные графики и плоскостные диаграммы,
построенные в прямоугольной системе
координат.
В
статистике выделяют две формы распределения
данных: нормальную
и несимметричную.
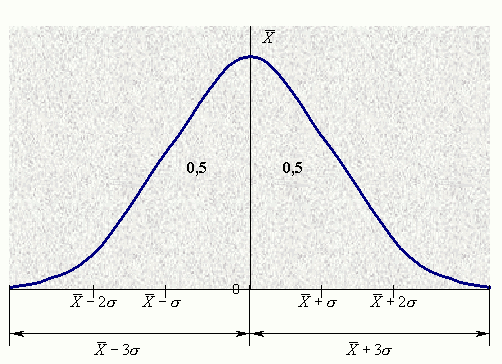
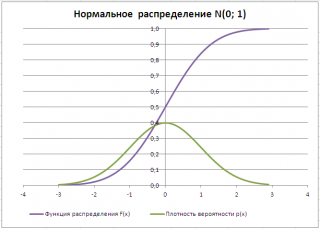
Нормальное
распределение (термин был впервые введен
Гальтоном в 1889 г.), иногда называемое
гауссовским, можно представить в виде
симметричной кривой в форме колокола
(рис. 3.1). Такая кривая представляет
идеальный набор данных, что редко
встречается на практике.
Рис.
3.1. Кривая нормального распределения
Тем
не менее, нормальное распределение
играет большую роль в статистике. С
помощью графического изображения
статистических данных важно определить,
являются ли данные нормально
распределенными, т.к. только в случае
распределения близкого к нормальному
можно использовать стандартные
статистические процедуры, в противном
случае полученные результаты анализа
данных могут быть неточными или неверными.
На
практике же чаще всего встречаются
несимметричные
формы распределения.
Для решения этой проблемы в статистике
используют специальное преобразование,
которое переводит несимметричное
распределение в более симметричное.
Наиболее распространенным типом
преобразования данных в экономике
является логарифмирование,
которое заключается в замене каждого
значения ряда данных его десятичным
или натуральным логарифмом.
В
статистике могут встречаться одновершинные
и многовершинные кривые распределения.
Однородные
совокупности описываются одновершинными
распределениями, а многовершинность
распределения свидетельствует о
неоднородности изучаемой совокупности
или о некачественном выполнении
группировки.
Одновершинные
кривые распределения делятся на
симметричные, умеренно асимметричные
и крайне асимметричные.
К
показателям положения центра распределения
относятся степенная средняя (средняя
арифметическая) и структурные средние
– мода и медиана.
Мода
и медиана являются дополнительными к
средней величине характеристиками
совокупности, по ним также можно судить
о форме рядов распределения.
Если
значение средней величины совпадает с
модой и медианой, то ряд является
симметричным. На практике строго
симметричные ряды встречаются довольно
редко, чаще исследователю приходится
иметь дело с асимметричными рядами.
Для
характеристики асимметрии используют
коэффициенты асимметрии.
Простейшим
показателем асимметрии может служить
разность между средней арифметической
величиной и модой.
Если
AS =

то в ряду имеет место правосторонняя
асимметрия, если AS =

то – левосторонняя.
Для
симметричных распределений может быть
рассчитан показатель эксцесса, который
показывает, насколько резкий скачок
имеет изучаемое
явление.
Если
показатель эксцесса больше нуля, то
распределение островершинное и скачок
считается значительным, если коэффициент
эксцесса меньше нуля, то распределение
считается плосковершинным и скачок
считается незначительным.
Однородность
статистических совокупностей
характеризуется величиной вариации
(рассеяния) признака, т.е. несовпадением
его значений у разных статистических
единиц. Для измерения вариации в
статистике используются абсолютные и
относительные показатели.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
Выбираем «Гистограмма»:
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData;C13:C22)=FREQUENCY(tblData,C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:
Содержание
- 2.2. Методика построения вариационных рядов и их графиков с помощью электронных таблиц Excel
- Функция распределения и плотность вероятности в EXCEL
- Генеральная совокупность и случайная величина
- Функция распределения
- Непрерывные распределения и плотность вероятности
- Вычисление плотности вероятности с использованием функций MS EXCEL
- Вычисление вероятностей с использованием функций MS EXCEL
- Обратная функция распределения (Inverse Distribution Function)
2.2. Методика построения вариационных рядов и их графиков с помощью электронных таблиц Excel
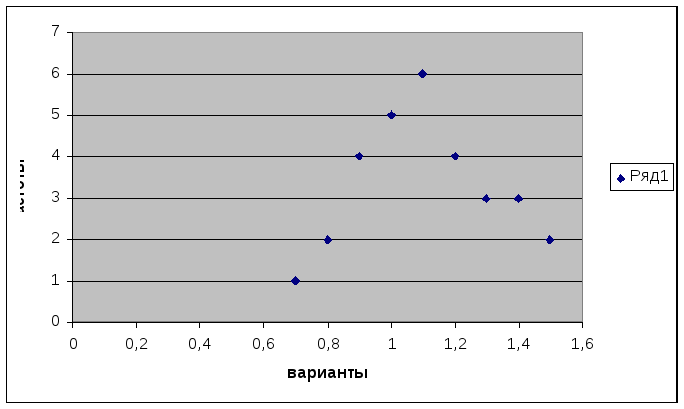
Построим дискретный вариационный ряд по затратам труда на 1 ц зерна.
Открываем лист Excel, в ячейку А1 записываем условное обозначение результативного признака – у, а в ячейки А2:А31 значения затрат труда на 1 ц зерна. В ячейки В2:В3 введём наименьшее и следующее за ним значения признака 0,7 и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем мышью правый нижний угол выделительной рамки и потянем вниз до значения 1,5 (наибольшее значение признака). В ячейках В2:В10 получим варианты признака в ранжированном порядке. Для определения частот проделаем следующие шаги:
1.Поставим курсор в ячейку С2.
2.Выберем Вставка, Функция.
Выберем в категории Статистические функции функцию Частота и нажмём ОК.
3.В поле данных укажем ячейки А2:А31, а в поле интервалов В2:В10.
4.Нажмём кнопку ОК.
5.Выделим ячейки С2:С10.
6.Нажмём F2, а затем комбинацию клавиш Shift+Ctrl+Enter.
В ячейках С2:С10 появятся частоты.
Вычислим накопленные частоты, которые потребуются для дальнейших расчётов, путём последовательного суммирования локальных частот (нарастающим итогом). Так, первая плюс вторая частоты дают накопленную частоту второго варианта (1+2=3); прибавляя к ней третью частоту, получим накопленную частоту третьего варианта (3+4=7) и т.д.
Скопируем полученный в Excel вариационный ряд и построим таблицу.
Дискретный вариационный ряд распределения затрат труда на 1 ц зерна
Построим полигон распределения частот с помощью Мастера диаграмм. Выберем точечную диаграмму, соединим полученные точки отрезками, а крайние точки с осью абсцисс в точках, отстоящих от крайних на расстоянии шага.
Р
Рассмотрим построение интервального вариационного ряда.
Рис. 2. Построение интервального вариационного ряда
На листе Excel в ячейку А1 записываем условное обозначение факторного признака – х, в ячейки А2:А31 – значения факторного признака – урожайности озимой пшеницы. Произведём сортировку данных, для чего выделяем диапазон данных, выбираем Данные – Сортировка и в появившемся окне «Сортировка диапазона» указываем «по возрастанию», нажимаем ОК. Данные в ячейках А2:А31 расположатся в ранжированном порядке по возрастанию признака. По формуле Стерджесса определяем количество групп (интервалов). Для вычисления десятичного логарифма lg30 выбираем Мастер функций – Математические – LOG10. В появившемся окне в поле Число записываем число 30, десятичный логарифм которого необходимо найти. Нажатием ОК получаем этот логарифм 1,477121. . Подставляя числовые данные в формулу (1), получим число групп (интервалов) 5,9, округляем до 6. По формуле (2) определяем величину интервалов – шаг с такой же точностью, с которой даны исходные данные (в данном случае с точностью до десятых: (30-20)/6≈1,7. Следовательно, совокупность надо разбить на 6 интервалов. Получаем шаг 1,7. Озаглавим следующие столбцы в Excel словами «Интервалы», «Частоты», «Накопленные частоты», «Середины интервалов». В ячейку В2 вписываем минимальное значение признака Хmin=20, в ячейку В3 формулу =В2+1,7, т.е. минимальное значение плюс шаг. Копируем эту формулу на 5 строк вниз. В результате в этих шести строках (В3:В8) получим верхние границы всех интервалов. Нижними границами интервалов будут данные в соседних верхних ячейках, т.е. для первого интервала нижней границей будет содержание ячейки В2, для второго В3 и для шестого В7.
Для расчёта частот выберем Сервис — Анализ данных – Гистограмма и нажмём ОК. В появившемся окне «Гистограмма» в поле «Входной интервал» копируем исходные данные (ячейки А2:А31), в поле «Интервал карманов» — верхние границы интервалов (ячейки В3:В8), в поле «Выходной интервал» ячейки частот (С3:С8), нажимаем ОК. В ячейки D3:D8 будут записаны частоты для всех шести интервалов. Накопленные частоты подсчитываем нарастающим итогом.
Для построения диаграммы необходимо найти середины интервалов. Для этого вводим формулу расчёта середины интервала: 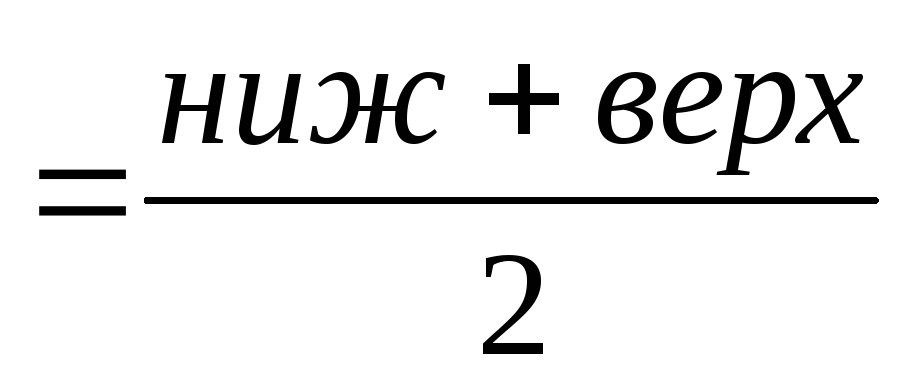
Для построения диаграммы выделяем массив частот и середин интервалов. Далее в Мастере диаграмм выбираем вид диаграммы — гистограмму определённого вида. Нажимаем кнопку Далее. В появившемся окне выбираем вкладку Ряд, удаляем ряд 1, а в поле «Подписи оси х» копируем середины интервалов. Нажимаем далее, в появившемся окне выбираем вкладку Заголовки. В поле «ось х (категорий)» вписываем название факторного признака (в данном случае урожайность, ц/га), в поле «Ось у (значений)» вписываем частоты. Нажимаем Далее, Готово. Появится диаграмма, состоящая из столбиков, отделённых друг от друга некоторым зазором. Щёлкаем правой кнопкой мыши на одном из столбиков диаграммы. В раскрывающемся списке элементов щёлкаем по кнопке Формат рядов данных. В появившемся диалоговом окне активизируем вкладку Параметры и в поле Ширина зазора устанавливаем значение 0. Нажимаем ОК, в результате чего гистограмма принимает стандартный вид.
Источник
Функция распределения и плотность вероятности в EXCEL
history 13 октября 2016 г.
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта ]]> www.excel2.ru ]]> . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL .
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).
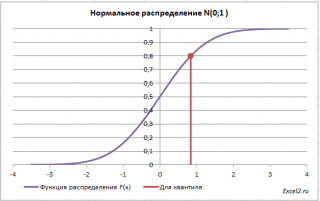
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):
В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x 1 Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
Непрерывные распределения и плотность вероятности
В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой функции плотности распределения p(x) . Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF) .
Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution ) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.
Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что плотность распределения является производной от функции распределения , т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения ).
Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.
Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.
Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
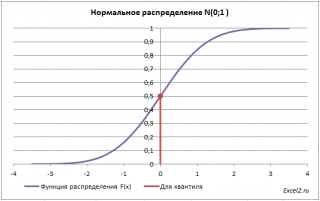
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.
Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .
Обратная функция распределения вычисляет квантили распределения , которые используются, например, при построении доверительных интервалов . Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения . В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Как построить вариационный ряд в Excel
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.