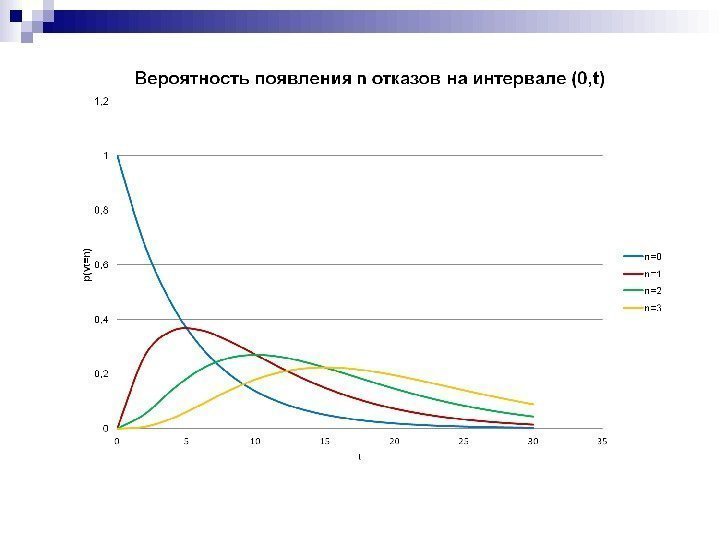
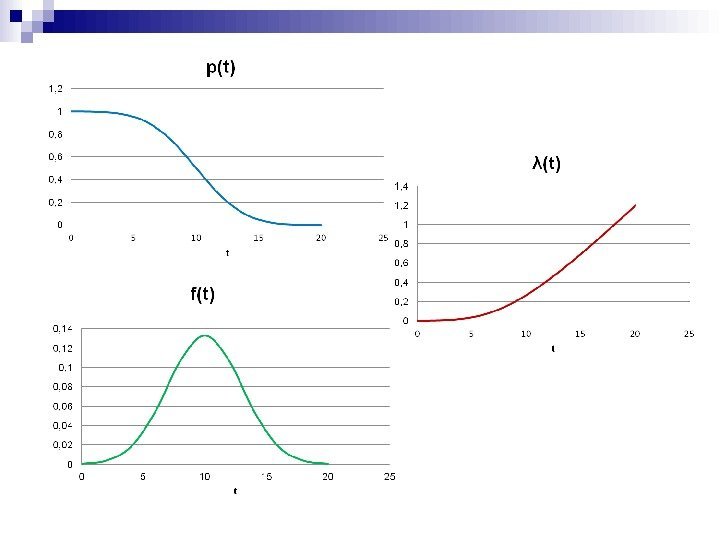
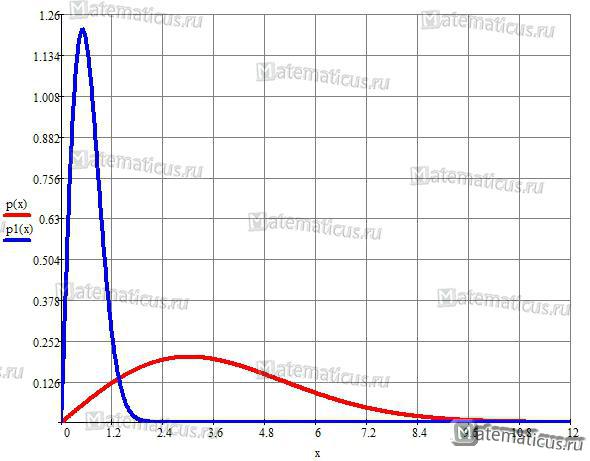
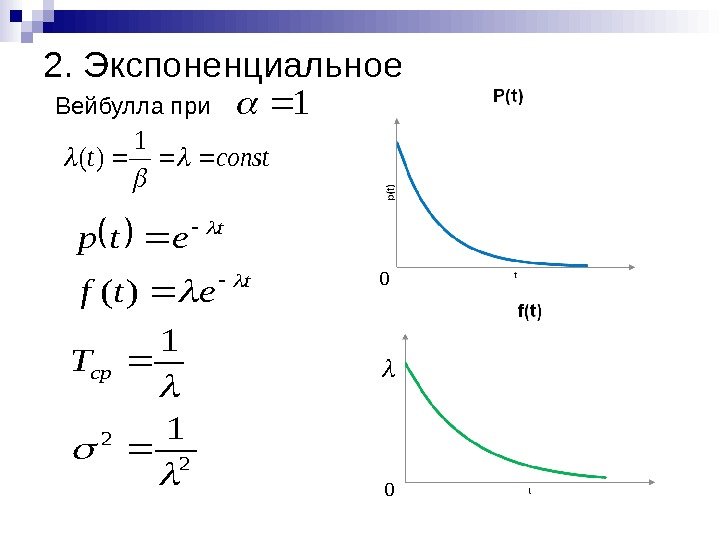
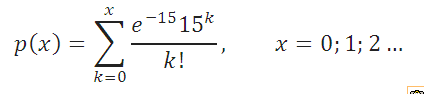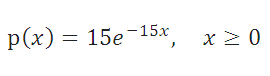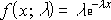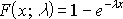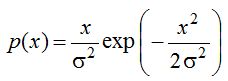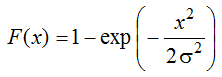Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL
ЭКСП.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение
(англ.
Exponential
distribution
)
часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение
Экспоненциального распределения
:
- Промежутки времени между появлением посетителей в кафе;
-
Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см.
Распределение Вейбулла
);
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности
Экспоненциального распределения
задается следующей формулой:
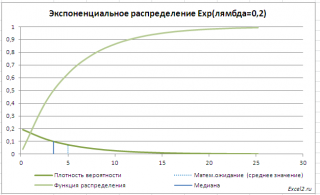
График
плотности распределения вероятности
и
интегральной функции
Экспоненциального
распределения выглядит следующим образом
(см. ниже).
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Среднее значение
(среднее время между 2-мя случайными событиями) равно
1/λ
. А
дисперсия (квадрат стандартного отклонения)
равна
1/
λ
^2
.
Экспоненциальное распределение
тесно связано с дискретным
распределением Пуассона
. Если
Распределение Пуассона
описывает число случайных событий, произошедших за определенный интервал времени, то
Экспоненциальное распределение
должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается
распределением Пуассона
со средним значением равным 15 машин в час (параметр распределения
λ
=15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра
экспоненциального распределения
, то параметр
λ
=15
, а плотность соответствующего
экспоненциального распределения
равна:
Экспоненциальное распределение в MS EXCEL
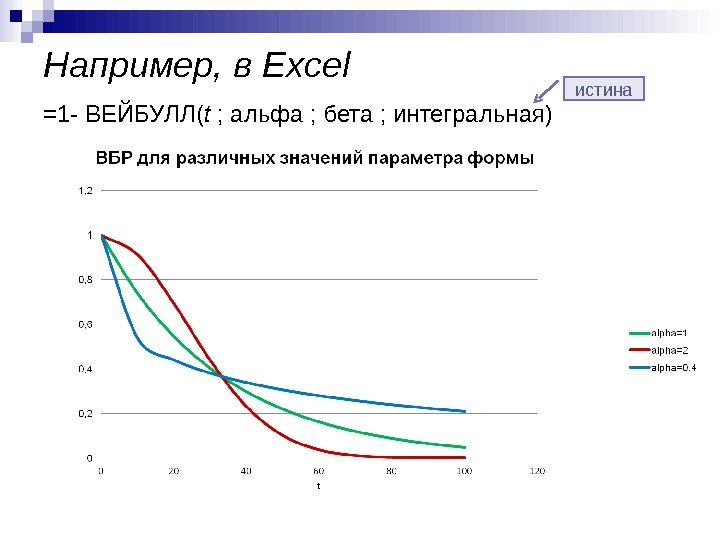
В MS EXCEL, начиная с версии 2010, для
Экспоненциального распределения
имеется функция
ЭКСП.РАСП()
, английское название — EXPON.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу в начале статьи) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
экспоненциальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение
имеет обозначение
Exp
(
λ
).
Примечание
: До MS EXCEL 2010 в EXCEL была функция
ЭКСПРАСП()
, которая позволяет вычислить
кумулятивную (интегральную) функцию распределения
и
плотность вероятности
.
ЭКСПРАСП()
оставлена в MS EXCEL 2010 для совместимости.
В
файле примера на листе Пример
приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции
экспоненциального распределения
:
=1-EXP(-
λ
*x)
;
=ГАММА.РАСП(x;1;1/
λ
;ИСТИНА)
, т.к.
экспоненциальное распределение
является частным случаемГамма распределения
;
=ВЕЙБУЛЛ.РАСП(x;1;1/
λ
;ИСТИНА)
, т.к.
экспоненциальное распределение
является частным случаемраспределения Вейбулла
;
Примечание
: Для удобства написания формул в
файле примера
создано
Имя
для параметра распределения —
λ
.
Графики функций
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Генерация случайных чисел
Для генерирования массива чисел, распределенных по
экспоненциальному закону
, можно использовать формулу
=-LN(СЛЧИС())/
λ
Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Если случайные числа содержатся в диапазоне
B14:B213
, то оценку параметра
экспоненциального распределения
λ
можно сделать с использованием формулы
=1/СРЗНАЧ(B14:B213)
.
Задачи
Экспоненциальное распределение
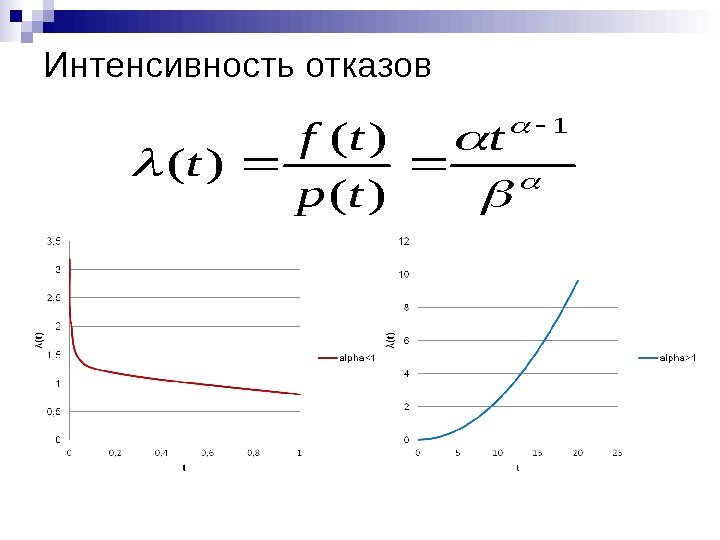
широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр
λ
называется
интенсивность отказов
, а
1/
λ
–
среднее время до отказа
.
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый
Экспоненциальным распределением
с
интенсивностью отказа
равной 10^(-3) в час, таким образом,
λ
=
10^(-3).
Среднее время до отказа
равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за
Среднее время до отказа,
то нужно записать формулу:
Т.е. результат не зависит от параметра
λ
.
В MS EXCEL решение выглядит так:
=ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача
.
Среднее время до отказа
некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы.
=ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЭКСП.РАСП в Microsoft Excel.
Возвращает экспоненциальное распределение. Функция ЭКСП.РАСП используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему. В частности, при помощи функции ЭКСП.РАСП можно определить вероятность того, что этот процесс займет не более 1 минуты.
Синтаксис
ЭКСП.РАСП(x;лямбда;интегральная)
Аргументы функции ЭКСП.РАСП описаны ниже.
-
x — обязательный аргумент. Значение функции.
-
Лямбда — обязательный аргумент. Значение параметра.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму экспоненциальной функции, которую следует использовать. Если аргумент «интегральная» имеет значение ИСТИНА, функция ЭКСП.РАСП возвращает интегральную функцию распределения; если имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
-
Если значение «x» или «лямбда» не является числом, функция ЭКСП.РАСП возвращает значение ошибки #ЗНАЧ!.
-
Если x < 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.
-
Если значение «лямбда» ≤ 0, функция ЭКСП.РАСП возвращает значение ошибки #ЧИСЛО!.
-
Уравнение для функции плотности вероятности имеет следующий вид:
-
Уравнение для интегральной функции распределения имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
0,2 |
Значение функции |
|
|
10 |
Значение параметра |
|
|
Формула |
Описание |
Результат |
|
=ЭКСП.РАСП(A2;A3;ИСТИНА) |
Интегральная экспоненциальная функция распределения |
0,86466472 |
|
=ЭКСП.РАСП(0,2;10;ЛОЖЬ) |
Экспоненциальная функция плотности распределения |
1,35335283 |
Нужна дополнительная помощь?






![5. Нормальное распределение для моделирования процессов «старения» ] 2 )( exp[ 2 1 )(2 5. Нормальное распределение для моделирования процессов «старения» ] 2 )( exp[ 2 1 )(2](https://present5.com/presentforday2/20170209/3_images/3_15.jpg)

![Усеченное нормальное распределение] 2 )( exp[ 2 )(2 0 0 mtc tf 00 Усеченное нормальное распределение] 2 )( exp[ 2 )(2 0 0 mtc tf 00](https://present5.com/presentforday2/20170209/3_images/3_18.jpg)





Probability describes the likelihood that some event occurs.
We can calculate probabilities in Excel by using the PROB function, which uses the following syntax:
PROB(x_range, prob_range, lower_limit, [upper_limit])
where:
- x_range: The range of numeric x values.
- prob_range: The range of probabilities associated with each x value.
- lower_limit: The lower limit on the value for which you want a probability.
- upper_limit: The upper limit on the value for which you want a probability. Optional.
This tutorial provides several examples of how to use this function in practice.
Example 1: Dice Probabilities
The following image shows the probability of a dice landing on a certain value on a given roll:
Since the dice is equally likely to land on each value, the probability is the same for each value.
The following image shows how to find the probability that the dice lands on a number between 3 and 6:
The probability turns out to be 0.5.
Note that the upper limit argument is optional. So, we could use the following syntax to find the probability that the dice lands on just 4:
The probability turns out to be 0.166667.
Example 2: Sales Probabilities
The following image shows the probability of a company selling a certain number of products in the upcoming quarter:
The following image shows how to find the probability that the company makes either 3 or 4 sales:
The probability turns out to be 0.7.
Additional Resources
How to Calculate Relative Frequency in Excel
How to Calculate Cumulative Frequency in Excel
How to Create a Frequency Distribution in Excel
17 авг. 2022 г.
читать 2 мин
Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.
Это распределение может быть использовано для ответа на такие вопросы, как:
- Как долго владельцу магазина нужно ждать, пока покупатель войдет в его магазин?
- Как долго батарея будет продолжать работать, прежде чем она умрет?
- Как долго компьютер будет продолжать работать, прежде чем он сломается?
В каждом сценарии нас интересует вычисление того, как долго нам придется ждать, пока не произойдет определенное событие. Таким образом, каждый сценарий может быть смоделирован с использованием экспоненциального распределения.
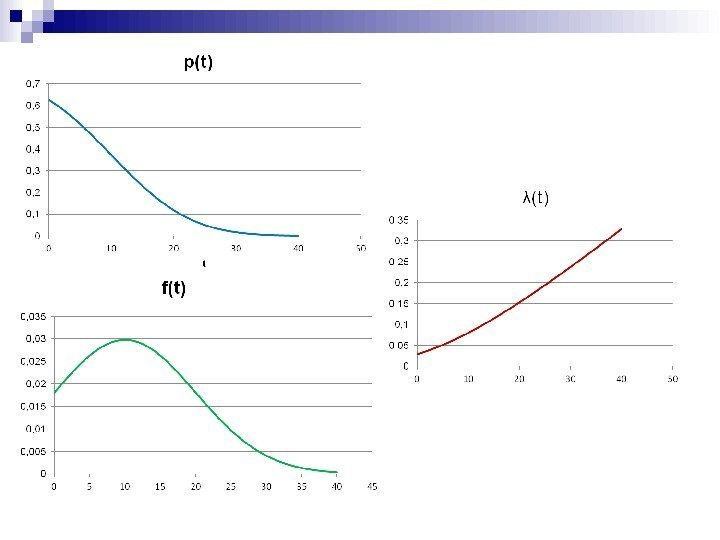
Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция плотности X может быть записана как:
F (х; λ) = 1 – e -λx
куда:
- λ: параметр скорости (рассчитывается как λ = 1/μ)
- e: константа, примерно равная 2,718.
Чтобы рассчитать вероятности, связанные с кумулятивной функцией плотности экспоненциального распределения в Excel, мы можем использовать следующую формулу:
=EXPON.DIST(x, lambda, cumulative)
куда:
- x : значение экспоненциально распределенной случайной величины
- lambda : параметр скорости
- cumulative : использовать функцию кумулятивной плотности или нет (ИСТИНА или ЛОЖЬ)
Следующие примеры показывают, как использовать эту формулу на практике.
Пример 1: время до прихода следующего клиента
В среднем новый покупатель заходит в магазин каждые две минуты. После прихода клиента найти вероятность того, что новый клиент прибудет менее чем за одну минуту.
Решение: Среднее время между клиентами составляет две минуты. Таким образом, ставка может быть рассчитана как:
- λ = 1/мк
- λ = 1/2
- λ = 0,5
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что новый клиент прибудет менее чем за одну минуту:
Вероятность того, что следующего клиента придется ждать менее одной минуты, равна 0,393469 .
Пример 2: Время до следующего землетрясения
Предположим, землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения найти вероятность того, что следующее землетрясение произойдет не ранее, чем через 500 дней.
Решение: Среднее время между землетрясениями составляет 400 дней. Таким образом, ставка может быть рассчитана как:
- λ = 1/мк
- λ = 1/400
- λ = 0,0025
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующее землетрясение произойдет менее чем через 500 дней:
Вероятность того, что следующее землетрясение произойдет менее чем через 500 дней, равна 0,7135.
Таким образом, вероятность того, что следующего землетрясения придется ждать более 500 дней, равна 1 – 0,7135 = 0,2865 .
Пример 3: время до следующего телефонного звонка
Предположим, колл-центр получает новый звонок в среднем каждые 10 минут. После звонка клиента найти вероятность того, что новый клиент позвонит в течение 10–15 минут.
Решение: Среднее время между вызовами составляет 10 минут. Таким образом, ставка может быть рассчитана как:
- λ = 1/мк
- λ = 1/10
- λ = 0,1
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующий клиент позвонит в течение 10-15 минут:
Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1447 .
Дополнительные ресурсы
Введение в экспоненциальное распределение
Свойство экспоненциального распределения без памяти
Как построить экспоненциальное распределение в R
Skip to content
matematicus.ru
matematicus включает разделы – высшая математика, аналитическая геометрия в пространстве и на плоскости, теория вероятностей, Arduino, Android Studio, Excel, программирование, программы, Windows, ошибки, таблицы, формулы, примеры, физика, химия
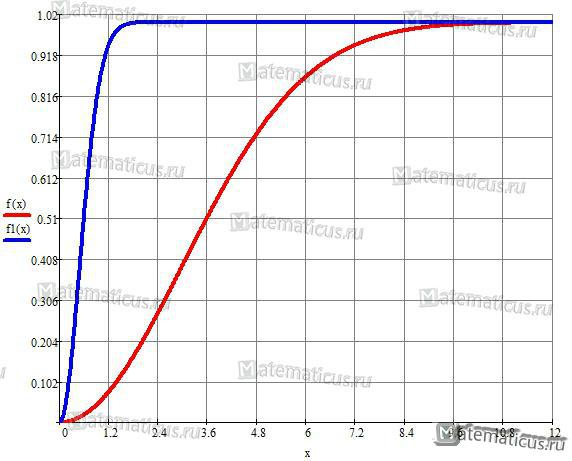
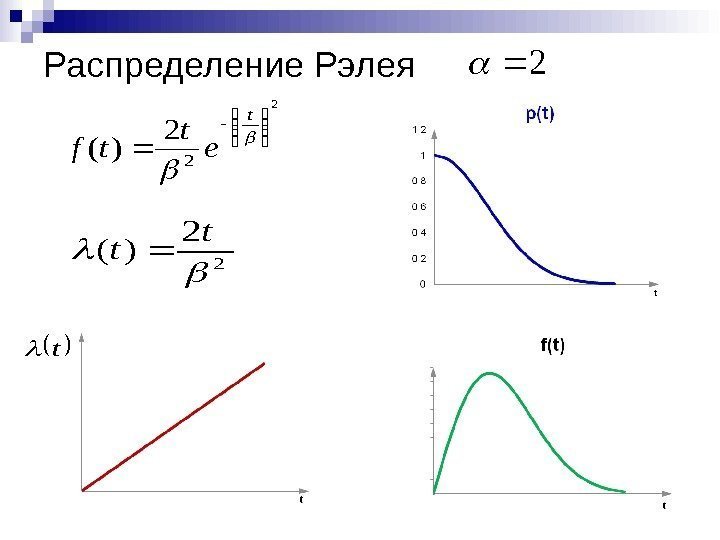
Распределение Рэлея
Рэлеевским распределением называют распределение вида:
Функция распределения определяется выражением:
σ — среднеквадратическое отклонение (параметр распределения).
График функции вероятности при σ=3 и σ=0.5
График плотности вероятности при σ=3 и σ=0.5
Возможное применение распределение Рэлея в колебательных процессах со случайными фазами и амплитудами, электроснабжении, малые частоты излучения, надежности изделий, связанных с выраженным старением элементов.
3406
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Пермская государственная сельскохозяйственная академия имени академика Д.Н.Прянишникова»
Факультет прикладной информатики Кафедра ИТАП
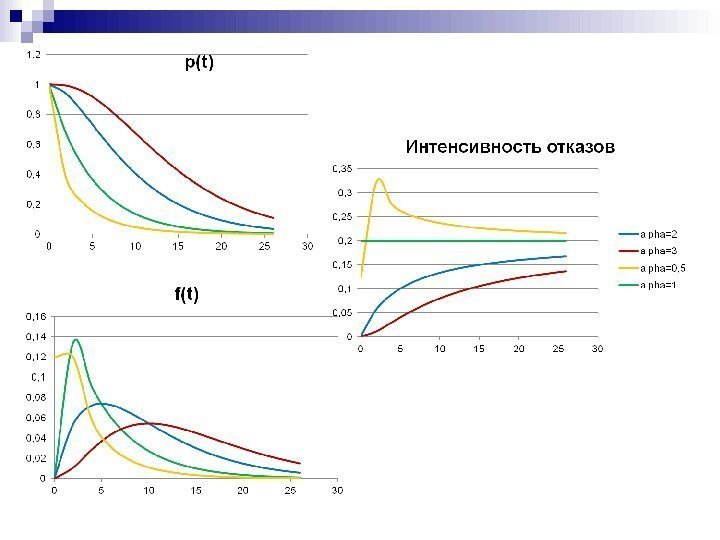
НАДЕЖНОСТЬ ИНФОРМАЦИОННЫХ СИСТЕМ
специальность 230201 «Информационные системы и технологии»
ЛАБОРАТОРНАЯ РАБОТА №2
тема: «РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ»
(различные законы распределения времени работы до отказа)
Структура:
1.Сведения из теории
2.Постановка задачи
3.Последовательность решения
4.Задание для самостоятельного решения
Пермь, 2011

I.СВЕДЕНИЯ ИЗ ТЕОРИИ
Вбольшинстве случаев решение вопросов, связанных с обеспечением надежно-
сти, предполагает качественное и количественное изучение объектов исследования. Ис-
следование в каждом конкретном случае специфики объектов на качественном уровне по-
зволяет установить основные критерии отказов, причины их возникновения, пути повы-
шения надежности и т.д. Решение этих задач невозможно без использования теории веро-
ятностей, математической статистики, методов оптимизации. В частности, приемы и ме-
тоды количественного анализа дают возможность исследовать функции распределения вероятностей случайных величин и оценки их основных моментов и квантилей, проведе-
ния структурного анализа и моделирования систем и процессов. В теории надежности ис-
пользуются следующие законы распределения времени работы до отказа объекта (систе-
мы): Вейбулла, гамма-распределение, Релея, экспоненциальный, усеченный нормальный,
нормальный, равномерный. В предложенной работе рассматривается лишь часть законов,
для определения которых приняты следующие обозначения:
W – Вейбулла;
Г – гамма;
R – Рэлея;
Exp – экспоненциальный.
Распределения Вейбулла и гамма-распределение являются двухпараметрическими
(имеют два параметра распределения).
Математическое ожидание и среднее квадратическое отклонение имеют следую-
щую взаимосвязь с параметрами распределений:
Таблица 1. Связь параметров распределений с математическим ожиданием и средним квадратическим отклонением
|
Распределение |
m |
||||||||||||||||||
|
Экспоненциальное |
1 |
1 |
|||||||||||||||||
|
Exp( ) |
|||||||||||||||||||
|
Гамма Г( , ) |
|||||||||||||||||||
|
Рэлея R( ) |
4 |
||||||||||||||||||
|
4 |
4 |
||||||||||||||||||
|
Вейбулла W( , ) |
Г(1 1/ ) |
||||||||||||||||||
|
Г(1 2/ ) Г2 (1 1/ ) |
|||||||||||||||||||
|
В таблице принято |
следующее обозначение: |
Гамма-функция — Г( ) x 1e xdx.
0
2
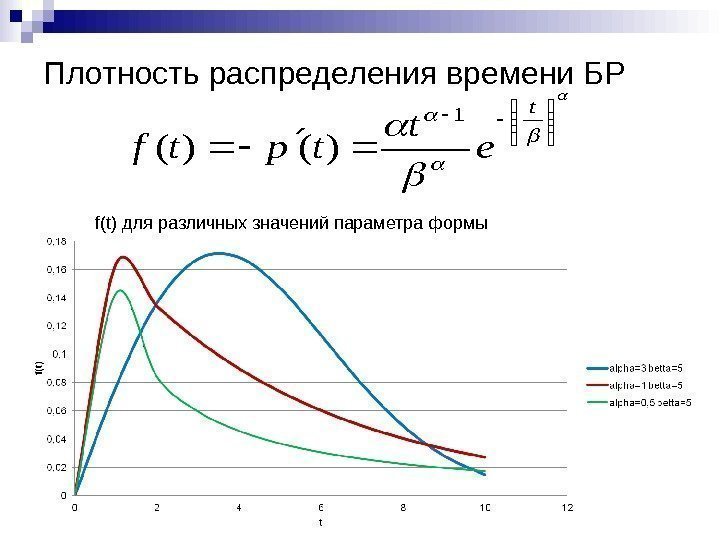
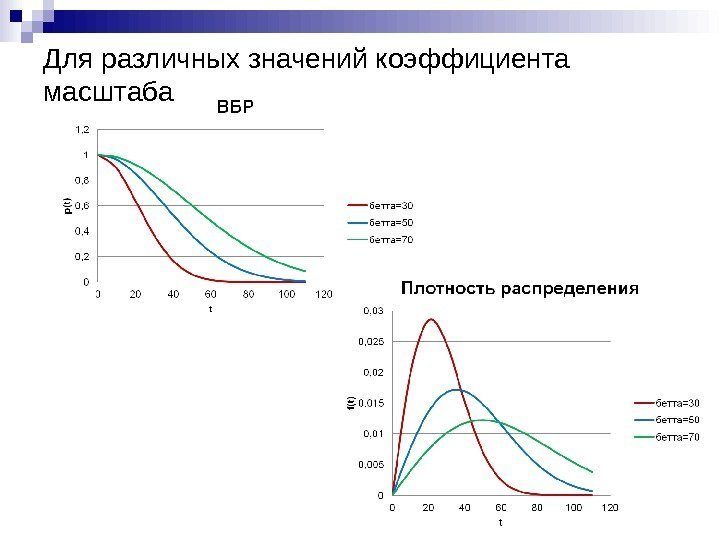
Для вычисления вероятности безотказной работы и плотности распределения времени до отказа элементов используют аналитические выражения, приведенные в таблице 2.
Таблица 2. Некоторые законы распределения вероятностей
|
Распределение |
f(t) |
P(t) |
|||||||||||||||||||
|
Экспоненциальное |
e— t |
e— t |
|||||||||||||||||||
|
Exp( ) |
|||||||||||||||||||||
|
Гамма Г( , ) |
t |
1 |
t |
t |
|||||||||||||||||
|
e |
1 I , |
||||||||||||||||||||
|
( ) |
|||||||||||||||||||||
|
Рэлея R( ) |
2 |
te |
— t2 |
e t2 |
|||||||||||||||||
|
Вейбулла W( , ) |
t |
1 |
( |
t |
) |
t |
|||||||||||||||
|
e |
|||||||||||||||||||||
|
e |
|||||||||||||||||||||
|
1 |
|||||||||||||||||||||
|
В гамма-распределении функция |
I( ,t) |
x 1e xdx есть неполная гамма- |
|||||||||||||||||||
|
( ) |
|||||||||||||||||||||
|
0 |
|||||||||||||||||||||
функция*.
II. ПОСТАНОВКА ЗАДАЧИ
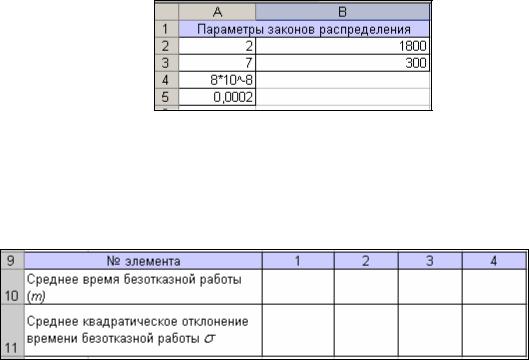
Нерезервированная система состоит из 4 элементов. Элементы имеют различные законы распределения времени работы до отказа. Виды законов распределения приведены в таблице 3. В скобках указаны параметры распределений.
Таблица 3. Законы распределения времени до отказа
|
№ элемента |
1 |
2 |
3 |
4 |
|
Закон распределения времени до |
W (2;1800) |
Г (7;300) |
R (8*10-8) |
Exp (0,0002) |
|
отказа |
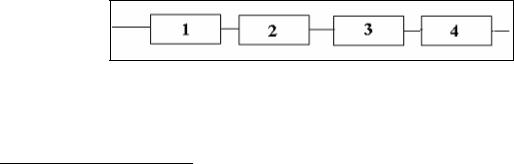
Элементы в данной нерезервированной невосстанавливаемой системе имеют последовательное (основное) соединение (рис.1).
Рис. 1. Нерезервированная система, состоящая из 4 элементов
споследовательным соединением.
*В Excel неполная гамма-функция реализуется следующий образом: в ячейку А1 помещают первый аргумент (значение ), в ячейку А2 – второй аргумент (значение t), в ячейку А3 – функция:
А3=ГАММАРАСП(А2; А1;1;1). Результатом является значение неполной гамма-функции.
3
Необходимо определить среднее время безотказной работы, среднее квадратиче-
ское отклонение времени безотказной работы, вероятность безотказной работы, для каж-
дого элемента и всей системы за время 2000 часов с шагом 100 часов. Для показателей,
зависящих от времени, решение получить в виде таблиц и графиков.
III. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ
Решение поставленной задачи рекомендуется производить с помощью электрон-
ных таблиц Microsoft Excel.
Этапы нахождения показателей надежности для данной системы:
1.Создать новый лист Microsoft Excel.
2.Необходимо создать область для ввода параметров законов распределения.
Вячейки А2:В5 вносятся параметры законов распределения времени до отказа (из усло-
вия задачи). Результат представлен на рис.1.
Рис.2. Область для ввода параметров законов распределения.
3. Далее вычисляются начальные моменты распределений: математическое ожидание m среднее квадратическое отклонение . В диапазоне ячеек А9:Е11 создать область для вычисления моментов распределения (рис.2).
Рис. 2. Область для вычисления моментов распределения.
4.Для вычисления среднего времени безотказной работы и среднего квадрати-
ческого отклонения необходимо использовать формулы связи моментов (m и ) с пара-
метрами распределений (формулы связи приведены в табл.1).
Элемент №1. Распределение Вейбулла с параметром формы 2 и парамет-
ром масштаба 1800: для вычисления математического ожидания в случае распреде-
ления Вейбулла необходимо знать и значение гамма-функции. Найти значение гамма-
функции в Excel можно по следующей технологии: в ячейке А2 находится аргумент (па- 4
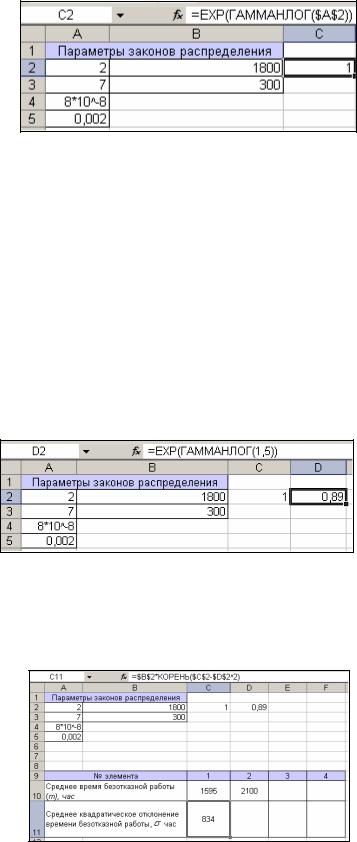
раметр формы), а в ячейку С2 необходимо поместить функцию
ЕХР(ГАММАНЛОГ(А2)), результатом является значение гамма-функции (рис.3).
Рис.3. Вычисление значения гамма-функции.
Учитывая формулу для нахождения математического ожидания (табл.1) —
Г(1 1/ ), в ячейку С10 необходимо ввести: =$B$2*EXP(ГАММАНЛОГ(1+1/$A$2)).
Для нахождения значения среднего квадратического отклонения времени без-
отказной работы необходимо знать значение гамма-функции с параметром, равным
(1+1/ ) и (1 2/ ) (табл.1). Значение гамма-функции с параметром (1 2/ ) уже извест-
но – в ячейке С2 (так как 1+2/2=2). Значение гамма-функции с параметром (1+1/ ) вы-
числяется по следующему принципу: в ячейку D2 ввести формулу
ЕХР(ГАММАНЛОГ(1,5)). Аргумент равен 1,5 исходя из условия: 1+1/2. Результат на
рис. 4.
Рис. 4. Значение гамма-функции с параметром (1 2/ ).
Теперь возможно найти . Для этого необходимо в ячейку С11 ввести формулу
=$B$2*КОРЕНЬ($C$2-$D$2^2). Результат представлен на рис.5.
Рис. 5. Результат нахождения .
5
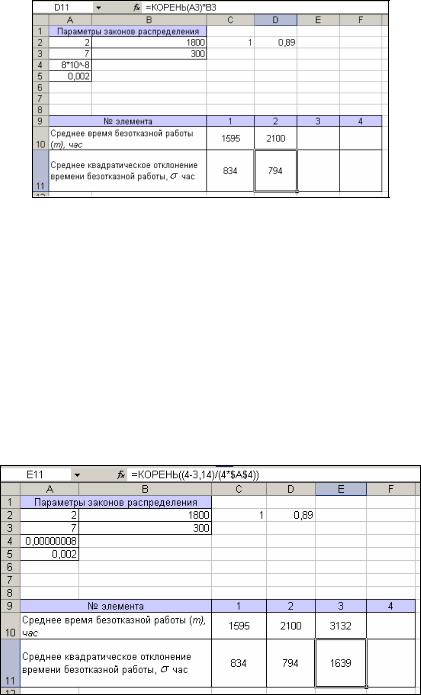
Элемент №2. Гамма-распределение с параметром формы 7 и параметром
масштаба 300: согласно формуле для нахождения математического ожидания в гамма-распределении (табл.1) в ячейку D10 ввести =A3*B3 (так как m=7*300). Для нахождения используем формулу из таблицы 1, вводя ее в ячейку D11. Результат на рис.6:
Рис.6. Вычисление среднего квадратического отклонения времени безотказной работы
Элемент №3. Распределение Рэлея с параметром 8*10 8 : для расчета матожидания значение параметра лучше вычислить заранее. Для этого в ячейку А4 перед данными параметра ставиться знак = и нажимается Enter. Значение параметра приняло вид
0,00000008.
Согласно описанным в таблице 1 формулам для m и , в ячейку E10 помещаем выражение =КОРЕНЬ(3,14/(4*$A$4)), в ячейку E11 =КОРЕНЬ((4-3,14)/(4*$A$4)). Результат представлен на рис.7:
Рис. 7. Вычисление m и для элемента №3.
Элемент №4. Экспоненциальное распределение с параметром 0,0002: при
экспоненциальном законе m= . Для ячеек F10, F11 имеет смысл =1/$A$5. Результат
представлен на рис.8:
6
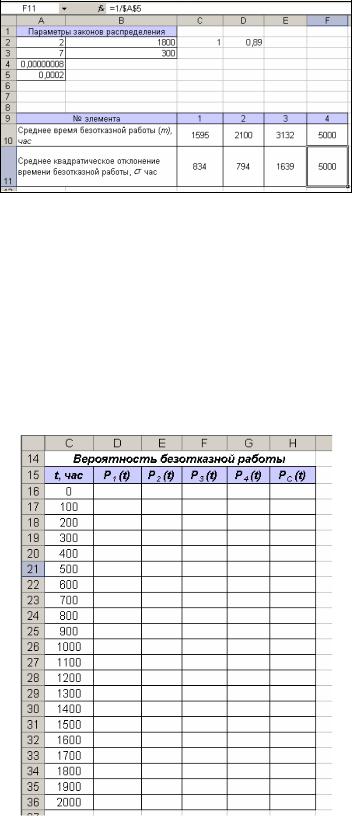
Рис. 8. Вычисление m и для элемента №4.
Таким образом, были найдены среднее время безотказной работы и среднее квадратическое отклонение времени безотказной работы для всех элементов данной системы
5.Для вычисления вероятности безотказной работы и плотности распреде-
ления времени до отказа элементов потребуются аналитические выражения, приведенные в таблице 2.
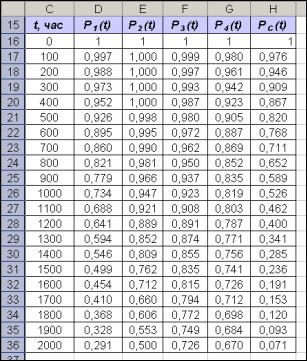
Создается область для вычисления вероятности безотказной работы элементов и системы в диапазоне ячеек C15:Н36, время – 2000 ч., шаг – 100 ч. (рис.9).
Рис. 9. Область для вычисления вероятности безотказной работы.
6. Используя формулы, приведенные в таблице 2, и подставляя значения параметров, получаем вероятности безотказной работы для элементов:
Элемент №1. Распределение Вейбулла:
7
P1(t) e 1800 таким образом, для ячейки D16 необходима следующая формула =
=EXP(-(СТЕПЕНЬ(C16/$B$2;2))).
Элемент №2. Гамма-распределение:
|
t |
||||||
|
P2 |
(t) 1 I |
7, |
, таким образом, для ячейки E16 необходима следующая фор- |
|||
|
300 |
||||||
мула =1-ГАММАРАСП(C16/$B$3;$A$3;1;1).
Элемент №3. Распределение Рэлея:
P3(t) e 8*10 8t2 , таким образом, формула для ячейки F16 имеет вид =EXP(- $A$4*(СТЕПЕНЬ(C16;2))).
Элемент №4. Экспоненциальное распределение:
P4(t) e 0,0002t, таким образом, формула для ячейки G16 =EXP(-$A$5*C16).
Необходимо табулировать эти функции от 0 до 2000 часов с шагом 100 часов.
7.Самостоятельно вычислите вероятность безотказной работы для всей систе-
мы. Сравните полученный результат со значениями, приведенными на рис.10.
Рис.10. Вероятность безотказной работы каждого элемента и всей системы за время 2000 ч., с интервалом 100 ч.
8.По полученным данным постройте графики функций, соответствующие ве-
роятностям безотказной работы элементов (рис.11) и вероятности безотказной работы
8
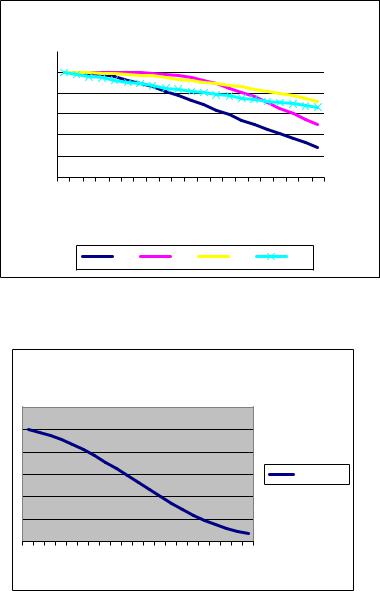
системы (рис.12). По первому графику проследите различное поведение вероятностей безотказной работы элементов. Какие элементы оказываются наиболее надежными при большом времени работы?
|
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙРАБОТЫ |
||||||||
|
ЭЛЕМЕНТОВ |
||||||||
|
Э3 |
||||||||
|
P(t) |
Э4 |
|||||||
|
Э2 |
||||||||
|
Э1 |
||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 1200 |
1400 1600 1800 2000 |
t, час |
|
|
Э1 |
Э2 |
Э3 |
Э4 |
|||||
|
Рис.11. График вероятностей безотказной работы элементов. |
|
ВЕРОЯТНОСТЬБЕЗОТКАЗНОЙРАБОТЫ |
||||||||||
|
СИСТЕМЫ |
||||||||||
|
Система |
||||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
|
Рис. 12. График вероятности безотказной работы системы. |
IV. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Самостоятельное определение плотность распределения времени до отказа, ин-
тенсивность отказов каждого элемента. Решение необходимо получить в виде таблиц и графиков.
9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #