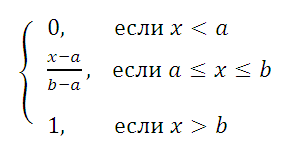СУММПРОИЗВ (SUMPRODUCT) в Excel. Гораздо больше, чем сумма произведений
Разберем, казалось бы, простую функцию СУММПРОИЗВ ( SUMPRODUCT ). В конце будет просто бомба для тех, кто строит отчеты в одних файлах, а хранит данные — в других.
Из русскоязычного написания функции можно догадаться, что СУММПРОИЗВ — это сумма произведений. Классический и самый примитивный способ её использования — перемножить значения из двух или более диапазонов и затем просуммировать. Посмотрим, как это работает.
Как посчитать в Экселе сумму столбца
С точки зрения логики выражение должно звучать следующим образом: если проверяемый город — это Москва ИЛИ Санкт-Петербург, то учитываем факт продаж, в противном случае — не учитываем. Т.е. нам достаточно, чтобы проверяемое значение соответствовало только одному из двух допустимых (МСК/СПБ)
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Вычислить сумму конкретных чисел в столбцах Excel можно как автоматически, так и вручную, используя стандартные инструменты программы. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: =D2/СУММ($D1500:$D$15) .
Как посчитать процент от числа и долю в Эксель
Вычислить сумму конкретных чисел в столбцах Excel можно как автоматически, так и вручную, используя стандартные инструменты программы. Помимо этого, имеется возможность просто просмотреть итоговый результат, не записывая его в ячейку. Начнем с последнего и самого простого способа.
Вариант №1: просматриваем всю сумму
В том случае, когда необходимо просто посмотреть всю сумму по столбцу, где ячейки содержат конкретные данные, и при этом не нужно постоянно удерживать сумму для дальнейших расчетов, делаем следующее:
Примечание: с левой стороны от суммы указываются число выделенных ячеек и усредненное значение по выбранному диапазону.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Дата отгрузки дата первого по времени составления первичного документа, оформленного на покупателя заказчика , перевозчика письмо Минфина от 01. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Если подрядчик обратится в суд, который подтвердит выполнение работ – НДС начисляется на дату вступления в законную силу решения суда (письмо Минфина от 02.02.2015 № 03-07-10/3962). Суды поддерживают такое мнение (см. постановление Восьмого ААС от 16.12.2014 № 08АП-11734/2014 по делу № А70-5069/2014).
EXCEL — как распределить сумму X на N месяцев — CodeRoad
При необходимости проверки большего количества условий, выполняемых одновременно (аналог логическому оператору И ), добавляем их в формулу через знак умножения и не забываем взять новое условие в круглые скобки.
Находим процент от числа
А сейчас давайте попробуем вычислить процент от числу в виде абсолютного значения, т.е. в виде другого числа.
Математическая формула для расчета выглядит следующим образом:
Например, давайте узнаем, какое число составляет 15% от 90.
Подобные знания помогают решать множество математических, экономических задач, физических и других задач. Допустим, у нас есть таблица с продажами обуви (в парах) за 1 квартал, и мы планируем в следующем продать на 10% больше. Нужно определить, какому количеству пар для каждого наименования соответствуют эти 10%.
В случаях, когда нам нужно получить разные проценты от разных чисел, соответственно, нужно создать отдельный столбец не только для вывода результатов, но и для значений процентов.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Таким образом, даже такую простую задачу, как вычисление суммы значений в ячейках и столбцах, можно выполнить в Excel несколькими способами, каждый из которых наилучшим образом подойдет в зависимости от ситуации и поставленных задач. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Если товар не отгружается и не транспортируется, но происходит передача права собственности на него, днем отгрузки признается дата передачи права собственности (п. 3 ст. 167 НК РФ, письмо Минфина от 01.11.2012 № 03-07-11/473).
Расчет пропорций при распределении расходов | Такском
Чтобы использовать эту функцию, на вкладке «Данные» выберите кнопку «Из интернета» и вставьте адрес надежного источника, например cbr.ru. Эксель предложит выбрать, какую именно таблицу нужно загрузить с сайта — отметьте нужную галочкой.
1 ответ
Возможный Дубликат : Пропорционально распределить (пропорционально распределить) значение по набору значений Я искал алгоритм, чтобы распределить общую сумму ежемесячно на основе количества дней в году в C# так, чтобы сумма всех пропортонов была равна общей стоимости. Диапазон дат в течение года и.

B1 , B2 и B3 являются входными ячейками. B1 должна быть датой, а не строкой.
D1 — O1 — это месяцы. Значения должны быть датами, а не строками, но затем могут быть отформатированы так, чтобы показывать только месяц и год. Например, формат MMM YYYY .
Вам нужно только ввести D1 и E1 в качестве дат 2017-01-01 и 2017-02-01 , затем выберите D1:E1 и заполните справа. Затем будет создана серия , имеющая от шага к шагу разницу в E1 — D1 , что в данном примере составляет 1 месяц.
и может быть заполнен справа по мере необходимости. В примере до O2 .
Теперь, если вы изменяете какую-либо из входных ячеек, значения в D2 на O2 также изменятся из-за формулы.
СУММПРОИЗВ (SUMPRODUCT) в Excel. Гораздо больше, чем сумма произведений | Excellent — Всё про Excel | Яндекс Дзен
Когда таблицы большие и многое происходит автоматически, легко пропустить что-то важное. От этого спасает функция выделения цветом. Для ее активации на главной вкладке выберите «Условное форматирование» и задайте условия и цвет выделения.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
В этом случае ячейка может быть зеленой, пока вы вписываетесь в бюджет, желтой, если на грани, и красной, когда вы вышли за лимит. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Таким образом, даже такую простую задачу, как вычисление суммы значений в ячейках и столбцах, можно выполнить в Excel несколькими способами, каждый из которых наилучшим образом подойдет в зависимости от ситуации и поставленных задач.
7 полезных формул для тех, кто считает деньги в эксель-таблице
То, что я рассказываю вам в своей статье это детский лепет. Если посмотреть, что вытворяют ребята завершившие обучение на курсе “EXCEL”, то захочется научиться делать также. Поэтому посоветую вам зарегистрироваться на обучение.
Распределение суммы по базе
Афиняне! Повсему вижу я, что Вы как-то по-особеному набожны, ибо проходя и осматривая Ваши святыни, я наткнулся и на жертвенник неведомому богу.
Где-то в библии в адрес древних греков.
В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.
Итак, классика!
Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).
Таким образом все сводится к такому вот методу:
Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) («Шесть в скобках» — это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе — проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.
В принципе мы получили то, что хотели — распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением — в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло — это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал.
Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно — давайте распределим 10 на 3:
В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить — 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, «чтобы не нарушать отчетности» (с).
Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:
В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет «золотым» )))
Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.
Новое решение!
Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз «родил» (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))
В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:
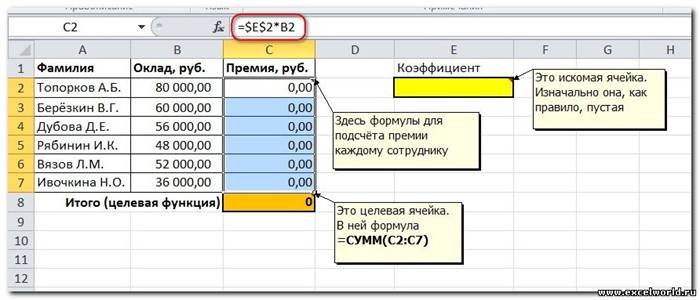
Пример 1. Распределение премии
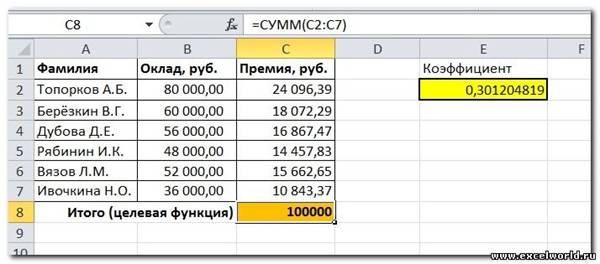
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
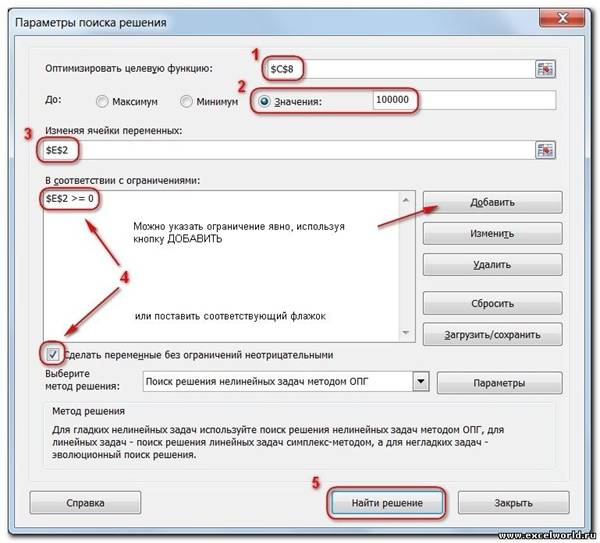
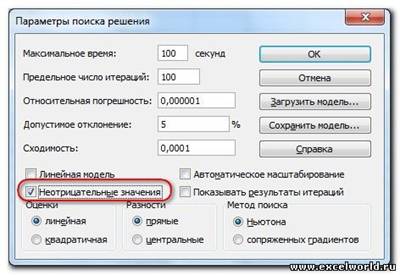
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
1. Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
2. Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
3. Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
4. Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=,
5. Кнопка, включающая итеративные вычисления с заданными параметрами.
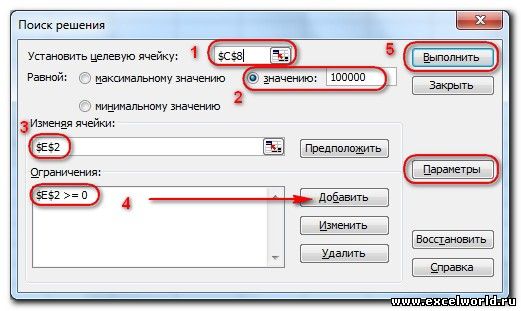
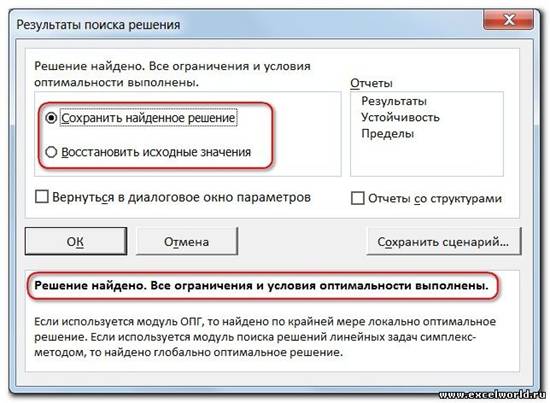
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
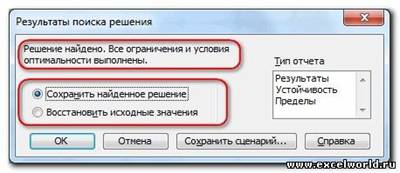
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОКи фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отменаи возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
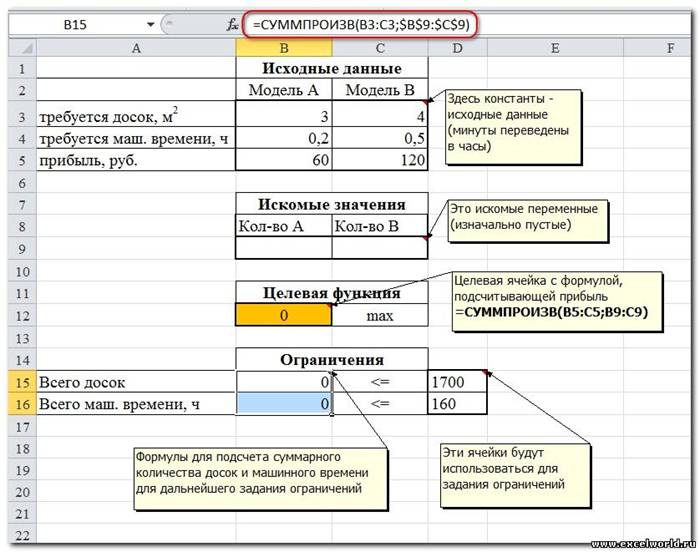
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
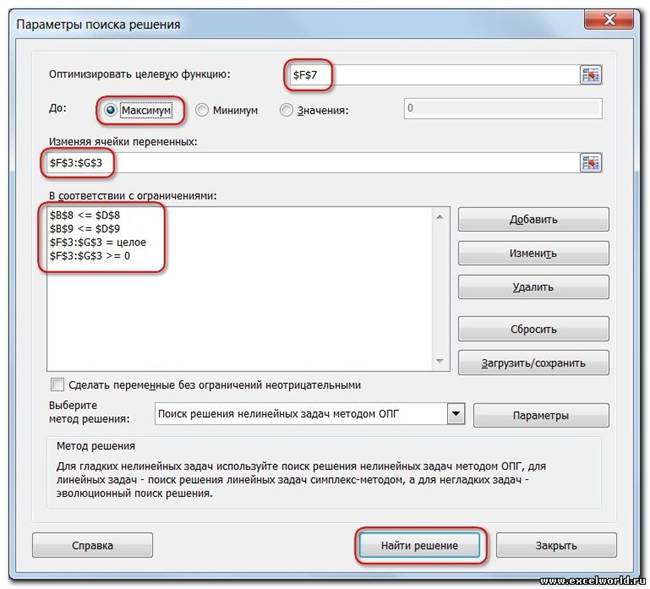
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
1. Целевая ячейка F7 содержит формулу для расчёта прибыли
2. Параметр оптимизации — максимум
3. Изменяемые ячейки F3:G3
4. Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D9); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D8). Здесь вместо ссылок на ячейки D8 и D9 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
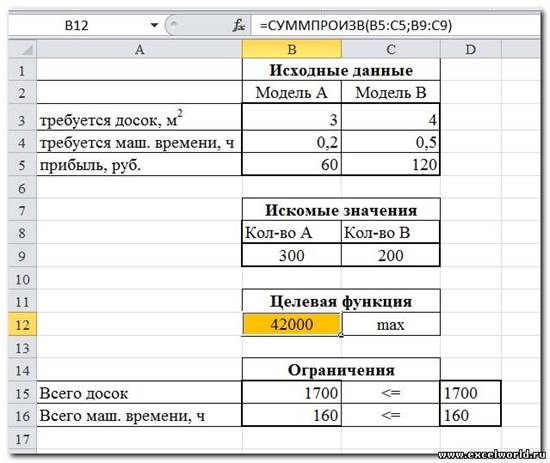
5. Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
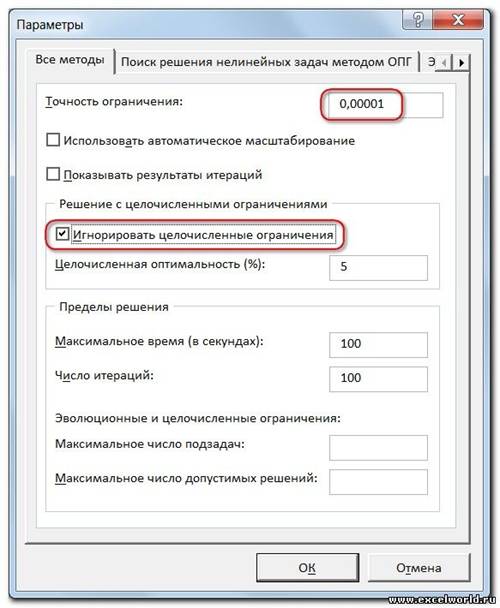
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметрыи попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
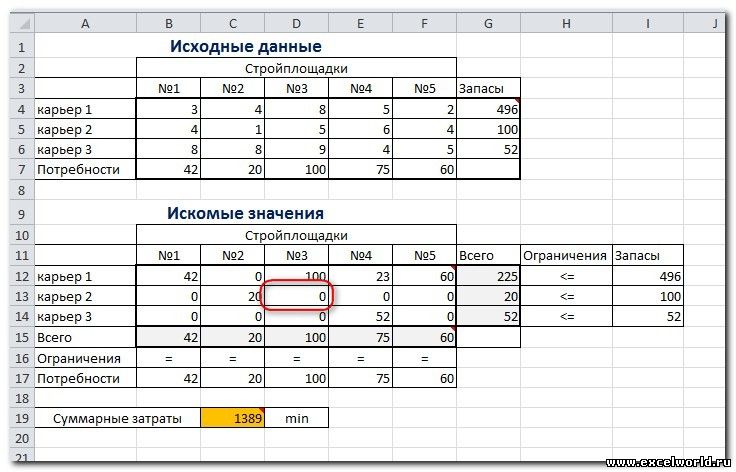
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
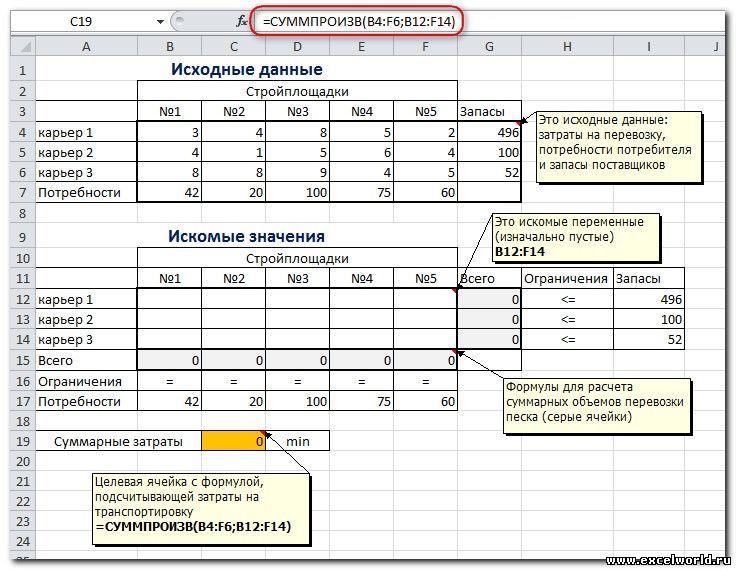
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
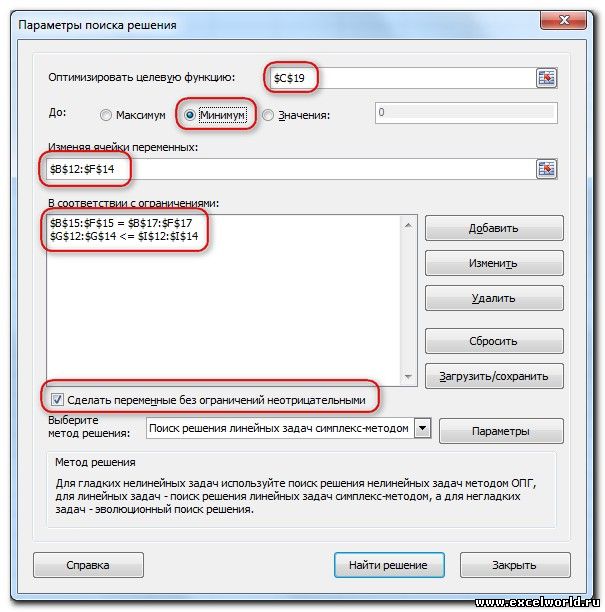
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
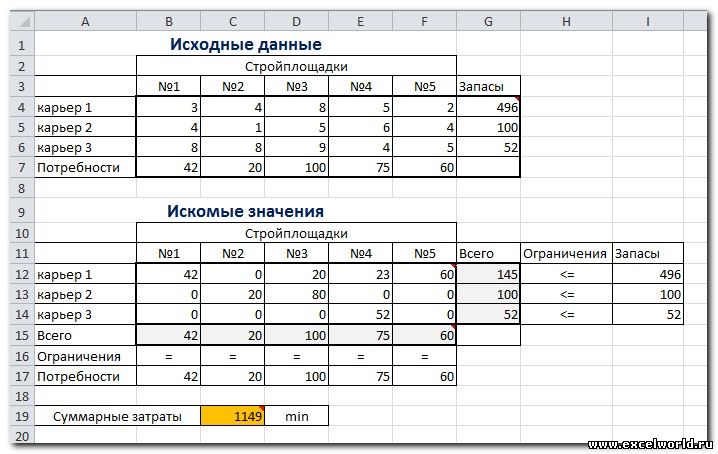
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Поиск решения EXCEL (1.3). Распределение ресурсов (ограничение по количеству оборудования, несколько периодов)
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.
Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования) , и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта www.solver.com ).
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Задача
Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача Поиска решения выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.
Переменные (выделено зеленым) . В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены имена Машин_Задействовано и Продукции_выпущено.
Ограничения (выделено синим) . Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются именованные диапазоны Alpha XXXX _Задействовано и Alpha XXXX _в_наличии ). Всего должно быть выпущено продукции не меньше чем величина заказа (используется именованный диапазон Продукции выпущено_Итого ). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются именованные диапазоны Продукции выпущено и Макс_производительность_задейств_машин ).
Целевая функция (выделено красным) . Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой =СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные) B19:B21 – количество продукции, выпущенной в определенный день. B13:B15 — количество задействованных машин в определенный день.
Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.
Убедитесь, что метод решения соответствует линейной задаче. Параметры Поиска решения были выбраны следующие:
Теперь в диалоговом окне можно нажать кнопку Найти решение .
Результаты расчетов
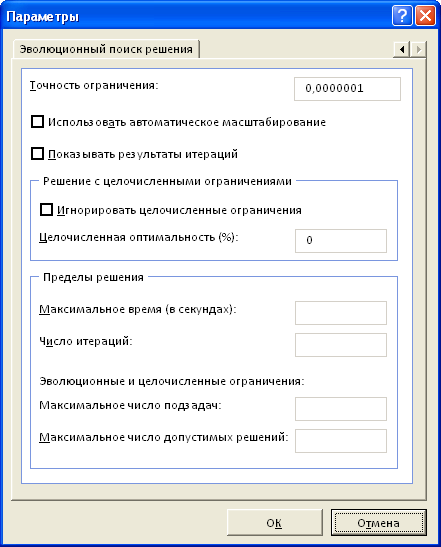
Поиск решения подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше, Целочисленная оптимальность была выбрана 0% ( Целочисленная оптимальность (Integer Optimality) позволяет Поиску решения остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных Поиску решения решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив Целочисленную оптимальность 1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при Целочисленной оптимальности не равной 0%.
Распределение суммы по базе
Афиняне! Повсему вижу я, что Вы как-то по-особеному набожны, ибо проходя и осматривая Ваши святыни, я наткнулся и на жертвенник неведомому богу.
Где-то в библии в адрес древних греков.
В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.
Итак, классика!
Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).
Таким образом все сводится к такому вот методу:
Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) («Шесть в скобках» — это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе — проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.
В принципе мы получили то, что хотели — распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением — в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло — это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал.
Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно — давайте распределим 10 на 3:
В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить — 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, «чтобы не нарушать отчетности» (с).
Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:
В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет «золотым» )))
Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.
Новое решение!
Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз «родил» (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))
В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:
5 основ Excel (обучение): как написать формулу, как посчитать сумму, сложение с условием, счет строк и пр.
Здравствуйте!
Многие кто не пользуются Excel — даже не представляют, какие возможности дает эта программа! ☝
Подумать только: складывать в автоматическом режиме значения из одних формул в другие, искать нужные строки в тексте, создавать собственные условия и т.д. — в общем-то, по сути мини-язык программирования для решения «узких» задач (признаться честно, я сам долгое время Excel не рассматривал за программу, и почти его не использовал) .
В этой статье хочу показать несколько примеров, как можно быстро решать повседневные офисные задачи: что-то сложить, вычесть, посчитать сумму (в том числе и с условием) , подставить значения из одной таблицы в другую и т.д.
То есть эта статья будет что-то мини гайда по обучению самому нужному для работы (точнее, чтобы начать пользоваться Excel и почувствовать всю мощь этого продукта!) .
Возможно, что прочти подобную статью лет 17-20 назад, я бы сам намного быстрее начал пользоваться Excel (и сэкономил бы кучу своего времени для решения «простых» задач. 👌
Обучение основам Excel: ячейки и числа
Примечание : все скриншоты ниже представлены из программы Excel 2016 (как одной из самой новой на сегодняшний день).
Многие начинающие пользователи, после запуска Excel — задают один странный вопрос: «ну и где тут таблица?». Между тем, все клеточки, что вы видите после запуска программы — это и есть одна большая таблица!
Теперь к главному : в любой клетке может быть текст, какое-нибудь число, или формула. Например, ниже на скриншоте показан один показательный пример:
- слева : в ячейке (A1) написано простое число «6». Обратите внимание, когда вы выбираете эту ячейку, то в строке формулы (Fx) показывается просто число «6».
- справа : в ячейке (C1) с виду тоже простое число «6», но если выбрать эту ячейку, то вы увидите формулу «=3+3» — это и есть важная фишка в Excel!
Просто число (слева) и посчитанная формула (справа)
👉 Суть в том, что Excel может считать как калькулятор, если выбрать какую нибудь ячейку, а потом написать формулу, например «=3+5+8» (без кавычек). Результат вам писать не нужно — Excel посчитает его сам и отобразит в ячейке (как в ячейке C1 в примере выше)!
Но писать в формулы и складывать можно не просто числа, но и числа, уже посчитанные в других ячейках. На скриншоте ниже в ячейке A1 и B1 числа 5 и 6 соответственно. В ячейке D1 я хочу получить их сумму — можно написать формулу двумя способами:
- первый: «=5+6» (не совсем удобно, представьте, что в ячейке A1 — у нас число тоже считается по какой-нибудь другой формуле и оно меняется. Не будете же вы подставлять вместо 5 каждый раз заново число?!);
- второй: «=A1+B1» — а вот это идеальный вариант, просто складываем значение ячеек A1 и B1 (несмотря даже какие числа в них!).
Сложение ячеек, в которых уже есть числа
Распространение формулы на другие ячейки
В примере выше мы сложили два числа в столбце A и B в первой строке. Но строк то у нас 6, и чаще всего в реальных задачах сложить числа нужно в каждой строке! Чтобы это сделать, можно:
- в строке 2 написать формулу «=A2+B2» , в строке 3 — «=A3+B3» и т.д. (это долго и утомительно, этот вариант никогда не используют) ;
- выбрать ячейку D1 (в которой уже есть формула) , затем подвести указатель мышки к правому уголку ячейки, чтобы появился черный крестик (см. скрин ниже) . Затем зажать левую кнопку и растянуть формулу на весь столбец. Удобно и быстро! ( Примечание : так же можно использовать для формул комбинации Ctrl+C и Ctrl+V (скопировать и вставить соответственно)) .
Кстати, обратите внимание на то, что Excel сам подставил формулы в каждую строку. То есть, если сейчас вы выберите ячейку, скажем, D2 — то увидите формулу «=A2+B2» (т.е. Excel автоматически подставляет формулы и сразу же выдает результат) .
Как задать константу (ячейку, которая не будет меняться при копировании формулы)
Довольно часто требуется в формулах (когда вы их копируете), чтобы какой-нибудь значение не менялось. Скажем простая задача: перевести цены в долларах в рубли. Стоимость рубля задается в одной ячейке, в моем примере ниже — это G2.
Далее в ячейке E2 пишется формула «=D2*G2» и получаем результат. Только вот если растянуть формулу, как мы это делали до этого, в других строках результата мы не увидим, т.к. Excel в строку 3 поставит формулу «D3*G3», в 4-ю строку: «D4*G4» и т.д. Надо же, чтобы G2 везде оставалась G2.
Чтобы это сделать — просто измените ячейку E2 — формула будет иметь вид «=D2*$G$2». Т.е. значок доллара $ — позволяет задавать ячейку, которая не будет меняться, когда вы будете копировать формулу (т.е. получаем константу, пример ниже) .
Константа / в формуле ячейка не изменяется
Как посчитать сумму (формулы СУММ и СУММЕСЛИМН)
Можно, конечно, составлять формулы в ручном режиме, печатая «=A1+B1+C1» и т.п. Но в Excel есть более быстрые и удобные инструменты.
Один из самых простых способов сложить все выделенные ячейки — это использовать опцию автосуммы (Excel сам напишет формулу и вставить ее в ячейку) .
Что нужно сделать, чтобы посчитать сумму определенных ячеек:
- сначала выделяем ячейки (см. скрин ниже 👇) ;
- далее открываем раздел «Формулы» ;
- следующий шаг жмем кнопку «Автосумма» . Под выделенными вами ячейками появиться результат из сложения;
- если выделить ячейку с результатом (в моем случае — это ячейка E8) — то вы увидите формулу «=СУММ(E2:E7)» .
- таким образом, написав формулу «=СУММ(xx)» , где вместо xx поставить (или выделить) любые ячейки, можно считать самые разнообразные диапазоны ячеек, столбцов, строк.
Автосумма выделенных ячеек
Как посчитать сумму с каким-нибудь условием
Довольно часто при работе требуется не просто сумма всего столбца, а сумма определенных строк (т.е. выборочно). Предположим простую задачу: нужно получить сумму прибыли от какого-нибудь рабочего (утрировано, конечно, но пример более чем реальный) .
Я в своей таблицы буду использовать всего 7 строк (для наглядности) , реальная же таблица может быть намного больше. Предположим, нам нужно посчитать всю прибыль, которую сделал «Саша». Как будет выглядеть формула:
- » =СУММЕСЛИМН( F2:F7 ; A2:A7 ;»Саша») » — ( прим .: обратите внимание на кавычки для условия — они должны быть как на скрине ниже, а не как у меня сейчас написано на блоге) . Так же обратите внимание, что Excel при вбивании начала формулы (к примеру «СУММ. «), сам подсказывает и подставляет возможные варианты — а формул в Excel’e сотни!;
- F2:F7 — это диапазон, по которому будут складываться (суммироваться) числа из ячеек;
- A2:A7 — это столбик, по которому будет проверяться наше условие;
- «Саша» — это условие, те строки, в которых в столбце A будет «Саша» будут сложены (обратите внимание на показательный скриншот ниже) .
Сумма с условием
Примечание : условий может быть несколько и проверять их можно по разным столбцам.
Как посчитать количество строк (с одним, двумя и более условием)
Довольно типичная задача: посчитать не сумму в ячейках, а количество строк, удовлетворяющих какомe-либо условию.
Ну, например, сколько раз имя «Саша» встречается в таблице ниже (см. скриншот). Очевидно, что 2 раза (но это потому, что таблица слишком маленькая и взята в качестве наглядного примера). А как это посчитать формулой?
«=СЧЁТЕСЛИ( A2:A7 ; A2 )» — где:
- A2:A7 — диапазон, в котором будут проверяться и считаться строки;
- A2 — задается условие (обратите внимание, что можно было написать условие вида «Саша», а можно просто указать ячейку).
Результат показан в правой части на скрине ниже.
Количество строк с одним условием
Теперь представьте более расширенную задачу: нужно посчитать строки, где встречается имя «Саша», и где в столбце «B» будет стоять цифра «6». Забегая вперед, скажу, что такая строка всего лишь одна (скрин с примером ниже) .
Формула будет иметь вид:
=СЧЁТЕСЛИМН( A2:A7 ; A2 ; B2:B7 ;»6″) — (прим.: обратите внимание на кавычки — они должны быть как на скрине ниже, а не как у меня) , где:
A2:A7 ; A2 — первый диапазон и условие для поиска (аналогично примеру выше);
B2:B7 ;»6″ — второй диапазон и условие для поиска (обратите внимание, что условие можно задавать по разному: либо указывать ячейку, либо просто написано в кавычках текст/число).
Счет строк с двумя и более условиями
Как посчитать процент от суммы
Тоже довольно распространенный вопрос, с которым часто сталкиваюсь. Вообще, насколько я себе представляю, возникает он чаще всего — из-за того, что люди путаются и не знают, что от чего ищут процент (да и вообще, плохо понимают тему процентов (хотя я и сам не большой математик, и все таки. ☝) ).
👉 В помощь!
Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel] — заметка для начинающих
Самый простой способ, в котором просто невозможно запутаться — это использовать правило «квадрата», или пропорции.
Вся суть приведена на скрине ниже: если у вас есть общая сумма, допустим в моем примере это число 3060 — ячейка F8 (т.е. это 100% прибыль, и какую то ее часть сделал «Саша», нужно найти какую. ).
По пропорции формула будет выглядеть так: =F10*G8/F8 (т.е. крест на крест: сначала перемножаем два известных числа по диагонали, а затем делим на оставшееся третье число).
В принципе, используя это правило, запутаться в процентах практически невозможно 👌.
Пример решения задач с процентами
PS
Собственно, на этом я завершаю данную статью. Не побоюсь сказать, что освоив все, что написано выше (а приведено здесь всего лишь «пяток» формул) — Вы дальше сможете самостоятельно обучаться Excel, листать справку, смотреть, экспериментировать, и анализировать. 👌
Скажу даже больше, все что я описал выше, покроет многие задачи, и позволит решать всё самое распространенное, над которым часто ломаешь голову (если не знаешь возможности Excel) , и даже не догадывается как быстро это можно сделать. ✔
СУММПРОИЗВ (SUMPRODUCT) в Excel. Гораздо больше, чем сумма произведений
Разберем, казалось бы, простую функцию СУММПРОИЗВ ( SUMPRODUCT ). В конце будет просто бомба для тех, кто строит отчеты в одних файлах, а хранит данные — в других.
Из русскоязычного написания функции можно догадаться, что СУММПРОИЗВ — это сумма произведений. Классический и самый примитивный способ её использования — перемножить значения из двух или более диапазонов и затем просуммировать. Посмотрим, как это работает.
Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: =D2/СУММ($D1500:$D$15) .
Как посчитать процент от числа и долю в Эксель
Вычислить сумму конкретных чисел в столбцах Excel можно как автоматически, так и вручную, используя стандартные инструменты программы. Помимо этого, имеется возможность просто просмотреть итоговый результат, не записывая его в ячейку. Начнем с последнего и самого простого способа.
Вариант №1: просматриваем всю сумму
В том случае, когда необходимо просто посмотреть всю сумму по столбцу, где ячейки содержат конкретные данные, и при этом не нужно постоянно удерживать сумму для дальнейших расчетов, делаем следующее:
Примечание: с левой стороны от суммы указываются число выделенных ячеек и усредненное значение по выбранному диапазону.
EXCEL — как распределить сумму X на N месяцев — CodeRoad
При необходимости проверки большего количества условий, выполняемых одновременно (аналог логическому оператору И ), добавляем их в формулу через знак умножения и не забываем взять новое условие в круглые скобки.
Находим процент от числа
А сейчас давайте попробуем вычислить процент от числу в виде абсолютного значения, т.е. в виде другого числа.
Математическая формула для расчета выглядит следующим образом:
Например, давайте узнаем, какое число составляет 15% от 90.
Подобные знания помогают решать множество математических, экономических задач, физических и других задач. Допустим, у нас есть таблица с продажами обуви (в парах) за 1 квартал, и мы планируем в следующем продать на 10% больше. Нужно определить, какому количеству пар для каждого наименования соответствуют эти 10%.
В случаях, когда нам нужно получить разные проценты от разных чисел, соответственно, нужно создать отдельный столбец не только для вывода результатов, но и для значений процентов.
Расчет пропорций при распределении расходов | Такском
Чтобы использовать эту функцию, на вкладке «Данные» выберите кнопку «Из интернета» и вставьте адрес надежного источника, например cbr.ru. Эксель предложит выбрать, какую именно таблицу нужно загрузить с сайта — отметьте нужную галочкой.
1 ответ
Возможный Дубликат : Пропорционально распределить (пропорционально распределить) значение по набору значений Я искал алгоритм, чтобы распределить общую сумму ежемесячно на основе количества дней в году в C# так, чтобы сумма всех пропортонов была равна общей стоимости. Диапазон дат в течение года и.
B1 , B2 и B3 являются входными ячейками. B1 должна быть датой, а не строкой.
D1 — O1 — это месяцы. Значения должны быть датами, а не строками, но затем могут быть отформатированы так, чтобы показывать только месяц и год. Например, формат MMM YYYY .
Вам нужно только ввести D1 и E1 в качестве дат 2017-01-01 и 2017-02-01 , затем выберите D1:E1 и заполните справа. Затем будет создана серия , имеющая от шага к шагу разницу в E1 — D1 , что в данном примере составляет 1 месяц.
и может быть заполнен справа по мере необходимости. В примере до O2 .
Теперь, если вы изменяете какую-либо из входных ячеек, значения в D2 на O2 также изменятся из-за формулы.
7 полезных формул для тех, кто считает деньги в эксель-таблице
То, что я рассказываю вам в своей статье это детский лепет. Если посмотреть, что вытворяют ребята завершившие обучение на курсе “EXCEL”, то захочется научиться делать также. Поэтому посоветую вам зарегистрироваться на обучение.
Как посчитать процентное распределение в Excel по формуле
Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.
Формула процентного распределения в Excel
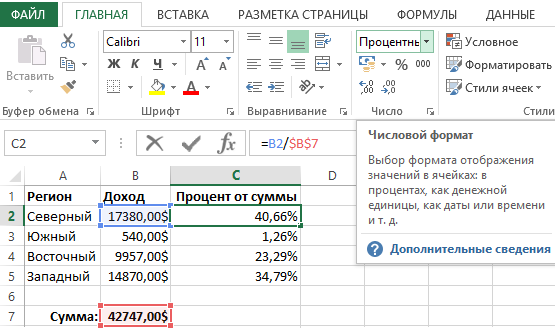
Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.
Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.
Процентное распределение по динамической формуле Excel
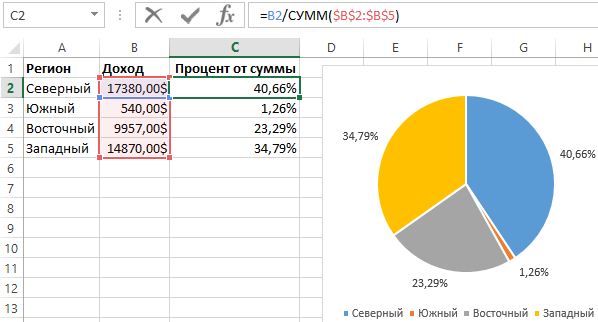
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.
Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.
Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.
Как раскидать сумму пропорционально в excel
В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.
Итак, классика!
Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).
Таким образом все сводится к такому вот методу:
Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) («Шесть в скобках» — это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе — проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.
В принципе мы получили то, что хотели — распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением — в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло — это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал.
Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно — давайте распределим 10 на 3:
В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить — 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, «чтобы не нарушать отчетности» (с).
Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:
В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет «золотым» )))
Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.
Новое решение!
Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз «родил» (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))
В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:
Пример 1. Распределение премии
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
1. Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
2. Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
3. Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
4. Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=,
5. Кнопка, включающая итеративные вычисления с заданными параметрами.
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОКи фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отменаи возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
1. Целевая ячейка F7 содержит формулу для расчёта прибыли
2. Параметр оптимизации — максимум
3. Изменяемые ячейки F3:G3
4. Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D9); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D8). Здесь вместо ссылок на ячейки D8 и D9 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
5. Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
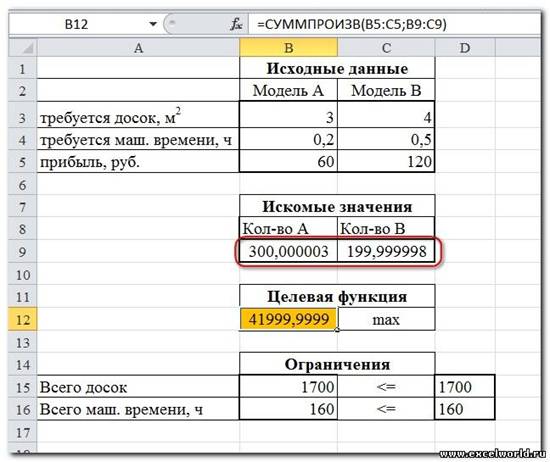
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметрыи попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Поиск решения EXCEL (1.3). Распределение ресурсов (ограничение по количеству оборудования, несколько периодов)
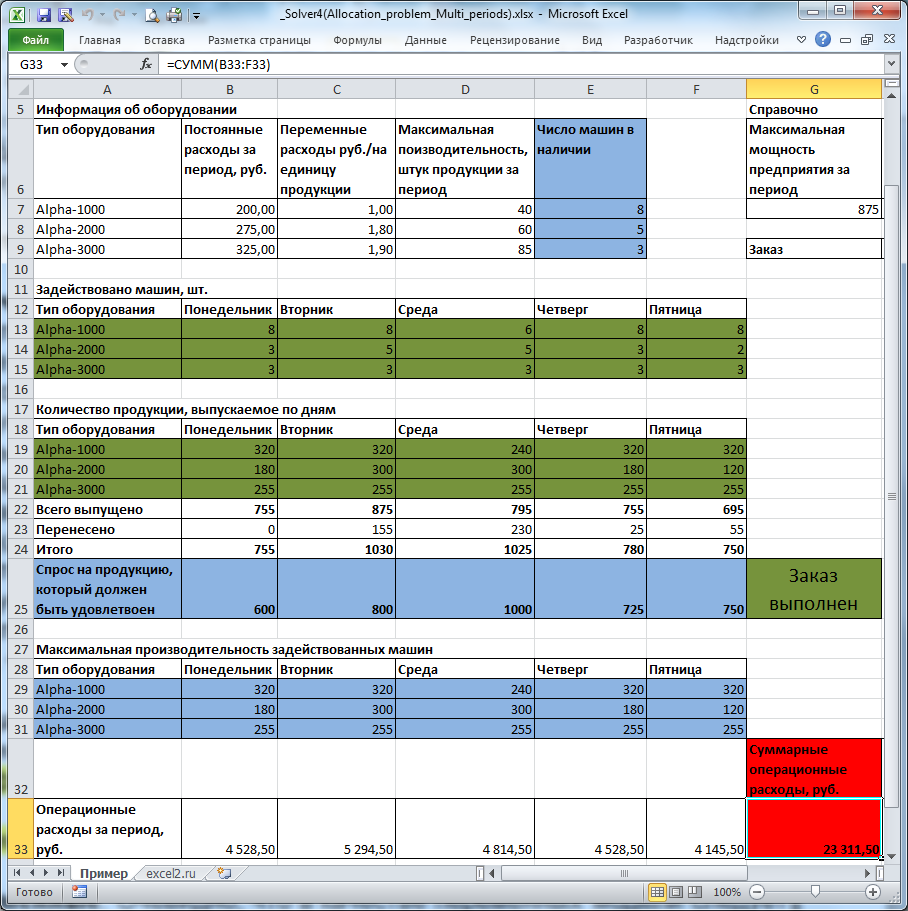
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.
Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования) , и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта www.solver.com ).
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Задача
Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача Поиска решения выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.
Переменные (выделено зеленым) . В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены имена Машин_Задействовано и Продукции_выпущено.
Ограничения (выделено синим) . Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются именованные диапазоны Alpha XXXX _Задействовано и Alpha XXXX _в_наличии ). Всего должно быть выпущено продукции не меньше чем величина заказа (используется именованный диапазон Продукции выпущено_Итого ). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются именованные диапазоны Продукции выпущено и Макс_производительность_задейств_машин ).
Целевая функция (выделено красным) . Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой =СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные) B19:B21 – количество продукции, выпущенной в определенный день. B13:B15 — количество задействованных машин в определенный день.
Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.
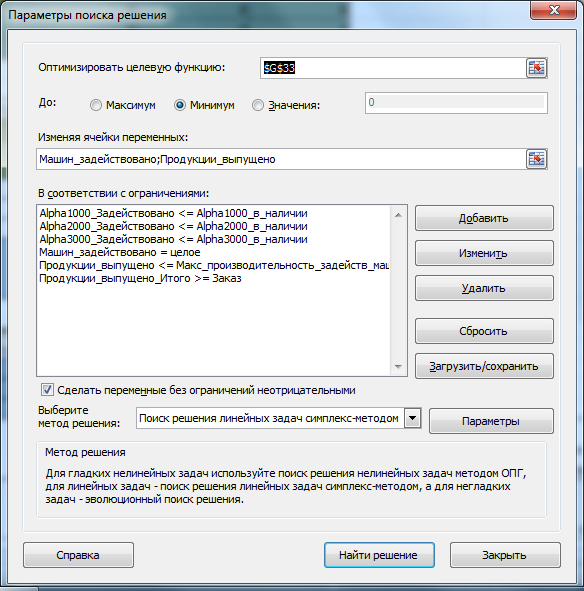
Убедитесь, что метод решения соответствует линейной задаче. Параметры Поиска решения были выбраны следующие:
Теперь в диалоговом окне можно нажать кнопку Найти решение .
Результаты расчетов
Поиск решения подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше, Целочисленная оптимальность была выбрана 0% ( Целочисленная оптимальность (Integer Optimality) позволяет Поиску решения остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных Поиску решения решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив Целочисленную оптимальность 1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при Целочисленной оптимальности не равной 0%.
Распределение суммы по базе
Афиняне! Повсему вижу я, что Вы как-то по-особеному набожны, ибо проходя и осматривая Ваши святыни, я наткнулся и на жертвенник неведомому богу.
Где-то в библии в адрес древних греков.
В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.
Итак, классика!
Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).
Таким образом все сводится к такому вот методу:
Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) («Шесть в скобках» — это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе — проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.
В принципе мы получили то, что хотели — распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением — в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло — это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал.
Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно — давайте распределим 10 на 3:
В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить — 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, «чтобы не нарушать отчетности» (с).
Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:
В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет «золотым» )))
Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.
Новое решение!
Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз «родил» (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))
В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:
5 основ Excel (обучение): как написать формулу, как посчитать сумму, сложение с условием, счет строк и пр.
Многие кто не пользуются Excel — даже не представляют, какие возможности дает эта программа! ☝
Подумать только: складывать в автоматическом режиме значения из одних формул в другие, искать нужные строки в тексте, создавать собственные условия и т.д. — в общем-то, по сути мини-язык программирования для решения «узких» задач (признаться честно, я сам долгое время Excel не рассматривал за программу, и почти его не использовал) .
В этой статье хочу показать несколько примеров, как можно быстро решать повседневные офисные задачи: что-то сложить, вычесть, посчитать сумму (в том числе и с условием) , подставить значения из одной таблицы в другую и т.д.
То есть эта статья будет что-то мини гайда по обучению самому нужному для работы (точнее, чтобы начать пользоваться Excel и почувствовать всю мощь этого продукта!) .
Возможно, что прочти подобную статью лет 17-20 назад, я бы сам намного быстрее начал пользоваться Excel (и сэкономил бы кучу своего времени для решения «простых» задач. 👌
Обучение основам Excel: ячейки и числа
Примечание : все скриншоты ниже представлены из программы Excel 2016 (как одной из самой новой на сегодняшний день).
Многие начинающие пользователи, после запуска Excel — задают один странный вопрос: «ну и где тут таблица?». Между тем, все клеточки, что вы видите после запуска программы — это и есть одна большая таблица!
Теперь к главному : в любой клетке может быть текст, какое-нибудь число, или формула. Например, ниже на скриншоте показан один показательный пример:
- слева : в ячейке (A1) написано простое число «6». Обратите внимание, когда вы выбираете эту ячейку, то в строке формулы (Fx) показывается просто число «6».
- справа : в ячейке (C1) с виду тоже простое число «6», но если выбрать эту ячейку, то вы увидите формулу «=3+3» — это и есть важная фишка в Excel!
Просто число (слева) и посчитанная формула (справа)
👉 Суть в том, что Excel может считать как калькулятор, если выбрать какую нибудь ячейку, а потом написать формулу, например «=3+5+8» (без кавычек). Результат вам писать не нужно — Excel посчитает его сам и отобразит в ячейке (как в ячейке C1 в примере выше)!
Но писать в формулы и складывать можно не просто числа, но и числа, уже посчитанные в других ячейках. На скриншоте ниже в ячейке A1 и B1 числа 5 и 6 соответственно. В ячейке D1 я хочу получить их сумму — можно написать формулу двумя способами:
- первый: «=5+6» (не совсем удобно, представьте, что в ячейке A1 — у нас число тоже считается по какой-нибудь другой формуле и оно меняется. Не будете же вы подставлять вместо 5 каждый раз заново число?!);
- второй: «=A1+B1» — а вот это идеальный вариант, просто складываем значение ячеек A1 и B1 (несмотря даже какие числа в них!).
Сложение ячеек, в которых уже есть числа
Распространение формулы на другие ячейки
В примере выше мы сложили два числа в столбце A и B в первой строке. Но строк то у нас 6, и чаще всего в реальных задачах сложить числа нужно в каждой строке! Чтобы это сделать, можно:
- в строке 2 написать формулу «=A2+B2» , в строке 3 — «=A3+B3» и т.д. (это долго и утомительно, этот вариант никогда не используют) ;
- выбрать ячейку D1 (в которой уже есть формула) , затем подвести указатель мышки к правому уголку ячейки, чтобы появился черный крестик (см. скрин ниже) . Затем зажать левую кнопку и растянуть формулу на весь столбец. Удобно и быстро! ( Примечание : так же можно использовать для формул комбинации Ctrl+C и Ctrl+V (скопировать и вставить соответственно)) .
Кстати, обратите внимание на то, что Excel сам подставил формулы в каждую строку. То есть, если сейчас вы выберите ячейку, скажем, D2 — то увидите формулу «=A2+B2» (т.е. Excel автоматически подставляет формулы и сразу же выдает результат) .
Как задать константу (ячейку, которая не будет меняться при копировании формулы)
Довольно часто требуется в формулах (когда вы их копируете), чтобы какой-нибудь значение не менялось. Скажем простая задача: перевести цены в долларах в рубли. Стоимость рубля задается в одной ячейке, в моем примере ниже — это G2.
Далее в ячейке E2 пишется формула «=D2*G2» и получаем результат. Только вот если растянуть формулу, как мы это делали до этого, в других строках результата мы не увидим, т.к. Excel в строку 3 поставит формулу «D3*G3», в 4-ю строку: «D4*G4» и т.д. Надо же, чтобы G2 везде оставалась G2.
Чтобы это сделать — просто измените ячейку E2 — формула будет иметь вид «=D2*$G$2». Т.е. значок доллара $ — позволяет задавать ячейку, которая не будет меняться, когда вы будете копировать формулу (т.е. получаем константу, пример ниже) .
Константа / в формуле ячейка не изменяется
Как посчитать сумму (формулы СУММ и СУММЕСЛИМН)
Можно, конечно, составлять формулы в ручном режиме, печатая «=A1+B1+C1» и т.п. Но в Excel есть более быстрые и удобные инструменты.
Один из самых простых способов сложить все выделенные ячейки — это использовать опцию автосуммы (Excel сам напишет формулу и вставить ее в ячейку) .
Что нужно сделать, чтобы посчитать сумму определенных ячеек:
- сначала выделяем ячейки (см. скрин ниже 👇) ;
- далее открываем раздел «Формулы» ;
- следующий шаг жмем кнопку «Автосумма» . Под выделенными вами ячейками появиться результат из сложения;
- если выделить ячейку с результатом (в моем случае — это ячейка E8) — то вы увидите формулу «=СУММ(E2:E7)» .
- таким образом, написав формулу «=СУММ(xx)» , где вместо xx поставить (или выделить) любые ячейки, можно считать самые разнообразные диапазоны ячеек, столбцов, строк.
Автосумма выделенных ячеек
Как посчитать сумму с каким-нибудь условием
Довольно часто при работе требуется не просто сумма всего столбца, а сумма определенных строк (т.е. выборочно). Предположим простую задачу: нужно получить сумму прибыли от какого-нибудь рабочего (утрировано, конечно, но пример более чем реальный) .
Я в своей таблицы буду использовать всего 7 строк (для наглядности) , реальная же таблица может быть намного больше. Предположим, нам нужно посчитать всю прибыль, которую сделал «Саша». Как будет выглядеть формула:
- » =СУММЕСЛИМН( F2:F7 ; A2:A7 ;»Саша») » — ( прим .: обратите внимание на кавычки для условия — они должны быть как на скрине ниже, а не как у меня сейчас написано на блоге) . Так же обратите внимание, что Excel при вбивании начала формулы (к примеру «СУММ. «), сам подсказывает и подставляет возможные варианты — а формул в Excel’e сотни!;
- F2:F7 — это диапазон, по которому будут складываться (суммироваться) числа из ячеек;
- A2:A7 — это столбик, по которому будет проверяться наше условие;
- «Саша» — это условие, те строки, в которых в столбце A будет «Саша» будут сложены (обратите внимание на показательный скриншот ниже) .
Сумма с условием
Примечание : условий может быть несколько и проверять их можно по разным столбцам.
Как посчитать количество строк (с одним, двумя и более условием)
Довольно типичная задача: посчитать не сумму в ячейках, а количество строк, удовлетворяющих какомe-либо условию.
Ну, например, сколько раз имя «Саша» встречается в таблице ниже (см. скриншот). Очевидно, что 2 раза (но это потому, что таблица слишком маленькая и взята в качестве наглядного примера). А как это посчитать формулой?
«=СЧЁТЕСЛИ( A2:A7 ; A2 )» — где:
- A2:A7 — диапазон, в котором будут проверяться и считаться строки;
- A2 — задается условие (обратите внимание, что можно было написать условие вида «Саша», а можно просто указать ячейку).
Результат показан в правой части на скрине ниже.
Количество строк с одним условием
Теперь представьте более расширенную задачу: нужно посчитать строки, где встречается имя «Саша», и где в столбце «B» будет стоять цифра «6». Забегая вперед, скажу, что такая строка всего лишь одна (скрин с примером ниже) .
Формула будет иметь вид:
=СЧЁТЕСЛИМН( A2:A7 ; A2 ; B2:B7 ;»6″) — (прим.: обратите внимание на кавычки — они должны быть как на скрине ниже, а не как у меня) , где:
A2:A7 ; A2 — первый диапазон и условие для поиска (аналогично примеру выше);
B2:B7 ;»6″ — второй диапазон и условие для поиска (обратите внимание, что условие можно задавать по разному: либо указывать ячейку, либо просто написано в кавычках текст/число).
Счет строк с двумя и более условиями
Как посчитать процент от суммы
Тоже довольно распространенный вопрос, с которым часто сталкиваюсь. Вообще, насколько я себе представляю, возникает он чаще всего — из-за того, что люди путаются и не знают, что от чего ищут процент (да и вообще, плохо понимают тему процентов (хотя я и сам не большой математик, и все таки. ☝) ).
👉 В помощь!
Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel] — заметка для начинающих
Самый простой способ, в котором просто невозможно запутаться — это использовать правило «квадрата», или пропорции.
Вся суть приведена на скрине ниже: если у вас есть общая сумма, допустим в моем примере это число 3060 — ячейка F8 (т.е. это 100% прибыль, и какую то ее часть сделал «Саша», нужно найти какую. ).
По пропорции формула будет выглядеть так: =F10*G8/F8 (т.е. крест на крест: сначала перемножаем два известных числа по диагонали, а затем делим на оставшееся третье число).
В принципе, используя это правило, запутаться в процентах практически невозможно 👌.
Пример решения задач с процентами
PS
Собственно, на этом я завершаю данную статью. Не побоюсь сказать, что освоив все, что написано выше (а приведено здесь всего лишь «пяток» формул) — Вы дальше сможете самостоятельно обучаться Excel, листать справку, смотреть, экспериментировать, и анализировать. 👌
Скажу даже больше, все что я описал выше, покроет многие задачи, и позволит решать всё самое распространенное, над которым часто ломаешь голову (если не знаешь возможности Excel) , и даже не догадывается как быстро это можно сделать. ✔
|
Как распределить сумму пропорционально между др. ячейками |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная на отрезке [a; b] случайная величина имеет плотность распределения (вероятности) :
Функция распределения определяется следующим образом:
Равномерное непрерывное распределение (англ. Continuous uniform d istribution или Rectangular distribution ) часто встречается на практике.
Пример1. Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2. Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
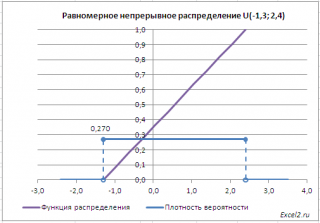
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Математическое ожидание и дисперсия
Математическое ожидание для равномерного непрерывного распределения вычисляется по формуле =(a+b)/2.
Генерация случайных чисел
Случайные числа, имеющие равномерное непрерывное распределение на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL СЛЧИС() . В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу =СЛЧИС()*(b-a)+a можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание : Чтобы сгенерировать случайные числа, имеющие равномерное дискретное распределение , воспользуйтесь функцией СЛУЧМЕЖДУ() .
Сгенерировать случайные числа, извлеченные из непрерывного равномерного распределения, можно также с помощью надстройки Пакет анализа .
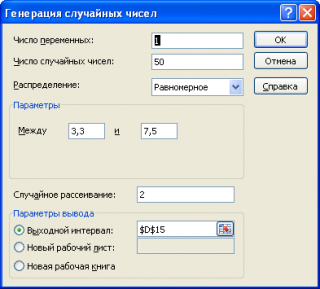
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне Генерация случайных чисел установим следующие параметры (см. файл примера лист Генерация ):
Как видно из рисунка выше, в поле Случайное рассеивание установлен необязательный параметр равный 2. Параметр Случайное рассеивание может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках B4:B5 . Сгенерируем 50 чисел ( выборку ) и поместим их в диапазоне С14:С63 .
Математическое ожидание этого распределения =(B4+B5)/2 и равно 5,4. Стандартное отклонение распределения равно =КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить математическое ожидание воспользуемся значениями выборки =СУММ(C14:C63)/СЧЁТ(C14:C63) .
Оценить стандартное отклонение можно с помощью формулы =СТАНДОТКЛОН.В(C14:C63) в MS EXCEL 2010 или =СТАНДОТКЛОН(C14:C63) для более ранних версий.
Чтобы оценить дисперсию используйте формулу =ДИСП.В(C14:C63) в MS EXCEL 2010 или =ДИСП(C14:C63) для более ранних версий. Также можно использовать формулу =СТАНДОТКЛОН.В(C14:C63)^2 .
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Как посчитать процентное распределение в Excel по формуле
Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.
Формула процентного распределения в Excel
Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.
Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.
Процентное распределение по динамической формуле Excel
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.
Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.
Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.
Распределение суммы в таблице Excel помесячно
Добрый день, друзья!
Помогите, если не трудно, справиться с задачкой.
Нужно распределить потребность равномерно помесячно по году. Допускается создание дополнительной таблицы. Но единица измерения меньше единицы не допускается.
Буду Вам очень признателен!
Вложения
Книга1.xlsx (11.6 Кб, 13 просмотров)
В ТАБЛИЦЕ EXCEL РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВА СООТВЕТСТВУЮЩЕМУ НАИМЕНОВАНИЮ
ЗДРАВСТВУЙТЕ. ПЕРВЫЙ РАЗ НА ФОРУМЕ, НЕ СУДИТЕ СТРОГО. ВОПРОС В ТОМ, ЧТО НАДО СДЕЛАТЬ.
распределение суммы
помогите решить следующую задачу есть общая сумма 2750, которую надо разбить на 70 разных.
Распределение суммы переменной
Здравствуйте у меня вопрос. Я хочу вместо нескольких массивов использовать один. Если я буду их.
Распределение суммы по ФИФО
Необходимо высчитать сколько осталось товара с каждой поставки. За основу взять алгоритм ФИФО.
Вложения
Книга1-4.xlsx (12.7 Кб, 23 просмотров)
Сообщение от andrei_g1

Решение
А можете это сделать в моей табличке? А то я совсем «чайник», боюсь что не правильно пропишу формулы.
Спасибо огромное заранее.
Добавлено через 39 минут
Все. Формулы вставил, все получилось.
Ребята, спасибо огромное. Вы мне здорово помогли
Вложения
Книга1-4.xlsx (13.7 Кб, 21 просмотров)

Решение
заинтересовавшись этим вопросом также выяснил,
что для разных отчётов можно ещё использовать
т.н. банковское (бухгалтерское) округление
также известное, как округление до ближайшего чётного
суть его в том, что все числа, у которых «отбрасываемая» цифра не равна 5,
округляются по правилам математического округления,
а если равна, то цифра округляется до ближайшего кратного целого числа
т.е. 6,5 до 6 а 7,5 до 8.
приводят следующий пример:
Сумма исходных чисел: 1.5 + 2.5 + 3.5 +4.5 = 12
Сумма округленных чисел классическим методом: 2 + 3 + 4 + 5 = 14
Сумма округленных чисел бухгалтерским методом: 2 + 2 + 4 + 4 = 12
Распределение суммы акций
Введите фамилии сотрудников (не менее 20), для всех них укажите даты приема на работу (в диапазоне.
Пропорциональное распределение суммы ЗП
Здравствуйте.:) Поставлена задача распределения суммы з/п сотрудника, которая указана в.

Родитель дает ребенку X рублей на месяц, в месяце Y дней (каждый месяц разный). Нужно.
Пропорциональное распределение потока с проверкой суммы
ПОжалуйста помогите написать формулу: Спримерно : J6= ЕСЛИ СУММ (F6: I6)<E6, то D6*J5/(d6+d7) .
Распределение по командам в Excel
Уважаемые коллеги! Помогите решить задачу через Excel Дано: Список 14 учеников в первой.
Распределение задач в Excel
Добрый день, форумчане! Задали не простую задачку над которой бьюсь уже второй день. Общая.
|
0 / 0 / 0 Регистрация: 15.07.2020 Сообщений: 4 |
|
|
1 |
|
|
15.07.2020, 17:16. Показов 8104. Ответов 8
Добрый день, друзья! Буду Вам очень признателен!
0 |
|
866 / 510 / 162 Регистрация: 30.03.2013 Сообщений: 1,048 |
|
|
15.07.2020, 19:53 |
2 |
|
1 |
|
0 / 0 / 0 Регистрация: 15.07.2020 Сообщений: 4 |
|
|
16.07.2020, 07:08 [ТС] |
3 |
|
Спасибо большое за ответ!
0 |
|
5942 / 3154 / 698 Регистрация: 23.11.2010 Сообщений: 10,524 |
|
|
16.07.2020, 08:20 |
4 |
|
меньше единицы не допускается. в случаях где всего 1, 2 и 16 как быть?
1 |
|
65 / 22 / 7 Регистрация: 28.02.2018 Сообщений: 211 |
|
|
16.07.2020, 08:44 |
5 |
|
Решениеandrei_g1, я обычно делаю округление до нуля а в последней ячейке считаю разницу для большей равномерности (и, в данном случае, чтобы избавиться от минусов), Код F6:=ЕСЛИ(ОКРУГЛ($C6/4;0)-СУММ($D6:E6)>0;ОКРУГЛ($C6/4;0)-СУММ($D6:E6);0) i6:=ЕСЛИ(ОКРУГЛ($C6/2;0)-СУММ($D6:H6)>0;ОКРУГЛ($C6/2;0)-СУММ($D6:H6);0) L6:=ЕСЛИ(ОКРУГЛ($C6*3/4;0)-СУММ($D6:K6)>0;ОКРУГЛ($C6*3/4;0)-СУММ($D6:K6);0) O6:=ЕСЛИ(C6-СУММ(D6:N6)>0;C6-СУММ(D6:N6);0) Добавлено через 8 минут
1 |
|
0 / 0 / 0 Регистрация: 15.07.2020 Сообщений: 4 |
|
|
16.07.2020, 10:39 [ТС] |
6 |
|
А можете это сделать в моей табличке? А то я совсем «чайник», боюсь что не правильно пропишу формулы. Спасибо огромное заранее!!! Добавлено через 39 минут
0 |
|
866 / 510 / 162 Регистрация: 30.03.2013 Сообщений: 1,048 |
|
|
16.07.2020, 10:44 |
7 |
|
Тогда так Код =IF(COLUMNS($D:D)<=(12-(ROUNDUP($C6/12;0)*12-$C6));ROUNDUP($C6/12;0);ROUNDDOWN($C6/12;0))
1 |
|
65 / 22 / 7 Регистрация: 28.02.2018 Сообщений: 211 |
|
|
17.07.2020, 10:21 |
8 |
|
Решениеandrei_g1, Не по теме: заинтересовавшись этим вопросом также выяснил, приводят следующий пример: Код =ОКРУГЛТ(A2;2) =ЦЕЛОЕ(A2/2+0,5)*2 в данном случае такое округление не подходит
1 |
|
0 / 0 / 0 Регистрация: 15.07.2020 Сообщений: 4 |
|
|
17.07.2020, 16:32 [ТС] |
9 |
|
Вот умом понимаю, а в формулах прописать тяму не хватает, даже сказал бы, навыков.
0 |
Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.
Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.
Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.
Процентное распределение по динамической формуле Excel
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.
Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.
Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.
1С:Предприятие 8.2 /
Бухгалтерия для Украины /
Учет НДС
Когда предприятие одновременно ведет хозяйственную деятельность, не облагаемую НДС и облагаемую НДС, тогда часть расходов можно соотнести с конкретным видом деятельности. Но часть расходов организации не может быть соотнесена с одним из видов деятельности. Обычно это расходы, связанные с обеспечением организации в целом — аренды помещений, коммунальные платежи, связь и т. д. Хотя, могут быть и запасы , используемые для обоих видов деятельности, и необоротные активы, работающие в обоих видах деятельности.
Например, организация одновременно продает фармацевтические препараты (освобожденные от НДС) и косметические средства (облагаемые НДС по ставке 20%). Другой пример, организация производит различную печатную продукцию — периодические издания и обычную художественную литературу (освобожденные от НДС), а также учебники и учебные пособия (облагаемые НДС по ставке 20%).
При этом для учета входящего НДС при покупках любых запасов, необоротных активов и услуг действуют такие правила:
-
Если закупаемый актив можно четко отнести к использованию в облагаемой НДС хозяйственной деятельности, то при наличии входящего НДС (ставка 20%) вся сумма НДС включается в налоговый кредит. Налоговая и бухгалтерская стоимость актива определяется по стоимости закупки без НДС. Налоговое назначение НДС при закупке указывается «Обл. НДС»,
-
Если закупаемый актив можно четко отнести к использованию в не облагаемой НДС хозяйственной деятельности, то независимо от наличия входящего НДС (ставка 20% или без НДС) вся стоимость закупки включается в налоговую и бухгалтерскую стоимость актива. Сумма НДС не включается в налоговый кредит. Налоговое назначение закупки указывается «Необл. НДС, любая хоз. «,
-
Если закупаемый актив используется для обоих видов хозяйственной деятельности, то согласно ст. 199 НКУ входящий НДС может быть включен в налоговый кредит только в той части, которая используется в налогооблагаемых операциях. Другая часть НДС включается в бухгалтерскую и налоговую стоимость актива. Налоговое назначение закупки указывается «Пропорц. обл. НДС».
Если приобретаемый актив используется не в хозяйственной деятельности, то его налоговая сумма определяется нулевой, и права на налоговый кредит не возникает. Ни о каком пропорциональном распределении НДС между хозяйственной и не хозяйственной деятельностью речи быть не может. Налоговое назначение указывается «Необл. НДС, нехоз. «. Для операций продажи налоговое назначение «Пропорц. обл. НДС» не используется, так как для реализуемого актива должна быть указана определенная ставка НДС и определенное облагаемое или не облагаемое назначение.
Для пропорционального распределения НДС следует в начале года или первого месяца, когда появились два вида деятельности с точки зрения обложения НДС — зафиксировать коэффициент распределения. Операция отражается документом «Установка коэффициента пропорционального отнесения НДС на кредит».
Рис.1. Установка коэффициентов пропорционального распределения НДС
Коэффициент можно рассчитать автоматически, если в ИБ есть данные прошлого года (или первого месяца в 2011 году, когда появились два вида деятельности НДС). Такой расчет производится по кнопке «Заполнить и рассчитать». При этом выбираются данные в зависимости от установленного переключателя — объемы продаж или прошлого года, или указанного месяца. Если такой информации в ИБ нет, то коэффициент можно рассчитать вручную и ввести в поле «Коэфф. (доля использования)». Если весь объем продаж взять за единицу, то коэффициент показывает — какова доля облагаемых НДС продаж.
В документах приобретения, оплат поставщикам (для договоров с упрощенным налоговым учетом) и в регламентном документе » Регистрация авансов в налоговом учете » (для договоров со сложным налоговым учетом) указываются такие налоговые параметры операций:
-
Ставка НДС,
-
Сумма НДС — полная в соответствие с документами поставщика,
-
Налоговое назначение НДС = «Пропорц. обл. НДС».
Само пропорциональное распределение НДС производится только для операций закупки по ставке 20%, т. к. в противном случае нет суммы НДС и нет предмета распределения. Но для контроля целевого использования и для дальнейшей возможности включения актива в расходы и облагаемой, и не облагаемой НДС деятельности рекомендуется указывать именно это налоговое назначение даже в случае приобретения без НДС. При этом актив с налоговым назначением «Пропорц. обл. НДС» может списываться (амортизироваться) и на облагаемую, и на не облагаемую НДС хозяйственную деятельность без изменения налогового назначения. Однако при списании на не хозяйственную деятельность налоговое назначение следует предварительно изменить.
Указанные выше налоговые параметры должны устанавливаться одинаковыми и в первичных документах, регистрирующих ожидаемый налоговый кредит, и в налоговых документах, регистрирующих подтвержденный налоговый кредит.
При отражении покупки запасов с налоговым назначением НДС «Пропорц. обл. НДС» при проведении документа автоматически рассчитывается сумма налогового кредита в соответствие с установленным коэффициентом (см. Рис. 6.35).
Рис.2. Покупка запасов на распределяемую по НДС деятельность
Остальная часть НДС включается в бухгалтерскую и налоговую стоимость запаса. Аналогичным образом отражаются и другие операции:
-
При покупке необоротного актива часть НДС включается в налоговый кредит, а остальная сумма — в стоимость будущего необоротного актива,
-
При получении услуг часть НДС включается в налоговый кредит, а остальная сумма — в затраты, на которые отнесены полученные услуги,
-
В платежных документах и при регистрации авансов —» рассчитывается только; сумма НДС, включаемая в налоговый кредит — для формирования проводки по НДС; налоговая стоимость актива не формируется по причине отсутствия в операции актива.
Для регистрации подтвержденного налогового кредита вводится документ » Регистрация входящего налогового документа «.
Рис.3. Регистрация входящего налогового документа
При этом сумма операции разбивается по двум строкам документа:
-
База и НДС, включенный в налоговый кредит — с видом «облагаемая НДС деятельность» и соответствующей строкой налоговой декларации,
-
База и НДС, включенные в стоимость запаса — с видом «не облагаемая НДС деятельность» и соответствующей строкой налоговой декларации.
Но в обеих строчках должен быть установлен флаг «Пропорционально». Проводка по подтвержденному НДС формируется только в части НДС, включенной в налоговый кредит.
Такое разбиение на две строки производится:
-
Либо автоматически при создании налогового документа вводом на основании первичного документа с указанными налоговыми параметрами и зафиксированным «событием» по НДС,
-
Либо полуавтоматически — по кнопке «Добавить строки по пропорциональному НДС» — при наличии в документе одной строки с общей суммой операции и флагом «Пропорционально». Второй вариант используется, когда налоговый документ:
-
заполняется вручную,
-
или создается вводом на основании платежного документа для договоров со сложным налоговым учетом (в этом случае налоговые параметры операции не заполняются в платежке и не фиксируются в регистрах), о или создается вводом на основании документа, не являющегося в полной сумме документом «первого события».
-
Такое заполнение документа «Регистрация входящего налогового документа» обеспечивает заполнение отчета «Реестр налоговых документов» в соответствии с п. 11.10 Порядка 1002, а также расшифровку сумм, включаемых и не включаемых в налоговый кредит, в Приложении 5 к Декларации.
Другие материалы по теме:
вводом на основании, сумма ндс, регистрация авансов в налоговом учете, закупки, деятельность, налоговый кредит, регистрация входящего налогового документа, актив., актив, ставка, коэффициент, налоговое назначение, регистрация, назначение, кредит, стоимость, значение, сумма, регистр, организация, операции, документа, документ
Распределение начислений по платежам
- Подробности
- Создано 26 Январь 2012
| Содержание |
|---|
| Программа на VBA |
| Формулы рабочего листа |
| Итеративный расчет |
| Заключение |
При ведении финансового учета в электронных таблицах обычно ограничиваются, так называемым «котловым» методом расчета задолженности контрагентов. То есть начисления и платежи не связываются между собой, а рассчитывается только разница, образующая кредиторскую или дебиторскую задолженности. Используя нормативы отсрочки платежа можно также определить уровень просроченной задолженности без точной привязки оплаты и отгрузки. Этой информации вполне достаточно для целей управленческого учета (т.е. для предоставления информации руководству). При этом иногда такой расчет может противоречить информации бухгалтерского учета – контрагент может потерять или пропустить счета для оплаты. В этой ситуации поиск расхождений представляет достаточно сложную задачу в зависимости от количества операций. Аналогичная задача сверки и распределения оплат по начислениям возникает при предоплатной схеме работы с контрагентом. Типичный случай – это работа с таможенными органами, когда средства списываются с депозитов на основании данных государственных таможенных деклараций (ГТД).
Подбор счетов к оплатам или анализ списаний, несмотря на кажущуюся простоту, представляет собой нетривиальную для решения в электронных таблицах задачу. Требуется указать список и сумму начислений, относящихся к каждой оплате. При этом суммы платежей и начислений могут быть произвольными, нет ограничений на кратность или размер оплаты. Алгоритм расчета носит циклический характер, что затрудняет решение с использованием формул рабочего листа. Тем не менее, при известных ограничениях можно построить последовательность формул.
В файлах, приложенных к статье, задача решена тремя различными методами:
- программа на VBA
- формулы рабочего листа
- итеративный расчет Excel без VBA.
Все файлы примеров используют один и тот же набор исходных данных. Следует заметить, что общую сумму неиспользованных платежей определить очень просто – надо вычесть сумму начислений из суммы платежей. Но задача состоит не в поиске этого значения, а в подборе информации о списании затрат по платежам. Решением задачи является текстовая информация с номерами ГТД и суммами по ним в каждой строке оплаты. Для сокращения текста принято условие, что если ГТД списана полностью, то указывается только ее номер, а если частично, то номер и сумма.
Программа на VBA
После открытия файла необходимо включить поддержку макросов. Для запуска расчетной процедуры необходимо нажать кнопку «Расчет».
При редактировании исходных данных, обратите внимание на именованные диапазоны rngCosts и rngPayments (границы выделены жирной рамкой) – программа анализирует информацию только в их пределах. Можно свободно добавлять строки внутрь диапазонов. Подбор будет производиться в порядке расположения строк, вне зависимости от поля даты или других параметров.
Как ни странно, этот способ, пожалуй, самый простой для понимания из всех представленных. Трудности могут возникнуть у тех, кто совсем не знаком с программированием. Алгоритм расчетной процедуры предельно прост:
- копируются данные о начальных остатках по ГТД и оплатам
- запускается цикл по двум диапазонам данных
- на каждом этапе анализируется текущее значение для списания и уменьшается остаток ГТД и остаток платежа на меньшую из этих величин. Таким образом, сумма в остатке одного из диапазонов становится равной нулю.
- в поле результата добавляется информация о списании
- производится переход к следующей строке того диапазона, сумма в котором достигла нуля
- цикл завершается, когда будет достигнут конец любого из диапазонов
Код основной процедуры расчета:
Private Sub Process_()
Dim nRowCost As Long
Dim nRowPay As Long
Dim fValue As Double
Dim sText As String
nRowCost = 1
nRowPay = 1
Do While (nRowCost <= RngCosts_.Rows.Count) And (nRowPay <= RngPay_.Rows.Count)
If RngCosts_.Cells(nRowCost, 4) > RngPay_.Cells(nRowPay, 4) Then
fValue = RngPay_.Cells(nRowPay, 4)
RngPay_.Cells(nRowPay, 4) = 0
RngCosts_.Cells(nRowCost, 4) = RngCosts_.Cells(nRowCost, 4) - fValue
Else
fValue = RngCosts_.Cells(nRowCost, 4)
RngCosts_.Cells(nRowCost, 4) = 0
RngPay_.Cells(nRowPay, 4) = RngPay_.Cells(nRowPay, 4) - fValue
End If
sText = RngCosts_.Cells(nRowCost, 2)
If (fValue <> RngCosts_.Cells(nRowCost, 3)) Then
sText = sText & "=" & Format(fValue, "0")
End If
If RngPay_.Cells(nRowPay, 5) <> "" Then
RngPay_.Cells(nRowPay, 5).Value = RngPay_.Cells(nRowPay, 5).Value & ","
End If
RngPay_.Cells(nRowPay, 5) = RngPay_.Cells(nRowPay, 5) & sText
If (RngPay_.Cells(nRowPay, 4) = 0) Then nRowPay = nRowPay + 1
If (RngCosts_.Cells(nRowCost, 4) = 0) Then nRowCost = nRowCost + 1
Loop
End Sub
Private Function RngCosts_() As Excel.Range
Set RngCosts_ = ThisWorkbook.Names("rngCosts").RefersToRange
End Function
Private Function RngPay_() As Excel.Range
Set RngPay_ = ThisWorkbook.Names("rngPayments").RefersToRange
End Function
Функции RngCost_ и RngPay_ служат в основном для удобства восприятия текста программы.
Формулы рабочего листа
Как уже отмечалось, алгоритм расчета носит циклических характер – т.е. требует повторения одних и тех же действий несколько раз. Через формулы рабочего листа впрямую этот механизм не реализуется. В нормальной ситуации при стандартных параметрах вычислений Excel – такой алгоритм приводит к ошибке «циклическая ссылка» в тот момент, когда формула попытается быть рассчитанной второй раз. Для реализации подобных расчетных процедур требуется ввести ограничение на возможное количество повторяющихся действий и создать последовательность одинаковых формул.
В представленном файле-примере используются ограничения:
- максимум 10 платежей
- максимум 20 ГТД
Имеется 2 служебных массива расчетов по ГТД и по оплатам.
В служебном массиве справа от диапазона ГТД хранится информация об оплатах. Каждая оплата разбита на два столбца, где рассчитывается:
1) остаток оплаты
Если текущий шаг, то уменьшается остаток по ГТД.
H8:
=IF(SUMIF($F$6:F$6;">0";$F8:F8)>0;H7;IF(H7-G8>0;H7-G8;0))
Функция SUMIF($F$6:F$6;»>0″;$F8:F8) выбирает для анализа только нечетные столбцы служебного диапазона.
2) остаток начисления по ГТД по данной оплате
Если текущий шаг, то уменьшается остаток по оплате.
I8:
=IF(SUMIF($F$6:F$6;">0";$F8:F8)>0;0;IF(H7-G8>0;0;G8-H7))
В служебном массиве справа от строк платежей хранится информация о всех ГТД. Рассчитывается:
1) сумма ГТД в данной оплате
Выбирается разность значений из служебной таблицы ГТД по остаткам до и после шага.
H25:
=IF(H$23=0;0;OFFSET($F$6;H$23;$F25*2)-OFFSET($F$6;H$23+1;$F25*2))
Функция OFFSET используется для вычисления адреса в служебном диапазоне ГТД.
2) формируется информационный текст платежа
Формируется текст служебной информации для данного шага. Этот значение добавляется к тексту, сформированному на предыдущем шаге.
I25:
=IF(H25<>0;G25&","&OFFSET($B$7;H$23;0)&IF(OFFSET($C$7;H$23;0)=H25;"";"="&TEXT(H25;"0"));IF(G25="";"";G25))
Функция TEXT(H25;»0″) преобразует число в текст без дробной части.
На последнем этапе формируется полный текст с информацией о платеже. Данные берутся из последнего служебного столбца:
E25:
=IF(AU25="";"";RIGHT(AU25;LEN(AU25)-1))
Формула убирает запятую, сформированную при добавлении информации на каждом шаге.
Все ячейки, имеющие одинаковый цвет фона, содержат копируемые формулы (идентичные в записи R1C1).
Недостатки этого метода очевидны – необходимо предварительно заготовить служебные диапазоны на определенное количество строк. Для расширения лимитов можно скопировать формулы в служебных столбцах вправо. Кроме того, при добавлении строк необходимо аккуратно копировать формулы, так как в некоторых служебных ячейках использованы ссылки вверх. Если применять эту модель для реальной работы, то лучше перенести массив формул из столбцов в строки на других служебных листах – таким образом можно существенно расширить ограничения.
Итеративный расчет
Данный способ уже неоднократно описан в других статьях на нашем сайте. Назвать его популярным в использовании довольно сложно, но показать еще раз возможности этого метода решения задач в Excel будет нелишним.
По описанию задачи сразу можно заметить, что там, где используются циклические вычисления, можно попытаться решить задачу методом итераций.
Обратите внимание на включенный параметр итерационных вычислений после открытия файла. Файл необходимо открывать в отдельном приложении Excel, либо после закрытия всех остальных открытых файлов.
Для запуска расчета требуется ввести в ячейку B5 любое, отличное от нуля, число, затем запустить расчет – проще всего нажать клавишу [F9]. Для изменения исходных данных надо очистить ячейку B5 (или ввести туда «0») и также запустить пересчет. Ячейке B5 присвоено имя flag, используемое во всех расчетных формулах.
Алгоритм расчета с использованием итераций аналогичен примеру, реализованному на VBA. Но для понимания он гораздо сложнее. Используются два служебных диапазона с текущими остатками по ГТД и платежам – скрытый столбец F. Основной механизм цикла находится в скрытых строках 6-8.
Рассмотрим формулы поподробнее.
Ячейки B6 и B7 содержат информацию о текущем шаге для массивов.
B6:
=IF(flag=0;0;IF(COUNTIF($F$13:$F$24;0)=ROWS($F$13:$F$24);0;COUNTIF($F$13:$F$24;0)))
B7:
=IF(flag=0;0;IF(COUNTIF($F$30:$F$35;0)=ROWS($F$30:$F$35);0;COUNTIF($F$30:$F$35;0)))
Текущий шаг определяется через сравнение общего количества строк с нулевыми остатками (уже обработанными строками).
Во всех формулах начальная часть текста =IF(flag=0;0;… предназначена для сброса значения в исходное состояние при выключенном механизме итеративного расчета.
Ячейки C6 и C7 содержат формулы с вычисляемой адресацией для выборки значений остатков ГТД и платежа по текущему шагу. Формула в ячейке С8 выбирает сумму, которая должна быть списана на текущем шаге.
Служебные диапазоны в столбце F содержат копируемые формулы, вычисляющие новое значение остатка для текущего шага.
F13
=IF(flag=0;C13;IF($B$6<>ROWS(F$12:F13)-1;F13;F13-$C$8))
Условие IF($B$6<>ROWS(F$12:F13)-1;… является проверкой соответствия строки текущему шагу массива ГТД.
F30
=IF(flag=0;C30;IF($B$7<>ROWS(F$29:F30)-1;F30;F30-$C$8))
Аналогично условие IF($B$7<>ROWS(F$29:F30)-1;… является проверкой соответствия строки текущему шагу массива платежей.
В ячейках D6 и D8 формируется текстовая информация для платежа текущего шага.
D6 – код ГТД
=IF(B6=0;"";OFFSET($B$12;B6;0))
D8 – сумма списания по ГТД
=IF(C8=0;"";IF(C8=OFFSET($C$12;$B$6;0);"";"="&TEXT(C8;"0")))
В результате в ячейках со светло-желтым фоном формируются остатки по платежам и заполняется текстовая информация о списанных ГТД.
D30
Выбирается текущее значение из служебного массива платежей.
E30
=IF(flag=0;"";IF(OR($B$7<>ROWS(F$29:F30)-1;$D$6="");E30;E30&IF(E30="";"";",")&$D$6&$D$8))
К текущему значению ячейки добавляется текст из ячеек D6 и D8.
Заключение
Все методы решения задачи можно применять на практике.
Пример с использованием итераций, пожалуй, наиболее сложен для понимания формул, и рекомендуется только для «продвинутых» пользователей, принципиально не желающих изучать VBA. Главным недостатком итеративного метода расчета, помимо сложности для понимания, является неудобство его использования вместе с другими расчетными процедурами в составе больших файлов, так как параметры вычислений Excel будут действовать на все открытые рабочие книги.
Пример с использованием формул рабочего листа имеет существенные недостатки из-за введения искусственных ограничений. Зато он может применяться в файлах с дальнейшими расчетами.
Однозначно настаивать на методе решения задачи при помощи VBA также нельзя. Во-первых, это требует от пользователя знания основ программирования. Во-вторых, VBA может быть просто отключен стандартами корпоративной безопасности на предприятии.
Вообще-то есть смутное подозрение, что рассмотренная в примерах задача может быть решена гораздо проще без «заумных» методов. Если кто-то знает, подскажите. Но даже в этом случае, описанные методы работы могут пригодиться на практике для других задач.
Смотри также
» Перекрестный расчет себестоимости
При разработке экономических моделей одной из самых интересных задач является решение проблемы перекрестных связей между формулами….
» Объединение строк
У продвинутых пользователей Excel очень популярен вопрос о возможности объединения диапазона ячеек, содержащих текст, в одну строку при…
» Календарный план выпуска изделий
Одной из самых сложных задач экономического менеджмента является составление календарного плана выпуска продукции в условиях…
» Судоку
Пример решения головоломки «Судоку 9х9» без программирования. К экономике отношения не имеет, зато отлично показывает возможности Excel в…
» Поиск кратчайшего маршрута
При решении сложных алгоритмических задач с использование электронных таблиц иногда приходится сталкиваться с ошибками из-за…
Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.
Формула процентного распределения в Excel
Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.
Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.
Процентное распределение по динамической формуле Excel
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.
Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.
Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.