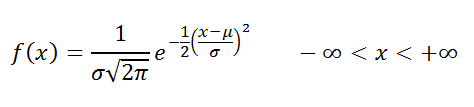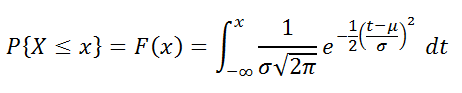Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
-
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равно (=). Excel интерпретирует символы после знака равно как формулу. После знака равно вычисляются элементы (операнды), например константы или ссылки на ячейки. Они разделены операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
-
Приоритет операторов в формулах Excel
Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом ( например, если формула содержит операторы умножения и деления), Excel оценивает операторы слева направо.
Оператор
Описание
: (двоеточие)
(один пробел)
, (запятая)
Операторы ссылок
–
Знак «минус»
%
Процент
^
Возведение в степень
* и /
Умножение и деление
+ и —
Сложение и вычитание
&
Объединение двух текстовых строк в одну
=
< >
<=
>=
<>Операторы сравнения
-
Использование скобок в Excel формулах
Чтобы изменить порядок выполнения формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, результатом приведенной ниже формулы будет число 11, поскольку в Microsoft Excel умножение выполняется раньше сложения. В данной формуле число 2 умножается на 3, а затем к результату добавляется число 5.
=5+2*3
Если же с помощью скобок изменить синтаксис, Microsoft Excel сложит 5 и 2, а затем умножит результат на 3; результатом этих действий будет число 21.
=(5+2)*3
В приведенном ниже примере скобки, в которые заключена первая часть формулы, задают следующий порядок вычислений: определяется значение B4+25, после чего полученный результат делится на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Нужна дополнительная помощь?
Наши советы помогут работать с обычными суммами значений в выбранном диапазоне ячеек или сложными вычислениями с десятками аргументов. Главное, что при большом количестве формул их будет легко расположить в нужных местах.
1 Простое протягивание формулы
Это самый простой и привычный для многих пользователей способ распространения формулы сразу на несколько ячеек строки или столбца. Он требует выполнения следующих действий:
- В первую ячейку с одной из сторон (например, сверху) надо записать нужную формулу и нажать Enter.
- После появления рассчитанного по формуле значения навести курсор в нижний правый угол ячейки. Подождать, пока толстый белый крестик не превратиться в тонкий черный.
- Нажать на крестик и, удерживая его, протянуть формулу в нужном направлении. В указанном примере — вниз.
Аргументы в формуле будут изменяться соответственно новому расположению. И если в самой первой ячейке это были F7 и G7, в последней позиции столбца это будет уже F12 и G12. Соответственно, если начинать распространять формулы по строкам, изменяться будут не цифры, а буквы в обозначениях ячеек.
Способ отличается простотой и высокой скоростью. Но не всегда подходит для больших таблиц. Так, если в столбце несколько сотен или даже тысяч значений, формулу проще растягивать другими способами, чтобы сэкономить время. Один из них — автоматическое копирование, требующее всего лишь двойного клика кнопкой мыши.
2 Быстрое автозаполнение
Еще один способ в Excel протянуть формулу до конца столбца с более высокой по сравнению с первой методикой скоростью. Требует от пользователя применить такие действия:
- Ввести в верхнюю ячейку формулу, в которой применяются аргументы из соседних столбцов. Нажать кнопку Enter.
- Навести курсор на правый нижний угол, чтобы он приобрел форму черного крестика.
- Кликнуть два раза по нижнему правому углу ячейки. Результатом станет автоматическое распространение формулы по столбцу с соответствующим изменением аргументов.
Стоит отметить, что автоматическое протягивание выполняется только до первой пустой ячейки. И если столбец был прерван, действия придется повторить для следующего диапазоне.
Еще одна особенность такого автоматического копирования формул — невозможность использования для строки. При попытке распространить значение ячейки не вниз, а в сторону, ничего не происходит. С другой стороны, длина строк обычно намного меньше по сравнению со столбцами, которые могут состоять из нескольких тысяч пунктов.
3 Протягивание без изменения ячеек в формуле
Еще один способ позволяет распространять формулы в Excel без изменения некоторых аргументов. Это может понадобиться в тех случаях, когда одно или несколько значений будут содержаться в одной и той же ячейке. Поможет в закреплении формулы специальная функция фиксации ссылок.
Для распределения без изменения адреса ячейки выполняются те же действия, что и при обычном протягивании или автоматическом копировании. Но при вводе формулы следует зафиксировать адреса, которые не будут меняться. Для этого используются символы доллара — $. Если в каждом новом пункте столбца при расчетах используется одна и та же ячейка, значки надо будет поставить и перед номером строки, и перед литерой, которая указывает на колонку. Как в примере: $G$6.
Ставить знак $ перед названием только строки или столбца при распределении функции не имеет смысла. Потому что, когда формула протягивается, в ней автоматически меняются только нужные части аргументов. Для столбцов это будут номера строк, для строк — названия колонок.
4 Простое копирование
Еще один способ представляет собой не совсем протягивание, а копирование. Но только более простое и позволяющее выделить конкретный диапазон, а не доверять такое выделение компьютеру. Процесс распределения требует выполнить следующие действия:
- Записать в одну из крайних ячеек строки или столбца нужную формулу и нажать Enter.
- Скопировать значение функции — с помощью контекстного меню, иконки на панели или комбинации клавиш Ctrl + C.
- Установить курсор в противоположную часть столбца или строки.
- Нажать на клавиши Ctrl + Shift + «Стрелка вверх». Результатом становится выделение нужного диапазона, даже если на этом участке столбца будет несколько сотен или тысяч пунктов.
- Вставить формулу. Самый простой способ сделать это — нажать комбинацию Ctrl + V.
Результатом будет такое же распределение функции по столбцу, как и при использовании способа №2. Но в отличие от него здесь можно выделить только часть диапазона. Или, наоборот, продлить такое протягивание дальше даже при наличии пустых строк. Правда, во втором случае лишнее значение придется удалить вручную.
Эта небольшая хитрость подходит и для распределения вдоль строки. В этом случае вместо комбинации Ctrl + Shift + «Стрелка вверх» придется нажать Ctrl + Shift + «Стрелка влево» (или вправо, если копируемая формула находится в крайнем левом столбце).
5 Протягивание формул в таблице Excel
Распределять формулы можно и в том случае, если данные размещены не на практически бесконечном листе, а в границах таблицы.
Для преобразования в табличную форму достаточно выделить одну из ячеек и нажать комбинацию Ctrl + T, чтобы вызвать диалоговое окно и указать диапазон данных таблицы.
Перед тем, как протянуть формулу в Excel, достаточно всего лишь ввести нужную функцию в самой верхней строчке таблицы и нажать Enter. Способ работает только при отсутствии других значений в столбце с формулой.
Формула автоматически распределяется по колонке. Преимущества способа — скорость, сравнимая с применением макроса. Недостаток — работает он только при использовании табличной формы размещения данных в Excel и позволяет протянуть формулу сразу до конца таблицы, а не до нужной строки.
Читайте также:
- Лучшие веб-камеры для дома и офиса: рейтинг 2021 года=«content_internal_link»>
- Нумерация страниц в Опен Офис: простая инструкция=«content_internal_link»>
Рассмотрим Нормальное распределение. С помощью функции
MS EXCEL
НОРМ.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения
.
Нормальное распределение
(также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения
Нормального распределения
(англ.
Normal
distribution
)
во многих областях науки вытекает из
Центральной предельной теоремы
теории вероятностей.
Определение
: Случайная величина
x
распределена по
нормальному закону
, если она имеет
плотность распределения
:
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Нормальное распределение
зависит от двух параметров: μ
(мю)
— является
математическим ожиданием (средним значением случайной величины)
, и σ (
сигма)
— является
стандартным отклонением
(среднеквадратичным отклонением). Параметр μ определяет положение центра
плотности вероятности
нормального распределения
, а σ — разброс относительно центра (среднего).
Примечание
: О влиянии параметров μ и σ на форму распределения изложено в статье про
Гауссову кривую
, а в
файле примера на листе Влияние параметров
можно с помощью
элементов управления Счетчик
понаблюдать за изменением формы кривой.
Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Нормального распределения
имеется функция
НОРМ.РАСП()
, английское название — NORM.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
нормальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Вышеуказанное распределение имеет обозначение
N
(μ; σ).
Так же часто используют обозначение через
дисперсию
N
(μ; σ
2
).
Примечание
: До MS EXCEL 2010 в EXCEL была только функция
НОРМРАСП()
, которая также позволяет вычислить функцию распределения и плотность вероятности.
НОРМРАСП()
оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением
называется
нормальное распределение
с
математическим ожиданием
μ=0 и
дисперсией
σ=1. Вышеуказанное распределение имеет обозначение
N
(0;1).
Примечание
: В литературе для случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение z.
Любое
нормальное распределение
можно преобразовать в стандартное через замену переменной
z
=(
x
-μ)/σ
. Этот процесс преобразования называется
стандартизацией
.
Примечание
: В MS EXCEL имеется функция
НОРМАЛИЗАЦИЯ()
, которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то
нормализацией
. Формулы
=(x-μ)/σ
и
=НОРМАЛИЗАЦИЯ(х;μ;σ)
вернут одинаковый результат.
В MS EXCEL 2010 для
стандартного нормального распределения
имеется специальная функция
НОРМ.СТ.РАСП()
и ее устаревший вариант
НОРМСТРАСП()
, выполняющий аналогичные вычисления.
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации
нормального распределения
N
(1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по
нормальному закону
N(1,5; 2)
, меньше или равна 2,5. Формула выглядит так:
=НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА)
=0,691462. Сделав замену переменной
z
=(2,5-1,5)/2=0,5
, запишем формулу для вычисления
Стандартного нормального распределения:
=НОРМ.СТ.РАСП(0,5; ИСТИНА)
=0,691462.
Естественно, обе формулы дают одинаковые результаты (см.
файл примера лист Пример
).
Обратите внимание, что
стандартизация
относится только к
интегральной функции распределения
(аргумент
интегральная
равен ИСТИНА), а не к
плотности вероятности
.
Примечание
: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле
=НОРМ.СТ.РАСП(z;ИСТИНА)
. Вычисления производятся по формуле
В силу четности функции
плотности стандартного нормального
распределения f(x), а именно f(x)=f(-х), функция
стандартного нормального распределения
обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция
НОРМ.СТ.РАСП(x;ИСТИНА)
вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется
квантилем
стандартного
нормального распределения
.
В MS EXCEL для вычисления
квантилей
используют функцию
НОРМ.СТ.ОБР()
и
НОРМ.ОБР()
.
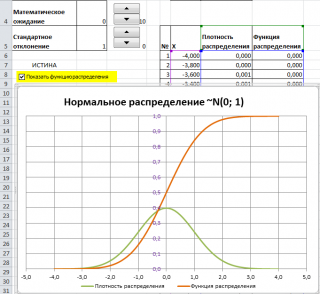
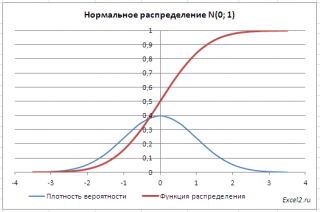
Графики функций
В
файле примера
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
Как известно, около 68% значений, выбранных из совокупности, имеющей
нормальное распределение
, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для
стандартного нормального распределения
можно записав формулу:
=
НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от
среднего
(см.
лист График в файле примера
).
В силу четности функции
плотности стандартного нормального
распределения:
f
(
x
)=
f
(-х)
, функция
стандартного нормального распределения
обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
=
2*НОРМ.СТ.РАСП(1;ИСТИНА)-1
Для произвольной
функции нормального распределения
N(μ; σ) аналогичные вычисления нужно производить по формуле:
=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1
Вышеуказанные расчеты вероятности требуются для
построения доверительных интервалов
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении
диаграмм
читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметров распределения: μ и σ.
Генерация случайных чисел
С помощью надстройки
Пакет анализа
можно сгенерировать случайные числа, распределенные по
нормальному закону
.
СОВЕТ
: О надстройке
Пакет анализа
можно прочитать в статье
Надстройка Пакет анализа MS EXCEL
.
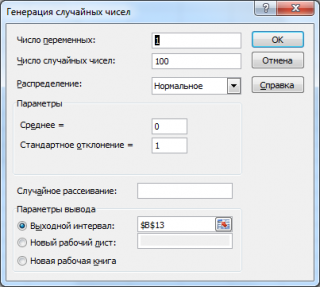
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне
Генерация
случайных чисел
установим следующие значения для каждой пары параметров:
Примечание
: Если установить опцию
Случайное рассеивание
(
Random Seed
), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции
Случайное рассеивание
может запутать. Лучше было бы ее перевести как
Номер набора со случайными числами
.
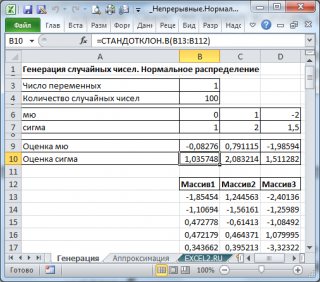
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ
.
Оценку для μ можно сделать с использованием функции
СРЗНАЧ()
, а для σ – с использованием функции
СТАНДОТКЛОН.В()
, см.
файл примера лист Генерация
.
Примечание
: Для генерирования массива чисел, распределенных по
нормальному закону
, можно использовать формулу
=НОРМ.ОБР(СЛЧИС();μ;σ)
. Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Задачи
Задача1
. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.
Решение1
: =
1-НОРМ.РАСП(36;41;2;ИСТИНА)
Задача2
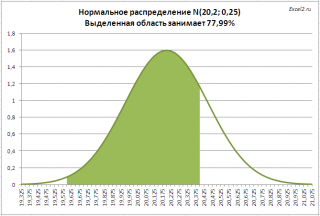
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?
Решение2
: =
НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)
На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.
Решение приведено в
файле примера лист Задачи
.
Задача3
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?
Решение3
: =
НОРМ.ОБР(0,975; 20,20; 0,25)
=20,6899 или =
НОРМ.СТ.ОБР(0,975)*0,25+20,2
(произведена «дестандартизация», см. выше)
Задача 4
. Нахождение параметров
нормального распределения
по значениям 2-х
квантилей
(или
процентилей
). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я
процентиля
(например, 0,5-
процентиль
, т.е. медиана и 0,95-я
процентиль
). Т.к. известна
медиана
, то мы знаем
среднее
, т.е. μ. Чтобы найти
стандартное отклонение
нужно использовать
Поиск решения
. Решение приведено в
файле примера лист Задачи
.
Примечание
: До MS EXCEL 2010 в EXCEL были функции
НОРМОБР()
и
НОРМСТОБР()
, которые эквивалентны
НОРМ.ОБР()
и
НОРМ.СТ.ОБР()
.
НОРМОБР()
и
НОРМСТОБР()
оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин
x
(
i
)
с параметрами μ
(
i
)
и σ
(
i
)
также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ
(1)+ μ(2)
и
КОРЕНЬ(σ(1)^2+ σ(2)^2).
Убедимся в этом с помощью MS EXCEL.
С помощью надстройки
Пакет анализа
сгенерируем 2 массива по 100 чисел с различными μ и σ.
Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
вычислим
среднее
и
дисперсию
получившейся
выборки
и сравним их с расчетными.
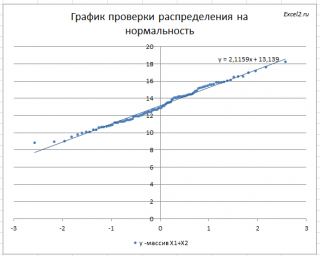
Кроме того, построим
График проверки распределения на нормальность
(
Normal
Probability
Plot
), чтобы убедиться, что наш массив соответствует выборке из
нормального распределения
.
Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой
стандартного отклонения
, а пересечение с осью y (параметр b) –
среднего
значения.
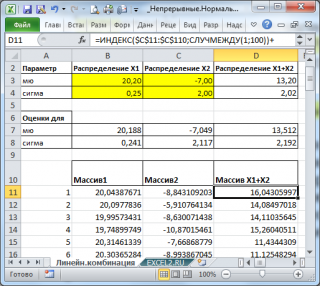
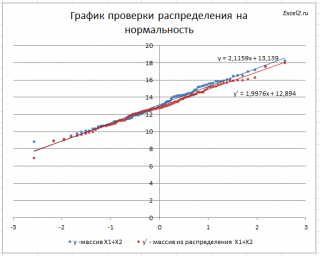
Для сравнения сгенерируем массив напрямую из распределения
N
(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)
).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.
В качестве примера можно провести следующую задачу.
Задача
. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.
Решение
. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и
стандартным отклонением
=КОРЕНЬ(СУММКВ(1,5;1,2))
, запишем решение =
1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)
Ответ
: 15% (см.
файл примера лист Линейн.комбинация
)
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры
Биномиального распределения
B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то
Биномиальное распределение
можно аппроксимировать
Нормальным распределением
.
При значениях
λ
>15
,
Распределение Пуассона
хорошо аппроксимируется
Нормальным распределением
с параметрами: μ
=λ
, σ
2
=
λ
.
Подробнее о связи этих распределений, можно прочитать в статье
Взаимосвязь некоторых распределений друг с другом в MS EXCEL
. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Иногда бывает необходимо навязать программе другой порядок вычисления, нежели тот, который используется по умолчанию в программе. Например, если вы купили что-либо по цене 11,21 рублей, включая 18% налог с продаж, и хотите рассчитать стоимость товара без налога, вы будете использовать формулу =11.21/(1 + 0.18), что дает вам ответ 9,5 рублей.
В общем случае формула расчета такова: Цена налога = Общая стоимость / (1+налог);
По умолчанию в русскоязычной локализации Excel в качестве разделителя целой и дробной части используется запятая. Приведенную выше формулу для этого случая придется переписать как =11/21/(1 + 0,18). В данной книге в качестве разделителя используется точка. Вы можете предписать Excel трактовать точку как разделитель целой и дробной части следующим образом. Зайдите в диалоговое окно Язык и региональные стандарты (Пуск → Настройка → Панель управления → Язык и региональные стандарты). На вкладке Региональные параметры нажмите кнопку Настройка. Введите точку в строку Разделитель целой и дробной части. Нажмите кнопку ОК. Закройте окно Язык и региональные стандарты. На рис. 1.1 показан пример расчета такой формулы. В ячейке D6 находится переменная, задающая полную стоимость товара, а в D7 — величина налога. При использовании данных параметров первым желанием будет использование формулы =D6/1+D7 для вычисления начальной стоимости.
Рис. 1.1. Лист расчета цены товара до налога
Эта формула представлена в ячейке J11, а ее результат в I11. Как вы можете наблюдать, результат вычисления неверен. Почему это произошло? В результате действий правил приоритетов при вычислениях Excel выполнил деление до сложения, таким образом значение ячейки D6 поделилось на 1 и затем сложилось со значением в ячейке D7. Для получения правильного результата необходимо каким-то образом преодолеть правила приоритетов, для того чтобы сложение 1+D7 выполнилось в первую очередь. Это возможно при заключении данного выражения в скобки, как показано в ячейке J12 рисунка 1.1. Как только это действие будет произведено, вы получите правильный результат в ячейке I12.
В общем случае с помощью круглых скобок вы можете контролировать порядок, по которому Excel производит вычисления формул. Вы можете удалить файл который не удаляется. Выражения внутри скобок всегда вычисляются в первую очередь. Например, если вы хотите с помощью Excel вычислить корень любой степени из числа, используйте формулу =number ^ (1/n), где n — необходимая степень корня. Для того чтобы ещё больше усилить контроль над вычислениями, вы можете использовать одни круглые скобки внутри других. При этом Excel вначале вычисляет самые внутренние из скобок. Вот несколько формул для примера.
| Формула | 1-й шаг | 2-й шаг | 3-й шаг | Результат |
|---|---|---|---|---|
| 3^(15/5)*2-5 | 3^3*2-5 | 27*2-5 | 54-5 | 49 |
| 3^((15/5)*2-5) | 3^(3*2-5) | 3^(6-5) | 3^1 | 3 |
| 3^(15/(5*2-5)) | 3^(15/(10-5)) | 3^(15/5) | 3^3 | 27 |
Обратите внимание, что порядок вычислений сохраняется внутри каждых скобок. Например, в выражении (5-5*2)5*2 вычисляется перед вычитанием из числа 5. Таким образом, применение скобок в Excel дает вам полный контроль над формулами. Только так вы можете быть уверены в том, что результат, выдаваемый формулой, соответствует вашим ожиданиям.
Одной из самых распространенных ошибок при использовании скобок является невнимательность при их закрытии. В этом случае Excel выведет сообщение об ошибке (и предложит решение проблемы). Для проверки подсчитывайте все открывающиеся и закрывающиеся скобки. Если их количество не совпадает, значит, в формуле допущена такого рода ошибка.
Самая популярная программа для работы с электронными таблицами «Microsoft Excel» упростила жизнь многим пользователям, позволив производить любые расчеты с помощью формул. Она способна автоматизировать даже самые сложные вычисления, но для этого нужно знать принципы работы с формулами. Мы подготовили самую подробную инструкцию по работе с Эксель. Не забудьте сохранить в закладки 😉
Содержание
-
Кому важно знать формулы Excel и где выучить основы.
-
Элементы, из которых состоит формула в Excel.
-
Основные виды.
-
Примеры работ, которые можно выполнять с формулами.
-
22 формулы в Excel, которые облегчат жизнь.
-
Использование операторов.
-
Использование ссылок.
-
Использование имён.
-
Использование функций.
-
Операции с формулами.
-
Как в формуле указать постоянную ячейку.
-
Как поставить «плюс», «равно» без формулы.
-
Самые распространенные ошибки при составлении формул в редакторе Excel.
-
Коды ошибок при работе с формулами.
-
Отличие в версиях MS Excel.
-
Заключение.
Кому важно знать формулы Excel и где изучить основы
Excel — эффективный помощник бухгалтеров и финансистов, владельцев малого бизнеса и даже студентов. Менеджеры ведут базы клиентов, а маркетологи считают в таблицах медиапланы. Аналитики с помощью эксель формул обрабатывают большие объемы данных и строят гипотезы.
Эксель довольно сложная программа, но простые функции и базовые формулы можно освоить достаточно быстро по статьям и видео-урокам. Однако, если ваша профессиональная деятельность подразумевает работу с большим объемом данных и требует глубокого изучения возможностей Excel — стоит пройти специальные курсы, например тут или тут.
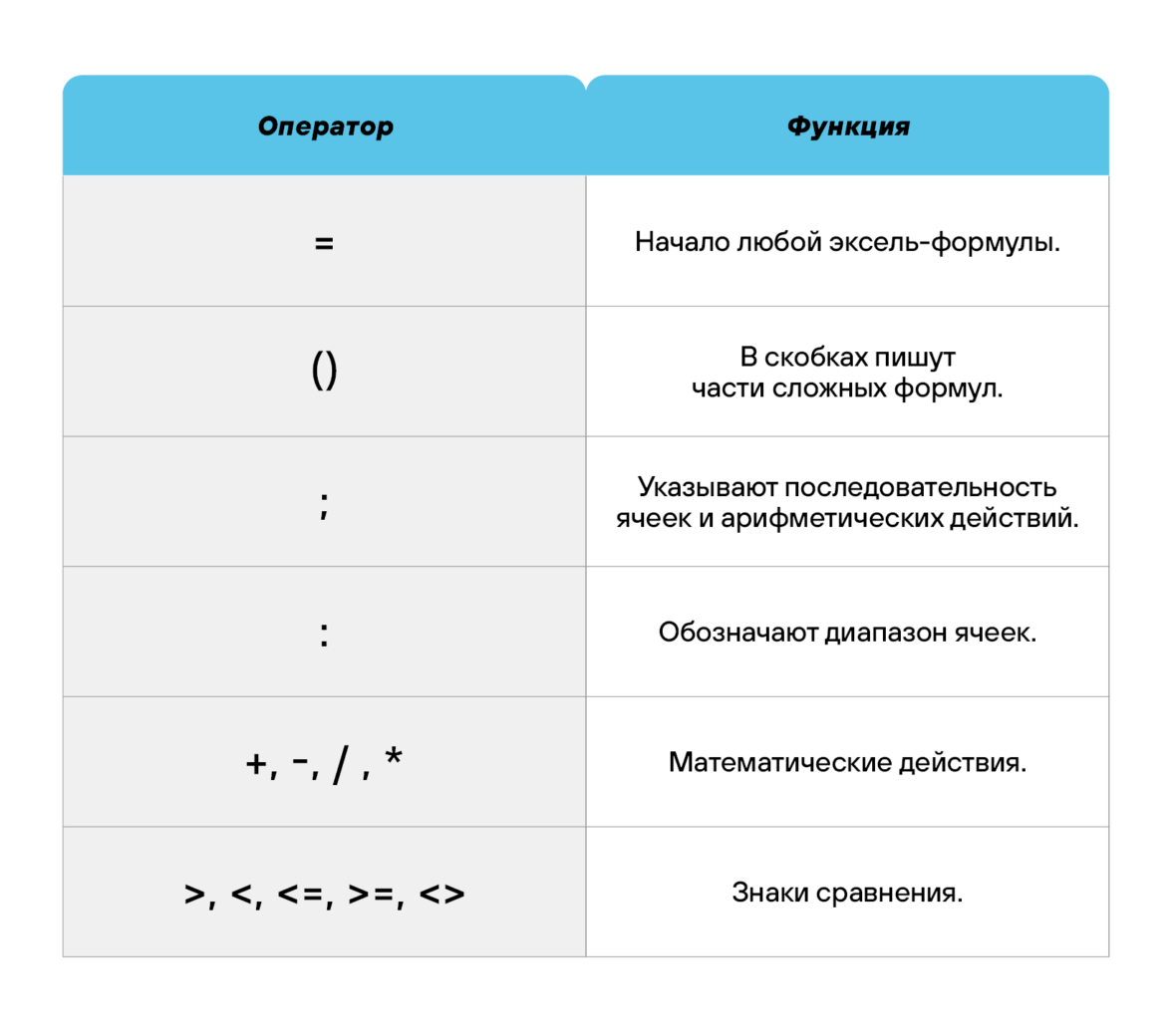
Элементы, из которых состоит формула в Excel
Формулы эксель: основные виды
Формулы в Excel бывают простыми, сложными и комбинированными. В таблицах их можно писать как самостоятельно, так и с помощью интегрированных программных функций.
Простые
Позволяют совершить одно простое действие: сложить, вычесть, разделить или умножить. Самой простой является формула=СУММ.
Например:
=СУММ (A1; B1) — это сумма значений двух соседних ячеек.
=СУММ (С1; М1; Р1) — сумма конкретных ячеек.
=СУММ (В1: В10) — сумма значений в указанном диапазоне.
Сложные
Это многосоставные формулы для более продвинутых пользователей. В данную категорию входят ЕСЛИ, СУММЕСЛИ, СУММЕСЛИМН. О них подробно расскажем ниже.
Комбинированные
Эксель позволяет комбинировать несколько функций: сложение + умножение, сравнение + умножение. Это удобно, когда, например, нужно вычислить сумму двух чисел, и, если результат будет больше 100, его нужно умножить на 3, а если меньше — на 6.
Выглядит формула так ↓
=ЕСЛИ (СУММ (A1; B1)<100; СУММ (A1; B1)*3;(СУММ (A1; B1)*6))
Встроенные
Новичкам удобнее пользоваться готовыми, встроенными в программу формулами вместо того, чтобы писать их вручную. Чтобы найти нужную формулу:
-
кликните по нужной ячейке таблицы;
-
нажмите одновременно Shift + F3;
-
выберите из предложенного перечня нужную формулу;
-
в окошко «Аргументы функций» внесите свои данные.
Примеры работ, которые можно выполнять с формулами
Разберем основные действия, которые можно совершить, используя формулы в таблицах Эксель и рассмотрим полезные «фишки» для упрощения работы.
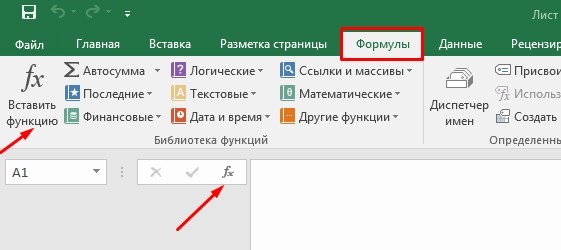
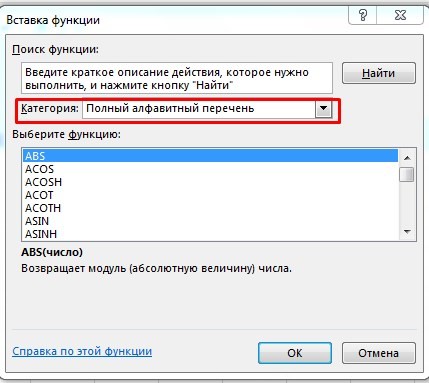
Поиск перечня доступных функций
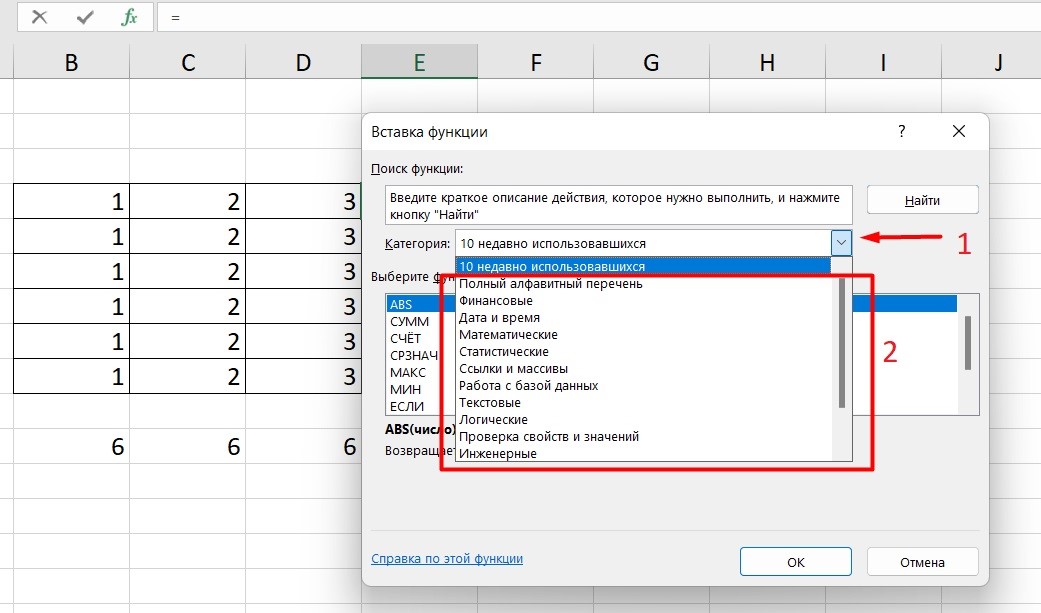
Перейдите в закладку «Формулы» / «Вставить функцию». Или сразу нажмите на кнопочку «Fx».
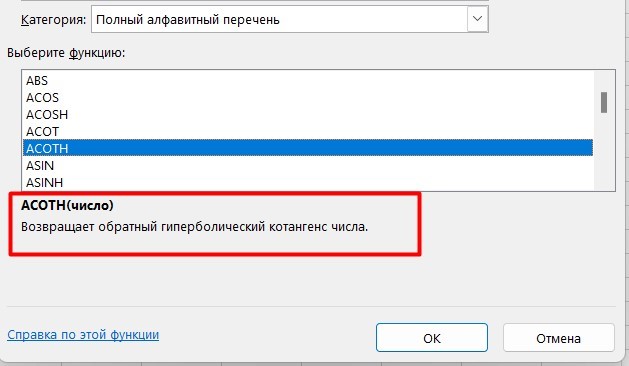
Выберите в категории «Полный алфавитный перечень», после чего в списке отобразятся все доступные эксель-формулы.
Выберите любую формулу и прочитайте ее описание. А если хотите изучить ее более детально, нажмите на «Справку» ниже.
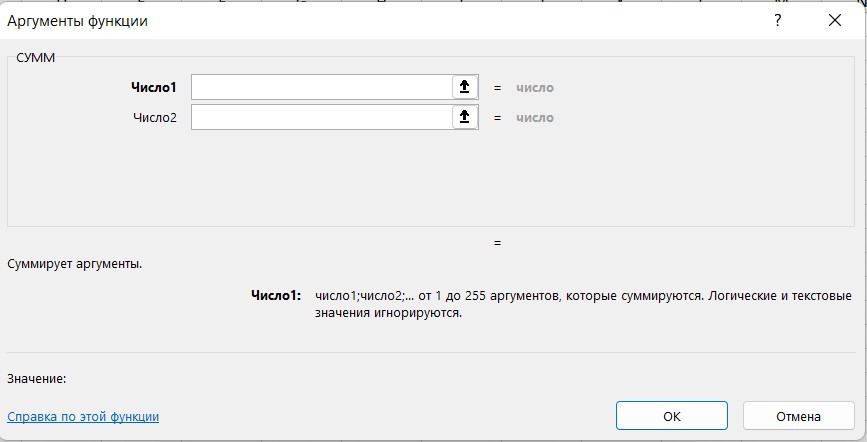
Вставка функции в таблицу
Вы можете сами писать функции в Excel вручную после «=», или использовать меню, описанное выше. Например, выбрав СУММ, появится окошко, где нужно ввести аргументы (кликнуть по клеткам, значения которых собираетесь складывать):
После этого в таблице появится формула в стандартном виде. Ее можно редактировать при необходимости.
Использование математических операций
Начинайте с «=» в ячейке и применяйте для вычислений любые стандартные знаки «*», «/», «^» и т.д. Можно написать номер ячейки самостоятельно или кликнуть по ней левой кнопкой мышки. Например: =В2*М2. После нажатия Enter появится произведение двух ячеек.
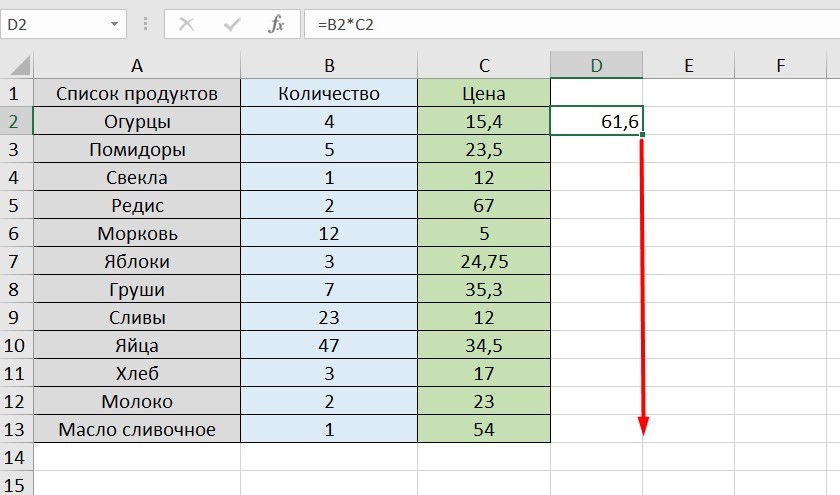
Растягивание функций и обозначение константы
Введите функцию =В2*C2, получите результат, а затем зажмите правый нижний уголок ячейки и протащите вниз. Формула растянется на весь выбранный диапазон и автоматически посчитает значения для всех строк от B3*C3 до B13*C13.
Чтобы обозначить константу (зафиксировать конкретную ячейку/строку/столбец), нужно поставить «$» перед буквой и цифрой ячейки.
Например: =В2*$С$2. Когда вы растяните функцию, константа или $С$2 так и останется неизменяемой, а вот первый аргумент будет меняться.
Подсказка:
-
$С$2 — не меняются столбец и строка.
-
B$2 — не меняется строка 2.
-
$B2 — константой остается только столбец В.
22 формулы в Эксель, которые облегчат жизнь
Собрали самые полезные формулы, которые наверняка пригодятся в работе.
МАКС
=МАКС (число1; [число2];…)
Показывает наибольшее число в выбранном диапазоне или перечне ячейках.
МИН
=МИН (число1; [число2];…)
Показывает самое маленькое число в выбранном диапазоне или перечне ячеек.
СРЗНАЧ
=СРЗНАЧ (число1; [число2];…)
Считает среднее арифметическое всех чисел в диапазоне или в выбранных ячейках. Все значения суммируются, а сумма делится на их количество.
СУММ
=СУММ (число1; [число2];…)
Одна из наиболее популярных и часто используемых функций в таблицах Эксель. Считает сумму чисел всех указанных ячеек или диапазона.
ЕСЛИ
=ЕСЛИ (лог_выражение; значение_если_истина; [значение_если_ложь])
Сложная формула, которая позволяет сравнивать данные.
Например:
=ЕСЛИ (В1>10;”больше 10″;»меньше или равно 10″)
В1 — ячейка с данными;
>10 — логическое выражение;
больше 10 — правда;
меньше или равно 10 — ложное значение (если его не указывать, появится слово ЛОЖЬ).
СУММЕСЛИ
=СУММЕСЛИ (диапазон; условие; [диапазон_суммирования]).
Формула суммирует числа только, если они отвечают критерию.
Например:
=СУММЕСЛИ (С2: С6;»>20″)
С2: С6 — диапазон ячеек;
>20 —значит, что числа меньше 20 не будут складываться.
СУММЕСЛИМН
=СУММЕСЛИМН (диапазон_суммирования; диапазон_условия1; условие1; [диапазон_условия2; условие2];…)
Суммирование с несколькими условиями. Указываются диапазоны и условия, которым должны отвечать ячейки.
Например:
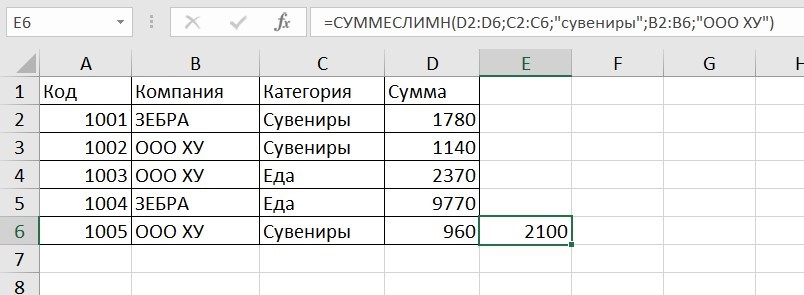
=СУММЕСЛИМН (D2: D6; C2: C6;”сувениры”; B2: B6;”ООО ХУ»)
D2: D6 — диапазон, где суммируются числа;
C2: C6 — диапазон ячеек для категории; сувениры — обязательное условие 1, то есть числа другой категории не учитываются;
B2: B6 — дополнительный диапазон;
ООО XY — условие 2, то есть числа другой компании не учитываются.
Дополнительных диапазонов и условий может быть до 127 штук.
СЧЕТ
=СЧЁТ (значение1; [значение2];…)Формула считает количество выбранных ячеек с числами в заданном диапазоне. Ячейки с датами тоже учитываются.
=СЧЁТ (значение1; [значение2];…)
Формула считает количество выбранных ячеек с числами в заданном диапазоне. Ячейки с датами тоже учитываются.
СЧЕТЕСЛИ и СЧЕТЕСЛИМН
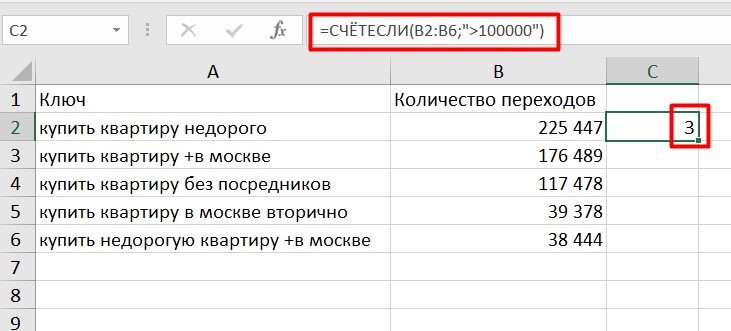
=СЧЕТЕСЛИ (диапазон; критерий)
Функция определяет количество заполненных клеточек, которые подходят под конкретные условия в рамках указанного диапазона.
Например:
=СЧЁТЕСЛИМН (диапазон_условия1; условие1 [диапазон_условия2; условие2];…)
Эта формула позволяет использовать одновременно несколько критериев.
ЕСЛИОШИБКА
=ЕСЛИОШИБКА (значение; значение_если_ошибка)
Функция проверяет ошибочность значения или вычисления, а если ошибка отсутствует, возвращает его.
ДНИ
=ДНИ (конечная дата; начальная дата)
Функция показывает количество дней между двумя датами. В формуле указывают сначала конечную дату, а затем начальную.
КОРРЕЛ
=КОРРЕЛ (диапазон1; диапазон2)
Определяет статистическую взаимосвязь между разными данными: курсами валют, расходами и прибылью и т.д. Мах значение — +1, min — −1.
ВПР
=ВПР (искомое_значение; таблица; номер_столбца;[интервальный_просмотр])
Находит данные в таблице и диапазоне.
Например:
=ВПР (В1; С1: С26;2)
В1 — значение, которое ищем.
С1: Е26— диапазон, в котором ведется поиск.
2 — номер столбца для поиска.
ЛЕВСИМВ
=ЛЕВСИМВ (текст;[число_знаков])
Позволяет выделить нужное количество символов. Например, она поможет определить, поместится ли строка в лимитированное количество знаков или нет.
ПСТР
=ПСТР (текст; начальная_позиция; число_знаков)
Помогает достать определенное число знаков с текста. Например, можно убрать лишние слова в ячейках.
ПРОПИСН
=ПРОПИСН (текст)
Простая функция, которая делает все литеры в заданной строке прописными.
СТРОЧН
Функция, обратная предыдущей. Она делает все литеры строчными.
ПОИСКПОЗ
=ПОИСКПОЗ (искомое_значение; просматриваемый_массив; тип_сопоставления)
Дает возможность найти нужный элемент в заданном блоке ячеек и указывает его позицию.
ДЛСТР
=ДЛСТР (текст)
Данная функция определяет длину заданной строки. Пример использования — определение оптимальной длины описания статьи.
СЦЕПИТЬ
=СЦЕПИТЬ (текст1; текст2; текст3)
Позволяет сделать несколько строчек из одной и записать до 255 элементов (8192 символа).
ПРОПНАЧ
=ПРОПНАЧ (текст)
Позволяет поменять местами прописные и строчные символы.
ПЕЧСИМВ
=ПЕЧСИМВ (текст)
Можно убрать все невидимые знаки из текста.
Использование операторов
Операторы в Excel указывают, какие конкретно операции нужно выполнить над элементами формулы. В вычислениях всегда соблюдается математический порядок:
-
скобки;
-
экспоненты;
-
умножение и деление;
-
сложение и вычитание.
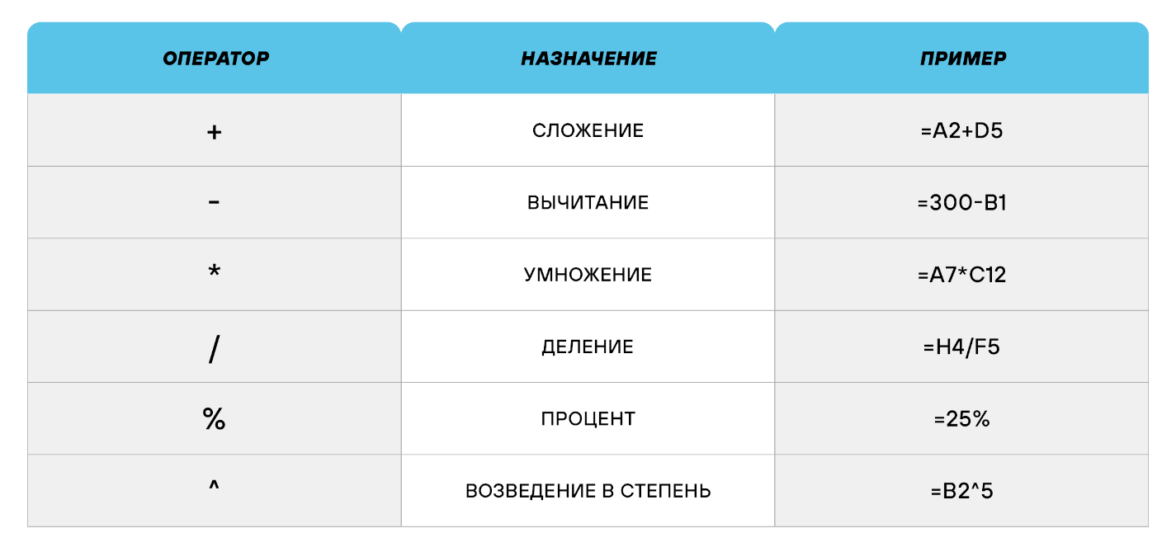
Арифметические
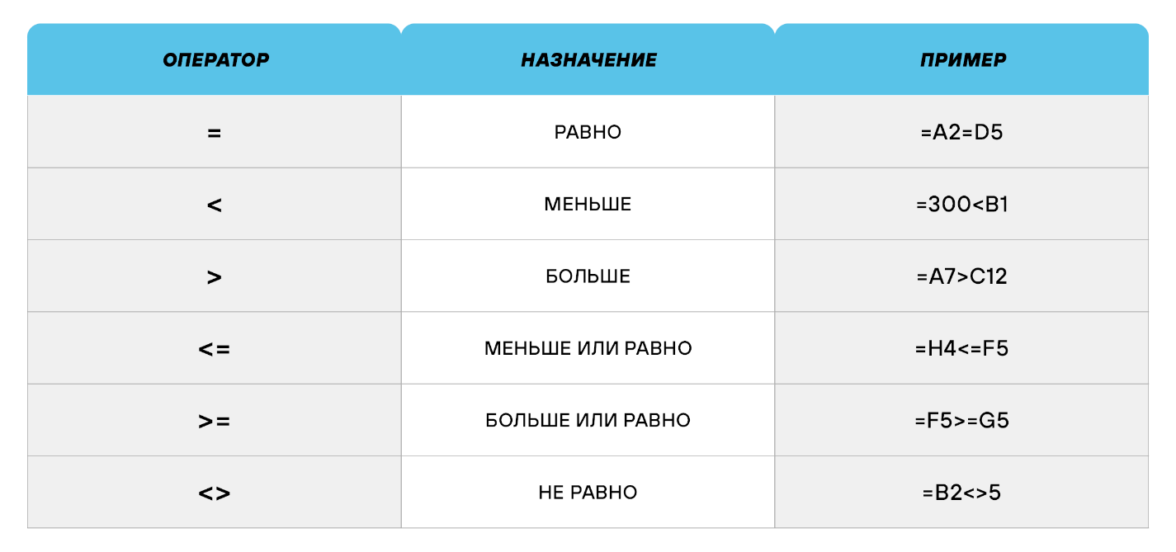
Операторы сравнения
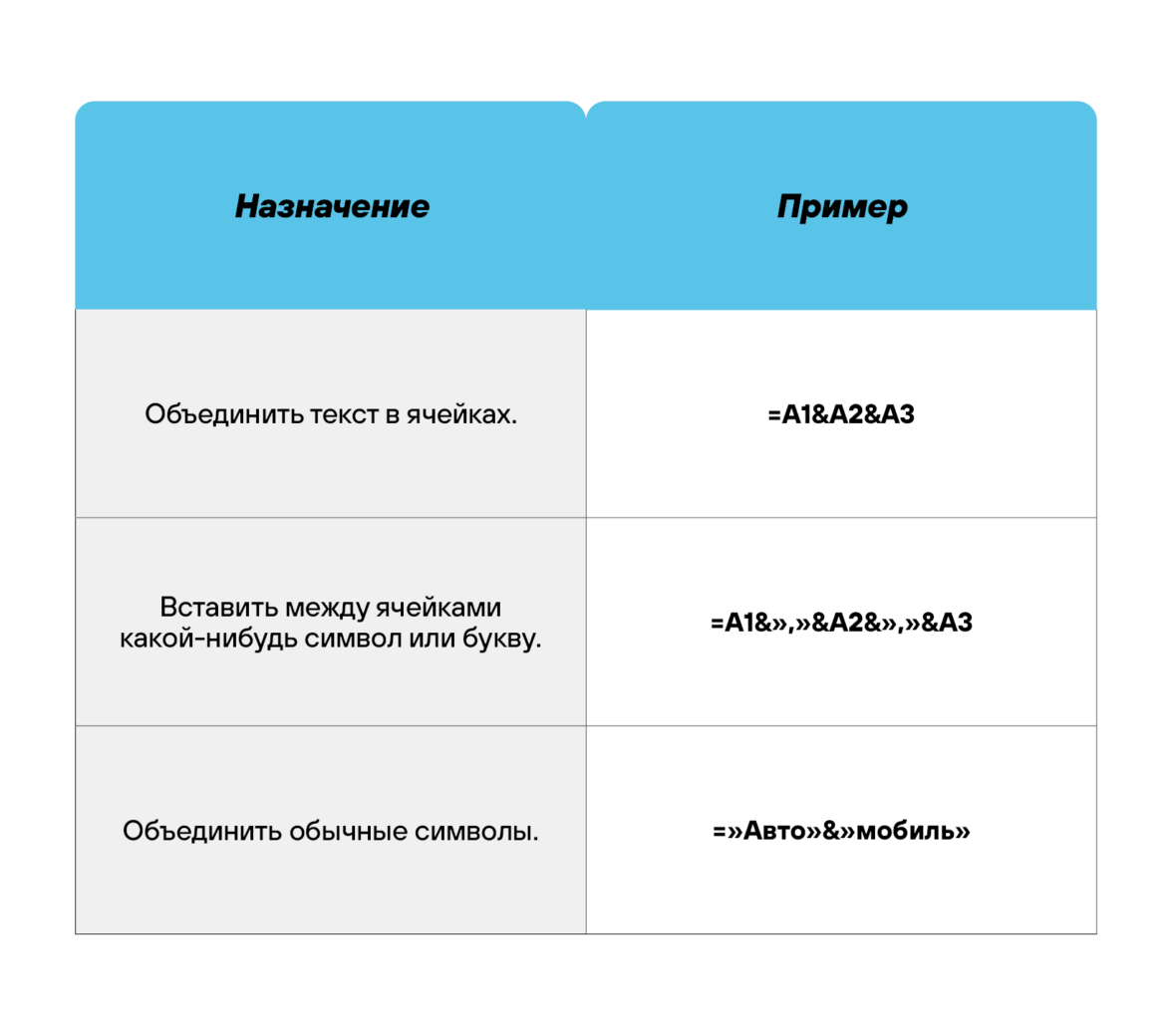
Оператор объединения текста
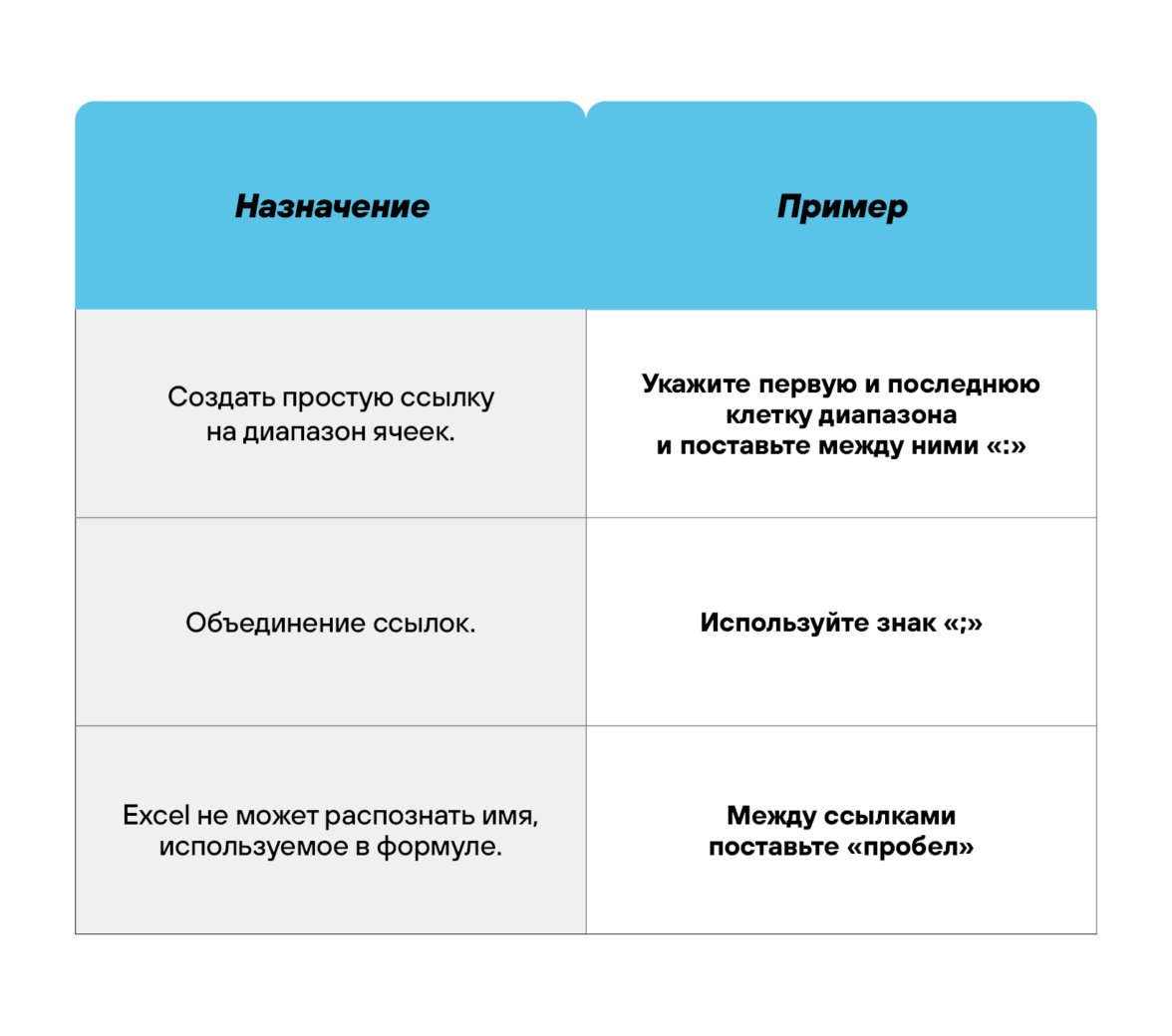
Операторы ссылок
Использование ссылок
Начинающие пользователи обычно работают только с простыми ссылками, но мы расскажем обо всех форматах, даже продвинутых.
Простые ссылки A1
Они используются чаще всего. Буква обозначает столбец, цифра — строку.
Примеры:
-
диапазон ячеек в столбце С с 1 по 23 строку — «С1: С23»;
-
диапазон ячеек в строке 6 с B до Е– «B6: Е6»;
-
все ячейки в строке 11 — «11:11»;
-
все ячейки в столбцах от А до М — «А: М».
Ссылки на другой лист
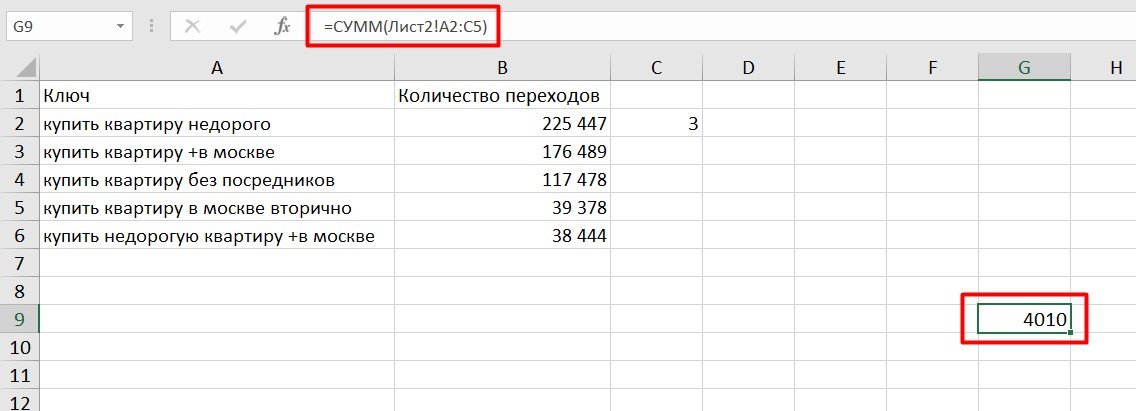
Если необходимы данные с других листов, используется формула: =СУММ (Лист2! A5: C5)
Выглядит это так:
Абсолютные и относительные ссылки
Относительные ссылки
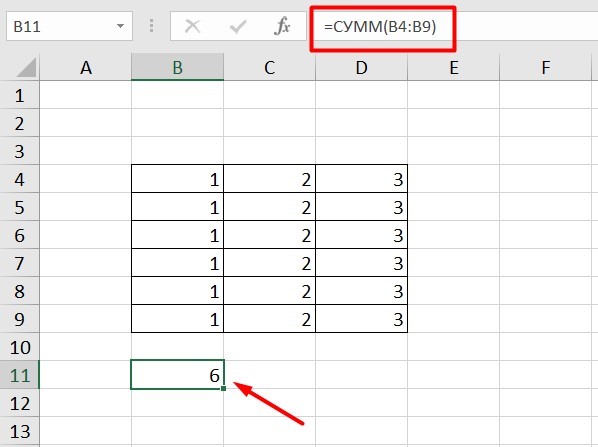
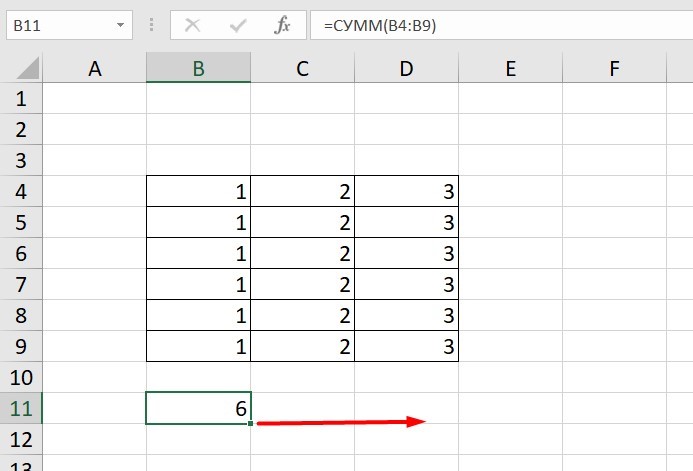
Рассмотрим, как они работают на примере: Напишем формулу для расчета суммы первой колонки. =СУММ (B4: B9)
Нажимаем на Ctrl+C. Чтобы перенести формулу на соседнюю клетку, переходим туда и жмем на Ctrl+V. Или можно просто протянуть ячейку с формулой, как мы описывали выше.
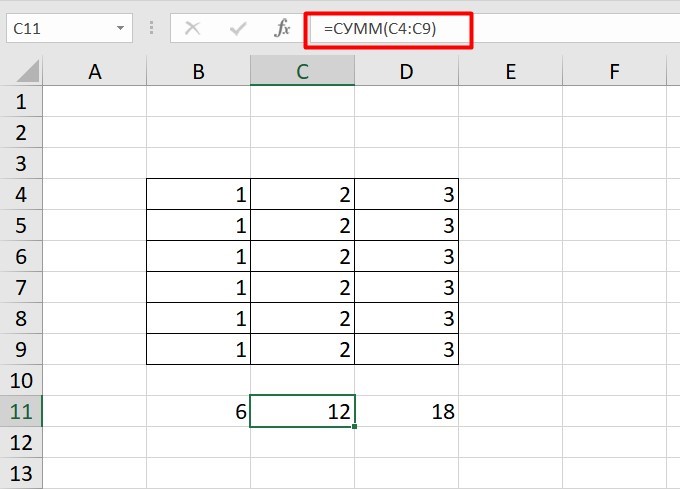
Индекс таблицы изменится автоматически и новые формулы будут выглядеть так:
Абсолютные ссылки
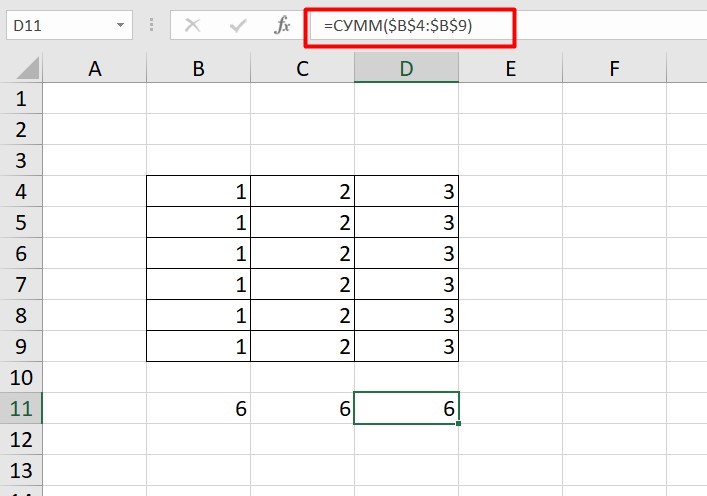
Чтобы при переносе формул ссылки сохранялись неизменными, требуются абсолютные адреса. Их пишут в формате «$B$2».
Например, есть поставить знак доллара в предыдущую формулу, мы получим: =СУММ ($B$4:$B$9)
Как видите, никаких изменений не произошло.
Смешанные ссылки
Они используются, когда требуется зафиксировать только столбец или строку:
-
$А1– сохраняются столбцы;
-
А$1 — сохраняются строки.
Смешанные ссылки удобны, когда приходится работать с одной постоянной строкой данных и менять значения в столбцах. Или, когда нужно рассчитать результат в ячейках, не расположенных вдоль линии.
Трёхмерные ссылки
Это те, где указывается диапазон листов.
Формула выглядит примерно так: =СУММ (Лист1: Лист5! A6)
То есть будут суммироваться все ячейки А6 на всех листах с первого по пятый.
Ссылки формата R1C1
Номер здесь задается как по строкам, так и по столбцам.
Например:
-
R9C9 — абсолютная ссылка на клетку, которая расположена на девятой строке девятого столбца;
-
R[-2] — ссылка на строчку, расположенную выше на 2 строки;
-
R[-3]C — ссылка на клетку, которая расположена на 3 ячейки выше;
-
R[4]C[4] — ссылка на ячейку, которая распложена на 4 клетки правее и 4 строки ниже.
Использование имён
Функционал Excel позволяет давать собственные уникальные имена ячейкам, таблицам, константам, выражениям, даже диапазонам ячеек. Эти имена можно использовать для совершения любых арифметических действий, расчета налогов, процентов по кредиту, составления сметы и табелей, расчётов зарплаты, скидок, рабочего стажа и т.д.
Все, что нужно сделать — заранее дать имя ячейкам, с которыми планируете работать. В противном случае программа Эксель ничего не будет о них знать.
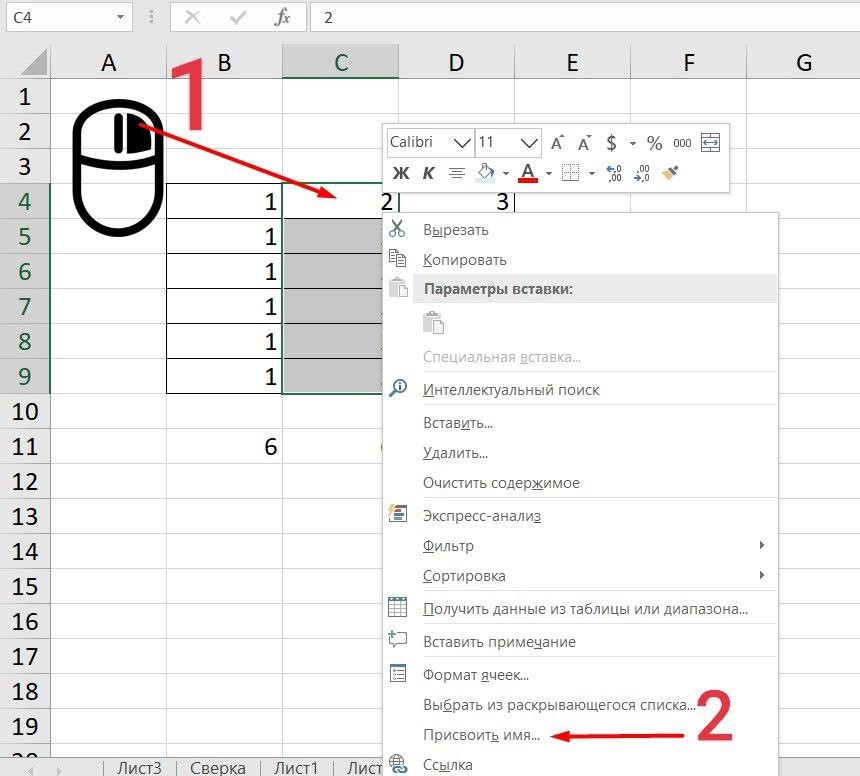
Как присвоить имя:
-
Выделите нужную ячейку/столбец.
-
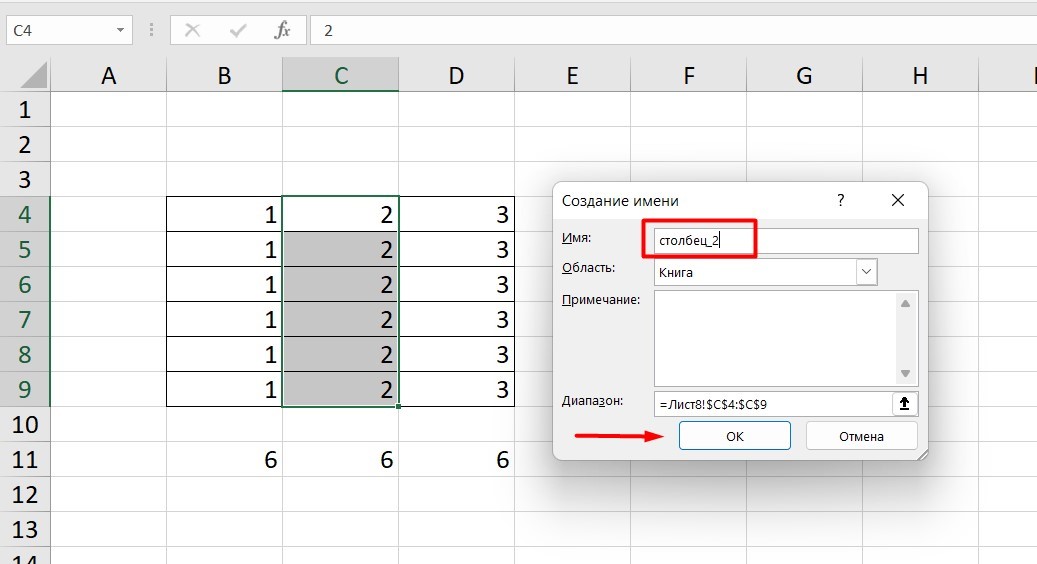
Правой кнопкой мышки вызовите меню и перейдите в закладку «Присвоить имя».
-
Напишите желаемое имя, которое должно быть уникальным и не повторяться в одной книге.
-
Сохраните, нажав Ок.
Использование функций
Чтобы вставить необходимую функцию в эксель-таблицах, можно использовать три способа: через панель инструментов, с помощью опции Вставки и вручную. Рассмотрим подробно каждый способ.
Ручной ввод
Этот способ подойдет тем, кто хорошо разбирается в теме и умеет создавать формулы прямо в строке. Для начинающих пользователей и новичков такой вариант покажется слишком сложным, поскольку надо все делать руками.
Панель инструментов
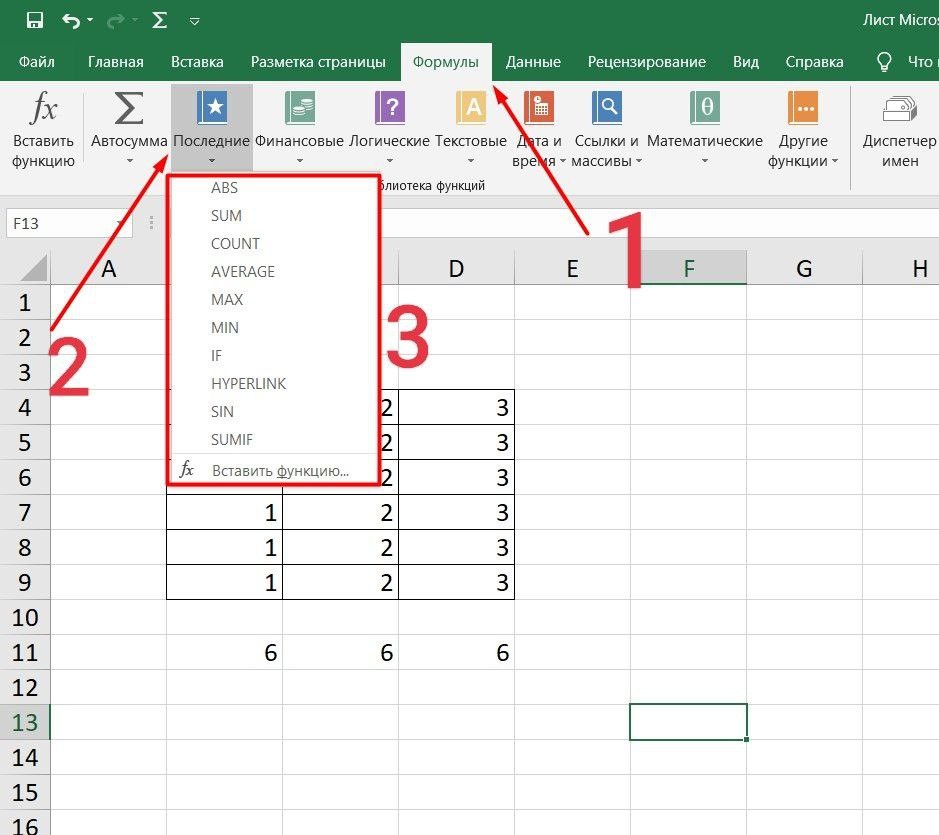
Это более упрощенный способ. Достаточно перейти в закладку «Формулы», выбрать подходящую библиотеку — Логические, Финансовые, Текстовые и др. (в закладке «Последние» будут наиболее востребованные формулы). Остается только выбрать из перечня нужную функцию и расставить аргументы.
Мастер подстановки
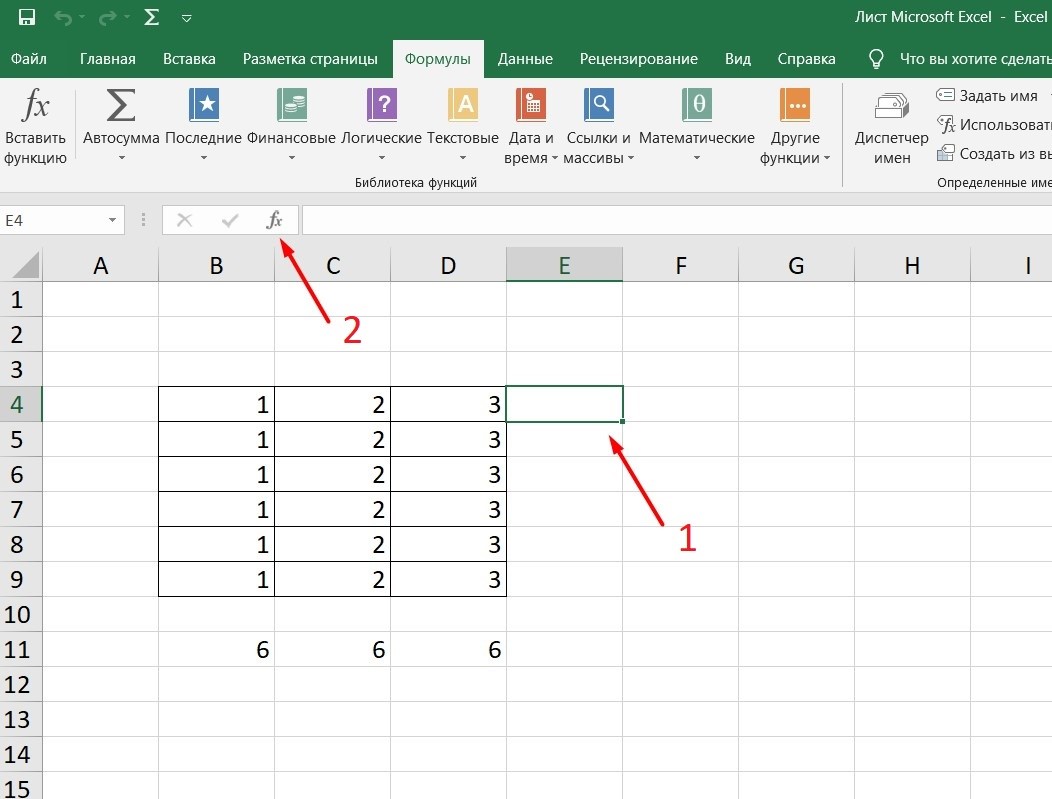
Кликните по любой ячейке в таблице. Нажмите на иконку «Fx», после чего откроется «Вставка функций».
Выберите из перечня нужную категорию формул, а затем кликните по функции, которую хотите применить и задайте необходимые для расчетов аргументы.
Вставка функции в формулу с помощью мастера
Рассмотрим эту опцию на примере:
-
Вызовите окошко «Вставка функции», как описывалось выше.
-
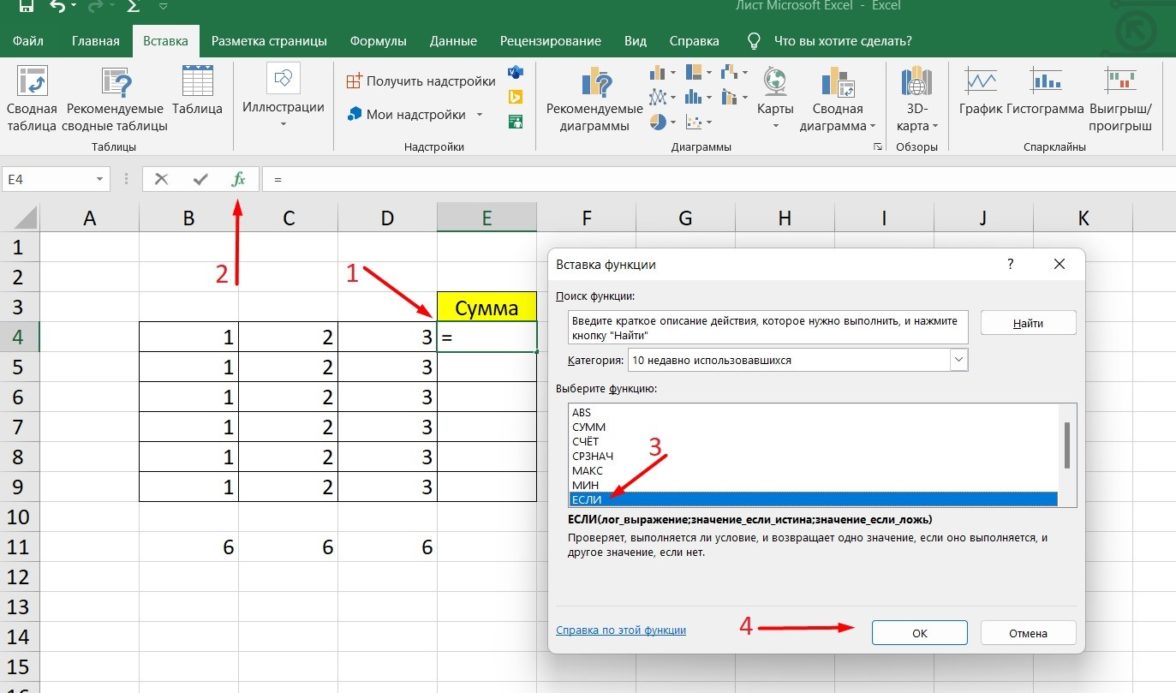
В перечне доступных функций выберите «Если».
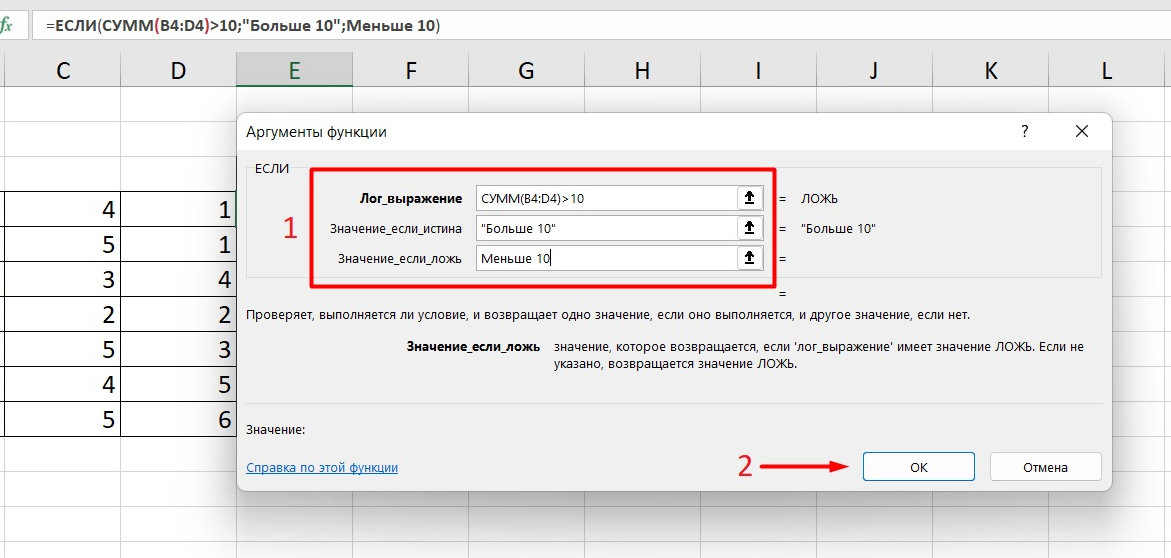
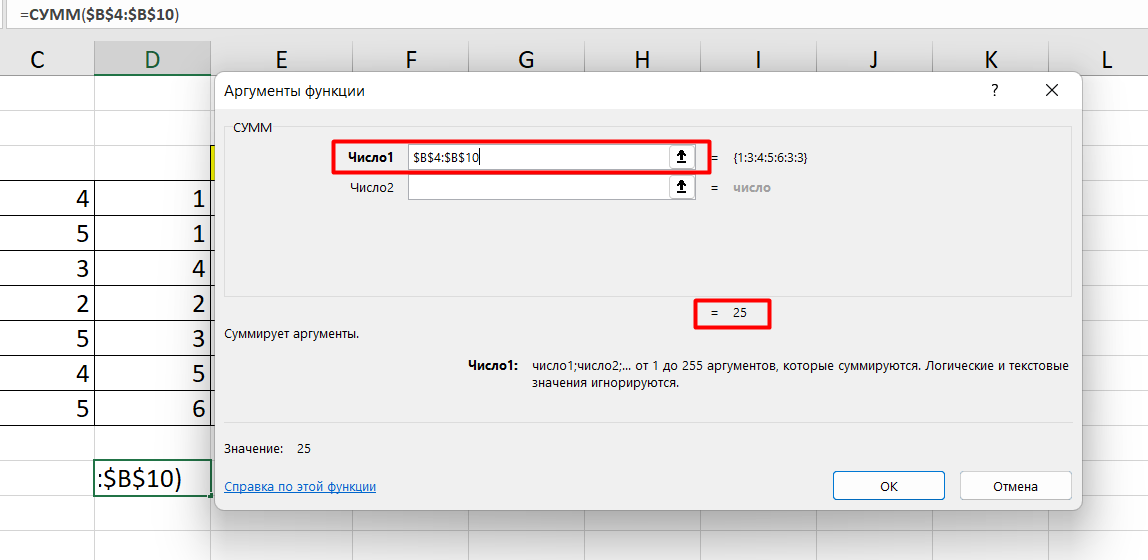
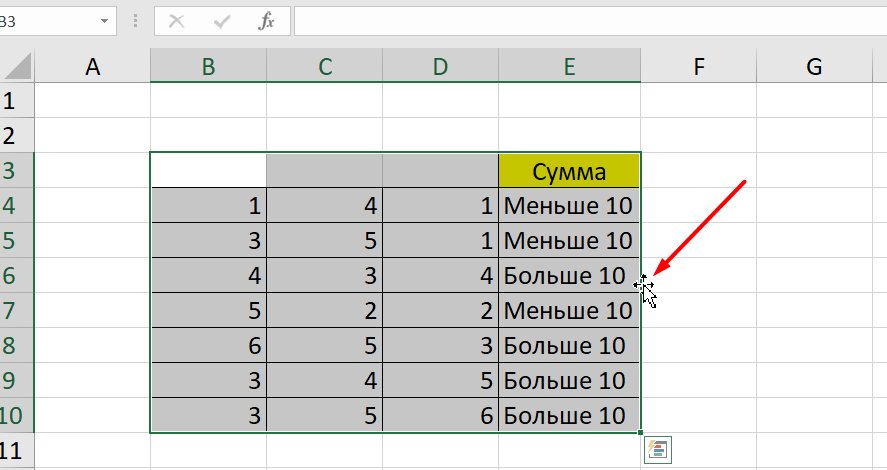
Теперь составим выражение, чтобы проверить, будет ли сумма трех ячеек больше 10. При этом Правда — «Больше 10», а Ложь — «Меньше 10».
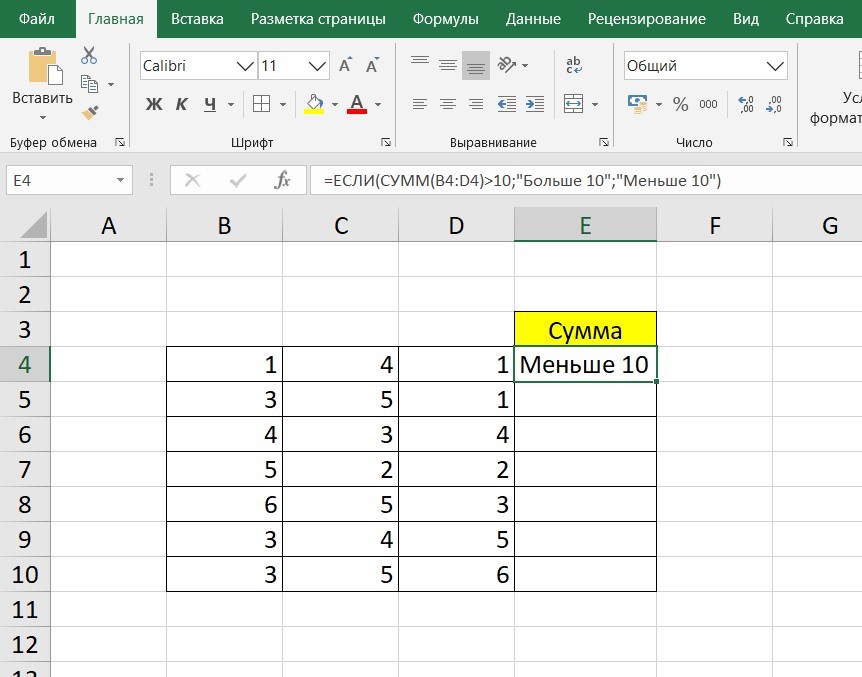
=ЕСЛИ (СУММ (B3: D3)>10;”Больше 10″;»Меньше 10″)
Программа посчитала, что сумма ячеек меньше 10 и выдала нам результат:
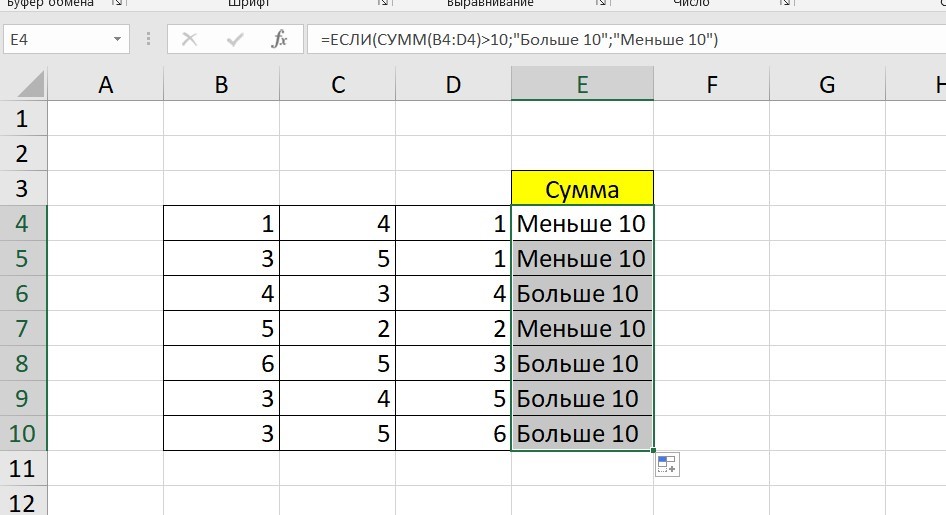
Чтобы получить значение в следующих ячейках столбца, нужно растянуть формулу (за правый нижний уголок). Получится следующее:
Мы использовали относительные ссылки, поэтому программа пересчитала выражение для всех строк корректно. Если бы нам нужно было зафиксировать адреса в аргументах, тогда мы бы применяли абсолютные ссылки, о которых писали выше.
Редактирование функций с помощью мастера
Чтобы отредактировать функцию, можно использовать два способа:
-
Строка формул. Для этого требуется перейти в специальное поле и вручную ввести необходимые изменения.
-
Специальный мастер. Нажмите на иконку «Fx» и в появившемся окошке измените нужные вам аргументы. И тут же, кстати, сможете узнать результат после редактирования.
Операции с формулами
С формулами можно совершать много операций — копировать, вставлять, перемещать. Как это делать правильно, расскажем ниже.
Копирование/вставка формулы
Чтобы скопировать формулу из одной ячейки в другую, не нужно изобретать велосипед — просто нажмите старую-добрую комбинацию (копировать), а затем кликните по новой ячейке и нажмите (вставить).
Отмена операций
Здесь вам в помощь стандартная кнопка «Отменить» на панели инструментов. Нажмите на стрелочку возле нее и выберите из контекстного меню те действия. которые хотите отменить.
Повторение действий
Если вы выполнили команду «Отменить», программа сразу активизирует функцию «Вернуть» (возле стрелочки отмены на панели). То есть нажав на нее, вы повторите только что отмененную вами операцию.
Стандартное перетаскивание
Выделенные ячейки переносятся с помощью указателя мышки в другое место листа. Делается это так:
-
Выделите фрагмент ячеек, которые нужно переместить.
-
Поместите указатель мыши над одну из границ фрагмента.
-
Когда указатель мыши станет крестиком с 4-мя стрелками, можете перетаскивать фрагмент в другое место.
Копирование путем перетаскивания
Если вам нужно скопировать выделенный массив ячеек в другое место рабочего листа с сохранением данных, делайте так:
-
Выделите диапазон ячеек, которые нужно скопировать.
-
Зажмите клавишу и поместите указатель мыши на границу выбранного диапазона.
-
Он станет похожим на крестик +. Это говорит о том, что будет выполняться копирование, а не перетаскивание.
-
Перетащите фрагмент в нужное место и отпустите мышку. Excel задаст вопрос — хотите вы заменить содержимое ячеек. Выберите «Отмена» или ОК.
Особенности вставки при перетаскивании
Если содержимое ячеек перемещается в другое место, оно полностью замещает собой существовавшие ранее записи. Если вы не хотите замещать прежние данные, удерживайте клавишу в процессе перетаскивания и копирования.
Автозаполнение формулами
Если необходимо скопировать одну формулу в массив соседних ячеек и выполнить массовые вычисления, используется функция автозаполнения.
Чтобы выполнить автозаполнение формулами, нужно вызвать специальный маркер заполнения. Для этого наведите курсор на нижний правый угол, чтобы появился черный крестик. Это и есть маркер заполнения. Его нужно зажать левой кнопкой мыши и протянуть вдоль всех ячеек, в которых вы хотите получить результат вычислений.
Как в формуле указать постоянную ячейку
Когда вам нужно протянуть формулу таким образом, чтобы ссылка на ячейку оставалась неизменной, делайте следующее:
-
Кликните на клетку, где находится формула.
-
Наведите курсор в нужную вам ячейку и нажмите F4.
-
В формуле аргумент с номером ячейки станет выглядеть так: $A$1 (абсолютная ссылка).
-
Когда вы протяните формулу, ссылка на ячейку $A$1 останется фиксированной и не будет меняться.
Как поставить «плюс», «равно» без формулы
Когда нужно указать отрицательное значение, поставить = или написать температуру воздуха, например, +22 °С, делайте так:
-
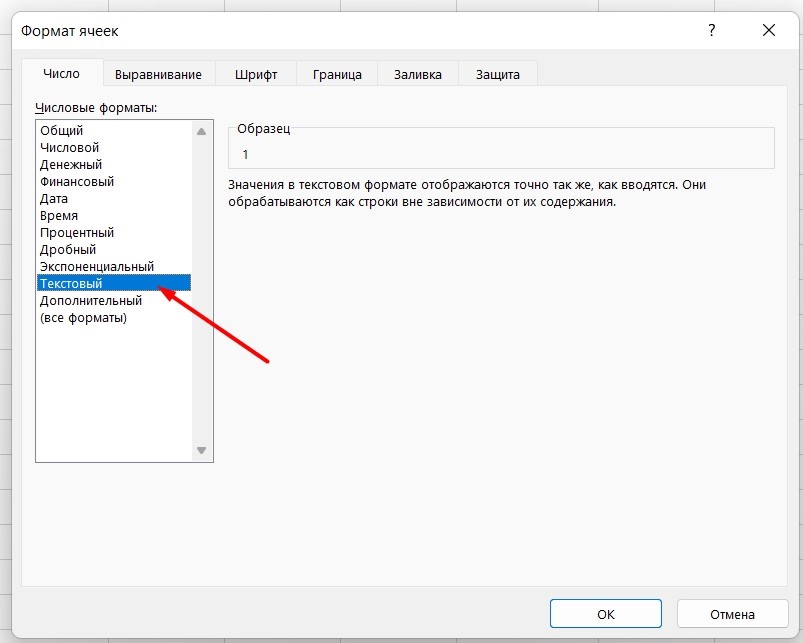
Кликаете правой кнопкой по ячейке и выбираете «Формат ячеек».
-
Отмечаете «Текстовый».
Теперь можно ставить = или +, а затем нужное число.
Самые распространенные ошибки при составлении формул в редакторе Excel
Новички, которые работают в редакторе Эксель совсем недавно, часто совершают элементарные ошибки. Поэтому рекомендуем ознакомиться с перечнем наиболее распространенных, чтобы больше не ошибаться.
-
Слишком много вложений в выражении. Лимит 64 штуки.
-
Пути к внешним книгам указаны не полностью. Проверяйте адреса более тщательно.
-
Неверно расставленные скобочки. В редакторе они обозначены разными цветами для удобства.
-
Указывая имена книг и листов, пользователи забывают брать их в кавычки.
-
Числа в неверном формате. Например, символ $ в Эксель — это не знак доллара, а формат абсолютных ссылок.
-
Неправильно введенные диапазоны ячеек. Не забывайте ставить «:».
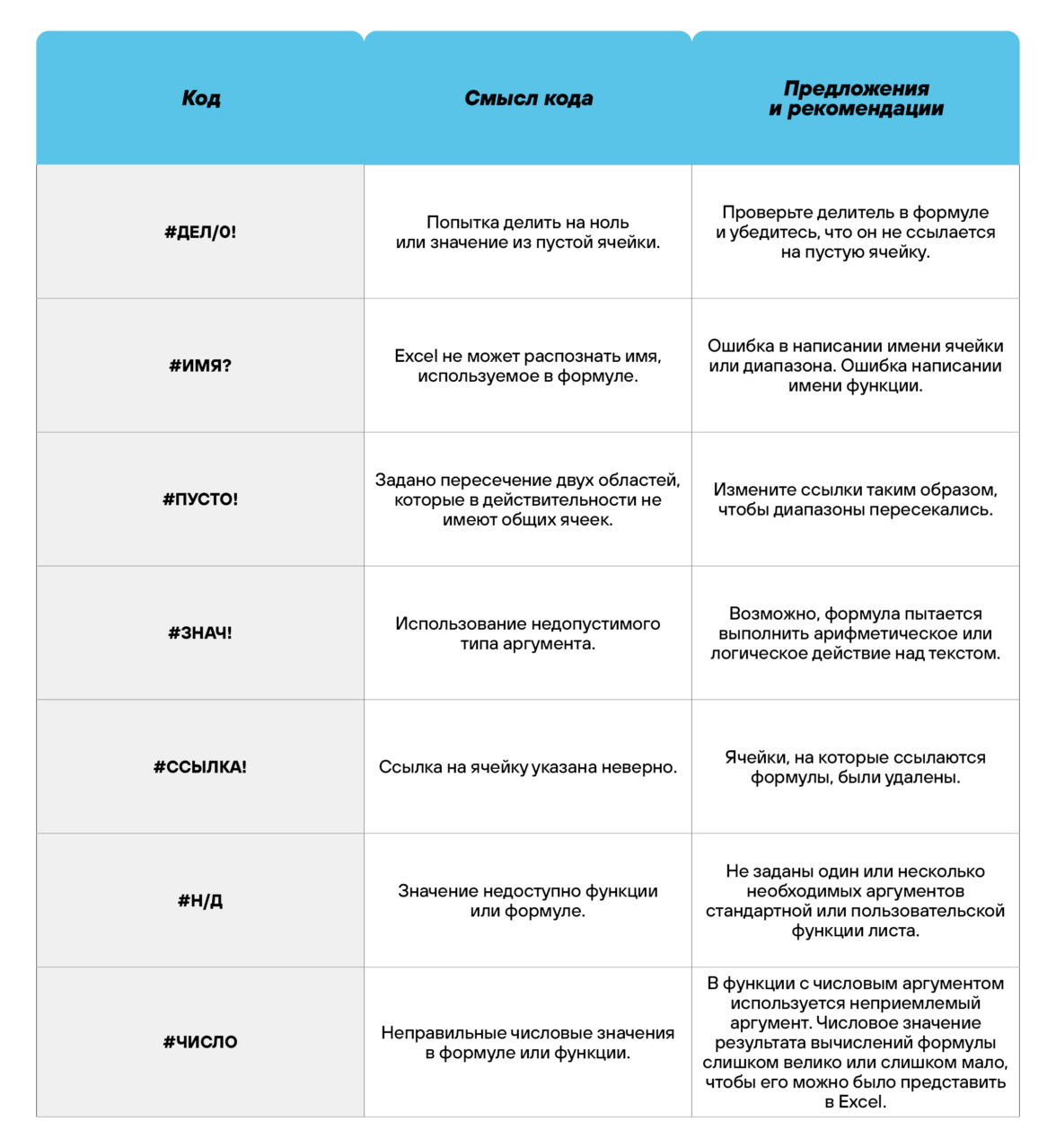
Коды ошибок при работе с формулами
Если вы сделаете ошибку в записи формулы, программа укажет на нее специальным кодом. Вот самые распространенные:
Отличие в версиях MS Excel
Всё, что написано в этом гайде, касается более современных версий программы 2007, 2010, 2013 и 2016 года. Устаревший Эксель заметно уступает в функционале и количестве доступных инструментов. Например, функция СЦЕП появилась только в 2016 году.
Во всем остальном старые и новые версии Excel не отличаются — операции и расчеты проводятся по одинаковым алгоритмам.
Заключение
Мы написали этот гайд, чтобы вам было легче освоить Excel. Доступным языком рассказали о формулах и о тех операциях, которые можно с ними проводить.
Надеемся, наша шпаргалка станет полезной для вас. Не забудьте сохранить ее в закладки и поделиться с коллегами.