Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
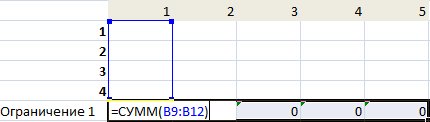
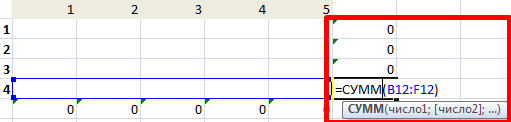
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
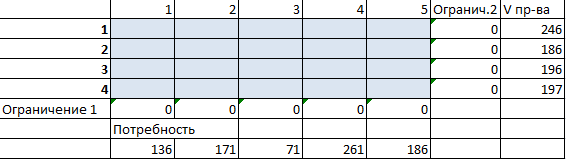
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
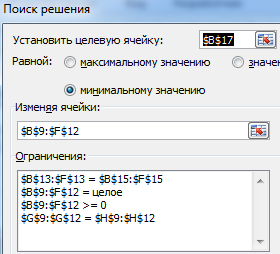
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Решение транспортных задач ЛП в Excel
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Алгоритм решения ТЗ в Эксель
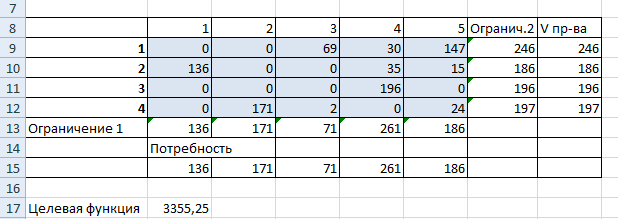
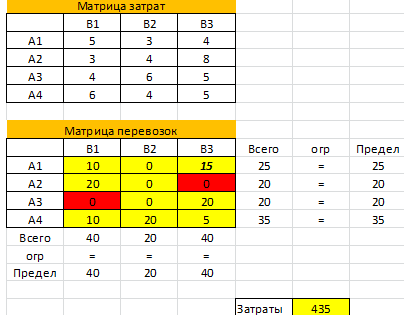
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Источник
Здесь Вы можете произвести расчёты загрузки автомобилей

Всякий, кто занимался организацией грузоперевозок или переездов задавал себе вопрос: сколько это стоит? Это один из основных вопросов и, пожалуй, самый главный, так как решает целесообразность перемещения грузов на расстояния. Эра открытий прошла, уже не осталось белых пятен на картах, наступила эпоха прагматичной целесообразности.
Вопрос: «Во что это обойдется?» решает все.
Вот здесь и пригодятся наши программы расчетов грузоперевозок и переездов.
Калькуляционные расчеты помогут определить целесообразность перемещения практически любых грузов, подобрать нужный транспорт от бычка и газели до большегрузных фур в соответствии с габаритами и тоннажём груза.
Расчеты стоимости перевозок (переездов) нужны как для крупных фирм, с грузопотоком в десятки тысяч тонн, так и частным предпринимателям и домохозяйкам, заказывающим перевозку мебели или крупногабаритной техники.
Мы представляем калькуляционные программы выбора автотранспорта по объему и тоннажу перевозимого груза, а также программы расчетов стоимости перевозок.
3D расчёт загрузки
Пример программы расчёта загрузки 
Вы можете скачать эту программу с нашего сайта ввиде zip-архива, в который входят: инструкция и лицензионное соглашение (формат rtf), а так же файлы программы. Данная программа распространяется бесплатно, с обязательным упоминанием этого сайта и ссылкой на эту страницу. Запрещается продавать эту программу и сдавать в аренду, получать коммерческую выгоду. Программа защищена законом © www.wiraj-perevozki.ru, 2011.
Скачать программу 3D загрузки (2,39 МБ)
После скачивания программы распакуйте ZIP архив в любую папку, затем почитайте инструкцию и лицензионное соглашение.
2D расчёт загрузки
Пример программы расчёта загрузки 
Вы можете связаться с нами, и мы ответим по вопросам приобретения данной программы.
Программа защищена законом © www.wiraj-perevozki.ru, 2014.
Универсальный расчёт загрузки автомобилей (в Excel)
Пример таблицы в Excel 
Скачать универсальный расчёт (41 кб, xls файл)
для работы этого файла вам потребуется MS Excel
Источник
Как решить транспортную задачу в Excel
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Источник
Автоматизация и моделирование бизнес-процессов в Excel
Глава 10
Модель для расчета максимальной загрузки автомобиля (контейнера)
Предположим, что размеры ящиков и кузова машины не кратны, и что эти ящики можно располагать как угодно, то есть на них нет маркировки «верх». В таком случае возможно шесть вариантов расположения груза, которые показаны на рис. 10.1.
Рис. 10.1. Возможное расположение прямоугольных ящиков с грузом в кузове машины
Рис. 10.2. Наименования сторон габаритов груза, применяемые в разрабатываемом приложении в качестве имен ячеек, в которые будет осуществляться ввод этих размеров
Рис. 10.3. Наименования сторон габаритов кузова автомобиля, применяемые в разрабатываемом приложении в качестве имен ячеек, в которые будет осуществляться ввод этих размеров
Книге, в которой будет производиться расчет оптимальной загрузки транспорта, присвойте имя Груз. Все расчеты будут производиться на одноименном листе Груз.
Исходные данные вводятся в две небольшие таблицы с указанием габаритов кузова машины (диапазон ячеек В1:С4) и габаритов груза (диапазон ячеек В6:С9), а также количество ящиков, которые желательно разместить в этом кузове (ячейка С11). Ячейкам, в которые будут вводиться габариты груза и кузова, присвойте имена, показанные на рис. 10.2. и 10.3.

Предполагаемая последовательность заполнения кузова автомобиля
Прежде чем приступить к созданию модели, необходимо продумать последовательность выполнения расчетов, которые в свою очередь предполагают виртуальную последовательность погрузки ящиков в кузов. Немаловажной деталью является и определение позиции наблюдающего за погрузкой, например, с целью- какой угол является правым или левым. Предполагаем, что наблюдение за погрузкой будет осуществляться от заднего борта автомобиля.
Предполагаем, что последовательность заполнения кузова автомобиля ящиками с грузом будет разделена на несколько этапов, каждый из которых предполагает погрузку партии ящиков.
На рис. 10.5. в качестве примера показано расположение первой партии груза по варианту 1.
Следовательно для последующих расчетов исходными данными будут служить уже значения габаритов оставшихся трех свободных объемов пространства кузова, не занятые ящиками первой партии.
Рис. 10.6. Заполнение свободного пространства кузова автомобиля второй партией ящиков с грузом по варианту 6 размещения
Рис. 10.7. Заполнение свободного пространства кузова автомобиля третьей партии по варианту 5 размещения
И последняя партия груза (партия-4) будет упаковываться, при наличии свободного пространства, поверх первой партии. Последовательность загрузки при желании может быть изменена, но результат от этого не изменится.
Определение оптимального варианта размещения первой партии груза
В зависимости от выбранного варианта размещения первой партии груза, в кузов автомобиля может поместиться различное количество ящиков этой партии. Создаваемая таблица должна учитывать выбираемый вариант размещения груза, производить расчет помещаемых ящиков по ширине, длине и высоте кузова, а также общее количество ящиков в первой партии и используемый объем кузова автомобиля.
Создание таблицы для расчета объема занимаемого первой партией груза
Определение оптимального заполнения кузова машины первой партией груза будет производиться в таблице, расположенной в области А13:Н21 (рис. 10.8.).
Рис. 10.8. Таблица для расчета количества помещаемых ящиков и заполнения пространства кузова при размещении первой партии груза с числовым примером
Автоматизация выбора варианта расположения груза первой партии
Для выбора варианта расположения первой партии груза в кузове автомобиля могут быть использованы шесть элементов управления Переключатель, которые связаны с ячейкой А16. В ячейку А17 введите формулу:
Формулы расчета количества ящиков первой партии
Формулы расчета должны определять количество размещаемых ящиков в один ряд по каждому параметру кузова автомобиля (по ширине, по длине и по высоте).
Например, в диапазоне ячеек D16:D21 необходимо произвести расчет количества ящиков, которые разместятся в один ряд по ширине автомобиля при каждом варианте размещения первой партии ящиков. Для этого необходимо произвести операцию деления значения размера ширины кузова автомобиля, находящегося в ячейке С2 (ячейке присвоено имя Машина_Ширина) на первый параметр габарита груза по варианту, текст которой указан в диапазоне ячеек В16:В21. В ячейке D16 будет находиться формула:
Аналогично производится и расчет количества ящиков, размещаемых по длине и высоте при различных вариантах расположения груза. В диапазоне G16:G21 производится расчет общего количества ящиков в первой партии по каждому варианту размещения, путем умножения количества ящиков, размещаемых в один ряд по ширине, по длине и по высоте.
Формулы находящиеся в этой таблице показаны на рис. 10.9.
Рис. 10.9. Таблица для расчета количества помещаемых ящиков и заполнения пространства кузова при размещении первой партии груза с формулами
Анализ и расчет свободного пространства кузова после загрузки первой партии ящиков
Создание таблицы расчета размеров оставшегося свободного пространства в кузове автомобиля
Рис. 10.10. Таблица расчета размеров оставшегося свободного пространства кузова после загрузки первой партии
Формулы в этих областях однотипны и проанализируем их по формуле, введенной в ячейку К16, которая производит вычисление свободного расстояния по длине кузова автомобиля:
В других ячейках таблицы находятся похожие формулы, но используют комбинацию различных габаритов груза и кузова.
Определение составляющих оставшегося свободного объема кузова автомобиля
Формулы таблицы расчета оставшегося свободного объема кузова
Рис. 10.11. Таблица расчета оставшегося свободного объема кузова
Рассмотрим формулы, находящиеся в первой строке указанных диапазонов таблицы.
Формула в ячейке N16 основана на функции СЦЕПИТЬ соединяющей текст, ссылки на ячейки, которым присвоены и не присвоены имена, а также производящая вычисление свободного объема, оставшегося по ширине автомобиля:
=СЦЕПИТЬ(J16;» х «;Машина_Длина;» х «;Машина_Высота;» = «;J16*Машина_Длина*Машина_Высота)
Формула в ячейке О16 аналогична предыдущей, но несколько сложнее:
И в формуле в ячейке Р16:
В ячейке Q16 формула суммарного свободного объема автомобиля:
Дальнейшее заполнение кузова
После загрузки первой партии ящиков, оставшееся свободное пространство кузова можно разделить на три части (описано выше).
Моделирование возможности дальнейшей автоматизации вычислений
Рис. 10.12. Габариты пространства, заполняемого второй партией груза
Тогда длина и высота останутся прежними, а ширина этого свободного объема будет равна ширине кузова автомобиля минус произведение, равное значению ширины груза, умноженное на 6 расположенных ящиков по ширине кузова:
Впрочем габариты этого свободного пространства (0,3м х 3,5 м х 2м) и его объем (2,1м3) рассчитаны и показаны в ячейке N16 (рис. 10.11.). Введите значение ширины этого пространства (0,3м) в ячейку С2 области ввода значения габаритов кузова автомобиля (рис. 10.4.) и тогда в таблице, показанной на рис. 10.8., будет произведен расчет, согласно которому возможно максимальное размещение в этом объеме семи ящиков по варианту 6 размещения груза.
Расчет заполнения свободного объема кузова второй партией груза
Рис. 10.13. Таблица оптимального размещения груза второй и третьей партии ящиков в свободном объеме кузова автомобиля
Находящаяся в ячейке С32 формула (показана в строке формул на рис. 10.13.), в качестве значения размера ширины габаритов свободного пространства, использует рассчитанные данные оставшегося не занятого расстояния ширины кузова автомобиля в области ячеек J16:J21 (рис. 10.10.). Эти данные она находит с помощью функции ВПР по значению 1, которая вводится в область ячеек А16:А21 активизацией выбранного элемента управления Переключатель. Данные свободного пространства, рассчитанные в области ячеек J16:J21 делятся на первый указанный в области ячеек В27:В32 элемент габарита груза (длина, ширина или высота).
Расчет заполнения свободного пространства кузова третьей партии груза
Рис. 10.14. Объем пространства, заполняемого третьей партией груза
Таблица расчета количества ящиков третьей партии находится в области ячеек G27:J33 (рис. 10.13.). Формула в ячейке G27:
производит с помощью функции ВПР поиск размера оставшегося свободного пространства по ширине кузова в области ячеек J16:J21 по выбранному варианту размещения первой партии груза, которое вычитается из ширины кузова автомобиля. И полученный результат делится на габарит груза, который указан первым в вариантах размещения в ячейках В27:В32.
Формула в ячейке Н27:
похожа на предыдущую формулу с той разницей, что поиск оставшегося свободного пространства кузова производится в диапазоне ячеек К16:К21, оставшейся после размещения первой партии груза.
Расчет заполнения свободного объема кузова четвертой партией груза
Рис. 10.15. Таблица расчета заполнения свободного объема кузова четвертой партии груза
Последовательность загрузки кузова на практике
Рис. 10.16. Итоговая таблица с анализом загрузки автомобиля
Расчет общего количества ящиков, которые могут поместиться в кузов автомобиля
Определение оптимального количества ящиков
При активизации переключателей, определяющей вариант размещения ящиков первой партии груза, вычисленные значения таблицы загрузки первой партии товара остаются неизменны. Изменяется только значение количества ящиков груза первой партии, которая отображается в ячейке Н4 таблицы с выходными параметрами, в которой находится формула, производящая поиск количества погруженных ящиков в первой партии рассчитанных в области L16:L21:
В ячейке Н8 находится формула суммирования количества ящиков во всех четырех партиях.
Формула в ячейке Н9 определяет загрузку объема кузова в процентном отношении:
Если в ячейку С11 введено количество ящиков, предполагаемое для загрузки, то формула в ячейке D11 сравнивает это значение, со значением в ячейке Н8:
В ячейке Е11, в зависимости от полученного результата вычислений в ячейке D11, формируется надписи: Остается свободный объем! или Груз не помещается! по формуле:
© Интернет-проект «Корпоративный менеджмент», 1998–2021
Источник
Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
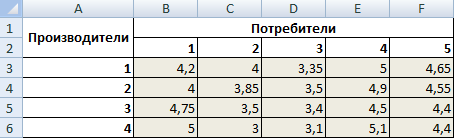
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Источник
Для фиксирования расходов на авто можно выделить несколько способов:
1. Банально завести тетрадку.
2. Скачать готовое приложение на телефон и радоваться (Нет).
3. Составить таблицу в Excel или Google Таблицы.
Тетрадь — самый надежный, но менее функциональный способ. Большинство, я думаю, в тетрадке и делают заметки о растратах (хотя некоторые не парятся по этому поводу и не ведут учет финансов вообще).
Приложение. Хочу сказать, приложения есть. Сильно не вникал, но по первым ощущениям — все корявое, большинство без русского языка, куча рекламы и, к тому же, приложение будет жрать память телефона, которой и так уже впритык. В общем, тоже не мой вариант.
Excel или Google Таблицы — то, что нужно. Именно по этому пути я и пошел. Почему? Да потому, что все данные по всем автомобилям останутся у меня навсегда, в отличии от приложения, где оно сегодня есть, а завтра его нет. Самый главный критерий — гибкость. Можно сформировать отчет на основе огромного количества данных именно так, как я хочу. По сути, таблицами можно добиться того же функционала, что и в приложении, но бесплатно и без рекламы.
Именно таким шаблоном Google таблицы для ведения бортжурнала и учета расходов на авто я хочу поделиться.
—————
Скачать Excel (Google Sheets) шаблон таблицы для учета расходов на авто.
—————
P.S. Конвертер валют будет работать только при использовании файла в Google Sheets. Если скачивать документ для Excel, обновление курса происходить не будет.
Реализованы такие функции как:
— Подсчет затрат без учета топлива, штрафов, докуметов, паркинга и платных доро
— Подсчет затрат с учетом всех статей расходов
— Подсчет полного пробега автомобиля на основе данных последней записи расходов
— Подсчет пробега с момента покупки авто
— Подсчет срока владения авто
— Подсчет оставшегося пробега до замены масла в двигателе
— Подсчет оставшегося пробега до замены масла в КПП/АКПП
— Подсчет оставшегося пробега до плановой диагностики
— Подсчет количества дней до окончания страховки
— Конвертер валют с автоматической конвертацией в выбранную в настройках валюту. Курс автоматически обновляется каждые 20 мин.
Руководство по настройке
Шаг 1. Указать требуемые данные в разделе «Настройки» (внизу листа «Главная»).
Шаг 2. Удалить демо записи.
Шаг 3. Можно добавлять расходы.
Что нужно помнить при добавлении расходов?
Расходы разделяются на категории. Каждой категории соответствует отдельный лист. При добавлении следует придерживаться следующих правил:
1. Все ячейки, к которым привязаны выпадающие списки, должны заполняться исключительно данными из этих выпадающих списков. В противном случае будет ошибочный итоговый подсчет растрат.
2. Даты указываются в формате «27.09.2021»
3. В некоторых категориях доставка детали и стоимость детали указываются в отдельных столбцах. Данные автоматически суммируются формулой и подставляются в соседний третий столбец, который править вручную не нужно. По такому же принципу работает и суммарная стоимость работ.
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
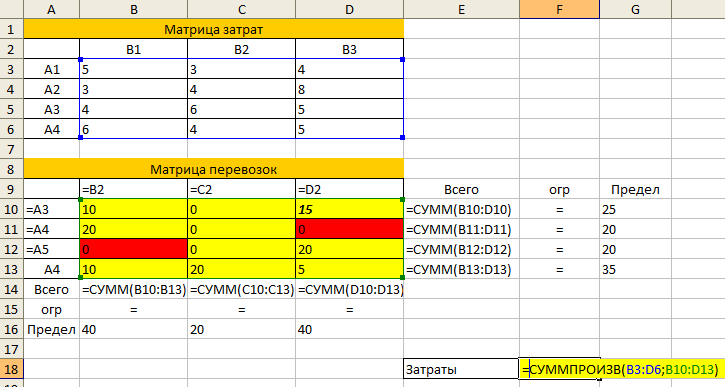
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
В режиме формул таблица будет выглядеть так:
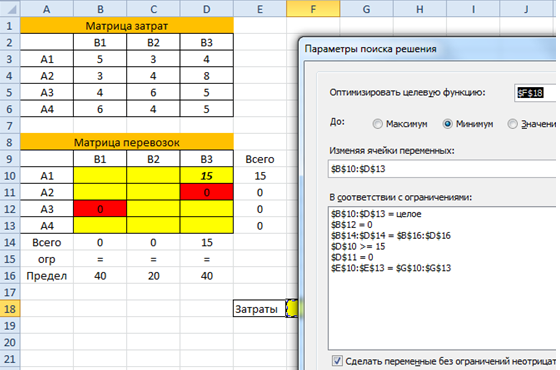
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Спасибо за ваши закладки и рекомендации
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|