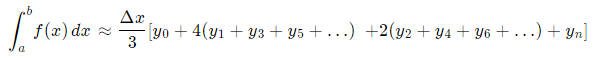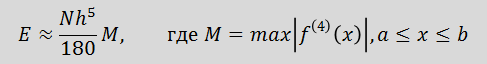history 27 ноября 2022 г.
- Группы статей
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
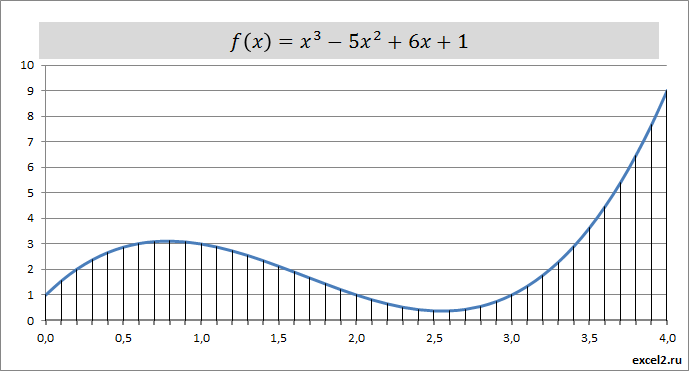
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
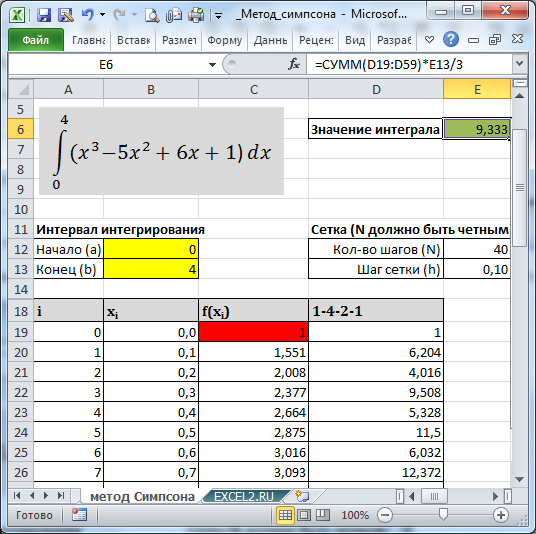
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
Настраиваемый интервал
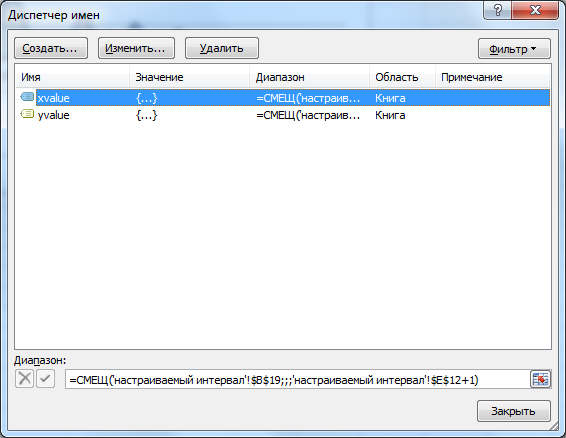
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.
1Постановка физической задачина расчёт определённого интеграла
Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (единицы измерений – микрозиверт в час, мкЗв/ч). Возможно, Вас это удивит, но при обычном перелёте на самолёте человек попадает под радиоактивное излучение, превышающее фоновый уровень до 10 раз и даже больше. Но воздействие это кратковременное, и поэтому не столь опасное. По результатам измерений у нас есть таблица вот такого формата: Время – Мощность дозы.
Необходимо посчитать суммарную накопленную за время полёта дозу.
2Геометрический смыслопределённого интеграла
Как мы помним из курса школьной алгебры, определённый интеграл – это площадь под графиком измеряемой величины. Чтобы определить накопленную дозу радиации в рассматриваемом примере, нужно определить площадь фигуры под графиком таблично заданной мощности дозы. Накопленная доза радиации равна площади фигуры под графиком мощности дозы
3Методика вычисленияопределённого интеграла
Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.
Площадь трапеции определяется как полусумма оснований, умноженная на высоту: Sтрап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.
4Согласованиеединиц измерения
В нашем примере измерения мощности дозы радиации даётся в мкЗв/час, а шкала времени – с точностью до минут. Мы не можем брать интеграл по времени, измеряемому в минутах, для величины, измеряемой в часах. Поэтому необходимо перевести мкЗв/час в мкЗв/мин.
Для перевода просто разделим мощность дозы в мкЗв/час построчно на количество минут в часе, т.е. на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации это столбец «D». В столбце «D» в строке 2 вписываем =С2/60 А потом с помощью маркера заполнения распространяем эту формулу на все остальные ячейки в столбце «D», (т.е. тянем мышью чёрный прямоугольник в правом нижнем углу ячейки). Таким образом, в столбце «D» у нас появятся значения мощности дозы радиации, измеряемые в микрозивертах в минуту для каждой минуты перелёта.
5Вычисление площадей отдельных трапеций
Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце «E» будем вычислять по приведённой выше формуле площади трапеций.
Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца «D». Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).
Получаем формулу в ячейке «E3»: =1/2*(D3+D2)*1. Понятно, что «×1» в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца «Е» посчитана накопленная доза за 1 минуту полёта.
Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.
5Определение площадипод графиком функции
Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке «F2» написать формулу: =СУММ(E:E) Это и будет сумма всех значений в столбце «E», т.е. численное значение искомого определённого интеграла. Но давайте сделаем вот что: определим накопленную дозу в разные моменты полёта. Для этого в ячейку «F4» впишем формулу =СУММ(E$3:E4) и маркером заполнения распространим на весь столбец «F».
Обозначение E$3 говорит программе Excel, что увеличивать индекс ячейки «3» в столбце «E» при переносе формулы на следующие строки не нужно. Т.е. в строке 4 формула будет определять сумму в ячейках с «Е3» по «Е4», в строке 5 – сумму с «Е3» по «Е5», в строке 6 – с «Е3» по «Е6» и т.д.
Построим график по столбцам «F» и «A». Это график изменения накопленной дозы радиации во времени. Наглядно видно монотонное увеличение накопленной дозы радиации за время полёта. Это говорит о том, что мы правильно рассчитали интеграл. И окончательное значение накопленной за двухчасовой полёт дозы радиации, которое получается в последней ячейке этого столбца, равно примерно 4,5 микрозиверт.
Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере. В качестве приложения к статье – файл Excel с нашим примером.

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
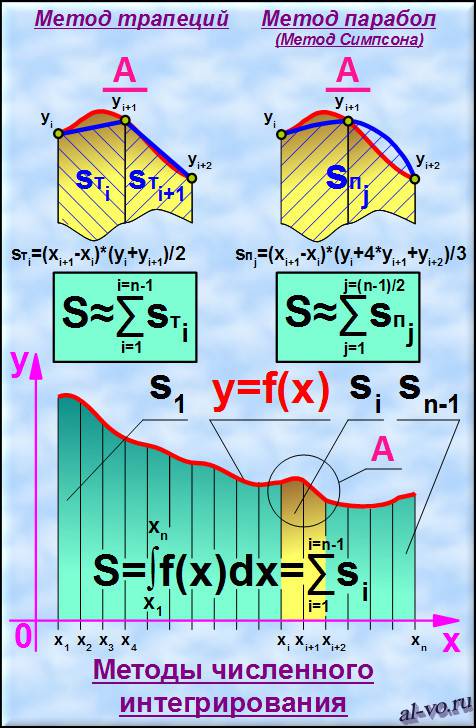
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Следите за анонсами, многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
1. В столбец B вписываем время проведения измерения τi .
2. В столбец C заносим температуры нагретого воздуха t2i , измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i , поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
5. Зная удельную теплоемкость воздуха c =1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G =0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni = c * G * dti
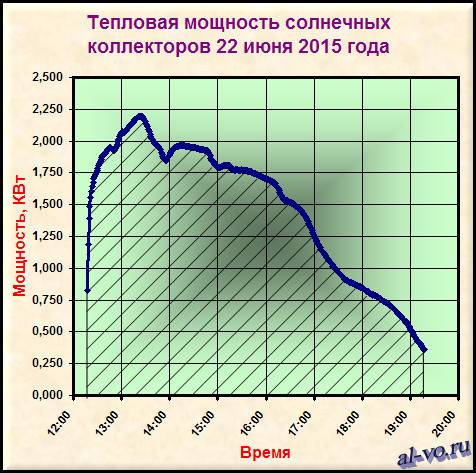
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
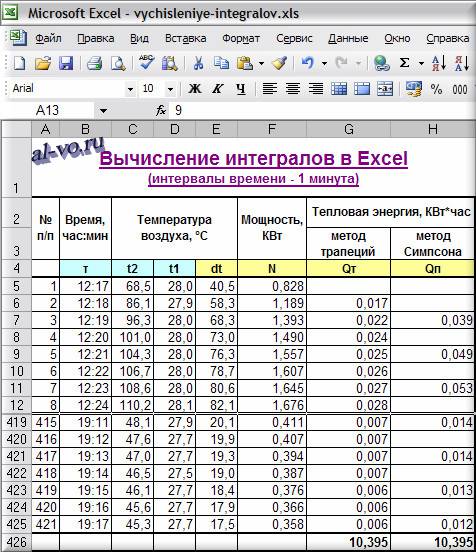
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Q =Σ Qi =10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Q =Σ Qj =10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
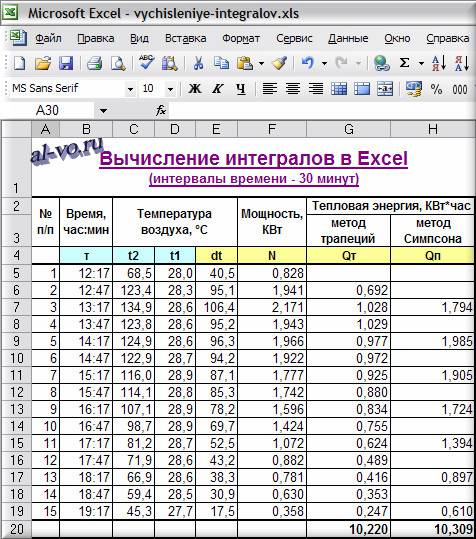
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q =10,220 КВт*час (-1,684%)
По методу Симпсона: Q =10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Отзывы и комментарии к статье, уважаемые читатели, пишите в блоке, расположенном ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи. Введите адрес своей электронной почты, нажмите на кнопку «Получать анонсы статей» и подтвердите подписку кликом по ссылке в письме, которое придет к вам на указанную почту. С этого момента к вам на почтовый ящик будет пару раз в месяц приходить небольшое уведомление о появлении на моем блоге новой статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Примеры интегрирования по частям логарифма и обратных тригонометрических функций
Интегрирование функций рационально зависящих от тригонометрических функций
1. Интегралы вида ∫ sin n xdx , ∫ cos n xdx , n>0
a) Если n нечётное, то одну степень sinx (либо cosx ) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
2. Интегралы вида ∫ tg n xdx , ∫ ctg n xdx , где n – целое.
Необходимо использовать формулы
3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n – нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n – нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x . Часто бывает удобным применить приём тригонометрической единицы.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx
Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:
- sin α·cos β = ½(sin(α+β)+sin(α-β))
- cos α·cos β = ½(cos(α+β)+cos(α-β))
- sin α·sin β = ½(cos(α-β)-cos(α+β))
- Решение онлайн
- Видеоинструкция
Примеры
1. Вычислить интеграл ∫ cos 4 x·sin 3 xdx .
Делаем замену cos(x)=t . Тогда ∫ cos 4 x·sin 3 xdx =
2. Вычислить интеграл 
Делая замену sin x=t , получаем
3. Найти интеграл 
Делаем замену tg(x)=t . Подставляя, получаем
Основные тригонометрические формулы
Ниже приведены некоторые тригонометрические формулы, которые могут понадобится при интегрировании тригонометрических функций.
sin 2 a + cos 2 a = 1
sin ( a+b ) = sin a cos b + cos a sin b
cos ( a+b ) = cos a cos b – sin a sin b
sin 2 a = 2 sin a cos a
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a
Примеры интегрирования тангенса и котангенса
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интеграла tan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5 .
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
Вычисление площадей отдельных трапеций
Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце “E” будем вычислять по приведённой выше формуле площади трапеций. Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца “D”. Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).
Получаем формулу в ячейке “E3”: =1/2*(D3+D2)*1. Понятно, что “×1” в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца “Е” посчитана накопленная доза за 1 минуту полёта.

Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Стандартные подстановки при интегрировании тригонометрических функций
Здесь мы рассмотрим стандартные подстановки, с помощью которых, в большинстве случаев, выполняется интегрирование тригонометрических функций.
Применение знаний, формирование умений и навыков
Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»
Состав задания:
- Ознакомиться с теоретической частью задания;
- Провести расчет для своего варианта индивидуального задания в Microsoft Excel
- Оформить презентацию в Ms PowerPoint, включающую:
– постановку задачи;
– алгоритм расчета;
– таблицу с расчетом из Ms Excel, график исходной функции;
– результат расчета и его анализ.
Индивидуальное расчетное задание:
- Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x 4 ) 1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка. - Представьте графически поставленную задачу.
Постановка задачи:
Найти: приближенное значение интеграла заданной функции по формуле трапеций, приняв предельное значение погрешности приближенного вычисления интеграла равным ε=0,02.
Таблица Исходная информация
Представление в Excel
Анализ заданной функции и результаты вычислений в Ms Excel
Расчет площади
xi
f(xi)
Коэффициенты формулы трапеций
Вычисление Ci*f(xi)
N=2
N=4
N=8
N=2
N=4
N=8
N=2
N=4
N=8
Ответ: приближенное значение интеграла заданной функции по формуле трапеций равна 1,60кв.мм, значение погрешности приближенного вычисления интеграла равным ε=0,008.
Задания для индивидуальной работы студентов по вариантам:
Найдите приближенное значение интеграла заданной функции f(x) на отрезке [a; b] (см. таблицу ) по формуле трапеций, разбивая отрезок [a; b] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.
Представьте графически поставленную задачу.
отрезок [a; b]
Функция f(x)
(х 4 /(1+x 4 ) 1/2 ) 1/2
(х 5 /(1+x 4 ) 1/2 ) 1/2
На сегодняшнем занятии мы отработали навыки вычисления определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработали умения применять теоретические знания в практических расчетах.
Распространенные примеры интегрирования косинуса
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6) .
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1 .
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0 . Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = – cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy) . Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории “ Интегрирование функций “.
Интегрирование обратных тригонометрических функций
Интегралы, содержащие обратные тригонометрические функции
arcsin φ , arctg φ , и т.д., где φ – некоторая алгебраическая функция от x , нередко интегрируются по частям, полагая u = arcsin φ , u = arctg φ , и т.д.
Общий подход
Вначале, если это необходимо, подынтегральное выражение нужно преобразовать, чтобы тригонометрические функции зависели от одного аргумента, который совпадал бы с переменной интегрирования.
Например, если подынтегральное выражение зависит от sin( x+a ) и cos( x+b ) , то следует выполнить преобразование:
cos ( x+b ) = cos ( x+a – ( a–b ) ) = cos ( x+a ) cos ( b–a ) + sin ( x+a ) sin ( b–a ) .
После чего сделать замену z = x+a . В результате, тригонометрические функции будут зависеть только от переменной интегрирования z .
Когда тригонометрические функции зависят от одного аргумента, совпадающим с переменной интегрирования (допустим это z ), то есть подынтегральное выражение состоит только из функций типа sin z , cos z , tg z , ctg z , то нужно сделать подстановку
.
Такая подстановка приводит к интегрированию рациональных или иррациональных функций (если есть корни) и позволяет вычислить интеграл, если он интегрируется в элементарных функциях.
Однако, часто можно найти другие методы, которые позволяют вычислить интеграл более коротким способом, основываясь на специфике подынтегрального выражения. Ниже дано изложение основных таких методов.
Методика вычисленияопределённого интеграла
Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.
Площадь трапеции определяется как полусумма оснований, умноженная на высоту: Sтрап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.

Интегрирование выражений вида R(sinx, cosx)
Пример №1 . Вычислить интегралы:
Решение.
а) Интегрирование выражений вида R(sinx, cosx) , где R — рациональная функция от sin x и cos x , преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t .
Тогда имеем
Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫ R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:
- Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx , то применяется подстановка cos x = t .
- Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx , то подстановка sin x = t .
- Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx , то подстановка tgx = t или ctg x = t .
В данном случае для нахождения интеграла
применим универсальную тригонометрическую подстановку tg(x/2) = t .
Тогда
Так как дробь неправильная, то, выделяя целую часть, получим
Возвращась к исходной переменной будем иметь
b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫ R(sinx, cosx) dx имеет вид ∫ sin m x·cos n xdx . В этом частном случае, если m нечетно, следует применить подстановку cos x = t . Если нечетно n , следует применить подстановку sin x = t . Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В данном случае
Вычисление определенных интегралов методом трапеции в среде Microsoft Excel
Цель урока: Совершенствование умений и навыков по теме «Численное интегрирование», применяя возможности MS Excel по вычисление определенных интегралов методом трапеции. Отработать практическое освоение соответствующих умений и навыков.
Задачи урока:
- Образовательные – совершенствование умений студентов при вычисление определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработать умение применять теоретические знания в практических расчетах;
- Развивающие – познакомить студентов с применением компьютеров в качестве помощников при решении уравнений. Развивать у студентов математическую речь: создать ситуацию для применения основных понятий в речи; творческого мышления через создание условий для самореализации творческого потенциала обучающихся;
- Воспитательные – выработать у студентов умение рационально использовать время и возможности компьютерных технологий при решении задач. Воспитывать интерес к предмету через ситуацию успеха и взаимодоверия.
Тип урока: комбинированный урок.
Вид урока: практическое занятие, продолжительность – 2 часа.
Оборудование урока:
- Компьютеры с OS MS Windows;
- Программа Microsoft Excel;
- Презентация по теме, выполненная в программе PowerPoint;
- Карточки с заданиями для самостоятельной работы.
Структура урока:
1.Актуализация знаний:
1.1. Мобилизующее начало, постановка целей и задач на урок;
1.2.Фронтальный опрос с целью выявления основных этапов решения задач интегрирования и методики решения;
1.3. Постановка задачи с целью повторения алгоритма вычисления определенных интегралов методом трапеции;
1.4.Подведение итогов 1 этапа урока.
2.Применение знаний, формирование умений и навыков:
2.1.Беседа с целью формулировки задания для самостоятельной работы и инструктажа по ее организации;
2.2.Самостоятельная работа в группах по выполнению задания вычисления определенных интегралов методом трапеции в среде Microsoft Excel.
2.3.Подведение итога урока.
В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft PowerPoint.
ХОД УРОКА
1. Актуализация знаний
1.1. Мобилизующее начало, постановка целей и задач на урок.
На прошлых уроках мы с Вами изучили приближенное вычисление определенных интегралов, выделили методы их решения и решали данные интегралы ручным счетом. А на сегодняшнем занятии мы будем совершенствовать умения и навыки при вычислении определенных интегралов методом трапеции в среде Microsoft Excel.
— В чем заключается вычисление интеграла?
— Важным средством вычисления определенных интегралов является формула Ньютона-Лейбница 
— Общий подход к ее решению состоит в том, чтобы аппроксимировать функцию 

— Тогда для решения задачи строим 



— Введем на отрезке 





— Рассмотрим простой вариант построения функции 
— При этом функция 





— Формулы такого рода (


Точность формулы трапеций зависит от гладкости функции 









Теоретические оценки погрешностей не всегда применяются. Если требуется вычислить интеграл с погрешностью 





Поэтому, вычисляя интеграл с небольшим числом узлов 






— Объясните алгоритм вычисления интеграла различными методами?
2. Применение знаний, формирование умений и навыков
Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»
Состав задания:
- Ознакомиться с теоретической частью задания;
- Провести расчет для своего варианта индивидуального задания в Microsoft Excel
- Оформить презентацию в Ms PowerPoint, включающую:
— постановку задачи;
— алгоритм расчета;
— таблицу с расчетом из Ms Excel, график исходной функции;
— результат расчета и его анализ.
Индивидуальное расчетное задание:
- Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x 4 ) 1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка. - Представьте графически поставленную задачу.
Постановка задачи:
Найти: приближенное значение интеграла заданной функции по формуле трапеций, приняв предельное значение погрешности приближенного вычисления интеграла равным ε=0,02.
Содержание
- Интегрирование в MS EXCEL. Метод Симпсона
- Построение модели
- Ошибка интегрирования
- Настраиваемый интервал
- Лирическое отступление
- Вычисление интегралов в Excel
- Теория.
- Практика вычисления интегралов в Excel.
- Определение тепловой энергии.
- Общие выводы.
- Статьи с близкой тематикой
- Отзывы
Интегрирование в MS EXCEL. Метод Симпсона
history 27 ноября 2022 г.
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥 3 −5𝑥 2 +6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера ).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы = ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)) . В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
Настраиваемый интервал
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ() .
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
Источник
Вычисление интегралов в Excel

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
1. В столбец B вписываем время проведения измерения τi .
2. В столбец C заносим температуры нагретого воздуха t2i , измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i , поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
5. Зная удельную теплоемкость воздуха c =1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G =0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni = c * G * dti
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Q =Σ Qi =10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Q =Σ Qj =10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q =10,220 КВт*час (-1,684%)
По методу Симпсона: Q =10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Статьи с близкой тематикой
Отзывы
13 комментариев на «Вычисление интегралов в Excel»
- Александр Попов 11 Авг 2015 10:29
Хотя и не часто но приходится сталкиваться с анализом функциональных зависимостей. Благодарю Вас за напоминание что есть интегралы и ,конечно, за Ваше решение в EXCEL.
Всегда интересные темы находите. Читаю с удовольствием.
очень интересная и полезная статья!
действительно очень просто в Екселе сделать подобное действие!
Александр, спасибо за Вашу очередную полезную работу
Всем спасибо за отзывы.
Большое спасибо за столь простое интересное и общедоступное объяснение, мне приходится иметь дела с фармакокинетическими кривыми вернее площадью под кривой лекарственных средств AUCt-0 (Кривая зависимости — концентрация лекарственного вещества в крови в теченеие времени), Ваша статья станет просто настольной инструкцией для всех фармакологов.
Неожиданный и очень приятный комментарий, Бахтиёр.
Очередная полезная штучка, спасибо
А можете мне уточнить почему в примере, в формулах делитель 120, и 180? это связано с тем чтобы перейти в размерность часы? почему у вас складывается размерность и появляется она в делителе? если я буду считать в 0,0001 секунды, то делитель будет 3? по методу Симпсона? и размерность получиться кг.*с.? Спасибо, заранее
Интервалы между строками — 1 минута = 1/60 часа.
В методе трапеций мощности складываются, делятся на 2 и умножаются на 1 минуту, выраженную в часах. Получается энергия в КВт*час = площади трапеции.
Аналогично и по формуле Симпсона.
Я не знаю, что Вы считаете, Иван, но делитель в формуле Симпсона, конечно, равен 3.
Что такое кг*с? У Вас по оси Y — кг, а по оси X -с?
Если так, то просто считайте по формуле Симпсона (делитель — 3) и получите кг*с.
Спасибо Александр, теперь понятно)) с этим моментом
Большое спасибо за статью , очень понятно и интересно написано, очень пригодилась )) в качестве благодарности рекомендую пару бесплатных приёмов по привлечению 1000 читателей.
При большом количестве замеров (в приведённом примере 425) метод прямоугольников тоже должен давать высокую точность. При этом погрешность измерений, скорее всего, больше, чем погрешность метода.
Источник
Опубликовано 10 Авг 2015
Рубрика: Справочник Excel | 13 комментариев

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Например:
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f (x) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y=f (x). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
Заполним таблицу.
1. В столбец B вписываем время проведения измерения τi.
2. В столбец C заносим температуры нагретого воздуха t2i, измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i, поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
dti=t2i—t1i
5. Зная удельную теплоемкость воздуха c=1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G=0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni=c*G*dti
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Qi=(Ni+1+Ni)*(τi+1—τi)/2
Q=ΣQi=10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Qj=(Ni+4*Ni+1+Ni+2)*(τi+1—τi)/3
Q=ΣQj=10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q=10,220 КВт*час (-1,684%)
По методу Симпсона: Q=10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Другие статьи автора блога
На главную