Расчеты по кредитам с помощью excel

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

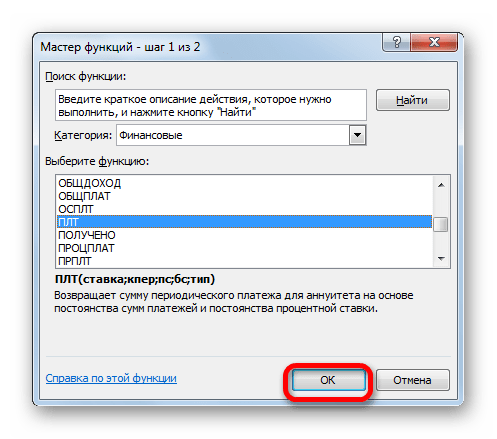
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

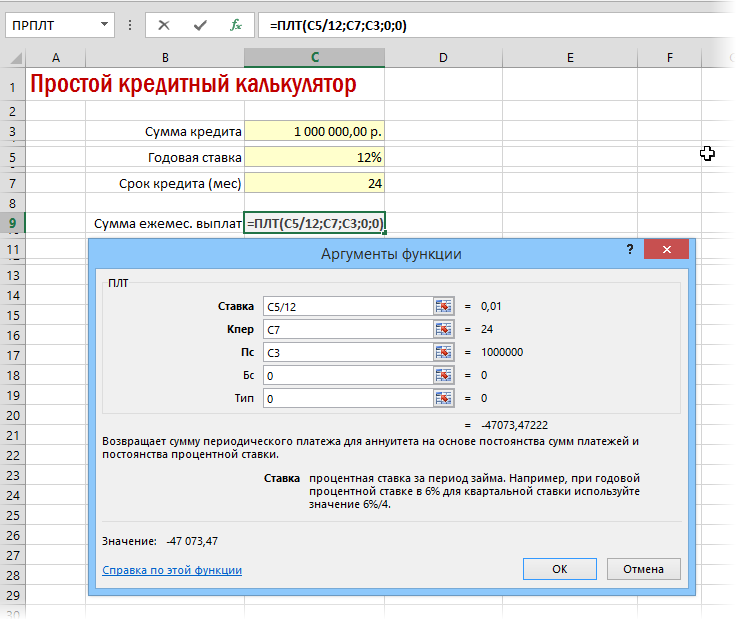
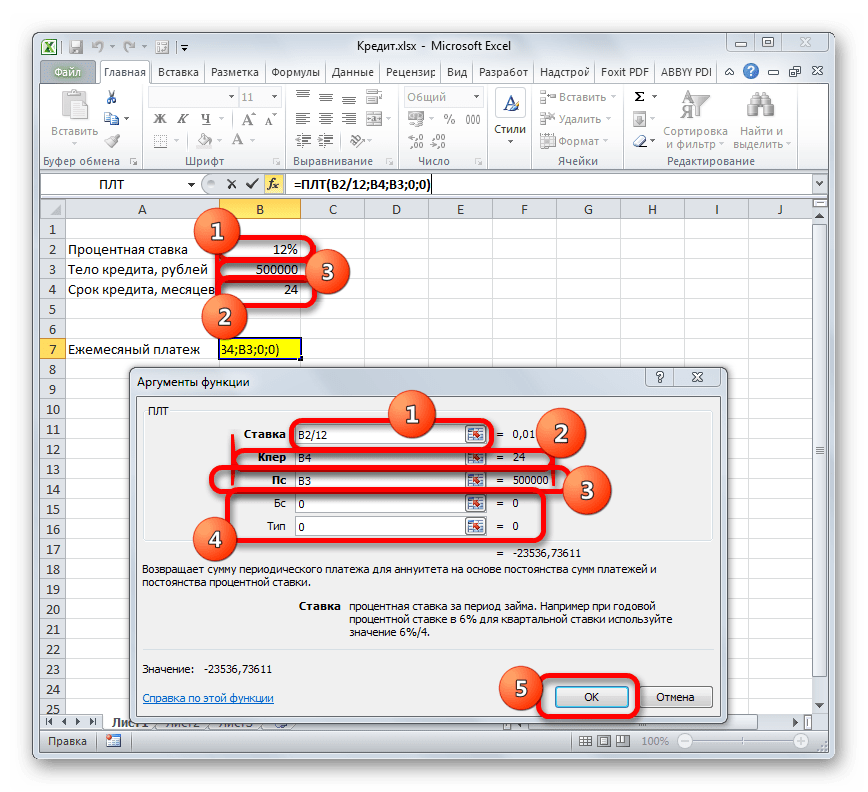
• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

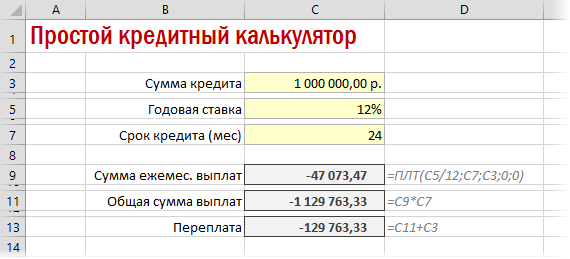
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

Вариант 2. Добавляем детализацию

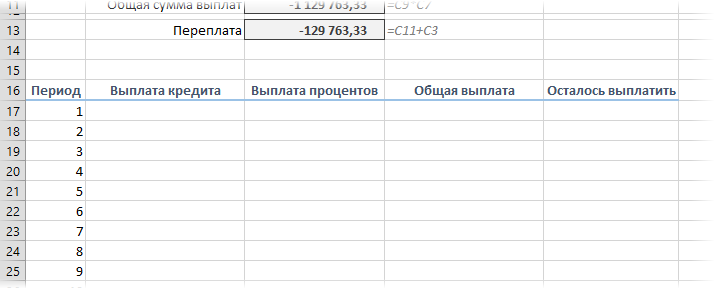
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

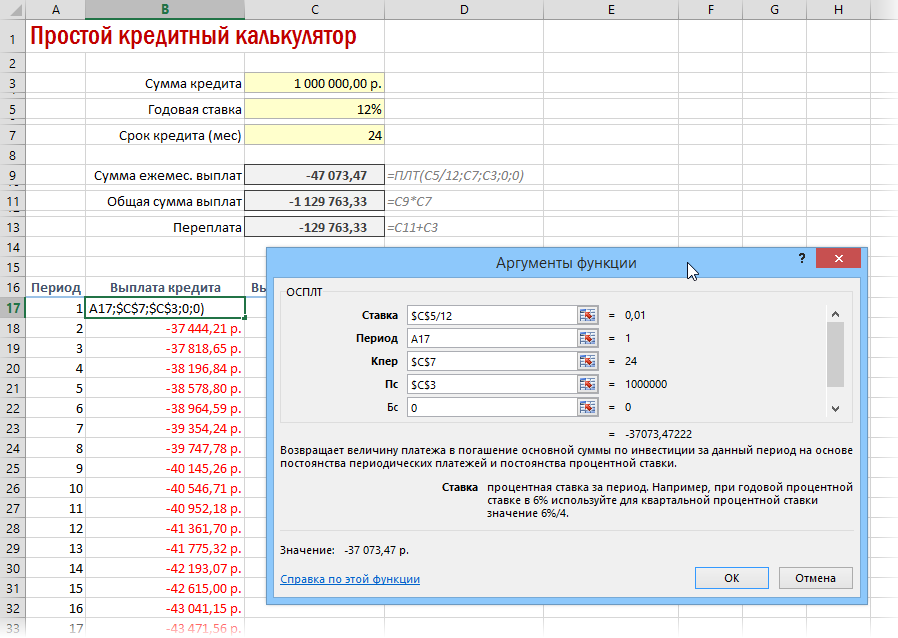
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

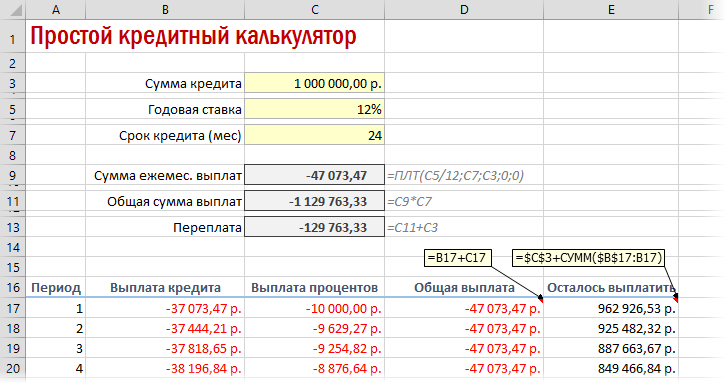
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

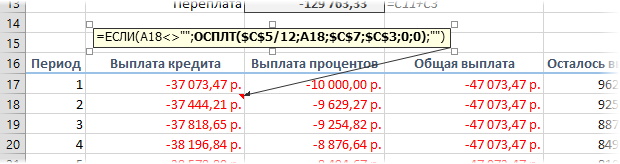
Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

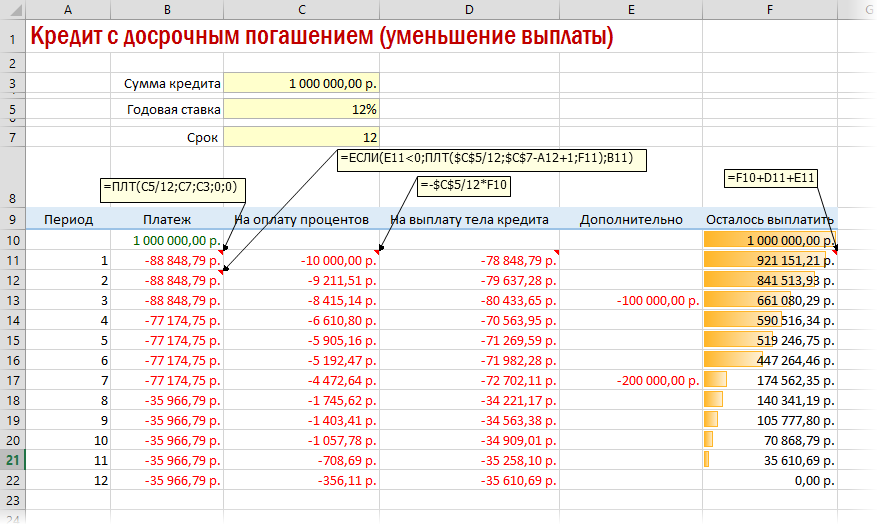
Вариант 3. Досрочное погашение с уменьшением срока или выплаты

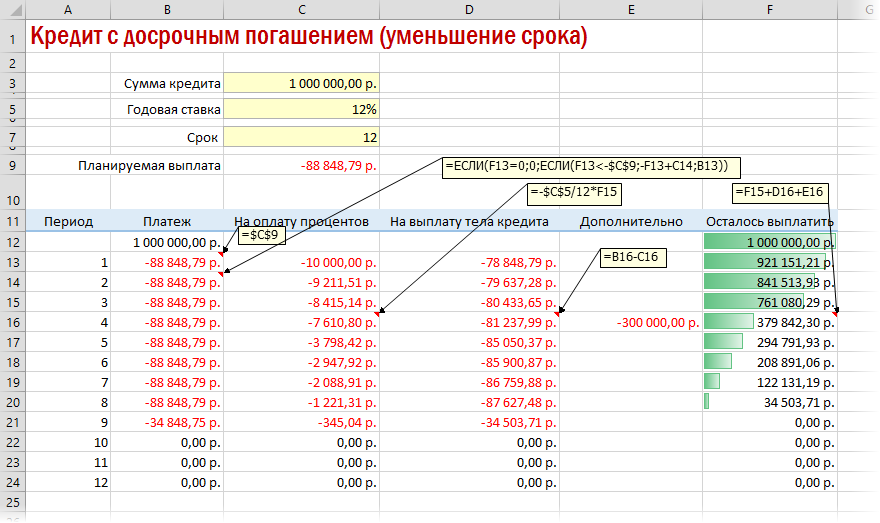
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

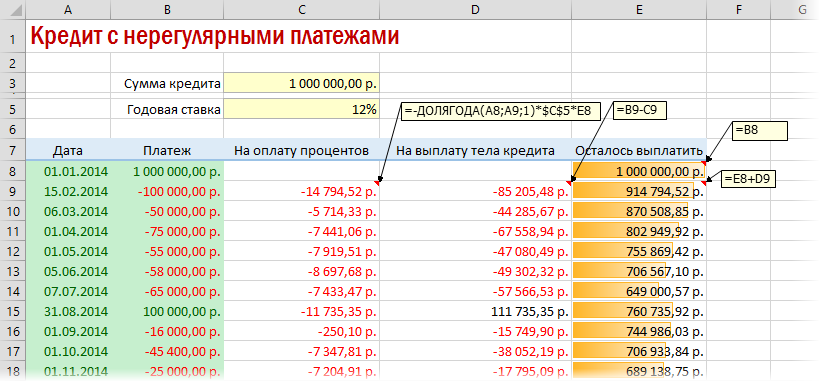
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

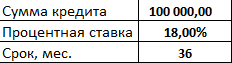
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.



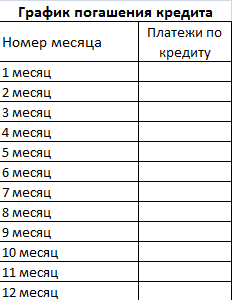
2. Составим график погашения кредита. Пока пустой.



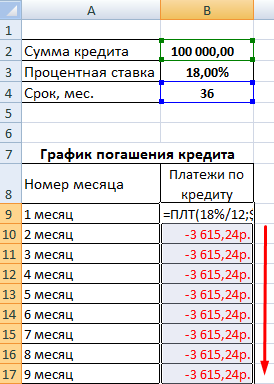
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.



Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

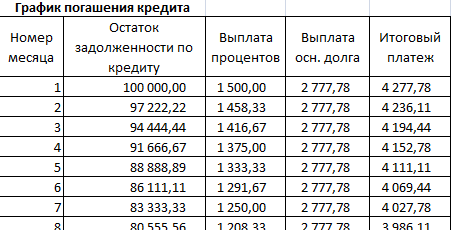
Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

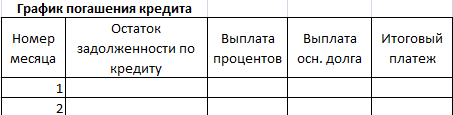
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

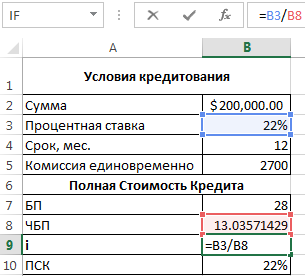
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

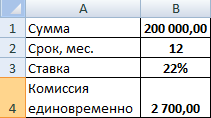
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:

• ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.

• КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.

• ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.

• БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.

Расчет ежемесячных платежей для погашения задолженности по кредитной карте

Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.

С помощью функции ПЛТ(ставка;КПЕР;ПС)

=ПЛТ(17%/12;2*12;5400)

получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.

• Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.

• Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.

• Аргумент ПС или приведенной стоимости составляет 5400 долларов США.

Расчет ежемесячных платежей по ипотеке

Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.

С помощью функции ПЛТ(ставка;КПЕР;ПС)

=ПЛТ(5%/12;30*12;180000)

получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.

• Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.

• Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.

• Аргумент ПС составляет 180 000 (нынешняя величина кредита).

Расчет суммы ежемесячных сбережений, необходимой для отпуска

Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.

С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)

=ПЛТ(1,5%/12;3*12;0;8500)

получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.

• Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.

• Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.

• Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.

• Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.

Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.

С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)

=ПС(1,5%/12;3*12;-175;8500)

мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.

• Аргумент «Ставка» составляет 1,5%/12.

• Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).

• Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).

• Аргумент БС (будущая стоимость) составляет 8500.

Расчет срока погашения потребительского кредита

Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.

С помощью функции КПЕР(ставка;ПЛТ;ПС)

=КПЕР(3%/12;-150;2500)

выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.

• Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.

• Аргумент ПЛТ составляет -150.

• Аргумент ПС (приведенная стоимость) составляет 2500.

Расчет суммы первого взноса

Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.

С помощью функции ПС(ставка;КПЕР;ПЛТ)

= 19000-ПС(2,9%/12; 3*12;-350)

выясняем, что первый взнос должен составлять 6946,48 долларов США.

• Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.

• Аргумент «Ставка» составляет 2,9%, разделенных на 12.

• Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).

• Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).

Оценка динамики увеличения сбережений

Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?

С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)

=БС(1,5%/12;10;-200;-500)

получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.

• Аргумент «Ставка» составляет 1,5%/12.

• Аргумент КПЕР составляет 10 (месяцев).

• Аргумент ПЛТ составляет -200.

• Аргумент ПС (приведенная стоимость) составляет -500.

См. также

ПЛТ

КПЕР

ПС

БС

Прежде, чем брать заем, неплохо было бы рассчитать все платежи по нему. Это убережет заёмщика в будущем от различных неожиданных неприятностей и разочарований, когда выяснится, что переплата слишком большая. Помочь в данном расчете могут инструменты программы Excel. Давайте выясним, как рассчитать аннуитетные платежи по кредиту в этой программе.

Расчет оплаты

Прежде всего, нужно сказать, что существует два вида кредитных платежей:

• Дифференцированные;
• Аннуитетные.

При дифференцированной схеме клиент вносит в банк ежемесячно равную долю выплат по телу кредита плюс платежи по процентам. Величина процентных выплат каждый месяц уменьшается, так как уменьшается тело займа, с которого они рассчитываются. Таким образом и общий ежемесячный платеж тоже уменьшается.

При аннуитетной схеме используется несколько другой подход. Клиент ежемесячно вносит одинаковую сумму общего платежа, который состоит из выплат по телу кредита и оплаты процентов. Изначально процентные взносы насчитываются на всю сумму займа, но по мере того, как тело уменьшается, сокращается и начисление процентов. Но общая сумма оплаты остается неизменной за счет ежемесячного увеличения величины выплат по телу кредита. Таким образом, с течением времени удельный вес процентов в общем ежемесячном платеже падает, а удельный вес оплаты по телу растет. При этом сам общий ежемесячный платеж на протяжении всего срока кредитования не меняется.

Как раз на расчете аннуитетного платежа мы и остановимся. Тем более, это актуально, так как в настоящее время большинство банков используют именно эту схему. Она удобна и для клиентов, ведь в этом случае общая сумма оплаты не меняется, оставаясь фиксированной. Клиенты всегда знают сколько нужно заплатить.

Этап 1: расчет ежемесячного взноса

Для расчета ежемесячного взноса при использовании аннуитетной схемы в Экселе существует специальная функция – ПЛТ. Она относится к категории финансовых операторов. Формула этой функции выглядит следующим образом:

=ПЛТ(ставка;кпер;пс;бс;тип)

Как видим, указанная функция обладает довольно большим количеством аргументов. Правда, последние два из них не являются обязательными.

Аргумент «Ставка» указывает на процентную ставку за конкретный период. Если, например, используется годовая ставка, но платеж по займу производится ежемесячно, то годовую ставку нужно разделить на 12 и полученный результат использовать в качестве аргумента. Если применяется ежеквартальный вид оплаты, то в этом случае годовую ставку нужно разделить на 4 и т.д.

«Кпер» обозначает общее количество периодов выплат по кредиту. То есть, если заём берется на один год с ежемесячной оплатой, то число периодов считается 12, если на два года, то число периодов – 24. Если кредит берется на два года с ежеквартальной оплатой, то число периодов равно 8.

«Пс» указывает приведенную стоимость на настоящий момент. Говоря простыми словами, это общая величина займа на начало кредитования, то есть, та сумма, которую вы берете взаймы, без учета процентов и других дополнительных выплат.

«Бс» — это будущая стоимость. Эта величина, которую будет составлять тело займа на момент завершения кредитного договора. В большинстве случаев данный аргумент равен «0», так как заемщик на конец срока кредитования должен полностью рассчитаться с кредитором. Указанный аргумент не является обязательным. Поэтому, если он опускается, то считается равным нулю.

Аргумент «Тип» определяет время расчета: в конце или в начале периода. В первом случае он принимает значение «0», а во втором – «1». Большинство банковских учреждений используют именно вариант с оплатой в конце периода. Этот аргумент тоже является необязательным, и если его опустить считается, что он равен нулю.

Теперь настало время перейти к конкретному примеру расчета ежемесячного взноса при помощи функции ПЛТ. Для расчета используем таблицу с исходными данными, где указана процентная ставка по кредиту (12%), величина займа (500000 рублей) и срок кредита (24 месяца). При этом оплата производится ежемесячно в конце каждого периода.

1. Выделяем элемент на листе, в который будет выводиться результат расчета, и щелкаем по пиктограмме «Вставить функцию», размещенную около строки формул.



2. Производится запуск окошка Мастера функций. В категории «Финансовые» выделяем наименование «ПЛТ» и жмем на кнопку «OK».



3. После этого открывается окно аргументов оператора ПЛТ.

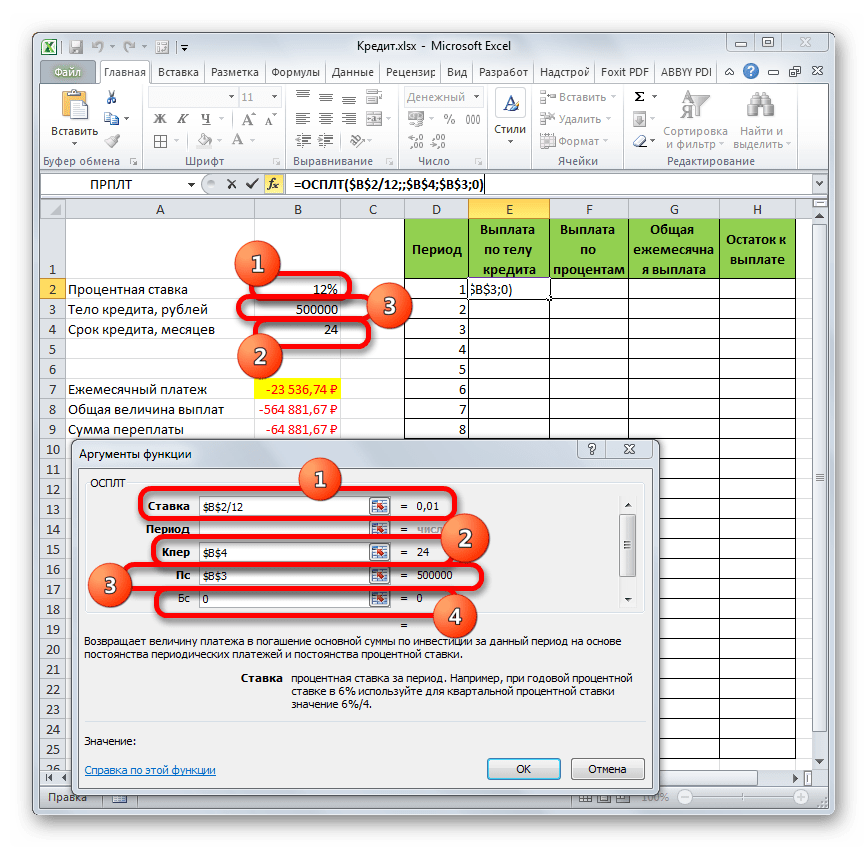
   В поле «Ставка» следует вписать величину процентов за период. Это можно сделать вручную, просто поставив процент, но у нас он указан в отдельной ячейке на листе, поэтому дадим на неё ссылку. Устанавливаем курсор в поле, а затем кликаем по соответствующей ячейке. Но, как мы помним, у нас в таблице задана годовая процентная ставка, а период оплаты равен месяцу. Поэтому делим годовую ставку, а вернее ссылку на ячейку, в которой она содержится, на число 12, соответствующее количеству месяцев в году. Деление выполняем прямо в поле окна аргументов.

   В поле «Кпер» устанавливается срок кредитования. Он у нас равен 24 месяцам. Можно занести в поле число 24 вручную, но мы, как и в предыдущем случае, указываем ссылку на месторасположение данного показателя в исходной таблице.

   В поле «Пс» указывается первоначальная величина займа. Она равна 500000 рублей. Как и в предыдущих случаях, указываем ссылку на элемент листа, в котором содержится данный показатель.

   В поле «Бс» указывается величина займа, после полной его оплаты. Как помним, это значение практически всегда равно нулю. Устанавливаем в данном поле число «0». Хотя этот аргумент можно вообще опустить.

   В поле «Тип» указываем в начале или в конце месяца производится оплата. У нас, как и в большинстве случаев, она производится в конце месяца. Поэтому устанавливаем число «0». Как и в случае с предыдущим аргументом, в данное поле можно ничего не вводить, тогда программа по умолчанию будет считать, что в нем расположено значение равное нулю.

   После того, как все данные введены, жмем на кнопку «OK».



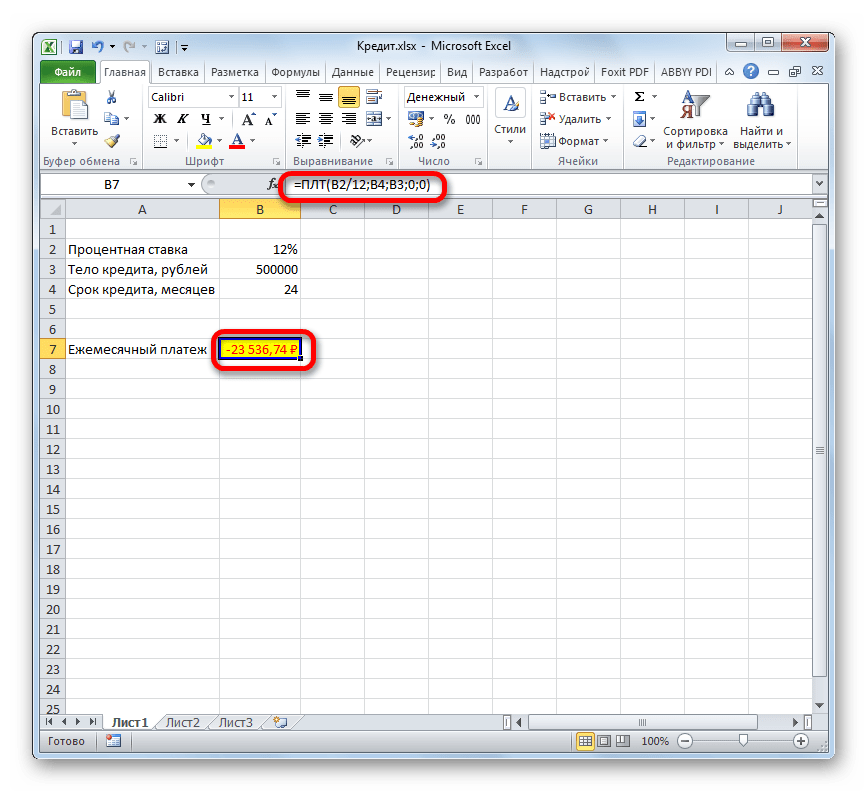
4. После этого в ячейку, которую мы выделили в первом пункте данного руководства, выводится результат вычисления. Как видим, величина ежемесячного общего платежа по займу составляет 23536,74 рубля. Пусть вас не смущает знак «-» перед данной суммой. Так Эксель указывает на то, что это расход денежных средств, то есть, убыток.



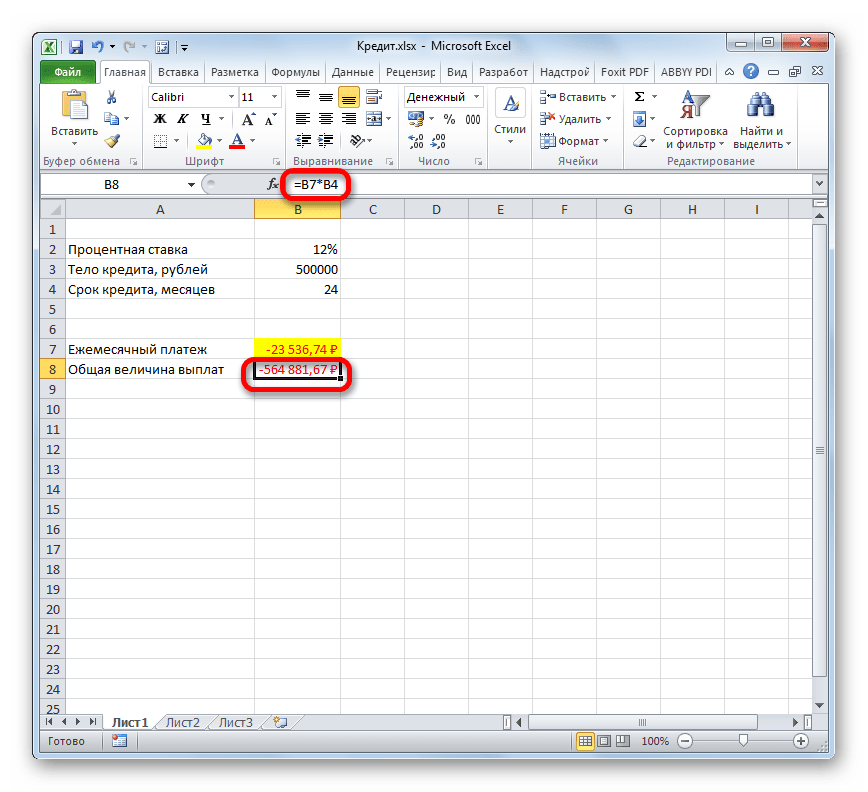
5. Для того, чтобы рассчитать общую сумму оплаты за весь срок кредитования с учетом погашения тела займа и ежемесячных процентов, достаточно перемножить величину ежемесячного платежа (23536,74 рубля) на количество месяцев (24 месяца). Как видим, общая сумма платежей за весь срок кредитования в нашем случае составила 564881,67 рубля.



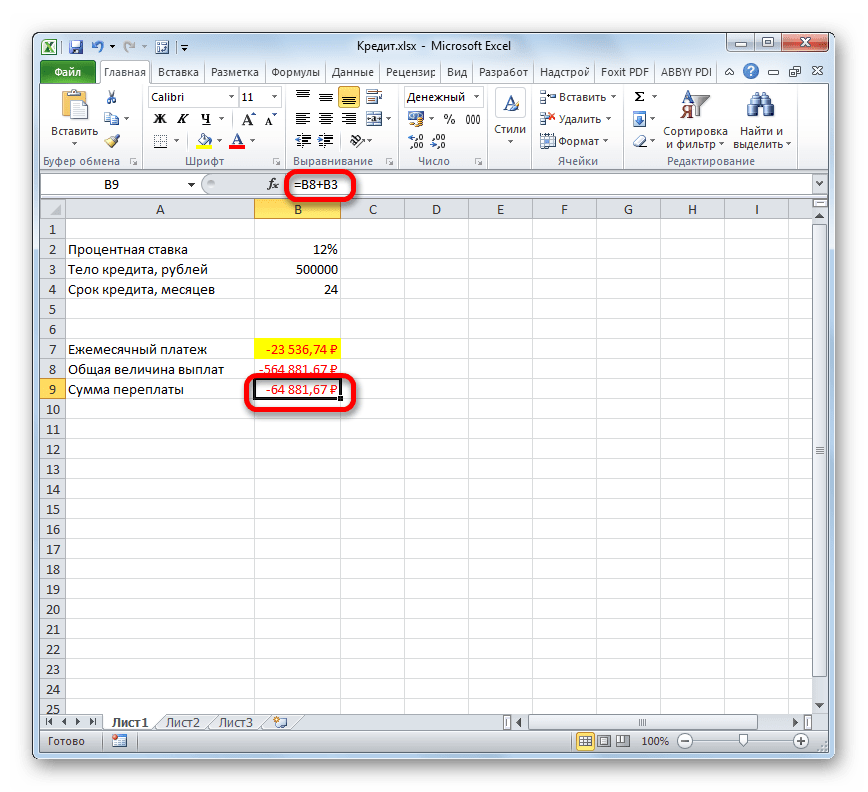
6. Теперь можно подсчитать сумму переплаты по кредиту. Для этого нужно отнять от общей величины выплат по кредиту, включая проценты и тело займа, начальную сумму, взятую в долг. Но мы помним, что первое из этих значений уже со знаком «-». Поэтому в конкретно нашем случае получается, что их нужно сложить. Как видим, общая сумма переплаты по кредиту за весь срок составила 64881,67 рубля.

Урок: Мастер функций в Эксель

Этап 2: детализация платежей

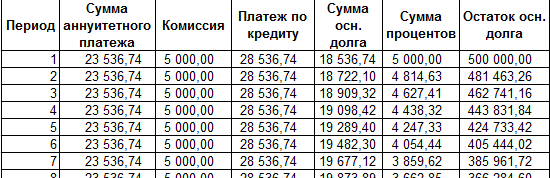
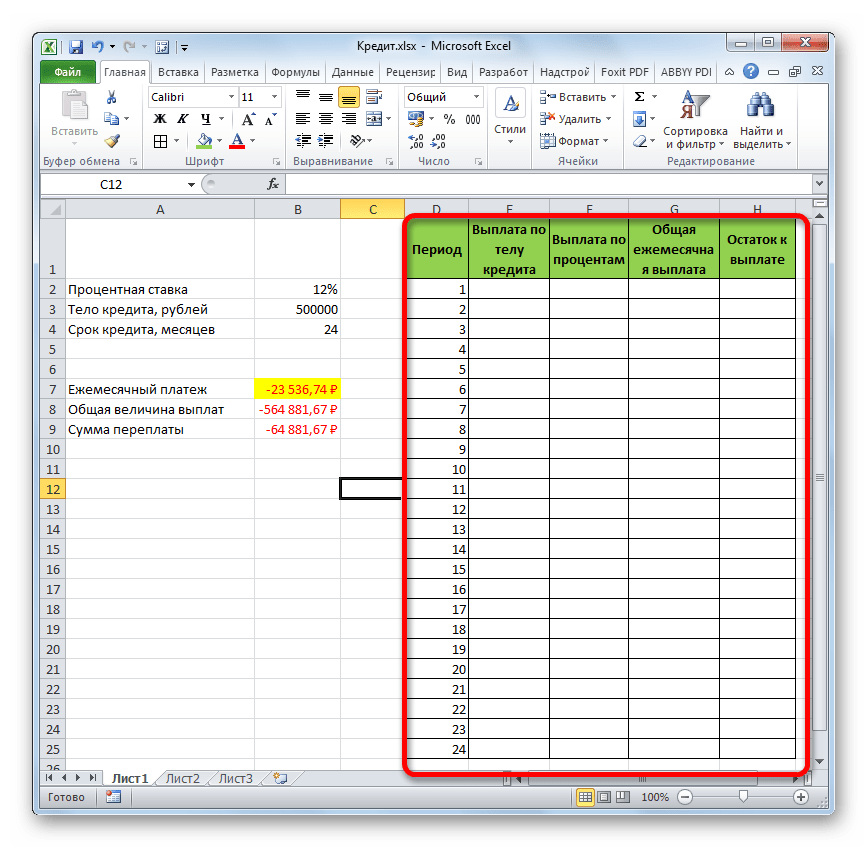
А теперь с помощью других операторов Эксель сделаем помесячную детализацию выплат, чтобы видеть, сколько в конкретном месяце мы платим по телу займа, а сколько составляет величина процентов. Для этих целей чертим в Экселе таблицу, которую будем заполнять данными. Строки этой таблицы будут отвечать соответствующему периоду, то есть, месяцу. Учитывая, что период кредитования у нас составляет 24 месяца, то и количество строк тоже будет соответствующим. В столбцах указана выплата тела займа, выплата процентов, общий ежемесячный платеж, который является суммой предыдущих двух колонок, а также оставшаяся сумма к выплате.

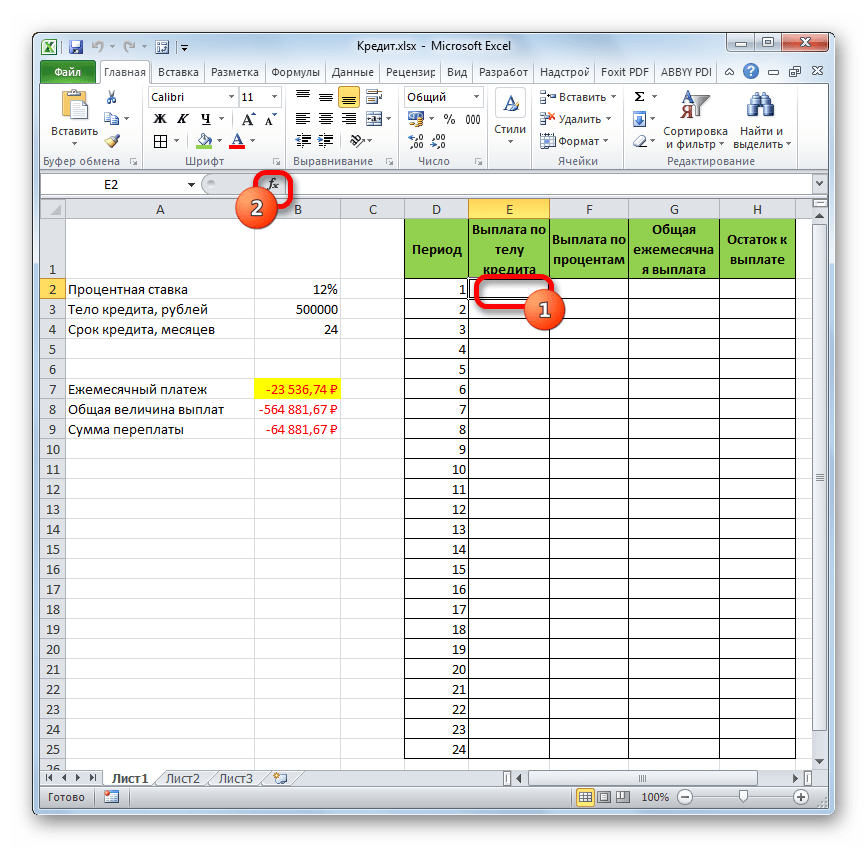
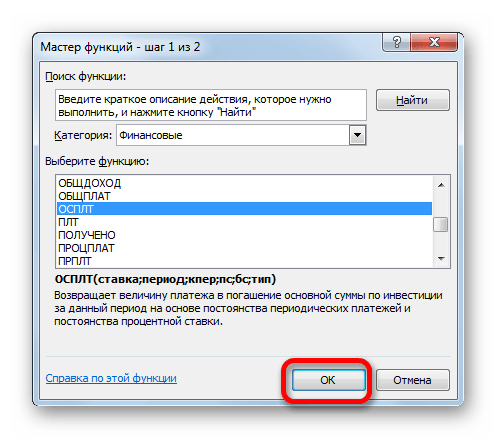
1. Для определения величины оплаты по телу займа используем функцию ОСПЛТ, которая как раз предназначена для этих целей. Устанавливаем курсор в ячейку, которая находится в строке «1» и в столбце «Выплата по телу кредита». Жмем на кнопку «Вставить функцию».



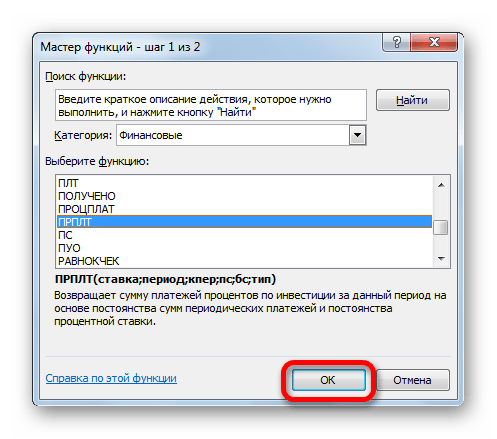
2. Переходим в Мастер функций. В категории «Финансовые» отмечаем наименование «ОСПЛТ» и жмем кнопку «OK».



3. Запускается окно аргументов оператора ОСПЛТ. Он имеет следующий синтаксис:

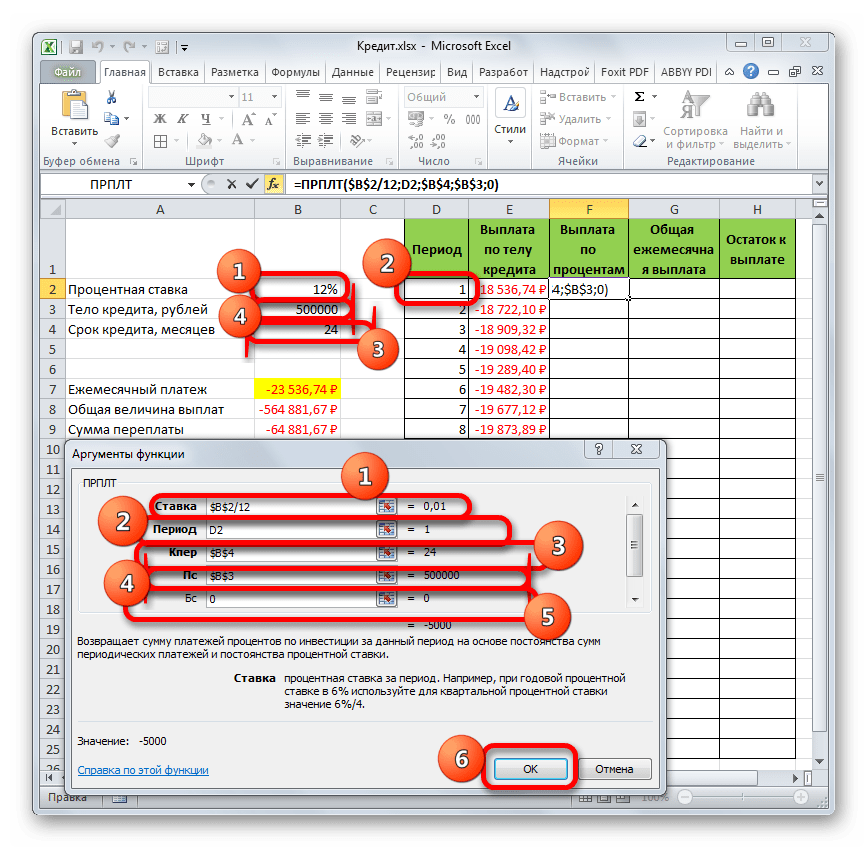
   =ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)

   Как видим, аргументы данной функции почти полностью совпадают с аргументами оператора ПЛТ, только вместо необязательного аргумента «Тип» добавлен обязательный аргумент «Период». Он указывает на номер периода выплаты, а в нашем конкретном случае на номер месяца.

   Заполняем уже знакомые нам поля окна аргументов функции ОСПЛТ теми самыми данными, что были использованы для функции ПЛТ. Только учитывая тот факт, что в будущем будет применяться копирование формулы посредством маркера заполнения, нужно сделать все ссылки в полях абсолютными, чтобы они не менялись. Для этого требуется поставить знак доллара перед каждым значением координат по вертикали и горизонтали. Но легче это сделать, просто выделив координаты и нажав на функциональную клавишу F4. Знак доллара будет расставлен в нужных местах автоматически. Также не забываем, что годовую ставку нужно разделить на 12.



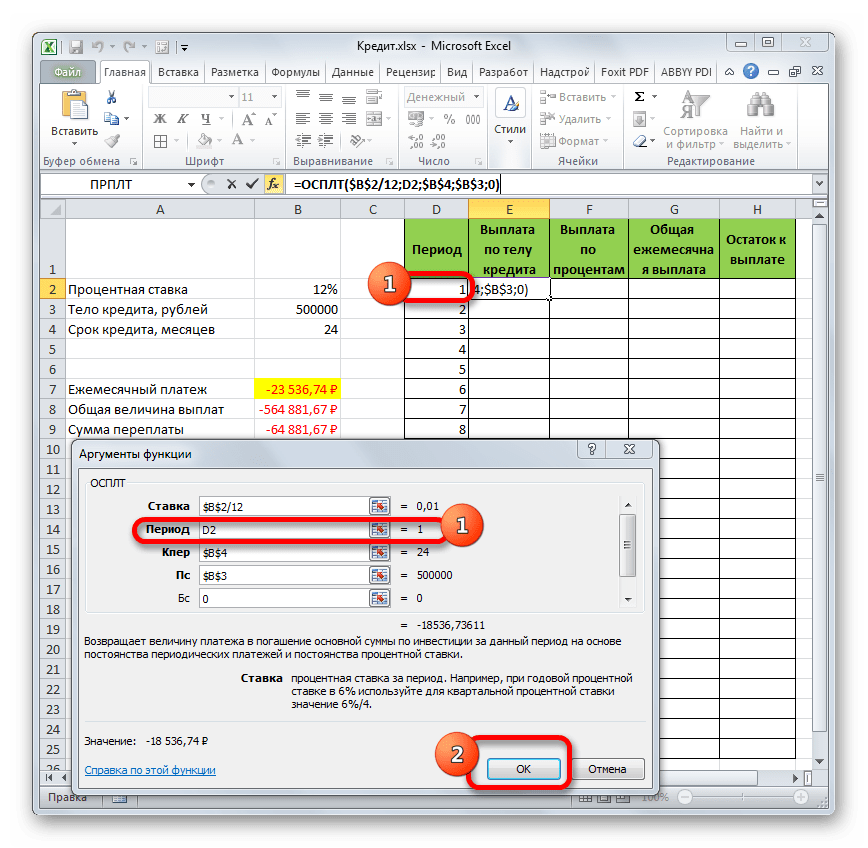
4. Но у нас остается ещё один новый аргумент, которого не было у функции ПЛТ. Этот аргумент «Период». В соответствующее поле устанавливаем ссылку на первую ячейку столбца «Период». Данный элемент листа содержит в себе число «1», которое обозначает номер первого месяца кредитования. Но в отличие от предыдущих полей, в указанном поле мы оставляем ссылку относительной, а не делаем из неё абсолютную.

   После того, как все данные, о которых мы говорили выше, введены, жмем на кнопку «OK».



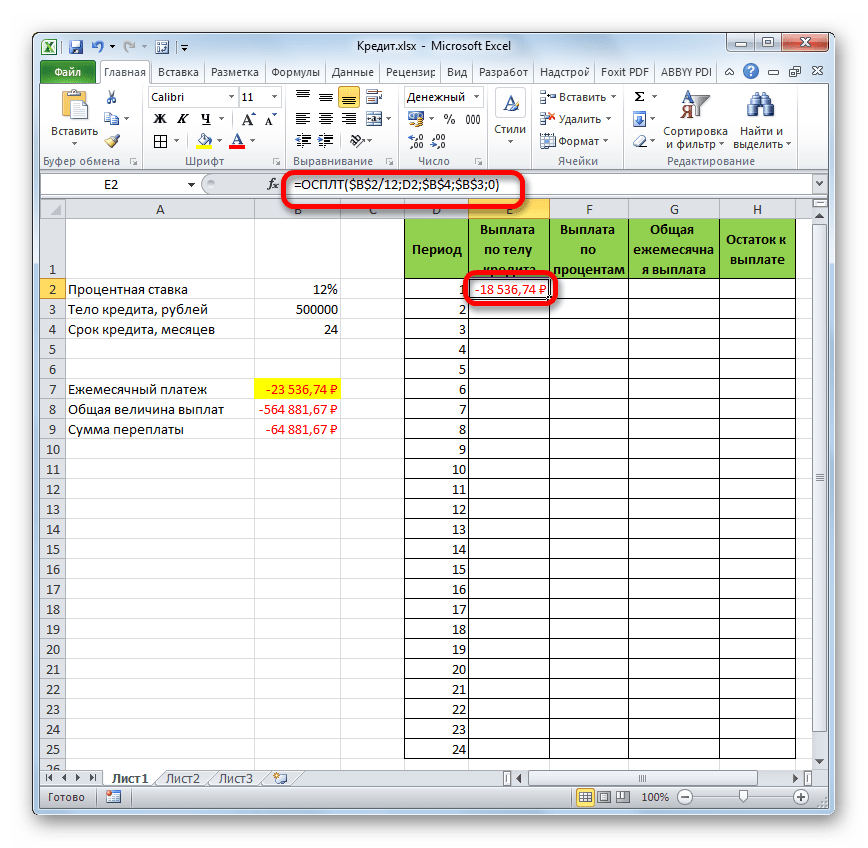
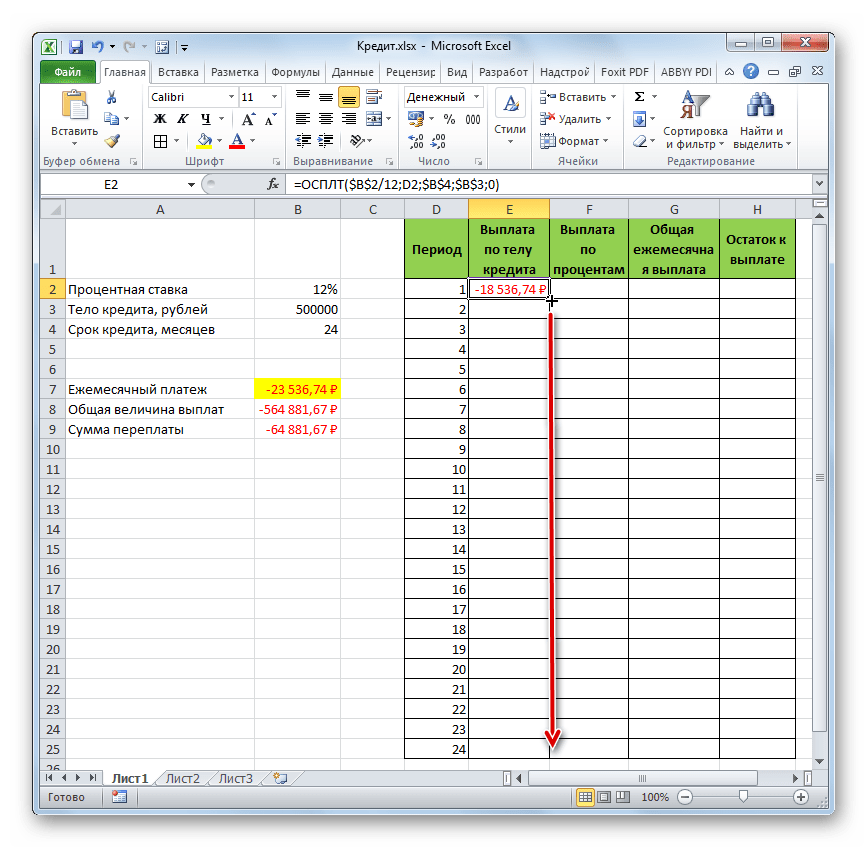
5. После этого в ячейке, которую мы ранее выделили, отобразится величина выплаты по телу займа за первый месяц. Она составит 18536,74 рубля.



6. Затем, как уже говорилось выше, нам следует скопировать данную формулу на остальные ячейки столбца с помощью маркера заполнения. Для этого устанавливаем курсор в нижний правый угол ячейки, в которой содержится формула. Курсор преобразуется при этом в крестик, который называется маркером заполнения. Зажимаем левую кнопку мыши и тянем его вниз до конца таблицы.



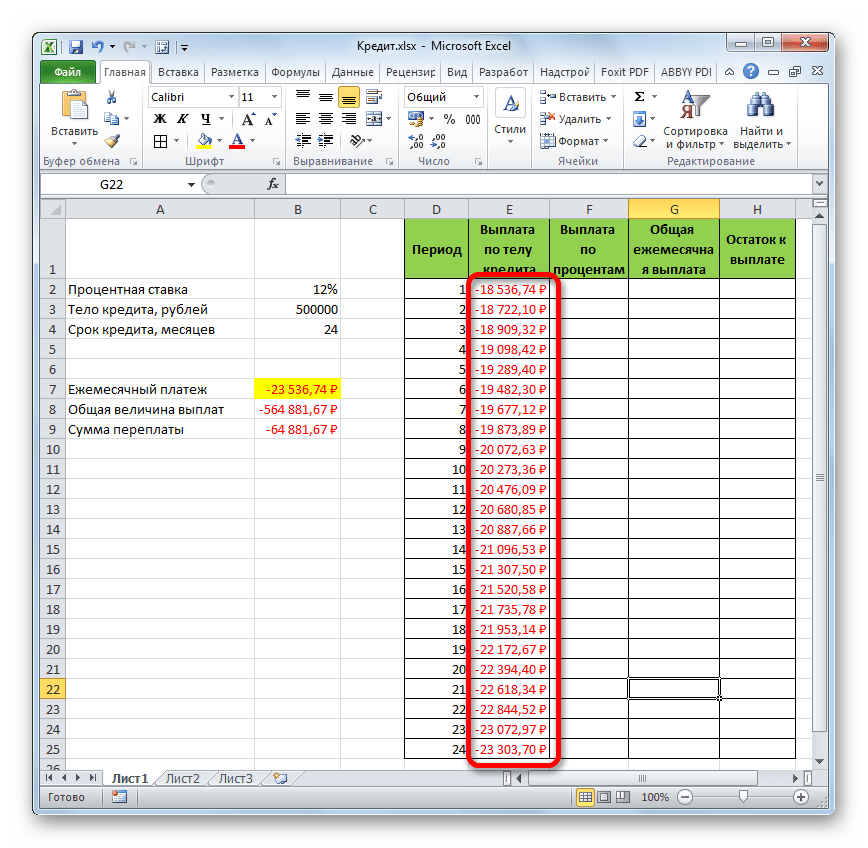
7. В итоге все ячейки столбца заполнены. Теперь мы имеем график выплаты тела займа помесячно. Как и говорилось уже выше, величина оплаты по данной статье с каждым новым периодом увеличивается.



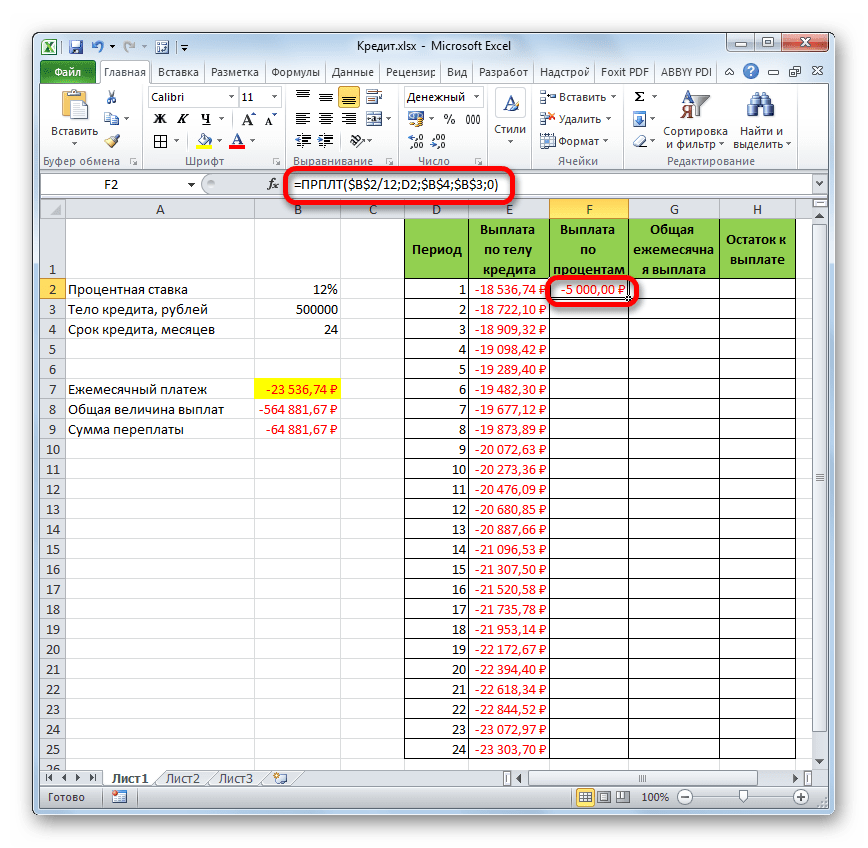
8. Теперь нам нужно сделать месячный расчет оплаты по процентам. Для этих целей будем использовать оператор ПРПЛТ. Выделяем первую пустую ячейку в столбце «Выплата по процентам». Жмем на кнопку «Вставить функцию».



9. В запустившемся окне Мастера функций в категории «Финансовые» производим выделение наименования ПРПЛТ. Выполняем щелчок по кнопке «OK».



10. Происходит запуск окна аргументов функции ПРПЛТ. Её синтаксис выглядит следующим образом:

    =ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)

    Как видим, аргументы данной функции абсолютно идентичны аналогичным элементам оператора ОСПЛТ. Поэтому просто заносим в окно те же данные, которые мы вводили в предыдущем окне аргументов. Не забываем при этом, что ссылка в поле «Период» должна быть относительной, а во всех других полях координаты нужно привести к абсолютному виду. После этого щелкаем по кнопке «OK».



11. Затем результат расчета суммы оплаты по процентам за кредит за первый месяц выводится в соответствующую ячейку.



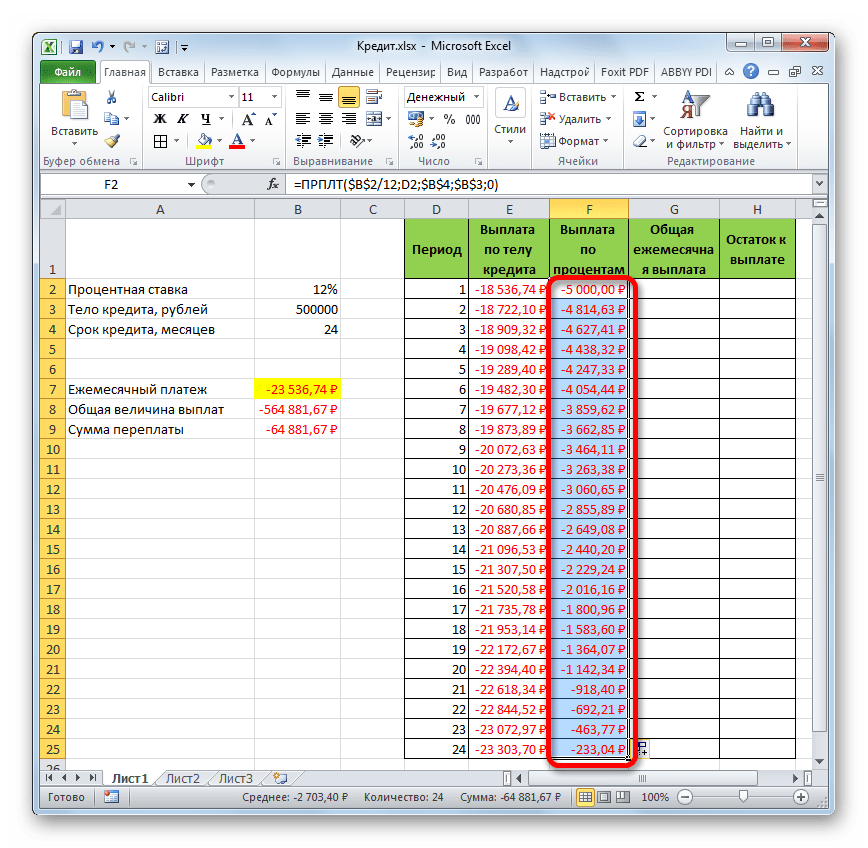
12. Применив маркер заполнения, производим копирование формулы в остальные элементы столбца, таким способом получив помесячный график оплат по процентам за заём. Как видим, как и было сказано ранее, из месяца в месяц величина данного вида платежа уменьшается.



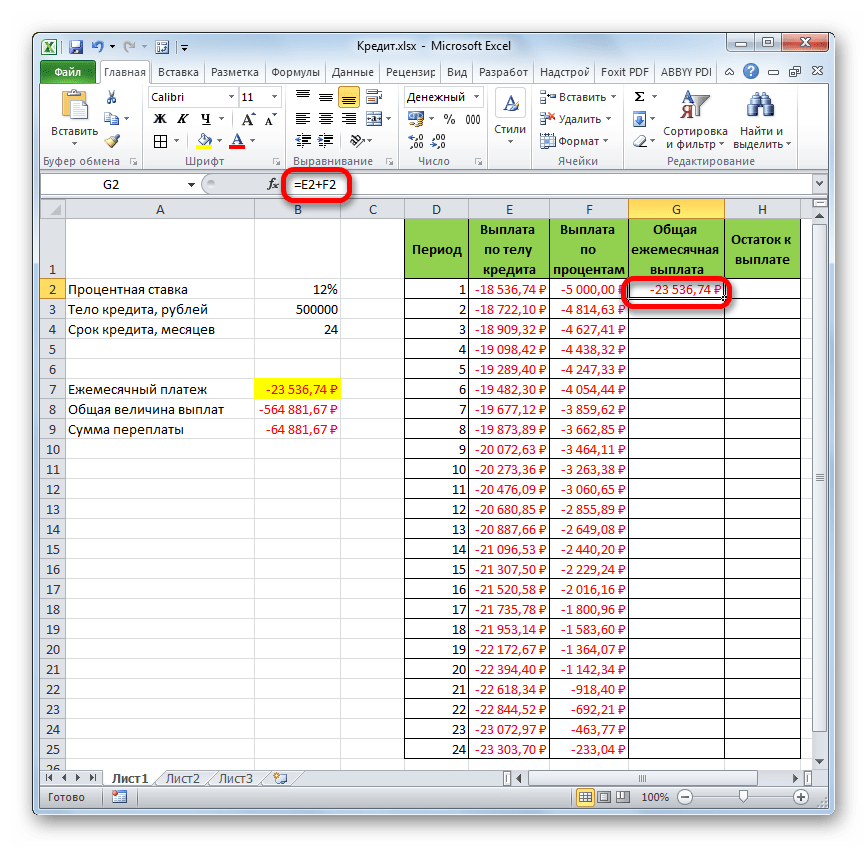
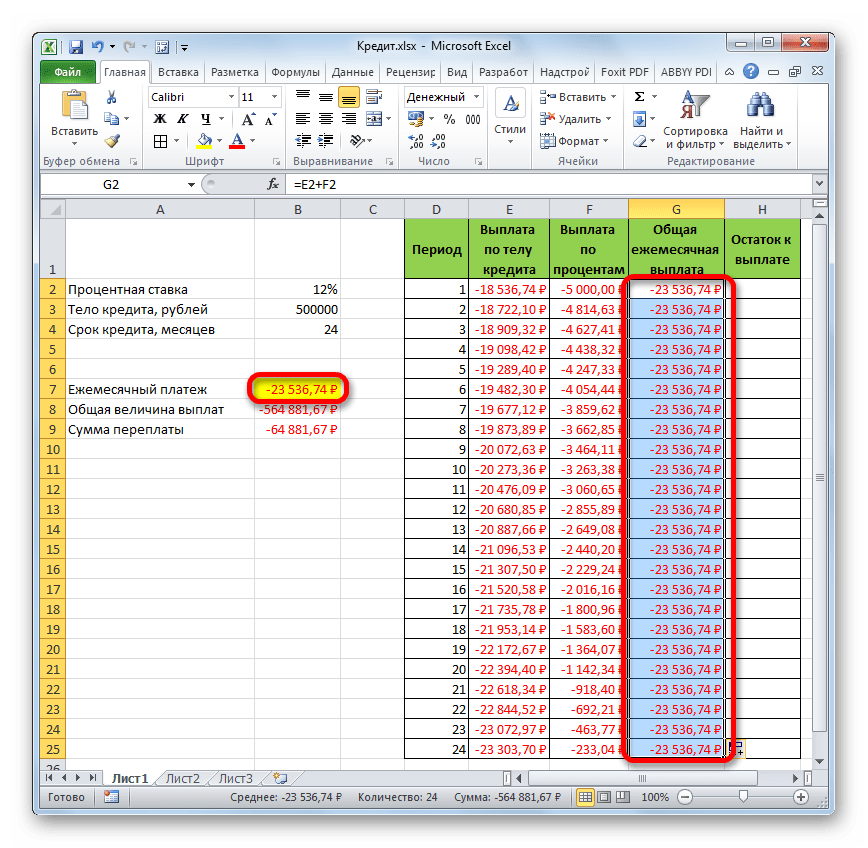
13. Теперь нам предстоит рассчитать общий ежемесячный платеж. Для этого вычисления не следует прибегать к какому-либо оператору, так как можно воспользоваться простой арифметической формулой. Складываем содержимое ячеек первого месяца столбцов «Выплата по телу кредита» и «Выплата по процентам». Для этого устанавливаем знак «=» в первую пустую ячейку столбца «Общая ежемесячная выплата». Затем кликаем по двум вышеуказанным элементам, установив между ними знак «+». Жмем на клавишу Enter.



14. Далее с помощью маркера заполнения, как и в предыдущих случаях, заполняем колонку данными. Как видим, на протяжении всего действия договора сумма общего ежемесячного платежа, включающего платеж по телу займа и оплату процентов, составит 23536,74 рубля. Собственно этот показатель мы уже рассчитывали ранее при помощи ПЛТ. Но в данном случае это представлено более наглядно, именно как сумма оплаты по телу займа и процентам.



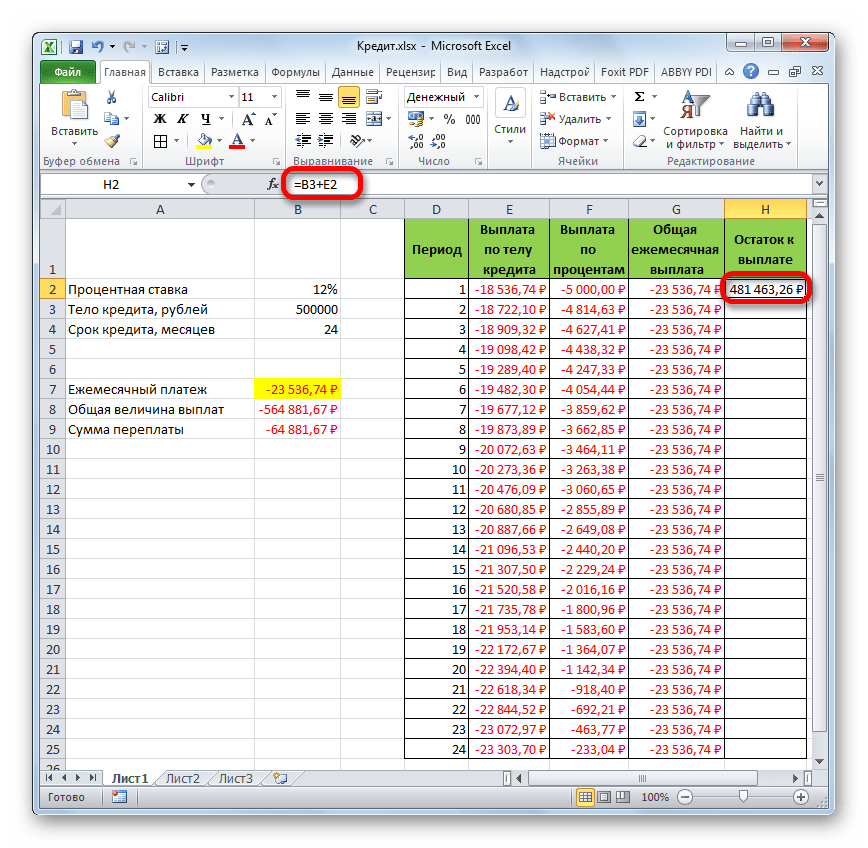
15. Теперь нужно добавить данные в столбец, где будет ежемесячно отображаться остаток суммы по кредиту, который ещё требуется заплатить. В первой ячейке столбца «Остаток к выплате» расчет будет самый простой. Нам нужно отнять от первоначальной величины займа, которая указана в таблице с первичными данными, платеж по телу кредита за первый месяц в расчетной таблице. Но, учитывая тот факт, что одно из чисел у нас уже идет со знаком «-», то их следует не отнять, а сложить. Делаем это и жмем на кнопку Enter.



16. А вот вычисление остатка к выплате после второго и последующих месяцев будет несколько сложнее. Для этого нам нужно отнять от тела кредита на начало кредитования общую сумму платежей по телу займа за предыдущий период. Устанавливаем знак «=» во второй ячейке столбца «Остаток к выплате». Далее указываем ссылку на ячейку, в которой содержится первоначальная сумма кредита. Делаем её абсолютной, выделив и нажав на клавишу F4. Затем ставим знак «+», так как второе значение у нас и так будет отрицательным. После этого кликаем по кнопке «Вставить функцию».



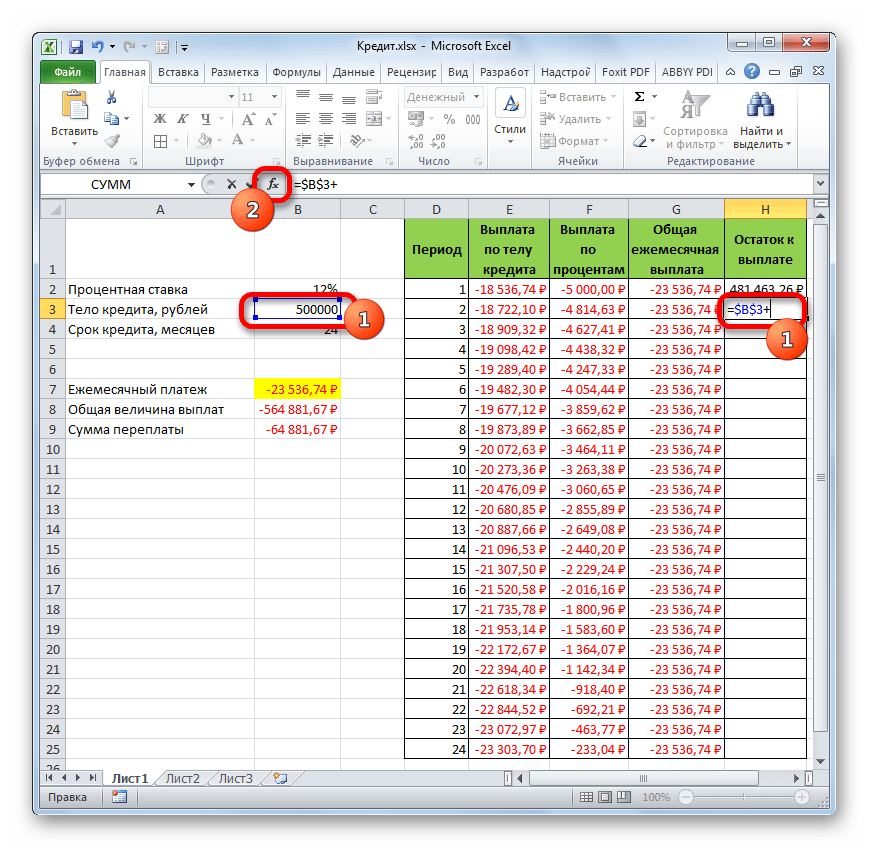
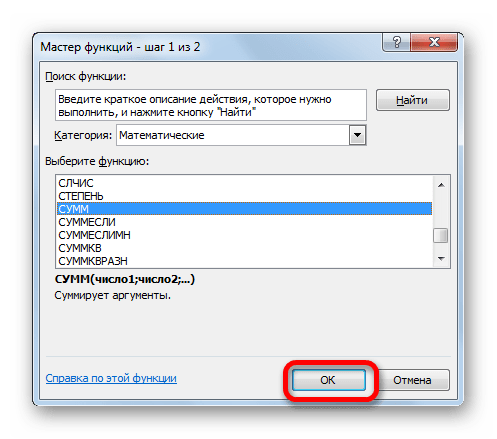
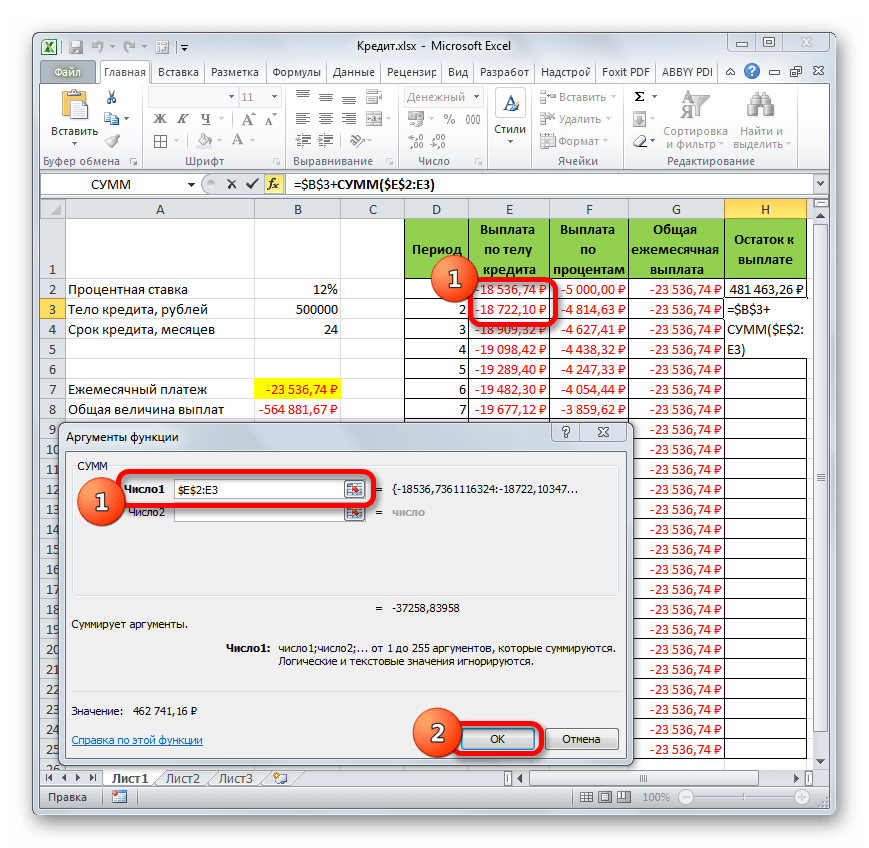
17. Запускается Мастер функций, в котором нужно переместиться в категорию «Математические». Там выделяем надпись «СУММ» и жмем на кнопку «OK».



18. Запускается окно аргументов функции СУММ. Указанный оператор служит для того, чтобы суммировать данные в ячейках, что нам и нужно выполнить в столбце «Выплата по телу кредита». Он имеет следующий синтаксис:

    =СУММ(число1;число2;…)

    В качестве аргументов выступают ссылки на ячейки, в которых содержатся числа. Мы устанавливаем курсор в поле «Число1». Затем зажимаем левую кнопку мыши и выделяем на листе первые две ячейки столбца «Выплата по телу кредита». В поле, как видим, отобразилась ссылка на диапазон. Она состоит из двух частей, разделенных двоеточием: ссылки на первую ячейку диапазона и на последнюю. Для того, чтобы в будущем иметь возможность скопировать указанную формулу посредством маркера заполнения, делаем первую часть ссылки на диапазон абсолютной. Выделяем её и жмем на функциональную клавишу F4. Вторую часть ссылки так и оставляем относительной. Теперь при использовании маркера заполнения первая ячейка диапазона будет закреплена, а последняя будет растягиваться по мере продвижения вниз. Это нам и нужно для выполнения поставленных целей. Далее жмем на кнопку «OK».



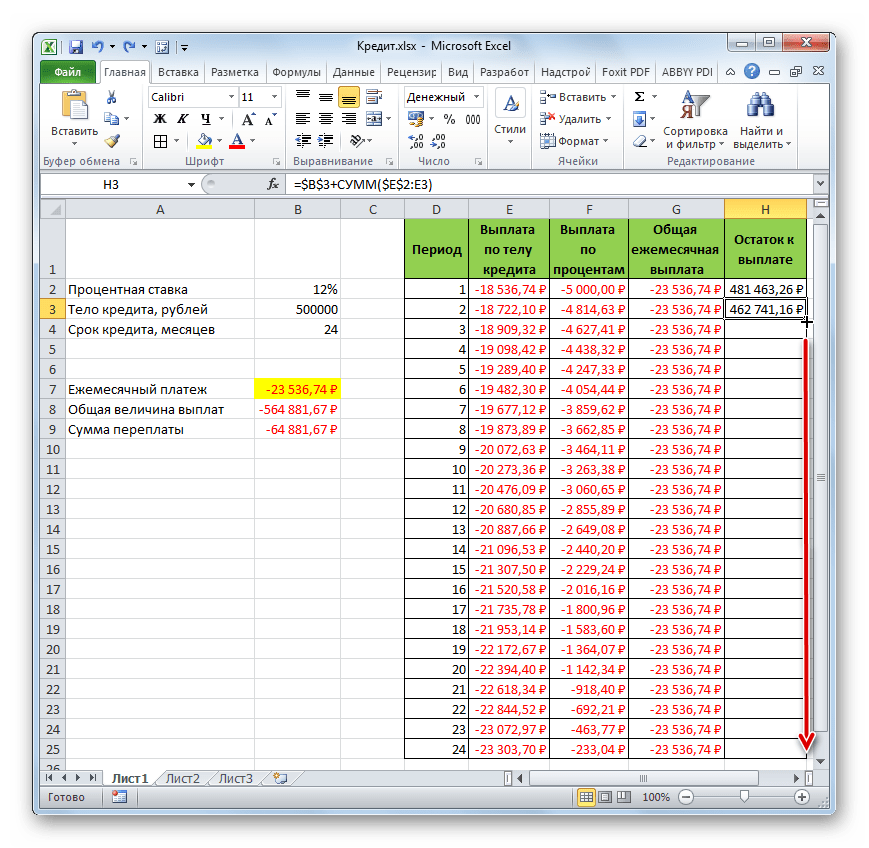
19. Итак, результат остатка кредитной задолженности после второго месяца выводится в ячейку. Теперь, начиная с данной ячейки, производим копирование формулы в пустые элементы столбца с помощью маркера заполнения.



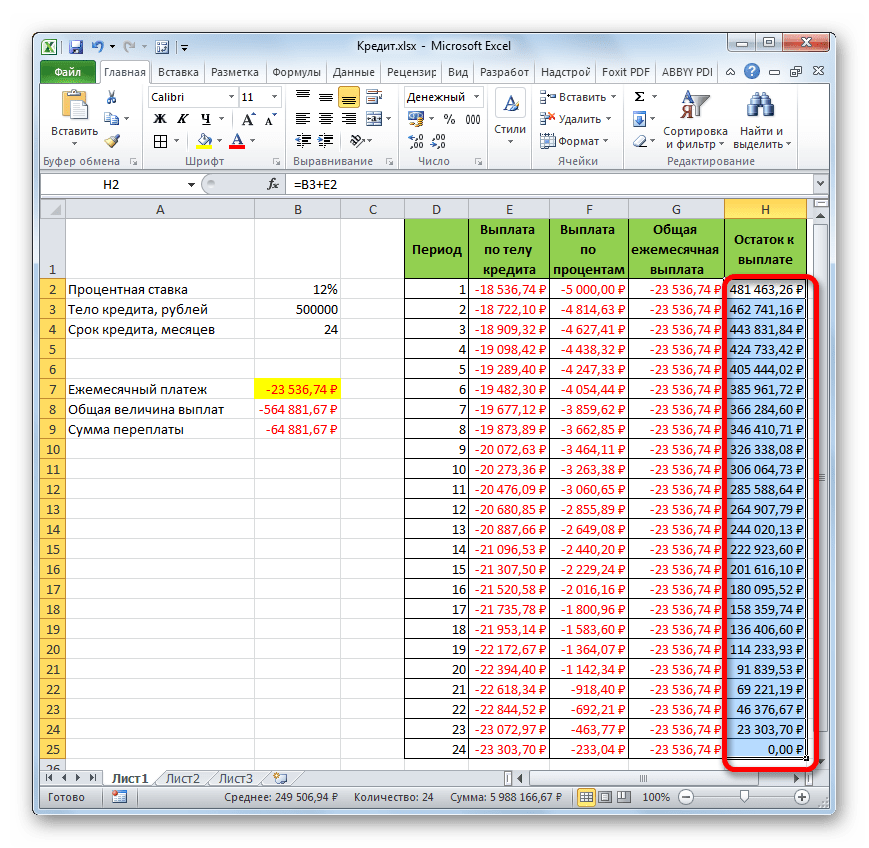
20. Помесячный расчет остатков к оплате по кредиту сделан за весь кредитный период. Как и положено, на конец срока эта сумма равна нулю.

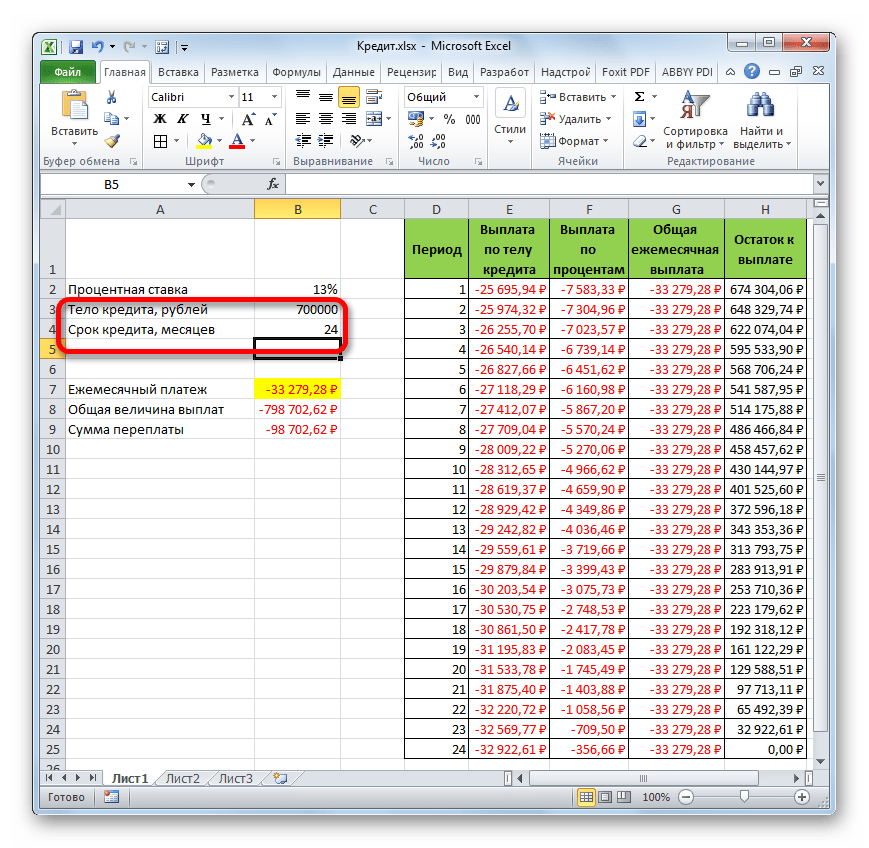
Таким образом, мы произвели не просто расчет оплаты по кредиту, а организовали своеобразный кредитный калькулятор. Который будет действовать по аннуитетной схеме. Если в исходной таблице мы, например, поменяем величину займа и годовой процентной ставки, то в итоговой таблице произойдет автоматический пересчет данных. Поэтому её можно использовать не только один раз для конкретного случая, а применять в различных ситуациях для расчета кредитных вариантов по аннуитетной схеме.

Урок: Финансовые функции в Excel

Как видим, при помощи программы Excel в домашних условиях можно без проблем рассчитать общий ежемесячный кредитный платеж по аннуитетной схеме, используя для этих целей оператор ПЛТ. Кроме того, при помощи функций ОСПЛТ и ПРПЛТ можно произвести расчет величины платежей по телу кредита и по процентам за указанный период. Применяя весь этот багаж функций вместе, существует возможность создать мощный кредитный калькулятор, который можно будет использовать не один раз для вычисления аннуитетного платежа.

В
пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:

• определение
  наращенной суммы (будущей стоимости),

• определение
  начального значения (текущей стоимости),

• определение
  срока платежа и процентной ставки,

• расчет
  периодических платежей, связанных с
  погашением займов.

Общая
формула расчета, которуюExcel
использует при вычислении финансовых
аргументов, связанных с денежными
потоками, имеет вид:

где
pmt
– фиксированная
(неизменная) периодическая сумма платежа;

n
– общее
число периодов выплат,

r
– процентная
ставка за один период,

type
– число 0
или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 – в конце
периода),

—
текущая стоимость вклада (займа), по
которому начисляются проценты по ставке
r%
n—ное
число периодов или текущая стоимость
серии фиксированных платежей,

—будущая стоимость вклада (займа) или
будущая стоимость серии фиксированных
периодических платежей.

Если
процентная ставка за период начисления
r=0, то используется следующая формула:

Эти
формулы используют встроенные функцииБC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.

ПС
— текущий объём вклада

Позволяет
рассчитать текущий объем вклада.

Синтаксис

ПС
(норма;кпер;выплата;бс;тип)

норма
— процентная
ставка за период. Так, если Вы по­лучили
ссуду под станок под 15% годовых и делаете
ежемесяч­ные выплаты, то ставка
процента за месяц составит 15%/12, или
1,25%. Аргумент норма
в данном
случае может принимать значения 15%/12
или 1,25% или 0,0125.

кпер
— общее число
периодов выплат годовых процентов. Так,
если Вы получили ссуду на 3 года под
станок и делаете ежемесячные платежи,
то Ваша ссуда имеет 3*12 (или 36) периодов.
Аргумент кпер
в данном случае принимает значение 36.

выплата
—
размер выплаты, производимой в каждом
периоде и не меняющейся в течение всего
времени выплаты процентов. Обычно,
выплата включает основные платежи и
платежи по процентам без учета других
сборов или налогов. Напри­мер,
ежемесячная выплата по четырехгодичному
займу в 10 000 руб. под 12% годовых составит
308,3 руб. Аргумент выплата
в данном случае принимает значение
-308,3.

бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если бс
опущено, оно полагается равным 0 (будущая
стоимость займа, например, равна 0).
Например, если Вы хотите накопить 50000
руб. в течение18 лет, то 50 000 руб. это и
есть будущая стоимость. Вы можете сделать
предположение о сохранении заданной
процентной ставки и определить, сколько
нужно откладывать каждый месяц.

тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 означает — выплата в конце периода,
1 — выплата в начале периода.

• Выбранные
  единицы измерения для аргументов норма
  и кпер
  должны соответствовать друг другу.
  Если Вы делаете ежемесячные выплаты
  по четырехгодичному займу под 12% годовых,
  то используйте 12%/12 для задания аргумента
  норма,
  4*12 для задания аргумента кпер.
  Если Вы делаете ежегодные платежи по
  тому же займу, то используйте 12% для
  задания аргумента норма
  и 4 для задания аргумента кпер.

• В
  функциях, связанных с интервалами
  выплат, выплачи­ваемые деньги
  представляются отрицательным числом,
  а получаемые деньги представляются
  положительным числом. Например, депозит
  в банк на сумму 1 000 руб. представляется
  для вкладчика аргументом -1000, а для
  банка аргументом 1000.

Пример

Фирме
потребуется 5000 руб. через 12 лет. В
настоящее время фирма располагает
деньгами и готова положить их на депозит
единым вкладом, чтобы через 12 лет он
достиг 5000 руб. Определим необходимую
сумму текущего вклада, если ставка
процента по нему составляет 12% годовых.

Необходимая
сумма текущего вклада составит:

ПС
(12%;12;;5000)=-1283.38 руб.

БС
— стоимость постоянных платежей в
определенные периоды на основе постоянной
процентной ставки

Позволяет
рассчитать объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.

Синтаксис

БС(норма;кпер;выплата;пс;тип)

ставка
— процентная
ставка за период.

кпер
— количество
периодов, в которые производится вы­плата
годовых процентов.

выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.

пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.

тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.

Более
подробная информация об аргументах
функции БЗ и о других функциях выплат
по процентным вкладам приведена в
описании функции ПЗ.

• Единицы
  измерения для аргументов норма
  и кпер
  должны быть согласованы. Если производятся
  ежемесячные платежи по четырехгодичному
  займу из расчета 12% годовых, то норма
  должна быть 12%/12 , а кпер
  должно быть 4*12. Если про­изводятся
  ежегодные платежи по тому же займу, то
  норма
  должна быть
  12%, а кпер
  должно быть 4.

• Ваш
  вклад представляется отрицательным
  числом, а деньги, которые вы получите,
  представляются положительным числом.

Пример

Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.

Через
год на счете будет:

БС
(0,5%;12;-100;-1000;1)=2301,40 р.

ПРПЛТ
— платежи по процентам за период на
основе постоянных периодических выплат
и постоянной процентной ставки

С
помощью данной функции можно рассчитать
процентные платежи за текущий период
при периодических постоянных выплатах
и постоянной процентной ставке. Полное
описание аргументов функции ПРПЛТ
и более подробная информация о функциях,
связанных с ежегодными выплатами,
приведены в описании функции ПС.

Синтаксис

ПРПЛТ(норма;период;кпер;тс;бс;тип)

норма
—
процентная ставка за период.

период
— текущий
период, в котором требуется определить
прибыль (может принимать значения от 1
до кпер).

кпер
— общее число
периодов выплат.

тс
— сумма,
которую составят будущие платежи с
настоящего момента.

бс
— баланс
платежей, который нужно достичь после
последней выплаты.

тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплаты в конце периода, 1 — выплаты
в начале периода.

• Единицы
  измерения для аргументов норма
  и кпер
  должны быть согласованы. Если производятся
  ежемесячные платежи по трехгодичному
  займу из расчета 10% годовых, то норма
  должна быть 10%/12 , а кпер
  должно быть 3*12. Если производятся
  ежегодные платежи по тому же займу, то
  норма
  должна быть 10%, а кпер
  должно быть 3.

• Выплачиваемые
  денежные средства представляются
  отрицательным числом, а получаемые
  денежные средства представляются
  положительным числом.

Пример

Требуется
определить доход за первый месяц от
четырех­годичного займа в 1000000 рублей
из расчета 15% годовых:

ПРПЛТ(0,15/12;1;48;1000000)
равняется -12500 рублей.

ПЛТ
— расчет постоянных периодических
выплат

Функция
вычисляет величину выплаты за один
период на основе фиксированных
периодических выплат и постоянной
процентной ставки. Выплаты, рассчитанные
функцией ПЛТ, включают основные платежи
и платежи по процентам.

Синтаксис

ПЛТ(норма;кпер;нз;бс;тип)

норма
– норма
прибыли за период займа.

кпер
– общее
число периодов выплат годовой ренты

нз
– текущая стоимость: общая сумма всех
будущих платежей с настоящего момента.

бс
– будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты.

тип
— число,
определяющее, когда должна производиться
выплата.

Пример

Предположим,
что необходимо накопить 4000 руб. за 3
года, откладывая постоянную сумму в
конце каждого месяца. Какой должна быть
эта сумма, если норма процента по вкладу
составляет 12% годовых?

Величина
ежемесячных выплат составит:

ПЛТ(12%/12;12*3;;4000)=-92.86
руб.

ОСПЛТ
— расчет основных платежей по займу

Функция
вычисляет величину основного платежа
(выплаты задолженности) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
на указанный период.

Синтаксис

ОСПЛТ(норма;период;кпер;тс;бс;тип)

норма
– норма
прибыли за период.

период
– период,
который должен быть в интервале от 1 до
кпер.

кпер
– общее
число периодов выплат годовой ренты.

тс
– текущая
стоимость: общая сумма всех будущих
платежей с настоящего периода.

бс
– будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.

тип
—
число,
определяющее, когда должна производиться
выплата.

Пример

Банком
выдан кредит в 7000 руб. на 3 года под 17%
годовых, начисляемых один раз в конце
каждого периода.

Определите
размер ежегодных основных выплат по
займу.

Основная
часть платежа на каждый из трех периодов
составит соответственно:

ОСПЛТ(17%;1;3;-70000)=19780.16
руб.

ОСПЛТ(17%;2;3;-70000)=23142.78
руб.

ОСПЛТ(17%;3;3;-70000)=27077.06
руб.

ОБЩПЛТ
— расчет суммы платежей по процентам
по займу между двумя периодами выплат

Функция
вычисляет накопленный доход (сумму
платежей по процентам) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
между двумя периодами выплат.

Синтаксис

ОБЩПЛТ(ставка;кол_пер;нз;нач_период;кон_период;тип)

ставка
– процентная ставка.

кол_пер
– общее
количество периодов выплат.

нз
– текущее
значение.

нач_период
– первый
период.

кон_период
— последний период.

Пример

Пусть
заем под недвижимость сделан на следующих
условиях: процентная ставка –9% годовых;
срок-30 лет, размер ссуды – 125000 руб.,
проценты начисляются ежемесячно.

Найти
сумму выплат по процентам за 2-й год и
за 1-й месяц займа.

Общая
выплата по процентам за второй год
составит:

ОБЩПЛТ(9%/12;30*12;125000;13;24)=-11135.23
руб.

Одна
выплата за первый месяц составит:

ОБЩПЛТ(9%/12;30*12;125000;1;1)=-937.50
руб.

ОБЩДОХОД
— расчет суммы основных выплат по займу
между двумя периодами

Функция
вычисляет сумму основных выплат по
займу, который погашается равными
платежами в конце или начале каждого
расчетного периода, между двумя периодами.

Синтаксис

ОБЩДОХОД
(ставка;кол_пер;нз;нач_период; нач_период;)

ставка
– процентная ставка.

кол_пер
– общее
количество периодов выплат.

нз
– текущее
значение.

нач_период
– первый
период.

кон_период
— последний период.

Пример

Выдана
ссуда размером 1000$ сроком на 6 лет под
15% годовых; проценты начисляются
ежеквартально.

Определите
величину основных выплат за 5 год.

Если
ссуда погашается равными платежами в
конце каждого расчетного периода, то
размер выплаты задолженности за пятый
год составит:

ОБЩДОХОД(15%/4;6*4;1000;17;20)=-201.43$.

Комплексный
пример

Банком
выдан кредит в 10000$ на 5 лет под 12% годовых,
начисляемых один раз в конце каждого
периода. По условиям договора кредит
должен быть погашен равными долями в
течение указанного срока, выплачиваемыми
в конце каждого периода.

Разработать
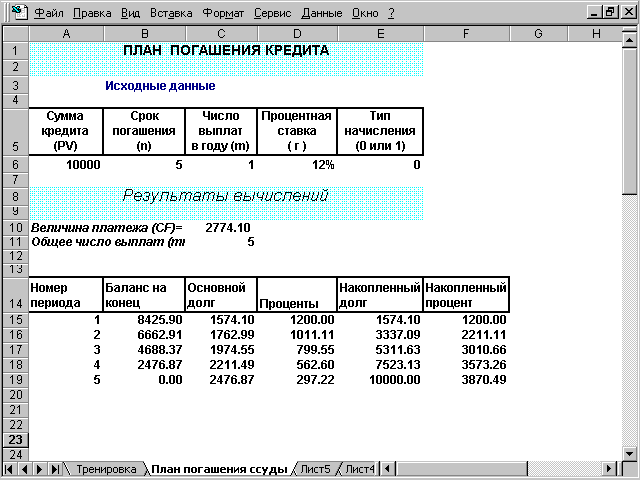
план погашения кредита.

Периодический
платеж по данной операции составит:

ПЛТ(12%;5;-10000)=2774.10$.

Процентная
часть платежа на первый период составит:

ПРПЛТ(12%;1;5;-10000)=1200,00$.

Основная
часть платежа, направленная на погашение
долга за первый период, составит:

ОСПЛТ(12%;1;5;-10000)=1574.10$.

Как
видно выполняется тождество:

ПРПЛТ()+ОСПЛТ()=ПЛТ()=2774.10$.

Будущее
значение суммы, которую банк получит в
результате проведения операции:

ПЛТ(12%;5;-10000)*5=13870.50$.

Накопленная
сумма процентов за весь период составит:

ОБЩПЛТ(12%;5;10000;1;5;0)=-3870,49$.

Накопленная
сумма в счет погашения по займу за 5 лет
составит:

ОБЩДОХОД(12%;5;10;1;5;0)=-10000.00$.

Как
видно, сумма полученных величин равна
общей сумме, выплаченной по данному
займу:

ОБЩДОХОД()+ОБЩПЛАТ()=13870.49$.

(В
силу заложенного алгоритма расчета
функции ОБЩДОХОД() и ОБЩПЛАТ возвращают
отрицательные значения. Для получения
положительных значений можно задать
их со знаком минус).

На
рис. 1 приведена таблица с планом погашения
кредита.

ЭФФЕКТ
— эффективная годовая процентная ставка

Позволяет
рассчитать фактическую годовую процентную
ставку, если известны годовая процентная
ставка и количество периодов в году.

Синтаксис

ЭФФЕКТ(нoмuнaльнaя_cmaвкa;кол_пep)

номинальная_ставка

—
номинальная годовая процентная ставка.

кол_пер
— количество
периодов в году.

Рис.
1. План погашения кредита

• Число
  периодов в году округляется до целого.

• Функция
  ЭФФЕКТ
  выдает значение ошибки #ЗНАЧ! в случае,
  если один из аргументов — не число либо,
  если номинальная_ставка
  меньше 0 или
  кол_пер
  меньше 1.

Пример

Рассчитаем
эффективную годовую процентную ставку
при став­ке 5,25% и четырех периодах в
году.

ЭФФЕКТ(5,25%;4)
равняется 0,053543 или 5,35%.

КПЕР
— определение срока платежа

Эта
функция вычисляет общее число периодов
выплат как для единой суммы вклада
(займа), так и для периодических постоянных
выплат на основе постоянной процентной
ставки. Если платежи производятся
несколько раз в год, найденное значение
необходимо разделить на число расчетных
периодов в году, чтобы найти число лет
выплат.

Синтаксис

КПЕР(норма;выплата;нз;бс;тип)

норма
– норма
прибыли за период.

выплата—
размер выплаты, производимой в каждом
периоде.

нз
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент нз опущен, то он
полагается равным 0.

бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.

тип
— число,
определяющее, когда должна производиться
выплата.

Пример

Ожидается,
что ежегодные доходы от реализации
проекта составят 33 млн. руб. Необходимо
рассчитать срок окупаемости проекта,
если инвестиции к началу поступления
доходов составят 100 млн. руб., норма
дисконтирования 12.11%.

Срок
окупаемости проекта составит:

КПЕР(12.11%;33;-100)=4года.

Определение
скорости оборота инвестиций

ВНДОХ
— процентная ставка дохода для ряда
последо­вательных периодических
выплат или поступлений

Позволяет
рассчитать процентную ставку дохода
от инвестиций для ряда последовательных
операций с денежными средствами,
представленными числовыми значениями.
Объемы операций могут быть различны.
Однако они должны происходить через
равные промежутки времени, например,
ежемесячно или ежегодно. Процентная
ставка дохода, полученного от инвестиции,
состоит из выплат (отрицательные
значения) и поступлений (положительные
значения), которые происходят в регулярные
периоды времени.

Синтаксис

ВНДОХ
(значения;предположение)

значения
— массив или
ссылка на ячейки, содержащие числа, для
которых вычисляется процентная ставка
инвестиций.

предположение
—
прогнозируемая величина.

• Аргумент
  значения
  должен включать в себя по крайней мере
  одно положительное значение и одно
  отрицательное значение, для того, чтобы
  можно было вычислить процентную ставку.

• Начиная
  со значения прогноз, функция ВНДОХ
  выполняет
  циклические вычисления, пока не получит
  результат с точностью 0,00001 процента
  (такой метод вычисления на­зывается
  методом итераций).

• Функция
  ВНДОХ выдает значение ошибки #ЧИСЛО! в
  том случае, если не может получить
  результат после 20 попыток.

• Обычно
  нет необходимости задавать аргумент
  прогноз
  для вычислений с помощью функции ВНДОХ.
  Если прогноз
  опущен, то
  он полагается равным 0,1 (10 процентов).
  Если ВНДОХ
  выдает значение ошибки
  #ЧИСЛО!,
  можно попытаться вы­полнить вычисления
  еще раз с другим значением аргумента
  прогноз.

Пример

Предположим,
что затраты по проекту составят 500 тыс.
руб. Ожидаемые доходы составят 50 , 100 ,
300 и 200 тыс. руб. в течение последующих
4 лет. Оценим
экономическую целесообразность проекта
по скорости оборота инвестиций, если
рыночная норма дохода 12%.

Ячейки
А1:А5 содержат следующие значения: -500,
50, 100, 300 и 200 соответственно.

Внутренняя
скорость оборота инвестиций составит:

ВНДОХ(А1:А5)=9.25%.

Это
меньше, чем рыночная норма, поэтому
проект должен быть отвергнут.

В
том случае, если эта какая-либо из
финансовых функций недоступна из Excel,
следует установить надстройку Пакет
Анализа (Analysis
ToolPak),
а затем подключить его с помощью команды
Сервис
— Надстройки…

ЗАДАЧИ