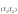Расчетно графическая работа по excel

НЕКОММЕРЧЕСКОЕ
АКЦИОНЕРНОЕ ОБЩЕСТВО

АЛМАТИНСКИЙ
УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Дисциплина:

«Информационно-коммуникационные
технологии»

Вариант
№3

Выполнила
: Деш.Я.А

Группа
: ЭЭ-16-6

Проверила
: Турганбай К.Е

_____________
_____________ «____» ___________ 20___г.

(оценка) (подпись)

Алматы,
2017

Содержание

1
Содержание……………………………………………………………………..2

2
Цель работы…………………………………………………………………….3

3
Задания 2.1.1 –2.1.10…………………………………………………………3-14

4
Вывод…………………………………………………………………………..15

5
Список литературы…………………………………….………………………16

2 Расчетно-графическая работа №1. Решение вычислительных задач с помощью табличного процессора ms Excel

Цель
работы

Цель
работы – изучение расширенных возможностей
табличного процессора MS
Excel
и их использование при решении
вычислительных задач. Научиться решать
финансовые, экономические, математические
и статические задачи. С помощью электронной
таблицы решать задачи, как обработка
заказов и планирование производства,
расчет налогов и заработной платы, учет
кадров и издержек, управление сбытом,
составление прайс-листов и др. Правильно
использовать функции из категории
инженерные, математические, ссылки и
массивы и др. Научиться строить графики,
выполнять по различным критериям
автофильтрацию, определить некоторые
основные характеристики потоков
различных жидкостей, решать систему
уравнении методом Крамера и методом
обратной матрицы.

2.1 Задание на расчетно-графическую работу

2.1.1. Используя
методику перевода чисел (таблица В.1), а
также ресурсы MS
Excel:

— создать таблицу
перевода заданного числа (таблица Б.1)
из десятичной системы счисления в
предлагаемую систему счисления (двоичную,
восьмеричную, шестнадцатеричную);

— создать таблицу
обратного перевода полученного результата
в десятичную систему. Выполнить те же
действия, используя встроенную функцию
из категории Инженерные
(подключить Пакет
анализов).
Объяснить возможные ошибки;

— с помощью
специальной функции из категории
Математические
перевести заданное число (таблица Б.1)
из десятичной системы счисления в
римскую систему счисления и получить
тот же результат.

Пояснение: было
задано число в десятичной системе, мне
нужно было перевести это число в
шестнадцатеричную систему, для этого
я сначала делил заданное число в
десятичной системе на основание системы,
до тех пор пока не получил число меньше
основания системы, при этом сразу
использовал функцию ЦЕЛОЕ, после этого
с помощью функции ОСТАТ я получила
остатки деления, затем с помощью функции
СЦЕПИТЬ объединила результат.

Задание 2.1.1
перевод с помощью функции:
исходное число	число в шестнадцатеричной системе
210236	3353С

Используя методику перевода чисел:
исходное число		остаток	число в шестнадцатеричной системе
210236		3	3353С
13139		3
821		5
51		3
3		12

Пояснение: с помощью
функции ВОС.В.ДЕС я перевёла
число из шестнадцатеричной системы
обратно в десятичную систему.

перевод в римские цифры
2689	MMDCXXXIX
обратный перевод
2000	MM
600	DC
40	LXXX
9	IX
2689	MMDCXXXIX

Пояснение: заданное
число в десятичной системе я переёла в
римскую систему исчисления, с помощью
функции РИМСКОЕ, и сделала обратное
действие, перевёла из римской системы
счисления в десятичную.

выполнение операции над числами
a	b	действие	результат
12	456	умножение	5472

Пояснение: над
заданными числами a
и b
я совершила заданную мне арифметическую
операцию, число а умножила на число b.

2.1.2. Используя
функцию преобразования из категории
Инженерные,
составить таблицу перевода данных из
одних единиц измерения (таблица Б.1) в
другие.

перевод
Ньютон	Дин
300	30000000

Пояснение: для
того чтобы перевести Ньютон в Дину я
использовал функцию ПРЕОБР (число –
заданное число, исходная единица
измерения – “N”,
конечная единица измерения – “dyn”).

2.1.3.
Построить график функции (таблица Б.3).

Построение
графика функции r=a(1+cosn) 
— кардиоида

№точки	Угол (t)	x	y	x окр	y окр
1	0,000	2,388456	0,197928	1,782013	0,907981
2	0,157	2,618034	0,449028	1,618034	1,175571
3	0,314	2,828427	0,828427	1,414214	1,414214
4	0,471	2,969175	1,333955	1,175571	1,618034
5	0,628	2,991533	1,945992	0,907981	1,782013
6	0,785	2,854102	2,628656	0,618034	1,902113
7	0,942	2,527851	3,332719	0,312869	1,975377
8	1,100	2	4	1,23E-16	2
9	1,257	1,276375	4,568787	-0,31287	1,975377
10	1,414	0,381966	4,979797	-0,61803	1,902113
11	1,571	-0,64039	5,18206	-0,90798	1,782013
12	1,728	-1,73311	5,138181	-1,17557	1,618034
13	1,885	-2,82843	4,828427	-1,41421	1,414214
14	2,042	-3,8541	4,253254	-1,61803	1,175571
15	2,199	-4,7396	3,433996	-1,78201	0,907981
16	2,356	-5,42226	2,411638	-1,90211	0,618034
17	2,513	-5,85287	1,243772	-1,97538	0,312869
18	2,670	-6	9,8E-16	-2	2,45E-16
19	2,827	-5,85287	-1,24377	-1,97538	-0,31287
20	2,985	-5,42226	-2,41164	-1,90211	-0,61803
21	3,142	-4,7396	-3,434	-1,78201	-0,90798
22	3,299	-3,8541	-4,25325	-1,61803	-1,17557
23	3,456	-2,82843	-4,82843	-1,41421	-1,41421
24	3,613	-1,73311	-5,13818	-1,17557	-1,61803
25	3,770	-0,64039	-5,18206	-0,90798	-1,78201
26	3,927	0,381966	-4,9798	-0,61803	-1,90211
27	4,084	1,276375	-4,56879	-0,31287	-1,97538
28	4,241	2	-4	-3,7E-16	-2
29	4,398	2,527851	-3,33272	0,312869	-1,97538
30	4,555	2,854102	-2,62866	0,618034	-1,90211
31	4,712	2,991533	-1,94599	0,907981	-1,78201
32	4,869	2,969175	-1,33395	1,175571	-1,61803
33	5,027	2,828427	-0,82843	1,414214	-1,41421
34	5,184	2,618034	-0,44903	1,618034	-1,17557
35	5,341	2,388456	-0,19793	1,782013	-0,90798
36	5,498	2,186192	-0,0605	1,902113	-0,61803
37	5,655	2,04864	-0,0077	1,975377	-0,31287
38	5,812	2	0	2	0
39	5,969	2	0	2	0
40	6,126	2	0	2	0

Пояснение: для
того чтобы построить график функции
сначала я построила таблицу, значение
«а» и «n»
я взял произвольное затем значения «а»
«n»
перевел в радианы r. Затем полученные
значения r
подставил в заданные функции получил
значения х и y после
всего этого я построил диаграмму,
подставив в диапазон данных столбцы со
значениями x
и y,
для построения графика выбрал тип
диаграммы Точечная.

2.1.4. Имеется
резервуар с емкостью V,
рабочим объемом Vr,
объем жидкости в резервуаре Vg.
Резервуар в основании имеет круг радиусом
r
или прямоугольник со сторонами a
и b
и высоту заполнения h
(таблица Б.4). Как только объем жидкости
станет превышать рабочий объем резервуара,
оператору необходимо отправить сообщение,
используя логическую функцию ЕСЛИ.
Сообщение “перекрыть
клапан”
должно быть написано на красном фоне,
в противном случае, должно быть выведено
сообщение – “не
требуется”.
Используя условное форматирование,
проиллюстрировать заполнение резервуара.

Пояснение: вначале
я нашла площадь основания S(п*r^2),
затем после этого записал формулу для
нахождения объёма жидкости (=G8*E8), потом
с помощью функции ЕСЛИ отправила нужное
сообщение (=ЕСЛИ(F8>D8;»закрыть кран»;»не
требуется»)), затем построила диаграмму
использовав условное форматирование,
и сообщение «закрыть кран» сделала
красным шрифтом.

а	b	Рабочий объем Vr	Высота H	Объем заполненный V	Команда
7	5,5	210	10,90909091	60	не требуется
7	5,5	210	17,27272727	95	не требуется
7	5,5	210	81,81818182	450	закрыть кран
7	5,5	210	146,3636364	805	закрыть кран
7	5,5	210	29,09090909	160	не требуется
7	5,5	210	89,09090909	490	закрыть кран

2.1.5. Решить систему
уравнений (таблица Б.5) методом обратной
матрицы и методом Крамера.

система уравнений
2	-1	2	0
4	1	4	0
1	1	2	4

обратная матрица
-0,333	0,6667	-1
-0,667	0,3333	0
0,5	-0,5	1
решение
X1	1
X2	0
X3	0

Пояснение: сначала
записала уравнение в матричной форме,
затем с помощью функции МОПРЕД нашла
определитель матрицы, после этого с
помощью функции МОБР нашла обратную
матрицу, потом нашла значения матрицы
X,
для этого умножила обратную матрицу на
правую часть уравнения или матрицу С,
с помощью функции МУМНОЖ. 6- определитель
матрицы.

Решить
систему уравнений методом Крамера.

Пояснение:
нашла вспомогательные определители
матриц 1, 2 , 3 с помощью функции МОПРЕД,
после этого для того чтобы найти x1,
x2,
x3
разделила соответствующее определители
на определитель матрицы А, и получил
нужные мне значения.

1 матрица
0	-1	2
0	1	4	Х1	= 1
4	1	2
2 матрица
2	0	2
4	0	4	Х2	= 0
1	4	2
3 матрица
2	-1	0
4	1	0	Х3	= 0
1	1	4

2.1.6. Используя
функцию MS
Excel,
выполнить с заданным массивом (таблица
Б.6) следующие действия:

— транспонировать
исходный и транспонированный массивы;

— перемножить
исходный и транспонированный массивы;

— найти позицию
элемента равного заданному числу А.

исходная таблица
8	-4	1	6
2	8	6	1
0	1	8	4
6	2	0	8

Пояснение: заданный
массив я транспонировала с помощью
функции ТРАНСП, и получила матрицу В,
затем перемножила матрицу В на её
транспонированную матрицу с помощью
функции МУМНОЖ и получила результат,
после этого с помощью функции ПОИСКПОЗ
нашла позицию числа А.

Транспонировать
матрицу B

транспонированная
8	2	0	6
-4	8	1	2
1	6	8	0
6	1	4	8

Перемножить
матрицу B и транспонированную матрицу
B результатом стало число 117.

2.1.7. Определить
некоторые основные характеристики
потоков различных жидкостей:

а) вода течет по
трубе с внутренним диаметром D
(таблица Б.7). Средняя скорость потока
равна v.
Вычислить площадь сечения трубы S=
(π/4)*D²
и объемную скорость потока V= v*S.
Определить какого диаметра должна быть
труба, чтобы скорость потока жидкости
снизилась до 1,3 м/с при неизменной
объемной потока;

б) на практике
широко применяется правило: средняя
скорость легкоподвижных жидкостей
(вязкость которых по порядку величины
совпадает с вязкостью воды ) в трубе не
должна превышать 1м/с. Определите
минимальный диаметр трубы, по которой
должно поступать 6000м³ воды в день при
соблюдений сформулированного правила;

в) число Рейнольдса
определяется соотношением Re=
, где D
– внутренний диаметр трубы, ν – средняя
скорость потока жидкостей в трубе, ρ —
плотность жидкости, μ — абсолютная
вязкость жидкости. Если для потока
жидкости в трубе величина числа Рейнольдса
не превышает 2100, поток считается
ламинарным. Если же его величина превышает
10000, поток считается турбулентным. Для
значений, лежащих в диапазоне от 2100 до
10000, невозможно заранее определить тип
потока. Найти число Рейнольдса и
определить тип потока (ламинарный,
турбулентный или неизвестный) для
жидкостей, характеристики которых
указаны в таблице Б.7

Вычислить
площадь поперечного сечения трубы и
объёмную скорость потока

Пояснение:
по исходным мне данным и формулам,
вначале я вычислил площадь поперечного
сечения (=ПРЕОБР(B10;»mm»;»m»)^2*ПИ()/4),
затем нашёл объёмную скорость потока
(=D10*E10), потом площадь поперечного сечения
(=B19/C19) и диаметр трубы
(=ПРЕОБР((4*D19/ПИ())^0,5;»m»;»mm»)) при
скорости 1,3 м/с, затем определил площадь
поперечного сечения
(=(C28/ПРЕОБР(1;»day»;»sec»))/1) и диаметр
трубы (=ПРЕОБР((4*D28/ПИ())^0,5;»m»;»mm»))
при средней скорости потока 1 м/с и
объёмной скорости потока 6000 м^3/день,
затем определил число Рейнольдса
(=C37*D37*ПРЕОБР(B37;»mm»;»m»)/E37) по
исходным данным, и с помощью функции
ЕСЛИ указал тип потока
(=ЕСЛИ(F37<2100;»ламинарный»;
ЕСЛИ(F37>10000;»турбулентный»;»неизвестный»)).

S=π*D^2/4

V=v*S

Определить
диаметр трубы при средней скорости
потока жидкости 1,3 м/с, и неизменной
объёмной скорости

Условия
D, м	Вид жидкости	v, м/с	p, кг/м3	µ, 10-4Па*с	v2, м/с
0,98	Нефть	1,5	870	2,8	1,3
А)
S, кв м	V, куб м/c	D2, м
0,055152959	0,033091776	0,180032
Б)
V, куб м	t,c	v, м/с	D, м
6000	86400	1	0,297358

В) Re=ламинарный

2.1.8. Резисторный
датчик температуры – это прибор, в
котором для изменения температуры
используется металлическая проволока
или пластинка. Электрическое сопротивление
металла зависит от температуры, поэтому
температуры можно вычислить на основе
измерений сопротивления металла.
Уравнение, связывающее температуру и
сопротивление, имеет вид:

Rt
= R0(1+άT)

где
Rt
– сопротивление
при изменяемой температуре Т;

R0
– сопротивление
при температуре 0ºС;

ά
– линейный
температурный коэффициент.

Для платины ά
= 0,00385 Ом/ ºС.
Вычислить (таблица Б.8)

а) сопротивление
платинового терморезистора в заданном
интервале температур (Т;Т)
с указанным шагом hпри
известном сопротивлении R;

б) температуру,
при которой сопротивление терморезистора
равно заданным значениям R
c
указанным шагом h.

Вычислить
сопротивление платинового терморезистора
в интервале температур (T1; T2)

Rt=R0*(1+αT)

№ вар.	R0	(Т1; Т2)	hT	R(T1; T2)	hR
3	50	(80;140)	10	(60;100)	5		α = 0,00385 Ом/°С

Пояснение:
по исходным данным и формуле я определилa
сопротивления на данном промежутке
температур (пример: =$B$11*(1+$C$11*G11) и т.д.),
затем наоборот по данным сопротивлениям
определила температуры (пример:
=((G38-$B$38)/$B$38)/$C$38
и т.д.).

T	Rt
80	130,8
90	134,65
100	138,5
110	142,35
120	146,2
130	150,05
140	153,9

Вычислить
температуру при которой сопротивление
терморезистора равно заданным значениям
R(t1;t2)

t=((Rt-R0)/R0)/α

R	T
80	259,7403
90	324,6753
100	389,6104
110	454,5455
120	519,4805
130	584,4156
140	649,3506

2.1.9. Сформировать
предложенную таблицу, заполнить не
менее 10 записей и выполнить выборку
данных по различным критериям (три
простых запроса с помощью автофильтрации
и три сложных запроса с использованием
расширенного фильтра).

Исходная таблица:

Абонентская плата за телефон
ФИО абонента	Телефон	Год установки	Статус абонента	Плата за телефон
Иванов И.И.	566-852	2001	подключен	8500
Перова Г.С.	456-555	1995	подключен	1200
Сидоров В.С	859-693	2008	отключен	9600
Ким А.Л.	485-963	2017	отключен	4500
Тагай А.Д.	123-954	1999	подключен	4589
Дюсебаева К.М.	565-963	2015	отключен	5263
Автофильтрация
ФИО абонента	Телефон	Год установки	Статус абонента	Плата за телефон
Дюсебаева К.М.	565-963	2015	отключен	5263
Иванов И.И.	566-852	2001	подключен	8500
Ким А.Л.	485-963	2017	отключен	4500
Перова Г.С.	456-555	1995	подключен	1200
Сидоров В.С	859-693	2008	отключен	9600
Тагай А.Д.	123-954	1999	подключен	4589

Расширенный фильтр
ФИО абонента	Телефон	Год установки	Статус абонента	Плата за телефон
				3000>
		2000<
ФИО абонента	Телефон	Год установки	Статус абонента	Плата за телефон
Иванов И.И.	566-852	2001	подключен	8500
Перова Г.С.	456-555	1995	подключен	1200
Сидоров В.С	859-693	2008	отключен	9600
Ким А.Л.	485-963	2017	отключен	4500
Тагай А.Д.	123-954	1999	подключен	4589
Дюсебаева К.М.	565-963	2015	отключен	5263

2.1.10. Сформировать
заданные основную и вспомогательную
таблицы. Выполнить в основной таблице
все необходимые вычисления, используя
данные вспомогательной таблицы.

Пояснение: я
сформировала основную и вспомогательную
таблицы, для связи таблиц я использовала
функцию ВПР.

Основная
таблица:

Наименование металла	Количество э/энергии на переработку 1 т металла	Количество металла (т)	Расход э/энергии	Стоимость 1т, $
Медь черновая	140	3000	420000	40125
Титан	250	500	125000	298000
Цинк	100	2000	200000	250000
Магний	95	1500	142500	547500
Цинк	100	1700	170000	212500
Титан	250	200	50000	119200
Медь черновая	140	4000	560000	1284000
Магний	140	1200	168000	438000
Цинк	100	1900	190000	237500

Вспомогательная
таблица:

Наименование металла	Количество э/энергии на переработку 1 т металла	Стоимость за 1т, $
Цинк	100	125
Титан	250	596
Медь черновая	140	321
Магний	95	365

Соседние файлы в папке local

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Слайды презентации

Инфоурок

›

Другое

›Презентации›Расчетно-графическая работа по работе Excel.

1


Расчетно-графическая работа по Microsoft Excel Выполнил: ст.гр. ЭУТ-11 Штейнгарт А.Л. Проверил: Терещенко Н.В.

2


Оглавление Задача 1 Задача 1 Задача 2 Задача 2 Задача 3 Задача 3 Задача 4 Задача 4 Задача 5 Задача 5

3


Задача 1 Число оборотов двигателя y функционально зависит от температуры x. Вычислить число оборотов двигателя y(x) при температуре a и b. Построить график этой функциональной зависимости на интервале [a,b] с шагом 0,05l; l – длина отрезка [a,b]. xy -3,83814, , , ,01099, ,597357, ,18385, , , ,356714, , , ,529614, , , ,297514, , , ,124614, , , ,951714, ,365255, ,77887, , , ,605913, , , ,43319, Оглавление

4


Задача 2 Число оборотов f, как и в предыдущей задаче функционально зависит от температуры x. Требуется найти температуру, при которой число оборотов равно нулю, то есть найти все корни уравнения f(x)=0 на отрезке локализации [-4;4] и точностью 0,0001 xy ,641, ,218, ,85, , , ,6-0, ,20, ,81, ,40, , , ,8-2,2544 1,21,4576 1,611, ,464,0496 2,8115,1216 3,2189,3616 3,6292, Оглавление

5


Задача 3 Построить таблицу значений функции z(x,y) и ее отображение в виде поверхности на области с шагом 0,1 по каждому направлению. Оглавление

6


Задача 4 Организация использует пять складов, на которых находится S1, S2, S3, S4, S5 тонн сырья. Его требуется доставить на 8 предприятий организации. Потребности предприятий в сырье равны P1, P2, P3, P4, P5, P6, P7, P8 соответственно, причем Si = Pj. Стоимость перевозки 1 тонны сырья с i-го склада на j-е предприятие равна Aji (матрица {A} задана). Средствами поиска решения определить план перевозок, при котором фирма понесет наименьшие издержки по перевозкам, и определить эти издержки. Оглавление

7


Задача 5 Требуется составить план выпуска трех видов продукции П1, П2, П3. Для выпуска каждой единицы каждого вида продукции нужны ресурсы (сырье) четырех видов С1, С2, С3, С4 в количестве aij, где i – продукция, j – сырье. Запасы сырья C1, C2, C3, C4 – c1, c2, c3, c4 соответственно. Прибыль от выпуска единицы каждой продукции П1, П2, П3 – р 1, р 2, р 3. Требуется максимизировать прибыль. При этом следует учесть ограничения: Σaij·xicj, j=1..4, где xi – количество произведенной продукции. Оглавление