В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.
Ключевые слова:
безотказная работа, доверительный интервал, испытания, нормальный закон распределения, число отказов.
Определение показателей надёжности необходимо для формулирования требования по надежности к проектируемым устройствам или системам. Показатель надежности — это количественная характеристика одного или нескольких свойств, составляющих надежность объекта [1].
Поскольку отказы и сбои элементов являются случайными событиями, то теория вероятностей и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности должны выбираться из числа показателей, принятых в теории вероятностей [2, с. 13].
Количественные характеристики надежности при нормальном законе распределения отказов могут быть определены из следующих выражений:
(1)
P(t)=
(2)
λ(
)=
(3),
где
нормированная и центрированная функция Лапласа.
Произведем расчет параметров надежности испытаний, проведенных в течение 100 часов на 100 деталях, 34 из которых вышли из строя.
Для построения статистического ряда время испытаний разбивают на интервалы (разряды) и подсчитывают частоту, интенсивность и вероятность отказов, используя выражения (1), (2) и (3). Определяют доверительные интервалы математического ожидания и среднеквадратичного отклонения при нормальном законе распределения отказов и заданном коэффициенте доверия [3, с. 60].
Результаты вычислений представлены в таблице Excel (Таблица 1).
Таблица 1
Результаты расчета основных показателей испытаний
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
5 |
3 |
5 |
2 |
2 |
3 |
3 |
3 |
5 |
3 |
|
|
0,935 |
0,917 |
0,896 |
0,870 |
0,841 |
0,805 |
0,767 |
0,725 |
0,680 |
0,633 |
|
|
0,983 |
0,986 |
0,988 |
0,990 |
0,991 |
0,992 |
0,993 |
0,993 |
0,994 |
0,994 |
|
|
1,050 |
1,074 |
1,102 |
1,137 |
1,178 |
1,232 |
1,294 |
1,369 |
1,460 |
1,570 |
|
|
0,064 |
0,082 |
0,103 |
0,129 |
0,158 |
0,194 |
0,232 |
0,274 |
0,319 |
0,366 |
|
|
0,014 |
0,002 |
0,026 |
0,020 |
0,011 |
0,005 |
0,002 |
0,014 |
0,009 |
0,026 |
|
|
0,085065269 |
|||||||||
Листинг фрагмента программы расчета показателей при нормальном законе распределения:
‘Вычислим 43 строку таблицы(45)=============================Рн(t)
СтрокаТаблицы = 45
‘a=(t-Tср)/Сигма
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
a = Abs(Sheets(«ОсновнаяТаблица»).Cells(3, n).Value — Tcp) / Сигма
‘b=Фо
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
If a <= Sheets(«Таблица функции Лапласа»).Cells(2, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(2, 2).Value
GoTo далее
End If
If a >= Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
GoTo далее
End If
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value = a Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
GoTo далее3
End If
If a < Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value And a > Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value — a < a — Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
Else
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
End If
GoTo далее3
End If
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
далее3:
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 0.5 + ф0
Next
‘Вычислим 44 строку таблицы(46)=============================fн(t)
СтрокаТаблицы = 46
СтолбецТаблицы = 4
Pi = Application.WorksheetFunction.Pi
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 1 — 1 / (Сигма * Sqr(2 * Pi)) * Exp((Sheets(«ОсновнаяТаблица»).Cells(3, n).Value — Tcp) ^ 2 / (2 * (Сигма ^ 2)))
Next
‘Заполним 45 строку таблицы(47)=============================Лямбда н(t)
СтрокаТаблицы = 47
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Sheets(«ОсновнаяТаблица»).Cells(46, n).Value / Sheets(«ОсновнаяТаблица»).Cells(45, n).Value
Next
Для определения доверительного интервала для математического ожидания по таблице квантилей распределения Стьюдента находят квантиль вероятности. Используя выражения (4) и (5) проводят расчеты
(4)
(5)
‘Заполним 30 строку таблицы(32)=============================Tср min
СтрокаТаблицы = 32
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp — Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 31 строку таблицы(33)=============================Tср max
СтрокаТаблицы = 33
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp + Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
|
Тср, min = |
79,29380755 ч. |
|
Тср, max = |
172,43129 ч. |
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей χ
2
– квадрат распределения определяют квантили для заданных вероятностей
P
1
и
P
2
.
|
(0,05) = |
3,32511 |
|
(0,95) = |
16,919 |
‘Заполним 32 строку таблицы(34)=============================X1(0,05)
СтрокаОсновнойТаблицы = 34
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск10:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.05
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск11
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск11
End If
СледующийПоиск11:
СтолбецТаблКвантили = 11
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск12
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск12
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск12:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 33 строку таблицы(35)=============================X2(0,95)
СтрокаОсновнойТаблицы = 35
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск13:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.95
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск14
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск14
End If
СледующийПоиск14:
СтолбецТаблКвантили = 2
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск15
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск15
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск15:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
Получим минимальное σ
min
и максимальное σ
max
значения среднеквадратического отклонения:
(6)
(7)
‘Заполним 34 строку таблицы(36)=============================Сигма min
СтрокаТаблицы = 36
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(35, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 35 строку таблицы(37)=============================Сигма max
СтрокаТаблицы = 37
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(34, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
|
|
52,40646615 |
|
|
118,2140815 |
Число разрядов, на которые следует группировать статистический ряд, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и часто в нем обнаруживают незакономерные колебания), с другой стороны, оно не должен быть слишком малым (свойства распределения при этом описываются статистическим рядом слишком грубо).
Литература:
- ГОСТ 27.002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
- Федотов, А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск : Изд-во ОмГТУ, 2010 – 64 с.
- Коваленко, В. Н. Надежность устройств железнодорожной автоматики, телемеханики : учеб. пособие / В. Н. Коваленко. – Екатеринбург : Изд-во УрГУПС, 2013. – 87 с.
Основные термины (генерируются автоматически): Таблица функции, строка таблицы, доверительный интервал, Сигма, математическое ожидание, распределение отказов, среднеквадратичное отклонение, статистический ряд, таблица, теория вероятностей.
history 23 ноября 2016 г.
- Группы статей
- Статистический вывод
Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .
СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:
Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу , когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность ошибки первого рода (type I error).
Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.
Например, при построении доверительного интервала для оценки среднего значения распределения , его ширину рассчитывают таким образом, чтобы вероятность события « выборочное среднее (Х ср ) находится за пределами доверительного интервала » было равно уровню значимости . Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о равенстве среднего заданному значению .
Ошибка первого рода часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина ошибки первого рода задается перед проверкой гипотезы , таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.
Чрезмерное уменьшение уровня значимости α (т.е. вероятности ошибки первого рода ) может привести к увеличению вероятности ошибки второго рода , то есть вероятности принять нулевую гипотезу , когда на самом деле она не верна. Подробнее об ошибке второго рода см. статью Ошибка второго рода и Кривая оперативной характеристики .
Уровень значимости обычно указывается в аргументах обратных функций MS EXCEL для вычисления квантилей соответствующего распределения: НОРМ.СТ.ОБР() , ХИ2.ОБР() , СТЬЮДЕНТ.ОБР() и др. Примеры использования этих функций приведены в статьях про проверку гипотез и про построение доверительных интервалов .
Уровень надежности
Уровень доверия (этот термин более распространен в отечественной литературе, чем Уровень надежности ) — означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.
Уровень доверия равен 1-α, где α – уровень значимости .
Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).
В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.
Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание : Стоит отметить, что математически не корректно говорить, что Уровень доверия является вероятностью, того что оцениваемый параметр распределения принадлежит доверительному интервалу , вычисленному на основе выборки . Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что доверительный интервал , с вероятностью равной Уровню доверия, накроет истинное значение оцениваемого параметра распределения.
Уровень надежности в MS EXCEL
В MS EXCEL Уровень надежности упоминается в надстройке Пакет анализа . После вызова надстройки, в диалоговом окне необходимо выбрать инструмент Описательная статистика .
После нажатия кнопки ОК будет выведено другое диалоговое окно.
В этом окне задается Уровень надежности, т.е.значениевероятности в процентах. После нажатия кнопки ОК в выходном интервале выводится значение равное половине ширины доверительного интервала . Этот доверительный интервал используется для оценки среднего значения распределения, когда дисперсия не известна (подробнее см. статью про доверительный интервал ).
Необходимо учитывать, что данный доверительный интервал рассчитывается при условии, что выборка берется из нормального распределения . Но, на практике обычно принимается, что при достаточно большой выборке (n>30), доверительный интервал будет построен приблизительно правильно и для распределения, не являющегося нормальным (если при этом это распределение не будет иметь сильной асимметрии ).
Примечание : Понять, что в диалоговом окне речь идет именно об оценке среднего значения распределения , достаточно сложно. Хотя в английской версии диалогового окна это указано прямо: Confidence Level for Mean .
Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):
или эквивалентную ей
где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))
Решение задач описательной статистики средствами пакета анализа Microsoft Excel Текст научной статьи по специальности « Компьютерные и информационные науки»
CC BY
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Трущелёв Сергей Андреевич
Представлено определение описательной статистики , изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Трущелёв Сергей Андреевич
Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel
The paper presents a definition of descriptive statistics , and its main indicators. The necessity of their calculation is set out step by step in the procedure of statistical analysis. The message is a training component with.
Текст научной работы на тему «Решение задач описательной статистики средствами пакета анализа Microsoft Excel»
МЕТОДОЛОГИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ
Уважаемые читатели, коллеги!
В связи с возрастающими требованиями к качеству публикаций результатов научно-исследовательских работ в «Российском психиатрическом журнале» открыта новая рубрика «Методология научно-исследовательской деятельности». Планируется публикация обучающих и информационно-разъяснительных материалов по разным разделам науковедения, организации научной работы, биоинформатике, биостатистике, биоэтике и т.д. Приглашаем ученых и исследователей поделиться опытом в этой области. Надеемся, что наша инициатива будет поддержана не только в научном сообществе, но и воспринята в среде практикующих специалистов.
© С.А. Трущелёв, 2013 Для корреспонденции
УДК 311:004 Трущелёв Сергей Андреевич — кандидат медицинских наук,
доцент, ведущий научный сотрудник ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»
Адрес: 107076, г. Москва, ул. Потешная, д. 3 Телефон: (495) 963-25-31 E-mail: sat-geo@mail.ru
Решение задач описательной статистики средствами пакета анализа Microsoft Excel
Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel
The paper presents a definition of descriptive statistics, and its main indicators. The necessity of their calculation is set out step by step in the procedure of statistical analysis. The message is a training component with. Key words: science of science, biostatistics, descriptive statistics, data analysis toolpak, Excel
ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»
Moscow Research Institute of Psychiatry
Представлено определение описательной статистики, изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.
Ключевые слова: науковедение, биостатистика, описательная статистика, пакет анализа, Excel
Каждое явление (предмет исследования) определяется многими факторами. В научном исследовании полностью учесть все факторы и обеспечить их стабильность удается редко. Следовательно, явление, определяемое этими факторами, не поддается точному предсказанию — оно приобретает вероятностные черты, т.е. ведет себя случайным образом. Этому подвержены многие явления, поэтому они определяются случайной величиной, которая принимает в результате опыта или наблюдения одно из множества значений. Случайные величины могут быть дискретными (прерывными) и непрерывными. Немаловажно их распределение — правило, которое устанавливает связь между значениями случайной величины и вероятностями (частотами) их появления.
Наглядное представление о распределении случайных величин дает разброс песчинок, образующих кучу при высыпании (рассеивании) из некоторого точечного источника. Его проекция является параметром положения и соответствует математическому ожиданию распределения, если куча симметрична. Разброс песчинок (параметр рассеяния) характеризуется радиусом кучи на высоте примерно 2/3. Такой параметр рассеяния соответствует так называемому стандартному (среднеквадратичному) отклонению случайных величин в распределении. Горизонтальные расстояния песчинок от проекции источника (математического ожидания) моделируют рассеяние случайной величины. Поверхность кучи (ее высоты) соответствует частоте случайных величин на разных расстояниях от центра. Вершина кучи, расположенная под источником, отвечает максимуму частоты. На периферии высота кучи уменьшается до нуля, что соответствует уменьшению частот больших отклонений от центра рассеяния. Статистическая обработка совокупности данных состоит в некоторых осредняющих вычислительных процедурах, погашающих сугубо индивидуальные особенности — отклонения от общей закономерности и подчеркивающих типичные (популяцион-ные) свойства явления в целом. Начальный раздел математической статистики — описательная статистика — занимается характеристикой (описанием) картины случайного рассеяния по совокупности данных. В соответствии с законом распределения данных решаются вопросы выбора и вычислений надлежащих показателей. Описательная статистика включает методы организации, суммирования и описания данных. Дескриптивные (от англ. descriptive — описательный) показатели позволяют быстро обобщать данные. К описательным методам относят частотные распределения, меры централь-
ной тенденции и меры относительного положения [4, с. 95].
К основным показателям описательной статистики относятся среднее значение (среднее арифметическое, медиана, мода), усредненное значение, разброс (диапазон разброса данных), дисперсия, стандартное среднеквадратное отклонение (СКО), квартили, доверительный интервал [2, с. 28].
Статистическая обработка результатов исследований и получение показателей описательной статистики в недалеком прошлом обычно занимали много времени, однако с внедрением средств компьютерной техники многое изменилось — вычислительные процессы стали происходить очень быстро. Для проведения статистических расчетов в электронной таблице Microsoft Excel имеется пакет анализа. Надстройка «Анализ данных» располагается во вкладке «Данные», в крайне правом блоке ленты (рис. 1).
Для демонстрации вычислений будем использовать гипотетический набор данных. Далее приведем пошаговую инструкцию по созданию описательной статистики признака (показателя систолического давления), измеренного до лечения и после него, в группе наблюдения (n=60).
Для проведения вычисления обратитесь к ленте: Данные ^ Анализ данных ^ Описательная статистика ^ ОК. Затем, перейдя в окно инструмента, выберите входной интервал, группирование (по столбцам), поставьте галочку, если в первой строке выделены метки; в параметрах вывода на поле электронной страницы выберите ячейку вывода результатов, установите галочку рядом с итоговой статистикой. Потом нажмите кнопку ОК. После этого вы получите результаты описательной статистики выбранных признаков (рис. 2 и 3).
[й1 A «ï- V m И^ЭгшИ Главная Ш I» 1 Описательная статистика — Microsoft Excel □ 0 й Вставка Разметка страницы Формулы Данные Рецензирование Вид Разработчик Надстройки MetaXL Л □ S3
П внец m 1олучение jних данныхт ч [^Подключения ^Свойства Обновить все т && Изменить связи Подключения A I AIЯ I Я + Я 1А1 Я| Сортировка Со pi ч Ш ^ Очистить ^ Повторить Фильтр ™ № Дополнительно ировка и фильтр S Ii ы» вш а в Текст по Удалить ,—, столбцам дубликаты » Работа сданными Ф Фор» орма Jbi ssprfa ф ^ ^Анализданных Поиск решения Стр^И^ра Анализ
А в с D Е F G У 1 J К 1 L _
1 Номер_исс Признак_1 Признак_2 у
3 2 178 143 Анализ данным lia
Инструменты анализа У _ 1 о, 1
4 3 320 188 Двухфакторный дисперсионный^нализ без повторений Корреляция Л* 3 J d Отмена |
6 5 159 161 Экспоненциальное сглаживание Двухвыборочный Р-тест для дисперсии Анализ Фурье Гистограмма Скользящее среднее 1 Генерация случайных чисел_| Справка
Рис. 1. Пошаговый выбор инструмента анализа данных
Рис. 2. Окно инструмента описательной статистики
Среднее (арифметическое; М; х ) — одна из наиболее распространенных мер центральной тенденции, представляющая собой сумму всех значений, деленную на их количество. Если значения интересующего нас признака у большинства объектов близки к их среднему и с равной вероятностью отклоняются от него в большую или меньшую сторону, лучшими характеристиками совокупности будут само среднее значение и стандартное отклонение. Напротив, когда значения признака распределены несимметрично относительно среднего, совокупность лучше описать с помощью медианы и процен-тилей [1, с. 27].
Стандартная ошибка (т) — показатель надежности расчетного параметра; стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка — это убывающая функция объема выборки: чем меньше стандартная ошибка, тем более достоверной является оценка параметра. Весьма часто для описания непрерывных количественных данных используют стандартную ошибку, которая (в отличие от СКО) является не характеристикой, описывающей распределение наблюдений исследуемой выборки по области значений, а только мерой точности оценки популяционного среднего и, следовательно, не характеризует дисперсию (разброс) в анализируемой выборке. Однако часто именно стандартную ошибку среднего приводят в качестве параметра описательной статистики, пытаясь продемонстрировать тем самым малую вариабельность своих данных, так как всегда (по определению) т Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
60 Среднее 161,77 Среднее 134,03
61 Стандартная ошибка 12,46 Стандартная ошибка 6.59
62 Медиана 167 Медиана 121,5
63 Мода 72 Мода 141
64 Стандартное отклонение 96.54 Стандартное отклонение 51,03
65 Дисперсия выборки 9320.59 Дисперсия выборки 2604.34
66 Эксцесс 0.89 Эксцесс 2.75
67 Асимметричность 0.96 Асимметричность 1,43
68 Интервал 420 Интервал 254
69 Минимум 50 Минимум 55
70 Максимум 470 Максимум 309
71 Сумма 9706 Сумма 8042
72 Счет 60 Счет 60
73 74 Уровень надежности(95.0%) 24.94 Уровень надежности(95.0%) 13,18
Коэффициент вариации 60% Коэффициент вариации 38%
Рис. 3. Результаты описательной статистики двух признаков
Медиану и интерквартильный размах рекомендуется применять для описания распределения, не являющегося нормальным (а это большинство распределений медико-биологических параметров) [1, с. 34]. Интерквартильный размах указывают в виде процентилей. Рекомендуется указывать уровни 25 и 75%, которые соответствуют верхней границе 1-го и нижней границе 4-го квартилей. Пример описания: Me (25%; 75%) = 60 (23; 78).
Мода (Мо) — значение, которое встречается наиболее часто во множестве. Иногда в совокупности встречается более одной моды. Тогда говорят, что совокупность мультимодальна — свидетельство того, что набор данных не подчиняется нормальному распределению. Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Например, в группе пациентов наибольшая частота тяжести болезни будет равна моде. При экспертной оценке с помощью этого показателя определяют предпочтения участников исследования. Недостаток — показатель не учитывает поведение распределения в других точках.
Стандартное отклонение (синонимы: среднеквадратичное отклонение, квадратичное отклонение; стандартный разброс; СКО; в; о) — в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Измеряется в единицах случайной величины. Равно корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчете стандартной ошибки среднего арифметического, построении доверительных интервалов, статистической проверке гипотез, измерении линейной взаимосвязи между случайными величинами. Большое значение СО показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения во множестве сгруппированы вокруг среднего. Если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратичного отклонения), то полученные значения или метод их получения следует перепроверить.
Дисперсия (D; о2) — мера разброса случайной величины, т.е. ее отклонения от математического ожидания. Квадратный корень из дисперсии называется стандартным отклонением. Дисперсия измеряется в квадратах единицы измерения. Однако в самостоятельном виде (как, например, средняя арифметическая) дисперсия используется редко. Это скорее вспомогательный и промежуточный показатель, который применяют в других методах статистического анализа.
Эксцесс — скалярная характеристика островершинности графика плотности вероятности унимо-
дального распределения, которую используют в качестве некоторой меры отклонения рассматриваемого распределения от нормального. Если коэффициент эксцесса равен нулю или близок к нему, то плотность вероятности распределения имеет нормальный эксцесс. Если коэффициент эксцесса сильно больше нуля, то плотность вероятности имеет положительный эксцесс. Это, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. Когда коэффициент эксцесса сильно больше нуля, говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона. Для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.
Асимметричность (коэффициент асимметрии или скоса) — величина, характеризующая асимметрию распределения данной случайной величины. Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в альтернативном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
Интервал — размах показателей, т.е. разность между максимумом и минимумом значений вариант.
Максимум — наибольшее значение вариант.
Минимум — наименьшее значение вариант.
Сумма — сумма значений вариант.
Счет — количество вариант.
Уровень надежности — свойство объекта сохранять в установленных пределах значения всех параметров. Показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.
Коэффициент вариации случайной величины -мера относительного разброса случайной величины. Показывает, какую долю среднего значения этой величины составляет ее средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от стандартного отклонения, он измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. В Excel нет готовой функции для расчета коэффициента вариации. Расчет можно провести простым делением стандартного отклонения на среднее значение. Эти значения имеются в таблице описательной статистики. Для вычисления этого важного показателя в ячейке ниже надписи Уровень надежности пишем Коэффициент вариации, затем в ячейке справа делаем запись: =G64/G60. То же необходимо по-
вторить для вычисления коэффициента вариации для другого измерения.
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на панели инструментов в закладке «Главная». Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что совокупность данных является однородной, если коэффициент вариации менее 33%, неоднородной — если более 33%. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений.
Анализ показателей описательной статистики
При сравнении значений среднего, медианы, моды в каждом измерении следует отметить, что эти показатели сильно отличаются друг от друга.
Коэффициенты эксцесса и асимметрии значимо отличаются от установленных границ, коэффициенты вариации больше критического (предельного) значения. Следовательно, распределение данных в обеих группах измерений отлично от нормального. В последующем необходимо применять непараметрические методы статистического анализа. Для быстрой сравнительной оценки можно использовать показатели доверительных интервалов.
Для представления результатов сравнения обычно используют формат в виде М (95% ДИ) — значение среднего и указание 95% доверительного интервала. В тексте публикации запись может выглядеть следующим образом: Средний уровень систолического давления в группе пациентов до лечения составил 161,77 мм рт. ст. (95% ДИ от 136,83 до 186,71 мм рт. ст.), после лечения -134,03 мм рт. ст. (95% ДИ от 120,85 до 147,21 мм рт. ст.). Указанные доверительные интервалы имеют зону совмещения, следовательно, существенного различия в изменении признака нет. Исходя из этого с большой долей вероятности можно утверждать, что для данной группы пациентов лекарственный препарат, примененный для снижения уровня систолического артериального давления, был не эффективен.
1. Гланц С. Медико-биологическая статистика / Пер. с англ. -М., Практика, 1998. — 459 с.
2. Ланг Т.А., Сесик М. Как описывать статистику в медицине. Аннотированное руководство для авторов, редакторов и рецензентов / Пер. с англ. под ред. В.П. Леонова. -М.: Практическая медицина, 2011. — 480 с.
3. Леонов В.П. Ошибки статистического анализа биомедицинских данных // Междунар. журн. мед. практики. — 2007. -№ 2. — С. 19-35.
4. Трущелев С.А. Медицинская диссертация: руководство: 3-е изд. / Под ред. проф. И.Н. Денисова. — М.: ГЭОТАР-Медиа, 2009. — 416 с.
Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в
MS
EXCEL
.
Уровень значимости
(Level of significance) используется в
процедуре проверки гипотез
и при
построении доверительных интервалов
.
СОВЕТ
: Для понимания терминов
Уровень значимости и
Уровень надежности
потребуется знание следующих понятий:
-
выборочное распределение среднего
;
-
стандартное отклонение
;
-
проверка гипотез
;
-
нормальное распределение
.
Уровень значимости
статистического теста – это вероятность отклонить
нулевую гипотезу
, когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность
ошибки первого рода
(type I error).
Уровень значимости
обычно обозначают греческой буквой α (
альфа
). Чаще всего для
уровня значимости
используют значения 0,001; 0,01; 0,05; 0,10.
Например, при построении
доверительного интервала для оценки среднего значения распределения
, его ширину рассчитывают таким образом, чтобы вероятность события «
выборочное среднее (Х
ср
) находится за пределами доверительного интервала
» было равно
уровню значимости
. Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о
равенстве среднего заданному значению
.
Ошибка первого рода
часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина
ошибки первого рода
задается перед
проверкой гипотезы
, таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.
Чрезмерное уменьшение
уровня значимости α
(т.е. вероятности
ошибки первого рода
) может привести к увеличению вероятности
ошибки второго рода
, то есть вероятности принять
нулевую гипотезу
, когда на самом деле она не верна. Подробнее об
ошибке второго рода
см. статью
Ошибка второго рода и Кривая оперативной характеристики
.
Уровень значимости
обычно указывается в аргументах
обратных функций MS EXCEL
для вычисления
квантилей
соответствующего распределения:
НОРМ.СТ.ОБР()
,
ХИ2.ОБР()
,
СТЬЮДЕНТ.ОБР()
и др. Примеры использования этих функций приведены в статьях про
проверку гипотез
и про построение
доверительных интервалов
.
Уровень надежности
Уровень
доверия
(этот термин более распространен в отечественной литературе, чем
Уровень надежности
) — означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Уровень
доверия
равен
1-α,
где α –
уровень значимости
.
Термин
Уровень надежности
имеет синонимы:
уровень доверия, коэффициент доверия, доверительный уровень
и
доверительная вероятность (англ.
Confidence
Level
,
Confidence
Coefficient
).
В математической статистике обычно используют значения
уровня доверия
90%; 95%; 99%, реже 99,9% и т.д.
Например,
Уровень
доверия
95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор
уровня доверия
полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание
: Стоит отметить, что математически не корректно говорить, что
Уровень
доверия
является вероятностью, того что оцениваемый параметр распределения принадлежит
доверительному интервалу
, вычисленному на основе
выборки
. Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что
доверительный интервал
, с вероятностью равной
Уровню
доверия,
накроет истинное значение оцениваемого параметра распределения.
Уровень надежности в MS EXCEL
В MS EXCEL
Уровень надежности
упоминается в
надстройке Пакет анализа
. После вызова надстройки, в диалоговом окне необходимо выбрать инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно.
В этом окне задается
Уровень надежности,
т.е.значениевероятности в процентах. После нажатия кнопки
ОК
в
выходном интервале
выводится значение равное
половине ширины
доверительного интервала
. Этот
доверительный интервал
используется для оценки
среднего значения распределения, когда дисперсия не известна
(подробнее см.
статью про доверительный интервал
).
Необходимо учитывать, что данный
доверительный интервал
рассчитывается при условии, что
выборка
берется из
нормального распределения
. Но, на практике обычно принимается, что при достаточно большой
выборке
(n>30),
доверительный интервал
будет построен приблизительно правильно и для распределения, не являющегося
нормальным
(если при этом это распределение не будет иметь
сильной асимметрии
).
Примечание
: Понять, что в диалоговом окне речь идет именно об оценке
среднего значения распределения
, достаточно сложно. Хотя в английской версии диалогового окна это указано прямо:
Confidence
Level
for
Mean
.
Если
Уровень надежности
задан 95%, то
надстройка Пакет анализа
использует следующую формулу (выводится не сама формула, а лишь ее результат):
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР.2Х(1-0,95;СЧЁТ(Выборка)-1)
или эквивалентную ей
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР((1+0,95)/2;СЧЁТ(Выборка)-1)
где
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка))
– является
стандартной ошибкой среднего
(формулы приведены в
файле примера
).
или
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))
Подробнее см. в
статьях про доверительный интервал
.
50000 ₽
После получения оплаты я высылаю на вашу почту расчетный модуль “Надежность”. Оплатить можно через сайт по кнопке “в корзину” или напрямую на карту Сбера или Тинькова.
Если покупаете через организацию, свяжитесь со мной для уточнения деталей.
После покупки и вы получаете:
– расчетный модуль “Надежность” в эксель
– пример оформления пояснительной записки реального расчета надежности
– основные формулы в формате ворд для использования в ваших проектах
– шаблоны структурных схем надежности для быстрого прототипирования ваших проектов
- Описание
- Отзывы (0)
Описание
Расчет надежности в эксель| areliability.com блог инженера по надежности
Расчет надежности в эксель
Описание функций модуля:
1. Расчет вероятности безотказной работы единичного компонента в зависимости от интенсивности отказов и времени работы;
2. Расчет вероятности безотказной работы единичного компонента в зависимости от наработки на отказ и времени работы;
3. Перевод наработки на отказ в интенсивность отказов и обратно;
4. Определение наработки на отказ всей системы через вероятность безотказной работы;
5. Расчет вероятности события, что произойдет ровно n отказов;
6. Расчет гамма-процентной наработки до отказа;
7. Расчет вероятности безотказной работы системы при последовательном соединении элементов;
8. Расчет вероятности безотказной работы системы при нагруженном резервировании («горячий» резерв);
9. Расчет вероятности безотказной работы системы при ненагруженном резервировании («холодный» резерв);
10. Расчет вероятности безотказной работы системы при мажоритарном принципе резервирования;
11. Расчет вероятности безотказной работы системы при резервировании k из n компонентов (пример: из 24 насосов возможен отказ 6);
12. Расчет вероятности безотказной работы комбинированных систем, включающих в себя разные типы резервирования;
13. Расчет вероятности восстановления технической системы;
14. Расчет коэффициента готовности технической системы;
15. Расчет коэффициента оперативной готовности технической системы;
16. Расчет своевременного завершения операции (готовность к вылету самолета, предстартовой подготовки, начала технологического процесса);
17. Расчет времени простоя технической системы;
18. Расчет стоимости простоя технической системы.
Скриншот расчетного модуля «Надежность»:
Расчетный модуль не требует установки на компьютер дополнительных компонентов (макросов и т.д.), не требует подключения к Сети, работает на любом компьютере (Windows, Mac, Linux) с установленным ПО Excel.
Позволяет не зависеть от продления и получения лицензий зарубежного ПО в условиях санкций, исключает возможность передачи информации о том, что именно считалось в этом модуле в отличии от ПО из США, Европы и Израиля.
Расчетный модуль используют организации, выполняющие расчеты для нужд Армии и Флота РФ на компьютерах не имеющих подключения к Сети. Их список по понятным причинам я приводить не буду.
Позволяет выполнять профессиональные расчеты надежности без привлечения дорогостоящего зарубежного ПО.
Расчетный модуль создан на основе ГОСТ Р МЭК 61078-2021 “Надежность в технике. Структурная схема надежности”.
Если вам нужен онлайн калькулятор надежности — нажмите на эту ссылку или на кнопку ниже.
Внимание! Если вас интересует корпоративное групповое обучение специалистов вашей компании, пожалуйста перейдите по ссылке ниже. Возможна адаптация учебной программы под ваши требования/пожелания/возможности как по объёму учёбы срокам обучения, формату обучения, так и по балансу теория/практика.
До встречи на обучении! С уважением, Алексей Глазачев. Инженер и преподаватель по надежности.
1.Включить ПК, войти в пакет Microsoft Excel.
2.В меню «Файл» на панели инструментов
выбрать команду «Создать».
3.Ввести в таблицу первый набор исходных
данных (гамма-распределение наработок
до отказов), которому соответствуют
невосстанавливаемые элементы (N=100),
работающие до первого отказа. Время до
отказа (наработка) каждого невосстанавливаемого
элемента соответствует одной ячейке
электронной таблицы и выражается в
часах.
4.Ввести количество элементов, находящихся
на испытании:
|
N= |
100 |
5.Определить среднее время работы
элемента до отказа. Для этого воспользоваться
стандартной функцией СРЗНАЧ (для
указанного закона распределения):
|
T1= |
242,55 |
ч |
6.Определить число элементов, для которых
отказ произошел не позднее момента
времени t. Для этого воспользоваться
стандартной функцией СЧЕТЕСЛИ
v(t)=
СЧЕТЕСЛИ(A1:J10;»<242,55″)
|
V(t)= |
61 |
7.Определить вероятность отказа элемента.
Для этого воспользоваться формулой для
вычисления вероятности отказа элемента
|
Q(t)=V(t)/N= |
0,61 |
8.Определить вероятность безотказной
работы. Для этого воспользоваться
формулой для вычисления вероятности
безотказной работы
|
P(t)=1-Q(t)= |
0,39 |
9.Определить интенсивность отказов за
время испытаний t, полагая, что она
постоянна во времени: λ(t)=λ. Для этого
воспользоваться зависимостями между
показателями надежности
|
λ=1/T1= |
0,0412 |
1/ч |
10.Определить плотность распределения
наработки до отказа. Для этого
воспользоваться зависимостями между
показателями:
|
f(t)=λ*P(t)= |
0,0106 |
1/ч |
11.Ввести второй набор исходных данных
(равномерное распределение наработок
на отказ). Этому набору данных соответствует
работа восстанавливаемых или ремонтируемых
элементов.
12.Составить таблицу отказов элементов.
Для этого разбить интервал, равный
времени испытаний (в нашем случае это
700 ч), на 14 равных частей длительностью
по 50 ч каждая.
13.Ввести определенный (условный) интервал
времени
|
Δt= |
50 |
ч |
14.Посчитать количество отказавших
элементов на каждом интервале Δti.
Для этого воспользоваться стандартной
функцией СЧЕТЕСЛИ (В50:B63;’’<=50’’).
15.Результат занести в электронную
таблицу
|
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
Δti |
|
0 |
4 |
6 |
7 |
3 |
5 |
5 |
4 |
7 |
1 |
9 |
4 |
5 |
3 |
15.Ввести общее число элементов, участвующих
в испытаниях
|
N= |
10 |
16.Определить параметр потока отказов
элемента ωi. Для
этого воспользоваться зависимостью
количества фиксированных отказов Δniот интервала времени Δti,
в который этот отказ произошел:
ωi=∆ni/(N∆t).
17.Зная поток отказов на каждом интервале,
найти среднее значение потока отказов
за время испытаний (в нашем случае за
700 ч). Для этого воспользоваться стандартной
функцией СРЗНАЧ: ωср= СРЗНАЧ(В50:B63)
|
ωср= |
0,009 |
1/ч |
18.Определить время между отказами для
каждого отдельного элемента. Для этого
воспользоваться функцией вычитания
1=С30-В30….
19.Определить среднюю наработку на отказ
по массиву данных. Для этого воспользоваться
стандартной функцией Т = СРЗНАЧ(B68:J77)
|
Т1= |
87,82 |
ч |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.
Ключевые слова:
безотказная работа, доверительный интервал, испытания, нормальный закон распределения, число отказов.
Определение показателей надёжности необходимо для формулирования требования по надежности к проектируемым устройствам или системам. Показатель надежности — это количественная характеристика одного или нескольких свойств, составляющих надежность объекта [1].
Поскольку отказы и сбои элементов являются случайными событиями, то теория вероятностей и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности должны выбираться из числа показателей, принятых в теории вероятностей [2, с.
13].
Количественные характеристики надежности при нормальном законе распределения отказов могут быть определены из следующих выражений:
(1)
P(t)=
(2)
λ(
)=
(3),
где
нормированная и центрированная функция Лапласа.
Произведем расчет параметров надежности испытаний, проведенных в течение 100 часов на 100 деталях, 34 из которых вышли из строя.
Для построения статистического ряда время испытаний разбивают на интервалы (разряды) и подсчитывают частоту, интенсивность и вероятность отказов, используя выражения (1), (2) и (3). Определяют доверительные интервалы математического ожидания и среднеквадратичного отклонения при нормальном законе распределения отказов и заданном коэффициенте доверия [3, с. 60].
Результаты вычислений представлены в таблице Excel (Таблица 1).
Таблица 1
Результаты расчета основных показателей испытаний
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
5 |
3 |
5 |
2 |
2 |
3 |
3 |
3 |
5 |
3 |
|
|
0,935 |
0,917 |
0,896 |
0,870 |
0,841 |
0,805 |
0,767 |
0,725 |
0,680 |
0,633 |
|
|
0,983 |
0,986 |
0,988 |
0,990 |
0,991 |
0,992 |
0,993 |
0,993 |
0,994 |
0,994 |
|
λн(t) |
1,050 |
1,074 |
1,102 |
1,137 |
1,178 |
1,232 |
1,294 |
1,369 |
1,460 |
1,570 |
|
|
0,064 |
0,082 |
0,103 |
0,129 |
0,158 |
0,194 |
0,232 |
0,274 |
0,319 |
0,366 |
|
|
0,014 |
0,002 |
0,026 |
0,020 |
0,011 |
0,005 |
0,002 |
0,014 |
0,009 |
0,026 |
|
|
0,085065269 |
|||||||||
Листинг фрагмента программы расчета показателей при нормальном законе распределения:
‘Вычислим 43 строку таблицы(45)=============================Рн(t)
СтрокаТаблицы = 45
‘a=(t-Tср)/Сигма
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
a = Abs(Sheets(«ОсновнаяТаблица»).
‘b=Фо
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
If a <= Sheets(«Таблица функции Лапласа»).Cells(2, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(2, 2).Value
GoTo далее
End If
If a >= Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
GoTo далее
End If
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value = a Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
GoTo далее3
End If
If a < Sheets(«Таблица функции Лапласа»).
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value — a < a — Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
Else
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
End If
GoTo далее3
End If
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
далее3:
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 0.5 + ф0
Next
‘Вычислим 44 строку таблицы(46)=============================fн(t)
СтрокаТаблицы = 46
СтолбецТаблицы = 4
Pi = Application.WorksheetFunction.Pi
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).
Next
‘Заполним 45 строку таблицы(47)=============================Лямбда н(t)
СтрокаТаблицы = 47
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Sheets(«ОсновнаяТаблица»).Cells(46, n).Value / Sheets(«ОсновнаяТаблица»).Cells(45, n).Value
Next
Для определения доверительного интервала для математического ожидания по таблице квантилей распределения Стьюдента находят квантиль вероятности. Используя выражения (4) и (5) проводят расчеты
(4)
(5)
‘Заполним 30 строку таблицы(32)=============================Tср min
СтрокаТаблицы = 32
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).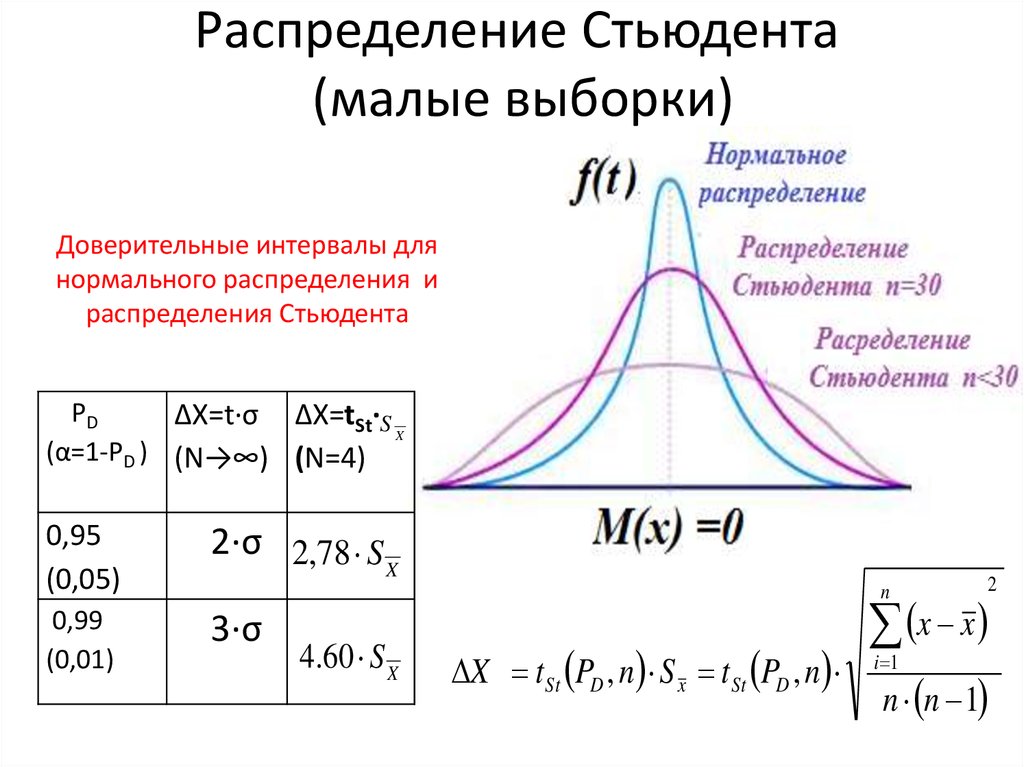
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 31 строку таблицы(33)=============================Tср max
СтрокаТаблицы = 33
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp + Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
|
Тср, min = |
79,29380755 ч. |
|
Тср, max = |
172,43129 ч. |
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей χ
2
– квадрат распределения определяют квантили для заданных вероятностей
P
1
и
P
2
.
|
(0,05) = |
3,32511 |
|
(0,95) = |
16,919 |
‘Заполним 32 строку таблицы(34)=============================X1(0,05)
СтрокаОсновнойТаблицы = 34
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).
СтрокаТабл = 4
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск10:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.05
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск11
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск11
End If
СледующийПоиск11:
СтолбецТаблКвантили = 11
While Sheets(«Квантили распределения хи»).
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск12
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск12
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск12:
x1 = Sheets(«Квантили распределения хи»).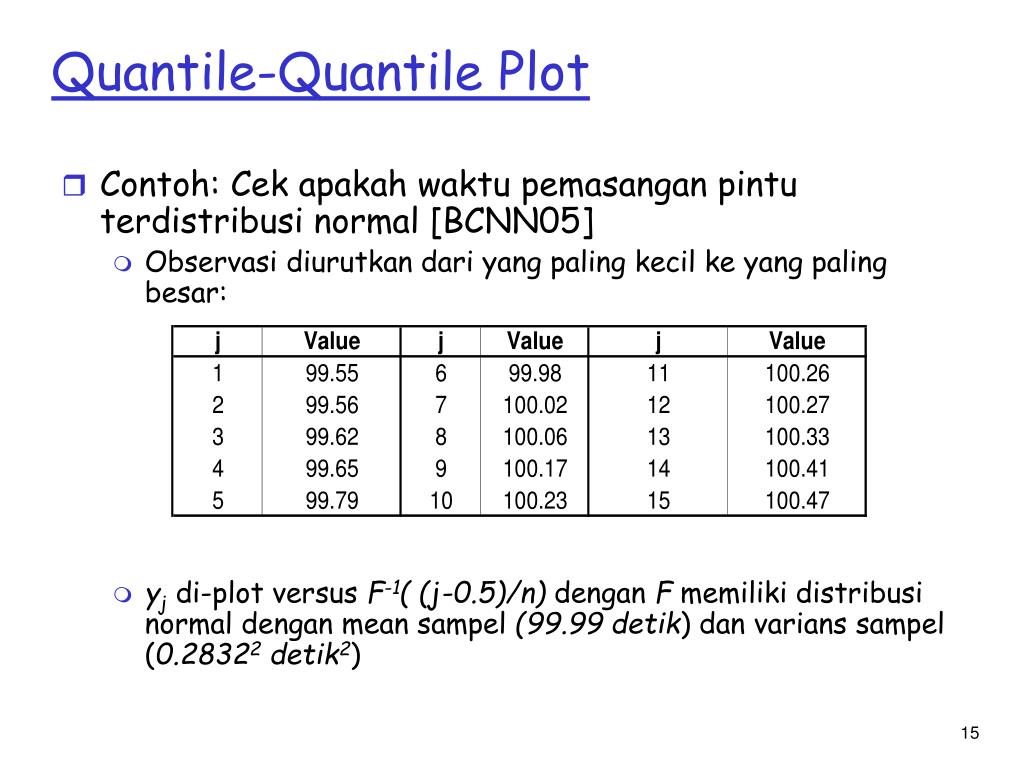
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 33 строку таблицы(35)=============================X2(0,95)
СтрокаОсновнойТаблицы = 35
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск13:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск14
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск14
End If
СледующийПоиск14:
СтолбецТаблКвантили = 2
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск15
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).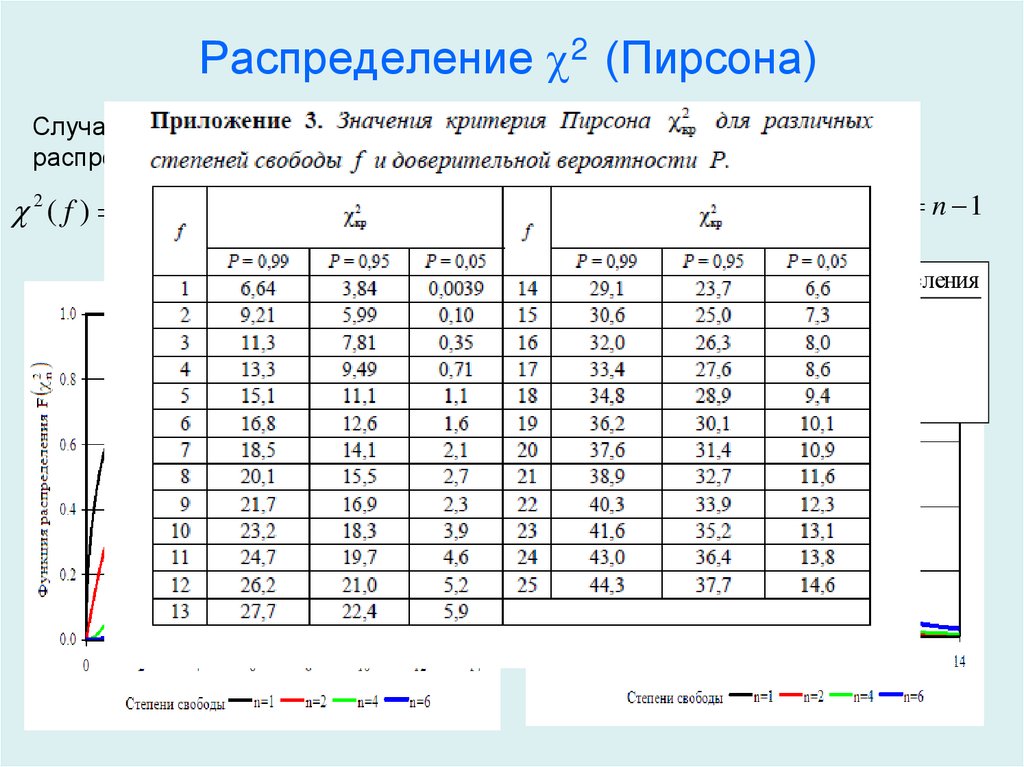
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск15
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск15:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).
Получим минимальное σ
min
и максимальное σ
max
значения среднеквадратического отклонения:
(6)
(7)
‘Заполним 34 строку таблицы(36)=============================Сигма min
СтрокаТаблицы = 36
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(35, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 35 строку таблицы(37)=============================Сигма max
СтрокаТаблицы = 37
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
Число разрядов, на которые следует группировать статистический ряд, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и часто в нем обнаруживают незакономерные колебания), с другой стороны, оно не должен быть слишком малым (свойства распределения при этом описываются статистическим рядом слишком грубо).
Литература:
-
ГОСТ 27.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
- Федотов, А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск : Изд-во ОмГТУ, 2010 – 64 с.
- Коваленко, В. Н. Надежность устройств железнодорожной автоматики, телемеханики : учеб. пособие / В. Н. Коваленко. – Екатеринбург : Изд-во УрГУПС, 2013. – 87 с.
Основные термины (генерируются автоматически): Таблица функции, строка таблицы, доверительный интервал, Сигма, математическое ожидание, распределение отказов, среднеквадратичное отклонение, статистический ряд, таблица, теория вероятностей.
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ
КОРРЕЛЯЦИИ В ПРОГРАММЕ EXCEL
t-статистика=0,99*(КОРЕНЬ(20-2)/КОРЕНЬ(1-0,99*0,99))=29,7745296027549
Коэффициент корреляции=0,991477169252612
Распределение Стьюдента=2,10092204024104
Расчетное значение t-статистики больше квантиля распределения Стьюдента, следовательно величина коэффициента корреляции является значимой.
2. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ
МЕЖДУ ДВУМЯ ВЕЛИЧИНАМИ
1-ый способ
| a1= 0,5014 | a0= 2,5326 |
| Se1= 0,0155 | Se0= 0,7075 |
| R2= 0,9830 | Se= 0,5561 |
| Se= 0,5561 | n-k-1= 18 |
| QR= 322,4250 | Qe= 5,5670 |
Для проверки адекватности
модели нашли квантиль распределения Фишера Ff. с помощью функции FРАСПОБР
FРАСПОБР=4,4139
Проверили адекватность
построенной модели, используя расчетный уровень значимости (P):
2,18499711496499E-17
2 –й способ
|
а=2,532579627 |
|
в=0,50139175 |
Для данного примера
уравнение модели имеет вид:Y=2,53+0,5X
Проверка адекватности модели выполняется по расчетному уровню значимости P,
указанному в столбце Значимость F.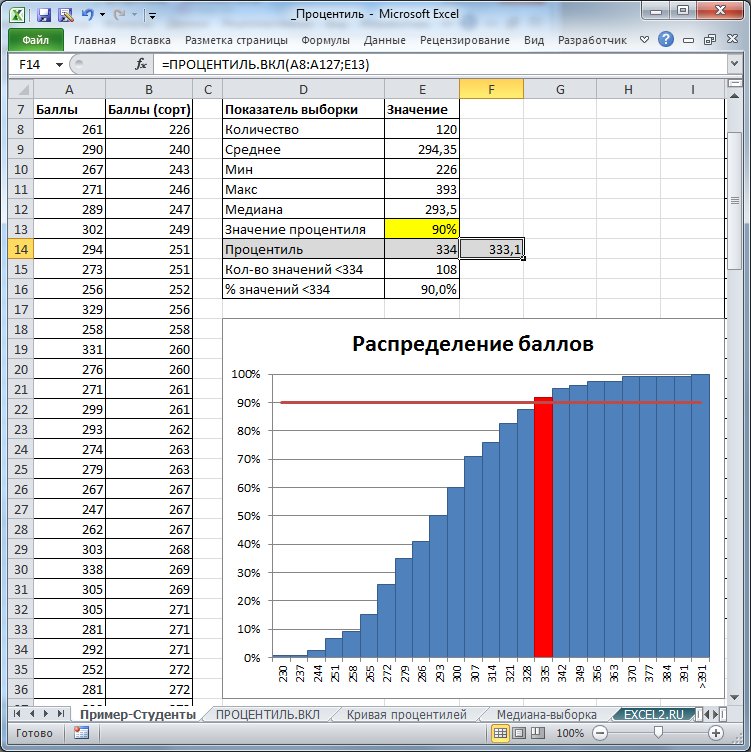
расчетный уровень значимости меньше заданного уровня значимости α =0,05, то модель адекватна.
Проверка статистической значимости коэффициентов модели выполняется по расчетным
уровням значимости P, указанным в столбце P-значение. Если расчетный уровень значимости меньше заданного
уровня значимости α =0,05, то соответствующий
коэффициент модели статистически значим.
Множественный R – коэффициент корреляции. Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями. Для данного примера R= 0,99. Это позволяет сделать
вывод, что качество земли – один из основных факторов, от которого зависит
урожайность зерновых культур.
R-квадрат – коэффициент
детерминации. Он получается возведением в квадрат коэффициента корреляции –
R2=0,98. Он
показывает, что урожайность зерновых культур на 98% зависит от качества почвы,
а на долю других факторов приходится 0,02%.
3-ий способ (графический)
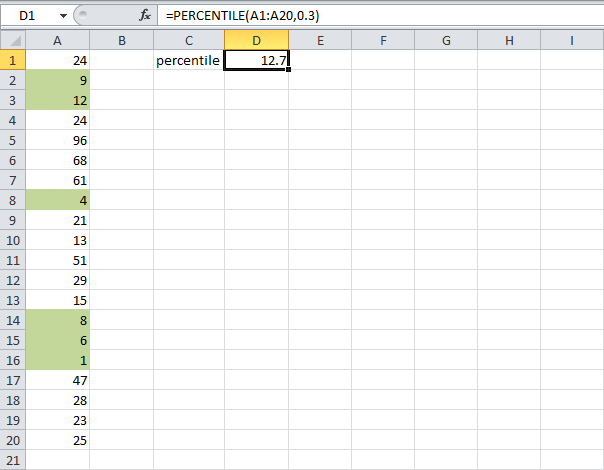
Расчет квантилей или процентилей в Excel
В этом руководстве показано, как вычислять квантили или процентили, связанные с доверительными интервалами, в Excel с помощью программного обеспечения XLSTAT.
Квантиль и процентили
XLSTAT имеет полный инструмент для вычисления квантилей или процентилей, их доверительного интервала и графического представления.
Квантили являются важными статистическими показателями, их легко понять. Квантиль 0,5 — это значение, при котором половина выборки находится ниже, а другая половина — выше. Его еще называют средним. Квантиль называется процентилем, если он основан на шкале от 0 до 100. 0,95-квантиль эквивалентен 95-процентилю и таков, что 95 % выборки ниже его значения, а 5 % выше.
Набор данных для создания квантиля
Набор данных был получен от [Lewis T. and Taylor L.R. (1967). Введение в экспериментальную экологию, Нью-Йорк: Academic Press, Inc. Это касается 237 детей, описанных по полу и росту в сантиметрах (1 см = 0,4 дюйма).
Настройка расчета определенного квантиля
После открытия XLSTAT выберите XLSTAT / Description / Quantiles , или нажмите на соответствующую кнопку панели инструментов «Описание» (см.
После нажатия кнопки появится диалоговое окно Quantile . Выберите данные на листе Excel.
В нашем случае; переменная — это «Высота». Данные должны быть количественными .
Поскольку для переменных был выбран заголовок столбца, необходимо активировать опцию Метки переменных .
Мы выбираем метод оценки по умолчанию ( средневзвешенное значение при x(Np) ) и оба типа доверительных интервалов с доверительной вероятностью 95 % .
Подробную информацию о статистических методах можно найти в справке XLSTAT.
Во вкладке диаграммы выбираем все диаграммы и нас интересует 67-процентиль (две трети детей меньше, а одна треть выше).
Вычисления начинаются после того, как вы нажмете на ОК . Затем будут отображены результаты.
Интерпретация результатов генерации квантилей
В первой таблице показаны некоторые описательные статистические данные о переменной высоты.
Затем отображается значение 67-процентиля. Две трети детей меньше 164,58 см.
Первый график (см. ниже) позволяет нам визуализировать эмпирическую кумулятивную функцию распределения со значением 67-го процентиля.
Вторая и третья диаграммы представляют собой коробчатую диаграмму и диаграмму рассеяния. 67-процентиль отображается синей линией.
Вы также можете использовать подвыборки, например пол можно использовать в качестве групповой переменной. Веса, связанные с наблюдениями, также могут быть включены.
Была ли эта статья полезной?
- Да
- №
Квантиль (квартиль, дециль и процентиль): расчет вручную + Microsoft
Квантиль — важная статистическая концепция, позволяющая разделить данные на равные группы.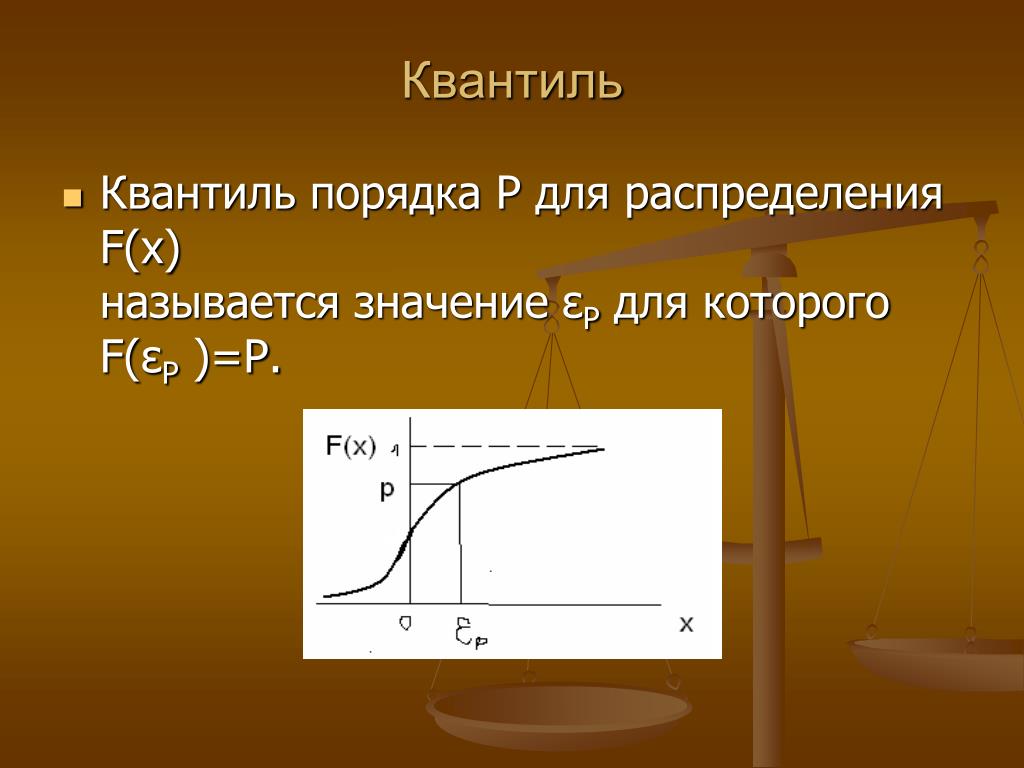
Квантиль
Квантиль — это мера, указывающая значение, ниже которого падает определенная доля наблюдений в группе наблюдений. Квантиль используется в статистике для разделения группы наблюдений на группы одинакового размера. Например, квантиль 0,25 — это значение, ниже которого падают 25% наблюдений; квантиль 0,50 — это значение, ниже которого падает 50%, и так далее. Другим родственным измерением является медиана, которая совпадает с квантилем 0,50, поскольку 50% данных находятся ниже медианы.
Какие общие квантили существуют?
Некоторые распространенные квантили включают:
1. Квартиль
Квартиль — это тип квантиля, который делит группу наблюдений на четыре группы одинакового размера.
2. Дециль
Дециль – это мера, которая делит группу наблюдений на десять групп одинакового размера. Например, в группе наблюдений первый дециль (D1) — это значение, ниже которого попадают первые 10% наблюдений, второй дециль (D2) — это значение, ниже которого попадают первые 20% наблюдений, и скоро. 9-й дециль (D9) — это значение, ниже которого опускаются последние 10% наблюдений.
3. Процентиль
Процентиль — это мера, указывающая значение, ниже которого находится определенный процент наблюдений в группе наблюдений. Например, в группе наблюдений 20-й процентиль (P20) — это значение, ниже которого опускаются первые 20% наблюдений, 50-й процентиль (P50) — это значение, ниже которого опускаются средние 50% наблюдений, и 95-й процентиль (P95) — это значение, ниже которого падают последние 95% наблюдений.
50-й процентиль также является медианой, вторым квартилем и 5-м децилем.
Процентиль: Расчет вручную / Microsoft Excel
Процентиль — это мера, используемая в статистике для указания значения, ниже которого находится определенный процент наблюдений в группе наблюдений.
Чтобы найти местоположение определенного процентиля, такие программы, как Minitab, Python, R и Excel, используют следующие шаги:
- Расположите наблюдения в порядке возрастания.
- Используйте формулу для определения положения процентиля, чтобы вычислить положение, в котором будет располагаться значение процентиля, используя желаемое значение процентиля и общее количество наблюдений в качестве входных данных. Существует два подхода: EXC (Exclusive) и INC (Inclusive). Процентное положение в подходе EXC определяется формулой (K(N+1)), а положение в подходе INC определяется формулой (K(N-1)+1).
- Если местоположение процентиля является целым числом, значение в этой позиции в упорядоченном списке наблюдений является значением процентиля.
- Если местоположение процентиля не является целым числом, значение процентиля рассчитывается путем вычисления значения на пропорциональной основе между этими двумя числами.
Чтобы найти 65-й процентиль в группе из 8 наблюдений, вы должны сначала расположить наблюдения в порядке возрастания: 8, 9, 12, 22, 23, 33, 55, 61.
Затем вы должны использовать формулу для местоположения процентиля, чтобы вычислить положение, в котором будет расположен 65-й процентиль:
Для ПРОЦЕНТИЛЬ.ИСКЛ рассчитанный ранг равен (K(N+1)).
Расположение в процентиле (с использованием эксклюзивного подхода) = (left(frac{65}{100}right)(8+1)) = 5,85
Поскольку положение в процентиле не является целым числом, 65-й процентиль будет между 5-м пунктом (номер 23) и 6-м пунктом (номер 33) на пропорциональной основе. Это будет (23+0,85(33-23) = 31,5).
Для PERCENTILE.INC (и PERCENTILE) рассчитанный ранг равен (K(N-1)+1).
Расположение в процентах (с использованием инклюзивного подхода) = ((65/100) (8-1)+1) = 5,55
Поскольку местоположение процентиля не является целым числом, 65-й процентиль будет почти посередине между 5-м элементом (число 23) и 6-м элементом (число 33).
Квартиль: пример расчета вручную
Квартиль — это статистическое значение, которое делит набор данных на четыре равные части или четверти. Первый квартиль, также известный как нижний квартиль или Q1, — это значение, которое отделяет самые низкие 25 % данных от остальных. Второй квартиль, также известный как медиана или Q2, представляет собой значение, которое отделяет самые низкие 50% данных от самых высоких 50% данных. Третий квартиль, также известный как верхний квартиль или Q3, — это значение, которое отделяет самые высокие 25% данных от остальных.
Например, если у нас есть следующие числа: 14, 9, 10, 11, 11 и 6, мы можем разделить данные на четыре равные группы, найдя первый, второй и третий квартили.
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Затем нам нужно найти медиану, или Q2, которая является средним значением в наборе данных.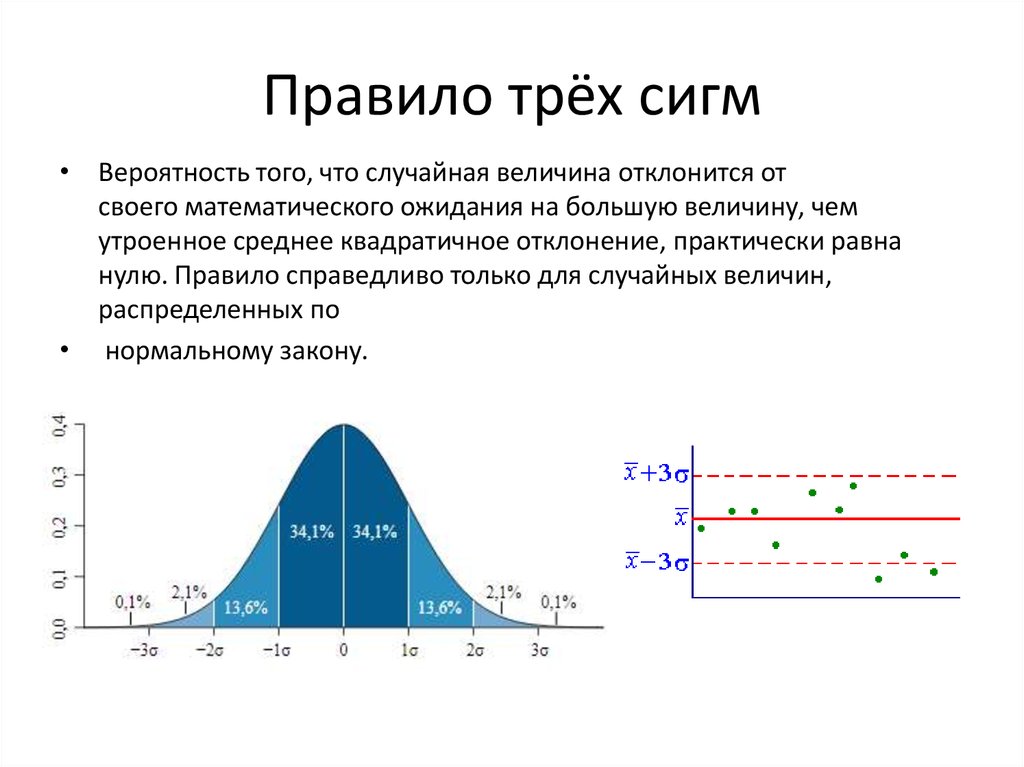
Чтобы найти нижний квартиль или Q1, мы берем медиану значений ниже медианы. В данном случае это будет медиана 9. Чтобы найти верхнюю квартиль или Q3, мы берем медиану значений выше медианы. В данном случае это будет медиана 11, 11 и 14, что равно 11.
Таким образом, для этого набора данных квартили: эти числа расчета квартиля не совпадают с расчетом Excel?
Квартиль Использование Excel:
Для расчета квартилей такие программы, как Microsoft Excel и Minitab, используют метод процентилей, как объяснялось ранее. Q1 рассчитывается как 25-й процентиль, Q2 — как 50-й и Q3 — как 75-й процентиль. Это приводит к тому, что значение квартиля иногда отличается от значения, рассчитанного с использованием обычного ручного метода расчета.
Возьмем тот же пример, который мы использовали ранее в ручном расчете для расчета первого квартиля (Q1).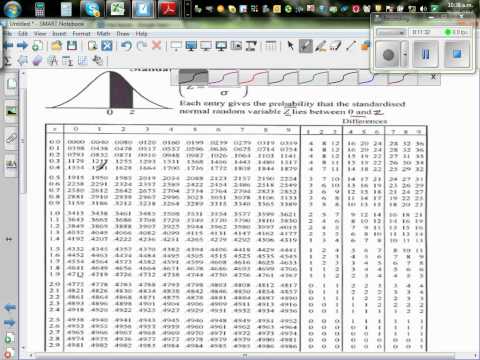
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Вы можете использовать функцию КВАРТИЛЬ.ИСКЛ или КВАРТИЛЬ.ВКЛ. найти квартили набора чисел в Excel.
Quartile.Exc
Для QUARTILE.EXC расчетный ранг равен K*(N+1). Чтобы рассчитать положение Q1 (или 25-го процентиля), подставим в эту формулу соответствующие значения.
Местоположение 1-го квартиля (с использованием эксклюзивного подхода) = (25/100) * (6+1) = 1,75
Поскольку положение процентиля не является целым числом, 1-й квартиль будет между 1-м элементом (номер 6) и 2-м элементом (номер 9) на пропорциональной основе. Получится (6 + (9-6)*0,75) = 8,25.
Использование Minitab: Если вы используете Minitab для расчета Q1, это значение (8,25), которое вы получите в описательной статистике. Minitab использует метод EXC для расчета процентилей и квартилей.
Квартиль.Вкл
Для КВАРТИЛЬ.

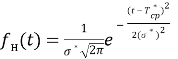
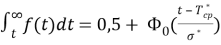
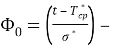
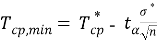
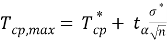
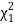
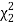
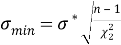
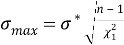
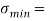


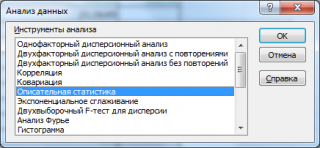









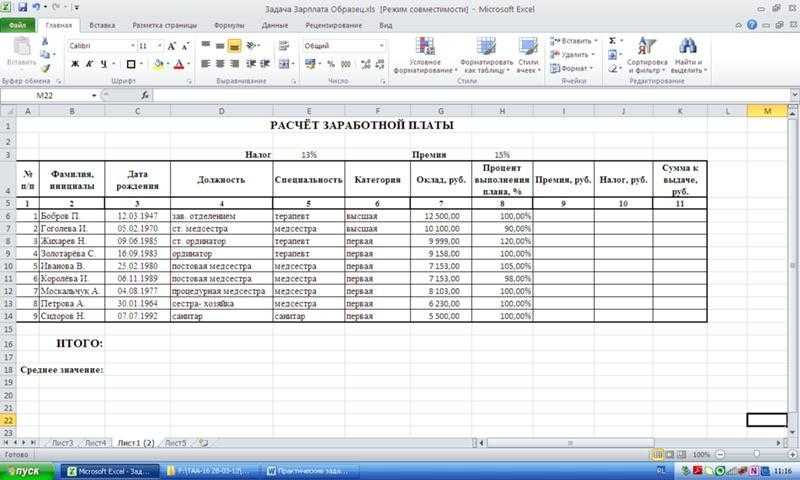
 002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.