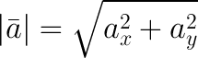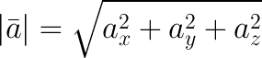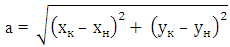6.1. Векторы
В
- сложение — два вектора а и b с одинаковым числом компонент образуют новый вектор с:сi= ai+ bi ;
- умножение на число — каждая компонента вектора умножается на число, т.е. b = λа означает bi= λаi
здесь i — номер компоненты вектора.
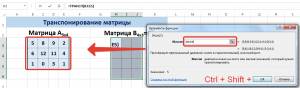
Упражнение 6.1.1. Сложить два вектора:
- Ввести в первую строку вектор Х — (А1:Е1)
- Ввести во вторую строку вектор Y — (А2:Е2)
- Найти сумму векторов –
- выделить блок ячеек для результата в третьей строке ( А3:Е3 );
- ввести в строке формул =А1:Е1+А2:Е2
- нажать Ctrl+Shift+Enter.
Иллюстрация к примеру — рис. 14.

Рис. 14. Иллюстрация к упражнению 6.1.1.
Задача 6.1.1 . Умножить вектор на число.
Умножение вектор-столбца на вектор-строку.

1-й способ: записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5.
2 -й способ (более экономный): выделить блок B2:D5. Запишем в него формулу массива <=А2:А5*B1:D1>.
А
Примечание. Если ввести формулу <=B1:D1* А2:А5>, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомножителе должно равняться числу строк во втором сомножителе).
У
пражнение 6.1.3. Вычислить скалярное произведение двух векторов.
- У
становить курсор в ячейку, где нужен результат.
- Щёлкнуть кнопку автосуммы — .
- Выделить массив Х (А5:А12).
- Нажать знак умножить —*.
- Выделить массив Y (B5:B12).
- Нажать Ctrl + Shift + Enter.
Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12).
6.2. Матричные операции
Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.
Упражнение 6.2.1. Сложение матриц.
Задание. Сложить матрицы М и N, где
Решение.
M= 

1-й способ:
- Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2.
- В блок А4:С5 ввести табличную формулу <= А1:С2 + E1:G2>.
Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.
Использование имен делает процедуру ввода табличной формулы намного проще:
- Задать диапазонам А1:С2 и E1:G2 имена М и N.
- В блок E4:G5 ввести табличную формулу < = М + N >.
Результат, естественно, тот же: M+N =
Упражнение 6.2.2 . Вычислить линейную комбинацию матриц 2*М — N (матрицы М.и N из упражнения 6.2.1.).
Решение. В блок А7:С8 ввести табличную формулу <= 2*М — N >.
Результат: 2*M — N =
Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение.
Д
МОБР — вычисление обратной матрицы;
МУМНОЖ — перемножение матриц;
Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.
У
Решение. Разместить исходную матрицу в блоке А1 :СЗ.
- В ячейке Е2 поместить формулу для вычисления определителя = МОПРЕД (А1:СЗ).
- В блок А5:С7 ввести формулу для вычисления обратной матрицы:
- выделить блок А5:С7 (он имеет три строки и три столбца, как и исходная матрица).
- Ввести формулу <=МОБР (А1:СЗ)>.
Примечания:
- При использовании Мастера функций нужно завершать ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке «ОК»).
- Для удобства работы рекомендуется задавать имена исходной матрице и обратной матрице.
- Проверить правильность вычисления обратной матрицы умножением ее на исходную:
- задать имена исходной матрице — А и обратной матрице — АО;
- в блок D5:F7 ввести формулу .
- к
ак и следовало ожидать, получилась матрица, близкая к единичной.
Рис. 16. Иллюстрация к упражнению 6.2.3.
У
Решение:
пражнение 6.2.4. Вычислить абсолютные отклонения величин в матрицах.
В блок А9:С11 ввести табличную формулу <= abs (A-AО)>.

Пример вычисления определителя матрицы
А, введенной в формулу как массив констант: =МОПРЕД(<-73; 78; 24:
Задача 6.2.2 . При каком значении элемента а33 определитель матрицы А обратится в нуль.
Задача 6.2.3. Дана матрица S = 
Е — единичная матрица.
Задача 6.2.4. Вычислить обратную матрицу для
и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.
Набор матричных операций в Excel беден.
Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive .
Вычисление длины (модуля) вектора в EXCEL
history 14 декабря 2015 г.
- Группы статей
- Пользовательский формат
- Векторы
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
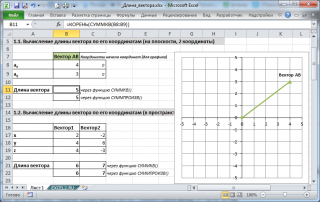
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
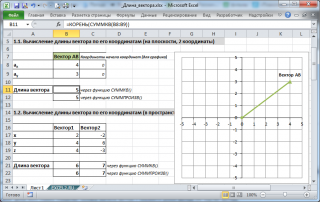
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
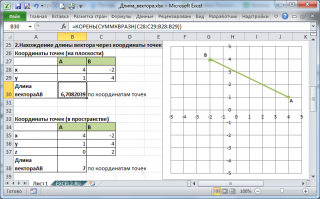
2. Нахождение длины вектора через координаты точек
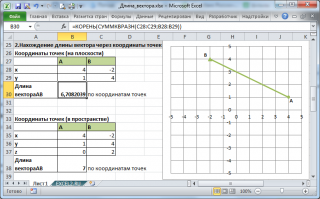
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
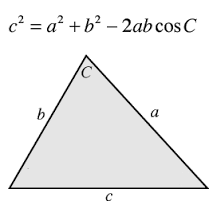
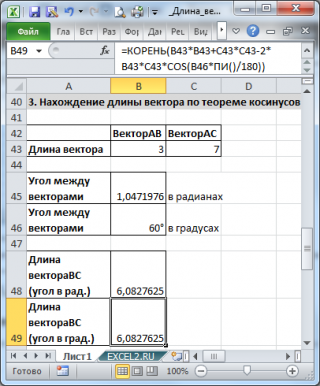
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
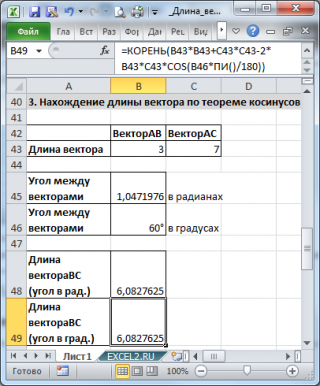
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL
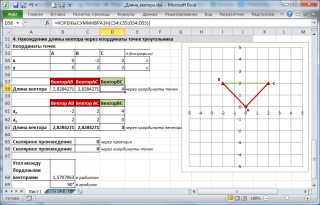
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
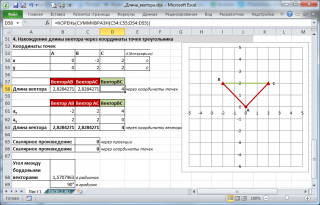
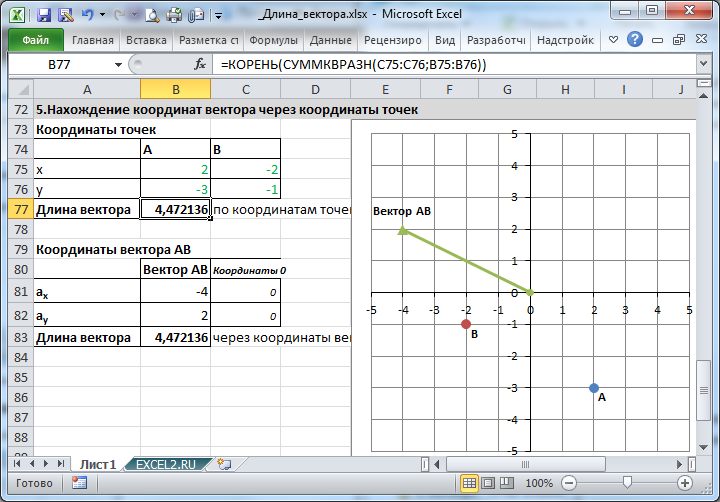
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
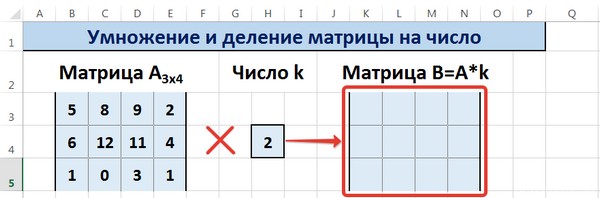
Умножение и деление матрицы на число в Excel
Способ 1
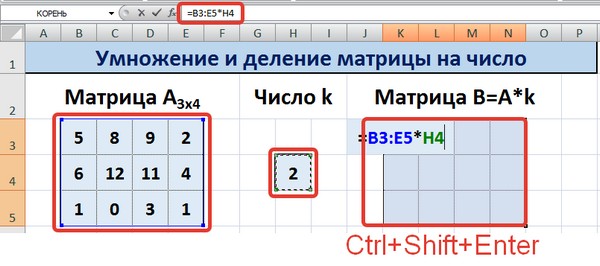
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
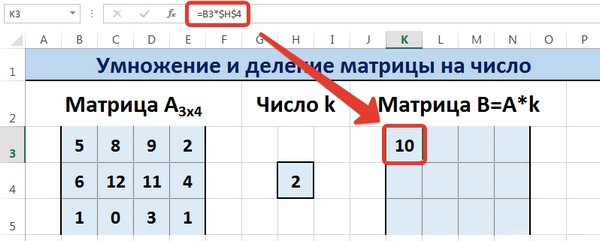
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
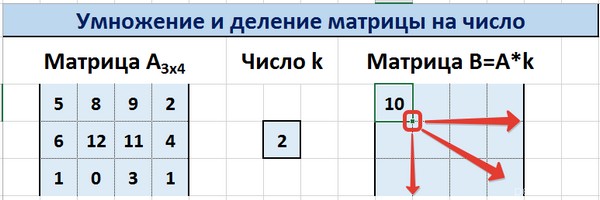
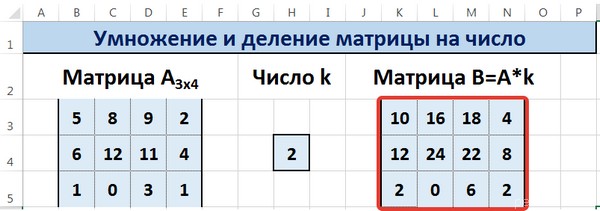
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
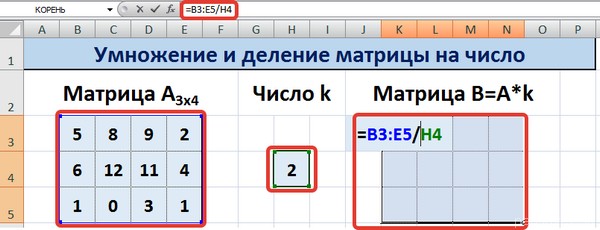
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
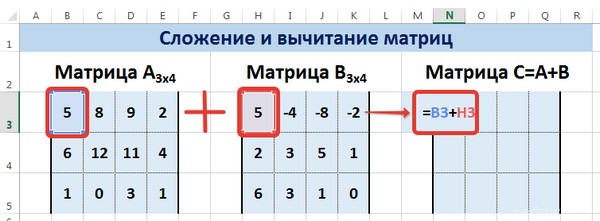
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
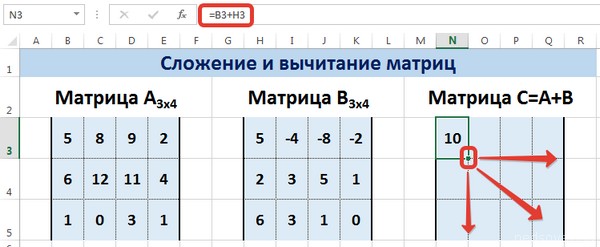
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
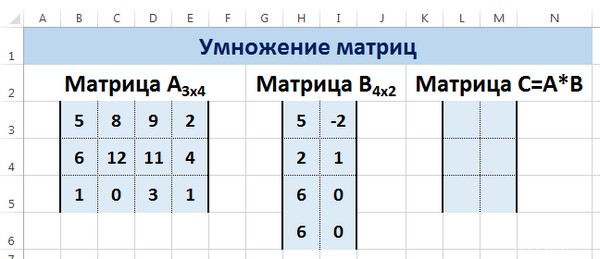
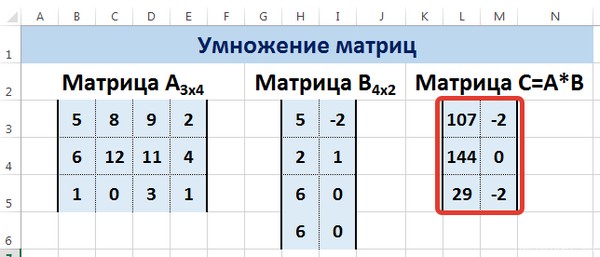
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
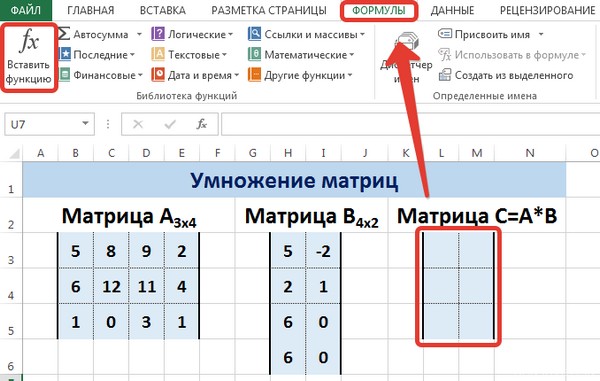
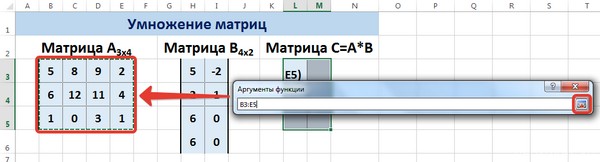
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
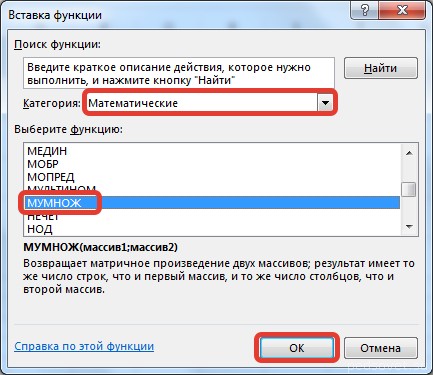
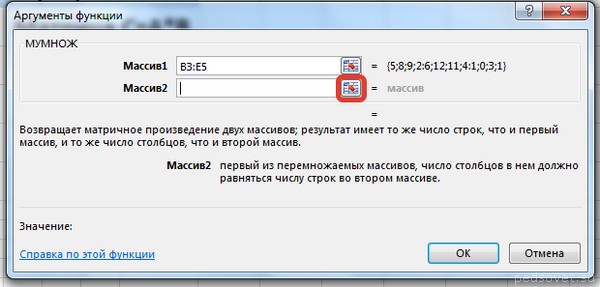
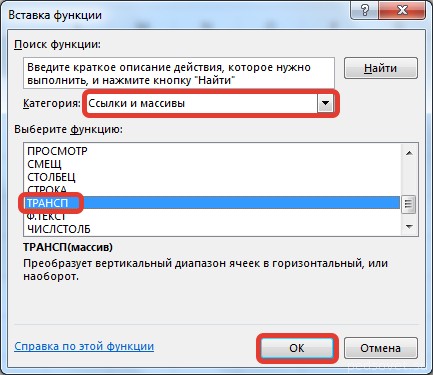
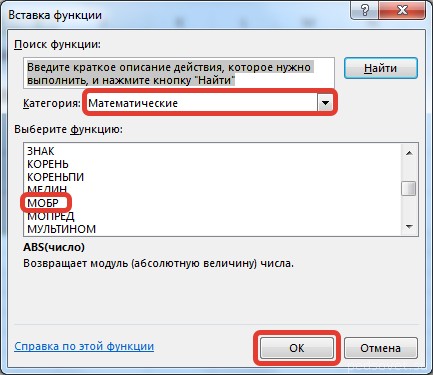
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
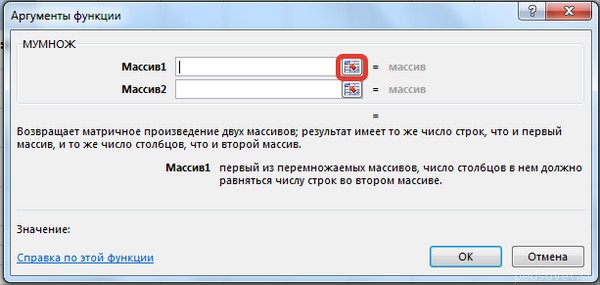
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
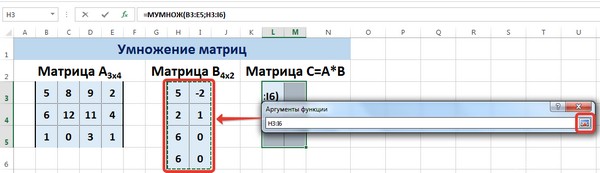
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
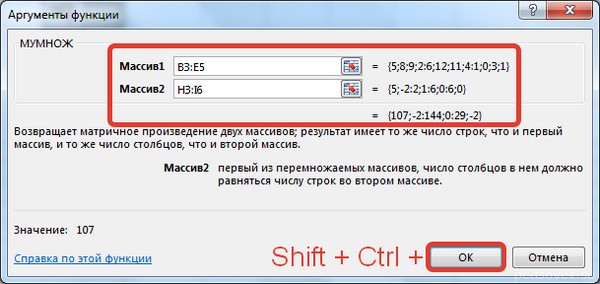
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
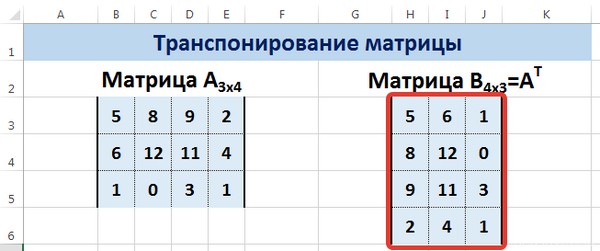
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
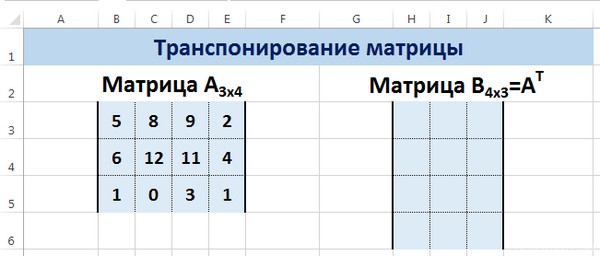
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
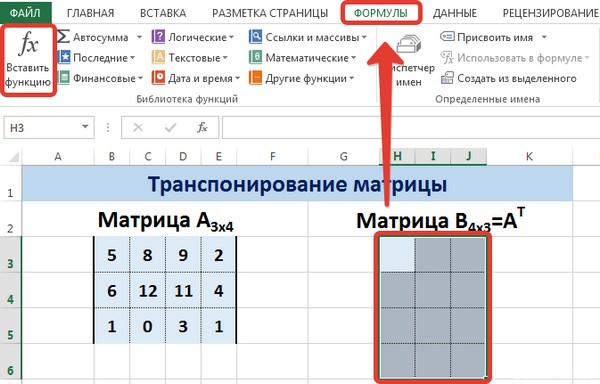
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
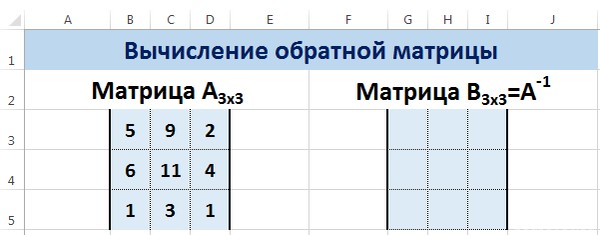
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
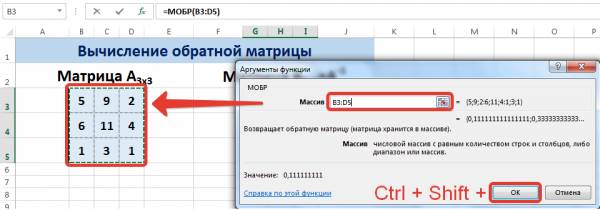
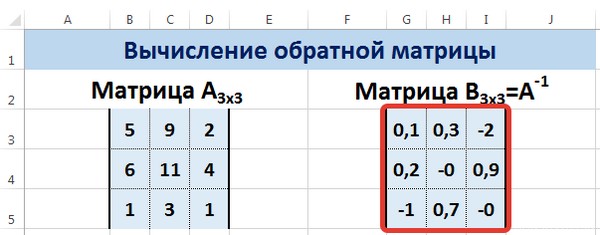
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
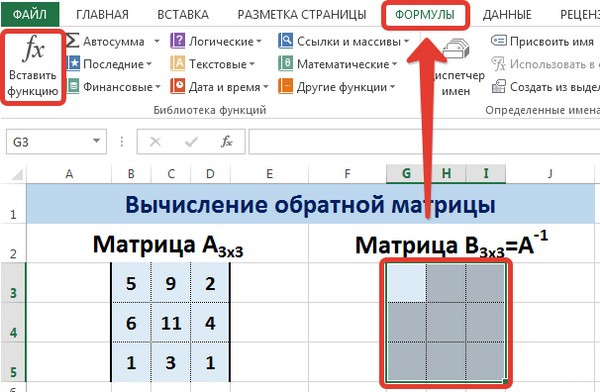
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
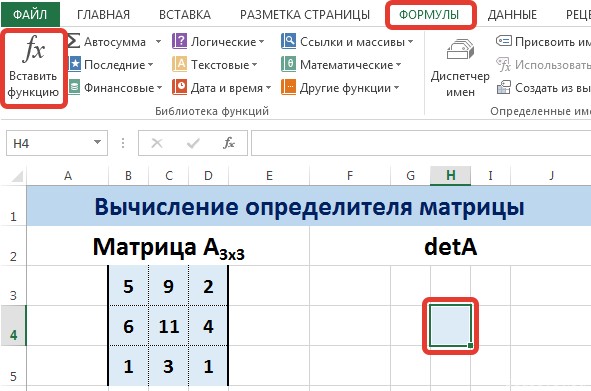
Как найти определить матрицы в Excel
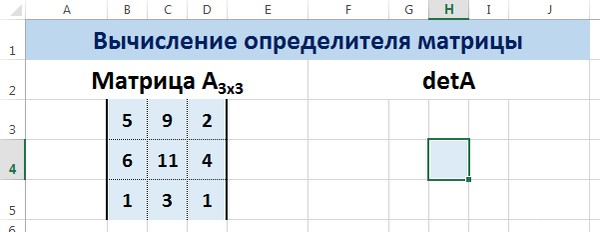
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
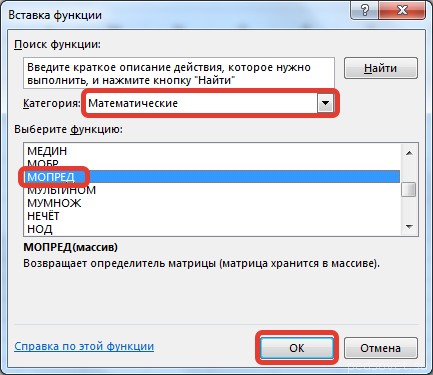
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
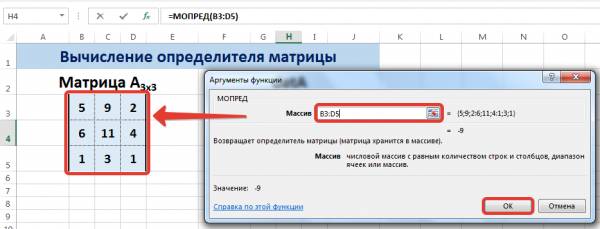
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
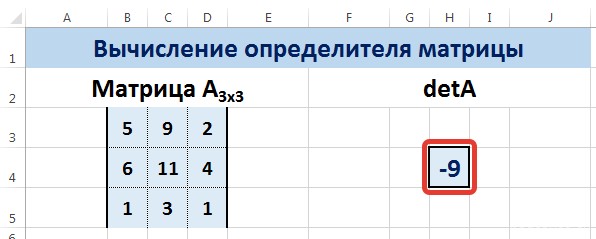
Нажмите для увеличения
Мы вычислили определитель матрицы А.
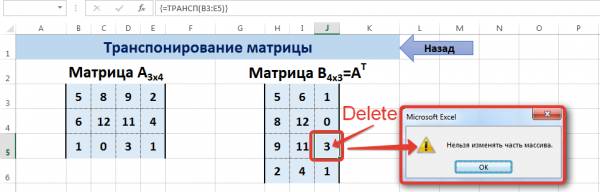
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
источники:
http://excel2.ru/articles/vychislenie-dliny-modulya-vektora-v-ms-excel
http://pedsovet.su/excel/6080_operacii_s_matricami
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор
– это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a
x
и a
y
, то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение
=КОРЕНЬ(СУММКВ(B8:B9))
позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки
B8:B9
, см.
файл примера
).
Функция
СУММКВ()
возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =
B8*B8+B9*B9
.
В
файле примера
также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение
=КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9))
.
2. Нахождение длины вектора через координаты точек
Если вектор
задан через координаты точек его начала и конца, то формула будет другой
=КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны
C28:C29
и
B28:B29
соответственно.
Функция
СУММКВРАЗН()
в
озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу
=КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках
B43:B43
содержатся длины векторов а и b, а в ячейке
В45
— угол между ними в радианах (в долях числа
ПИ()
).
Если угол задан в градусах, то формула будет немного отличаться
=КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание
: для наглядности в ячейке со значением угла в градусах можно применить
пользовательский формат
, см. например, статью
Отображение широты и долготы в MS EXCEL
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле
=КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55))
.
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
17 авг. 2022 г.
читать 2 мин
В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.
Что такое скалярный продукт?
Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:
а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3
Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:
а · б = 2*4 + 5*3 + 6*2
а · б = 8 + 15 + 12
а · б = 35
По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.
Как найти точечный продукт в Excel
Чтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:
1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:
2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:
СУММПРОИЗВ(массив1, [массив2], …)
- array — первый массив или диапазон, который необходимо умножить, а затем добавить.
- array2 — второй массив или диапазон для умножения, а затем добавления.
В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :
=СУММПРОИЗВ(A1:A3, B1:B3)
Это дает значение 35 , которое соответствует ответу, который мы получили вручную.
Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:
=СУММПРОИЗВ(A1:A20, B1:B20)
Возможные ошибки при вычислении скалярного произведения
Функция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.
Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.
Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:
Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84
Министерство
образования и науки Российской Федерации
Саратовский
государственный технический университет
имени Гагарина Ю.А.
Методические
указания и задания для студентов
Саратов
2012
Введение
Методические
указания представлены в виде набора
практических и лабораторных работ для
развития навыков моделирования и
реализации решения инженерных задач.
Задачи сопровождаются инструкциями
выполнения. Предлагаемые упражнения и
задания помогут усвоить технику
использования MS Excel и найти эффективные
способы решения практических задач.
Основные понятия Массивы
Массив
данных – это совокупность однотипных
элементов. Тип элементов в MS Excel
определяется с помощью Формат Ячейки.
В MS Excel можно работать с одномерными
и двумерными массивами.
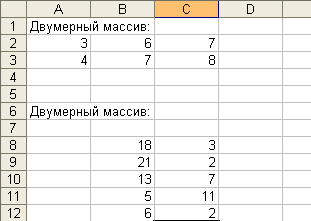
Одномерные
массивы (векторы), состоят из элементов
строк или столбцов, например, B2:B5, C9:G9
(рис. 1).
Рис. 1
Двумерные
массивы (матрицы) состоят из элементов,
располагающихся в прямоугольном
диапазоне, например, A2:C3,
B8:C12 (рис.
2).
Рис. 2
Формулы массивов
Формулы
массивов используются для того, чтобы
производить вычисления над несколькими
значениями (массивом значений), не
производя копирования и заполнения.
П
ример.
Выполним сложение и вычитание двух
векторов А=(а1,а2,…аn)
и B=(b1,b2,…bn),
где n = 4, например, (рис.
3).
Рис. 3
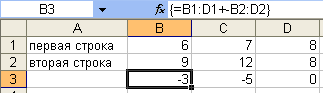
Инструкция
для сложения элементов двух векторов
(рис. 3):
-
Выделить
диапазон (строка) D3:G3,
где будет результат сложения; -
Ввести
знак равенства в строку формул; -
Выделить
первый массив D1:G1; -
Вставить
знак «плюс»; -
Выделить
второй массив D2:G2; -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1+
D2:G2}.
Инструкция
для вычитания элементов двух векторов
(рис. 3):
-
Выделить диапазон (строка) D4:G4.
-
Ввести
знак равенства. -
Выделить
первый массив D1:G1. -
Вставить
знак «минус». -
Выделить
второй массив D2:G2. -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1-
D2:G2}.
Изменить
содержимое ячеек полученных строк
(векторов) невозможно. Нельзя вставить
столбец в вектор. При таких попытках
будет выдано сообщение, что нельзя
изменить часть массива.
Если
при выполнении пункта 6 инструкций,
нажать на клавиатуре клавишу Enter вместо
клавиш Ctrl+Shift+Enter, то в этом случае формула
вычислит только одно, первое значение
вектора. Перейти в режим редактирования
нужно нажатием клавиши F2. Затем
одновременно нажать Ctrl+Shift+Enter.
Ошибки в формулах
При
наборе формул могут быть допущены
ошибки, например:
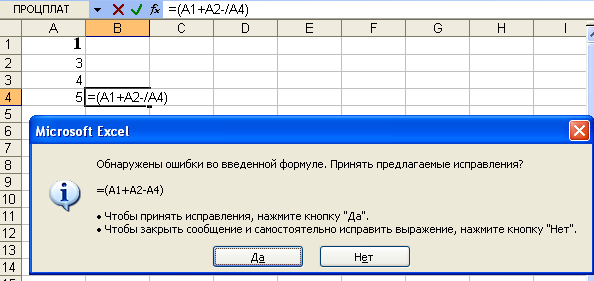
Набраны
две арифметические операции подряд,
пропущен оператор, например, (рис. 4 а)
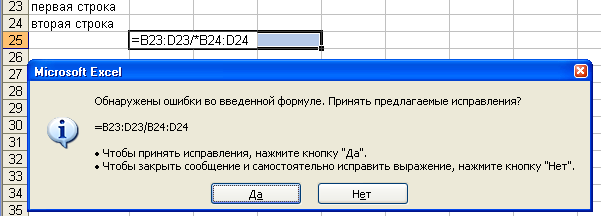
вод формулы =(A1+A2-/A4), при наборе допущена
элементарная ошибка или пропущен адрес
ячейки или ошибочно введены подряд две
арифметические операции вычитания и
деления (рис. 4 б–4 г).
Рис. 4 а
Рис. 4 б
Рис. 4 в
Рис. 4 г
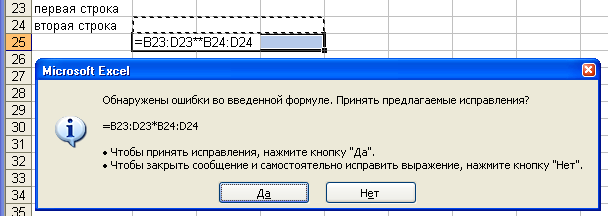
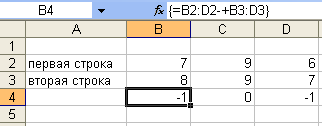
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «+», а затем «–», то не будет
ошибки, выполнится операция вычитания
(рис. 5).
Рис. 5
Рис. 6
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «–», а затем «+», то не будет
ошибки, опять выполнится операция
вычитания (рис. 6).
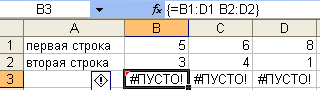
Пробел
между вектором А1:D1 и
В2:D2 означает пересечение
диапазонов (рис. 7). Пересечения ячеек
#ПУСТО!
Точка
с запятой – это объединение диапазонов
(рис. 8). В формуле ошибка.
Рис. 7
Рис. 8
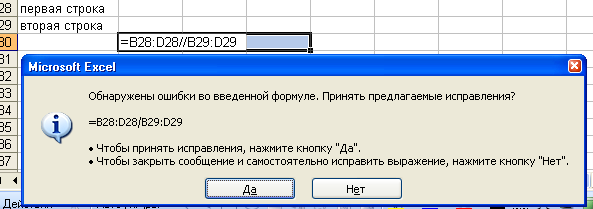
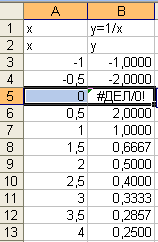
Могут
возникать ошибки в формулах при попытках
деления на 0
Рис. 9
Рис. 10
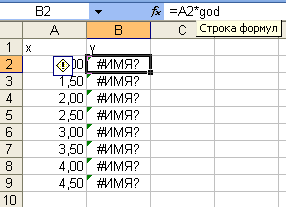
Ошибки
могут быть связаны с неопределенными
именами ячеек, использованных в формулах:
ошибка #ИМЯ? – не распознается имя,
используемое в формуле (рис. 11–12).
Имя адреса ячейки qod не
было присвоено;
Рис. 11
Рис. 12
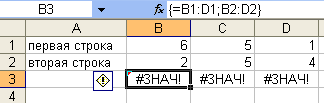
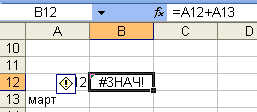
Ошибка
#ЗНАЧ! – используются операторы или
аргументы недопустимого типа (рис. 13).
В ячейке B12 возникла ошибка
#ЗНАЧ! В этом случае это значит, что
складываются содержимое ячеек А12 и А13
разного типа. A13 определено
как тип дата, а A12 — как
число.
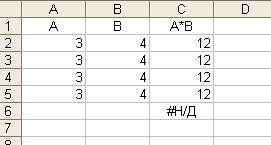
Ошибка
#Н/Д возникла в C6
неопределенных данных, т.е. не определены
значения ячеек A6 и B6
(рис. 14).
Рис.13
Рис. 14
В этом
примере ошибка #ПУСТО! возникает при
пересечении двух диапазонов, которые
в действительности не имеют общих ячеек
(рис. 15).
Рис. 15
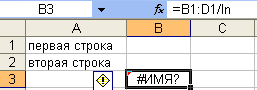
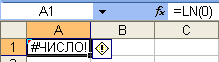
Ошибка
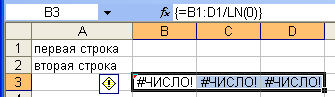
#ЧИСЛО! На рис. 16, 17 возникает при вычислении
натурального логарифма от нуля, что
невозможно.
Рис. 16
Рис. 17
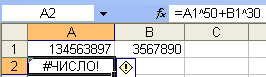
Такого
рода ошибка, как на рис. 18, происходит
при «переполнении», когда числовое
значение вычисляемой формулы слишком
велико или слишком мало для используемого
формата.
Рис. 18
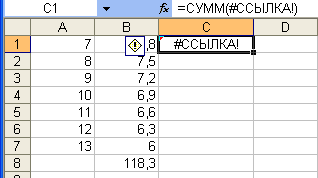
Ошибка
#ССЫЛКА! – неправильная ссылка на
ячейку. В ячейке В8 (рис. 19) вычислена
сумма элементов массива A1:B7.
При попытке скопировать содержимое
ячейки В8 в ячейку С1 и произошла ошибка.
При копировании часто возникает ошибка
#ССЫЛКА.
Рис.19
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Автор:
Monica Porter
Дата создания:
14 Март 2021
Дата обновления:
13 Апрель 2023
Содержание
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
Вектор — это список из двух или более чисел. В векторе-строке числа выровнены в строке, а в векторе-столбце они выровнены в столбце. Два вектора можно складывать или вычитать, если они одного типа и имеют одинаковую размерность. Два вектора можно перемножить, если они имеют одинаковую размерность, и один — вектор-столбец, а другой — вектор-строка. Если A — вектор-строка с 5 числами, а B — вектор-столбец с 5 числами, при выполнении умножения A * B в результате вы получите матрицу 5 * 5, а при умножении B * A вы получите только одно число. (также называемый скаляром). В Microsoft Excel есть функции для выполнения всех этих вычислений. Они известны как матричные функции.
Шаг 1
Откройте Excel и введите векторы. Например, если A равно 1, 2, 3, 4 и 5, а B равно 2, 4, 6, 8 и 10, введите эти числа в столбцы для A и B.
Шаг 2
Добавьте векторы. Выделите область того же размера, что и A, а затем введите = (A1: Ap) + (B1: Bp), где p — количество строк. Затем одновременно нажмите клавиши «Ctrl», «Shift» и «Enter». В этом примере выделите ячейки с C1 по C5, введите = (A1: A5) + (B1: B5), а затем нажмите «Ctrl», «Shift» и «Enter». Результатом должно быть 3, 6, 9, 12 и 15 в ячейках с C1 по C5.
Шаг 3
Вычтите векторы. Это похоже на сложение чисел, за исключением того, что вы пишете — вместо + в формуле. В этом примере выделите от D1 до D5, введите = (A1: A5) — (B1: B5) и нажмите «Ctrl», «Shift» и «Enter». Результат должен быть -1, -2, -3, -4 и -5 в ячейках с D1 по D5.
Умножьте матрицу A на матрицу B.Помните, что две матрицы могут быть перемножены, только если одна является вектором-строкой, а другая — вектором-столбцом. Изменение вектора-строки на вектор-столбец называется транспонированием. Чтобы умножить вектор строки A на вектор столбца B, выделите матрицу pxp и введите = MMULT (TRANSPOSE (A1: Ap), (B1: Bp)) и нажмите клавиши «Ctrl», «Shift» и «Enter». «. В этом примере в ячейках, помеченных с E1 по J5, введите = MMULT (TRANSPOSE (A1: A5), (B1: B5)) и нажмите клавиши «Ctrl», «Shift» и «Enter». Результат должен заполнить все ячейки.
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9))
позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9
, см. файл примера
).
Функция СУММКВ()
возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9
.
В файле примера
также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9))
.
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29
и B28:B29
соответственно.
Функция СУММКВРАЗН()
в
озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43
содержатся длины векторов а и b, а в ячейке В45
— угол между ними в радианах (в долях числа ПИ()
).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание
: для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
модуль вектора
— величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …
модуль вектора
— vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
— (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора
— — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей
— — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
Абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Модуль вектора
можно найти, если мы знаем его проекции на координатные оси
.
на плоскости задан вектор
а
(рис. 15).
Опустим с начала и конца вектора перпендикуляры на координатные оси для нахождения его проекций. В соответствии с теоремой Пифагора
. Отсюда
.
Эту формулу надо знать НАИЗУСТЬ.
Запомните!
Чтобы найти модуль вектора
надо извлечь корень квадратный из суммы квадратов его проекций.
Вы уже знаете, что проекцию вектора на ось можно найти, если из координаты точки конца вектора вычесть координату точки его начала. Тогда для нашего вектора, если он задан на плоскости, а x = х к − х н,
а y = y к − y н. Следовательно, модуль вектора
можно найти по формуле
.
Нетрудно сообразить, как будет выглядеть формула, если вектор
задан в пространстве.
Обратите еще внимание вот на что. Ведь модуль вектора
— это длина отрезка, заключенного между двумя точками: точкой начала вектора и точкой его конца. А это ни что иное, как расстояние между двумя этими точками. Поэтому чтобы найти расстояние между любыми двумя точками, нужно вычислить модуль вектора
, соединяющего эти точки.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Euclidean distance is the distance between two real-valued vectors. It is calculated by the square root of the sum of the squared differences of the elements in the two vectors.
The formula to calculate Euclidean distance is :
In this article we are going to discuss how to calculate the Euclidean distance in Excel using a suitable example.
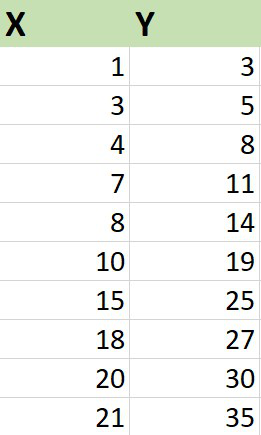
Example : Consider the dataset which consists of information about X and Y coordinates of ten points in a 2-D plane.
Implementation :
The functions used are :
1. SUMXMY2: It finds the sum of squared differences of the elements in array X and array Y.
2. SQRT: It is used to find the square root of the squared difference.
The steps to calculate Euclidean distance are :
1. Insert the coordinates in the Excel sheet as shown above.
Column X consists of the x-axis data points and column Y contains y-axis data points.
2. Write the Excel formula in any one of the cells to calculate the Euclidean distance.
=SQRT(SUMXMY2(array_x,array_y))
The observations in array X are stored from A2 to A11.
The observations in array Y are stored from B2 to B11.
3. Click on Enter.
The Euclidean distance turns out to be 25.18 units approximately.
It is important to note that the number of observations in X and that of Y has to be the same. While calculating the distance Excel takes pairwise values of X and Y simultaneously.
If any one of the values is missing in the worksheet then Excel will ignore that and move to the next data point. So, while entering the dataset we need to be careful to enter the observations X and Y pair-wise such that no data is missing.
Like Article
Save Article




 становить курсор в ячейку, где нужен результат.
становить курсор в ячейку, где нужен результат.



 ак и следовало ожидать, получилась матрица, близкая к единичной.
ак и следовало ожидать, получилась матрица, близкая к единичной.