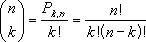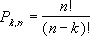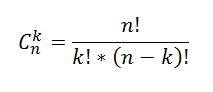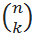Расчет вариантов в excel - Word и Excel - помощь в работе с программами

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ЧИСЛКОМБ в Microsoft Excel.

Описание

Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.

Синтаксис

ЧИСЛКОМБ(число;число_выбранных)

Аргументы функции ЧИСЛКОМБ описаны ниже.

Число — обязательный аргумент. Количество элементов.
Число_выбранных — обязательный аргумент. Количество элементов в каждой комбинации.

Замечания

Числовые аргументы усекаются до целых чисел.
Если хотя бы один из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
Если число < 0, number_chosen < 0 или < number_chosen, то #NUM! значение ошибки #ЗНАЧ!.
Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.
Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:

где

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ЧИСЛКОМБ(8;2)	Возможные команды по два человека, которые могут быть сформированы из восьми кандидатов.	28

Нужна дополнительная помощь?

Источник

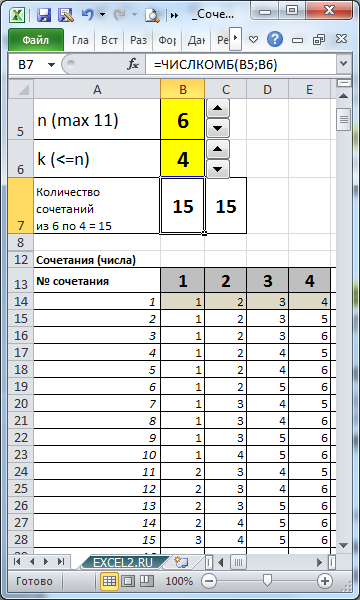
Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание

: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.

Отличие Сочетаний от Размещений

В отличие от

Размещений

следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор

Сочетаний

включается только одна из этих комбинаций. Очевидно, что для тех же n и k число

Сочетаний

всегда меньше чем число

Размещений

(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.

Подсчет количества Сочетаний

Число всех

Сочетаний

из n элементов по k можно вычислить по формуле:

Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)

Примечание

: Для

Сочетаний

из n элементов по k также используется и другая запись:

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .

Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.

Примечание

: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье

Сочетания с повторениями: Комбинаторика в MS EXCEL

Вывод всех комбинаций Сочетаний

В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью

элементов управления Счетчик

количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.

Задача

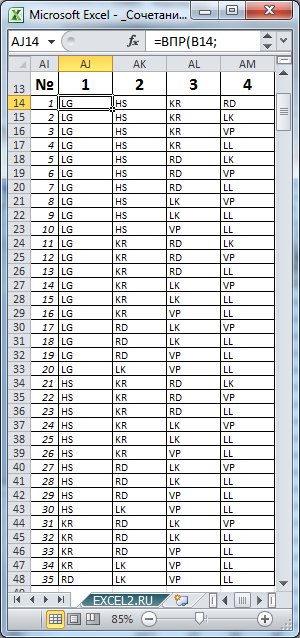
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число

Сочетаний

7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.

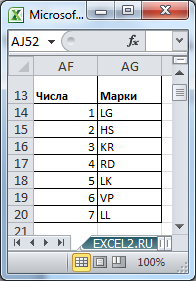
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках

В5

и

В6

значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).

Примечание

: О Перестановках можно прочитать в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

, а о Размещениях в статье

Размещения без повторений: Комбинаторика в MS EXCEL

Источник

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

Лучшее спасибо — порекомендовать эту страницу

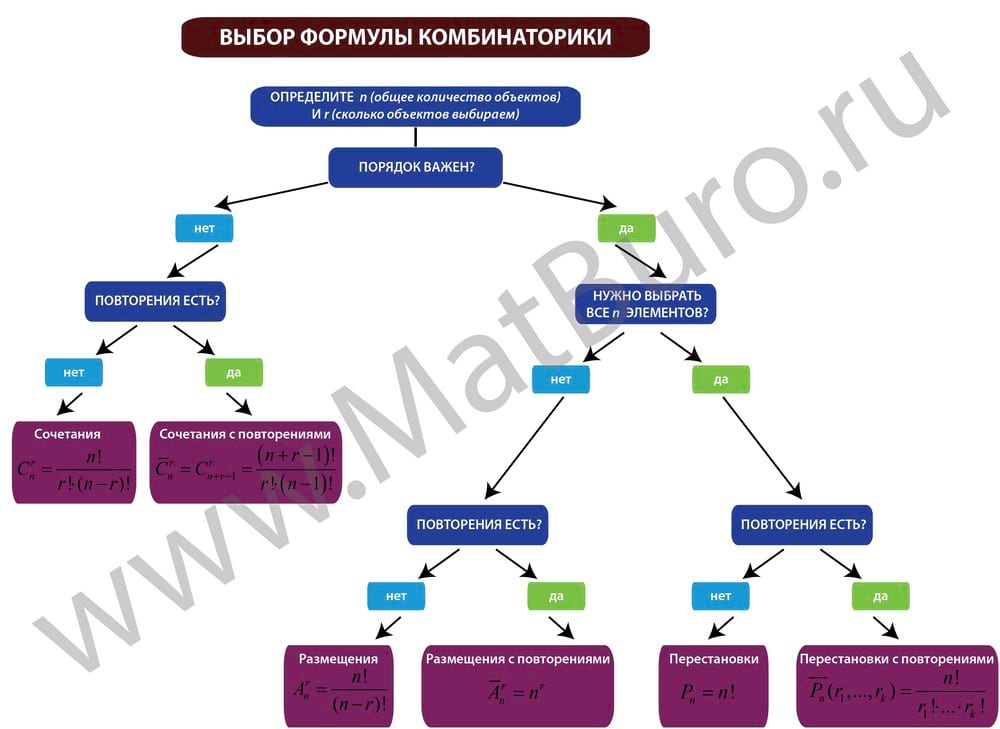
Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

Сколько у нас есть объектов (число $n$)?
Важен ли их порядок в комбинации?
Могут ли встречаться повторяющиеся элементы?
Нужно выбрать все элементы или только $klt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Схема выбора формул с примерами задач

Консультируем по решению задач комбинаторики

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

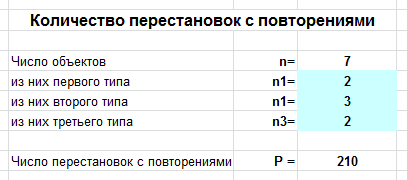
Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

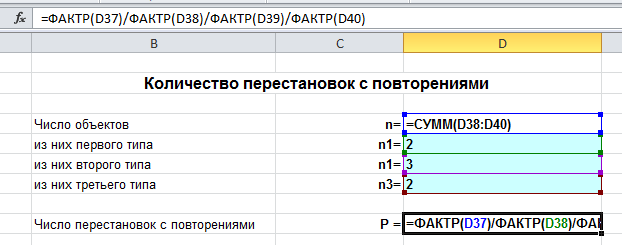
Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=frac{n!}{(n-k)!cdot k!} $$

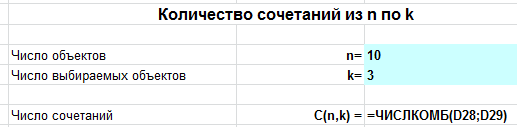
Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний.

Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Онлайн калькуляторы
Онлайн учебник: Элементы комбинаторики
Примеры решений

Как решать задачи по комбинаторике?
Видеоуроки по комбинаторике
Решение на заказ

Решебник задач по комбинаторике

Источник

Содержание

Использование таблицы данных
- Способ 1: применение инструмента с одной переменной
- Способ 2: использование инструмента с двумя переменными
Вопросы и ответы

Довольно часто требуется рассчитать итоговый результат для различных комбинаций вводных данных. Таким образом пользователь сможет оценить все возможные варианты действий, отобрать те, результат взаимодействия которых его удовлетворяет, и, наконец, выбрать самый оптимальный вариант. В Excel для выполнения данной задачи существует специальный инструмент – «Таблица данных» («Таблица подстановки»). Давайте узнаем, как им пользоваться для выполнения указанных выше сценариев.

Читайте также: Подбор параметра в Excel

Использование таблицы данных

Инструмент «Таблица данных» предназначен для того, чтобы рассчитывать результат при различных вариациях одной или двух определенных переменных. После расчета все возможные варианты предстанут в виде таблицы, которую называют матрицей факторного анализа. «Таблица данных» относится к группе инструментов «Анализ «что если»», которая размещена на ленте во вкладке «Данные» в блоке «Работа с данными». До версии Excel 2007 этот инструмент носил наименование «Таблица подстановки», что даже более точно отражало его суть, чем нынешнее название.

Таблицу подстановки можно использовать во многих случаях. Например, типичный вариант, когда нужно рассчитать сумму ежемесячного платежа по кредиту при различных вариациях периода кредитования и суммы займа, либо периода кредитования и процентной ставки. Также этот инструмент можно использовать при анализе моделей инвестиционных проектов.

Но также следует знать, что чрезмерное применение данного инструмента может привести к торможению системы, так как пересчет данных производится постоянно. Поэтому рекомендуется в небольших табличных массивах для решения аналогичных задач не использовать этот инструмент, а применять копирование формул с помощью маркера заполнения.

Оправданным применение «Таблицы данных» является только в больших табличных диапазонах, когда копирование формул может отнять большое количество времени, а во время самой процедуры увеличивается вероятность допущения ошибок. Но и в этом случае рекомендуется в диапазоне таблицы подстановки отключить автоматический пересчет формул, во избежание излишней нагрузки на систему.

Главное отличие между различными вариантами применения таблицы данных состоит в количестве переменных, принимающих участие в вычислении: одна переменная или две.

Способ 1: применение инструмента с одной переменной

Сразу давайте рассмотрим вариант, когда таблица данных используется с одним переменным значением. Возьмем наиболее типичный пример с кредитованием.

Итак, в настоящее время нам предлагаются следующие условия кредитования:

Срок кредитования – 3 года (36 месяцев);
Сумма займа – 900000 рублей;
Процентная ставка – 12,5% годовых.

Выплаты происходят в конце платежного периода (месяца) по аннуитетной схеме, то есть, равными долями. При этом, вначале всего срока кредитования значительную часть выплат составляют процентные платежи, но по мере сокращения тела процентные платежи уменьшаются, а увеличивается размер погашения самого тела. Общая же выплата, как уже было сказано выше, остается без изменений.

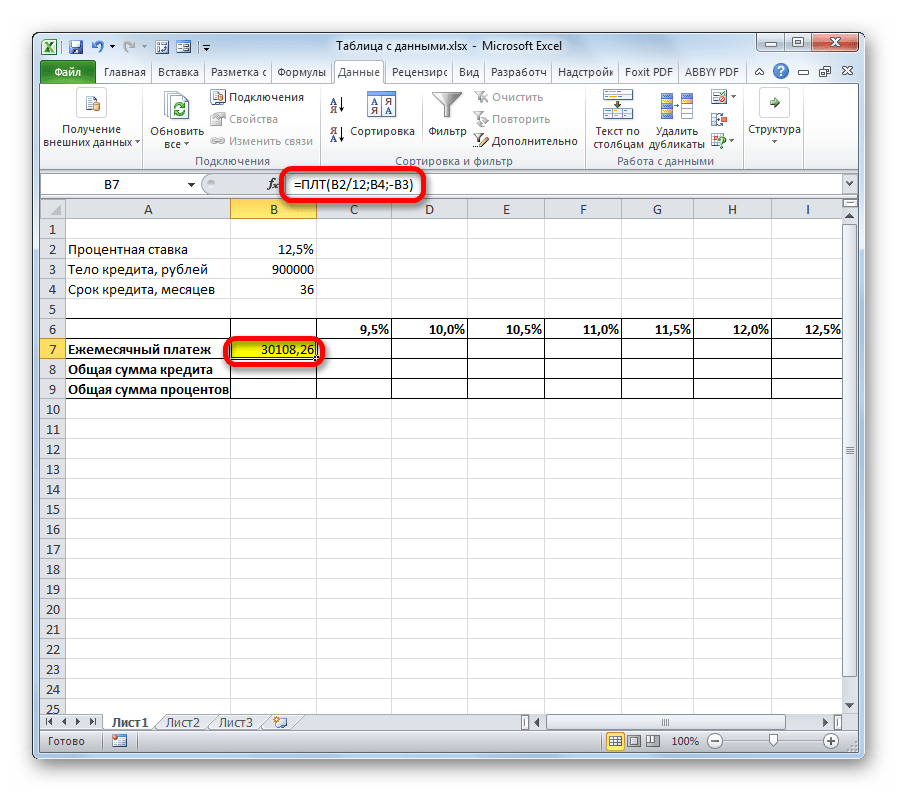
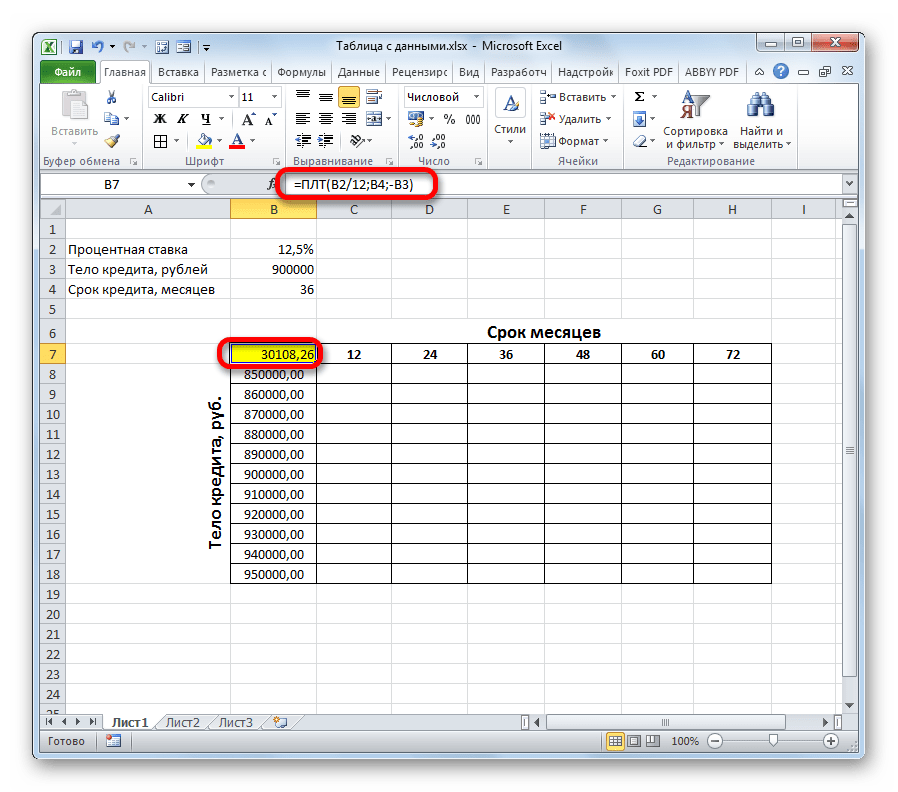
Нужно рассчитать, какова будет сумма ежемесячного платежа, включающего в себя погашение тела кредита и выплат по процентам. Для этого в Экселе имеется оператор ПЛТ.

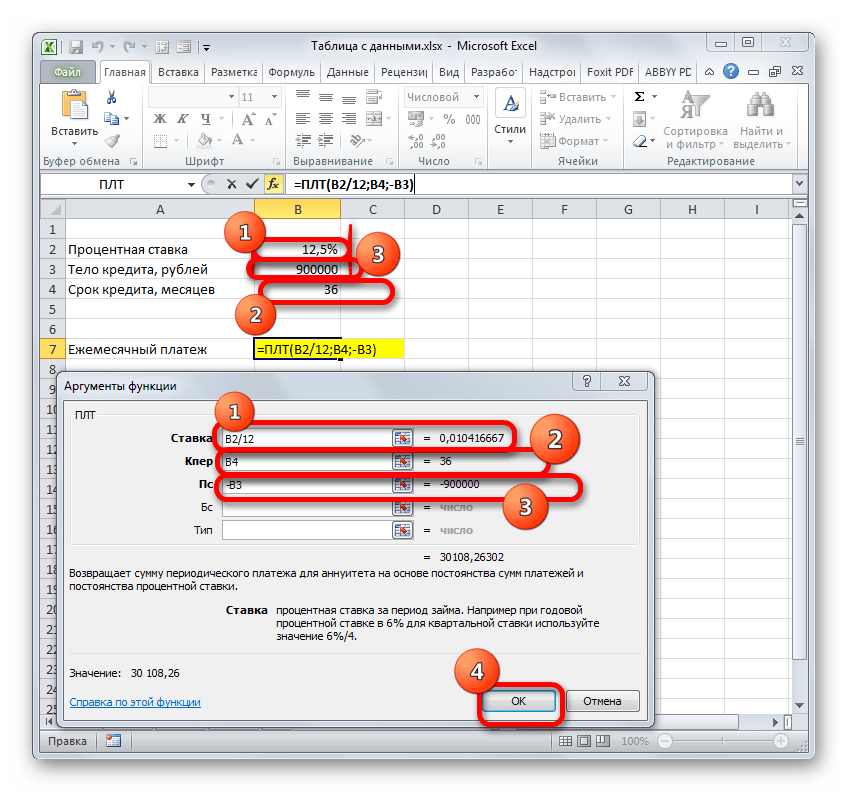
ПЛТ относится к группе финансовых функций и его задачей является вычисление ежемесячного кредитного платежа аннуитетного типа на основании суммы тела кредита, срока кредитования и процентной ставки. Синтаксис этой функции представлен в таком виде

=ПЛТ(ставка;кпер;пс;бс;тип)

«Ставка» — аргумент, определяющий процентную ставку кредитных выплат. Показатель выставляется за период. У нас период выплат равен месяцу. Поэтому годовую ставку в 12,5% следует разбить на число месяцев в году, то есть, 12.

«Кпер» — аргумент, определяющий численность периодов за весь срок предоставления кредита. В нашем примере период равен одному месяцу, а срок кредитования составляет 3 года или 36 месяцев. Таким образом, количество периодов будет рано 36.

«ПС» — аргумент, определяющий приведенную стоимость кредита, то есть, это размер тела кредита на момент его выдачи. В нашем случае этот показатель равен 900000 рублей.

«БС» — аргумент, указывающий на величину тела кредита на момент его полной выплаты. Естественно, что данный показатель будет равен нулю. Этот аргумент не является обязательным параметром. Если его пропустить, то подразумевается, что он равен числу «0».

«Тип» — также необязательный аргумент. Он сообщает о том, когда именно будет проводиться платеж: в начале периода (параметр – «1») или в конце периода (параметр – «0»). Как мы помним, у нас платеж проводится в конце календарного месяца, то есть, величина этого аргумента будет равна «0». Но, учитывая то, что этот показатель не является обязательным, и по умолчанию, если его не использовать, значение и так подразумевается равным «0», то в указанном примере его вообще можно не применять.

Итак, приступаем к расчету. Выделяем ячейку на листе, куда будет выводиться расчетное значение. Клацаем по кнопке «Вставить функцию».

Запускается Мастер функций. Производим переход в категорию «Финансовые», выбираем из перечня наименование «ПЛТ» и клацаем по кнопке «OK».

Вслед за этим происходит активация окошка аргументов вышеуказанной функции.
Ставим курсор в поле «Ставка», после чего кликаем по ячейке на листе со значением годовой процентной ставки. Как видим, в поле тут же отображаются её координаты. Но, как мы помним, нам нужна месячная ставка, а поэтому производим деление полученного результата на 12 (/12).

В поле «Кпер» таким же образом вносим координаты ячеек срока кредита. В этом случае делить ничего не надо.

В поле «Пс» нужно указать координаты ячейки, содержащей величину тела кредита. Выполняем это. Также ставим перед отобразившемся координатами знак «-». Дело в том, что функция ПЛТ по умолчанию выдает итоговый результат именно с отрицательным знаком, справедливо считая ежемесячный кредитный платеж убытком. Но нам для наглядности применения таблицы данных нужно, чтобы данное число было положительным. Поэтому мы и ставим знак «минус» перед одним из аргументов функции. Как известно, умножение «минус» на «минус» в итоге дает «плюс».

В поля «Бс» и «Тип» данные вообще не вносим. Клацаем по кнопке «OK».

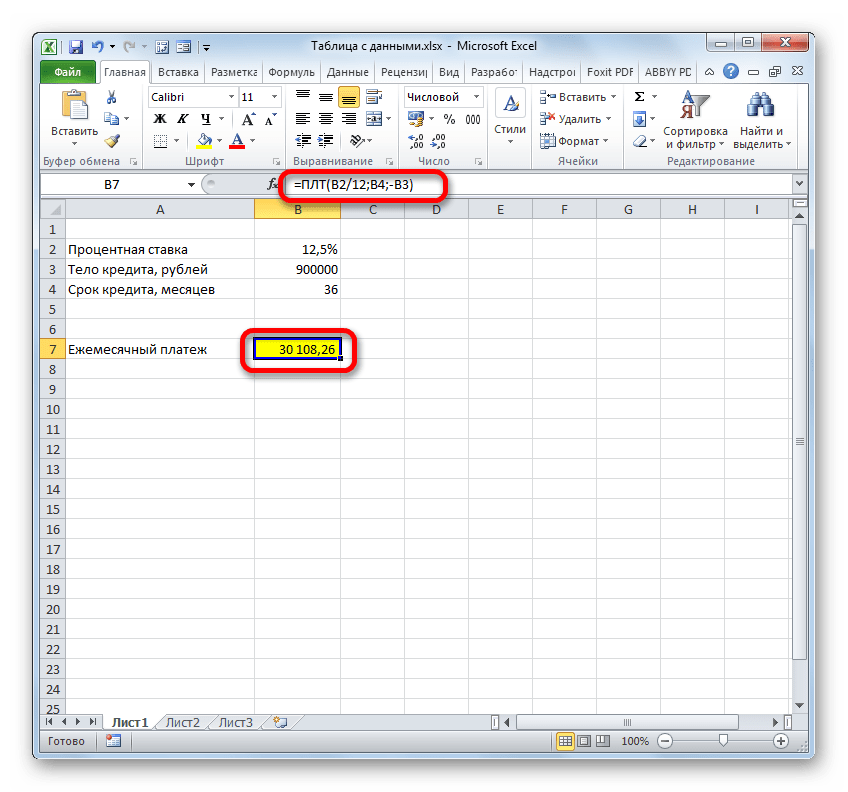
После этого оператор производит подсчет и выводит в заранее обозначенную ячейку результат общего ежемесячного платежа – 30108,26 рублей. Но проблема состоит в том, что заёмщик в состоянии платить максимум 29000 рублей в месяц, то есть, ему следует либо найти банк, предлагающий условия с более низкой процентной ставкой, либо уменьшить тело займа, либо увеличить срок кредитования. Просчитать различные варианты действий нам поможет таблица подстановок.

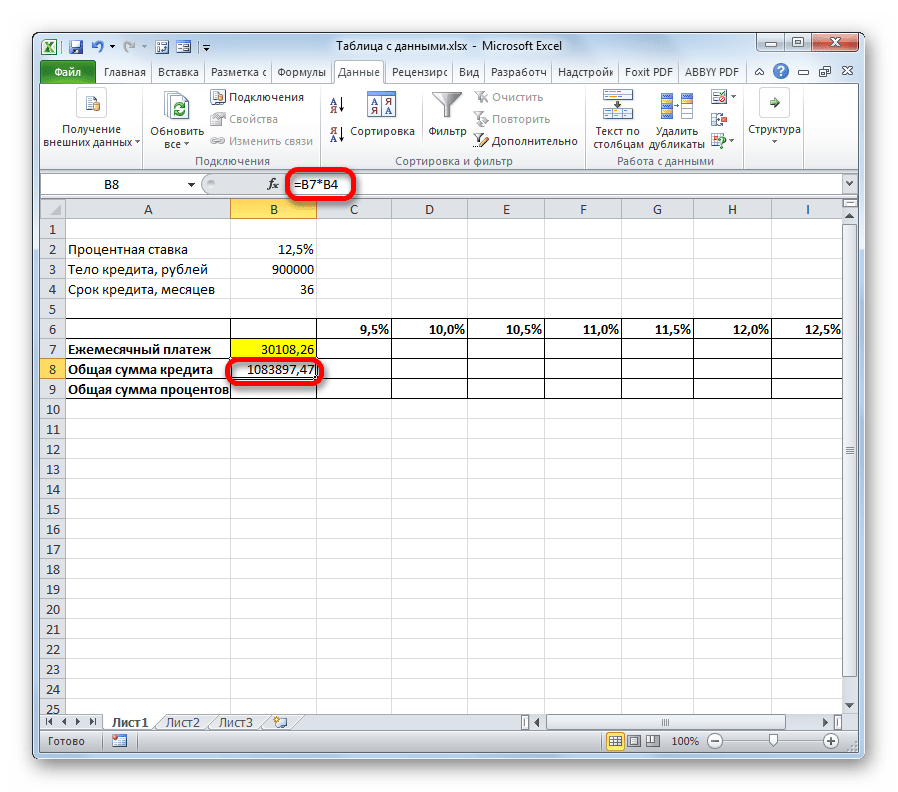
Для начала используем таблицу подстановок с одной переменной. Посмотрим, как будет изменяться величина обязательного месячного платежа при различных вариациях годовой ставки, начиная от 9,5% годовых и заканчивая 12,5% годовых с шагом 0,5%. Все остальные условия оставляем неизменными. Чертим табличный диапазон, наименования колонок которого будут соответствовать различным вариациям процентной ставки. При этом строку «Ежемесячные выплаты» оставляем так, как есть. В первой её ячейке должна содержаться формула, которую мы рассчитали ранее. Для большей информативности можно добавить строки «Общая сумма кредита» и «Общая сумма процентов». Столбец, в котором находится расчет, делаем без заголовка.

Далее рассчитаем общую сумму займа при текущих условиях. Для этого выделяем первую ячейку строки «Общая сумма кредита» и умножаем содержимое ячеек «Ежемесячный платеж» и «Срок кредита». После этого щелкаем по клавише Enter.

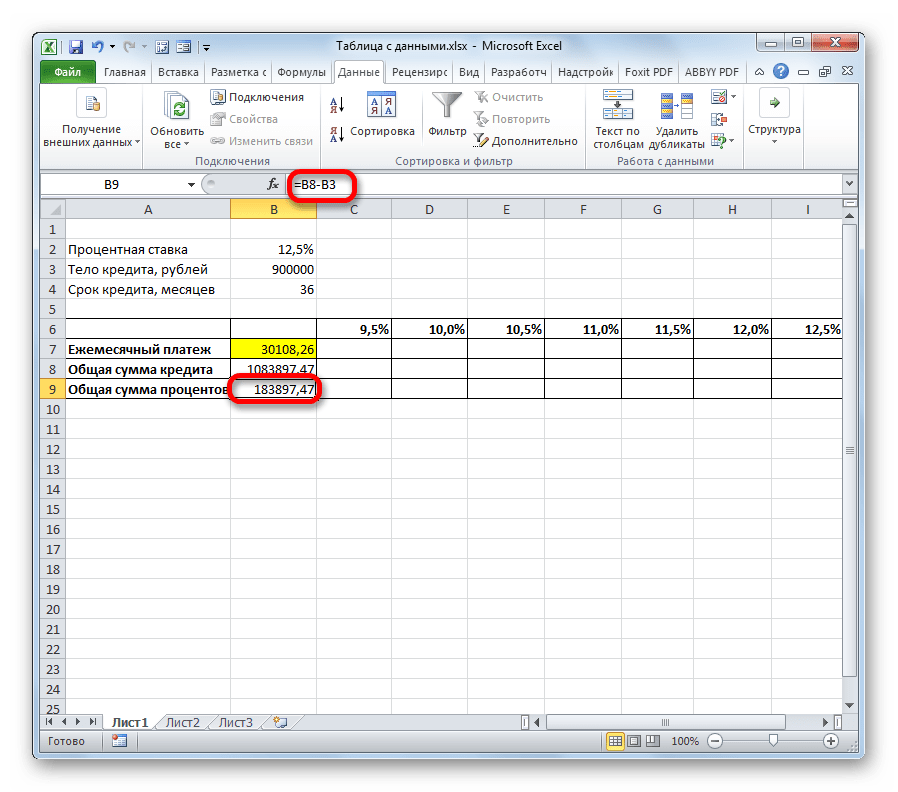
Для расчета общей суммы процентов при текущих условиях аналогичным образом отнимаем от общей суммы займа величину тела кредита. Для вывода результата на экран щелкаем по кнопке Enter. Таким образом мы получаем сумму, которую переплачиваем при возврате займа.

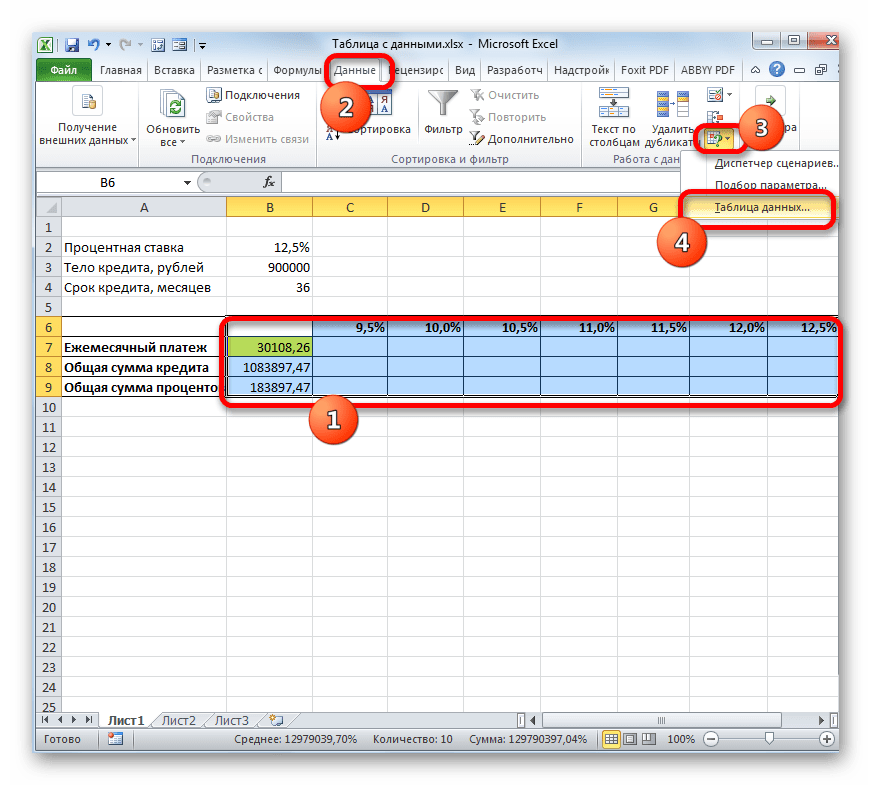
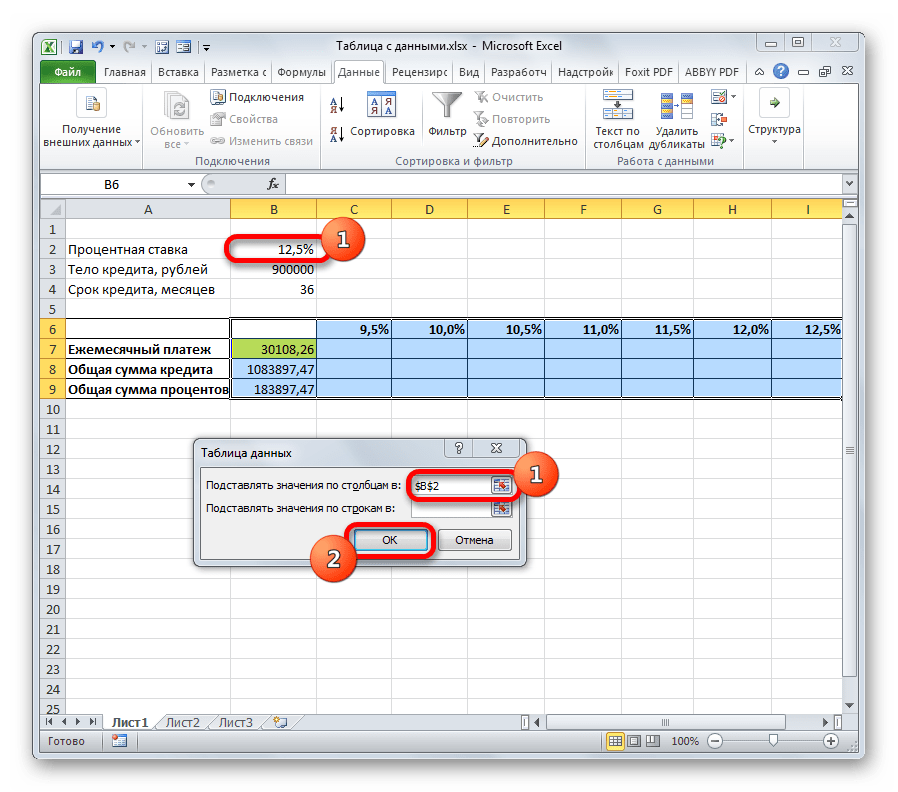
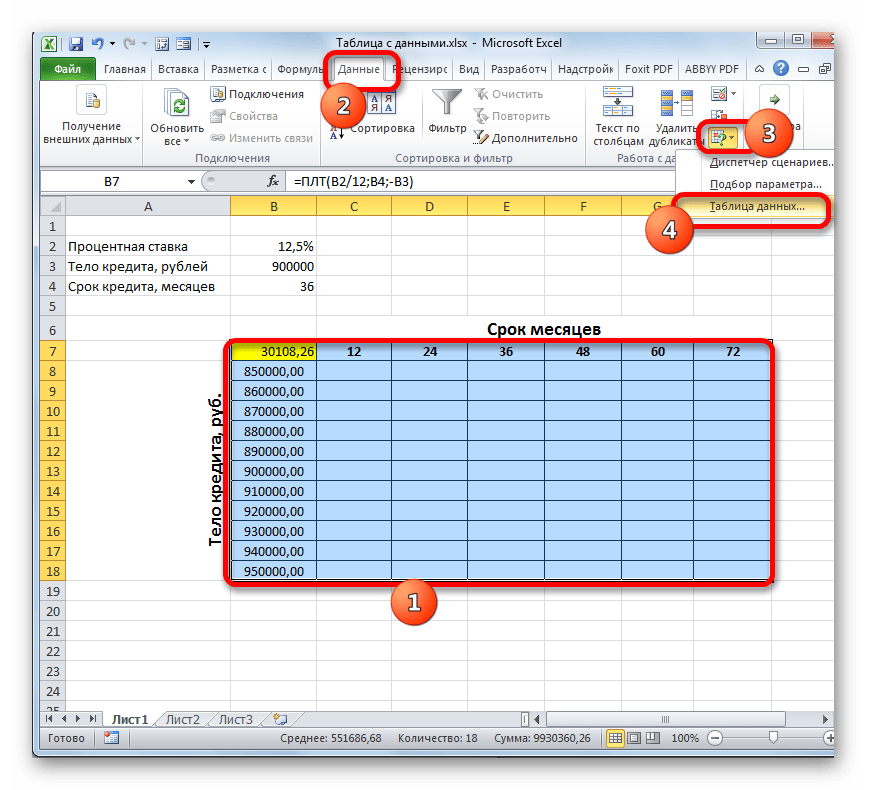
Теперь настало время применить инструмент «Таблица данных». Выделяем весь табличный массив, кроме наименований строк. После этого переходим во вкладку «Данные». Щелкаем по кнопке на ленте «Анализ «что если»», которая размещена в группе инструментов «Работа с данными» (в Excel 2016 группа инструментов «Прогноз»). Затем открывается небольшое меню. В нем выбираем позицию «Таблица данных…».

Открывается небольшое окошко, которое так и называется «Таблица данных». Как видим, у него имеется два поля. Так как мы работаем с одной переменной, то нам понадобится только одно из них. Так как у нас изменения переменной происходит по столбцам, то мы будем использовать поле «Подставить значения по столбцам в». Устанавливаем туда курсор, а затем кликаем по ячейке в исходном наборе данных, которая содержит текущую величину процентов. После того, как координаты ячейки отобразились в поле, жмем на кнопку «OK».

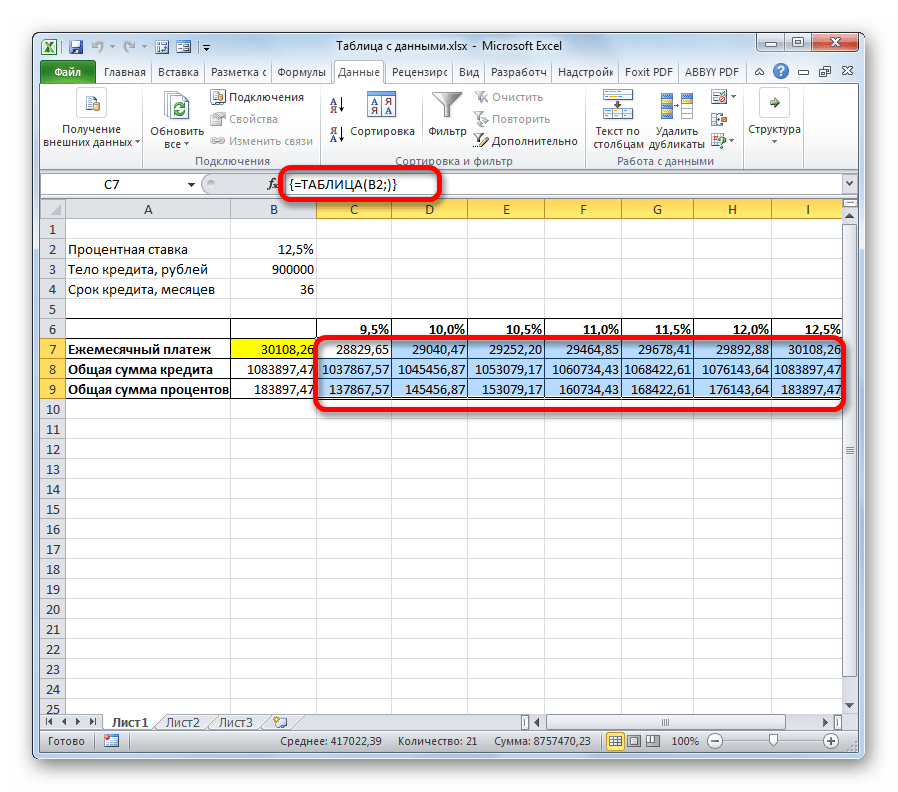
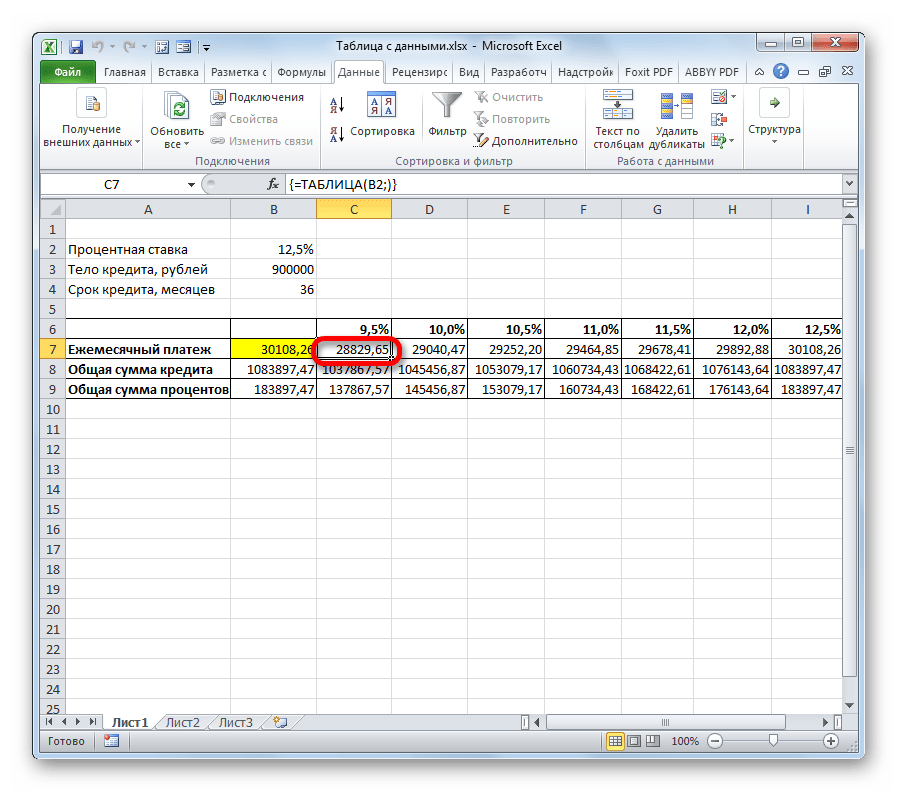
Инструмент производит расчет и заполняет весь табличный диапазон значениями, которые соответствуют различным вариантам процентной ставки. Если установить курсор в любой элемент данной табличной области, то можно увидеть, что в строке формул отображается не обычная формула расчета платежа, а специальная формула неразрывного массива. То есть, изменять значения в отдельных ячейках теперь нельзя. Удалять результаты расчета можно только все вместе, а не по отдельности.

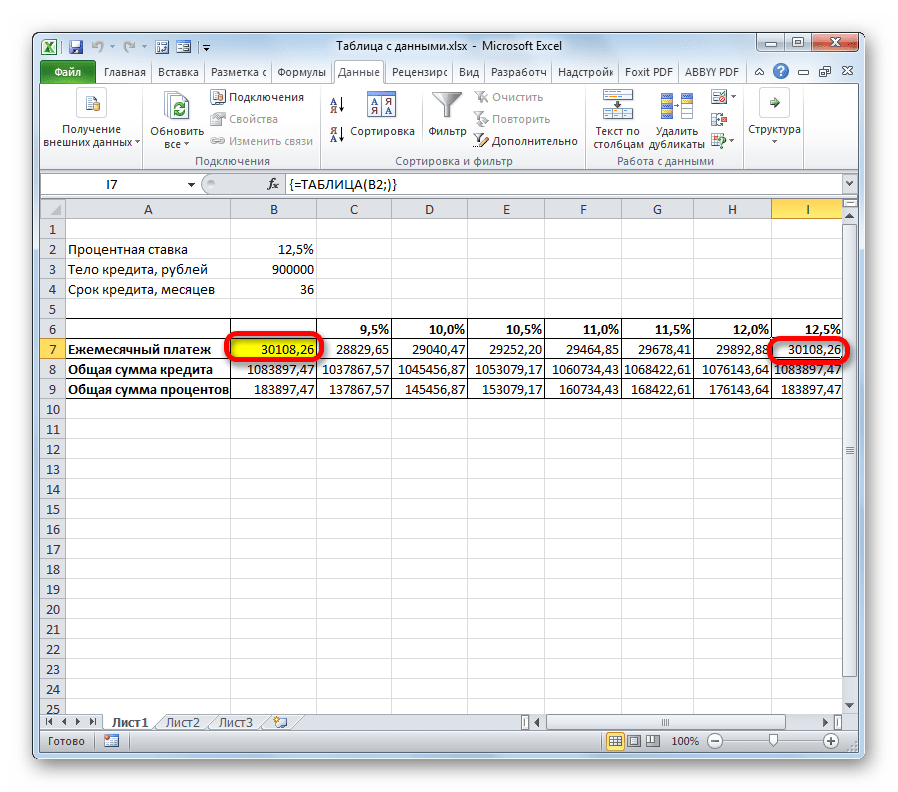
Кроме того, можно заметить, что величина ежемесячного платежа при 12.5% годовых, полученная в результате применения таблицы подстановок, соответствует величине при том же размере процентов, которую мы получили путем применения функции ПЛТ. Это лишний раз доказывает правильность расчета.

Проанализировав данный табличный массив, следует сказать, что, как видим, только при ставке 9,5% годовых получается приемлемый для нас уровень ежемесячного платежа (менее 29000 рублей).

Урок: Расчет аннуитетного платежа в Экселе

Способ 2: использование инструмента с двумя переменными

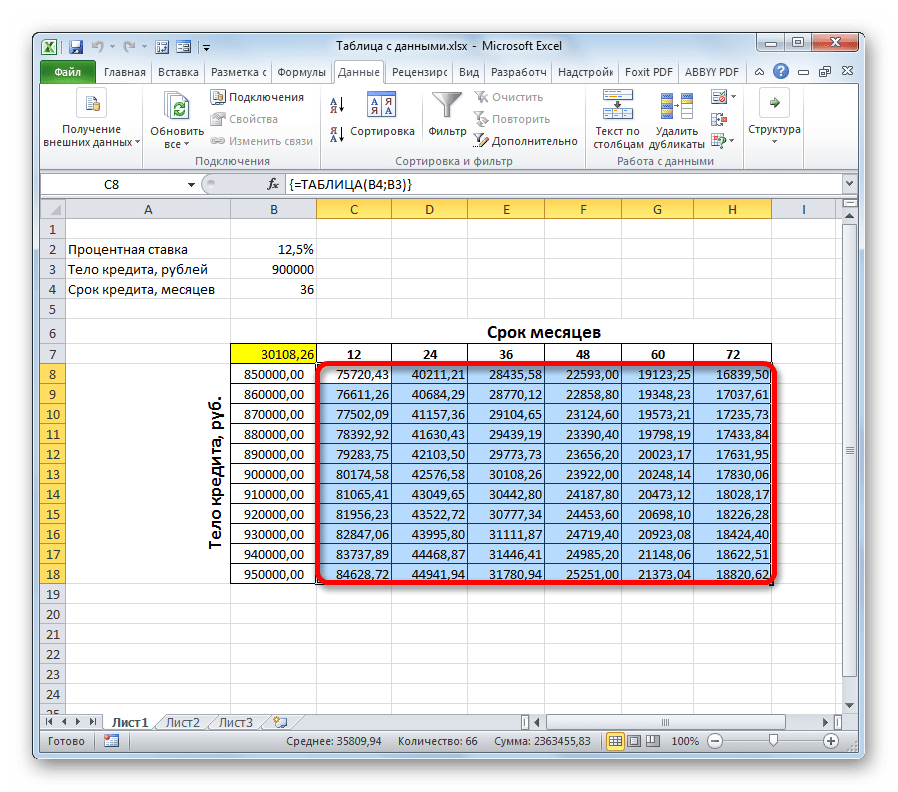
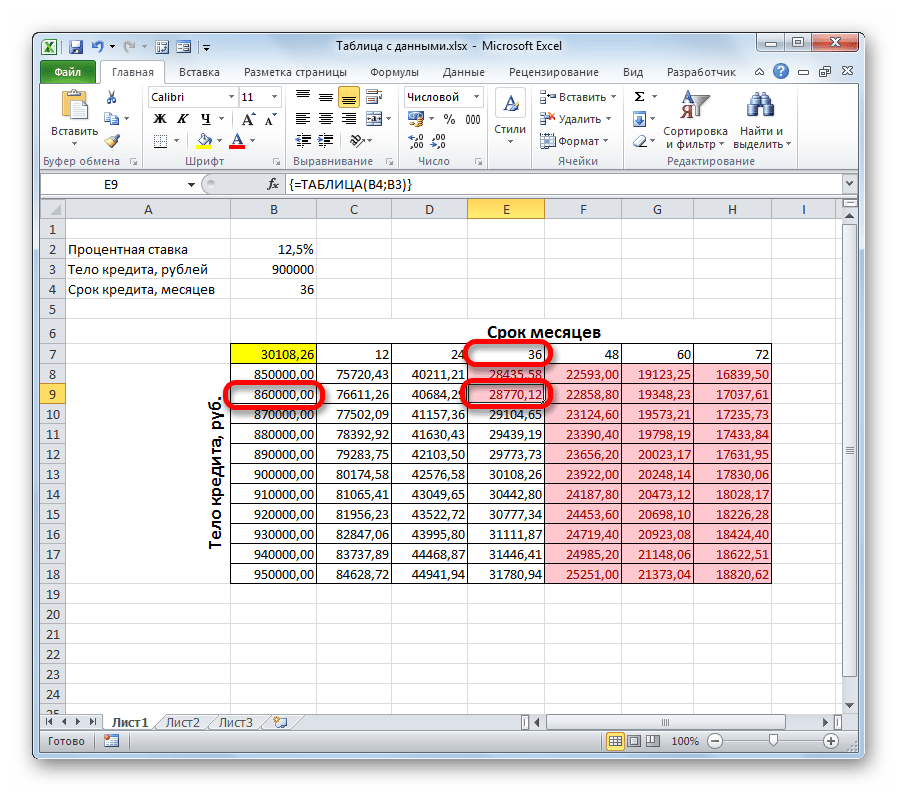
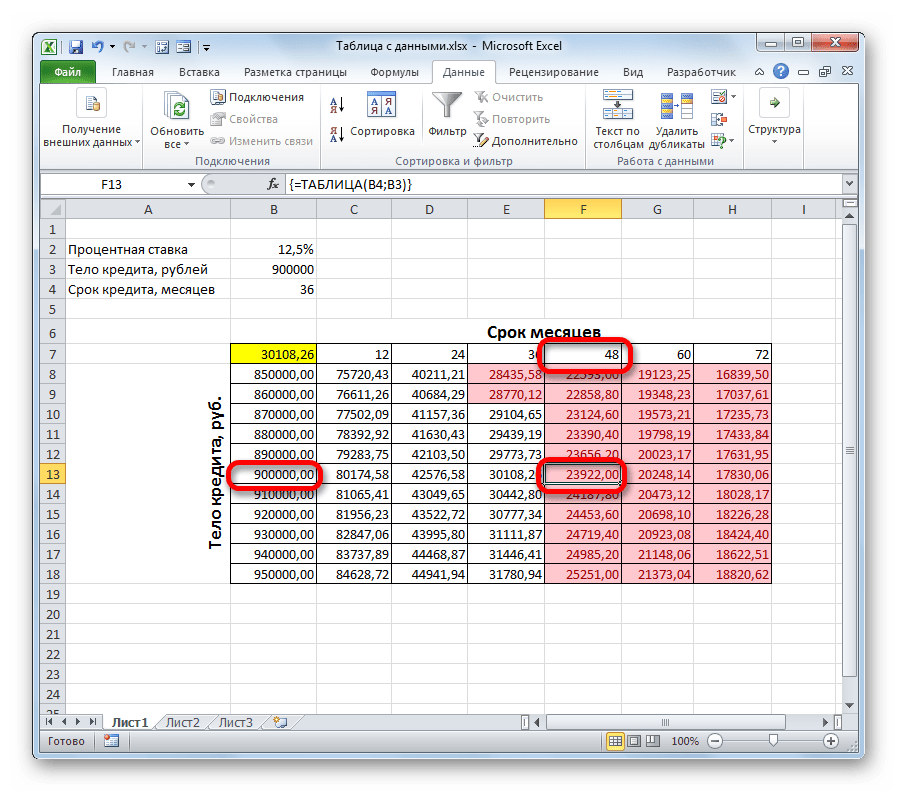
Конечно, отыскать в настоящее время банки, которые выдают кредит под 9,5% годовых, очень сложно, если вообще реально. Поэтому посмотрим, какие варианты существуют вложиться в приемлемый уровень ежемесячного платежа при различных комбинациях других переменных: величины тела займа и срока кредитования. При этом процентную ставку оставим неизменной (12,5%). В решении данной задачи нам поможет инструмент «Таблица данных» с использованием двух переменных.

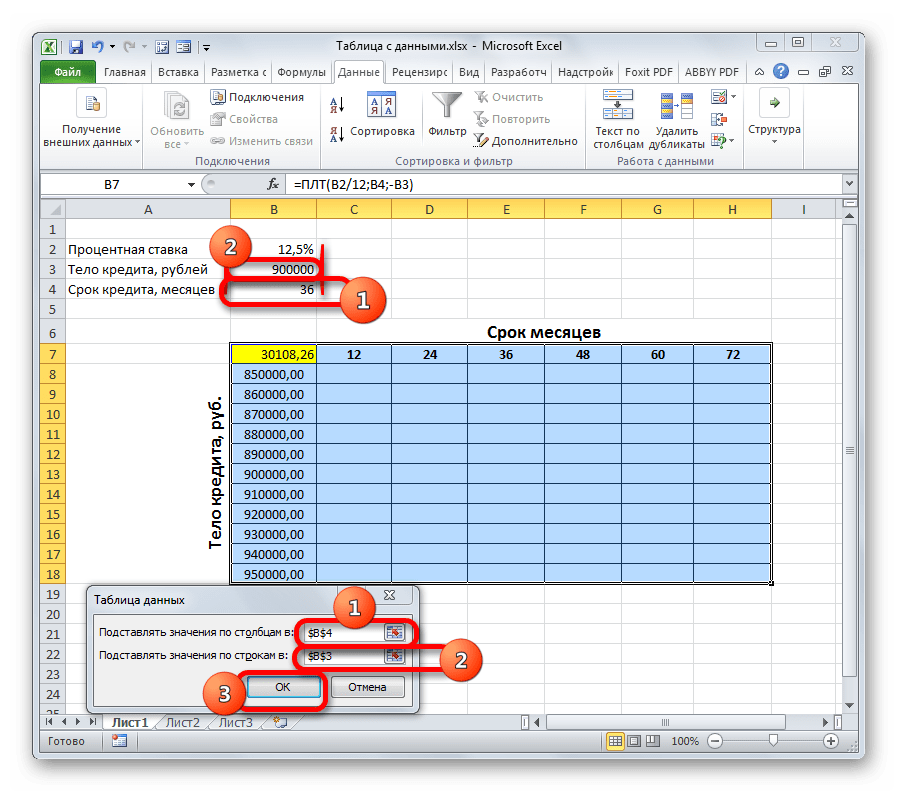
Чертим новый табличный массив. Теперь в наименованиях столбцов будет указываться срок кредитования (от 2 до 6 лет в месяцах с шагом в один год), а в строках — величина тела кредита (от 850000 до 950000 рублей с шагом 10000 рублей). При этом обязательным условием является то, чтобы ячейка, в которой находится формула расчета (в нашем случае ПЛТ), располагалась на границе наименований строк и столбцов. Без выполнения данного условия инструмент при использовании двух переменных работать не будет.

Затем выделяем весь полученный табличный диапазон, включая наименование столбцов, строк и ячейку с формулой ПЛТ. Переходим во вкладку «Данные». Как и в предыдущий раз, щелкаем по кнопке «Анализ «что если»», в группе инструментов «Работа с данными». В открывшемся списке выбираем пункт «Таблица данных…».

Запускается окно инструмента «Таблица данных». В данном случае нам потребуются оба поля. В поле «Подставлять значения по столбцам в» указываем координаты ячейки, содержащей срок кредита в первичных данных. В поле «Подставлять значения по строкам в» указываем адрес ячейки исходных параметров, содержащей величину тела кредита. После того, как все данные введены. Клацаем по кнопке «OK».

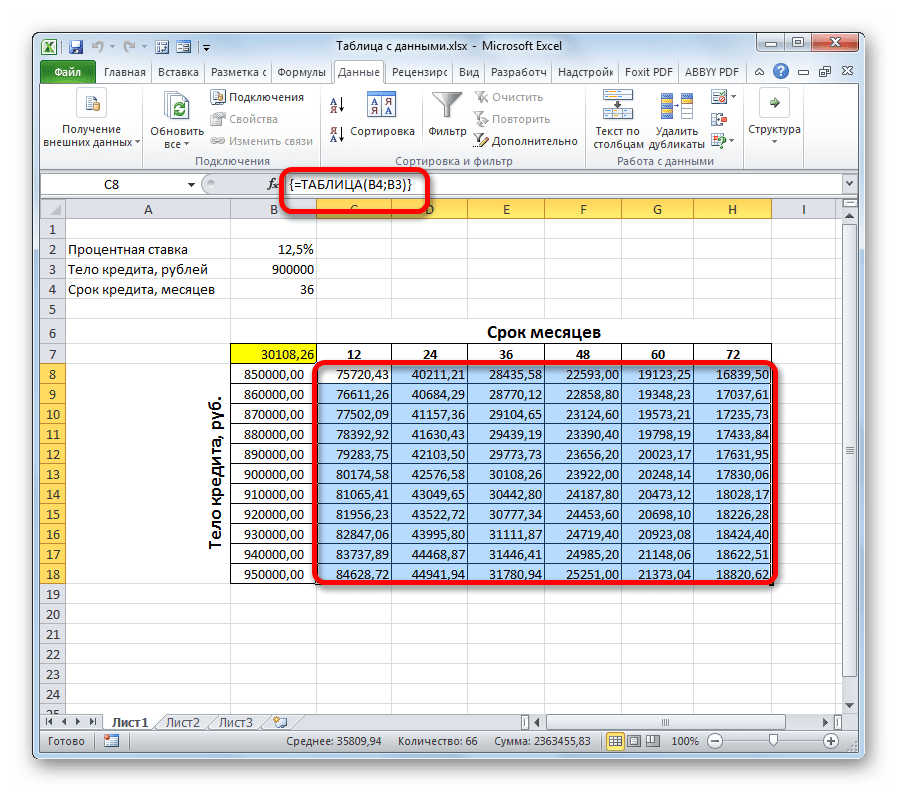
Программа выполняет расчет и заполняет табличный диапазон данными. На пересечении строк и столбцов теперь можно наблюдать, каким именно будет ежемесячный платеж, при соответствующей величине годовых процентов и указанном сроке кредитования.

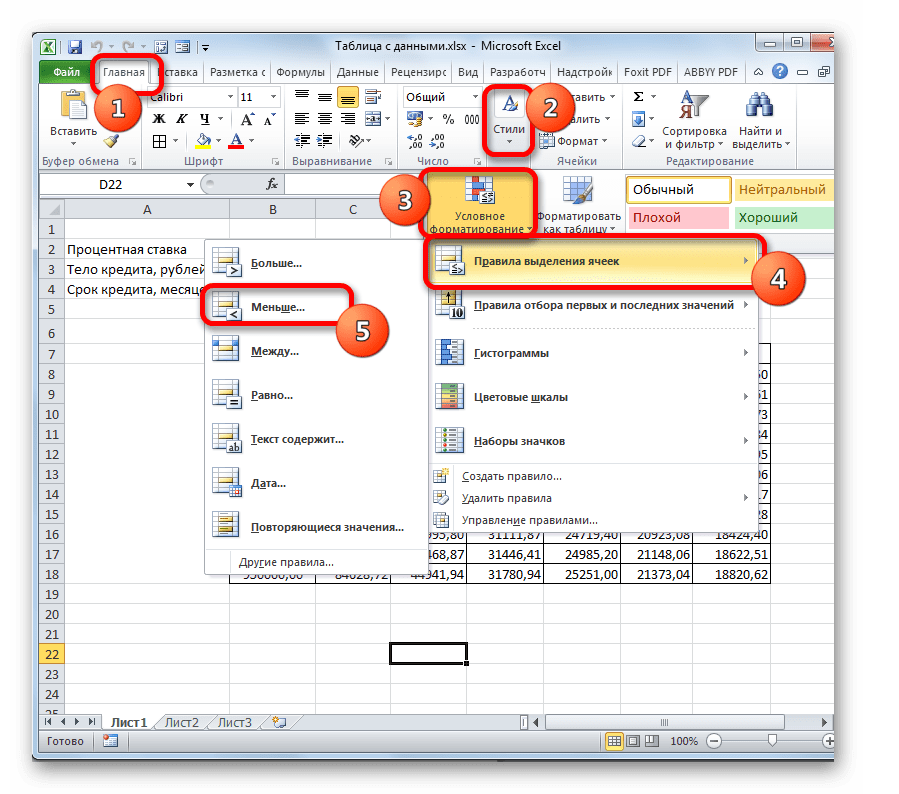
Как видим, значений довольно много. Для решения других задач их может быть ещё больше. Поэтому, чтобы сделать выдачу результатов более наглядной и сразу определить, какие значения не удовлетворяют заданному условию, можно использовать инструменты визуализации. В нашем случае это будет условное форматирование. Выделяем все значения табличного диапазона, исключая заголовки строк и столбцов.

Перемещаемся во вкладку «Главная» и клацаем по значку «Условное форматирование». Он расположен в блоке инструментов «Стили» на ленте. В раскрывшемся меню выбираем пункт «Правила выделения ячеек». В дополнительном списке кликаем по позиции «Меньше…».

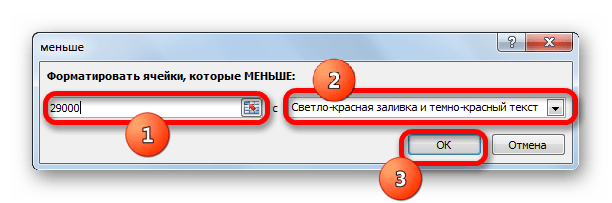
Вслед за этим открывается окно настройки условного форматирования. В левом поле указываем величину, менее которой ячейки будут выделены. Как помним, нас удовлетворяет условие, при котором ежемесячный платеж по кредиту будет составлять менее 29000 рублей. Вписываем данное число. В правом поле существует возможность выбора цвета выделения, хотя можно оставить его и по умолчанию. После того, как все требуемые настройки введены, клацаем по кнопке «OK».

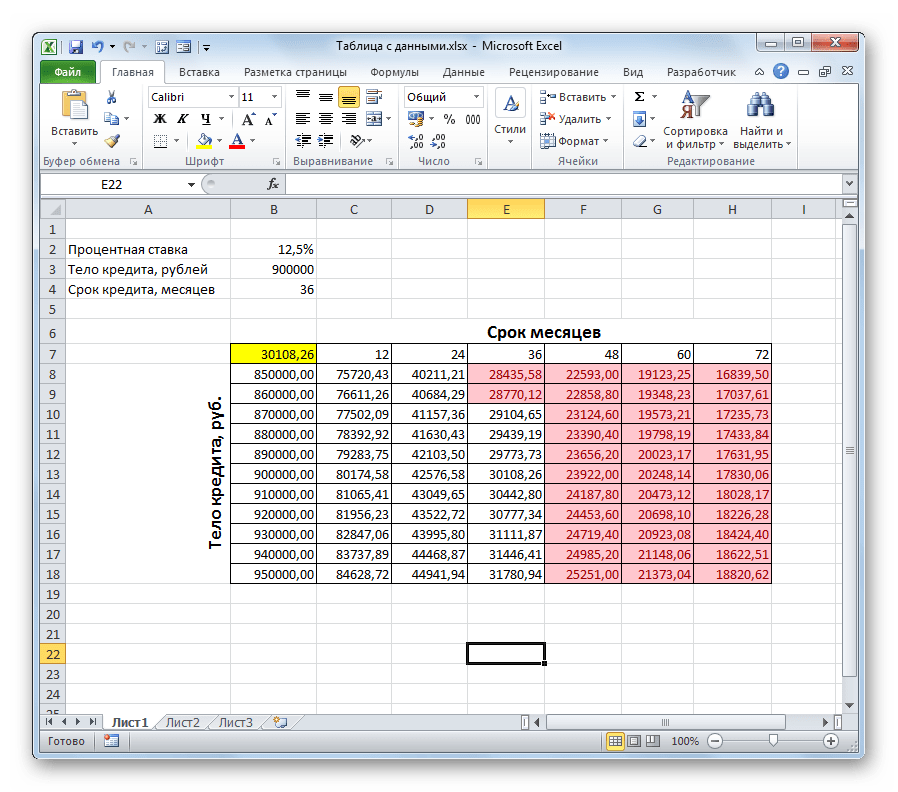
После этого все ячейки, значения в которых соответствуют вышеописанному условию, будут выделены цветом.

Проанализировав табличный массив, можно сделать некоторые выводы. Как видим, при существующем сроке кредитования (36 месяцев), чтобы вложиться в выше обозначенную сумму ежемесячного платежа, нам нужно взять заём не превышающий 860000,00 рублей, то есть, на 40000 меньше первоначально запланированного.

Если же мы все-таки намерены брать кредит размером 900000 рублей, то срок кредитования должен составлять 4 года (48 месяцев). Только в таком случае размер ежемесячного платежа не превысит установленную границу в 29000 рублей.

Таким образом, воспользовавшись данным табличным массивом и проанализировав «за» и «против» каждого варианта, заёмщик может принять конкретное решение об условиях кредитования, выбрав наиболее отвечающий его пожеланиям вариант из всех возможных.

Конечно, таблицу подстановок можно использовать не только для расчета кредитных вариантов, но и для решения множества других задач.

Урок: Условное форматирование в Экселе

В общем, нужно отметить, что таблица подстановок является очень полезным и сравнительно простым инструментом для определения результата при различных комбинациях переменных. Применив одновременно с ним условное форматирование, кроме того, можно визуализировать полученную информацию.

Источник

17 авг. 2022 г.
читать 2 мин

Коэффициент вариации , часто обозначаемый как CV, представляет собой способ измерения степени разброса значений в наборе данных по отношению к среднему значению. Он рассчитывается как:

CV = σ / μ

куда:

σ = стандартное отклонение набора данных

μ = среднее значение набора данных

Проще говоря, коэффициент вариации — это просто отношение между стандартным отклонением и средним значением.

Когда используется коэффициент вариации?

Коэффициент вариации часто используется для сравнения вариации между двумя разными наборами данных.

В реальном мире он часто используется в финансах для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций. Это позволяет инвесторам сравнивать соотношение риска и доходности между инвестициями.

Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:

Взаимный фонд A: среднее = 7%, стандартное отклонение = 12,4%

Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%

При расчете коэффициента вариации для каждого фонда инвестор находит:

CV для взаимного фонда A = 12,4% / 7% = 1,77

CV для взаимного фонда B = 8,2% / 5% = 1,64

Поскольку взаимный фонд B имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.

Как рассчитать коэффициент вариации в Excel

В Excel нет встроенной формулы для расчета коэффициента вариации для набора данных, но, к счастью, его относительно легко вычислить, используя пару простых формул. В следующем примере показано, как рассчитать коэффициент вариации для заданного набора данных.

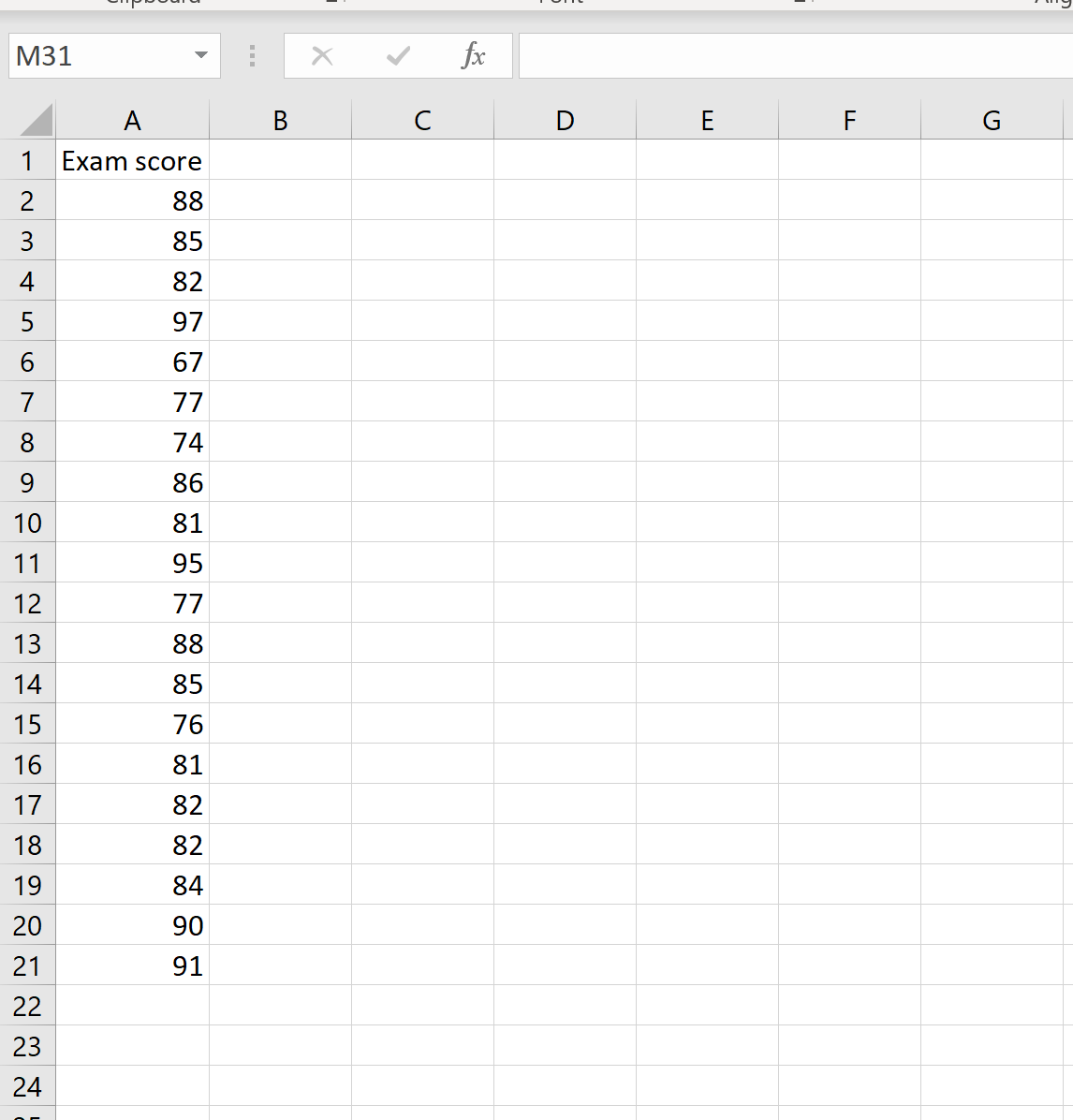
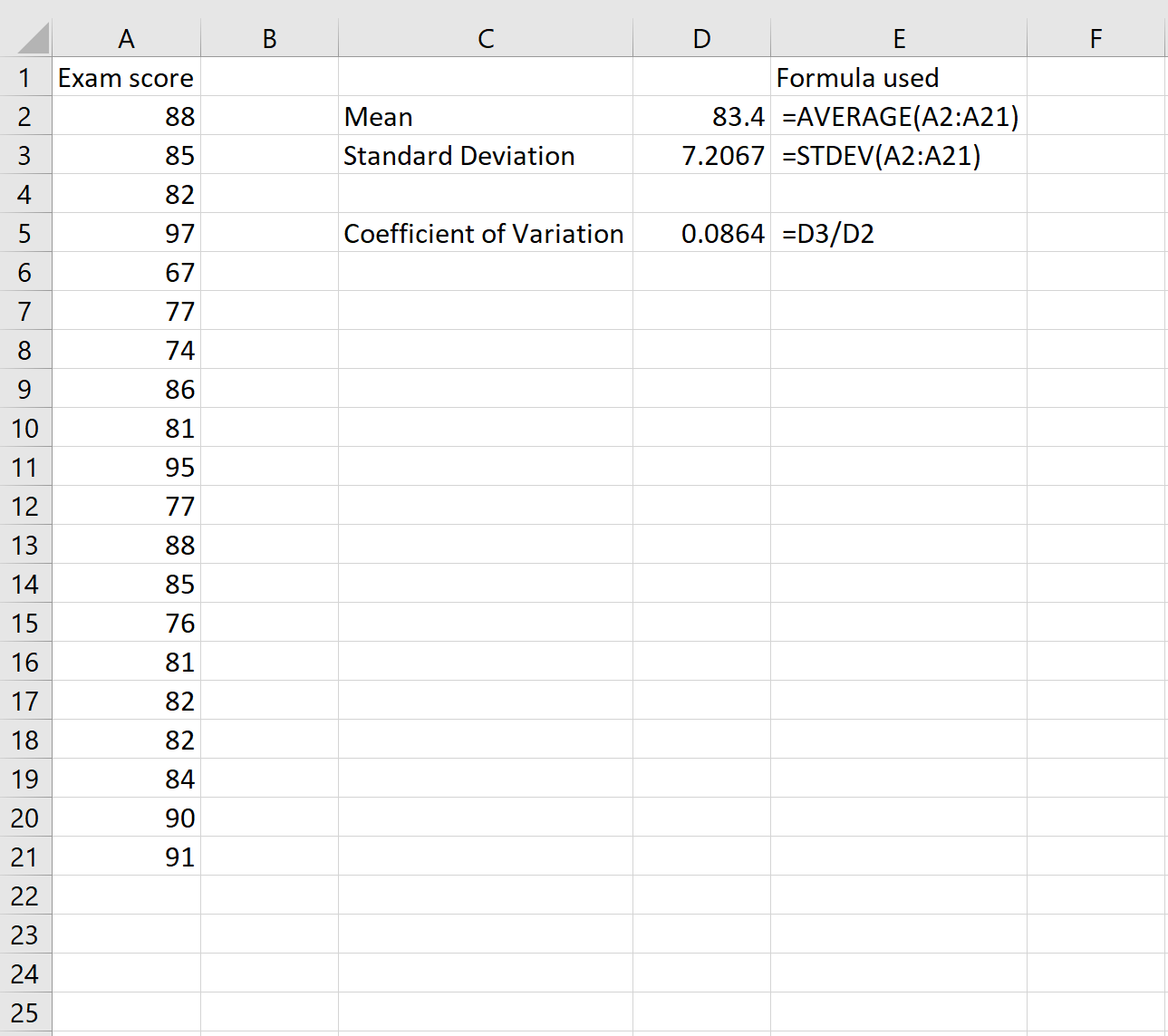
Предположим, у нас есть следующий набор данных, содержащий экзаменационные оценки 20 студентов:

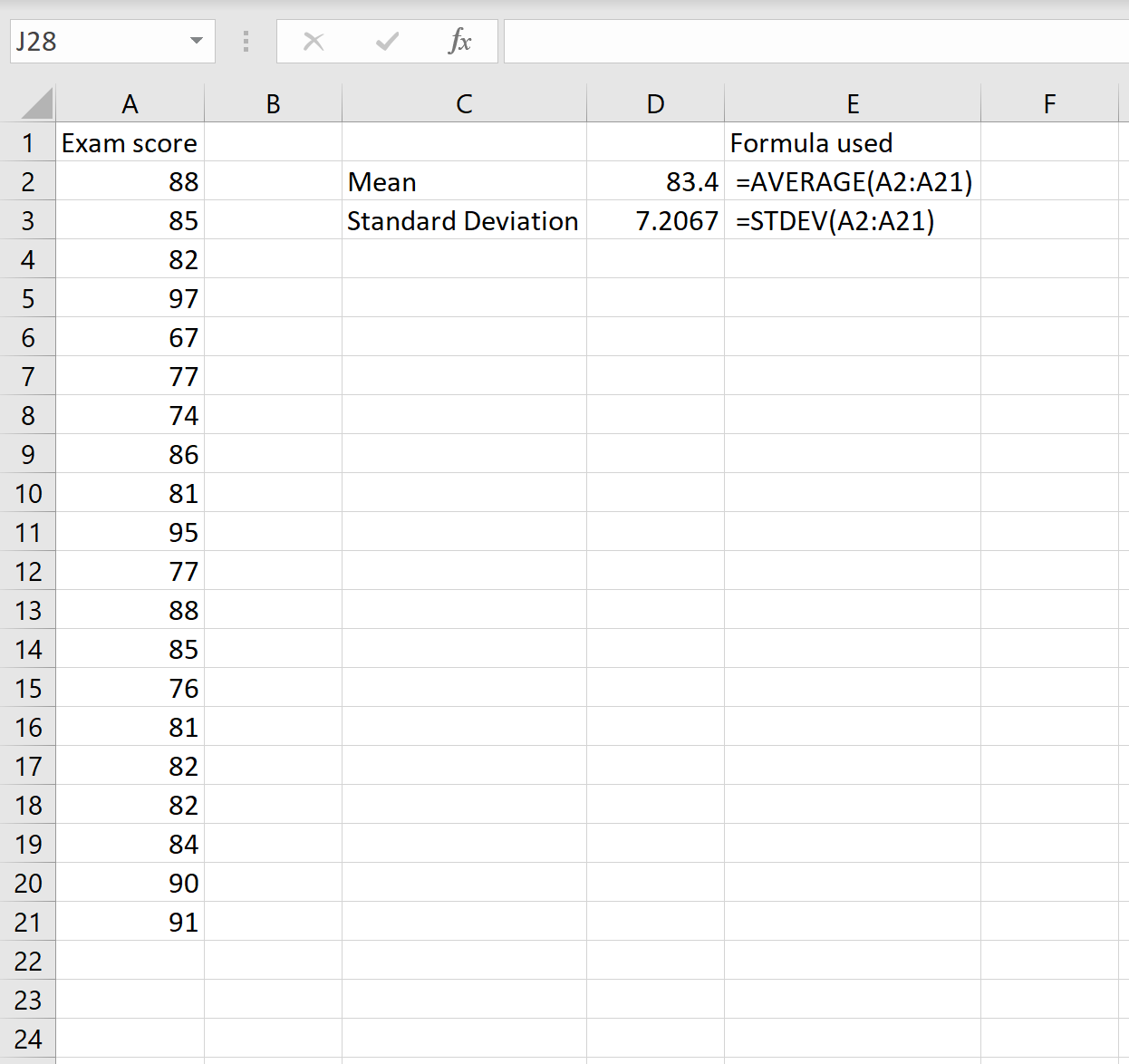
Чтобы рассчитать коэффициент вариации для этого набора данных, нам нужно знать только два числа: среднее значение и стандартное отклонение. Их можно рассчитать по следующим формулам:

Среднее значение: =СРЕДНЕЕ(A2:A21)

Стандартное отклонение: =СТАНДОТКЛОН(A2:A21)

Чтобы вычислить коэффициент вариации, мы затем делим стандартное отклонение на среднее значение:

Коэффициент вариации оказывается равным 0,0864 .

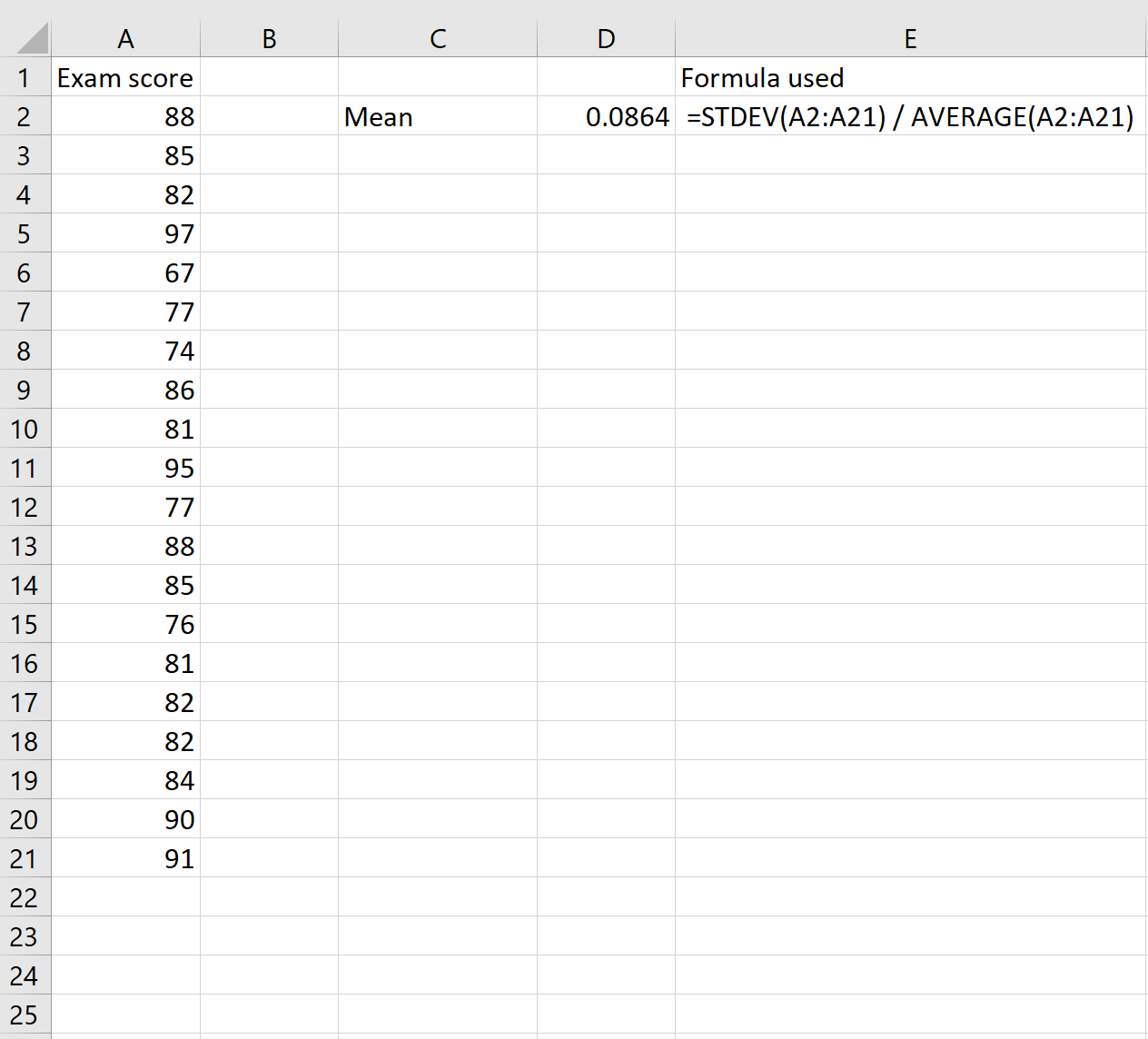
Обратите внимание, что мы также могли бы использовать только одну формулу для расчета CV:

Это приводит к тому же CV 0,0864 .

Источник

Хороший инструмент — это надстройка Поиск решения в MS Excel!

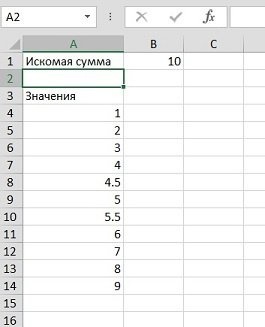
Например, его можно использовать в ситуации, когда вам нужно найти вариант, из которого с разных чисел могла быть добавлена определенная сумма (возможно, вы ищете, с каких счетов могла быть сформирована сумма платежа). Допустим, вам нужно найти сумму 10 из заданных чисел:

Для начала включаем надстройку или проверяем, что она включена (в Excel 2013): Файл/Параметры, раздел Надстройки, выберите Управление: Надстройки Excel, нажмите кнопку Перейти. Установите флажок Поиск решения, нажмите кнопку ОК

Найдите решение, которое появилось на ленте на вкладке «Данные»:

Теперь нам нужно понять, как мы можем использовать параметры в разных строках для «выбора» суммы. Я сделал вариант, когда мы указываем множитель 0 или 1 в одном столбце, подсчитываем произведение в соседнем столбце, а затем добавляем значения к итогу:

в ячейках столбца B указываем 0 или 1 (теперь неважно, что именно)
в ячейке C4 формула = A4 * B4
в ячейках C5: C14 — то же с учетом номера строки
в ячейке C3 формула = СУММ (C4: C14)

Теперь приступим к поиску решения. И заполните:

Оптимизация целевой функции: $ C $ 3
Раньше: Значения: 10
Изменение ячеек переменных: $ B $ 4: $ B $ 14
В соответствии с ограничениями: — добавьте (кнопка Добавить) три условия: 1) значения переменных должны быть целыми числами, 2) значения должны быть> = 0, 3) 2) значения должны быть быть

Не очень распространено, но и не экзотично. Во время моих обучающих курсов такой вопрос задавали не раз и не два. Суть в том, что у нас есть конечный набор некоторых чисел, из которых мы должны выбрать те, которые в сумме дают заданное значение.

В реальной жизни эта задача может показаться другой.

Например, мы загрузили из интернет-банка все платежи, поступившие на наш счет за последний месяц. Один из клиентов разделяет сумму платежа на несколько отдельных счетов и производит оплату в рассрочку. Мы знаем общую сумму к оплате и количество счетов, но не знаем сумму. В истории платежей необходимо выбрать те суммы, которые, как правило, дают заданное значение.
У нас есть несколько рулонов стали (линолеум, бумага.), Из которых мы должны выбрать те, которые придадут заказу заданную длину.
Блэкджек или обычно «пойнт». Необходимо собрать карты с общей стоимостью как можно ближе к 21 баллу, но не превышать этот порог.

В некоторых случаях может быть известна допустимая погрешность допуска. Он может быть нулевым (в случае счетов для снятия средств) и ненулевым (в случае бросков на снятие средств), либо ограничиваться снизу или сверху (в случае блэкджека).

Давайте рассмотрим разные способы решения такой задачи в Excel.

Способ 1. Надстройка Поиск решения (Solver)

Эта надстройка входит в стандартный набор Microsoft Office вместе с Excel и предназначена, как правило, для решения линейных и нелинейных задач оптимизации со списком ограничений. Для его подключения необходимо:

в Excel 2007 и более поздних версиях выберите Файл — Параметры Excel — Надстройки — Перейти
в Excel 2003 и более ранних версиях: откройте меню Инструменты — Надстройки

и поставьте галочку в соответствующем поле. Тогда нужная нам команда появится во вкладке или меню «Данные.

Чтобы использовать надстройку Поиск решения нашей проблемы, нам нужно будет немного модернизировать наш пример, добавив несколько вспомогательных ячеек и формул в список сумм для выбора:

Диапазон A1: A20 содержит наши числа, из которых мы выберем те, которые нам нужны, чтобы «уместить» заданное количество.
Диапазон B1: B20 будет своего рода набором переключателей, то есть он будет содержать ноль или один, указывая, выбираем ли мы данное число в образце или нет.
Ячейка E2 содержит обычную автоматическую сумму всех единиц в столбце B, в которой подсчитывается количество выбранных чисел.
В ячейке E3 функция СУММПРОИЗВ вычисляет сумму произведений пары ячеек из столбцов A и B (то есть A1 * B1 + A2 * B2 + A3 * B3 +.). Фактически, он вычисляет сумму чисел в столбце A, выбранных из чисел в столбце B.
В розовой ячейке E4 пользователь вводит желаемую сумму для вывода.
В ячейке E5 вычисляется абсолютное значение ошибки выбора, чтобы минимизировать ее в будущем.
Все желтые ячейки E8: E17 хотели бы получить список выбранных чисел, т.е тех чисел из столбца A, перед которыми стоят числа из столбца B. Для этого нужно выделить сразу все (!) Желтые ячейки и вставьте в них следующую формулу массива:

После ввода формулы ее нужно вводить не как обычную формулу, а как формулу массива, т.е нажимать не Enter, а Ctrl + Shift + Enter. Аналогичная формула используется в примере ВПР, который возвращает все найденные значения сразу (а не только первое).

Теперь перейдите на вкладку Data (или меню) и запустите инструмент Data — Solver):

В открывшемся окне вам необходимо:

Установить как целевую функцию (Целевая ячейка) — ячейка для расчета ошибки выбора E5. Чуть ниже выбираем вариант — Минимум, потому что мы хотим подбирать числа на заданную сумму с минимальной (или даже нулевой) ошибкой.
Установите диапазон столбцов переключателя B1: B20 как Edit Cells.
Используя кнопку Добавить, создайте дополнительное условие, что ячейки диапазона B1: B20 должны быть двоичными (т.е содержать только 0 или 1):

Используя ту же кнопку, при необходимости создайте ограничение на количество чисел в образце. Например, если мы знаем, что сумма разделена на 5 счетов, тогда:

После ввода всех параметров и ограничений запустите процесс выбора, нажав кнопку «Решить». Процесс выбора длится от нескольких секунд до нескольких минут (в самых серьезных случаях) и заканчивается появлением следующего окна:

Теперь вы можете оставить найденное решение выбора (Сохранить найденное решение) или вернуться к предыдущим значениям (Восстановить исходные значения).

Следует отметить, что для этого класса задач существует не одно, а целый набор решений, особенно если ошибка строго не равна нулю. Следовательно, выполнение поиска решения с разными начальными данными (например, с разными комбинациями нулей и единиц в столбце B) может привести к разным наборам чисел в выборках в указанных пределах. Поэтому имеет смысл запустить эту процедуру несколько раз, произвольно меняя переключатели в столбце B.

Найденные комбинации можно сохранить как сценарии (кнопка Сохранить сценарий), чтобы вы могли вернуться к ним позже, используя команду Данные — Анализ моделирования — Менеджер сценариев):

И все найденные решения, сохраненные в виде скрипта, будет очень удобно просматривать в единой сравнительной таблице с помощью кнопки Сводка):

Способ 2. Макрос подбора

В этом методе вся работа выполняется макросом, который по глупости прокручивает случайные комбинации чисел, пока не найдет требуемое количество в пределах допустимой ошибки. В этом случае нет необходимости добавлять столбец с нулями и единицами и формулами.

Чтобы использовать макрос, нажмите комбинацию Alt + F11, в открывшемся окне редактора Visual Basic вставьте новый модуль через меню Insert — Module и скопируйте туда этот код:

Подобно первому способу, запустив макрос несколько раз, вы можете получить несколько наборов подходящих чисел.

в Excel 2007 и более поздних версиях выберите Файл — Параметры Excel — Надстройки — Перейти
в Excel 2003 и более ранних версиях: откройте меню Инструменты — Надстройки

и поставьте галочку в соответствующем поле. После этого необходимая команда появится на вкладке или в меню «Данные».

Источник

Содержание

Использование описательной статистики
Подключение «Пакета анализа»
Размах вариации
Вычисление коэффициента вариации
Шаг 1: расчет стандартного отклонения
Шаг 2: расчет среднего арифметического
Шаг 3: нахождение коэффициента вариации
Простая формула для расчета объема выборки
Пример расчета объема выборки
Задачи о генеральной доле
По части судить о целом
Как рассчитать объем выборки
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Способ 1: применение расширенного автофильтра
Способ 2: применение формулы массива
СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

«Вставить функцию»

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

«Главная»

«Число»

«Процентный»

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Разделы: Математика

Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26
32 33 31 31 25 33 25 29 30 28
23 30 29 24 33 30 30 28 26 25
26 29 27 29 26 28 27 26 29 28
29 30 27 30 28 32 28 26 30 26
31 27 30 27 33 28 26 30 31 29
27 30 30 29 27 26 28 31 29 28
33 27 30 33 26 31 34 28 32 22
29 30 27 29 34 29 32 29 29 30
29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики:

моду
медиану
размах ряда
построить полигон частот
построить столбчатую и круговую диаграммы
раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Простая формула для расчета объема выборки

где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;

p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = (1 – p);

e – допустимая ошибка, в долях.

Пример расчета объема выборки

Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Получаем объем выборки n = 96 человек.

Задачи о генеральной доле

На вопрос «Накрывает ли доверительный интервал заданное значение p₀?» — можно ответить, проверив статистическую гипотезу H₀:p=p₀. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p^* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H₀ используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле

Гипотеза	H₀:p=p₀	H₀:p₁=p₂
Предположения	Схема испытаний Бернулли	Схема испытаний Бернулли
Оценки по выборке
Статистика K
Распределение статистики K	Стандартное нормальное N(0,1)	Стандартное нормальное N(0,1)

Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле

Значение u_кр находим по таблице функции Лапласа из соотношения 2Ф(u_кр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.

Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
Ф(2.23) = 0.49, u_кр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.

Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01

Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H₀:p=p₀=0,97 — неизвестная генеральная доля p равна заданному значению p₀=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H₁:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p₀=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства

По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-K_kp)= (-∞;-2,05). Наблюдаемое значение К_набл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.

Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H₀:p₁=p₂ — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H₀:p₁≠p₂ — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.

Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение K_набл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:

С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.

Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.

Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.

В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.

В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:

Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.

Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.

Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.

Способ 1: применение расширенного автофильтра

Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.

Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».

Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».

После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».

Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».

Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.

Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».

Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.

Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».

Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».

Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.

Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».

Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).

В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».

Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».

Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.

Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».

Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».

При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.

Способ 2: применение формулы массива

Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.

На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.

Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.

Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.

Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Жмем сочетание клавиш Ctrl+Shift+Enter.

Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Опять набираем сочетание клавиш Ctrl+Shift+Enter.

Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.

Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».

В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».

Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».

В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».

В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».

На кнопку с точно таким же названием жмем после возвращения в окно создания условий.

Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:

Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13

Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).

Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:

СРЗНАЧЕСЛИ()

Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:

В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.

Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:

Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.

МАКС()

Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

Источники

https://lumpics.ru/descriptive-statistics-in-excel/
https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
http://galyautdinov.ru/post/formula-vyborki-prostaya
https://math.semestr.ru/group/interval-estimation-share.php
https://tidydata.ru/sample-size
https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
https://lumpics.ru/how-to-make-a-sample-in-excel/
https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html

Источник

Большинство типовых
вычислительных алгоритмов в Excel оформлены
в виде стандартных функций и вызываются
с помощью программы Мастер функций (см.
подразд. 1.9). Самые популярные
из них:

ЕСЛИ() – позволяет
предусмотреть разные варианты заполнения
ячейки;
СУММ(), ПРОИЗВЕД()
– соответственно суммирование и
перемножение значений из одного или
нескольких блоков;
СУММПРОИЗВ() –
суммирование произведений соответствующих
элементов двух или нескольких массивов;
СРЗНАЧ(), СРГЕОМ()
– расчет соответственно среднего
арифметического и геометрического по
числам в заданных блоках;
СЧЕТ() – определение
количества чисел в заданном блоке.

Более сложные
алгоритмы оформлены в виде команд и
заказываются через меню Сервис. Наиболее
важные из них:

Подбор параметра…
– нахождение аргумента, при котором
функция примет нужное значение;
Поиск решения…
– решение систем уравнений и задач
оптимизации;
Пакет анализа –
содержит программы, необходимые при
статистической обработке данных.

Если нужная для
вычислений команда отсутствует в меню,
ее можно установить с помощью команды
Сервис Надстройки…

6.1. Общие сведения о функции если()

Функция ЕСЛИ()
позволяет предусмотреть разные способы
заполнения одной и той же ячейки. То,
каким из них следует воспользоваться
в данный момент, Excel определяет
самостоятельно по тому, выполняется
или нет при введенных данных указанное
в функции условие. Стандартный формат
функции имеет следующий вид:

ЕСЛИ(Логическое_выражение;
Значение_если_истина;Значение_если_ложь)

Здесь:

Логическое_выражение
– это условие, которое при одних
значениях введенных данных выполняется,
при других – нет;
Значение_если_истина
– алгоритм, по которому определяется
значение функции, когда условие
оказывается правильным;
Значение_если_ложь
– алгоритм, по которому определяется
значение функции, когда условие
оказывается неправильным.

В роли алгоритмов,
которые выбирает функция ЕСЛИ(), могут
выступать расчетные выражения, другие
функции, ссылки на ячейки, где находится
нужная информация, текстовые строки и
т. п.

Рассмотрим действие
этой функции на конкретных примерах.

6.2. Выбор из двух вариантов по одному условию

Пример

Поставщик ввел
оптовую скидку на цену для больших
партий товара. Надо составить шаблон
для расчета стоимости любой партии
товара.

Составим таблицу
из констант, необходимых для расчета.
В ячейки А1:А4 введем названия констант:
«ОбъемПартии», «ОптБарьер»,
«РознЦена», «ОптЦена». Присвоим
ячейкам В1:В4 такие же имена (удобно
пользоваться командой Вставка 
Имя 
Создать…). В ячейку С1 введем
текст «СтоимПартииТовара».

Сделаем активной
ячейку С2 и вызовем через Мастер функций
функцию ЕСЛИ(). В окне аргументов в
текстовые поля введем следующие значения:

В поле
«Логическое_выражение:» вводится
условие, по которому Excel будет выбирать
нужный вариант действий. Его можно
составить так:

ОбъемПартии<=ОптБарьер

В поле
«Значение_если_истина:» указывается
способ, по которому следует рассчитывать
функцию, если условие оказалось
правильным при тех данных, которые
введены во влияющие ячейки в данный
момент. Для нашего примера этот аргумент
выглядит следующим образом:

ОбъемПартии*
РознЦена

В поле
«Значение_если_ложь:» указывается,
как рассчитывать функцию, если условие
не выполняется. Для нашего примера
следует ввести

ОбъемПартии*ОптЦена

Расчетный шаблон
готов. Чтобы проверить его, введите
удобные для устных расчетов числа в
ячейки В1:В4 и проверьте, правильно ли
функция ЕСЛИ() выбрала формулу для
заполнения ячейки С2. Введите в В1 другой
объем партии, при котором требуется
использовать другую цену при расчете
стоимости покупки. Если в обоих случаях
получены верные результаты, можно
красиво отформатировать ячейки А1:С4
(см.
подразд. 1.13–1.16) и пользоваться
этим шаблоном, меняя только значения
констант в В1:В4.

Пример

В таблице значений
функции y = 2cos(x
+ 2)e^0,5^xнадо отметить символом «*» строку
с минимальным значением.

Введем в ячейки
А1 и В1 подписи «X» и
«Y», в блок А2:А11 –
значения аргументов, в блок В2:В11 –
формулу расчета функции. Столбец С
зарезервируем для заказанной в условии
метки. В ячейкуD1 введем
текст «минимум», в ячейкеD2
с помощью функции МИН() найдем это
значение в блоке В2:В11.

Выделим ячейку С2
и вызовем через Мастер функций функцию
ЕСЛИ(). Условие, по которому Excel выбирает
нужный вариант действий, составим так:
В2=$D$2. В строку второго
аргумента вводим символ «*» (без
кавычек), в третий – пробел и нажмем
после этого <ОК>. С помощью протяжки
скопируем полученную формулу на блок
С2:С11.

Задание

Посмотрите, какой
вид приняла функция в разных ячейках
этого блока.

Рассмотрим функцию
ЕСЛИ() в той строке, в которой появилась
«*». Значение функции y
в этой строке минимально. Левая и
правая части условия оказались
одинаковыми, т. е. первый аргумент –
правильный. Поэтому для заполнения
своей ячейки функция ЕСЛИ выбрала то,
что указано во втором аргументе. Для
значений функцииув других строках
условие, введенное в функцию ЕСЛИ(),
оказывается неверным, поэтому она
заполняет свои ячейки по варианту
третьего аргумента. В нашем случае это
пробел, который невидим на экране,
поэтому ячейки кажутся пустыми.

Измените аргументы,
введенные в А2:А11. «*» переместилась
в другую строку, хотя формулы в С2:С11 не
были изменены (после изменения данных
каждая функция ЕСЛИ() автоматически
проверила свой первый аргумент заново
и приняла новое управляющее решение,
каким правилом пользоваться для
заполнения своей ячейки).

Задание

В ячейку А1 введите
формулу:

=ЕСЛИ(С3=37;»СЕНО»;»СОЛОМА»)

Определите влияющую
ячейку (команда
Сервис 
Зависимости 
Влияющие ячейки) и введите в
нее такое число, при котором СОЛОМА
превратится в СЕНО.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Coefficient of Variation is a statistical term that is used to measure the dispersion of data points with the arithmetic mean of all the data points in the series. In mathematical terms, it is the ratio of standard deviation with the mean. The formula for the coefficient of variation can be expressed as:

$CV = frac{sigma}{overline{x}}$

where and denotes the standard deviation and arithmetic mean of all the data points in the series respectively.

The coefficient of variation is a dimensionless quantity and is often expressed in percentage. Intuitively, we can say the higher the value of the coefficient of variance the more the data points are dispersed around the mean. Since the coefficient of variation is a dimensionless entity, it can also be used to compare two completely different data series even though their arithmetic means differ significantly from one another. It makes it possible to compare two different entities whose scales of measurement do not match each other.

One real-world scenario where the coefficient of variation is used in calculating the risk-reward ratio in stock markets. The less value of the coefficient of variation signifies lesser volatility relative to the return generated. Hence, an investor can decide to take a position in such stocks/funds in which volatility is less.

In this article, we are going to read about the calculation of the coefficient of variation in Excel. Since Excel is an advanced tool that offers multiple pre-defined functions to perform statistical operations we can expect Excel to have one such pre-defined function for calculating the Coefficient of variation. But sadly it does not include any built-in function to perform this operation. Instead, we can have a workaround to complete this operation that we are going to learn in the next section. From the mathematical formula of the coefficient of variation, to calculate the coefficient of variation we require standard deviation and mean of all the points in the series.

Step 1: Calculate the standard deviation of all the points in the series. It can be calculated using any of the below given three functions based upon our requirements:

(i) STDEV(): Used for calculating the standard deviation of a general series.

(ii) STDEV.P(): Used for calculating the standard deviation of a population.

(iii) STDEV.S(): Used for calculating the standard deviation of a sample.

Step 2: Calculate the arithmetic mean of all the data points in the series using the AVERAGE() function.

Step 3: Calculate the ratio by dividing the standard deviation value by the mean value.

Источник

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28