Excel for Microsoft 365 Excel for Microsoft 365 for Mac Excel for the web Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 for Mac Excel 2016 Excel 2016 for Mac Excel 2013 Excel 2010 Excel 2007 Excel for Mac 2011 Excel Starter 2010 More…Less
Estimates variance based on a sample.
Important: This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.
For more information about the new function, see VAR.S function.
Syntax
VAR(number1,[number2],…)
The VAR function syntax has the following arguments:
-
Number1 Required. The first number argument corresponding to a sample of a population.
-
Number2, … Optional. Number arguments 2 to 255 corresponding to a sample of a population.
Remarks
-
VAR assumes that its arguments are a sample of the population. If your data represents the entire population, then compute the variance by using VARP.
-
Arguments can either be numbers or names, arrays, or references that contain numbers.
-
Logical values, and text representations of numbers that you type directly into the list of arguments are counted.
-
If an argument is an array or reference, only numbers in that array or reference are counted. Empty cells, logical values, text, or error values in the array or reference are ignored.
-
Arguments that are error values or text that cannot be translated into numbers cause errors.
-
If you want to include logical values and text representations of numbers in a reference as part of the calculation, use the VARA function.
-
VAR uses the following formula:
where x is the sample mean AVERAGE(number1,number2,…) and n is the sample size.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Strength |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Formula |
Description |
Result |
|
=VAR(A2:A11) |
Variance for the breaking strength of the tools tested. |
754.2667 |
Need more help?
Want more options?
Explore subscription benefits, browse training courses, learn how to secure your device, and more.
Communities help you ask and answer questions, give feedback, and hear from experts with rich knowledge.
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
Инвестору чрезвычайно важно знать степень риска, которому подвержены открытые позиции. Определить меру риска VaR (Value-at-Risk) для единичного актива можно по формуле:
95% VaR = 1.65 X Волатильность * Размер позиции * SQRT(Время)
где
(SQRT – корень квардатный) и 95% – это 95%-ный доверительный уровень;
Волатильность – стандартное отклонение изменения цен (выясняется как натуральный логарифм «сегодня/вчера»);
Размер позиции – лицевая стоимость торгуемого контракта;
Время – горизонт оценки.
Полученный результат трактуют так: ценовые изменения в данный промежуток времени не приведут к потерям выше полученного результата в 95% случаев. Иными словами, есть только 5%-ная вероятность потери, превышающей значение 95% VaR.
В банковской практике чаще применяется 99% VaR, отличие которого от представленной формулы в коэффициенте: 2.33 вместо 1.65. Соответственно, 99% VaR говорит нам, что цены с вероятностью 99% не способны измениться настолько, чтобы убытки превысили вычисленное значение.
Пользуясь указанной выше формулой, можно определить риск широкого спектра финансовых активов, попадающих в категорию простых инструментов и линейных производных. К ним относятся: акции, иностранные валюты, облигации обычные и с плавающим купоном (не имеющие высокую дюрацию), процентные и валютные свопы, валютные форвардные контракты, FRA. Тем самым формулировка доступна для применения практически на всех рынках, традиционно вызывающих интерес у отечественных инвесторов, в первую очередь – на рынке акций и FOREX.
Обычно проблемы оценки риска рассматриваются на стадии портфеля, состоящего из двух активов. Для большего числа инструментов предлагаются формулы, труднопонимаемые без специальной математической подготовки. Но данная задача решается просто, если подойти к ней сугубо с практической точки зрения, исключив теоретические аспекты.
Поэтому здесь дается только то, что необходимо знать, чтобы самостоятельно составить программу в электронных таблицах (Excel), обеспечивающую вычисления VaR портфеля. Для иллюстрации использованы случайно выбранные пять российских акций в произвольно взятый период времени: с 1 по 29 апреля 2003 года.
Шаг 1. Первичная обработка данных
Сначала выясним значение среднего изменения цен и волатильности. Для этого нам потребуется как минимум объем данных, удовлетворяющих выбранному периоду оценки.
Предположим, используется 20-периодный цикл, тогда нужно не менее 21 дня, если анализ выполняется по дневным данным. Для каждого дня необходимо выяснить натуральный логарифм отношения цен «сегодня/вчера» (см. значение «Изм.» в табл. 1).
«Изменение» = ln (сегодня / вчера)

Теперь можно найти среднедневное изменение и величину стандартного отклонения, используя полученный ряд (колонки «Изм.»).
Среднедневное изменение – это среднеарифметическое, которое в Excel записывается «=average()», а стандартное отклонение как «=stdev()», которое и является дневной волатильностью.
При этом калькуляция охватывает область переменных, находящихся на строчках от 2 до 21 в колонке «Изм.» (результат см. в табл. 2).

Следует иметь в виду: предлагаемый алгоритм оценки волатильности основан на методе постоянных, а не экспоненциально взвешенных ковариаций. Но к ним можно перейти, используя полученные ряды изменения цен, для чего необходимо ввести соответствующие поправки, обеспечивающие больший вклад более поздних наблюдений.
Хороший аналог данного метода оценки волатильности – взвешенная скользящая средняя по сравнению с обычной скользящей средней. Характерно, что множитель, практикуемый в методологии J.P. Morgan RiskMetrics, равен 0.98, как и в установках по умолчанию в программах, предназначенных для технического анализа рынка.
Шаг 2. Необходимый минимум теории
Прежде чем перейти к вычислению VaR портфеля, обратимся к некоторым сведениям, которые дают понимание расчетных алгоритмов. В целом VaR портфеля из многих активов можно определить по следующей формуле:
VaR портфеля = Среднее изменение – К * Волатильность портфеля,
где
Среднее изменение – просто сумма средних изменений всех компонентов портфеля;
К – число стандартных отклонений, требуемых для заданного доверительного уровня, вычисляемое по формуле в Excel «=NORMSINV()», где аргумент – соответствующий доверительный уровень.
Волатильность портфеля калькулируется с использованием формулы, предложенной Г. Марковицем:
Волатильность портфеля = SQRT (Вектор волатильной компоненты *Корреляционная матрица * Транспонированный вектор волатильной компоненты)
Вектор волатильной компоненты можно вычислить, пользуясь формулой:
Компонента волатильности = Стоимость позиции * Волатильность позиции
Помимо уже выполненных расчетов для вычисления VaR портфеля потребуется построить корреляционную матрицу, основываясь на данных, обработанных в шаге 1.
Она представляет собой совокупность коэффициентов, отражающих корреляцию между каждым из инструментов, входящих в портфель.
Вычисления в Excel выполняются с помощью соответствующей функции «=correl()», причем построение матрицы лучше выполнить на странице, где будут размещены все прочие расчеты, в том числе и VaR. Это уже будет шаг 3.
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
Шаг 3. Вычисление VaR портфеля
Протокол расчета, позволяющий видеть все промежуточные этапы, представлен в таблице 3. Здесь же даны формулы, с помощью которых производятся вычисления.
Следует иметь в виду: данная таблица есть копия рабочего листа Excel, поэтому при написании программы рекомендуется придерживаться указанного порядка, пользуясь для подсказки формулами, выложенными в крайней колонке «Н» справа. Позже, если возникнет желание, структуру таблицы можно изменить.
Остается сделать ряд важных замечаний
Во-первых, в зависимости от задачи число входящих в портфель активов можно увеличить или уменьшить.
Во-вторых, при оценке по ценам внутри дня при вычислениях надо придерживаться единого масштаба, поэтому VaR будет получаться для задаваемого числа часов в параметре «время». Для перевода в дневной масштаб следует учесть число торговых часов в одном дне.
Для обращающихся на бирже активов обычно это не вызывает трудностей, но в ряде случаев можно столкнуться с проблемами. Как, скажем, на рынке FOREX, где трудно предложить однозначное решение, поскольку приходится учитывать неравномерный характер торговой активности.
В-третьих, следует иметь в виду: портфель может содержать различные активы. Единственное условие – они должны быть выражены в одной валюте.
Например, если бы мы пожелали оценить риск портфеля, состоящего из акций в рублях, валютной позиции по евро/доллар и процентного фьючерса в британских фунтах, нам пришлось бы прежде выбрать счетную валюту.
Если мы выбрали евро, то потребуется пересчитать все ценовые ряды в евро по соответствующему курсу для каждого дня. После этого нам удастся без труда получить результирующую цифру, которая также будет в евро.
Шаг 4. Оптимизация портфеля
Поняв процедуру оценки риска, можно решать такие серьезные задачи, как поиск более эффективных решений. В Excel существует опция «Solver» в разделе «Tools», позволяющая выполнять поиск решений по заданным условиям. О других полезных функциях Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Например, если мы укажем, что нас устраивает иное значение 95% VaR – скажем, -500, а не -844 – и определим при этом возможность изменения числа всех акций, то программа вычислит: «Акция 1» следует иметь 119 акций, «Акция 2» – 1193, «Акция 3» – 11, «Акция 4» – 2 и «Акция 5» – 227 акций. Причем с длинными позициями по всем бумагам.
Легко заметить: подобный подход отличается ограниченностью, поскольку мы никак не определяем имеющийся в нашем распоряжении капитал, а указываем лишь уровень принимаемого риска.
Эта проблема легко разрешима: имеющиеся данные позволяют производить любые вычисления, необходимые для определения стоимости портфеля, а также размера требуемого капитала как при торговле с маржой, так и без нее. После этого определить степень риска в относительных величинах не представляет труда, это будет частное от VaR и рабочего капитала или размера счета – в зависимости от того, что необходимо оценить.
С полученной величиной мы можем обращаться точно так же, как и со значением VaR в денежных единицах. Скажем, если нам для создания портфеля, представленного в таблице 3, потребуется капитал в размере 42 тыс. руб. (исходя из правил брокера), то 1-дневный 95% VaR составит 2.01%, а 10-дневный – 3.41%.
Данные цифры говорят: существует 95%-ная вероятность, что потери портфеля за 1 день не превысят 2.01% от работающего капитала, а за 10 дней – 3.41%. Естественно, если нам нужна более полная картина, следует проводить расчеты также и для всего капитала, с учетом резервов.
Опираясь на эти цифры, можно выполнять оптимизацию, пользуясь алгоритмом, описанным выше. Например, задавая 1-дневные потери в размере 1% от работающего капитала при доверительном уровне в 95%, мы узнаем, что это достигается за счет увеличения короткой позиции в «Акция 3» (с 20 до 23 акций) и покупки 18, а не одной, акций «Акция 4», при неизменности числа прочих бумаг.
Обратите внимание: не введя в данную процедуру ограничений на капитал, мы обнаружим, что эта возможность для нас нереальна или не отвечает нашим намерениям, поскольку для создания портфеля требуется 163 тыс. руб. Поэтому следующий этап усложнения алгоритмов оценки риска – ввод ограничений.
Шаг 5. Ввод ограничений
Ввод ограничений, позволяющих решать проблему оптимизации, требует немного больше знаний об электронных таблицах. Полностью описать то, как можно решить ту или иную задачу, здесь не представляется возможным.
Во-первых, можно найти немало подходящих алгоритмов, позволяющих достичь поставленной цели. Во-вторых, многие из них связаны с уровнем квалификации инвесторов – пользователей среды Windows, а обучение не является нашей задачей. В-третьих, как показывает практика, пользователям лучше всего самостоятельно создавать интерфейс, если работа ведется с Excel.
Поэтому в шаге 5 только указывается путь, ведущий к построению потокового процесса контроля над риском и управления им.
Наиболее простой способ решить задачу – ввести условия, опираясь на соотношение между показателем меры риска и размером имеющегося в нашем распоряжении капитала. Если одновременно мы хотим автоматизировать процесс, нам потребуется ввести дополнительные ограничения, описывающие наши реальные возможности. Обычно это реализуется через совместное использование таких функций, как «=IF(), OR(), AND()».
Дополнительные возможности появляются, если изменениям будет подвергаться не число акций, а их доля в портфеле. Описание связей в таком случае будет легче, так как мы заранее указываем размер капитала, под который формируется портфель. Число акций уже будет не задаваться пользователем, как это предложено в таблице 3, а вычисляться на основе весовой доли в портфеле.
Причем подходы, основанные на оценке веса, могут иметь и другие решения. Вводя граничные условия с целью автоматизации процесса оценки риска, мы неминуемо столкнемся с проблемой управления резервами.
И здесь следует обратить внимание на важную деталь. Дело в том, что непосредственное применение VaR – это определение, какой капитал необходимо резервировать, чтобы иметь достаточное покрытие рыночного риска. В практике рядового инвестора – это решение вопроса, сколько надо иметь свободных средств на счете, чтобы не потерять свыше заданной величины или не получить margin call (при маржевой торговле).
В банковской практике рекомендуемые резервы – 3-кратный 10-дневный 99% VaR (для портфеля из таблицы 3 такие резервы составят 8299 рублей). Поскольку резервы, оцениваемые через VaR, – величина «плавающая» и зависит от волатильности, этот аспект может оказаться для кого-то привлекательным. В таком случае вполне естественно включить данный параметр в алгоритмы, обеспечивающие обсчет риска.
Наконец, следует включить и ожидаемую прибыль. Это дополнение позволяет получать новые оценочные коэффициенты, играющие важную роль в торговой практике. Скажем, мы можем вывести соотношение «прибыль/возможный убыток». Если при этом учтены издержки на транзакции, а также соответствуют горизонты, использованные для оценки потерь и прибыли, то у нас получится формулировка для оценки рисков RAROC по методике Bankers Trust.
Решений автоматизации процедур, связанных с риск-менеджментом, существует много. Окажутся ли они эффективными, в значительной степени зависит от точности поставленной задачи и желания получить действительно простую и понятную процедуру оценки меры риска.
Вершиной здесь является построение потокового процесса управления ценовыми и финансовыми рисками, решающего с максимально возможной эффективностью основную задачу инвестора – как понадежней заработать.
Автор: Михаил Чекулаев
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
Трейдинг21 октября 2020 в 08:0036 498
Формулы для расчёта в Excel
Разновидности риска
Метод VAR
Рис. 1. Список авторизованных вендоров
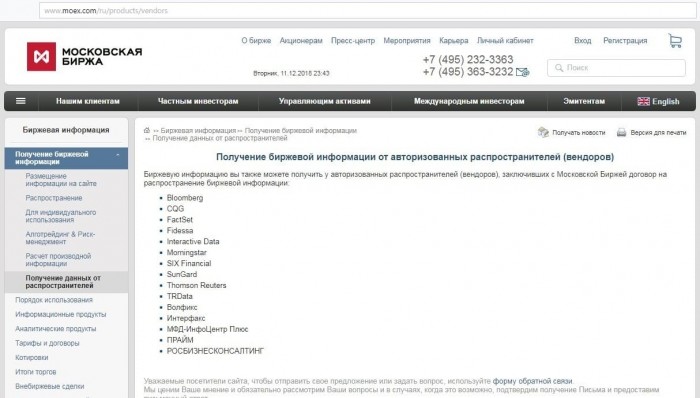
Рис. 2. Вычисление математического ожидания и стандартного отклонения
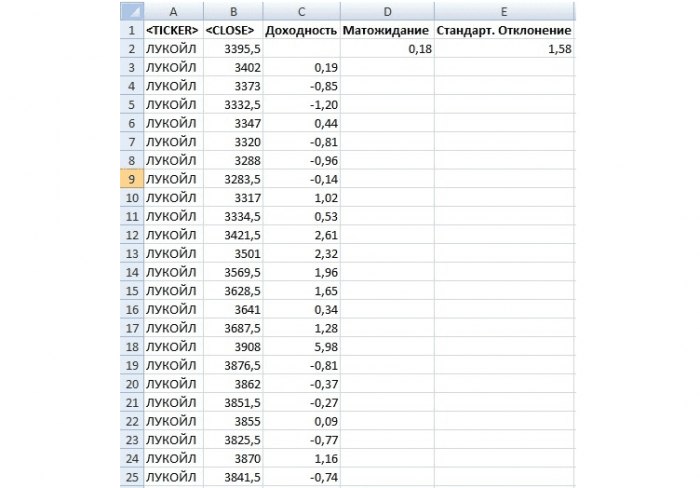
Рис. 3. Определение квантиля
Рис. 4. Определение минимальной стоимости акции с вероятностью 99% на следующий день
Рис. 5. Определение минимальной стоимости акции с вероятностью 99% через пять дней
Рис. 6. Определение риска ценового изменения на следующий день и через пять дней
Больше интересных материалов
Value at Risk (VaR) is one of the most widely known measurements for risk assessment and risk management. The goal of risk management is to identify and understand exposures to risk, measure that risk, and then apply the knowledge to address those risks.
Key Takeaways
- Value at Risk statistically measures the likelihood of a specific loss occurring.
- Value at Risk is an industry-wide, commonly-used risk assessment technique.
- The confidence interval of a VaR computation is the chance a specific outcome will occur. The higher the confidence interval, the more likely the outcome.
- There are several different ways to calculate VaR with the historical method being among the easiest to manually calculate.
- Excel can be very helpful in calculating the mean return, standard deviation, and VaR outcomes for various confidence intervals.
What Is Value at Risk (VaR)?
Value at Risk (VaR) is a measurement showing a normal distribution of past losses. The measurement is often applied to an investment portfolio for which the calculation gives a confidence interval about the likelihood of exceeding a certain loss threshold. The VaR calculation is a probability-based estimate of the minimum loss in dollar terms expected over a period. This data is used by investors to strategically make investment decisions.
Pros and Cons of Value at Risk (VaR)
There are a few pros and some significant cons to using VaR in risk measurement. On the plus side, the measurement is widely used by financial industry professionals and is easy to interpret. VaR computations can be compared across different types of assets or portfolios. Due to its popularity, VaR is also frequently included and calculated for you in various financial software tools such as a Bloomberg terminal.
VaR is often criticized for offering a false sense of security as VaR does not report the maximum potential loss. VaR is also highly dependent on the confidence interval, and the outcome of models calculated with 95% confidence may still occur.
VaR is an estimation technique—it is not useful when attempting to determine what will occur. VaR indicates the chance something might happen and what the dollar impact will be at that likelihood.
Probabilities in VaR are based on a normal distribution of returns. Unfortunately, financial markets are known to have non-normal distributions. Financial markets have extreme outlier events on a regular basis—far more than a normal distribution would predict. For this reason, a limitation of VaR is the statistically most likely outcome isn’t always the actual outcome.
The VaR calculation also requires several statistical measurements such as variance, covariance, and standard deviation. With a two-asset portfolio, this is relatively straightforward. However, the complexity increases exponentially for a highly diversified portfolio. As with other quantitative analysis techniques, the calculation will only be as good as the underlying assumptions of the calculation.
Value at Risk Formula
As with many financial applications, the formula sounds easy as it only has a few inputs. However, manually calculating the VaR for a large portfolio is computationally intense. Also, though there are several different methods of calculating VaR, the historical method shown below is the most simple:
Value at Risk = vm (vi / v(i — 1))
M is the number of days from which historical data is taken, and vi is the number of variables on day i. The purpose of the formula is to calculate the percent change of each risk factor for the past 252 trading days. Each percent change is then applied to current market values to determine 252 scenarios for the security’s future value.
There are 252 trading days in a year, which is why we use that figure instead of 365 to calculate VaR for a daily timeframe.
Finding VaR in Excel
Below is the process of calculating VaR using a different method called the variance-covariance approach.
-
Import relevant historical financial data into Excel. For a single security, you’ll need the current price as well as the historical closing price for the specific period you want to analyze.
-
Calculate the daily rate of change for the price of the security. For each day, this is calculated by dividing the change in price over two days by the old price. For example, to find the return for today, subtract today’s price by yesterday’s price, then divide that calculation by yesterday’s price. Repeat this process for each historical day.
-
Calculate the mean of the historical returns from Step 2. In Excel, this can be achieved by using the average function.
-
Calculate the standard deviation of the historical returns compared to the mean determined in Step 3. In Excel, this can be achieved by using the STDEV function.
-
Calculate the VaR for various confidence intervals. In Excel, this can be achieved by using the NORM.INV function. This function requires the probability of an event occurring, mean, and standard deviation. For multiple calculations of VaR, repeat Step 5 using different probabilities.
What Is the Formula for VaR?
There are several different methods to calculate VaR, each with a different formula, The most simple method to manually calculate is the historical method where m is the number of days from which historical data is taken and vi is the number of variables on day i.
Value at Risk Formula (using the historical method): vm (vi / v(i — 1))
What Does Value at Risk Indicate?
Value at Risk measures the statistical likelihood that an investment might experience a loss given a specific probability. Value at Risk also quantifies what that loss might be at various confidence intervals.
Is a High VaR a Good Thing?
When analyzing VaR, a high value for the confidence internal percentage is a good thing. This means we are more confident in the likelihood of the projected outcome. Alternatively, a high value for the projected outcoming is not ideal. This means we statistically anticipate a higher dollar loss to occur.
Наблюдения и советы этой статьи мы подготовили на основании опыта команды Функция ВАР вычисляет дисперсию на основе заданной выборки.
Функция VAR и функция VAR.S:
Начиная с Excel 2010, Функция ВАР был заменен Функция VAR.S. Хотя обе они могут использоваться для оценки дисперсии на основе данной выборки, функция VAR.S более рекомендуется для использования в будущем, поскольку функция VAR может быть недоступна в будущих версиях Excel.
Функции дисперсии Excel
В следующей таблице перечислены все функции отклонения Excel и примечания к их использованию, которые помогут вам выбрать ту, которая лучше всего соответствует вашим потребностям.
| Имя и фамилия | Тип данных | Текст и логика в ссылках |
| VAR | Образец | Игнорируется |
| VAR.S | Образец | Игнорируется |
| ДИСПА | Образец | Оценивается |
| VARP | Население | Игнорировать |
| VAR.P | Население | Игнорируется |
| VARPA | Население | Оценивается |
Синтаксис
VAR(number1, [number2], …)
аргументы
- Number1 (обязательно): номер первой выборки, использованный в расчете;
- Номер 2, … (обязательно): Второй и более номер выборки, используемые в расчете.
Замечания
1. Одновременно может быть до 255 аргументов.
2. Аргументы могут быть любым из:
— Числа;
— Имена диапазонов, массивы или ссылки на ячейки, содержащие числа.
3. Функция VAR использует аргументы как выборку населения.
Советы: Если предоставленные вами данные представляют всю совокупность, рекомендуется использовать функцию ДИСП.П.
4. Логические значения и текстовые представления чисел, которые вы непосредственно вводите в аргументах, будут включены в расчет:
— Логические значения: ИСТИНА (1) или ЛОЖЬ (0);
— Текстовые представления чисел: числа, заключенные в двойные кавычки, например «2».
5. Пустые ячейки, логические значения, текст или значения ошибок будут игнорироваться в ссылках на массив или ячейки.
Советы: Если вы хотите включить в расчет логические значения, текстовые представления чисел в массиве или ссылки на ячейки, рекомендуется использовать функцию VARA.
6. #СТОИМОСТЬ! ошибка возникает, если какой-либо из предоставленных аргументов, которые вы ввели непосредственно в функцию, являются текстовыми строками, которые не могут быть интерпретированы Excel как числа.
7. # DIV / 0! ошибка возникает, если в функцию передано менее 2 числовых значений.
8. Уравнение функции VAR выглядит следующим образом:
где
— x представляет каждое значение в выборке.
— 
— n — количество ячеек в диапазоне выборки.
Возвращаемое значение
Возвращает числовое значение.
Пример
Следующая таблица представляет собой пример оценок. Чтобы оценить дисперсию на его основе, можно сделать следующее.
Выберите ячейку (в данном случае F6), введите приведенную ниже формулу и нажмите клавишу Enter, чтобы получить результат.
=VAR(C6:C13)
Примечание: Аргумент в приведенной выше формуле предоставляется в виде диапазона ячеек. Однако вы можете изменить формулу следующим образом:
=VAR(C6,C7,C8,C9,C10,C11,C12,C13)
=VAR({80;95;100;73;60;90;85;68})
=VAR(80,95,100,73,60,90,85,68)
Связанные функции
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
На чтение 10 мин Просмотров 72.8к.
Рассмотрим методы оценки риска, в частности рыночного, с помощью меры риска VaR (Value at Risk). Для этого разберем практический пример оценки риска для акции компании ОАО «Газпром».
Содержание
- Рыночный риск. Определение
- Методы оценки риска
- Метод оценки рыночного риска. Мера риска VaR (Value at Risk). Что такое VaR?
- Оценка риска по методу VaR на основе исторического моделирования в Excel
- Прогнозирование будущей стоимости акции на основе метода VaR
- Оценка меры риска VaR на основе «ручного способа» в Excel
- Сложность использования метода оценки риска VaR
Рыночный риск. Определение
Рыночный риск (англ. Market risk) – это вероятность неблагоприятного изменения стоимости активов. На изменение стоимости влияют множество макро-, мезо-, микроэкономических факторов, к которым можно отнести цены на сырье (нефть, сталь, платина и т.д.); цены на драгоценные металлы (золото, серебро); изменения отраслевых индексов производства, национальных показателей (ВВП, безработица, ключевая процентная ставка, инфляция), уровня спроса и предложения и т.д.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Рыночные риски находятся в системе финансовых рисков и можно выделить их следующие виды:
- Фондовый риск (Equity risk) – вероятность потерь в случае неблагоприятного изменения стоимости ценных бумаг на фондовом рынке.
- Процентный риск (Interest rate risk) – вероятность потерь при изменении банковских процентных ставок.
- Товарный риск (Commodity risk) – вероятность непредвиденных потерь в случае изменения стоимости товаров.
- Валютный риск (Currency risk) – вероятность потерь из-за изменения курса валют.
Рыночные риски оценивают различные инвестиционные компании, инвестиционные и хеджевые фонды, частные инвесторы, банки, предприятия, финансовые агенты, поставщики и т.д. для минимизации возможных убытков и создания резервов. Как мы видим, рыночные риски влияют на самых различных участников финансового рынка.
Методы оценки риска
Для того чтобы управлять возможными потерями и определять резервы для страхования потерь необходима количественная оценка риска. Основная аксиома любого управления заключается в том, что управлять можно только тем, что можно количественно измерить. Все методы оценки рыночных риском можно условно разделить на две группы:
- Статистические методы оценки риска
- Стандартное отклонение доходностей (σ)
- Метод Value at Risk (Var)
- Метод CVaR
- Экспертные методы оценки риска
- Рейтинговые методы
- Бальные методы
- Метод Дельфи
К преимуществам статистических методов можно отнести возможность объективной оценки вероятности возникновения непредвиденных убытков и их абсолютного размера. Экспертные методы оценки позволяют учесть слабоформализуемые факторы риска и разработать различные сценарии его снижения.
Г.Марковиц в начале 60-х годов предложил оценивать риск как изменчивость стоимости ценных бумаг на фондовом рынке. То есть чем сильнее изменяется цена актива, тем выше риск вложения в него. Недостатками данного способа были в неспособности спрогнозировать размер и вероятность будущих убытков.
Метод оценки рыночного риска. Мера риска VaR (Value at Risk). Что такое VaR?
В 80-е годы был предложен новый критерий риска – VaR (Value at Risk), который позволил комплексно оценить возможные убытки в будущем с выбранной вероятностью и за определенный промежуток времени. Для расчета меры риска VaR на практике используют несколько способов:
- Метод исторического моделирования («дельта нормальный», «ручной способ»).
- Метод параметрической модели.
- Статистическое (имитационное) моделирование с помощью метода Монте-Карло.
Оценка риска по методу VaR на основе исторического моделирования в Excel
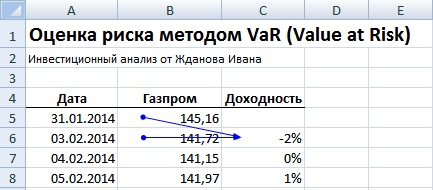
Рассмотрим пример оценки риска актива на фондовом рынке по модели VaR на основе дельта нормального моделирования вероятности и размера убытка. Возьмем котировки акции ОАО «Газпром» и рассчитаем возможные убытки по данному виду актива. Для этого необходимо закачать котировки с сервиса finam.ru («Экспорт данных») или с сайта finance.yahoo.com, если вы будете оценивать рыночный риск для иностранных компаний. По рекомендации Bank of International Settlements для расчета VaR необходимо использовать не менее 250 данных по стоимости акции. Были взяты дневные котировки по ОАО «Газпром» за период 31.01.2014 – 31.01.2015.
На следующем этапе необходимо рассчитать дневную доходность акции ОАО «Газпром», воспользовавшись следующей формулой.
Доходность акции ОАО «Газпром» =LN(B6/B5)
Следует отметить, что корректность использования дельта нормального метода оценки риска достигается только при подчинении факторов риска (доходности) нормальному закону распределения (Гауссовому). Для определения принадлежности распределения доходности Гауссовому распределению можно воспользоваться классическими статистическими критериями – Коломогорова-Смирнова или Пирсона.
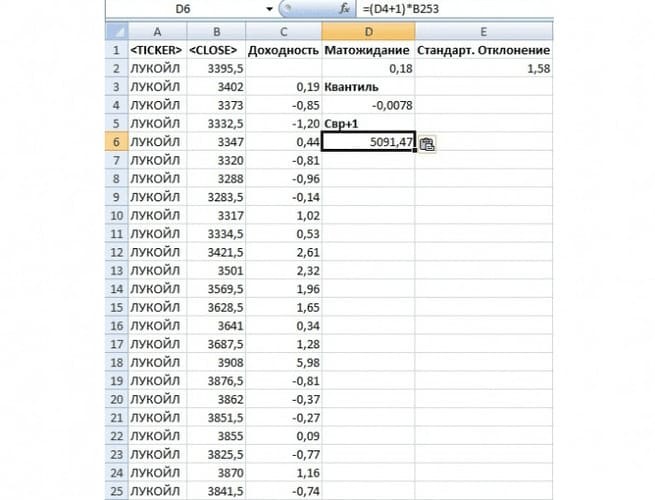
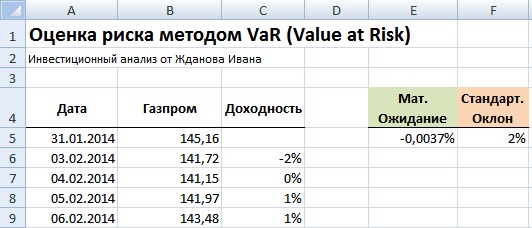
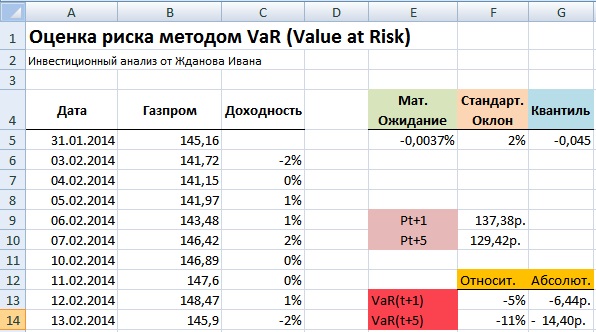
На следующем шаге необходимо рассчитать основные параметры распределения доходности: математическое ожидание и стандартное отклонение. Для этого воспользуемся встроенными формулами в Excel:
Математическое ожидание =СРЗНАЧ(C5:C255)
Стандартное отклонение =СТАНДОТКЛОН(C5:C255)
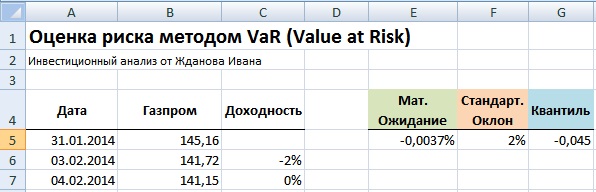
Следующим этапом в расчете меры риска VaR является определение квантиля данного нормального распределения. В статистике под квантилем понимают – значение функции распределения (Гаусса) по заданным параметрам (математического ожидания и стандартного отклонения) при которых функция не превышает данное значение с заданной вероятностью. В нашем примере уровень вероятности был взят 99%.
Рассчитаем в Excel значение квантиля для распределения доходностей акции ОАО «Газпром».
Квантиль =НОРМОБР(1%;E5;F5)
Прогнозирование будущей стоимости акции на основе метода VaR
Далее необходимо оценить какой возможно будет стоимость акции при заданных параметрах распределения доходности. Для этого можно воспользоваться следующей формулой:
где:
q – квантиль распределения доходностей акции;
Pt – стоимость акции в момент времени t;
Pt+1 – минимальная стоимость акции в следующем периоде времени t с заданным уровнем квантиля.
Для прогнозирования будущей стоимости акции (актива) на несколько периодов вперед следует использовать модификацию формулы:
где:
q – квантиль распределения доходностей акции;
Pt – стоимость акции в момент времени t;
Pt+1 – минимальная стоимость акции в следующем периоде времени t при заданном уровне квантиля;
n – глубина прогноза возможной минимальной стоимости акции.
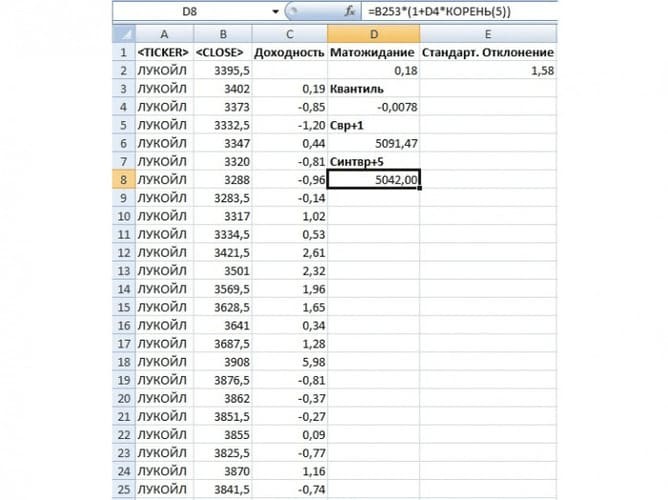
Формула расчета будущей стоимости акции в Excel будет иметь вид:
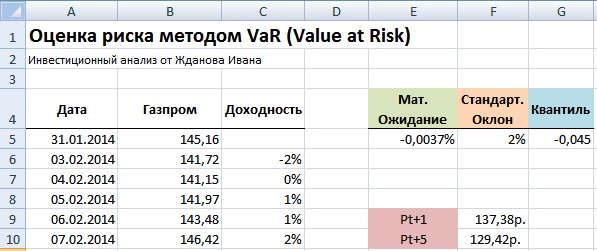
Минимальная стоимость акции ОАО «Газпром» на следующий день =(1+G5)*B255
Минимальная стоимость акции ОАО «Газпром» через 5 дней =B255*(1+G5*КОРЕНЬ(5))
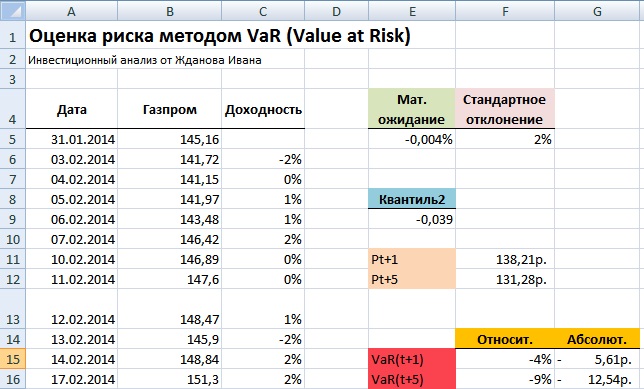
Значения Pt+1 показывает, что с вероятностью 99% акции ОАО «Газпром» не опустятся ниже цены равной 137.38руб, а значение Pt+5 показывает возможную минимальную стоимость акции с вероятностью 99% на 5 следующих дней. Для расчета абсолютного значения возможного убытка следует определить процентное изменение стоимости акции. Формулы расчета в Excel будут следующие:
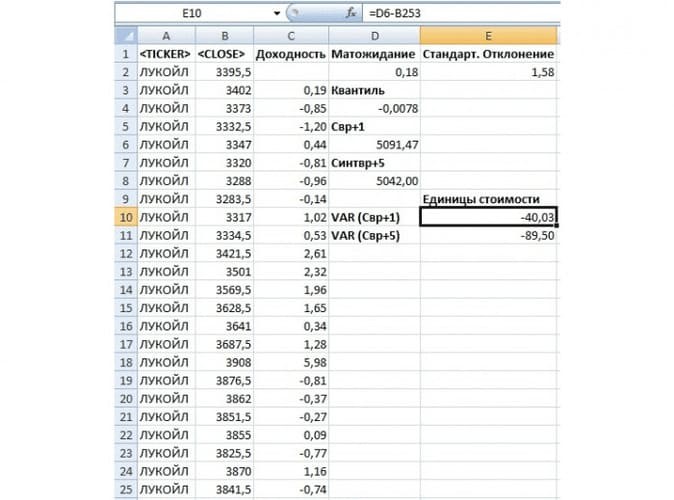
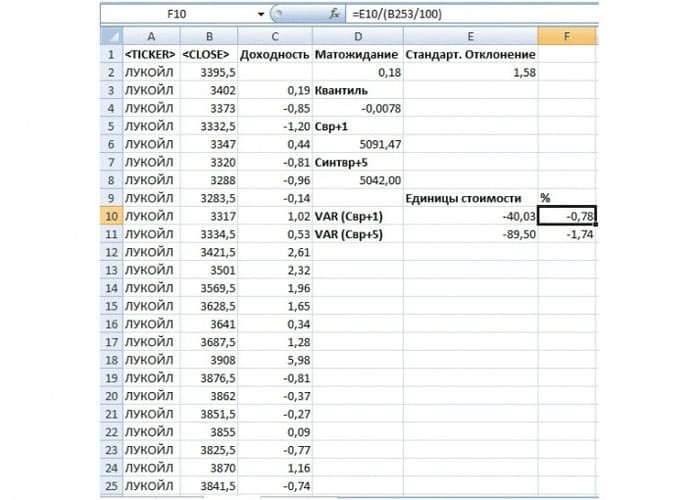
Относительное изменение стоимости акции
Относительное снижение стоимости акции на следующий день =LN(F9/B255)
Относительное снижение стоимости акции за пять дней =LN(F10/B255)
Абсолютное изменение стоимости акции
Абсолютное снижение стоимости акции на следующий день =F9-B255
Абсолютное снижение стоимости акции за пять дней =F10-B255
Таким образом читать экономический смысл показателя VaR заключается в следующем: в течение следующего дня стоимость акции ОАО «Газпром» с вероятностью 99% не окажется ниже 137,38руб. и абсолютные убытки не превысят 6,44руб (5%) на акцию. И аналогично для оценки VaR на пять дней вперед: в течение пяти дней стоимость акции ОАО «Газпром» с вероятностью 99% не опуститься ниже 129,42 руб., и потеря капитала не превысит 11% (14,4руб на акцию).
Оценка меры риска VaR на основе «ручного способа» в Excel
Второй метод расчета меры риска VaR называется «ручным способом», так как позволяет не привязываться к распределению, по которому изменяется стоимость актива. Это одно из его главных преимуществ по отношению к дельта нормальному методу. Для оценки рыночного рискам будем использовать те же входные данные – котировки ОАО «Газпром». Этапы расчета VaR следующие:
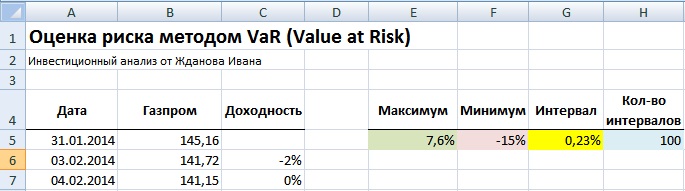
Расчет максимума и минимума доходностей акции ОАО «Газпром»
По рассчитанной доходности акции ОАО «Газпром» определяем максимум и минимум доходности. Для этого воспользуемся формулами:
Максимальное значение доходности акции =МАКС(C5:C255)
Минимальное значение доходности акции =МИН(C5:C255)
Выбор количества интервалов группировки доходностей/убытков акции
Для ручного способа оценки риска необходимо взять количество интервалов деления группировки доходностей. Количество может быть любое, в нашем примере мы возьмем N=100.
Определение ширины интервала группировки доходностей
Ширина интервала или шаг изменения группы необходим для построения гистограммы и рассчитывается как деление максимального разброса доходностей к количеству интервалов. Формула расчета интервала следующая:
Размер интервала доходностей акции =(E5-F5)/H5
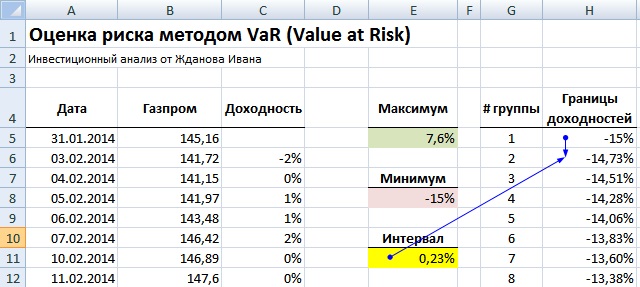
На следующем этапе необходимо построить гистограмму распределения доходностей по выбранным интервалам. Для этого рассчитываем границы всех групп доходностей (всего их 100). Формула расчета следующая:
Граница доходностей акции =H5+$E$11
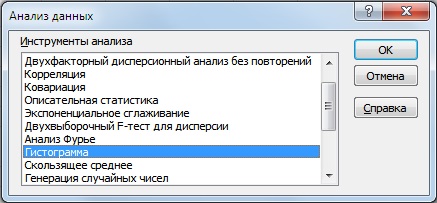
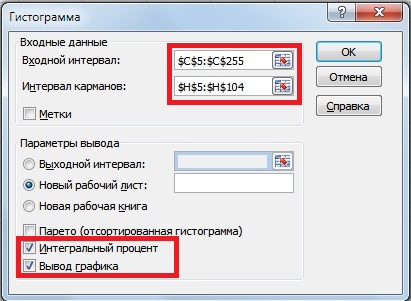
После определения границ групп доходностей строим накопительную гистограмму. Для этого заходим в надстройку «Данные» → «Анализ данных» → «Гистограмма».
В открывшемся окне заполняем «Входные интервалы», «Интервалы карманов», также выбираем опцию «Интегральный процент» и «Вывод графика».
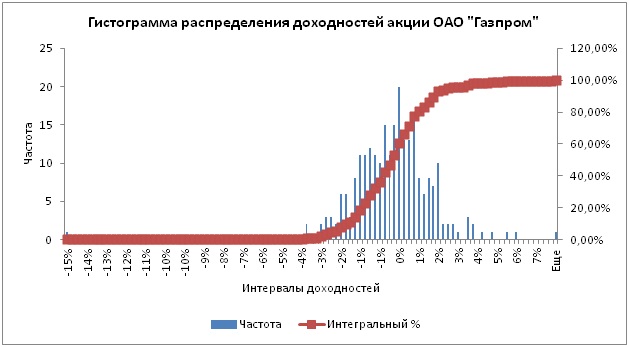
В результате будет сформирован новый рабочий лист с графиком и частотой попадания доходности/убытка в тот или иной интервал. График накопительным итогом имеет следующий вид:
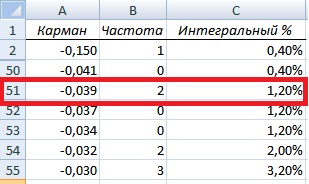
Итак первый столбец полученной таблицы это квантиль данного для распределения доходностей/убытков, вторая частота попадания доходностей в тот или иной интервал, третья отражает вероятность появления убытков. В таблице с накопительной вероятностью попадания в тот или иной интервал необходимо найти уровень ~1%.
Значение квантиля соответствует -0,039, тогда как при дельта нормальном способе оценки риска квантиль составил -0,045. Для оценки рисков воспользуемся уже полученными формулами оценки и рассчитаем размер убытков. На рисунке ниже показана оценка возможных убытков на следующий день и в течение пяти дней с вероятностью 1% составят 4 и 9% соответственно.
Сложность использования метода оценки риска VaR
Отечественный фондовый рынок имеет достаточно высокую степень волатильности, на рынке наблюдаются «тяжелые хвосты» – то есть возникновение частых кризисов с большим размером убытков. В результате модель VaR не может точно спрогнозировать возможные будущие потери инвестора. Следует отметить, что данная модель хорошо применима для товарных низковолательных рынков нежели фондовых.
Резюме
В данной статье мы рассмотрели методы оценки риска на примере акции ОАО «Газпром», для этого пошагово разобрали, как строится современная оценка риска Value at Risk (VaR) в Excel двумя способами: дельта нормальным моделированием и «ручным способом».
Автор: к.э.н. Жданов Иван Юрьевич
In this article, we will learn about the calculation of the variance(var) in Excel.
First, let’s learn about Variance. In real-life scenarios, we have populations like marks of students in a particular subject, salaries of multiple employees in a company. Let us consider, in a company named ABC, we have 5 employees.
| Name | Salary(USD) |
|---|---|
| a | 10k |
| b | 50k |
| c | 30k |
| d | 40k |
| e | 20k |
Now, it will tell us the expectation of standard deviation. In other words, the factor of difference in salaries.
The formula for std is –
sigma^{2} = sum_1^n (x_{i} - mu )^{2} / N
It will be shown as
Where x represents the value, and μ is the mean of the sample.
- Mean = 30
- N = 5
- Var = 200
Now, Let’s learn how to use it in Excel –
In Excel we have formulas for everything and as you might have guessed for var also.
We can have this list of formulas using ‘=’ symbol shown below
Let’s talk about them briefly,
1. VAR.P – It calculates the var assuming that the entire population is its argument. It returns an approximate value and is used with a large population. Uses the same formula shown above.
2. VAR.S – It calculates the var assuming that the sample of the population is its argument. It returns an approximate value and is used with a large population. Uses the same formula shown below
sigma^{2} = sum_1^n (x_{i} - mu )^{2} / (N -1)
3. VARA – It includes text and logical symbols whereas the above 2 functions don’t include text and logical symbols. It is used for a sample of the population. Uses “n-1” formula.
4. VARPA – It includes text and logical symbols. It is used for the whole population. Uses “n” formula.
Let’s see the difference here,
Here, the discrepancy occurs because VARPA and VARA read TRUE as 1 and VAR.P and VAR.S ignore it.
The formula goes like this –
1. =STDEV.P(A38:A43) [Formula used in A37 cell] 2. =STDEV.S(B38:B43) [Formula used in B37 cell] 3. =STDEVPA(C38:B43) [Formula used in C37 cell] 4. =STDEVA(D38:B43) [Formula used in D37 cell]
Note – VAR and VARP are for Excel 2007 or earlier. DVAR and DVARP are used for fetching data from Database.
Коротко: Коэффициент вариации, VAR или CV, — ключевой показатель в оценке риска проектов и доходности ценных бумаг. Он позволяет заранее проанализировать сразу два показателя, которые обладают меняющимися во времени значениями. Если показатель оказывается менее 0,1, направление инвестирования характеризуется низким уровнем риска. При показателе свыше 0,3 уровень риска необоснованно высок. Для расчета удобнее всего использовать функции СТАНДОТКЛОН и СРЗНАЧ табличного редактора Excel.
Подробно
Для того чтобы сформировать качественный инвестиционный портфель, инвесторам порой приходится прибегать к оценке входящих в него активов, которые обладают разным уровнем риска и доходности. Для этой цели используется широко известный в инвестиционном анализе и эконометрике показатель.
Коэффициент вариации (Coefficient of variation — CV, VAR) — относительный финансовый показатель, который демонстрирует сравнение рассеивания значений двух случайных показателей, которые имеют разные единицы измерения относительно ожидаемого значения.
Справка! Поскольку коэффициент вариации позволяет получить сопоставимые результаты, то его применение оптимально в рамках портфельного анализа. В ней он позволяет эффективно объединить значения риска и доходности и вывести результирующее значение.
Coefficient of variation — показатель из числа относительных методов статистики, который, как NPV и IRR, применяется в рамках инвестиционного анализа. Он измеряется в процентах и может применяться для сравнения вариаций двух несвязанных между собой критериев. Его чаще всего используют финансовые и инвестиционные аналитики.
Справка! На базе коэффициента вариации оценивается так называемый «унифицированный риск» (unitized risk), поскольку он оценивает относительный разброс двух показателей по отношению к прогнозному значению.
Для чего используют показатель VAR:
- в целях сравнения двух разных показателей;
- для определения степени устойчивости прогнозных моделей (в основном по инвестициям и портфельному инвестированию);
- для осуществления XYZ-анализа.
Справка! XYZ-анализ — аналитический инструмент, в рамках которого продукция компании оценивается по двум параметрам: стабильность потребления и продаж.
Формула расчета коэффициента вариации
Суть расчета коэффициента вариации состоит в том, что по множеству значений рассчитывается сначала среднее квадратичное отклонение, а затем — среднее арифметическое, а после — найти их соотношение.
В общем виде формула расчета показателя VAR выглядит следующим образом:
CV = σ / t ср, где:
CV — коэффициент вариации;
σ — среднее квадратическое отклонение;
t — среднее арифметическое значение для случайной величины.
Формула расчета показателя VAR может принимать самые разнообразные интерпретации в зависимости от объекта оценки.
Важный момент! Очевидно, что применение представленных выше формул вручную, в особенности при наличии широкого круга значений, весьма затруднительно. Оттого для расчета применяется инструментарий табличного редактора Excel.
Значения показателя VAR в инвестиционном анализе
CV — показатель, который можно считать более универсальным, чем дисперсия или среднее квадратичное отклонение: на его основе можно сопоставлять риски и доходности двух и более активов, существенно отличающихся друг от друга.
Нормативного значения этого показателя не существует. Однако имеются некоторые опорные критерии, которые помогают при его анализе и интерпретации.
Важный момент! Коэффициент CV имеет несколько недостатков — он не учитывает величины первоначальных вложений, предполагает симметричность разбросанных значений по отношению к среднему, а также не может использоваться для опционов, доходность которых может быть меньше 0. Оттого при наличии сомнений стоит дополнительно использовать показатели IRR и NPV.
Примеры расчета VAR в Excel
Расчет коэффициента вариации вручную − сложная и затяжная по времени процедура. Если выборка значительная, то расчёт по ней среднего квадратического отклонения вручную крайне чреват ошибками и неточностями.
Удобный способ определения VAR предлагает табличный редактор Excel. На его базе можно рассчитать:
- среднее квадратическое отклонение (функция СТАНДОТКЛОН);
- среднее арифметическое (функция СРЗНАЧ).
Для того чтобы разобраться в тонкостях использования CV, имеет смысл привести пример его расчета.
Пример расчета: оценка двух проектов с разной прибылью
Существует два бизнеса, которые на протяжении 5 лет демонстрируют разный финансовый результат. Для того чтобы сделать выбор между ними, инвестору стоит рассчитать коэффициент вариации.
Первоначально рассчитаем среднее квадратичное отклонение, используя статистическую функцию Excel СТАНДОТКЛОН.В.
Рисунок 1. Расчет среднего квадратического отклонения по проекту А.
Аналогичным образом на базе статистической функции СРЗНАЧ рассчитывается среднее арифметическое по обоим проектам
Рисунок 2. Расчет среднего арифметического значения по проекту А.
После этого остается разделить среднее квадратическое отклонение на среднее арифметическое и получить результат — значение коэффициента вариации.
Рисунок 3. Расчет VAR по проекту А.
Вывод! По проекту А уровень риска оказался равным 40%. При таком раскладе он представляется рискованным и неустойчивым. По проекту В уровень риска приемлемый — всего 11,64%. Инвестору уместно вложить средства в более надежный проект В, хотя в отдельные периоды проект А приносит большую прибыль.
Детальный алгоритм расчета показателя представлен в образце, составленном на базе табличного редактора Excel.
Детальный процесс расчета показателя вариации представлен в видеоролике.