Рассчитаем
Приведенную (к текущему моменту) стоимость
инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.
Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и
Будущей стоимости
важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты:
простые проценты
,
сложные проценты
или
аннуитет
(в
файле примера
приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание
. В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция
ПС()
используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить
ПС()
рассчитать Приведенную стоимость и по методу простых процентов (см.
файл примера
).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета
Будущей стоимости
(FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя
формулу наращения для сложных процентов
.
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,
т.е. PV = FV / (1+i)^n
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
Сложные проценты (несколько сумм)
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции
ПС()
или альтернативной формулы PV = FV / (1+i)^n
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см.
файл примера
).
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью
Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость
, где приведен расчет с помощью функции
ПС()
, а также вывод альтернативной формулы).
Здесь разберем другую задачу (см.
файл примера
):
Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?
Решение может быть найдено с помощью функции
ПС()
:
=ПС(12%/12;12;20000;-1000000;0)
= 662 347,68р.
Аргумент
Ставка
указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент
Кпер
– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент
Плт
— это 20000р., т.е. величина дополнительных взносов. Аргумент
Бс
— это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент
перечисляет
эти средства банку, а будущую сумму вклада клиент
получит
от банка. Это очень важное замечание касается всех
функций аннуитета
, т.к. в противном случае можно получить некорректный результат. Результат функции
ПС()
– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше
=ПС(12%/12;12;20000)
= -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость
= БС(12%/12;12;; 225 101,55+662 347,68)
= -1000000,0р., что и требовалось доказать.
Определение Приведенной стоимости в случае платежей произвольной величины
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция
ЧПС()
. Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция
ЧИСТНЗ()
. Об этих расчетах читайте в статье
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL
.
Что такое PV в Excel? Это функция для расчета текущей стоимости. В этом руководстве объясняется его синтаксис, показано, как построить правильную формулу PV для серии денежных потоков и одного платежа, описаны подводные камни, с которыми вы можете столкнуться, и способы их преодоления.
Предположим, вы думаете о покупке страхового аннуитета, чтобы обеспечить стабильный денежный поток в течение пенсионных лет. Или, может быть, вы думаете о том, чтобы положить немного денег на сберегательный счет с приличной годовой процентной ставкой. Что бы это ни было, вы задаетесь вопросом — это хорошая сделка? Чтобы узнать это наверняка, вам нужно найти текущую стоимость инвестиций. Для этого Microsoft Excel предоставляет функцию PV, которая означает «текущая стоимость».
PV — это финансовая функция Excel, которая возвращает текущую стоимость аннуитета, кредита или инвестиции на основе постоянной процентной ставки. Его можно использовать для серии периодических денежных потоков или одного единовременного платежа.
Функция PV доступна во всех версиях Excel 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010 и Excel 2007.
Синтаксис следующий:
PV(скорость, кпер, плт, [fv], [type])
Где:
- Ставка (обязательно) — процентная ставка за период. Если вы производите ежегодные платежи, укажите годовую процентную ставку; если вы платите ежемесячно, укажите ежемесячную процентную ставку и так далее.
- Кпер (обязательно) — общее количество периодов выплат на протяжении аннуитета.
- Pmt (необязательно) — сумма, выплачиваемая за каждый период. Если он опущен, предполагается, что он равен 0, а фв аргумент должен быть включен.
- Fv (необязательно) — будущая стоимость аннуитета после последнего платежа. Если он опущен, предполагается, что он равен 0, а пмт аргумент должен быть включен.
- Тип (необязательно) — когда будут производиться платежи:
- 0 или опущен (по умолчанию) — в конце периода (обычный аннуитет)
- 1 — на начало периода (аннуитетный платеж)
5 вещей, которые вы должны знать о функции PV
Чтобы функция Excel PV правильно работала на ваших листах, примите во внимание следующие примечания по использованию:
- Если фв аргумент равен нулю или опущен, пмт должны быть включены, и наоборот.
- оценивать Аргумент может быть представлен в виде процента или десятичного числа, например, 10% или 0,1.
- Любые деньги, которые вы выплачиваете (отток), должны быть представлены отрицательным числом. Любые деньги, которые вы получаете (приток), должны быть представлены положительным числом. Например, когда вы инвестируете деньги в страховой аннуитет, используйте отрицательное число для пмт. Когда страховая компания начнет выплачивать вам выплаты, выражайте платежи в виде положительных чисел.
- При расчете периодических денежных потоков соблюдайте оценивать а также Например единицы. Например, если вы делаете 5 ежегодных платежей по годовой процентной ставке 7%, используйте 5 для Например и 7% или 0,07 для оценивать. Если вы делаете ежемесячные платежи сроком на 5 лет, то используйте 5*12 (всего 60 периодов) для Например и 7%/12 для оценивать.
- Все аргументы должны быть числовыми, в противном случае функция PV возвращает ошибку #ЗНАЧ! ошибка.
Базовая формула PV в Excel
Чтобы получить общее представление о том, как использовать функцию PV в Excel, давайте создадим формулу приведенной стоимости в ее простейшей форме.
Предположим, вы делаете регулярные взносы для накопления пенсионных сбережений. Вы вносите 500 долларов на период по ставке 7% и делаете 50 таких платежей через равные промежутки времени.
Чтобы найти текущую стоимость аннуитета, настройте свой рабочий лист таким образом:
- Периодическая процентная ставка (C2): 7%
- Количество периодов (C3): 100
- Сумма платежа (С4): -500
- Тип аннуитета (C5): 0 (обычный аннуитет) или 1 (аннуитетный платеж)
Формула для расчета PV инвестиций выглядит следующим образом:
=PV(С2, С3, С4, ,С5)
Если вы сравните результаты порядкового аннуитета (платежи производятся в конце периода) и аннуитета к оплате (платежи производятся в начале периода), вы заметите, что в последнем случае текущая стоимость равна выше.
PV регулярного аннуитета:
PV аннуитета:
И вот еще несколько вещей, на которые стоит обратить внимание:
- В этом примере пмт аргумент является отрицательным числом, потому что мы вкладываем деньги. Если вы рассчитываете PV аннуитета, который выплачивается вам, введите пмт как положительное число, и в результате вы получите отрицательный PV.
- Будущая стоимость в данном расчете не используется, поэтому фв аргумент опущен.
- При составлении формулы PV для ежемесячных денежных потоков (или других периодических платежей, таких как еженедельные, ежеквартальные и т. д.) не забудьте преобразовать годовую процентную ставку в периодическую ставку, как показано на рис. этот пример.
Можно также посмотреть на проблему под другим углом. Чтобы найти процентную ставку, при которой PV равен 0, используйте функцию IRR.
Как использовать функцию PV в Excel — примеры формул
Следующие примеры дадут вам представление о том, как функция Excel PV работает в различных сценариях, чтобы вы могли настроить базовую формулу для своей конкретной задачи.
Рассчитать PV аннуитета
Допустим, вы купили аннуитет, по которому регулярный платеж в размере 200 долларов США должен производиться страховой компании в начале каждого месяца в течение следующих 10 лет. По аннуитету ежемесячно начисляются проценты по ставке 9% годовых. Вопрос — сколько сейчас стоит эта рента?
Для начала введите все данные в отдельные ячейки:
- Годовая процентная ставка (B2): 9%
- Количество лет (B3): 10
- Ежемесячный платеж (В4): -200
- Аннуитетный тип (B5): 1
- Количество периодов в году (B6): 12
В этом случае процентная ставка (оценивать) и оплата (пмт) относятся к разным периодам. Чтобы сделать PV правильно, нам нужно сделать пару преобразований:
Чтобы преобразовать годовую процентную ставку в периодическую, разделите годовую ставку на количество периодов в году:
оценивать = годовая процентная ставка / кол. периодов в год
Чтобы получить общее количество периодов, умножьте срок аннуитета в годах на количество периодов в году:
Например = нет. лет * нет. периодов в год
Так как у нас ежемесячная рента, мы можем делить и умножать на 12 или на ячейку В6, в которую вписано это число.
Полная формула PV в B8:
=PV(B2/B6, B3*B6, B4,, B5)
Аналогичным образом можно рассчитать текущую стоимость еженедельной, квартальной или полугодовой ренты. Для этого просто измените количество периодов в году в соответствующей ячейке:
- Еженедельно: 52
- Ежемесячно: 12
- Ежеквартально: 4
- Полугодовой: 2
- Годовой: 1
Рассчитать PV инвестиций на основе их будущей стоимости
В этом примере мы собираемся найти текущую стоимость инвестиции, которая принесет 50 000 долларов через 5 лет при годовой процентной ставке 7%. Цель состоит в том, чтобы выяснить, сколько денег нам нужно инвестировать сегодня, чтобы достичь целевой суммы в конце инвестиционного периода.
Как обычно, мы вводим данные аннуитета в отдельные ячейки:
- Годовая процентная ставка (B2): 7%
- Количество лет (B3): 5
- Будущая стоимость (B4): 50 000
- Тип аннуитета (B5): 0
Предполагая, что процентная ставка начисляется ежегодно, формула приведенной стоимости проста:
=PV(B2, B3, , B4, B5)
Пожалуйста, обратите внимание, что пмт аргумент в данном случае опущен, поскольку предполагается единовременное вложение без дополнительных периодических платежей.
Как показано на снимке экрана ниже, результат формулы PV отрицательный, потому что это отток, то есть деньги, которые вы инвестируете сейчас, чтобы заработать целевую сумму в будущем.
Но что, если у нас есть несколько предложений от разных инвестиционных компаний и мы хотим сравнить эффект разных периодов начисления процентов?
В этом случае мы вводим количество периодов начисления процентов в год в ячейки E2:E6, как показано на рисунке ниже. Затем мы вводим приведенную ниже формулу в F2 и перетаскиваем ее вниз через F6:
=PV($B$2/E2, $B$3* E2, ,$B$4)
Постоянные данные, такие как процентная ставка ($B$2), срок аннуитета ($B$3), будущая стоимость ($B$4) и тип ($B$5), должны быть указаны как абсолютные ссылки, чтобы формула копировала правильно. к нижним ячейкам.
Присмотревшись к результатам, вы можете заметить обратную зависимость между рассчитанным PV (абсолютное значение без учета знака) и количеством периодов начисления сложных процентов. Лучшее предложение для нас — это еженедельное начисление процентов — вложив сейчас наименьшую сумму денег, мы получим те же $50 000 через 5 лет.
Дополнительные примеры формул см. в разделе Как рассчитать текущую стоимость ренты в Excel.
Разница между формулой NPV и PV в Excel
Помимо PV, в финансах есть еще один термин, называемый NPV, который дисконтирует будущие денежные потоки по ожидаемой норме прибыли для оценки их текущей стоимости. Хотя эти два термина имеют много общего, они существенно различаются.
Текущая стоимость (PV) — относится к будущим поступлениям денежных средств в данный период.
Чистая приведенная стоимость (NPV) – это разница между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств. Другими словами, NPV учитывает первоначальные инвестиции, что делает текущую стоимость чистой величиной.
В Microsoft Excel есть два основных различия между функциями PV и NPV:
- Функция PV может рассчитывать только постоянные денежные потоки, которые не меняются в течение всего срока действия аннуитета. Функция NPV может рассчитывать переменные денежные потоки.
- PV работает как для обычного аннуитета, так и для аннуитета. NPV может обрабатывать только денежные потоки, возникающие в конце каждого периода.
Для получения дополнительной информации см. функцию Excel NPV с примерами формул.
Вот как рассчитать PV в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь для скачивания
Использование формулы PV в Excel (файл .xlsx)
Вас также могут заинтересовать:
Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.
Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel
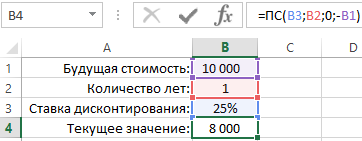
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?
Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:
Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.
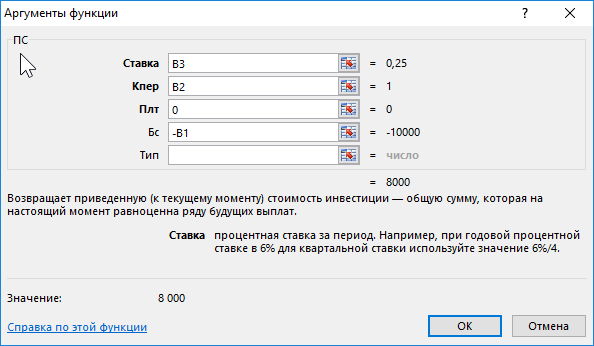
Функция ПС имеет 5 аргументов:
- Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
- Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
- Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
- Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
- Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.
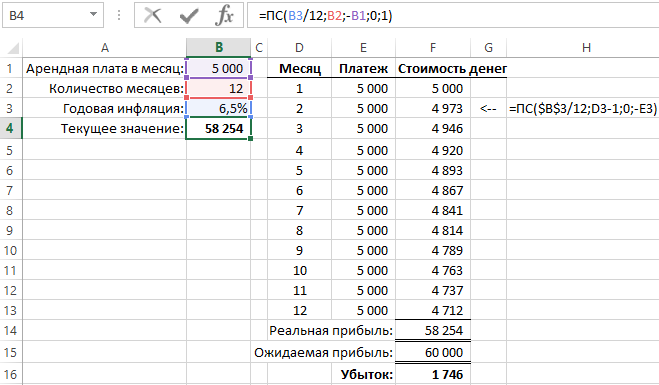
Формула расчета текущей стоимости денег с учетом инфляции в Excel
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:
В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.
В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.
Содержание
- Что такое NPV простыми словами
- Зачем нужен показатель NPV
- Формула расчета NPV
- Экономический смысл показателя NPV
- Значение ставки дисконтирования при расчёте NPV
- Расчет приведенной стоимости денежного потока в Excel
- Применение приведённой NPV на практике
- Плюсы и недостатки
- Тщательный анализ результата
- Вычисление приведенной стоимости
- Приведенная стоимость единовременной будущей выплаты
- Прогнозирование денежного потока в Excel
- Срок окупаемости в Excel: пример расчёта
- Алгоритм и формула расчета ЧДД
- ЧДД проектов: какой выбрать
- Анализ полученных результатов
- Как проводить анализ результатов
- Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
- Определите все денежные потоки, связанные с инвестициями – все притоки и оттоки.
- Определите соответствующую ставку дисконтирования или ставку альтернативной доходности r для инвестиционного проекта.
- Используя эту ставку дисконтирования, найдите текущую (приведенную) стоимость (PV) каждого денежного потока.
- Суммируйте все приведенные значения стоимости.
- Примените правило чистой приведенной стоимости.
- Простые проценты
- Сложные проценты
- Сложные проценты (несколько сумм)
Что такое NPV простыми словами
NPV называют чистую стоимость денежных потоков, приведенную к моменту расчета проекта. Благодаря формуле расчета NPV удается оценить собственную экономическую эффективность проекта и сравнить между собой несколько объектов инвестирования.
Английская аббревиатура NPV (Net Present Value) имеет в русском языке несколько аналогов:
- Чистая приведенная стоимость (ЧПС). Этот вариант является наиболее распространенным, даже в «Microsoft Excel» формула называется именно таким образом.
- Чистый дисконтированный доход (ЧДД). Название связано с тем, что денежные потоки дисконтируются и лишь после этого суммируются.
- Чистая текущая стоимость (ЧТС). Все доходы и убытки от деятельности за счет дисконтирования приводятся к текущей стоимости денег. Поясним: с точки зрения экономики, если мы заработаем 1000 руб., то получим потом на самом деле меньше, чем если бы мы получили ту же сумму прямо сейчас.
Дисконтирование — это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени.
NPV представляет собой уровень прибыли, который ожидает участников инвестиционного проекта. Математически этот показатель определяют за счет дисконтирования значений чистого денежного потока, при этом неважно, о каком потоке идет речь: отрицательном либо положительном.
Чистый дисконтированный доход можно рассчитать за любой период времени проекта с его начала (за 5, 7 лет, 10 лет, пр.) – все зависит от необходимости.
Если максимально упростить определение, то NPV – это доход, который получит владелец проекта за период планирования, оплатив все текущие затраты и рассчитавшись с налоговыми органами, персоналом, кредитором (инвестором), в том числе выплатив проценты (или с учетом дисконтирования).
Допустим, за 10 лет планирования предприятие получило выручку в 5,57 млрд руб., тогда как общая сумма налогов и всех затрат равна 2,21 млрд руб. Значит, сальдо от основной деятельности окажется 3,36 млрд руб.
Но это пока не искомый результат – из данной суммы нужно вернуть первоначальные инвестиции, допустим, 1,20 млрд руб. Чтобы упростить подсчет, будем считать, что проект финансируется за счет средств инвестора по нулевой ставке дисконтирования. Тогда, если рассчитать показатель NPV, он составит 2,16 млрд руб. за 10 лет планирования.
Если увеличить срок планирования, то увеличится и размер ЧДД. Смысл этого показателя в том, что он позволяет рассчитать еще на этапе разработки бизнес-плана, какой реальный доход может получить инициатор проекта.
Повторим, что NPV – один из ключевых показателей оценки эффективности инвестиционных проектов. Поэтому если рассчитать его даже с малейшей неточностью, можно столкнуться с потенциально неэффективным вложением средств.
Зачем нужен показатель NPV
Если у вас на примете есть перспективный бизнес-проект, в который вы готовы вложить деньги, советуем рассчитать его чистую приведенную стоимость.
Как рассчитать NPV проекта? Используйте такой порядок действий:
- Оцените денежные потоки от проекта, то есть первоначальное вложение (отток) и ожидаемые поступления (притоки) денежных средств.
- Определите стоимость капитала (cost of capital), так как этот показатель станет для вас ставкой дисконтирования.
- Продисконтируйте притоки и оттоки от проекта по ставке, которую вам удалось рассчитать на предыдущем шаге.
- Сложите все дисконтированные потоки – это и будет NPV проекта.
Далее можете принимать решение об инвестициях, но помните: в проект стоит вкладываться при NPV больше нуля, если же этот показатель ниже нуля, лучше отказаться от своей задумки.
На самом деле, все просто – если NPV равен нулю, значит, денежных потоков от проекта хватит, чтобы:
- возместить инвестированный капитал;
- обеспечить доход на этот капитал.
При положительном NPV проект принесет прибыль, и чем выше его уровень, тем выгоднее окажутся вложения в проект.
Кредиторы, то есть люди, дающие деньги в долг, имеют фиксированный доход, поэтому все средства, превышающие этот показатель, остаются акционерам. Если компания решает одобрить проект с нулевым NPV, акционеры сохранят свою позицию – компания станет больше, но акции не поднимутся в цене. При положительном NPV проекта акционеры станут богаче.
NPV позволяет рассчитать, какой из инвестиционных проектов выгоднее, когда их несколько, но компания не имеет средств на реализацию сразу всех. В этом случае приступают к проектам с наибольшей возможностью заработать или с самым высоким NPV.
Сегодня нужно просто рассчитать NPV, чтобы оценить выгодность инвестиционных проектов. Среди достоинств этого показателя аналитики называют:
- четкие критерии принятия решения об инвестировании – первоначальные инвестиции, выручка на каждом этапе, доходность альтернативных вложений;
- учет изменения стоимости денег с течением времени;
- учет рисков за счет использования различных ставок дисконтирования.
Но не стоит заблуждаться и считать этот показатель абсолютно точным коэффициентом. Нередко сложно корректно рассчитать ставку дисконтирования, особенно когда речь идет о многопрофильных проектах. Также отметим, что при расчете не учитывается вероятность исхода каждого проекта.
Формула расчета NPV
Как рассчитать чистый дисконтированный доход NPV? Казалось бы, все просто: нужно вычесть из всех притоков денежных средств все оттоки по каждому временному отрезку, после чего привести полученные значения к моменту расчета.
Но рассчитать этот показатель невозможно без формулы:

Где:
- IC – сумма первоначальных инвестиций;
- N – число периодов (месяцев, кварталов, лет), за которые нужно рассчитать оцениваемый проект;
- t – отрезок времени, для которого необходимо рассчитать чистую приведенную стоимость;
- i – расчетная ставка дисконтирования для оцениваемого варианта вложения инвестиций;
- CFt – ожидаемый денежный поток (чистый) за установленный временной период.
Экономический смысл показателя NPV
Если рассматривать показатель более глубоко, можно констатировать, что это результирующая величина, полученная при учёте всех исходящих и входящих денежных поступлений анализируемого инвестиционного проекта, приведённая ко времени выполнения подобного анализа.
Полученное значение даёт инвестору представление о том, на что он может рассчитывать при вложении (с учётом погашения первоначальных затрат, понесённых на начальном этапе развития проекта и периодических оттоков в процессе его реализации).
Благодаря тому, что все денежные потоки рассчитываются с учётом рисков и временной стоимости, величину NPV инвестиционного проекта можно охарактеризовать, как стоимость, которая добавляется проектом, либо как совокупную прибыль инвестора.
Главной целью любого бизнеса является получение прибыли.
Для того, чтобы не инвестировать в рисковые проекты, инвестор проводит предварительную оценку возможных вариантов инвестирования. Причём все такие предложения на стадии их предварительно изучения оцениваются в сравнении с доходностью безрисковых вложений (банковский депозит).
Для понимания алгоритма расчёта чистой приведённой стоимости следует учитывать, что в его основу положена методология дисконтирования всех имеющихся денежных потоков. Именно поэтому решение о инвестировании в тот или иной проект принимается после его предварительного расчёта NPV проекта, в рамках которого:
- оцениваются все ожидаемые притоки и оттоки капитала за расчётный период;
- определяется его стоимость (для инвестора эта величина рассматривается в качестве ставки дисконтирования);
- с учётом упомянутой ставки дисконтируются все поступающие и истекающие потоки;
- результаты суммируются. Полученный результат и является величиной приведённой стоимости проекта.
Полученное число может иметь такие значения.
NPV = 0. Это информирует инвестора, что у него имеется вероятность вернуть вложенные средства с минимальной прибылью.
NPV < 0. Подобные инвестиционные проекты дальнейшему рассмотрению не подлежат. NPV > 0. Вложение средств должно принести прибыль.
Значение ставки дисконтирования при расчёте NPV
Изучая чистую приведённую стоимость обязательно следует уделять серьёзное внимание показателю — ставка дисконтирования. Часто её именуют иначе — альтернативной стоимостью вложений. Показатель, используемый в формуле расчёта, обозначает минимальную величину доходности, которую инвестор считает для себя приемлемой при рисках, сопоставимых с имеющимися у реализуемого проекта.
Инвестор может оперировать средствами, привлекаемыми из различных источников (собственных либо заёмных).
1. В первом случае устанавливаемая ставка дисконтирования, является личной оценкой допустимых рисков рассматриваемого инвестиционного проекта.
Её оценка может иметь несколько подходов. Самые простые, это:
- Выбор безрисковой ставки, корректируемой с учётом вероятности возникновения специфических рисков.
В качестве таковой обычно рассматриваются доходность по ценным бумагам государства, в котором реализуется проект, ставка доходности по корпоративным облигациям компаний отрасли.
- Необходимая и минимально достаточная (с точки зрения потенциального инвестора) рентабельность (показатель ROE).
При этом, лицо, принимающее решение об инвестировании, определяет ставку дисконтирования по одному из возможных вариантов:
- в проект вкладываются средства, имеющиеся на депозите в конкретном банке. Следовательно, альтернативная стоимость не должна быть меньше имеющейся банковской ставки;
- В проект инвестируются средства, выведенные из бизнеса и являющиеся временно свободными. В случае возникновения потребности в них, оперативное изъятие всей суммы из проекта невозможно. Потребуется кредит. Поэтому в качестве текущей стоимости средств выбирается рыночная кредитная ставка;
- Средняя доходность основного бизнеса составляет Y%. Соответственно от инвестиционного проекта требуется получать не меньше.
2. При работе с заёмными средствами ставка будет рассчитана как величина производная от стоимости привлекаемых из различных источников средств.
Как правило ставка, устанавливаемая инвестором, в подобных случаях превышает аналогичный показатель стоимости заёмных денежных средств.
При этом не просто учитывается изменение стоимости средств во времени, но и закладываются возможные риски, связанные с неопределённостью поступления денежных потоков и их объёмов.
Это является главной причиной, по которой ставкой дисконтирования считают средневзвешенную стоимость привлекаемого для последующего инвестирования капитала (WACC).
Именно этот показатель рассматривается в качестве требуемой нормы доходности на средства, вложенные в конкретный инвестиционный проект.
Чем выше ожидаемые риски, тем выше ставка.
Расчётные методы определения данного параметра менее наглядны, чем графические. Особенно когда требуется сравнить привлекательность двух или более проектов.
Например, сравнивая проекты «А» и «Б» (смотри график) можно сделать следующие выводы:
При ставке, превышающей значение 7%, величина NPV проекта А выше, чем у Б (что предупреждает о возможной ошибке в выборе при арифметическом сопоставлении).
К тому же инвестиционный проект «Б», обозначенный на графике красной кривой, подвержен более значительным изменениям в связи с изменяющейся ставкой дисконтирования (такое может быть объяснено разновеликими величинами поступающих средств в одинаковый период времени).
Следует учитывать факт существенного снижения величины ставок дисконтирования во времени, что накладывает определённые временные ограничение. Рассчитать их можно не более, чем за 10 лет.
Анализ графиков позволяет сделать вывод о том, что меняющаяся ставка дисконтирования приводит к изменениям величины показателя NPV (причём последний меняется нелинейно).
Поэтому для более взвешенной оценки необходимо не просто сравнивать величины для разных инвестиционных проектов, но и учитывать изменения последних при разных величинах ставки.
По умолчанию при расчете в Excel, ставка дисконтирования принимается равной 10%.
Пример. Рассчитать значение чистой приведенной стоимости для финансовых потоков, представленных в таблице, с использованием функции ЧПС, сравнить данные, применив функцию ЧИСТНЗ, объяснить расхождения в полученных результатах.
Вид таблицы данных:

Вначале рассчитаем значение приведенной стоимости с использованием рассматриваемой функции:
В результате получим:

Если бы в табличном редакторе Excel отсутствовала формула ЧИСТНЗ, кроме ручного способа можно было бы рассчитать приведенную стоимость с помощью функции ЧПС следующим образом:
Поскольку функция ЧПС учитывает только платежи, к результатам ее вычислений добавлено значение первоначальных затрат (+C3).
Результат вычислений:

Как видно, результаты немного различны. Это обусловлено тем, что функция ЧИСТНЗ учитывает реальное количество дней в году (в високосном году дней больше на 1). Несмотря на то, что все платежи производились 2-го числа 11 месяца ежегодно, их нельзя считать периодичными, поскольку в списке дат есть високосный год и реальное число дней между 2.11.2016 и 2.11.2017 равен 366 дней. Функция ЧИСТНЗ в подобных расчетах дает более точный результат.
Применение приведённой NPV на практике
Универсальные формулы приведённой стоимости активно используют опытные и начинающие инвесторы. Такой подход помогает оценить целесообразность внесения финсредств. Эксперты рекомендуют использовать три варианта расчёта приведённой NPV:
- Если чистая стоимость в приведённый период =0, это указание, что инвестиции окупаются, но сам вкладчик не получит никакой прибыли. К примеру: если гражданин использовал кредитные деньги, то поступающие финпотоки благоприятствуют расчёту с кредитором полностью. Инвестор сможет выплатить все начисленные %, а сам счёт останется неизменным. Здесь лучше найти иные варианты вклада, с более оптимистичным приведённым результатом чистой итоговой стоимости.
- Когда при изучении приведённого показателя NPV было получено плюсовое значение стоимости, то инвестиция полностью окупается. А сама цифра отображает цифру прибыли вкладчика. Конечно, в этом случае инвестиции более чем оправданы, так как в итоге человек получает хорошую прибыль.
- В редких случаях после многочисленных расчётов стоимости выходит отрицательное значение приведённой цифры. В такой ситуации инвестиции пользователя не окупаются, а сам вкладчик остаётся с убытками. Если исследуемый проект с минусовым значением, от работы с ним правильнее отказаться.
К инвестпроектам могут относиться только те бизнес-идеи, у которых преобладают положительные значения цифр. Когда вкладчик не может определиться, тогда предпочесть лучше вариант с наибольшим показателем чистого приведённого NPV.
Плюсы и недостатки
Универсальный метод расчёта приведённой стоимости был разработан экспертами для того, чтобы каждый человек имел возможность получения итоговой прибыли. Но, как и у любого другого финансового инструмента, у чистого приведённого NPV есть выгодные и негативные стороны.
К основным преимуществам можно отнести:
- Проводить корректировку объёма финпотоков и приведённой стоимости во времени можно за счёт учёта дисконтставки проекта.
- Действуют простые однозначные правила, помогающие со сложными решениями, которые касаются инвестпривлекательности идеи.
- Можно ввести учёт премии за рисковую составляющую в составе дисконтставки. Стоит отметить, что для высокорисковых проектов допустимо использовать повышенный процент.
Несмотря на все вышеперечисленные преимущества, у чистого приведённого NPV есть и негативные стороны. Каждый специалист должен помнить о ряде ограничений:
- Неопытному человеку сложно спрогнозировать будущие денежные потоки. Если пользователь решил разобраться в столь ответственном этапе работы, то все полученные им расчёты должны быть точными, так как от этого зависит итоговый объём приведённого NPV.
- Трудно оценить сложные инвестпроекты. Особые сложности возникают из-за многочисленных рисков, которых очень много в долгосрочном горизонте. Специалист должен скорректировать дисконтставки.
- Приведённый NPV может использоваться только для отображения абсолютного показателя дохода. Чтобы результаты анализа были достоверными, нужно дополнительно рассчитывать относительные показатели (внутренней нормы по доходности, инвестрентабельности).
- Стандартная форма приведённого NPV не корректируется на реинвест финансовых потоков.
Тщательный анализ результата
Специалистами было разработана базовое правило, обязательное для оценки уровня КПД инвестиций — принять план-проект можно только в том случае, если итоговая величина имеет значение «+». Если же этот параметр «-», то рассматриваемый инвестиционный проект будет убыточным. Цифра «0» свидетельствует о том, что доходные потоки от реализуемой программы могут возместить затратную часть, без поступления прибыли.
Приведённый NPV напрямую связан с приведённой стоимостью (PV). Эксперты применяют эту терминологию для оценки интенсивности финпоступлений в будущие периоды, которые соотносятся с настоящим моментом дисконта. Вычисление чистого NPV чаще всего включает расчёт приведённой стоимости. Узнать параметр довольно просто, главное — использовать специальную формулу.
Такой подход позволяет узнать следующие данные: плотность, размещение средств, возвратность и единовременное погашение:
PV = FV / (1+ r), здесь:
- PV — это общая сумма финсредств для размещения на общих условиях срочности, плотности и возвратности.
- FV — сумма, которая может быть использована для погашения долга. Включает в себя размер займа, проценты.
- r — процентная ставка, используемая в качестве платы за те финансы, которые были взяты в кредит.
Вычисление приведенной стоимости
В примере, приведенном ниже в этом разделе, вычисляется приведенное значение серии будущих выплат, иногда называемых ежегодной рентой. Если каждый год в течение десяти лет вносится платеж размером в 1200 долларов, то приведенная стоимость этих платежей составляет 6780,27 долларов: =ПС(,12;10;1200;0;0). Другими словами, если плательщик в настоящий момент предложит вам 6800 долларов, вам будет выгоднее их взять, чем получать в течение 10 лет по 1200 долларов. Если он предложит меньшую сумму, лучше подождать регулярных ежегодных платежей.
В приведенной выше формуле вы, наверное, заметили, что процентная ставка взята как бы ниоткуда. Функция ПС обычно используется для определения, сколько стоят на настоящий момент будущие выплаты. В этих ситуациях конкретная процентная ставка недоступна.
Существует множество мнений относительно того, какую процентную ставку лучше использовать при определении приведенной стоимости. Выбор процентной ставки в значительной мере зависит от вас самих. Одни говорят, что нужно использовать текущую процентную ставку по банковским депозитам, другие утверждают, что нужно брать процентную ставку по инвестициям, не связанным с рисками, таким как казначейские облигации. В данном примере была использована процентная ставка по инвестициям в ценные бумаги.
В приведенном выше примере была использована процентная ставка 12%. В результате получилось, что инвестиция размером в 6800 долларов принесет тот же доход, что и десятилетнее ожидание платежей по 1 200 долларов. Если плательщик предложит вам 7000 долларов немедленно, вы можете вложить их и получить лучший финансовый результат. Теперь давайте вернемся к таблицам и предположим, что у вас есть обязательства, по которым вы должны ежегодно выплачивать кому-то по 1200 долларов в течение 10 лет. Формула выглядит следующим образом: =ПС(,12;10;-1200;0;0).
Вместо входящего, в этой формуле использован исходящий денежный поток. Результат (-$6 780,27) также имеет знак, противоположный предыдущему примеру. В обоих примерах сумма платежей формирует всю транзакцию, поэтому будущей стоимости не существует. Также в примере использовано значение по умолчанию аргумента Тип. Аргументы БС и Тип не являются обязательными; они были включены в пример только для наглядности. На рис. 1 этот расчет показан в рабочей книге.
Рис. 1. Вычисление приведенной стоимости
Из соображений простоты в формулах примеров, приведенных в тексте, используются только константы. На практике чаще всего в аргументы функций подставляются ссылки на ячейки.
Приведенная стоимость единовременной будущей выплаты
В предыдущих примерах мы имели дело с сериями последовательных регулярных выплат, однако иногда существует всего одна будущая единовременная выплата. В качестве примера представим себе, что некоторый богатый родственник решил дать вам 100 тысяч долларов, но вы не можете получить их до своего сорокалетия. Если сейчас вам 25 лет, приведенная стоимость будущего платежа составит 31524,17 долларов. Эта сумма получена с помощью следующей формулы: =ПС(,08;15;0;100000).
Таким образом, это будет единовременный платеж ровно через 15 лет. Если бы у вас были сейчас какие-либо деньги, вы смогли бы инвестировать их под 8% годовых. Так как периодических платежей не будет, аргумент Тип в формуле опущен. Результат формулы свидетельствует о том, что если бы у вас было сейчас 31524,17 долларов и вы бы инвестировали их под 8%, то через 15 лет получили бы сотню тысяч долларов.
Рис. 2. Приведенное значение будущей единовременной выплаты
Прогнозирование денежного потока в Excel
Заполните таблицу «Денежные потоки»:
- в ячейку В9 введите значение первоначальных инвестиций,
- в ячейку В10 — формулу «=B8-B9»
- в ячейку С8 введите сумму поступлений в первый год,
- в D8 – формулу «=C8*1,3»,
- в С9 — «=C8*0,8»,
- протяните формулу из ячейки D8 вправо до 2019 года, рассчитайте итоговое значение;
- протяните вправо формулы из ячеек С9 и В10,
- протяните формулу из ячейки G8 на две ячейки вниз.
- В ячейку В11 формулу «=B10», в ячейку С11 формулу =B11+C10, протяните ячейку С11 вправо до F11, сверьте значение в ячейке F11 cо значением в G10.
Теперь рассчитаны денежные потоки, в том числе нарастающим итогом.
Срок окупаемости в Excel: пример расчёта
Для расчёта срока окупаемости в примере Excel введите в ячейку В17 формулу «=СЧЁТЕСЛ?(B11:G11;»<1″)+1». Смысл этой формулы: подсчёт всех отрицательных значений и прибавление единицы даст номер года, в котором совокупный денежный поток станет неотрицательным.
Алгоритм и формула расчета ЧДД
ЧДД рассчитывается с использованием такой формулы:
NPV = сумма результатов за каждый год капиталовложения CF / ((1 + r) в степени t),
где обозначения имеют следующий смысл:
Расчет денежных потоков
- CF – сальдо потока денежного, рассчитанного как разница между тем, что предприятие получило, и тем, что потратило
- t – количество лет, за который производится расчет
- r – ставка дисконтирования инвестиции
- n – продолжительность внедрения самого инвестиционного проекта
При изучении денежных потоков и их приведенной стоимости очень важно подойти непосредственно к выбору ставки дисконтирования. При осуществлении ее выбора необходимо учитывать не только особенности теории стоимости денег во времени, но и учитывать в обязательном порядке риск неопределенности. Лучше в качестве ставки дисконтирования выбирать именно средневзвешенную стоимость капитала, вложенного в инвестиционный проект. По итогу такого выбора существует закономерность: чем будут больше риски неопределенности, тем больше будет сама ставка, и наоборот.
ЧДД проектов: какой выбрать
Есть два инвестиционных проекта с инвестиционными вложениями в 10 тыс. рублей. Известны денежные потоки по каждому проекту по годам. Проект А: 5, 4, 3, 1. Проект Б имеет такие денежные потоки: 1, 3, 4, 6. Ставка дисконтирования 10%. Какой проект лучше?
Для начала необходимо рассчитать ЧДД для проекта А за каждый год:
- 5 / (1 + 0,1) в 1-й степени = 4545,5
- 4 / (1 + 0,1) во 2-й степени = 3305,8
- 3 / (1 + 0,1) в 3-й степени = 2253,9
- 1 / (1 + 0,1) в 4-й степени = 683,0
По результатам расчета ЧДД потока по проекту инвестирования А за 4-е года составит: 10788,2 (все ЧДД за четыре года суммируются: 4545,5 +…+ 683). Если отнять первоначальные капиталовложения, то ЧДД = 10788,2 – 10000 = 788,2.
По аналогии рассчитывается ЧДД по проекту Б, где она составит 491,5.
Вывод: вкладывать деньги можно в оба проекта, но выгоднее в проект А.
Анализ полученных результатов
Таким образом, NPV – это тот способ изучения инвестиционной доходности проекта, позволяющий уже сегодня понять, сколько денег необходимо вложить, и какая от них будет отдача. Также можно понять, за сколько окупится проект.
Как проводить анализ результатов
Реализация метода NPV базируется на таких основах:
Полученные результаты
- Дисконтирование денежных потоков происходит в целом по стоимости вложенного в капитал. Перед проведением расчета необходимо всегда найти приведенный к текущему временному периоду размер как входящих, так и исходящих потоков, и только после этого осуществить расчет ЧДД.
- Все значения по дисконтированным денежным потокам всегда необходимо складывать, чтобы потом проводить оценку полученного результата.
- Проводится оценка полученного потока. При полученном NPV больше 0 инвестиционный проект можно реализовать в действительность. Если же такая стоимость равна 0, тогда все на усмотрение инвестора: проект может быть принят или отклонен. Связано это с тем, что ЧДД = 0 свидетельствует о том, что потоки покроют инвестированный капитал и может даже дадут получить небольшою норму прибыли, но больше никаких выгод для инвестора не будет. Стоимость акций проекта не изменится в будущем.
Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
Чистая приведенная стоимость характеризует стоимость инвестиций, а правило чистой приведенной стоимости – это метод выбора среди альтернативных инвестиций.
Чистая приведенная стоимость инвестиций (NPV, от англ. ‘net present value’) – это приведенная (текущая) стоимость притока денежных средств за вычетом приведенной стоимости оттока денежных средств.
Слово «чистая» (англ. ‘net’) в этом термине означает вычитание приведенной стоимости оттоков (затрат) инвестиций из приведенной стоимости притоков (доходов) для получения чистого финансового результата.
Процедура вычисления NPV и применения правила NPV заключаются в следующем:
Определите все денежные потоки, связанные с инвестициями – все притоки и оттоки.
При оценке денежных потоков мы руководствуемся двумя принципами.
- Во-первых, мы включаем в расчет только дополнительные денежные потоки, возникающие в результате осуществления проекта. Мы не учитывает невозвратные затраты (англ. ‘sunk costs’), т.е. расходы, которые были совершены до начала проекта и которые нельзя возместить в течение проекта.
- Во-вторых, мы учитываем налоговые последствия, используя стоимость денежных потоков после уплаты налогов.
Определите соответствующую ставку дисконтирования или ставку альтернативной доходности r для инвестиционного проекта.
Для дисконтирования денежных потоков часто используется средневзвешенная стоимость капитала (WACC).
Этот показатель представляет собой средневзвешенное значение ставок доходности после налогообложения для обыкновенных акций, привилегированных акций и долгосрочных долговых обязательств компании, где весом является доля каждого источника финансирования в целевой структуре капитала компании.
Используя эту ставку дисконтирования, найдите текущую (приведенную) стоимость (PV) каждого денежного потока.
Приток имеет положительный знак (+) и увеличивает NPV. Отток имеет отрицательный знак (-) и уменьшает NPV.
Суммируйте все приведенные значения стоимости.
Сумма приведенной стоимости всех денежных потоков (притоков и оттоков) является чистой приведенной стоимостью инвестиций.
Примените правило чистой приведенной стоимости.
Правило NPV (англ. ‘net present value rule’) заключается в следующем:
- Если NPV инвестиции является положительным значением, инвестор должен ее осуществить.
- Если NPV отрицательна, инвестор не должен осуществлять эту инвестицию.
- Если у инвестора есть две возможные инвестиции, но он может выбрать только одну (т.е. взаимоисключающие проекты), инвестору следует выбрать инвестицию с более высокой положительной NPV.
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание . В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция ПС() используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить ПС() рассчитать Приведенную стоимость и по методу простых процентов (см. файл примера ).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета Будущей стоимости (FV): FV = PV * (1+i*n) где PV – Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i – процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя формулу наращения для сложных процентов .
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i – годовая ставка, n – срок ссуды в годах,
т.е. PV = FV / (1+i)^n
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
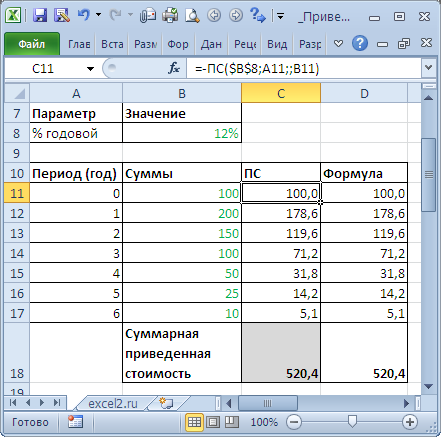
Сложные проценты (несколько сумм)
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции ПС() или альтернативной формулы PV = FV / (1+i)^n
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков.
Источники
- https://rdv-it.ru/company/press-center/blog/kak-rasschitat-npv/
- https://arakis.su/articles/npv-chistaja-privedennaja-stoimost-raschet/
- https://exceltable.com/funkcii-excel/raschet-privedennoy-stoimosti-chistnz
- https://vse-investicii.ru/razvitie-proektov/chistaya-privedyonnaya-stoimost
- http://Excel2010.ru/kak-v-excel-vychislit-privedennuyu-stoimost.html
- http://finexcel.ru/raschyot-pokazatelej-investicionnogo-proekta-v-excel/
- https://PravoDeneg.net/buhuchet/uchet/privedennaya-stoimost-denezhnogo-potoka.html
- https://fin-accounting.ru/cfa/l1/quantitative/cfa-nvp-and-net-present-value-rule
- https://excel2.ru/articles/raschet-privedennoy-nastoyashchey-tekushchey-stoimosti-v-ms-excel
Форма при выводе в эксель сметного расчета
Форма при выводе в эксель сметного расчета
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#1 Спасибо0 20.01.2020 11:58:10 Ребят, кто-нибудь знает как можно при выводе сметы в эксель сделать графу всего затрат, заказчик просит видеть реальную стоимость работ по каждой позиции, может кто сталкивался |
|
Светлана Специалист Сообщений: 505Регистрация: 03.12.2018 |
#2 Спасибо0 20.01.2020 12:03:58 Татьяна, в какой программе работаете? |
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#3 Спасибо0 20.01.2020 13:36:04 |
|
Светлана Специалист Сообщений: 505Регистрация: 03.12.2018 |
#5 Спасибо0 20.01.2020 13:47:15
Вы имеете ввиду в текущих ценах? Каким методом составлена смета баз-индексным или в текущих ценах? |
||
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#6 Спасибо0 20.01.2020 14:31:23 |
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#7 Спасибо0 20.01.2020 14:35:53 спасибо, все получилось;) |
|
Ирина Иванчикова Эксперт Проживает: Ростов ВеликийСообщений: 2949Регистрация: 24.10.2017 |
#8 Спасибо0 20.01.2020 14:37:58
Выбирайте форму Ресурсная смета (полная форма), 8-ой столбец — Сметная стоимость в текущих (прогнозных) ценах, руб. — общая |
||
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#9 Спасибо0 20.01.2020 14:42:57 спасибо, но нужно было с НР И СП, ТЕКУЩАЯ СТОИМОСТЬ без НДС, заказчик не понимает расчет |
|
Светлана Специалист Сообщений: 505Регистрация: 03.12.2018 |
#10 Спасибо0 20.01.2020 14:53:15 |
|
Ирина Иванчикова Эксперт Проживает: Ростов ВеликийСообщений: 2949Регистрация: 24.10.2017 |
#11 Спасибо0 20.01.2020 14:58:40
Выбирайте форму Ресурсная смета (полная форма) Теперь в 8 столбце в итогах каждой позиции сумма посчитана с учетом НР и СП
Если нужна текущая стоимость сразу с НДС введите коэффициент к итогам вот так: Теперь НДС считается в каждой позиции сметы, только из итогов не забудьте его убрать |
||||
|
Татьяна Участник Сообщений: 64Регистрация: 02.10.2019 |
#12 Спасибо0 20.01.2020 15:02:52 класс, спасибо, но базисно-индексным теперь не совсем понятно |
|
Noori Участник Сообщений: 8Регистрация: 23.06.2018 |
#13 Спасибо0 04.03.2020 08:26:32 Коллеги, подниму тему, пожалуйста уточните как это в баз-инд.методе сделать? чтобы примерно вот так было: Прикрепленные файлы |
|
Noori Участник Сообщений: 8Регистрация: 23.06.2018 |
#15 Спасибо0 04.03.2020 11:14:31 Я видела это, но не пойму как добавить 16 столбец… |
|
#16 Спасибо0 04.03.2020 11:24:57 Noori,выведите форму ЛСР по ЛЭУ |
|
|
Noori Участник Сообщений: 8Регистрация: 23.06.2018 |
#17 Спасибо0 04.03.2020 13:11:09 Вариант конечно, но не самый удобный… Спасибо) |
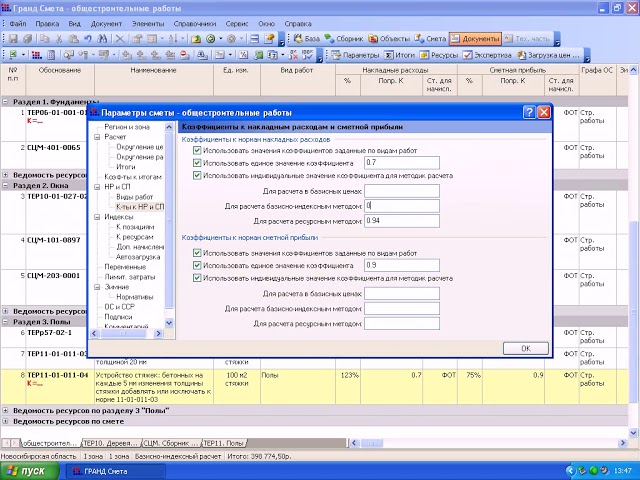
Видеоуроки
Видеурок учит вводить и использовать коэффициенты к накладным расходам и сметной прибыли в программе ГрандСмета
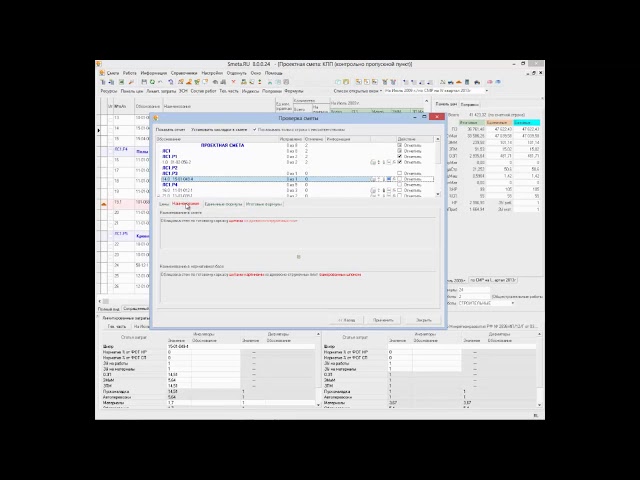
Проверка сметного расчета в программе Смета.ру
Документы сметчика
Об автомобильных дорогах и о дорожной деятельности в Российской Федерации и о внесении изменений в отдельные законодательные акты Российской Федерации
О внесении изменения в приказ Министерства строительства и жилищно-коммунального хозяйства Российской Федерации от 30 августа 2019 г. № 499/пр
Сертификация сметчиков
Подтвердите свою квалификацию в области ценообразования и сметного нормирования в строительстве — получите сертификат специалиста или специалиста высшей категории.