Как при помощи формул Excel решить теорему Пифагора для прямоугольных треугольников
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock] скачать бесплатно [/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2) . В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)) . Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)) .
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание) . Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)) . Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание) . Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание) .
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
Расчеты в Microsoft Excel: Решение и оформление задач
Лабораторная работа №5
1. Ознакомьтесь с задачей, представленной ниже.
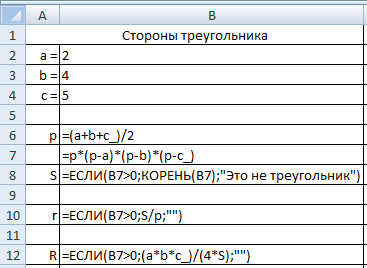
Вычисление элементов треугольника.Даны три стороны треугольника a, b, c. Требуется вычислить его площадь по формуле Герона 



1. Создайте в Microsoft Excel «Чистую книгу». Переименуйте, как показано на картинке Лист1 в «Треугольник».
2. Для получения красивых заголовков используйте возможности меню Формат à Ячейки à Выравнивание.[1]Шапка таблицы получена путем объединения ячеек. Оформите границы таблицы (кнопка 
3. Постройте модель решения задачи в среде Microsoft Excel, максимально автоматизировав расчеты. Для этого в ячейке, где должен находиться результат вычислений, необходимо вести формулы. Ввод всегда начинается со знака =. Вам понадобятся стандартная функция Excel 

4. Сравните полученные Вами результаты с теми, которые представлены в задании. Если Вы наблюдаете некоторые расхождения, значит формулы в вашей электронной таблице записаны ошибочно. В этом случае Ваша модель нуждается в корректировке.
5. Задайте формат ячеек с результатами вычислений Числовойс четырьмя десятичными знаками после запятой (Формат à Ячейки à Число).
6. Исследование зависимостей. Выделите D8 и выберите в меню Сервис à Зависимости формулà Влияющие ячейки. На экране протянутся синие стрелки от ячеек, содержащих длины сторон к ячейке D8. Исследуйте зависимости и влияния для других ячеек. Уберите стрелки соответствующей командой меню.
1. 
Будем вычислять отдельно подкоренное выражение р*(р-а)*(р-b)*(р-c) и определять его знак. Если оно положительно, вычисляем S, R и r. Если же нет, то в ячейке D9 выведем текстовую строку «Это не треугольник!», а в ячейках D11 и D12 выведем пустые строки.
Скопируйте формулу из D9 в D10. Отредактируйте D10, убрав КОРЕНЬ. В ячейке останется формула =D8*(D8-B4)*(D8-B5)*(D8-B6)
В D9 разместите формулу =ЕСЛИ(D10>0;КОРЕНЬ(D10);»Это не треугольник!»)[2].
В D11 формулу =ЕСЛИ(D10>0; D9/D8;»»). Аналогично измените формулу в D12.
2. Ограничение ввода. Разрешите пользователю вводить только положительные длины сторон треугольника (меню Данные à Проверка à Параметры.
3. Предъявите работу преподавателю.
[1] Обратите внимание, в ячейках Excel буквенные значения всегда автоматически отформатированы по левому краю ячейки, а численные – по правому. Также, заметьте, разделителем десятичных разрядов в Microsoft Excel 2003 является запятая.
[2] Обратите внимание на синтаксис функции ЕСЛИ. Разделителем трех переменных является точка с запятой ;
Задание в Microsoft Excel. Вычисления с использованием стандартных функций
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Задание в Microsoft Excel . Вычисления с использованием стандартных функций
Создать таблицу по образцу:
3 . Высоту подсчитать по формуле:
4 . Медиану подсчитать по формулам:
5 . Биссектрису подсчитать по формулам:
6. Углы подсчитать по формулам:
При вычислении углов функция arccos дает ответ в радианах, нужно перевести ответ в градусы, например: САВ =ACOS((E2*E2+G2*G2-C2*C2)/(2*E2*G2))*180/ПИ()
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 964 человека из 79 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 56 человек из 28 регионов
Курс повышения квалификации
Авторская разработка онлайн-курса
- Курс добавлен 02.12.2021
- Сейчас обучается 78 человек из 38 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 520 514 материалов в базе
Другие материалы
- 07.04.2016
- 486
- 0
- 07.04.2016
- 364
- 0
- 07.04.2016
- 966
- 5
- 07.04.2016
- 913
- 9
- 07.04.2016
- 794
- 2
- 07.04.2016
- 680
- 1
- 07.04.2016
- 1582
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 07.04.2016 975
- DOCX 36.6 кбайт
- 3 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Гнездилова Людмила Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 10360
- Всего материалов: 6
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Онлайн-тренинг о способах взаимодействия с разными категориями учащихся
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
Минобрнауки учредит стипендию для студентов — победителей международных олимпиад
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://mydocx.ru/10-2081.html
http://infourok.ru/zadanie-v-microsoft-ecel-vichisleniya-s-ispolzovaniem-standartnih-funkciy-1015391.html
|
Всем привет. угол А лежит напротив стороны а. угол B лежит напротив стороны b, угол С напротив стороны с. Я там набросал кое что. Но сомневаюсь что у меня там все правильно (см. вложение). И еще, я не знаю как проверить, можно ли построить треугольник с данными длинами сторон или нет. |
|
|
{quote}{login=CAHARD_76}{date=28.10.2011 08:27}{thema=Задача по геометрии в Excel. Найти углы треугольника по 3 сторонам.}{post}Всем привет. |
|
|
VLad777 Пользователь Сообщений: 5018 |
для проверки можно построить или нет: |
|
{quote}{login=V}{date=28.10.2011 08:45}{thema=}{post}для проверки можно построить или нет: А можно пожалуйста пример? А то я просто в excel пока не очень разбираюсь, и не знаю как это все в одну ячейку запихнуть. |
|
|
VLad777 Пользователь Сообщений: 5018 |
по вашему файлу. |
|
VLad777 Пользователь Сообщений: 5018 |
так |
|
{quote}{login=V}{date=28.10.2011 09:05}{thema=}{post}так Cпасибо большое) Очень помогли) |
|
|
Добрый день! Даны катеты прямоугольного треугольника. Подготовить лист для вычисления острых углов треугольника (в градусах). |
|
|
{quote}{login=V}{date=28.10.2011 09:05}{thema=}{post}так |
|
|
VLad777 Пользователь Сообщений: 5018 |
Оформление это не к нам, а вот на счет решения можем помочь. |
|
anvg Пользователь Сообщений: 11878 Excel 2016, 365 |
Нафиг ему теорема синусов? Для прямоугольного треугольника и обычного atan хватить. Для угла, противолежащего катету1 atan(катет1/катет2), для угла, противолежащего катету2, atan(катет2/катет1). Да и не забыть перевести в градусы |
|
{quote}{login=anvg}{date=20.01.2012 01:28}{thema=}{post}Нафиг ему теорема синусов? Для прямоугольного треугольника и обычного atan хватить. Для угла, противолежащего катету1 atan(катет1/катет2), для угла, противолежащего катету2, atan(катет2/катет1). Да и не забыть перевести в градусы{/post}{/quote} |
|
|
anvg Пользователь Сообщений: 11878 Excel 2016, 365 |
{quote}{login=}{date=20.01.2012 01:35}{thema=Re: }{post}{quote}{login=anvg}{date=20.01.2012 01:28}{thema=}{post}Нафиг ему теорема синусов? Для прямоугольного треугольника и обычного atan хватить. Для угла, противолежащего катету1 atan(катет1/катет2), для угла, противолежащего катету2, atan(катет2/катет1). Да и не забыть перевести в градусы{/post}{/quote} |
|
Guest Гость |
#15 20.01.2012 16:51:51 для общего случая угол В в рад=arcsin(b/a*(((a^2-b^2-c^2)/2/b/c)^2-1)^0,5) для других аналогично, если в сумме не Пи, треугольнику не жить |
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock]
скачать бесплатно
[/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2). В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)). Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)).
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание). Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)). Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание). Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание).
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
If you’re working with any triangle with a right angle in it somewhere, it’s simple to find the tangent angle, so long as you know the length of two sides of the triangle.
Doing so is even easier in Microsoft Excel because there are built-in functions you can use.
Information in this article applies to Excel for Microsoft 365, Excel 2019, 2016, 2013, 2010, and Excel for Mac.
What Is the Tangent Angle?
A tangent angle is an angle in the triangle where you know the length of the side opposite the angle and the side adjacent to it.
Imagine, for example, that your boss tells you to adjust a ladder at precisely 70 degrees from the ground. Unless you have some special tools, it would be complicated to measure whether the angle between the ladder and the ground is exactly 70 degrees.
However, if you have a measuring tape, you could measure the distance from the bottom of the ladder to the wall. Since the ladder against the wall forms a triangle, this would be the side that’s adjacent to the tangent angle you’re trying to calculate.
Next, you’d measure the distance from the bottom of the wall to where the top of the ladder touches it. This is the distance of the side that’s opposite from the tangent angle.
With the measurement of the opposite and adjacent sides, you can calculate the angle at the ladder base using the arctangent function.
If the wall (opposite) side is 10 feet, and the ground (adjacent) side is 5 feet, the formula for the tangent angle is the opposite side divided by the adjacent side. This is 10 divided by 5, or 0.5.
To find the value for the angle, you need to take the arctangent of 0.5.
Find the Tangent Angle With Excel
You could find a calculator that calculates the arctangent of a value, but Excel has a built-in function called ATAN that you can use.
The formula returns the angle in radians, which your boss probably won’t understand.
You’ll want to convert radians to degrees by multiplying it by 180/pi. Excel also has a PI function you can use for this purpose.
The answer, in this case, is 63.43 degrees. This means you’ll need to adjust one of the lengths until the angle is precisely 70 degrees.
Doing this is easy in Excel because you can change the opposite side’s value until the arctangent result is 70.
Using ASIN and ACOS in Excel
In this same scenario, let’s say you don’t have a tape measure long enough to measure the wall. You only know that the ladder is 15 feet and that it’s placed five feet from the wall.
Excel has two other functions that you can use to calculate the angle.
The ladder’s length is the hypotenuse of the triangle, and the ground distance is the adjacent side to the angle. So long as the triangle has one right (90 degree) angle, the information you have determines the formula you need to use.
- Cosine: Calculate the cosine angle if you know the length of the hypotenuse and the adjacent side.
- Sine: Calculate the sine angle if you know the length of the hypotenuse and the opposite side.
In this case, the angle is the arccosine of the adjacent side divided by the hypotenuse.
Since you know the adjacent side (the ground distance) is 5 feet, and the ladder length (hypotenuse) is 15 feet, the cosine of the angle is 5 divided by 15, or 0.333.
To calculate the angle, use the arccosine formula in Excel.
The result of the arccosine function is Excel is in radians, so you need to multiply it by 180/PI to convert it to degrees.
For a 15 foot ladder with its base 5 feet from the wall, the angle is 70.53 degrees.
If you knew that the height of the wall (the opposite side) is 10 feet, instead of the ground distance from the wall (the adjacent side), you’d use the arcsine formula in Excel.
In this case, the sine of the angle is the opposite side divided by the hypotenuse.
After converting to degrees, the angle, in this case, would be 48.12 degrees.
Why Use ATAN, ACOS, or ASIN?
Here are a few examples of situations where you may need to use one of these functions in Excel:
- In carpentry and construction, angles and lengths are used in all aspects of building houses and buildings.
- Photographers use angles to align lighting and their creative shots carefully.
- In sports, understanding angles can enhance skills and improve strategy.
- Ships and airplanes are located on radar using angles and distances.
- If you want to be sure furniture will fit right in your room, you’ll need to know how to calculate lengths and angles.
You may be able to accomplish these calculations on a scientific calculator. But if you don’t have one handy, Excel can help you make those calculations.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90 гр. (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Вспомните, как выглядит теорема Пифагора:
Высота^2+Основание^2=Гипотенуза^2
Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания:
=КОРЕНЬ(Гипотенуза^2-Основание^2 )
В другой формуле, вычисляющей основание прямоугольного треугольника, используются гипотенуза и высота:
=КОРЕНЬ((Гипотенуза^2)-(Высота^2))
Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту:
=КОРЕНЬ((Высота^2)+(Основание^2))
Верны также приведенные ниже тригонометрические тождества.
SIN(А) = Высота/Гипотенуза
SIN(В) = Основание/Гипотенуза
COS(А) = Основание/Гипотенуза
COS(В) = Высота/Гипотенуза
TAN(А) = Высота/Гипотенуза
Примечание
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А).
=ATAN(Высота/Основание)
Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу:
=ГРАДУСЫ(ATAN(Высота/Основание))
Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В):
=ПИ()/2-ATAN(Высота/Основание)
Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу:
=90-ГРАДУСЫ(ATAN(Высота/Основание)
В начало
Полезное
теорема Пифагора
Чтобы вычислить самую длинную сторону (гипотенузу) прямоугольного треугольника в Excel, вы можете использовать формулу, основанную на теореме Пифагора, адаптированную для использования математических операторов и функций Excel. В показанном примере формула в D5, скопированная ниже, имеет следующий вид:
который возвращает длину гипотенузы с учетом длины стороны a и стороны b, указанной в столбцах B и C соответственно.
Объяснение
Теорема Пифагора — ключевой принцип евклидовой геометрии. В нем говорится, что квадрат самой длинной стороны прямоугольного треугольника (гипотенуза) равен сумме квадратов двух других сторон. Теорема записывается в виде следующего уравнения:
Когда известны любые две стороны, это уравнение можно использовать для решения третьей стороны. Когда a и b известны, длину гипотенузы можно вычислить с помощью:
Когда известны b и c, длину стороны a можно рассчитать с помощью:
Когда a и c известны, длину стороны b можно рассчитать с помощью:
Чтобы перевести приведенное выше в синтаксис формулы Excel, используйте оператор возведения в степень (^) и функцию КОРЕНЬ, как показано ниже. Теорема Пифагора может быть записана как:
Приведенные ниже формулы можно использовать для решения каждой из трех сторон:
Вместо оператора возведения в степень вы также можете использовать функцию POWER следующим образом:
Приведенные выше формулы являются примером вложения одной функции в другую.
Как сделать таблицу пифагора в excel одной формулой
Создать таблицу умножения чисел от 1 до 9 (9 строк, 9 столбцов). В ячейке, соответствующей произведению 1*1, должна быть записана формула, которая затем должна быть скопирована во все остальные 80 ячеек. Решение в двух вариантах:
1)с использованием смешанных ссылок;
2)с использованием формулы массивов.
Метод 1. С использованием смешанных ссылок.
Составим таблицу. Введем по столбцам цифры от 1 до 9 и по строкам.
В ячейку В2 введем формулу: =$A2*Bкопируем эту ячейку во все остальные ячейки диапазона В2:J10. Получим таблицу умножения:
Метод 2. С использованием формулы массивов.
В ячейки В2:J2 введем цифры от1 до 9 и в ячейки А14:А22.
Выделим ячейки В14:J22 и введем формулу =B13:J13*A14:A22. Нажмем Ctrl+shift+Enter, чтобы формула вставилась как формула массива. Получим:
Excel: Абсолютные и относительные ссылки. Таблица Пифагора
Сегодняшняя статья для новичков. Помнится, не так давно на глаза попалась «экселевская» шутка, про то, что если ты не знаешь, чем $A$1 отличается от A1, то нам не о чем с тобой разговаривать. Но нам всегда есть о чём поговорить с нашими читателями и тем более о таком базовом вопросе, как абсолютные и относительные ссылки в Excel.
Итак, чем же эти ссылки отличаются одна от другой? Относительная ссылка в формуле вида A1 – это адресация на ячейку, которая удалена от ячейки с формулой на определённое расстояние. Поэтому, при протягивании формулы в сторону, она будет ссылаться на то же самое расстояние, а не на определённую ячейку. Например, если формулу протянуть вправо на одну ячейку, то она уже будет ссылаться не на A1, а на B1. Если вместо этого мы протянем формулу вниз, то ссылка окажется не на A1, а на A2. Таким образом, ссылки собьются и формула выдаст неправильный результат.
Если же мы вместо ссылки на ячейку A1, проставим $A$1, то куда бы мы не сдвигали формулу и на какое бы количество ячеек, формула всё равно будет ссылаться именно на ячейку A1. Сделать такую ссылку можно во время выбора ячейки в формуле, нажав клавишу F4.
Кроме жёсткой привязки к определённой ячейке может быть смешанная ссылка вида $A1 (фиксация столбца) или A$1 (фиксация строки). Это также достигается нажатием клавиши F4 два или три раза, пока знак $ не появится в нужном месте. Что это значит? При фиксации столбца $A1 во время сдвига формулы в сторону не будет происходить изменений. Ссылка будет изменяться только при движении по столбцу, то есть при протягивании формулы вверх или вниз. Соответственно, с учётом того, что ссылка идёт на ячейку A1, то при протягивании вверх, будет выдаваться ошибка #ССЫЛКА! (потому что выше A1 ячеек нет), а при протягивании формулы вниз, ссылка на ячейку примет вид $A2.
При создании ссылки вида A$1, будет зафиксирована строка, в результате, при протягивании формулы вверх или вниз, изменений в адресации ячейки не будет. При протягивании формулы влево будет выдаваться ошибка #ССЫЛКА! (слева от A1 нет ячеек), при протягивании формулы вправо, ссылка примет вид B$1 и выдаст значение из этой ячейки. Наглядным примером использования разной адресации ячеек служит таблица Пифагора. Если кто-то не помнит – это таблица умножения в шахматном виде, где перекрёстно перемножаются цифры из верхней строки (от 1 до 10) и из левого столбца (от 1 до 10).
Соответственно, мы получаем значения от 1 до 100. Если мы в ячейку B2 введём формулу =A2*B1 и протянем строки и столбцы, то формула будет считать неправильно, или, верней сказать, выдаст не те значения, которые нам нужны, так как, если вы помните, формула будет перемножать данные на определённом расстоянии от себя.
Если мы поставим формулу с жёсткой фиксацией (абсолютная адресация), то также не получим нужный результат. Формула просто скопирует одно и то же значение.
Лишь вводя смешанную адресацию, фиксируя левый столбец и верхнюю строку, мы получим правильный результат.
Наглядно ещё раз этот пример нам поможет проиллюстрировать короткое видео.
Как при помощи формул Excel решить теорему Пифагора для прямоугольных треугольников
Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.
Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock] скачать бесплатно [/lock]
Рис. 1. Элементы прямоугольного треугольника
Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2) . В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)) . Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)) .
Верны также приведенные ниже тригонометрические тождества:
- SIN(А) = Высота/Гипотенуза
- SIN(В) = Основание/Гипотенуза
- COS(А) = Основание/Гипотенуза
- COS(В) = Высота/Гипотенуза
- TAN(А) = Высота/Гипотенуза
Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.
Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание) . Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)) . Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание) . Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание) .
На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.
Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников
Вычисления на рабочем листе
Вычисление
– это процесс расчета формул с последующим
выводом результатов в виде значений в
ячейках, содержащих формулы. При изменении
значений в ячейках, на которые ссылаются
формулы, Excel обновляет
значения (выполняет повторное вычисление)
этих формул. Этот процесс называется
пересчетом, он затрагивает только те
ячейки, которые содержат ссылки на
изменившиеся ячейки.
Проектирование расчетов на рабочем
листе
Задание 1.
Вычисление элементов треугольника.
Даны
три стороны треугольника а, b,
с. Требуется вычислить по формуле
Герона площадь треугольника:

= p (p – a) (p – b) (p –
c),
где
полупериметр p равен:
|
p = |
a + b |
|
2 |
радиус
вписанной окружности r равен:
|
r = |
S |
|
p |
радиус
описанной окружности R равен:
|
R = |
abc |
|
4S |
-
Откройте
книгу Упражнения.xlsx. -
Добавьте
в книгу новый лист, переименуйте его в
Упр.11. -
В ячейки
В2, В3, В4 введите числа и присвойте им
соответствующие имена из левого столбца
(рис. 11.1).
Рис. 11.1. Исходные
данные
Обратите
внимание, какое имя получила ячейка
В4. Это связано с тем, что имена c и r
в Excel зарезервированы: c (column) –
столбец, r (row) – строка. Поэтому
Excel ввел в имя символ подчеркивания –
с_.
-
В ячейке
В8 вычислите площадь по предложенной
выше формуле. -
Задайте
длину стороны а, равную 10. В ячейках
с результатами появится сообщение об
ошибке – #ЧИСЛО! Дело в том, что стороны
10, 4, 5 не образуют треугольника. При
вычислении площади под корнем получается
отрицательное число. -
Необходимо
переделать формулы таким образом, чтобы
пользователь получал сообщение, почему
не могут быть вычислены значения S,
R и r, а в ячейках с результатами
вычислений R и r ничего не должно
выводиться. -
В ячейке
В7 отдельно вычислите подкоренное
выражение. Анализ подкоренного выражения
можно выполнить с помощью функции
ЕСЛИ(). Если подкоренное выражение
получится положительным, вычислите S,
R и r. Если же нет, то в ячейке В8 введите
текстовую строку «Это не треугольник!»,
а в ячейках В10 и В12 выведите пустые
строки (рис. 11.2).
Рис.11.2. Формулы с
учетом аналиа подкоренного выражения
Задание
2. Самостоятельно выполните следующие
примеры.
-
Вычислите
сторону треугольника а по
заданному R = 3. Используйте команду
Подбор параметра. -
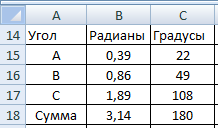
Вычислите углы
треугольника А, В, С (по теореме
косинусов), используя функцию ACOS().
В результате углы будут вычислены
в радианах.A =
arccos
b2 + c2 – a2
2bc
-
Переведите
углы, вычисленные в радианах в
градусы, используя функцию ГРАДУСЫ().
Вычислите отдельно сумму углов для
углов треугольника, выраженных в
радианах и в градусах соответственно
(рис. 11.3).
Рис. 11.3. Вычсление
углов треугольника
-
Вычислите
длину и площадь окружности по
заданному радиусу R по следующим
формулам: R2
и 2R. -
Вычислите
расстояние между двумя точками на
плоскости, заданными своими
координатами (рис. 11.4) по следующей
формуле: (Х2-Х1)^2+(Y2-Y2)^2.
В формуле должны быть использованы
имена координат.
Рис. 11.4. Коордитаты
точек
-
Вычислите
общее сопротивление трех параллельных
сопротивлений по формуле
|
R = |
1 |
|||
|
1 |
+ |
1 |
+ |
1 |
|
R1 |
R2 |
R3 |
Лабораторная работа 6. Проектирование
расчетов
на рабочем листе
Откройте
книгу Лабораторные работы.xls и на
листе Лаб_6 выполните следующие
задания.
Задание
1. Дан прямоугольный параллелепипед
со сторонами a, b, c. Вычислить:
-
Объем
V = abc
-
Площадь
поверхности
S = 2(ab + bc + ac)
-
Длину
диагонали

= a2 + b2
+ c2
-
Угол
между диагональю и плоскостью основания
=arctg
(c
)
a2 + b2 -
Угол
между диагональю и боковым ребром =
—
2
-
Объем
шара, диаметром которого является
диагональ,
|
Vш |
d3 |
|
6 |
Задание
2. В правильной четырехугольной
пирамиде заданы: длина стороны основания
а и высота h. Вычислить:
-
Объем
|
V = |
a2h |
|
3 |
-
Угол
наклона бокового ребра к плоскости
основания =
arctg
h
2a
-
Радиус
описанного около пирамиды шараR =
2h2
+ a24h
-
Угол
наклона боковой грани к основанию =
arctg
2h
a
-
Радиус
вписанного в пирамиду шараr =
a
tg
2
2
-
Площадь
полной поверхности пирамиды
|
S = |
3 V |
|
r |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для проведения вычислений можно использовать
вычислительные возможности программы Microsoft Excel.
Рассмотрим решение тестового примера по расчету углов треугольника с помощью программы MS Excel. Предположим, что
координаты вершин треугольника заданы в ячейках: x1®A2, y1®B2, x2®C2, y2®D2, x3®E2, y3®F2 (ячейки первой строки могут быть заполнены поясняющими подписями). Если запланировать ячейку G2, например, под хранение длины стороны AB, то в нее необходимо записать формулу:
=КОРЕНЬ((A2-C2)*(A2-C2)+(B2-D2)*(B2-D2)).
Здесь используется функция вычисления квадратного корня,
конструкция (A2-C2)*(A2-C2) соотвествует возведению в квадрат выражения в скобках (можно было бы так же использовать
конструкцию (A2-C2)^2). Для сторон BC и AC следует поступить
аналогично, выделив, например, под них ячейки H2 и I2.
Для вычисления величины угла А в ячейку J2 необходимо поместить формулу:
=(180/ПИ())*ACOS((G2*G2+I2*I2-H2*H2)/(2*G2*I2)).
Здесь ACOS обозначает вычисление функции арккосинус,
G2*G2 – возведение в квадрат, конструкция ПИ() возвращает значение математической константы p, множитель 180/ПИ() используется для превода в градусы величины полученной в радианах. Без этого множителя будет вычислена радианная мера
угла. Для перевода из градусов в радианы необходимо использовать множитель ПИ()/180.
Для вычисления величин углов B и C используем ячейки K2 и L2, поместив в них соотвествующие формулы, аналогичные последней.
Таким образом в ячейках J2, K2 и L2 будем иметь величины искомых углов в градусах и долях. Для проверки расчетов в ячейку
М2 следует поместить формулу: =СУММ(J2:L2). Она будет вычислять сумму углов треугольника, которая, как известно, должна
быть равна 180 градусам.
Для представления их в градусах – минутах – секундах и долях необходимо выполнить дополнительные вычисления.
Отведем для градусов угла А ячейку N2, для минут – O2, для секунд и долей — P2. Для получения градусов необходимо отбросить у
величины, хранящейся в ячейке J2 дробную часть. Это можно сделать помещением в N2 формулы: =ОКРВНИЗ(J2;1). Для получения минут в ячейку O2 поместим формулу:
=ОКРВНИЗ((J2-N2)*60;1).
Для получения секунд с долями в P2 поместим формулу:
=(J2-(N2+O2/60))*3600.
Для углов B и C необходимо поступать аналогично, выбрав для них по три ячейки, например, R2, S2, T2 и V2, W2, X2. Расчет
дает для углов А, В и С:
| Угол A | Угол B | Угол C | ||||||
| град | мин | сек | град | мин | сек | град | мин | сек |
| 11,2 | 10,1 | 38,6 |
Расчет неприступного расстояния
Рассмотрим решение тестового примера по расчету расстояния
до неприступной точки с помощью программы MS Excel.
Спланируем оформление вычислений так, что в ячейках A1-J1 разместим подписи к столбцам. В A2 поместим номер набора
данных, которые позволят получить одну величину неприступного
расстояния. В ячейке B2 будем задавать базис, в C2 и D2 разместим
градусы и минуты угла d. В ячейку Е2 поместим формулу
=C2+D2/60. Она будет содержать угол d в градусах с долями.
Ячейки F2, G2 и H2 будут содержать ту же информацию, но для угла
b, т.е. в H2 будет содержаться величина этого угла в градусах с долями (=F2+G2/60). По значениям, содержащимся в B2, E2 и H2 можно вычислить искомую величину неприступного расстояния с помощью формулы, помещенной в I2:
=B2*SIN(H2*ПИ()/180)/SIN((180-E2-H2)*ПИ()/180).
В этой формуле множитель ПИ()/180 служит для перевода градусов с долями в радианы. Таким образом, в ячейке I2 будет
находиться величина неприступного расстояния для первого набора
данных.
После этого описанные выше аналогичные действия произ- ведем с ячейкам третьей, четвертой и пятой строки, в результате че- го в ячейках I2-I5 получим четыре значения неприступного расстоя- ния. Последнее вычислительное действие, которое необходимо вы- полнить – это помещение в ячейку J2 формулы для вычисления среднего значения: =СУММ(I2:I5)/4. И, наконец, выполним объ- единение ячеек J2-J5. Для этого выделим с помощью мыши назван- ные ячейки, а затем выполним следующую последовательность дей- ствий: пункт главного меню Формат / Ячейки / вкладка Выравни- вание / по горизонтали – по центру / по вертикали – по центру / флажок объединение ячеек / кнопка Ок.
Для исходных данных тестового примера получаются следующие результаты:
| A | B | C | D | E | F | G | H | I | J |
| № | AC | d,г | d,м | d | b,г | b,м | b | AB | Среднее |
| 225,78 | 81,23 | 54,62 | 264,27456 | 264,29 |
|||||
| 227,38 | 88,92 | 49,92 | 264,29168 | ||||||
| 193,48 | 87,42 | 55,48 | 264,28703 | ||||||
| 241,19 | 89,82 | 47,72 | 264,29073 |
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах… |


















 Вычислите
Вычислите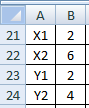

 Угол
Угол


