Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
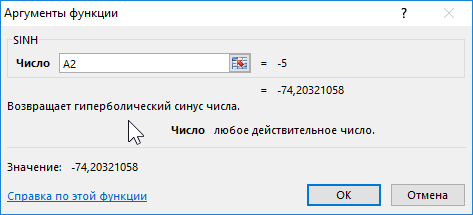
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
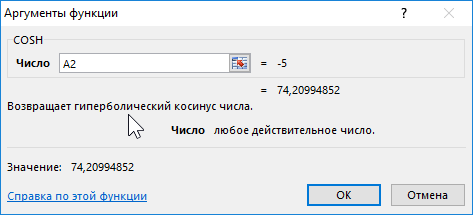
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
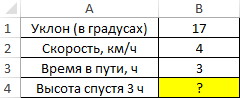
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
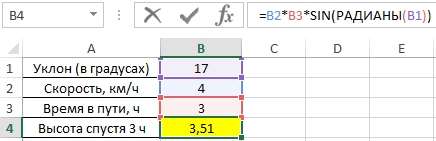
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
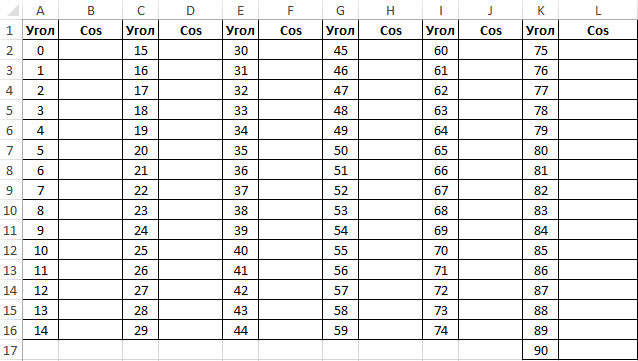
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
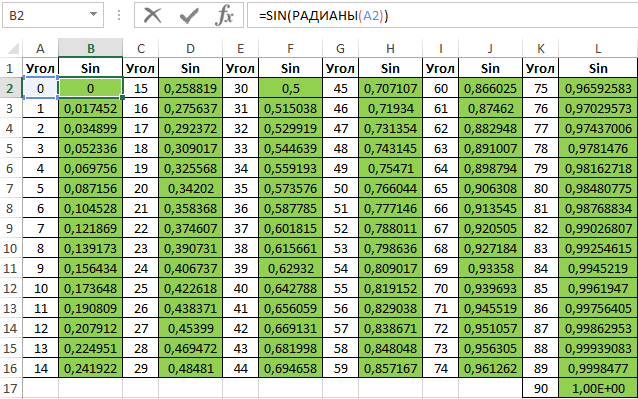
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
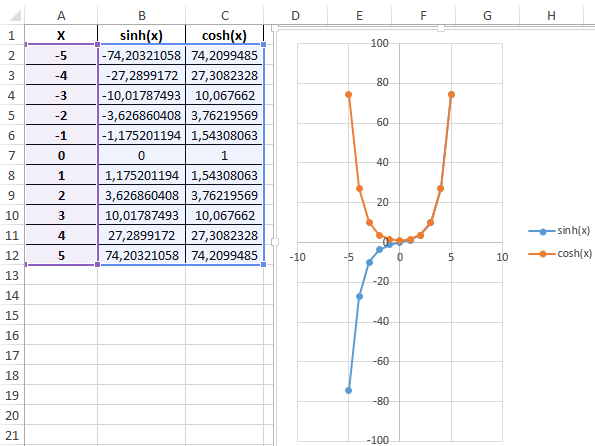
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
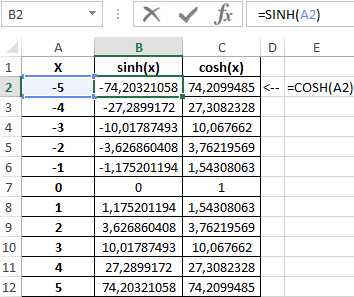
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
ABS |
Возвращает модуль (абсолютную величину) числа. |
|
ACOS |
Возвращает арккосинус числа. |
|
ACOSH |
Возвращает гиперболический арккосинус числа. |
|
ACOT |
Возвращает арккотангенс числа. |
|
ACOTH |
Возвращает гиперболический арккотангенс числа. |
|
АГРЕГАТ |
Возвращает агрегат для списка или базы данных. |
|
АРАБСКОЕ |
Преобразует римские числа в арабские в виде числа. |
|
ASIN |
Возвращает арксинус числа. |
|
ASINH |
Возвращает гиперболический арксинус числа. |
|
ATAN |
Возвращает арктангенс числа. |
|
ATAN2 |
Возвращает арктангенс для заданных координат x и y. |
|
ATANH |
Возвращает гиперболический арктангенс числа. |
|
ОСНОВАНИЕ |
Преобразует число в текстовое представление с данным основанием (базой). |
|
ОКРВВЕРХ |
Округляет число до ближайшего целого или кратного. |
|
ОКРВВЕРХ.МАТ |
Округляет число в большую сторону до ближайшего целого или кратного. |
|
ОКРВВЕРХ.ТОЧН |
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака. |
|
ЧИСЛКОМБ |
Возвращает количество комбинаций для заданного числа объектов. |
|
ЧИСЛКОМБА |
Возвращает количество комбинаций с повторами для заданного числа элементов. |
|
COS |
Возвращает косинус числа. |
|
COSH |
Возвращает гиперболический косинус числа. |
|
COT |
Возвращает котангенс угла. |
|
COTH |
Возвращает гиперболический котангенс числа. |
|
CSC |
Возвращает косеканс угла. |
|
CSCH |
Возвращает гиперболический косеканс угла. |
|
ДЕС |
Преобразует текстовое представление числа в заданном основании в десятичное число. |
|
ГРАДУСЫ |
Преобразует радианы в градусы. |
|
ЧЁТН |
Округляет число до ближайшего четного целого. |
|
EXP |
Возвращает число e, возведенное в указанную степень. |
|
ФАКТР |
Возвращает факториал числа. |
|
ДВФАКТР |
Возвращает двойной факториал числа. |
|
ОКРВНИЗ |
Округляет число до ближайшего меньшего по модулю значения. |
|
ОКРВНИЗ.МАТ |
Округляет число в меньшую сторону до ближайшего целого или кратного. |
|
ОКРВНИЗ.ТОЧН |
Округляет число в меньшую сторону до ближайшего целого или кратного. Число округляется в меньшую сторону независимо от знака. |
|
НОД |
Возвращает наибольший общий делитель. |
|
ЦЕЛОЕ |
Округляет число до ближайшего меньшего целого. |
|
ISO.ОКРВВЕРХ |
Округляет число в большую сторону до ближайшего целого или кратного. |
|
НОК |
Возвращает наименьшее общее кратное. |
|
LN |
Возвращает натуральный логарифм числа. |
|
LOG |
Возвращает логарифм числа по заданному основанию. |
|
LOG10 |
Возвращает десятичный логарифм числа. |
|
МОПРЕД |
Возвращает определитель матрицы массива. |
|
МОБР |
Возвращает обратную матрицу массива. |
|
МУМНОЖ |
Возвращает матричное произведение двух массивов. |
|
ОСТАТ |
Возвращает остаток от деления. |
|
ОКРУГЛТ |
Возвращает число, округленное с требуемой точностью. |
|
МУЛЬТИНОМ |
Возвращает мультиномиальный коэффициент множества чисел. |
|
МЕДИН |
Возвращает матрицу единицы или заданный размер. |
|
НЕЧЁТ |
Округляет число до ближайшего нечетного целого. |
|
ПИ |
Возвращает число пи. |
|
СТЕПЕНЬ |
Возвращает результат возведения числа в степень. |
|
ПРОИЗВЕД |
Возвращает произведение аргументов. |
|
ЧАСТНОЕ |
Возвращает целую часть частного при делении. |
|
РАДИАНЫ |
Преобразует градусы в радианы. |
|
СЛЧИС |
Возвращает случайное число в интервале от 0 до 1. |
|
Функция СЛУЧМАССИВ |
Возвращает массив случайных чисел в интервале от 0 до 1. Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные. |
|
Функция СЛУЧМЕЖДУ |
Возвращает случайное число в интервале между двумя заданными числами. |
|
РИМСКОЕ |
Преобразует арабские числа в римские в виде текста. |
|
ОКРУГЛ |
Округляет число до указанного количества десятичных разрядов. |
|
ОКРУГЛВНИЗ |
Округляет число до ближайшего меньшего по модулю значения. |
|
ОКРУГЛВВЕРХ |
Округляет число до ближайшего большего по модулю значения. |
|
SEC |
Возвращает секанс угла. |
|
SECH |
Возвращает гиперболический секанс угла. |
|
РЯД.СУММ |
Возвращает сумму степенного ряда, вычисленную по формуле. |
|
ЗНАК |
Возвращает знак числа. |
|
SIN |
Возвращает синус заданного угла. |
|
SINH |
Возвращает гиперболический синус числа. |
|
КОРЕНЬ |
Возвращает положительное значение квадратного корня. |
|
КОРЕНЬПИ |
Возвращает квадратный корень из значения выражения (число * пи). |
|
ПРОМЕЖУТОЧНЫЕ.ИТОГИ |
Возвращает промежуточный итог в списке или базе данных. |
|
СУММ |
Суммирует аргументы. |
|
СУММЕСЛИ |
Суммирует ячейки, удовлетворяющие заданному условию. |
|
СУММЕСЛИМН |
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям. |
|
СУММПРОИЗВ |
Возвращает сумму произведений соответствующих элементов массивов. |
|
СУММКВ |
Возвращает сумму квадратов аргументов. |
|
СУММРАЗНКВ |
Возвращает сумму разностей квадратов соответствующих значений в двух массивах. |
|
СУММСУММКВ |
Возвращает сумму сумм квадратов соответствующих элементов двух массивов. |
|
СУММКВРАЗН |
Возвращает сумму квадратов разностей соответствующих значений в двух массивах. |
|
TAN |
Возвращает тангенс числа. |
|
TANH |
Возвращает гиперболический тангенс числа. |
|
ОТБР |
Отбрасывает дробную часть числа. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Содержание
- Перевод (преобразование) тригонометрических функций: cos(a), sin(a), tg(a), ctg(a) в Excel. Формулы перевода.
- Такую шпаргалку мы для Вас подготовили и приводим ниже в тексте.
- Простые тригонометрические функции в программе «Excel» выглядят следующим образом:
- Тригонометрические функции SIN COS в Excel для синуса и косинуса
- Примеры использования функций SIN, SINH, COS и COSH в Excel
- Таблица синусов и косинусов в Excel
- Построение графика функций SINH и COSH в Excel
- Особенности использования тригонометрических функций в Excel
- Как в эксель посчитать синус в градусах
- SIN (функция SIN)
- Описание
- Синтаксис
- Замечание
- Пример
- Тригонометрические функции SIN COS в Excel для синуса и косинуса
- Примеры использования функций SIN, SINH, COS и COSH в Excel
- Таблица синусов и косинусов в Excel
- Построение графика функций SINH и COSH в Excel
- Особенности использования тригонометрических функций в Excel
- Как в экселе считать синус в градусах
- Описание
- Синтаксис
- Замечание
- Пример
- Примеры использования функций SIN, SINH, COS и COSH в Excel
- Таблица синусов и косинусов в Excel
- Построение графика функций SINH и COSH в Excel
- Особенности использования тригонометрических функций в Excel
Перевод (преобразование) тригонометрических функций: cos(a), sin(a), tg(a), ctg(a) в Excel. Формулы перевода.
Добрый день.
Очень часто работая с тригонометрическими функциями в программе «Эксель» приходится их переводить из одной в другую для проведения расчетов. Казалось бы нет ничего сложного в этих тригонометрических преобразованиях изученных нами еще в курсе алгебры школьной программы, но когда голова забита рабочими процессами и планами на ближайшие выходные, вспомнить формулу перевода косинуса в тангенс достаточно сложно и хочется иметь под рукой небольшую шпаргалку.
Она поможет Вам быстро без лишних затрат времени на поиск в интернете рассчитать cos и sin двойных и тройных углов, произвести перевод синуса в косинус, косинуса в тангенс, синуса в котангенс и наоборот.
Такую шпаргалку мы для Вас подготовили и приводим ниже в тексте.
Надеемся, что данная шпаргалка будет полезна для Вас.
Простые тригонометрические функции в программе «Excel» выглядят следующим образом:
- Косинус (cos) – COS()
- Синус (sin) – SIN()
- Тангенс (tg) – TAN()
- Котангенс (ctg) – 1/TAN()
- Угол следует указывать в радианах .
- Перевод градусов в радианы по формуле — угол°*Пи/180
Вопросы можно задавать в комментариях и на форуме.
Источник
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Источник
Как в эксель посчитать синус в градусах
SIN (функция SIN)
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Как в экселе считать синус в градусах
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
В этой практической задаче я покажу вам как при помощи возможностей Excel 2010 найти значение косинуса угла в 136 градусов. Задачка из школьной программы, так что этот практический урок будет полезен не только родителям, но и школьникам. Заодно вы узнаете какими тригонометрическими функциями обладает Excel 2010.
Обратите внимание на то, что в тригонометрических функциях программы Excel углы измеряются не в градусах, а в радианах. Поэтому, прежде чем вычислить косинус угла 136°, его нужно перевести в радианы. Это можно сделать двумя способами.
Первый: умножить 136 на число пи и разделить произведение на 180.
Второй: воспользоваться специальной функцией, которая переводит градусы в радианы.
Источник
Математические и тригонометрические функции (справочник)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
Возвращает модуль (абсолютную величину) числа.
Возвращает арккосинус числа.
Возвращает гиперболический арккосинус числа.
ACOT
Возвращает арккотангенс числа.
ACOTH
Возвращает гиперболический арккотангенс числа.
Возвращает агрегат для списка или базы данных.
АРАБСКОЕ
Преобразует римские числа в арабские в виде числа.
Возвращает арксинус числа.
Возвращает гиперболический арксинус числа.
Возвращает арктангенс числа.
Возвращает арктангенс для заданных координат x и y.
Возвращает гиперболический арктангенс числа.
ОСНОВАНИЕ
Преобразует число в текстовое представление с данным основанием (базой).
Округляет число до ближайшего целого или кратного.
ОКРВВЕРХ.МАТ
Округляет число в большую сторону до ближайшего целого или кратного.
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака.
Возвращает количество комбинаций для заданного числа объектов.
ЧИСЛКОМБА
Возвращает количество комбинаций с повторами для заданного числа элементов.
Возвращает косинус числа.
Возвращает гиперболический косинус числа.
COT
Возвращает котангенс угла.
COTH
Возвращает гиперболический котангенс числа.
CSC
Возвращает косеканс угла.
CSCH
Возвращает гиперболический косеканс угла.
ДЕС
Преобразует текстовое представление числа в заданном основании в десятичное число.
Преобразует радианы в градусы.
Округляет число до ближайшего четного целого.
Возвращает число e, возведенное в указанную степень.
Возвращает факториал числа.
Возвращает двойной факториал числа.
Округляет число до ближайшего меньшего по модулю значения.
ОКРВНИЗ.МАТ
Округляет число в меньшую сторону до ближайшего целого или кратного.
Округляет число в меньшую сторону до ближайшего целого или кратного. Число округляется в меньшую сторону независимо от знака.
Возвращает наибольший общий делитель.
Округляет число до ближайшего меньшего целого.
ISO.ОКРВВЕРХ
Округляет число в большую сторону до ближайшего целого или кратного.
Возвращает наименьшее общее кратное.
Возвращает натуральный логарифм числа.
Возвращает логарифм числа по заданному основанию.
Возвращает десятичный логарифм числа.
Возвращает определитель матрицы массива.
Возвращает обратную матрицу массива.
Возвращает матричное произведение двух массивов.
Возвращает остаток от деления.
Возвращает число, округленное с требуемой точностью.
Возвращает мультиномиальный коэффициент множества чисел.
МЕДИН
Возвращает матрицу единицы или заданный размер.
Округляет число до ближайшего нечетного целого.
Возвращает число пи.
Возвращает результат возведения числа в степень.
Возвращает произведение аргументов.
Возвращает целую часть частного при делении.
Преобразует градусы в радианы.
Возвращает случайное число в интервале от 0 до 1.
Возвращает массив случайных чисел в интервале от 0 до 1. Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.
Возвращает случайное число в интервале между двумя заданными числами.
Преобразует арабские числа в римские в виде текста.
Округляет число до указанного количества десятичных разрядов.
Округляет число до ближайшего меньшего по модулю значения.
Округляет число до ближайшего большего по модулю значения.
SEC
Возвращает секанс угла.
SECH
Возвращает гиперболический секанс угла.
Возвращает сумму степенного ряда, вычисленную по формуле.
Возвращает знак числа.
Возвращает синус заданного угла.
Возвращает гиперболический синус числа.
Возвращает положительное значение квадратного корня.
Возвращает квадратный корень из значения выражения (число * пи).
Возвращает промежуточный итог в списке или базе данных.
Суммирует ячейки, удовлетворяющие заданному условию.
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям.
Возвращает сумму произведений соответствующих элементов массивов.
Возвращает сумму квадратов аргументов.
Возвращает сумму разностей квадратов соответствующих значений в двух массивах.
Возвращает сумму сумм квадратов соответствующих элементов двух массивов.
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Возвращает тангенс числа.
Возвращает гиперболический тангенс числа.
Отбрасывает дробную часть числа.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://exceltable.com/funkcii-excel/primery-funkciy-sin-sinh-cos-cosh
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Excel поддерживает простые и легкие тригонометрические вычисления для пользователей. Особенно в сложных задачах этот инструмент очень помогает. В следующей статье представлены тригонометрические функции, поддерживаемые Excel.
1. Хам Син
— Синтаксис: Грех (число).
Где: число — значение угла Sin.
— Значение: возвращает значение Sin для 1 угла, значение находится в диапазоне от -1 до +1.
— Например:
Обратите внимание на работу с тригонометрическими функциями в Excel. Единица измерения — радианы.
Шаг 1. Преобразуйте единицы измерения в радианы. Вставьте еще 1 столбец и введите команду, как показано:
Шаг 2: Перетащите форматирование в оставшиеся ячейки. Введите формулу для расчета значения Sin, как показано ниже:
Наконец, вы перетаскиваете форматирование в оставшиеся ячейки со следующим результатом:
2. Хэм Кос
— Синтаксис: Cos (число) .
Где: число — это значение угла для вычисления Cos.
— Значение: возвращает значение Cos для 1 угла, значение находится в диапазоне от -1 до +1.
— Например:
Шаг 1: Вы вводите формулу, как показано.
Шаг 2: Перетащите формат в оставшиеся ячейки с результатами, как показано ниже:
3. Хам Тан
— Синтаксис: Загар (число) .
В котором: число — это значение угла, который необходимо вычислить.
— Значение: возвращает значение Tan для 1 угла, значение от -1 до +1.
— Например:
4. Функция Asin
— Синтаксис: Асин (число) .
Где :: число — значение угла для вычисления Asin.
— Значение: возвращает значение Asin для 1 угла, значение находится в диапазоне от -1 до +1.
— Например:
5. Функция Asinh
— Синтаксис: Асин (число) .
Где: число — значение угла для вычисления Asin.
— Значение: возвращает значение угла Asinh, но это значение в радианах.
— Например:
6. Функция Acos
— Синтаксис: Acos (число) .
Где: число — значение угла для вычисления Acos.
— Значение: возвращает значение Acos для 1 угла, значение находится в диапазоне от -1 до +1.
— Например:
7. Функция Акоша
— Синтаксис: Асин (число) .
Где: число — это значение угла, который нужно вычислить.
— Значение: возвращает значение угла Acosh, но это значение в радианах.
— Например:
8. сырой стрелок
— Синтаксис: Атан (число) .
В котором: число — это значение для вычисления Атана.
— Значение: возвращает значение угла Атана.
— Например:
9. Хам Атан2
— Синтаксис: Антан2 (x_num, y_num) .
Где: x_num, y_num — значения градусов и градусов. —
Значение: возвращает значение радиана в диапазоне от — Pi-> + Pi.
— Например:
10. Хам Атанх
— Синтаксис: Атан (число) .
В котором: число — это значение для вычисления Атана.
— Значение: возвращает значение радиана.
— Например:
11. Функция «Градусы».
— Синтаксис: Градусы (угол) .
Где: угол — это значение угла, который нужно преобразовать.
— Значение: преобразование измерения угла из радианов в градусы.
— Например:
12. Радианы Хэма
— Синтаксис: Радианы (угол) .
Где: угол — это значение угла, который нужно преобразовать.
— Значение: преобразование измерения угла из градусов в радианы.
— Например:
Удачи!
Электронные таблицы EXCEL можно
использовать при изучении многих разделов
физики, математики и других предметов. Одной из
тем, является математическая тема: «Анализ
тригонометрических функций». Данная работа
будет посвящена использованию электронных
таблиц EXCEL в анализе тригонометрических функций.
В ней, используя знания и навыки работы с
мастером функций и диаграмм Excel, будет проведен
анализ тригонометрических функций с проведением
расчетов по формулам и с построением графиков,
используя ссылки.
Для анализа элементарных функций необходимо
уметь решать следующие задачи:
- определение возрастания или убывания функции
на заданном интервале, - определение максимума (минимума) данной функции
на заданном интервале, - определение четности данной функции на
заданном интервале, - определение периодичности данной функции на
заданном интервале,
Каждая из этих задач может быть решена разным
способом. В данной работе рассмотрен один из
вариантов их решения.
ЗАДАЧА №1. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ВОЗРАСТАНИЕ.
Признаком возрастания или убывания заданной
функции на заданном отрезке можно предложить
результат действия функции EXCEL – ЗНАК(…) –,
определяющей знак числа: =ЗНАК(f(x2) – f(x1)),
где
x1, x2 – значения концов заданного интервала,
f(x2) – последующее значение функции,
f(x1) – предыдущее значение функции.
При результате действия функции ЗНАК(…) равном 1
функция возрастает; а если результат равен (–1),
то функция убывает на заданном отрезке.
ЗАДАЧА №2. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
МАКСИМУМ И МИНИМУМ.
Исследования поведения любой функции Y=f(X)
проводится в определенном интервале [A,B]. Для
этого в EXCEL имеются соответствующие функции.
Для этого воспользуемся следующим алгоритмом:
- выделить ячейку для результата,
- задать соответствующую функцию в мастере
функций, - замаркировать диапазон значений, для которых
определяем максимальное или минимальное
значение, - запустить на выполнение.
ЗАДАЧА №3. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ.
Предлагается определение четности или
нечетности данной функции в EXCEL проводится в два
этапа:
- проверка равенства модулей f(x) и f(–x) для всех
значений аргумента, - определение четности или нечетности заданной
функции.
Проверку равенства модулей можно проводить на
основе следующей формулы: ABS(ABS(f(x)) – ABS( f(–x)))
Значение данной сумы для всех без исключения
строк должно быть равно «0», в противном случае не
может быть речи о четности или нечетности
заданной функции.
Очевидно, что для четной или нечетной функции
автосумма столбца значений данной функции равна
«0».
Для определения четности заданной функции
воспользуемся формулой:
ABS (f(x) – f(–x))
И определим для полученных по этой формуле
значений автосумму. Если автосумма равна нулю, то
заданная функция – четная, иначе – не четная.
Просматривая результаты расчетов, можно сделать
вывод, что функция Y=SIN(X) НЕЧЕТНАЯ.
ЗАДАЧА №4. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ПЕРИОДИЧНОСТЬ.
Для полученных значений определяем для каждого
значения аргумента значение формулы: =ABS(Sin(x) –
Sin(x+Pi))
И для всех, полученных по данной формуле
значений, определяем автосумму. Если автосумма
равна нулю, то данная функция действительно
имеет период равный 2*Pi.
Просматривая результаты расчетов, можно сделать
вывод, что функция Y=SIN(X) ПЕРИОДИЧЕСКАЯ, период
этой функции T=2*PI .
Практические задания для выполнения в
электронных таблицах
ЗАДАНИЕ N 1: «АНАЛИЗ ФУНКЦИИ Y=SIN(X)
НА МАКСИМУМ, МИНИМУМ»
Фамилия
Класс
Написать на 1 листе, начиная в ячейке A1, А2
тему урока, A3 задание, в А4 фамилию, класс.
В пятой строке сделать надписи:Номер; Угол X; SIN(X).
С помощью автозаполнения с шестой строки ввести
в столбец A номера точек (17) от 0 до 16, в столбец B
значение углов X от –360 градусов до +360 через 45
градусов, по которым будут рассчитаны значения
функции в этих точках и построен график функции
Y=SIN(X).
В ячейке E24 сделать надпись: Конст. ПИ, в F24 ввести
значение константы ПИ, выбрав его с помощью
мастера функций из категории
«Математические».
В столбце С посчитать значения функции Y=SIN(X) ,
задав относительные ссылки (B6, B7,…, B22) на значения
угла в градусах для столбца В, и абсолютную
ссылку $F$24 на ячейку F24,при
переводе значений углов из градусов в радианы.
Пример формулы расчета в ячейке С6:
=SIN(B6*$F$24/180)
В ячейке B23 сделать надпись МАКС=, в C23 определить
значение максимума для функции SIN(X) по столбцу С
от C6 до C22.
В ячейке B24 сделать надпись МИН=, в C24 определить
значение минимума для функции SIN(X) по столбцу С
от C6 до C22.
Внизу под
вычислениями построить
точечный график функции Y=SIN(X) по диапазону
B6:C22.
| А | B | C | D | E | |
| Номер Nн– |
X | SIN(X) | |||
| 0 | –360 | 2,4503E–16 | |||
| 1 | –315 | 0,707106781 | |||
| 2 | –270 | 1 | |||
| 3 | –225 | 0,707106781 | |||
| 4 | –180 | –1,2251E–16 | |||
| 5 | –135 | –0,70710678 | |||
| 6 | –90 | –1 | |||
| 7 | –45 | –0,70710678 | |||
| 8 | 0 | 0 | |||
| 9 | 45 | 0,707106781 | |||
| 10 | 90 | 1 | |||
| 11 | 135 | 0,707106781 | |||
| 12 | 180 | 1,22515E–16 | |||
| 13 | 225 | –0,70710678 | |||
| 14 | 270 | –1 | |||
| 15 | 315 | –0,70710678 | |||
| 16 | 360 | –2,4503E–16 | |||
|
МАКСИМУМ |
1 | ||||
|
МИНИМУМ |
–1 | КОНС.PI | 3,141593 |
ЗАДАНИЕ N 2: « АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ПЕРИОДИЧНОСТЬ».
Фамилия
Класс
Скопировать с 1 листа на 2 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на ПЕРИОДИЧНОСТЬ
В пятой строке сделать надписи:
Номер; Угол X; SIN(X); SIN(X+2*ПИ); SIN(X)–SIN(X+2*ПИ)
Скопировать с 1 листа на 2 лист значения, формулы,
расчеты для диапазона A6:C24 c помощью команды
«Специальная вставка»,опция «ВСЕ».
Удалить на листе 2 надписи и значения для расчета
максимума и минимума в B23:C24.
В столбце D посчитать значения функции Y=SIN(X+2*ПИ),
скопировав формулу из С6 в D6, и добавив в скобках к
аргументу X значение +2*ПИ. Формула расчета в
ячейке D6: =SIN(B6*$F$24/180+2*ПИ)
В столбце E посчитать значения разности по модулю
двух функций SIN(X) и SIN(X+2*ПИ). Формула расчета
в ячейке E6: =ABS(C6–D6) .
В ячейке D23 сделать надпись:»Сумма
разностей»,в E23 сосчитать сумму разностей по
столбцу E в диапазоне E6:E22.Формула =СУММ(E6:E22)
Внизу под вычислениями построить совместный
точечный график функции Y=SIN(X) и график функции
Y=SIN(X+2*ПИ) по диапазону B6:D22.
| X | SIN(X) | Sin(X+2*ПИ) | Sin(X)–Sin(X+2*ПИ) | |
| –360 | 2,4503E–16 | 4,90059E–16 | 2,4503E–16 | |
| –315 | 0,707106781 | 0,707106781 | 7,77156E–16 | |
| –270 | 1 | 1 | 0 | |
| –225 | 0,707106781 | 0,707106781 | 4,44089E–16 | |
| –180 | –1,22515E–16 | –3,67545E–16 | 2,4503E–16 | |
| –135 | –0,707106781 | –0,707106781 | 7,77156E–16 | |
| –90 | –1 | –1 | 0 | |
| –45 | –0,707106781 | –0,707106781 | 1,11022E–16 | |
| 0 | 0 | 2,4503E–16 | 2,4503E–16 | |
| 45 | 0,707106781 | 0,707106781 | 2,22045E–16 | |
| 90 | 1 | 1 | 0 | |
| 135 | 0,707106781 | 0,707106781 | 1,11022E–16 | |
| 180 | 1,22515E–16 | –1,22515E–16 | 2,4503E–16 | |
| 225 | –0,707106781 | –0,707106781 | 1,11022E–16 | |
| 270 | –1 | –1 | 0 | |
| 315 | –0,707106781 | –0,707106781 | 2,22045E–16 | |
| 360 | –2,4503E–16 | 0 | 2,4503E–16 | |
| Сумма разностей | 4,00071E–15 | |||
| КОНС.PI | 3,14159265 |
ЗАДАНИЕ N 3: «АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ВОЗРАСТАНИЕ И УБЫВАНИЕ».
Фамилия
Класс
Скопировать с 1 листа на 3 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на ВОЗРАСТАНИЕ И УБЫВАНИЕ.
В пятой строке сделать надписи:
Номер; Угол X; SIN(X); ЗНАК РАЗНОСТИ; ВОЗРАСТАНИЕ ИЛИ
УБЫВАНИЕ
Скопировать с 1 листа на 3 лист
значения,формулы,расчеты для диапазона A6:C24 c
помощью команды «Специальная вставка»,опция
«ВСЕ». Удалить на листе 3 надписи и значения
для расчета максимума и минимума в B23:C24.
В столбце D посчитать значения функции ЗНАК
,начиная со второй ячейке столбца функций D7,
вычитая из предыдущего значения
функции последующее значение функции.Формула
расчета в ячейке D7:=ЗНАК(C7–C6) Если значение
разности>0,то результат вычисления 1,
если значение разности<0,то результат
вычисления –1.
В столбце E написать слово возрастает,если
результат вычисления 1, в соответствующей ячейки
столбца D, иначе написать слово убывает, если
результат вычисления –1 .
Внизу под вычислениями построить точечный
график функции Y=SIN(X) и график функции ЗНАК по
диапазону B6:D22.
| N | X | SIN(X) | знак разности | ||
| 0 | –360 | 2,4503E–16 | |||
| 1 | –315 | 0,70710678 | 1 | возрастает | |
| 2 | –270 | 1 | 1 | экстремум | |
| 3 | –225 | 0,70710678 | –1 | убывает | |
| 4 | –180 | –1,225E–16 | –1 | убывает | |
| 5 | –135 | –0,7071068 | –1 | убывает | |
| 6 | –90 | –1 | –1 | экстремум | |
| 7 | –45 | –0,7071068 | 1 | возрастает | |
| 8 | 0 | 0 | 1 | возрастает | |
| 9 | 45 | 0,70710678 | 1 | возрастает | |
| 10 | 90 | 1 | 1 | экстремум | |
| 11 | 135 | 0,70710678 | –1 | убывает | |
| 12 | 180 | 1,2251E–16 | –1 | убывает | |
| 13 | 225 | –0,7071068 | –1 | убывает | |
| 14 | 270 | –1 | –1 | экстремум | |
| 15 | 315 | –0,7071068 | 1 | возрастает | |
| 16 | 360 | –2,45E–16 | 1 | возрастает | |
| КОНС.PI | 3,141593 |
ЗАДАНИЕ N 4: «АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ЧЕТНОСТЬ».
Фамилия
Класс
Скопировать с 1 листа на 3 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на НА ЧЕТНОСТЬ
В пятой строке сделать надписи: Номер; Угол X; SIN(X);
SIN(–X); ABS(SIN(X)–SIN(–X));ABS(SIN(X))–ABS(SIN(–X))
Скопировать с 1 листа на 3 лист
значения,формулы,расчеты для диапазона A6:C24 c
помощью команды «Специальная вставка»,опция
«ВСЕ». Удалить на листе 3 надписи и значения
для расчета максимума и минимума в B23:C24.
В столбце D посчитать значения функции Y=SIN(–X),
скопировав формулу из С6 в D6, и добавив в скобках к
аргументу X ЗНАК – . Формула расчета в ячейке D6:
=SIN(–B6*$F$24/180)
В столбце E посчитать значения функции
Y=ABS(SIN(X)–SIN(–X)) , т.е. модуль разности функции Y=SIN(X)
и функции Y=SIN(–X).
Формула расчета в ячейке E6: =ABS(C6–D6) .
В столбце F посчитать значения функции
Y=ABS(SIN(X))–ABS(SIN(–X)) т.е. разность модулей
функции Y=SIN(X) и функции Y=SIN(–X). Формула
расчета в ячейке E6: =ABS(C6)–ABS(D6) .
В ячейке С23 сделать надпись:»Контрольные
суммы»,в E23 сосчитать сумму по столбцу E в
диапазоне E6:E22.Формула =СУММ(E6:E22), в F23 сосчитать
сумму по столбцу F в диапазоне F6:F22.Формула
=СУММ(F6:F22).
Внизу под вычислениями построить точечный
график функции Y=SIN(X) и график функции Y=SIN(–X) по
диапазону B6:D22.
| N | X | SIN(X) | SIN(–X) | ABS(SIN(X)–SIN(–X)) | ABS(SIN(X))– ABS(SIN(–X)) |
| 0 | –360 | 2,4503E–16 | –2,4503E–16 | 0 | |
| 1 | –315 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 2 | –270 | 1 | –1 | 2 | 0 |
| 3 | –225 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 4 | –180 | –1,225E–16 | 1,22515E–16 | 2,4503E–16 | 0 |
| 5 | –135 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 6 | –90 | –1 | 1 | 2 | 0 |
| 7 | –45 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 |
| 9 | 45 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 10 | 90 | 1 | –1 | 2 | 0 |
| 11 | 135 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 12 | 180 | 1,2251E–16 | –1,22515E–16 | 2,4503E–16 | 0 |
| 13 | 225 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 14 | 270 | –1 | 1 | 2 | 0 |
| 15 | 315 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 16 | 360 | –2,45E–16 | 2,4503E–16 | 4,90059E–16 | 0 |
| Контрольные суммы | 19,3137085 | 0 | |||
| КОНС.PI | 3,141592654 |
Данная работа посвящена исследованию
тригонометрических функций. Именно на примере
функции SIN(X) продемонстрированы возможности
электронных таблиц Excel для анализа функций. Было
показано, как можно определить участки
возрастания или убывания функции, как определить
их максимальное и минимальное значения на
заданном интервале аргумента, как можно
определить периодичность функции, ее четность
или нечетность.
В школе был проведен открытый
интегрированный урок: Информатика – Математика
по теме: «Исследование тригонометрических
функций с помощью электронных таблиц». На этом
уроке участники каждой группы с помощью
демонстрационной презентации рассказали о
постановке своих задач, а в Excel показали, как они
решаются.
Данная работа может использоваться в школах, как
дополнительное пособие при изучении
соответствующих разделов математики и
информатики.
Перейти к содержимому
Добрый день.
Очень часто работая с тригонометрическими функциями в программе «Эксель» приходится их переводить из одной в другую для проведения расчетов. Казалось бы нет ничего сложного в этих тригонометрических преобразованиях изученных нами еще в курсе алгебры школьной программы, но когда голова забита рабочими процессами и планами на ближайшие выходные, вспомнить формулу перевода косинуса в тангенс достаточно сложно и хочется иметь под рукой небольшую шпаргалку.
Она поможет Вам быстро без лишних затрат времени на поиск в интернете рассчитать cos и sin двойных и тройных углов, произвести перевод синуса в косинус, косинуса в тангенс, синуса в котангенс и наоборот.
Такую шпаргалку мы для Вас подготовили и приводим ниже в тексте.
Надеемся, что данная шпаргалка будет полезна для Вас.
Простые тригонометрические функции в программе «Excel» выглядят следующим образом:
- Косинус (cos) – COS()
- Синус (sin) – SIN()
- Тангенс (tg) – TAN()
- Котангенс (ctg) – 1/TAN()
- Угол следует указывать в радианах .
- Перевод градусов в радианы по формуле — угол°*Пи/180
Вопросы можно задавать в комментариях и на форуме.
Тригонометрия в Excel: основные функции
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Математические и тригонометрические функции
- ABS (ABS) — Находит модуль (абсолютную величину) числа.
- ACOS (ACOS) — Вычисляет арккосинус числа.
- ACOSH (ACOSH) — Вычисляет гиперболический арккосинус числа.
- ASIN (ASIN) — Вычисляет арксинус числа.
- ASINH (ASINH) — Вычисляет гиперболический арксинус числа.
- ATAN (ATAN) — Вычисляет арктангенс числа.
- ATAN2 (ATAN2) — Вычисляет арктангенс для заданных координат x и y.
- ATANH (ATANH) — Вычисляет гиперболический арктангенс числа.
- ОКРВВЕРХ (CEILING) — Округляет число до ближайшего целого или до ближайшего кратного указанному значению.
- ЧИСЛКОМБ (COMBIN) — Находит количество комбинаций для заданного числа объектов.
- COS (COS) — Вычисляет косинус числа.
- COSH (COSH) — Вычисляет гиперболический косинус числа.
- ГРАДУСЫ (DEGREES) — Преобразует радианы в градусы.
- ЧЁТН (EVEN) — Округляет число до ближайшего четного целого.
- EXP (EXP) — Вычисляет число e, возведенное в указанную степень.
- ФАКТР (FACT) — Вычисляет факториал числа.
- ОКРВНИЗ (FLOOR) — Округляет число до ближайшего меньшего по модулю целого.
- НОД (GCD) — Находит наибольший общий делитель.
- ЦЕЛОЕ (INT) — Округляет число до ближайшего меньшего целого.
- НОК (LCM) — Находит наименьшее общее кратное.
- LN (LN) — Вычисляет натуральный логарифм числа.
- LOG (LOG) — Вычисляет логарифм числа по заданному основанию.
- LOG10 (LOG10) — Вычисляет десятичный логарифм числа.
- МОПРЕД (MDETERM) — Вычисляет определитель матрицы, хранящейся в массиве.
- МОБР (MINVERSE) — Определяет обратную матрицу (матрица хранится в массиве).
- МУМНОЖ (MMULT) — Вычисляет произведение матриц, хранящихся в массивах.
- ОСТАТ (MOD) — Вычисляет остаток от деления.
- ОКРУГЛТ (MROUND) — Находит число, округленное с требуемой точностью.
- МУЛЬТИНОМ (MULTINOMIAL) — Вычисляет мультиномиальный коэффициент множества чисел.
- НЕЧЁТ (ODD) — Округляет число до ближайшего нечетного целого.
- ПИ (PI) — Вставляет число «пи».
- СТЕПЕНЬ (POWER) — Вычисляет результат возведения числа в степень.
- ПРОИЗВЕД (PRODUCT) — Вычисляет произведение аргументов.
- ЧАСТНОЕ (QUOTIENT) — Вычисляет целую часть частного при делении.
- РАДИАНЫ (RADIANS) — Преобразует градусы в радианы.
- СЛЧИС (RAND) — Выдает случайное число в интервале от 0 до 1.
- СЛУЧМЕЖДУ (RANDBETVEEN) — Выдает случайное число в заданном интервале.
- РИМСКОЕ (ROMAN) — Преобразует число в арабской записи к числу в римской как текст.
- ОКРУГЛ (ROUND) — Округляет число до указанного количества десятичных разрядов.
- ОКРУГЛВНИЗ (ROUNDDOWN) — Округляет число до ближайшего меньшего по модулю целого.
- ОКРУГЛВВЕРХ (ROUNDUP) — Округляет число до ближайшего по модулю большего целого.
- РЯД.СУММ (SERIESSUM) — Вычисляет сумму степенного ряда по заданной формуле.
- ЗНАК (SIGN) — Определяет знак числа.
- SIN (SIN) — Вычисляет синус заданного угла.
- SINH (SINH) — Вычисляет гиперболический синус числа.
- КОРЕНЬ (SQRT) — Вычисляет положительное значение квадратного корня.
- КОРЕНЬПИ (SQRTPI) — Вычисляет значение квадратного корня из числа «пи».
- ПРОМЕЖУТОЧНЫЕ.ИТОГИ (SUBTOTAL) — Вычисляет промежуточные итоги.
- СУММ (SUM) — Суммирует аргументы.
- СУММЕСЛИ (SUMIF) — Суммирует ячейки, удовлетворяющие заданному условию(читать подробнее).
- СУММЕСЛИМН (SUMIFS) — Суммирует ячейки, удовлетворяющие заданным критериям. Допускается указывать более одного условия(читать подробнее).
- СУММПРОИЗВ (SUMPRODUCT) — Вычисляет сумму произведений соответствующих элементов массивов(читать подробнее).
- СУММКВ (SUMSQ) — Вычисляет сумму квадратов аргументов.
- СУММРАЗНКВ (SUMX2MY2) — Вычисляет сумму разностей квадратов соответствующих значений в двух массивах.
- СУММСУММКВ (SUMX2PY2) — Вычисляет сумму сумм квадратов соответствующих элементов двух массивов.
- СУММКВРАЗН (SUMXMY2) — Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
- TAN (TAN) — Вычисляет тангенс числа.
- TANH (TANH) — Вычисляет гиперболический тангенс числа.
- ОТБР (TRUNC) — Отбрасывает дробную часть числа.
Математические функции Excel
Здесь рассмотрены наиболее часто используемые математические функции Excel (краткая справка). Дополнительную информацию о функциях можно найти в окне диалога мастера функций, а также в справочной системе Excel. Кроме того, множество математических функций включено в надстройку «Пакет анализа».
Функция СУММ (SUM)
Функция СУММ (SUM) суммирует множество чисел. Эта функция имеет следующий синтаксис:
=СУММ(числа)
Аргумент числа может включать до 30 элементов, каждый из которых может быть числом, формулой, диапазоном или ссылкой на ячейку, содержащую или возвращающую числовое значение. Функция СУММ игнорирует аргументы, которые ссылаются на пустые ячейки, текстовые или логические значения. Аргументы не обязательно должны образовывать непрерывные диапазоны ячеек. Например, чтобы получить сумму чисел в ячейках А2, В10 и в ячейках от С5 до К12, введите каждую ссылку как отдельный аргумент:
=СУММ(А2;В10;С5:К12)
Функции ОКРУГЛ, ОКРУГЛВНИЗ, ОКРУГЛВВЕРХ
Функция ОКРУГЛ (ROUND) округляет число, задаваемое ее аргументом, до указанного количества десятичных разрядов и имеет следующий синтаксис:
=ОКРУГЛ(число;количество_цифр)
Аргумент число может быть числом, ссылкой на ячейку, в которой содержится число, или формулой, возвращающей числовое значение. Аргумент количство_цифр, который может быть любым положительным или отрицательным целым числом, определяет, сколько цифр будет округляться. Задание отрицательного аргумента количество_цифр округляет до указанного количества разрядов слева от десятичной запятой, а задание аргумента количество_цифр равным 0 округляет до ближайшего целого числа. Excel цифры, которые меньше 5, с недостатком (вниз), а цифры, которые больше или равны 5, с избытком (вверх).
Функции ОКРУГЛВНИЗ (ROUNDDOWN) и ОКРУГЛВВЕРХ (ROUNDUP) имеют такой же синтаксис, как и функция ОКРУГЛ. Они округляют значения вниз (с недостатком) или вверх (с избытком).
Функции ЧЁТН и НЕЧЁТ
Для выполнения операций округления можно использовать функции ЧЁТН (EVEN) и НЕЧЁТ (ODD). Функция ЧЁТН округляет число вверх до ближайшего четного целого числа. Функция НЕЧЁТ округляет число вверх до ближайшего нечетного целого числа. Отрицательные числа округляются не вверх, а вниз. Функции имеют следующий синтаксис:
=ЧЁТН(число)
=НЕЧЁТ(число)
Функции ОКРВНИЗ, ОКРВВЕРХ
Функции ОКРВНИЗ (FLOOR) и ОКРВВЕРХ (CEILING) тоже можно использовать для выполнения операций округления. Функция ОКРВНИЗ округляет число вниз до ближайшего кратного для заданного множителя, а функция ОКРВВЕРХ округляет число вверх до ближайшего кратного для заданного множителя. Эти функции имеют следующий синтаксис:
=ОКРВНИЗ(число;множитель)
=ОКРВВЕРХ(число;множитель)
Значения число и множитель должны быть числовыми и иметь один и тот же знак. Если они имеют различные знаки, то будет выдана ошибка.
Функции ЦЕЛОЕ и ОТБР
Функция ЦЕЛОЕ (INT) округляет число вниз до ближайшего целого и имеет следующий синтаксис:
=ЦЕЛОЕ(число)
Аргумент — число — это число, для которого надо найти следующее наименьшее целое число.
Эта формула возвратит значение 10, как и следующая:
Функция ОТБР (TRUNC) отбрасывает все цифры справа от десятичной запятой независимо от знака числа. Необязательный аргумент количество_цифр задает позицию, после которой производится усечение. Функция имеет следующий синтаксис:
=ОТБР(число;количество_цифр)
Если второй аргумент опущен, он принимается равным нулю. Следующая формула возвращает значение 25:
Функции ОКРУГЛ, ЦЕЛОЕ и ОТБР удаляют ненужные десятичные знаки, но работают они различно. Функция ОКРУГЛ округляет вверх или вниз до заданного числа десятичных знаков. Функция ЦЕЛОЕ округляет вниз до ближайшего целого числа, а функция ОТБР отбрасывает десятичные разряды без округления. Основное различие между функциями ЦЕЛОЕ и ОТБР проявляется в обращении с отрицательными значениями. Если вы используете значение -10,900009 в функции ЦЕЛОЕ, результат оказывается равен -11, но при использовании этого же значения в функции ОТБР результат будет равен -10.
Функции СЛЧИС и СЛУЧМЕЖДУ
Функция СЛЧИС (RAND) генерирует случайные числа, равномерно распределенные между 0 и 1, и имеет следующий синтаксис:
=СЛЧИС()
Функция СЛЧИС является одной из функций EXCEL, которые не имеют аргументов. Как и для всех функций, у которых отсутствуют аргументы, после имени функции необходимо вводить круглые скобки.
Значение функции СЛЧИС изменяется при каждом пересчете листа. Если установлено автоматическое обновление вычислений, значение функции СЛЧИС изменяется каждый раз при воде данных в этом листе.
Функция СЛУЧМЕЖДУ (RANDBETWEEN), которая доступна, если установлена надстройка «Пакет анализа», предоставляет больше возможностей, чем СЛЧИС. Для функции СЛУЧМЕЖДУ можно задать интервал генерируемых случайных целочисленных значений.
=СЛУЧМЕЖДУ(начало;конец)
Аргумент начало задает наименьшее число, которое может возвратить любое целое число от 111 до 529 (включая и оба эти значения):
Функция ПРОИЗВЕД
Функция ПРОИЗВЕД (PRODUCT) перемножает все числа, задаваемые ее аргументами, и имеет следующий синтаксис:
=ПРОИЗВЕД(число1;число2. )
Эта функция может иметь до 30 аргументов. Excel игнорирует любые пустые ячейки, текстовые и логические значения.
Функция ОСТАТ
Функция ОСТАТ (MOD) возвращает остаток от деления и имеет следующий синтаксис:
=ОСТАТ(число;делитель)
Значение функции ОСТАТ — это остаток, получаемый при делении аргумента число на делитель. Например, следующая функция возвратит значение 1, то есть остаток, получаемый при делении 19 на 14:
Если число меньше чем делитель, то значение функции равно аргументу число. Например, следующая функция возвратит число 25:
Если число точно делится на делитель, функция возвращает 0. Если делитель равен 0, функция ОСТАТ возвращает ошибочное значение.
Функция КОРЕНЬ
Функция КОРЕНЬ (SQRT) возвращает положительный квадратный корень из числа и имеет следующий синтаксис:
=КОРЕНЬ(число)
Аргумент число должен быть положительным числом. Например, следующая функция возвращает значение 4:
Если число отрицательное, КОРЕНЬ возвращает ошибочное значение.
Функция ЧИСЛОКОМБ
Функция ЧИСЛОКОМБ (COMBIN) определяет количество возможных комбинаций или групп для заданного числа элементов. Эта функция имеет следующий синтаксис:
=ЧИСЛОКОМБ(число;число_выбранных)
Аргумент число — это общее количество элементов, а число_выбранных — это количество элементов в каждой комбинации. Например, для определения количества команд с 5 игроками, которые могут быть образованы из 10 игроков, используется формула:
Результат будет равен 252. Т.е., может быть образовано 252 команды.
Функция ЕЧИСЛО
Функция ЕЧИСЛО (ISNUMBER) определяет, является ли значение числом, и имеет следующий синтаксис:
=ЕЧИСЛО(значение)
Пусть вы хотите узнать, является ли значение в ячейке А1 числом. Следующая формула возвращает значение ИСТИНА, если ячейка А1 содержит число или формулу, возвращающую число; в противном случае она возвращает ЛОЖЬ:
Функция LOG
Функция LOG возвращает логарифм положительного числа по заданному основанию. Синтаксис:
=LOG(число;основание)
Если аргумент основание не указан, то Excel примет его равным 10.
Функция LN
Функция LN возвращает натуральный логарифм положительного числа, указанного в качестве аргумента. Эта функция имеет следующий синтаксис:
=LN(число)
Функция EXP
Функция EXP вычисляет значение константы e, возведенной в заданную степень. Эта функция имеет следующий синтаксис:
EXP(число)
Функция EXP является обратной по отношению к LN. Например, пусть ячейка А2 содержит формулу:
Тогда следующая формула возвращает значение 10:
Функция ПИ
Функция ПИ (PI) возвращает значение константы пи с точностью до 14 десятичных знаков. Синтаксис:
=ПИ()
Функция РАДИАНЫ и ГРАДУСЫ
Тригонометрические функции используют углы, выраженные в радианах, а не в градусах. Измерение углов в радианах основывается на константе пи и при этом 180 градусов равны пи радиан. Excel предоставляет две функции, РАДИАНЫ (RADIANS) и ГРАДУСЫ (DEGREES), чтобы облегчить работу с тригонометрическими функциями.
Вы можете преобразовать радианы в градусы, используя функцию ГРАДУСЫ. Синтаксис:
=ГРАДУСЫ(угол)
Здесь — угол — это число, представляющее собой угол, измеренный в радианах. Для преобразования градусов в радианы используется функция РАДИАНЫ, которая имеет следующий синтаксис:
=РАДИАНЫ(угол)
Здесь — угол — это число, представляющее собой угол, измеренный в градусах. Например, следующая формула возвращает значение 180:
В то же время следующая формула возвращает значение 3,14159:
Функция SIN
Функция SIN возвращает синус угла и имеет следующий синтаксис:
=SIN(число)
Здесь число — угол в радианах.
Функция COS
Функция COS возвращает косинус угла и имеет следующий синтаксис:
=COS(число)
Здесь число — угол в радианах.
Функция TAN
Функция TAN возвращает тангенс угла и имеет следующий синтаксис:
=TAN(число)
Здесь число — угол в радианах.
В начало страницы
В начало страницы