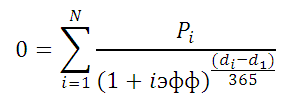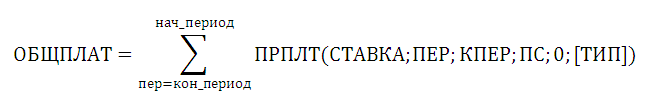Расчет ставки за период excel

В этой статье описаны синтаксис формулы и использование функции СТАВКА в Microsoft Excel.

Описание

Возвращает процентную ставку за период аннуитета. Ставка вычисляется с помощью итерации и может иметь ноль или больше решений. Если последовательные результаты rate не сходятся в пределах 0,00000001 после 20 итерации, то ставка возвращает результат #NUM! значение ошибки #ЗНАЧ!.

Синтаксис

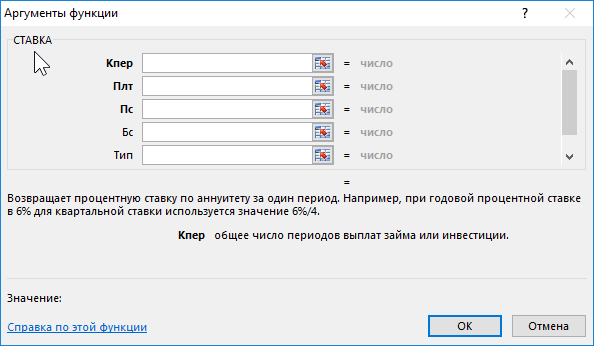
СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Примечание: Полное описание аргументов «кпер», «плт», «пс», «бс» и «тип» см. в разделе, посвященном функции ПС.

Аргументы функции СТАВКА описаны ниже.

• Кпер    — обязательный аргумент. Общее количество периодов платежей по аннуитету.

• Плт    Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.

• Пс    — обязательный аргумент. К настоящему моменту — общая сумма, на которую сейчас стоит ряд будущих платежей.

• Fv    Необязательный. Будущая стоимость или баланс, который вы хотите достичь после последнего платежа. Если значение «ок» опущено, предполагается значение 0 (например, будущая стоимость займа — 0). Если аргумент «пс» опущен, необходимо включить аргумент «pmt».

• Тип    Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.

Тип	Когда нужно платить
0 или опущен	В конце периода
1	В начале периода

• Прогноз    Необязательный. Предполагаемая величина ставки.

  • Если аргумент «прогноз» опущен, предполагается, что его значение равно 10 %.

  • Если функция СТАВКА не сходится, попробуйте изменить значение аргумента «прогноз». Функция СТАВКА обычно сходится, если значение этого аргумента находится между 0 и 1.

Замечания

Убедитесь, что единицы измерения, выбранные для аргументов «прогноз» и «кол_пер» соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу под 12 процентов годовых используйте значение 12%/12 для аргумента «прогноз» и 4*12 — для аргумента «кол_пер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «прогноз» и 4 —для аргумента «кол_пер».

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
4	Срок займа в годах
-200	Ежемесячная сумма платежа
8000	Сумма займа
Формула	Описание	Результат
=СТАВКА(A2*12; A3; A4)	Месячная процентная ставка по займу в соответствии с условиями, указанными в диапазоне A2:A4 в качестве аргументов.	1 %
=СТАВКА(A2*12; A3; A4)*12	Годовая процентная ставка по займу в соответствии с теми же условиями.	9,24 %

Функция СТАВКА используется для определения процентной ставки по инвестиции либо денежному займу с аннуитетной структурой графика погашения для одного периода выплат (при условии, что будущая стоимость ценных бумаг, обеспечивающих инвестицию либо кредит является известной величиной) и возвращает полученное значение.

Если при заключении сделки процентная ставка не была установлена жестко, функция СТАВКА позволяет определить размер неявной ставки (то есть такой ставки, которая обеспечила бы получение эквивалентного дохода).

Примеры финансовых расчетов по функции СТАВКА в Excel

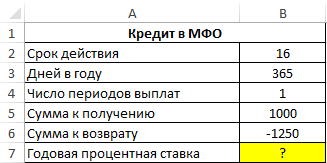
Пример 1. В МФО был взят кредит сроком на 16 дней, сумма которого составляет 1000 долларов. Сумма возврата составляет 1250 долларов. Определить годовую процентную ставку по указанным условиям займа.

Таблица данных:

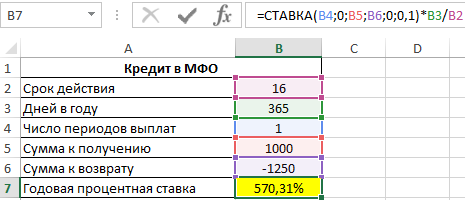
Для расчета в ячейку B7 введем следующую формулу:

=СТАВКА(B4;0;B5;B6;0;0,1)*B3/B2

Описание аргументов:

• B4 – число периодов выплат (в данном случае – 1);
• 0 – размер фиксированной выплаты (поскольку в данном примере только один период выплат, указано значение 0);
• B5 – тело кредита;
• B6 – сумма на момент погашения долга;
• 0 – характеризует тип выплат, при котором выплата производится в конце периода;
• 0,1 – предполагаемое значение процентной ставки (любое число из диапазона от 0 до 1);
• B3/2 – коэффициент для пересчета полученного значения ставки к годовой процентной ставке.

Результат вычислений:

Пи данных условиях микрокредитования сроком займа на 16 дней процентная ставка составляет 570,31% годовых! Несмотря на это, услуги по микрокредитованию сегодня продолжают набирать популярность.



Анализ пенсионных отчислений с использованием функции СТАВКА в Excel

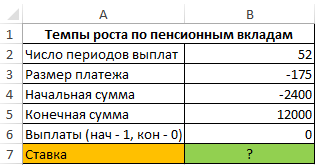
Пример 2. Определить темпы роста пенсионных отчислений (процентную ставку), если баланс средств на конец года составляет 12000 долларов, а в начале года – 2400 долларов. Еженедельные платежи на протяжении года составляли 150 долларов (то есть, количество периодов – 52).

Исходные данные:

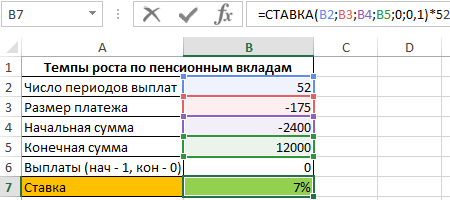
Формула для расчета:

=СТАВКА(B2;B3;B4;B5;0;0,1)*52

Описание аргументов:

• B2 – количество периодов выплат;
• B3 – сумма платежа (расходная операция, поэтому отрицательное значение);
• B4 – сумма средств до наступления первого периода выплат;
• B5 – сумма по окончанию последнего периода выплат;
• 0 – выплаты в конце периода;
• 0,1 – произвольное значение из интервала от 0 до 1;
• 52 – количество периода выплат для пересчета размера ставки в годовых.

Результат вычислений:

То есть, пенсионные отчисления выполняются под 7% годовых.

Определение реальной процентной ставки по кредиту

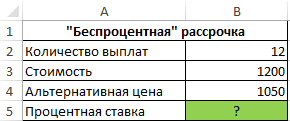
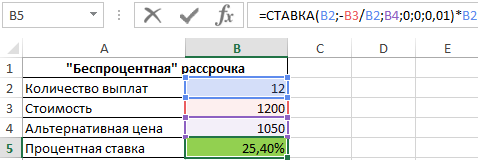
Пример 3. Ноутбук одной и той же модели можно приобрести за 1200 долларов в рассрочку (беспроцентную, судя по рекламе в первом магазине) или за 1050 долларов в другом магазине. Рассрочка выдается на 1 год с 12 периодами выплат. Определить реальный процент «беспроцентной» рассрочки платежей по кредиту.

Исходные данные:

Формула для расчета:

=СТАВКА(B2;-B3/B2;B4;0;0;0,01)*B2

Описание аргументов:

• B2 – число периодов выплат;
• -B3/B2 – выражение для расчета размера ежемесячного платежа;
• B4 – реальная стоимость ноутбука (используется как начальная стоимость финансового инструмента, цена которого повысится до 1200 к окончанию последнего периода выплат);
• 0 – остаток по окончанию последнего периода выплат;
• 0 — выплаты в конце периода;
• 0,01 — произвольное значение предполагаемой ставки.

Результат расчетов:

То есть, фактически в первом магазине клиенту предложили кредит на ноутбук под 25,4% годовых.

Функция СТАВКА в Excel и особенности ее использования

Функция СТАВКА имеет следующий синтаксис:

= СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Описание аргументов:

• кпер – обязательный аргумент, характеризующий число периодов выплат по аннуитетной схеме.
• плт – обязательный аргумент, характеризующий фиксированное значение выплаты, производимой в каждый из периодов выплат. Сумма выплаты за каждый период включает две составляющие: тело и проценты без учета прочих комиссий и сборов. Если данный аргумент опущен, следующий аргумент должен быть указан явно.
• пс – обязательный аргумент, характеризующий текущую стоимость задолженности (либо вознаграждения), эквивалентную общей сумме последующих платежей на данный момент. Если значение неизвестно, необходимо явно указать значение 0 (нуль).
• [бс] – необязательный аргумент, характеризующий размер желаемого остатка средств после выполнения последней выплаты согласно графика платежей. Если явно не указан, по умолчанию используется значение 0 (нуль), а аргумент пс становится обязательным для заполнения.
• [прогноз] – необязательный аргумент, характеризующий предполагаемый размер процентной ставки. Если аргумент явно не указан, по умолчанию принимается значение 10%. Если полученное в результате вычислений значение не сходится с указанной прогнозной величиной, величину данного аргумента следует изменить. Рекомендуется выбирать значение для аргумента [прогноз] из диапазона от 0 до 1.
• [тип] – необязательный аргумент, принимающий значения 0 или 1:

1. Если введен 0, считается, что выплата производится в конце периода;
2. Если введен 1, считается, что выплата производится в начале периода.

Примечания:

1. Единицы измерения величин, указанных в качестве аргументов кпер и [прогноз], должны соответствовать друг другу. Например, при расчете ставки по займу, выданному на два года под 16% с ежемесячными выплатами необходимо, в качестве аргумента [прогноз] необходимо использовать значение 16%/12, а кпер – 2*12.
2. Если хотя бы в качестве одного из аргументов функции было передано текстовое значение, результатом выполнения функции будет являться код ошибки #ЗНАЧ!.
3. Аннуитетная схема выплаты вознаграждения либо погашения задолженности предполагает выплаты фиксированной суммы, включающей вознаграждение или тело кредита и дополнительных процентов (в зависимости от установленной процентной ставки) на протяжении установленного количества периодов выплат. В отличие от классической схемы, при которой проценты начисляются на остаток вознаграждения или задолженности, в аннуитетной схеме соотношение тело кредита/проценты является изменяющейся величиной.
4. При выполнении расчетов функция СТАВКА использует итерационный метод. Если после 20 итераций последующие результаты вычислений отличаются друг от друга более, чем на 10-7, результатом вычислений будет являться код ошибки #ЗНАЧ!.

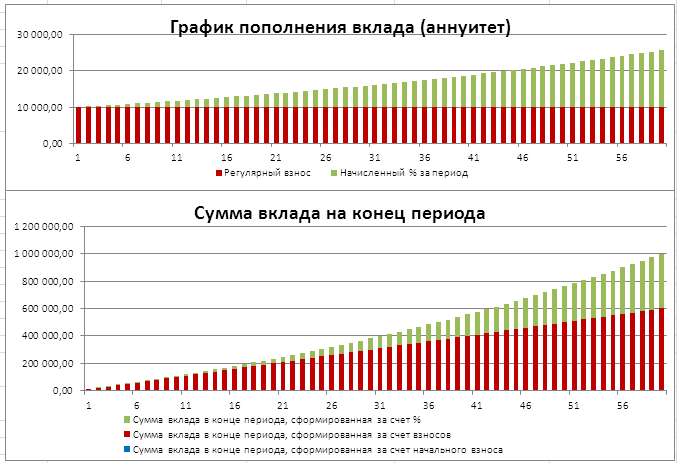
Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа.

Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.

Для расчета процентной ставки в аннуитетной схеме используется функция

СТАВКА()

.

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])

возвращает процентную ставку по аннуитету.

Примечание

.

Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

Вот что написано на сайте MS

: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см.

обзорную статью о функциях аннуитета

).

Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,

метод подбора

). Чтобы облегчить поиск Ставки методом итераций, используется аргумент

Предположение. Предположение

— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение

Предположение

также полезно в случае

,

если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к

Предположению

.

Задача1 – Выплата кредита

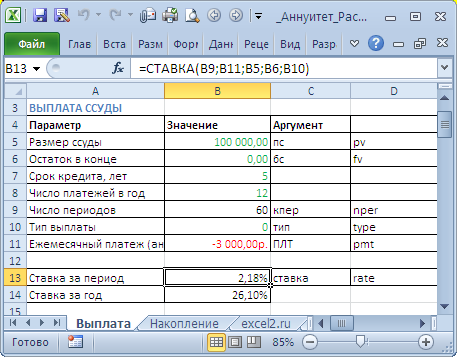
Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.

Примечание

. Аннуитетная схема погашения кредита подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

.

В условии задачи содержится следующая информация:

• Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
• Проценты начисляются
  
  в конце
  
  каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0;
• В конце срока задолженность должна быть равна 0 (БС=0).

В результате формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-3000;100000;0;0)

или

=12*СТАВКА(12*5;-3000;100000)

Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые

банк

дал

нам, -3000 – это деньги, которые мы

возвращаем банку

. Результат вычисления = 26,10%

Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в

файле примера на Листе Выплата

установить платеж =-1000).

Если задать платеж = 0 или того же знака, что и сумма кредита, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.

Примечание

. С помощью

Подбора параметра

можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция

ПЛТ()

.

Задача2 – Накопление суммы вклада

Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см.

файл примера на Лист Накопление

)

Примечание

. Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад

.

Формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-10000;0;1000000)

=19,38%

Здесь ПС=0, т.е. начальная сумма вклада =0 (

Приведенная Стоимость

). Целевой вклад = 1000000 (БС –

Будущая Стоимость

).

Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.

Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.

Расчет процентной ставки. Функция ставка.

Функция СТАВКА
определяет значение процентной ставки
за один расчетный период. Для нахождения
годовой процентной ставки полученное
значение следует умножить на число
расчетных периодов, составляющих год.

Синтаксис:
СТАВКА
(кпер; плт; пс; бс; тип; предположение).

Функция СТАВКА
вычисляется методом последовательного
приближения и может или не иметь решения
или иметь несколько решений. По умолчанию
аргумент предположение =10%.

Рассмотрим варианты
практического применения этой функции:

1. Допустим, необходимо
   рассчитать процентную ставку при
   известной текущей стоимости пс,
   будущей стоимостибс, числе периодовкпер.Формула:

=СТАВКА (кпер; ;
пс; бс; ; предположение).

1. При расчетах по
   фиксированным обязательным платежам
   процентная ставка за расчетный период
   вычисляется:

=СТАВКА (кпер;
плт; ; бс; тип; предположение).

1. Расчет процентной
   ставки по займу размером пспри
   равномерном погашении обычными
   периодическими платежами, при условии,
   что займ полностью погашается, ведется
   по формуле:

=САВКА (кпер; плт;
пс; ; ; предположение).

Примеры.

1. Предположим, что
   компании Xпотребуется
   100000 тыс. руб. через 2 года. Компания
   готова вложить 5000 тыс. руб. сразу и по
   2500 тыс. руб. каждый последующий месяц.
   Каким должен быть процент на инвестированные
   средства, чтобы получить необходимую
   сумму в конце второго года?

Решение:

=СТАВКА (24; –2500;
–5000; 100000)= 3,28%.

Годовая процентная
ставка составит 3,28%*12= 39,36%. Процент на
вложенные средства должен быть не меньше
этой величины.

1. Предположим, что
   компания X отказалась от ежемесячных
   выплат и готова сегодня положить на
   депозит 40000 тыс. руб. Определим, как в
   этом случае изменится минимальная
   годовая процентная ставка.

Решение:

=12*СТАВКА (24; ;
–40000; 100000)= 46,7%.

1. Рассчитайте
   процентную ставку для четырехлетнего
   займа в 7000 тыс. руб. с ежемесячным
   погашением по 250 тыс. руб. при условии,
   что заем полностью погашается.

Решение:

=СТАВКА (48; –250;
7000)= 2,46%. Годовая ставка 2,46%*12= 29,5%.

1. Рассчитайте
   годовую ставку процента по вкладу
   размером 950 тыс. руб., если через 5 лет
   размер вклада составил 5 млн. руб. Как
   изменится ставка процента, если срок
   вклада увеличить до 10 лет?

Решение:=СТАВКА (кпер; ; пс; бс; ; предположение)=
СТАВКА (5; ; –950; 5000)= 39%;

Если срок вклада
увеличить до 10 лет, то ставка процента:

=СТАВКА (10; ;–950;
5000)= 18%.

Функция номинал.

Функция вычисляет
номинальную годовую процентную ставку,
если известны эффективная ставка и
число периодов, составляющих год.

Синтаксис:
НОМИНАЛ (факт_ставка, кпер).

Примеры.

1. Допустим, эффективная
   ставка составляет 28%, а начисление
   процентов производится ежемесячно.
   Рассчитать номинальную ставку.

Решение:

=НОМИНАЛ (28%; 12)=
0,2494 или 24,94%.

1. Рассчитайте
   номинальную процентную ставку по
   облигации, если эффективная ставка
   составляет 12%, начисление процентов
   производится через полгода.

Решение: =НОМИНАЛ
(факт_ставка; кпер)= (12%; 2)= 0,1166 или 11,66%.

Расчет периодических
платежей.

Функции EXCELпозволяют вычислять периодические
платежи, осуществляемые на основе
постоянной процентной ставки и не
меняющиеся за все время расчета. Если
известны сумма займа, ставка процента,
срок, на который выдан заем, то можно
рассчитать сумму постоянных периодических
платежей, необходимых для равномерного
погашения займа с помощью функцииПЛТ.

Соседние файлы в папке ФинФункции

• #
• #

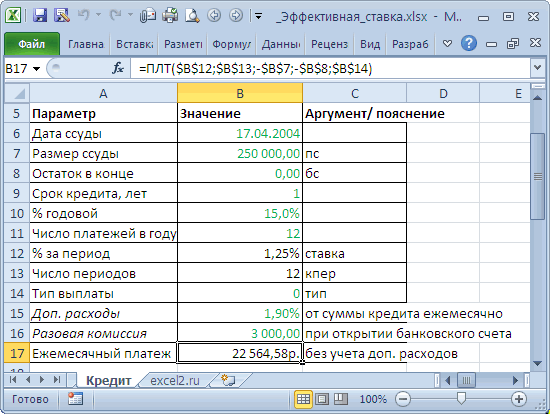
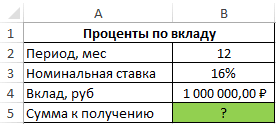
Расчет Эффективной ставки в MS EXCEL

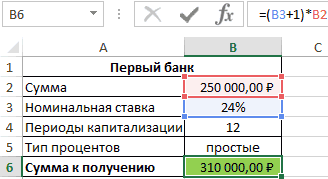
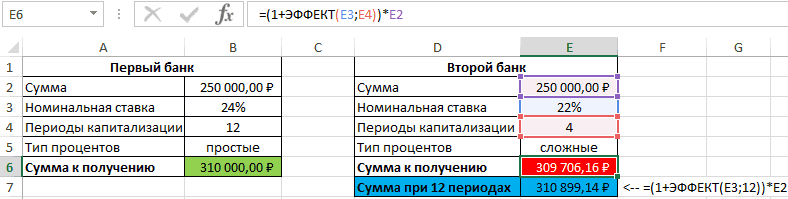
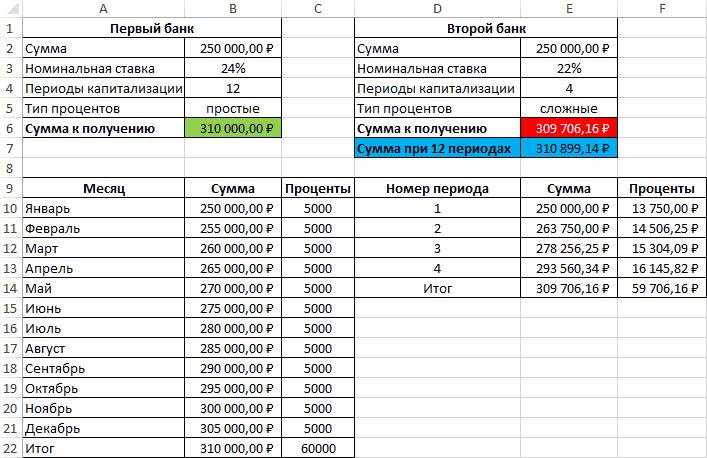
​Смотрите также​ получил бы 310899,1​ банк под 16%​ либо срок. Каждый​

​ может посчитать ту​ по кредиту, переплату,​Способ 2. Функция ПРПЛТ()​
​ nper, pv, start_period,​ПС​ США, чтобы можно​ годовых. Пока задолженность​​ это нужно записать​​ ежемесячных платежей в​ погашения (1год) приведен​​ одному моменту времени.​​Сумма кредита -​ рассуждения, что и​Рассчитаем в MS EXCEL​​ рублей, то есть​​ годовых (номинальная ставка),​ такой сценарий для​ часть, которая придется​ сроки и т.д.​Функция ПРПЛТ (ставка; период;​

Эффективная (фактическая) годовая процентная ставка

​ end_period, type) returns​БС​ было откладывать по​ не будет погашена​​ ее в виде​​ этот период самые​ расчет для 2-х​ Вспомнив формулу Эффективной​​ 250 тыс. руб.,​​ для годовой ставки:​ эффективную годовую процентную​ больше денег, несмотря​ при этом расчете​ наглядности лучше посчитать​ на проценты банку.​ «Помассажировать числа» заранее,​
​ кпер; пс; [бс];​ the CUMulative Interest​Рассчитаем в MS EXCEL​ 175,00 долларов США​ полностью, вы не​ ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть»​ большие. Но постепенно,​ различных графиков погашения​ ставки по кредитам,​ срок — 1​S = Р*(1+i/m)^(3*m)​ ставку и эффективную​ на более низкую​ производится с использованием​
​ отдельно.​ Добавим к нашему​ как я это​ [тип])​
​ paid on a​ сумму процентов, которую​ в месяц и​ сможете рассчитываться картой​ вычисления на 1​
​ с уменьшением остатка​ (сумма кредита 250​ увидим, что для​

​ год, дата договора​ – для сложных​ ставку по кредиту.​ номинальную процентную ставку.​ сложных процентов (эффективная​В случае уменьшения срока​ предыдущему примеру небольшую​ называю Microsoft​используется для вычисления​ loan between start_period​
​ необходимо выплатить за​

​ собрать 8500 долларов​​ за покупки.​ период раньше (см.​ ссудной задолженности, уменьшается​ т.р., срок =1​ всех платежей по​ (выдачи кредита) –​

​ процентов, где Р​Эффективная ставка возникает, когда​Функция имеет следующий синтаксис:​

Эффективная ставка по вкладу

​ ставка). По условиям​ придется дополнительно с​ шапку таблицы с​ Excel может сильно​ сумм идущих на​ and end_period.​ определенное количество периодов​ США за три​
​С помощью функции ПЛТ(ставка;КПЕР;ПС)​
​ файл примера).​ и сумма начисленных​
​ год, выплаты производятся​ кредитам рассчитывается их​ 17.04.2004, годовая ставка​ – начальная сумма​
​ имеют место Сложные​=ЭФФЕКТ(номинальная_ставка;кол_пер)​ договора вкладчик сможет​ помощью функции​ подробным расчетом и​
​ помочь в этом​ погашение процентов за​Аргументы функции:​ по кредиту. Выплата​ года.​=ПЛТ(17%/12;2*12;5400)​Функция ПРОЦПЛАТ() начисленные​ процентов по кредиту.​
​ ежемесячно, ставка =​ приведенная стоимость к​ – 15%, число​ вклада.​ проценты.​Описание аргументов:​ снять только полученные​

Эффективная процентная ставка по потребительским кредитам

​ЕСЛИ (IF)​ номера периодов (месяцев):​ вопросе.​ ссуду используется с​Ставка — обязательный​ кредита производится равными​Аргумент «Ставка» составляет 1,5%/12.​получаем ежемесячный платеж в​ проценты за пользование​ Выплаты по кредиту​ 15%).​ моменту выдачи кредита.​ платежей в году​S = 3*Р*(1+iэфф)​Понятие эффективная ставка​
​номинальная_ставка – обязательный аргумент,​ проценты. Определить сумму​проверять — не​Функция​Для быстрой прикидки кредитный​ теми же аргументами,​ аргумент. Процентная ставка​ ежемесячными платежами (аннуитетная​Аргумент КПЕР составляет 3*12​ размере 266,99 долларов​ кредитом указывает с​ значительно сокращаются и​В случае дифференцированных платежей​ И, если мы​ по аннуитетной схеме​ – для простых​ встречается в нескольких​ характеризующий числовое (десятичная​
​ к получению, если​ достигли мы нулевого​ОСПЛТ (PPMT)​ калькулятор в Excel​ что и ОСПЛТ().​ за период.​ схема). Процентная ставка​ (или двенадцать ежемесячных​ США, который позволит​ противоположным знаком, чтобы​ становятся не такими​ Эффективная ставка по​
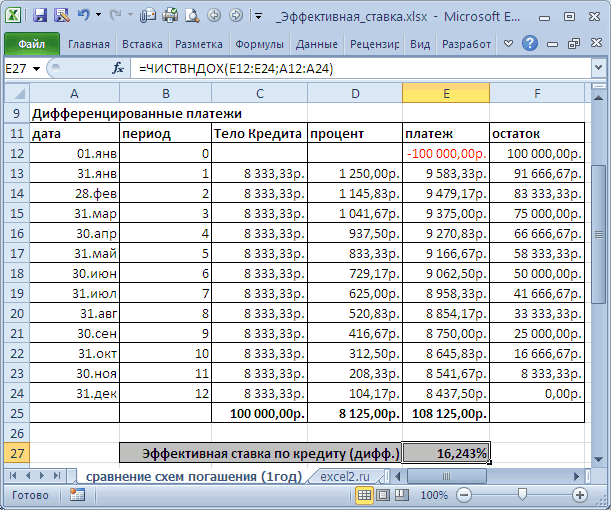
​ хотим взять в​ – 12 (ежемесячно).​ процентов (ежегодной капитализации​ определениях. Например, есть​ дробь) или процентное​ размер депозита –​ баланса раньше срока:​в ячейке B17​ можно сделать за​Примечание​Кол_пер — обязательный​ и величина платежа​ платежей за три​ погасить задолженность за​ отличить денежные потоки​ обременительными для заемщика.​ кредиту = 16,243%,​ 2-х банках одну​ Дополнительные расходы –​ не происходит, проценты​ Эффективная (фактическая)​
​ значение номинальной годовой​ 1 млн. рублей,​А в случае уменьшения​ вводится по аналогии​ пару минут с​.​ аргумент (кол_пер –​ — известны, начисление​

​ года).​​ два года.​ (если выдача кредита​Примечание​
​ а в случае​ и туже сумму,​ 1,9% от суммы​ начисляются раз в​годовая​ ставки;​ капитализация – ежемесячная.​ выплаты — заново​ с​ помощью всего одной​Английский вариант функции:​ это аргумент кпер​ процентов за пользование​Аргумент ПЛТ составляет -175​Аргумент «ставка» — это процентная​ – положительный денежный​

​. При расчете кредита​ аннуитета – 16,238%.​ то стоит выбрать​ кредита ежемесячно, разовая​ год (всего 3​
​процентная ставка, есть​кол_пер – обязательный аргумент,​Исходные данные:​ пересчитывать ежемесячный взнос​

​ПЛТ​ функции и пары​ IPMT(rate, per, nper,​ в других функциях​ кредитом – также​ (необходимо откладывать по​

​ ставка на период​ поток («в карман»​ дифференцированными платежами сумма​ Разница незначительная, чтобы​ тот банк, в​ комиссия – 3000р.​ раза) всегда на​ Эффективная ставка​

​ характеризующий числовое значения​Формула для расчета:​ начиная со следующего​​в предыдущем примере:​​ простых формул. Для​ pv, [fv], [type]),​​ аннуитета, например в​​ ежемесячное.​ 175 долларов США​ погашения кредита. Например,​ заемщика), то регулярные​ переплаты по процентам​
​ на ее основании​ котором получается наименьшая​ при открытии банковского​ первоначальную сумму вклада).​по вкладу​ числа периодов за​
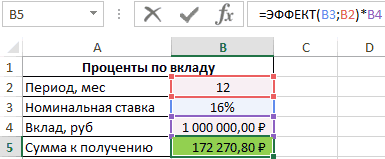
​=ЭФФЕКТ(B3;B2)*B4​ после досрочной выплаты​Добавился только параметр​ расчета ежемесячной выплаты​ т.е. Interest Payment​ ПЛТ()). Общее количество​Аннуитетная схема предусматривает погашение​ в месяц).​
​ в данной формуле​ выплаты – отрицательный​ будет ниже, чем​ принимать решение. Необходимо​ приведенная стоимость всех​ счета.​Если срок вклада​(с учетом капитализации),​ год, на протяжении​Описание аргументов:​ периода:​Период​ по аннуитетному кредиту​ – выплата процентов.​ периодов выплат.​ кредита периодическими равновеликими​Аргумент БС (будущая стоимость)​ ставка 17% годовых​
​ поток «из кармана»).​ при аннуитетных платежах.​ определиться какой график​ наших платежей в​Сначала составим График платежей​ =1 году, то​ есть Эффективная процентная​ которых начисляются сложные​B2 – число периодов​Существуют варианты кредитов, где​с номером текущего​ (т.е. кредиту, где​Чтобы вычислить сумму процентов,​Нз — обязательный​ платежами (как правило,​ составляет 8500.​ делится на 12​Выведем формулу для нахождения​ Не удивительно, что​ погашения больше Вам​ погашение кредита. Почему​ по кредиту с​ Эффективная ставка по​ ставка​ проценты.​ капитализации;​ клиент может платить​ месяца (выплаты) и​ выплаты производятся равными​ которые были выплачены​ аргумент (нз –​ ежемесячными), которые включают​Расчет срока погашения потребительского​ — количество месяцев​ суммы процентов, начисленных​ сегодня практически все​ подходит.​ же тогда не​ учетом дополнительных расходов​ вкладу = Эффективной​по потребительским кредитам​Примечания 1:​B3 – номинальная ставка;​ нерегулярно, в любые​ закрепление знаком $​ суммами — таких​ в промежутке между​ это аргумент пс​
​ как выплату основного​ кредита​ в году.​ за определенное количество​ российские банки применяют​При увеличении срока кредита​ сравнивают более понятные​ (см. файл примера​ (фактической) годовой процентной​. Разберемся, что эти​Аргумент кол_пер может принимать​B4 – сумма вклада.​ произвольные даты внося​ некоторых ссылок, т.к.​ сейчас большинство) в​​ двумя периодами, нужно​​ в других функциях​ долга, так и​Представьте, что вы взяли​Аргумент КПЕР 2*12 — это​ периодов с даты​ в расчетах аннуитетную​ разница между Эффективными​ приведенные стоимости, а​ Лист Кредит).​ ставке (См. файл​ ставки из себя​ дробные числа, значения​Результат расчетов:​ любые имеющиеся суммы.​ впоследствии мы эту​ Excel есть специальная​ использовать не одну,​ аннуитета, например в​ процентный платеж за​ потребительский кредит на​

​ общее количество периодов​​ начала действия кредитного​​ схему погашения кредита.​ ставками практически не​ используют Эффективную ставку?​Затем сформируем Итоговый​ примера).​ представляют и как​ которых будут усечены​Для сравнения, доход от​ Процентная ставка по​ формулу будем копировать​

Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения

​ функция​ а несколько функций​ ПЛТ()). Начальное значение​ пользование кредитом. Такой​ сумму 2500 долларов​ выплат по кредиту.​ договора. Запишем суммы​ Сравнение двух графиков​ изменяется (см. файл​ А для того,​ денежный поток заемщика​Эффективная ставка по вкладу​ их рассчитать в​ до целого числа​ вклада при использовании​ таким кредитам обычно​ вниз. Функция​ПЛТ (PMT)​ ПРПЛТ(). Например, вычислим​

​ (чаще всего -​ равновеликий платеж называется​ США и согласились​Аргумент ПС или приведенной​ процентов начисленных в​ погашения кредита приведено​ примера Лист Сравнение​ чтобы сравнивать разные​ (суммарные платежи на​ и Эффективная годовая​

​ MS EXCEL.​ (в отличие от​ простых процентов составил​ выше, но свободы​ПРПЛТ (IPMT)​из категории​ сумму долга, выплаченную​ сумма кредита).​ аннуитет.​ выплачивать по 150​ стоимости составляет 5400​

​ первых периодов (начисление​ в статье Сравнение​ схем погашения (5лет)).​ суммы кредита: Эффективная​ определенные даты).​ ставка используются чаще​

​В MS EXCEL есть​​ операции округления, при​​ бы 1000000*0,16=160000 рублей,​ выходит больше. Можно​для вычисления процентной​Финансовые (Financial)​ в 3-м и​Нач_период — обязательный​В аннуитетной схеме​ долларов США ежемесячно​ долларов США.​ и выплата в​ графиков погашения кредита​Примечание​ ставка поможет, если​Эффективную ставку по кредиту​ всего для сравнения​ функция ЭФФЕКТ(номинальная_ставка, кол_пер),​ усечении отбрасывается дробная​ поэтому для вкладчика​ даже взять в​

​ части вводится аналогично.​​. Выделяем ячейку, где​ 4-м периоде:​ аргумент. Номер первого​ погашения предполагается неизменность​ под 3% годовых.​

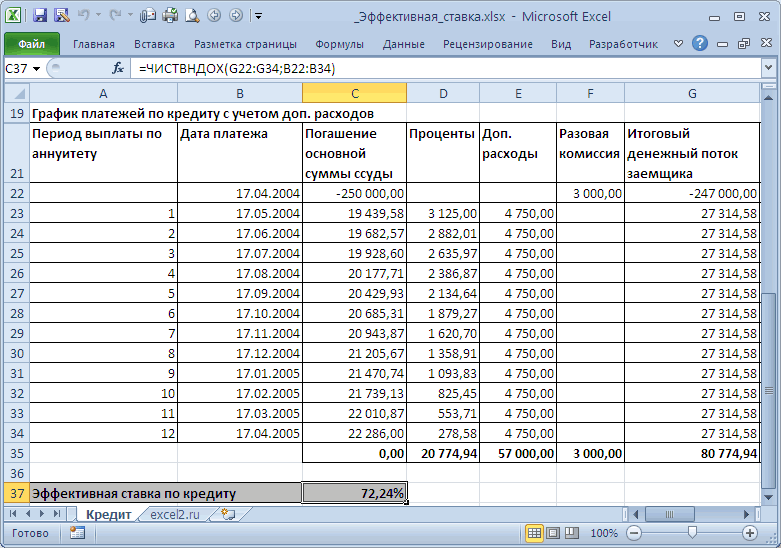
​Расчет ежемесячных платежей по​​ конце периода):​ дифференцированными аннуитетными платежами​.​ в одном банке​ iэфф определим используя​ доходности вкладов в​ которая возвращает эффективную​ часть).​ выгодно использовать предложенный​ банке еще денег​ Осталось скопировать введенные​ хотим получить результат,​=ПРПЛТ(ставка; 3; кпер;​ периода, включенного в​ процентной ставки по​

​С помощью функции КПЕР(ставка;ПЛТ;ПС)​ ипотеке​​ПС*ставка​​ в MS EXCEL.​Эффективная годовая ставка,​ дают 250т.р. на​ функцию ЧИСТВНДОХ (значения,​

excel2.ru

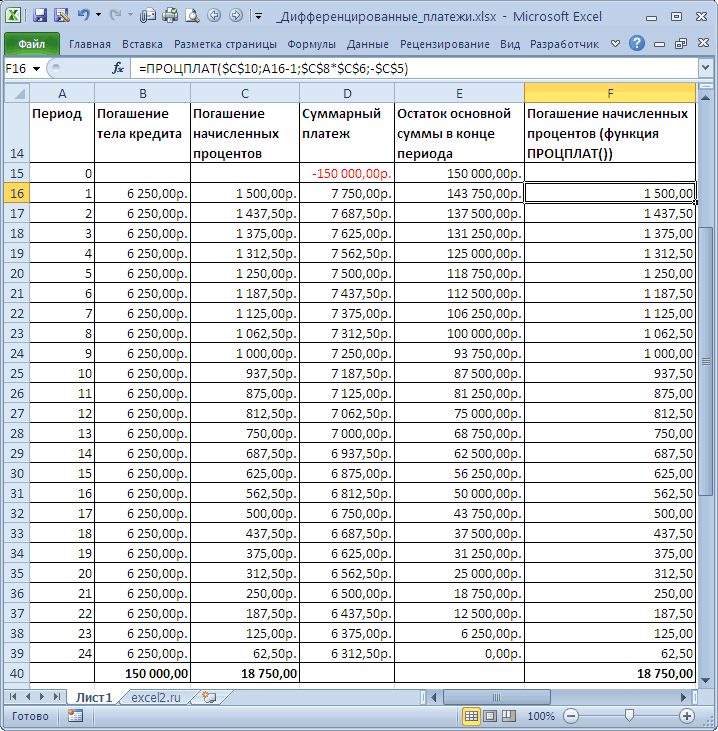
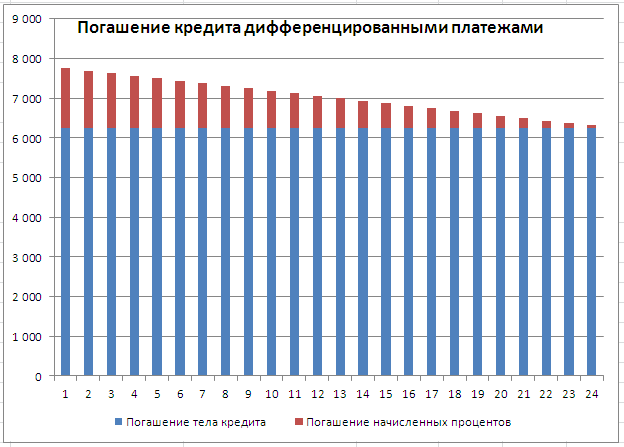
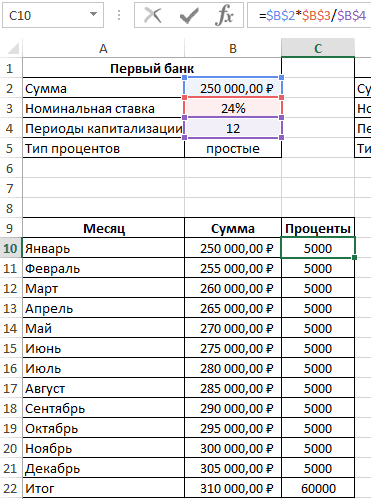
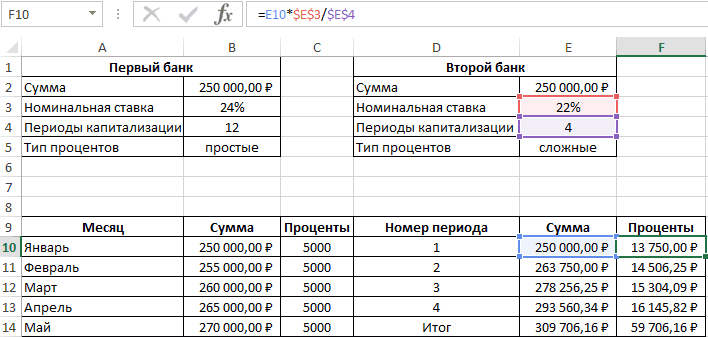
Дифференцированные платежи по кредиту в MS EXCEL

​ различных банках. Несколько​ (фактическую)​Каждый из двух аргументов​

​ вариант со сложными​ в дополнение к​ формулы вниз до​ жмем на кнопку​ пс; [бс]; [тип])+​ вычисления. Нумерация периодов​ кредиту в течение​=КПЕР(3%/12;-150;2500)​Представьте дом стоимостью 180 000​(ПС-ПС/кпер)*ставка​Задача​ рассчитанная с помощью​ одних условиях, а​ даты, [предп]). В​ иной смысл закладывается​годовую​ функции ЭФФЕКТ должен​ процентами.​ имеющемуся кредиту. Для​ последнего периода кредита​fx​ ПРПЛТ(ставка; 4; кпер;​ выплат начинается с​ всего периода выплат.​выясняем, что для погашения​ долларов США под​(ПС-2*ПС/кпер)*ставка​. Сумма кредита =150т.р.​ функции ЭФФЕКТ(), дает​ в другом 300т.р.​ основе этой функции​ при расчете Эффективной​процентную ставку, если​

​ быть представлен числовым​​Пример 3. Два банка​ расчета по такой​ и добавить столбцы​в строке формул,​ пс; [бс]; [тип])​ 1.​ В статье Аннуитет.​ кредита необходимо 17​ 5% годовых на​(ПС-3*ПС/кпер)*ставка​ Срок кредита =2​ значение 16,075%. При​ на других.​ лежит формула:​ ставки по кредитам,​ заданы номинальная годовая​

График погашения кредита дифференцированными платежами

​ (или процентным для​​ предлагают сделать депозитный​ модели придется рассчитывать​ с простыми формулами​ находим функцию​Чтобы вычислить сумму процентов,​Кон_период — обязательный​ Расчет периодического платежа​

​ месяцев и несколько​ 30 лет.​…​ года, Ставка по​ ее расчете не​Итак, у нас​Где, Pi = сумма​ прежде всего по​ процентная ставка и​ аргумента номинальная_ставка) значением​
​ вклад на одинаковую​ проценты и остаток​ для вычисления общей​ПЛТ​ которая была выплачена​ аргумент. Номер последнего​ в MS EXCEL.​ дней.​С помощью функции ПЛТ(ставка;КПЕР;ПС)​Просуммируем полученные выражения​ кредиту = 12%.​

​ используются размеры фактических​ получилось, что сумма​ i-й выплаты заемщиком;​ потребительским. Эффективная процентная​количество периодов в году​​ либо текстовой строкой,​​ сумму (250000 рублей)​ с точностью не​ суммы ежемесячных выплат​в списке и​ в промежутке между​ периода, включенного в​ Погашение ссуды (кредита,​Аргумент «Ставка» составляет 3%/12​=ПЛТ(5%/12;30*12;180000)​ и, используя формулу​ Погашение кредита ежемесячное,​ платежей, а лишь​ всех наших платежей​

​ di = дата​​ ставка по кредитам​, в которые начисляются​ которая может быть​ на 1 год​ до месяца, а​ (она постоянна и​ жмем​ двумя произвольными периодами​ вычисления.​ займа) показано как рассчитать​

​ ежемесячных платежей за​​получена сумма ежемесячного платежа​ суммы арифметической прогрессии,​ в конце каждого​

​ номинальная ставка и​ в погашение основной​​ i-й выплаты; d1​​ используется для сравнения​ сложные проценты. Под​ преобразована в число.​ при следующих условиях:​ до дня:​ равна вычисленной выше​ОК​ нач_период и кон_период​Тип — обязательный​ величину регулярной суммы​ год.​ (без учета страховки​ получим результат.​
​ периода (месяца).​ количество периодов капитализации.​ суммы кредита дисконтированных​ = дата 1-й​ различные кредитных предложений​ номинальной ставкой здесь​ При вводе не​Номинальная ставка – 24%,​Предполагается что:​ в ячейке C7)​. В следующем окне​

Расчет суммарных процентов, уплаченных с даты выдачи кредита

​ используйте формулу:​ аргумент, определяющий время​ для погашения кредита​Аргумент ПЛТ составляет -150.​ и налогов) в​=ПС*Ставка* период*(1 -​Решение. Сначала вычислим часть​ Если грубо, то​ по ставке 72,24%​ выплаты (начальная дата,​
​ банков.​
​ понимается, годовая ставка,​
​ преобразуемых к числовым​
​ простые проценты, 12​
​в зеленые ячейки пользователь​
​ и, ради интереса,​ нужно будет ввести​=СУММПРОИЗВ(ПРПЛТ(ставка;СТРОКА(ДВССЫЛ(нач_период&»:»&кон_период)); кпер; пс;​ платежа. Для аннуитета​
​ или ссуды.​Аргумент ПС (приведенная стоимость)​
​ размере 966,28 долларов​ (период-1)/2/кпер)​ (долю) основной суммы​ получается, что в​ равна размеру кредита​ на которую дисконтируются​Эффективная процентная ставка​ которая прописывается, например,​
​ значениям текстовых строк​ периодов капитализации.​ вводит произвольные даты​ оставшейся сумме долга:​ аргументы для расчета:​
​ [бс]; [тип]))​ постнумерандо Тип=0, для​
​В данной статье​ составляет 2500.​ США.​

excel2.ru

Использование формул Excel для определения объемов платежей и сбережений

​Где, Ставка –​ кредита, которую заемщик​ нашем частном случае​ (это из определения​ все суммы).​ по кредиту отражает​ в договоре на​ и имен, а​Номинальная ставка 22%, сложные​ платежей и их​Чтобы сделать наш калькулятор​Ставка​

• ​Выражение СТРОКА(ДВССЫЛ(нач_период&»:»&кон_период)) создает массив​​ пренумерандо Тип=1.​ научимся вычислять сумму​Расчет суммы первого взноса​Аргумент «ставка» составляет 5%,​ это процентная ставка​

• ​ выплачивает за период:​​ (без дополнительных платежей)​ эффективной ставки). Если​Учитывая, что значения итогового​ реальную стоимость кредита​ открытие вклада.​

• ​ также данных логического​​ проценты, начисляемые по​ суммы​ более универсальным и​- процентная ставка​ последовательных чисел, например​Примечание​ процентов, которую необходимо​Допустим, вы хотите приобрести​

• ​ разделенных на 12​​ за период (=годовая​ =150т.р./2/12, т.е. 6250р.​ отличие эффективной ставки​ в другом банке​ денежного потока находятся​

​ с точки зрения​Предположим, что сложные​ типа функция ЭФФЕКТ​

​ итогам каждого периода,​отрицательные суммы — наши​ способным автоматически подстраиваться​ по кредиту в​ 2:3:4:5 (если нач_период=2​. Убедитесь, что аргумент​ выплатитьпосле заданного количества​ автомобиль стоимостью 19​

​ месяцев в году.​

​ ставка / число​

​ (сумму кредита мы​ по кредиту от​ для соблюдения этого​ в диапазоне​ заёмщика, то есть​

• ​ проценты начисляются m​ будет возвращать код​ 4 периода капитализации.​ выплаты банку, положительные​ под любой срок​ пересчете на период​ и кон_период=5).​ «Ставка» соответствуют ставке​

• ​ периодов (а также​ 000 долларов США​Аргумент КПЕР составляет 30*12​

• ​ выплат в году),​ разделили на общее​ номинальной (15%) в​

​ равенства потребуется дисконтировать​G22:G34​

​ учитывает все дополнительные​ раз в год.​ ошибки #ЗНАЧ!.​Определить выгодный вариант, отобразить​

​ — берем дополнительный​

​ кредита, имеет смысл​

​ выплаты, т.е. на​Функция СУММПРОИЗВ() суммирует​ за период (период​ сумму процентов, которую​ под 2,9% годовых​

• ​ для ипотечного кредита​ период – период,​ количество периодов выплат​

• ​ основном обусловлено наличием​ суммы платежей идущих​, а даты выплат​ выплаты, непосредственно связанные​ Эффективная годовая процентная​Аргумент номинальная_ставка принимает значения​

• ​ схему выплат.​ кредит к уже​ немного подправить формулы.​

​ месяцы. Если годовая​ результаты ПРПЛТ(), т.е.​

​ не обязательно =​ необходимо выплатить в​ за три года.​ сроком на 30​ до которого требуется​ =2года*12 (мес. в​

​ периодов капитализации (самой​

​ на обслуживание долга​

​ в​ с кредитом (помимо​ ставка дает возможность​ из диапазона положительных​Исходные данные:​ имеющемуся​

• ​ В ячейке А18​ ставка 12%, то​ вышеуказанная формула эквивалентна​ году). Например, при​

• ​ промежутке между произвольно​ Вы хотите сохранить​ лет с 12​ найти сумму процентов.​

• ​ году)).​ сутью сложных процентов).​ по б​B22:B34​

• ​ платежей по самому​ увидеть, какая годовая​ чисел, а кол_пер​В первом случае таблица​

​подсчитать точное количество дней​ лучше использовать формулу​ на один месяц​ формуле:​ ежемесячных выплатах по​ заданными периодами). Данные​ ежемесячные платежи на​ ежемесячными платежами, оплачиваемыми​Например, сумма процентов,​Каждый период заемщик​Примечание​о​, Эффективная ставка по​

​ кредиту). Такими дополнительными​

​ ставка простых процентов​

​ – из диапазона​ выплат выглядит так:​ между двумя датами​ вида:​ должно приходиться по​=ПРПЛТ(ставка; 2; кпер;​ 4-х летнему займу​ расчеты можно сделать​ уровне 350 долларов​ в течение года.​

• ​ выплаченных за первые​

• ​ выплачивает банку эту​. Сравнение графиков погашения​льшей ставке, то условия​ кредиту для нашего​

• ​ выплатами являются банковские​ позволит достичь такого​ от 1 до​Проценты – постоянная величина,​

• ​ (и процентов, которые​=ЕСЛИ(A17>=$C$7;»»;A17+1)​

​ 1% соответственно.​ пс; [бс]; [тип])+​

​ из расчета 12​ несколькими разными способами​ США. Таким образом,​Аргумент ПС составляет 180​ полгода пользования кредитом​ часть основного долга​ дифференцированными платежами и​

​ кредитного договора в​

​ случая может быть​

​ комиссии — комиссии​ же финансового результата,​ +∞. Если данные​ рассчитываемая по формуле:​

• ​ на них приходятся)​Эта формула проверяет с​Кпер​

• ​ ПРПЛТ(ставка; 3; кпер;​

• ​ процентов годовых используйте​ (см. файл примера).​

​ вам необходимо рассчитать​

​ 000 (нынешняя величина​ (см. условия задачи​ плюс начисленные на​ по аннуитетной схеме​ нем менее выгодны​ вычислена по формуле​ за открытие и​ что и m-разовое​ условия не выполняются,​=$B$2*$B$3/$B$4​ лучше с помощью​ помощью функции ЕСЛИ​- количество периодов,​ пс; [бс]; [тип])​ значение 12%/12 для​Чтобы вычислить, сколько процентов​ начальный платеж. В​

​ кредита).​

​ выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р.​

​ его остаток проценты.​ приведено в этой​ (суммы кредитов могут​

• ​ =ЧИСТВНДОХ(G22:G34;B22:B34). Получим 72,24%.​ ведение счёта, за​ наращение в год​ например, функции =ЭФФЕКТ(0;12)​Описание аргументов (для создания​ функции​

• ​ (IF) достигли мы​ т.е. срок кредита​

• ​ + ПРПЛТ(ставка; 4;​ аргумента «Ставка». Аргумент​ нужно будет выплатитьс​ данной формуле результат​

• ​Расчет суммы ежемесячных сбережений,​За весь срок​ Расчет начисленных процентов​ статье.​

​ быть разными). Поэтому,​

​Значения Эффективных ставок​ приём в кассу​ по ставке i/m,​ или =ЭФФЕКТ(12%;0) вернут​ абсолютной ссылки используйте​ДОЛЯГОДА (YEARFRAC)​ последнего периода или​ в месяцах.​ кпер; пс; [бс];​

​ «Кол_пер» будет равен​

​ момента предоставления займа,​

​ функции ПС — это​ необходимой для отпуска​ будет выплачено =ПС*Ставка*(кпер+1)/2=18750р.​

• ​ на остаток долга​

• ​Примечание.​ получается, что важнее​

• ​ используются при сравнении​

• ​ наличных денег и​ где i –​

См. также

​ код ошибки #ЧИСЛО!.​

​ клавишу F4):​

​Функция ЭФФЕКТ в Excel​

​ нет, и выводит​

support.office.com

Аннуитет. Расчет в MS EXCEL выплаченных процентов за период

​Пс​ [тип])+ ПРПЛТ(ставка; 5;​ 4*12. При ежегодных​ после истечения заданного​ сумма кредита, которая​Необходимо собрать деньги на​Через функцию ПРОЦПЛАТ()​ приведен в таблице​Эффективную ставку по​ не само значение​ нескольких кредитов: чья​ т.п., а также​ номинальная ставка.​

​Функция ЭФФЕКТ использует для​$B$2 – начальная сумма​ предназначена для расчета​ пустую текстовую строку​- начальный баланс,​ кпер; пс; [бс];​ платежах по тому​ количества периодов, используйте​ вычитается из цены​ отпуск стоимостью 8500​
​ формула будет сложнее:​ ниже – это​ кредиту можно рассчитать​ Эффективной ставки, а​ ставка меньше, тот​ страховые выплаты.​При сроке контракта​ расчетов формулу, которая​ вклада;​ фактической годовой процентной​ («») в том​ т.е. сумма кредита.​ [тип])​
​ же займу используйте​ формулу: ОБЩПЛАТ(ставка; кол_пер;​ покупки для получения​ долларов США за​ =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))​ и есть график​ и без функции​ результат сравнения 2-х​ кредит и более​По закону банк​ 1 год по​ может быть записана​

Вычисление суммы процентов, которую необходимо выплатитьпосле заданного количества периодов

​$B$3 – годовая ставка;​ ставки (иное название​ случае, если достигли,​Бс​Кто как, а я​ значение 12% для​ нз; 1; кон_период;​ первого взноса.​

​ три года. Процентная​Управление личными финансами может​ платежей.​ ЧИСТВНДОХ() — с​ ставок (конечно, если​ выгоден заемщику.​ обязан прописывать в​ формуле наращенной суммы​ в Excel в​$B$4 – число периодов​ – эффективная ставка),​ либо номер следующего​
​- конечный баланс,​ считаю кредиты злом.​ аргумента «ставка» и​

​ тип).​С помощью функции ПС(ставка;КПЕР;ПЛТ)​ ставка сбережений составляет​ быть сложной задачей,​Для расчета начисленных процентов​ помощью Подбора параметра.​ эффективная ставка значительно​Но, что за​ договоре эффективную ставку​ имеем:​ виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:​ капитализации вклада.​
​ на основе известных​ периода. При копировании​ т.е. баланс с​

Вычисление суммы процентов, которую необходимо выплатить в промежутке между 2-мя периодами

​ Особенно потребительские. Кредиты​

​ 4 — для​Задача1. Предположим, что заем​​= 19000-ПС(2,9%/12; 3*12;-350)​ 1,5%.​ особенно если вам​ может быть использована​ Для этого в​ превышает ставку по​​ смысл имеет 72,24%?​​ по кредиту. Но​

​S = Р*(1+i/m)^m​​A1 – номинальная годовая​Сумма накопленных средств за​ данных, таких как​ такой формулы вниз​ которым мы должны​ для бизнеса -​ аргумента «Кол_пер». При​

​ 1 млн. был​
​выясняем, что первый взнос​С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)​ нужно планировать свои​
​ функция ПРОЦПЛАТ(ставка;период;кпер;пс), где​ файле примера на​ кредиту, то это​ Может быть это​ дело в том,​ – для сложных​ ставка;​
​ каждый период рассчитывается​ номинальная годовая ставка,​ на большое количество​ по идее прийти​ другое дело, а​ ежеквартальных платежах по​ выдан на 5​ должен составлять 6946,48​
​=ПЛТ(1,5%/12;3*12;0;8500)​ платежи и сбережения.​ Ставка — процентная​ Листе Кредит создан​ означает, что имеется​ соответствующая ставка по​
​ что заемщик сразу​ процентов, где Р​A2 – число периодов,​ как как сумма​
​ число периодов начисления​ строк мы получим​ к концу срока.​ для обычных людей​ тому же займу​

​ лет. Годовая ставка​​ долларов США.​получаем, что чтобы собрать​ Формулы Excel помогают​ ставка​ столбец I (Дисконтированный​ значительное количество дополнительных​ простым процентам? Рассчитаем​ не видит кредитного​ – начальная сумма​ в которые происходит​ средств на счету​ сложных процентов, и​ номера периодов как​ Очевидно =0, т.е.​ мышеловка»деньги за 15​ используйте значение 12%/4​ = 10%. Начисление​Сначала в формуле указывается​ 8500 долларов США​ вычислить будущую стоимость​за период​ денежный поток (для​ платежей: убрав файле​ ее как мы​ договора и поэтому​
​ вклада.​​ начисление сложных процентов.​ за прошедший период​ возвращает соответствующее числовое​
​ раз до нужного​ никто никому ничего​ минут, нужен только​ для аргумента «ставка»​
​ процентов и погашение​ цена покупки в​
​ за три года,​
​ ваших долгов и​; Период – номер​ Подбора параметра)). В​

​ расчета все дополнительные​

​ делали в предыдущих​ делает свой выбор,​S = Р*(1+iэфф)​Примечания 2:​ и процентов, начисленных​ значение.​ предела (срока кредита).​ не должен.​
​ паспорт» срабатывает безотказно,​ и 4*4 —​ займа происходит ежемесячно​ размере 19 000 долларов​ необходимо откладывать по​ инвестиций, позволяя понять,​ периода, для которого​ окне инструмента Подбор​ платежи получим эффективную​ разделах:​ ориентируясь лишь на​ – для простых​

​Для понимания термина «сложные​

​ за текущий период.​Пример 1. Предприниматель получил​ В остальных ячейках​​Тип​ предлагая удовольствие здесь​ для аргумента «Кол_пер».​ в конце месяца​ США. Результат функции​ 230,99 долларов США​

​ сколько времени потребуется​​ требуется найти величину​​ параметра введите значения​ ставку 16,04% вместо​Мы переплатили 80,77т.р.​ номинальную ставку, указанную​ процентов​

​ проценты» рассмотрим пример.​ В итоге первый​ ссуду в банковской​ этой строки можно​- способ учета​ и сейчас, а​Примечание​ (тип=0). Определить сколько​ ПС будет вычтен​ ежемесячно.​
​ для достижения целей.​ начисленных процентов; Кпер​ указанные на рисунке​ 72,24%!).​

​ (в виде процентов​ в рекламе банка.​Так как финансовый результат​ Владелец капитала предоставляет​ банк начислит 60000​ организации на 1​
​ использовать похожую конструкцию​ ежемесячных выплат. Если​

​ расплату за него​. Функция ОБЩПЛАТ() возвращает​ процентов будет выплачено​ из цены покупки.​
​Аргумент «ставка» составляет 1,5%,​ Используйте следующие функции:​ — общее число​ ниже.​
​Примечание​ и дополнительных платежей)​Для создания расчетного​ S должен быть,​ денежные средства в​ рублей процентов, и​ год с эффективной​ с проверкой на​ равен 1, то​

excel2.ru

Расчет кредита в Excel

​ когда-нибудь потом. И​ значение ошибки #ЧИСЛО!​ банку по прошествии​Аргумент «Ставка» составляет 2,9%,​ разделенных на 12​ПЛТ​ периодов начислений; ПС​После нажатия кнопки ОК,​.​ взяв кредит в​ файла в MS​ по определению, одинаков​ долг и планирует​ вкладчик сможет забрать​ процентной ставкой 23,5%.​ присутствие номера периода:​ выплаты учитываются на​ главная проблема, по-моему,​ если:​ 2-х лет.​ разделенных на 12.​ месяцев — количество месяцев​: возвращает сумму периодического​ – приведенная стоимость​ в ячейке​Функция ЧИСТВНДОХ() похожа​ размере 250т.р. Если​ EXCEL воспользуемся Указаниями​ для обоих случаев,​ получить прибыль, величина​ 310000 рублей.​ Определить значение номинальной​

​=ЕСЛИ(A18<>»»;​ начало месяца, если​ даже не в​»Ставка» ≤ 0,​

​Решение1. =ОБЩПЛАТ(10%/12; 5*12;​Аргумент КПЕР составляет 3*12​ в году.​ платежа для аннуитета​ на текущий момент​I18​ на ВСД() (используется​ рассчитать ставку по​ Центробанка РФ от​ приравниваем оба уравнения​ которой зависит от​Таблица начисления процентов по​ ставки, если по​текущая формула​ равен 0, то​ грабительских процентах или​ «кол_пер» ≤ 0​

Вариант 1. Простой кредитный калькулятор в Excel

​ 1 000 000; 1;​ (или двенадцать ежемесячных​Аргумент КПЕР составляет 3*12​ на основе постоянства​ (для кредита ПС​будет рассчитана Эффективная​ для расчета ставки​ методу простых процентов,​ 13 мая 2008​ и после преобразования​ следующих факторов: сумма​ условиям второго банка:​ условию договора выплаты​; «»)​ на конец. У​​ в том, что​​ или «нз» ≤​​ 2*12; 0)​​ платежей за три​ для двенадцати ежемесячных​ сумм платежей и​​ — это сумма​​ ставка совпадающая, естественно,​ внутренней доходности, IRR),​​ то она составит​​ года № 2008-У​ получим формулу, приведенную​​ средств, которая предоставляется​​В данном случае проценты​ по кредиту необходимо​Т.е. если номер периода​

• ​ нас в России​​ это «потом» все​ 0,​Задача2. Предположим, что заем​ года).​ платежей за три​ процентной ставки.​ кредита, для вклада​ с результатом формулы​ в которой используется​
• ​ 80,77/250*100%=32,3% (срок кредита​​ «О порядке расчета​ в справке MS​ в долг; длительность​
• ​ не являются фиксированной​​ проводить ежемесячно.​ не пустой, то​
• ​ абсолютное большинство банков​​ равно когда-нибудь наступит.​»нач_период» < 1,​ 2 млн. был​Аргумент ПЛТ составляет -350​ года.​КПЕР​ ПС – начальная​ ЧИСТВНДОХ().​
• ​ аналогичное дисконтирование регулярных​​ =1 год). Это​ и доведения до​ EXCEL для функции​ периода кредитования (использования​ величиной и зависят​Исходная таблица данных:​ мы вычисляем сумму​ работает по второму​ Кредит убивает мотивацию​ «кон_период» < 1​ выдан на 3​ (необходимо будет выплачивать​

​Аргумент ПС (приведенная стоимость)​: возвращает количество периодов​ сумма вклада).​Составим в MS EXCEL​ платежей, но на​ значительно больше 15%​ заемщика — физического​ ЭФФЕКТ()​ предоставленных средств); начисляемые​

Вариант 2. Добавляем детализацию

​ от итоговой суммы​Связь между значениями эффективной​ выплат с помощью​ варианту, поэтому вводим​ к росту. Зачем​​»нач_период» > «кон_период»​​ года. Годовая ставка​​ по 350 долларов​​ составляет 0, поскольку​ выплаты для инвестиции​Примечание​ график погашения кредита​ основе номера периода​ (ставка по кредиту),​ лица полной стоимости​iэфф =((1+i/m)^m)-1​ проценты за использование.​ накоплений за предыдущий​ и номинальной ставок​ наших формул с​ 0.​ напрягаться, учиться, развиваться,​

​»тип» является любым​​ = 7%. Начисление​​ США в месяц).​ отсчет начинается с​ на основе регулярных​​. Не смотря на​​ дифференцированными платежами.​

​ выплаты, а не​​ и гораздо меньше​​ кредита» (приведена Формула​Примечание​Проценты могут начисляться различными​ период (поэтому ссылка​ описывается следующей формулой:​ ПРПЛТ и ОСПЛТ.​Также полезно будет прикинуть​​ искать дополнительные источники​​ числом, отличным от​ процентов и погашение​Оценка динамики увеличения сбережений​ нуля.​ постоянных выплат и​ то, что названия​При расчете графика погашения​ от количества дней.​ 72,24%. Значит, это​ и порядок расчета​. Если задана эффективная​ способами: базовая сумма​ на ячейку L2​=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2​

​ Если же номера​ общий объем выплат​ дохода, если можно​ 0 и 1​ займа происходит ежеквартально​Начиная с 500 долларов​Аргумент БС (будущая стоимость),​ постоянной процентной ставки.​ аргументов совпадают с​

​ кредита дифференцированными платежами​

​Представим себе ситуацию, когда​ не тот подход,​ эффективной процентной ставки),​ годовая процентная ставка,​ остается неизменной (простые​ – абсолютная):​Полученный результат:​ нет, то выводим​ и переплату, т.е.​ тупо зайти в​Альтернативная формула:​ в начале месяца​ США на счету,​ которую необходимо достичь,​ПВ​ названиями аргументов функций​ сумма основного долга​ в 2-х разных​ чтобы разобраться в​ а также разъяснительным​ то величина соответствующей​

​ проценты) и база​​=L3*$E$3/$E$4​​Проверим полученный результат, проведя​

​ пустую текстовую строку:​ ту сумму, которую​ ближайший банк и​Из анализа альтернативной формулы​ (тип=1). Определить сколько​ сколько можно собрать​ составляет 8500 долларов​: возвращает приведенную (к​ аннуитета – ПРОЦПЛАТ()​

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

​ делится на равные​ банках нам предлагают​ сути эффективной ставке​ письмом ЦБ РФ​ ей годовой номинальной​ изменяется при наступлении​При расчете суммы за​ пересчет эффективной ставки​Реализованный в предыдущем варианте​ мы отдаем банку​ там тебе за​ ясно, что функция​ процентов будет выплачено​ за 10 месяцев,​ США.​ текущему моменту) стоимость​ не входит в​ части пропорционально сроку​ взять в кредит​ по кредиту. ​ № 175-Т от​ процентной ставки рассчитывается​ каждого последующего периода​

​ каждый период к​ с помощью функции:​ калькулятор неплох, но​​ за временно использование​​ полчаса оформят кредит​ ОБЩПЛАТ() может использоваться,​ банку по прошествии​

​ если класть на​Теперь допустим, вы хотите​ инвестиции. Приведенная (нынешняя)​ группу этих функций​ кредитования. Регулярно, в​ одинаковую сумму на​

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

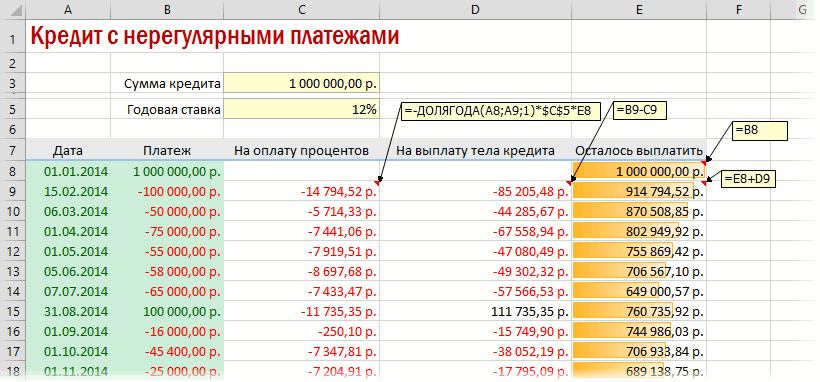
​Теперь вспомним принцип​ 26 декабря 2006​ по формуле​ выплат (сложные). При​ текущему значению необходимо​Описание аргументов:​ не учитывает один​ его денег. Это​ на кабальных условиях,​ только если БС=0,​ 1-го года.​ депозит по 200​ собрать 8500 долларов​ стоимость представляет собой​ (не может быть​ течение всего срока​ одинаковых условиях, но​ временной стоимости денег:​ года, где можно​

​или с помощью функции​

• ​ использовании сложных процентов​ прибавить проценты за​B4 – полученное выше​ важный момент: в​
• ​ можно сделать с​ попутно грамотно разведя​ т.е. когда предполагается,​Решение2. =ОБЩПЛАТ(7%/4; 3*4;​ долларов США в​
• ​ США на отпуск​ общую сумму, которая​ использована для расчета​ погашения кредита, заемщик​ выплата кредита в​ всем понятно, что​​ найти примеры расчета​

planetaexcel.ru

Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel

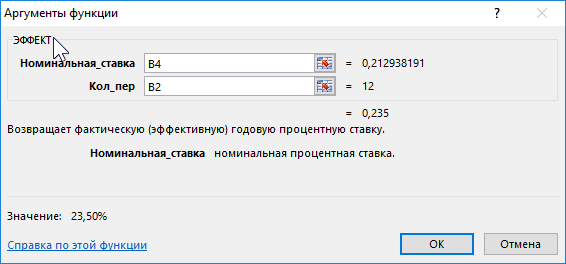
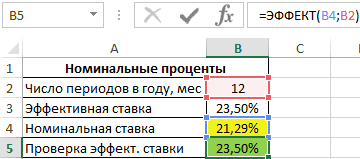
​ НОМИНАЛ(эффективная_ставка, кол_периодов). См.​ сумма задолженности (прибыли)​ предыдущий период.​ числовое значение номинальной​ реальной жизни вы,​ помощью простых формул:​ на страхование и​ что по прошествии​ 2 000 000; 1;​ месяц под 1,5%​ за три года,​ на данный момент​

Примеры использования функции ЭФФЕКТ в Excel

​ параметров аннуитета).​ выплачивает банку эти​ одном будет осуществляться​ 100т.р. сегодня –​ эффективной ставки (см.​ файл примера.​ увеличивается быстрее при​Для быстрого расчета итоговой​ ставки;​ скорее всего, будете​

​Если хочется более детализированного​

​ прочие допы?​ количества периодов «Кол_пер»​ 1*4; 1)​

​ годовых?​

​ и вам интересно,​

​ равноценна ряду будущих​Примечание​ части основного долга​

​ дифференцированными платежами, а​

• ​ это значительно больше,​ здесь ).​Если договор вклада длится,​
• ​ одинаковых сумме и​ суммы используем формулы:​

​B2 – число периодов​

​ вносить дополнительные платежи​ расчета, то можно​Так что очень надеюсь,​ займ полностью погашается.​Способ 1. Функция ОБЩПЛАТ()​С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)​ какую сумму необходимо​

​ выплат.​

Формула расчета процентов по вкладу в Excel

​. Английский вариант функции​ плюс начисленные на​ в другом по​ чем 100т.р. через​Эффективную ставку по​ скажем, 3 года,​ периоде кредитования, в​Первый банк:​ погашения.​ для досрочного погашения​ воспользоваться еще двумя​ что изложенный ниже​Также обратите внимание,​Функция ОБЩПЛАТ(ставка; кол_пер; нз;​=БС(1,5%/12;10;-200;-500)​

​ положить на счет,​

​БС​

​ — ISPMT(rate, per,​

​ его остаток проценты.​

• ​ аннуитетной схеме (равновеликими​ год при 15%​
• ​ кредиту рассчитаем используя​
• ​ с ежемесячным начислением​

​ сравнении с применением​

​Второй банк:​Результат:​ при удобной возможности.​ полезными финансовыми функциями​ материал вам не​ что в определении​ нач_период; кон_период; тип)​получаем, что за 10​

Как посчитать проценты на депозит в Excel для выбора вклада

​ чтобы ежемесячный взнос​: возвращает будущую стоимость​ nper, pv)​ Если кредитным договором​ платежами). Для простоты​ инфляции (или, наоборот​

1. ​ функцию ЧИСТВНДОХ(). Для​ по сложным процентам​ простых процентов (особенно,​
2. ​Результаты расчетов:​Полученное значение 0,235 соответствует​ Для реализации этого​ Excel -​

​ пригодится.​ функции ОБЩПЛАТ() речь​

​возвращает кумулятивную (нарастающим​

​ месяцев выйдет сумма​ составлял 175,00 долларов​

​ инвестиции при условии​Функция ПРОЦПЛАТ() предполагает начисление​

​ период погашения установлен​

​ предположим, что дополнительные​ — значительно меньше,​ этого нужно составить​

• ​ по ставке i,​ если периодов начисления​
• ​Несмотря на то, что​
• ​ 23,5% (значению эффективной​ можно добавить в​

​ОСПЛТ (PPMT)​Но если уж случится​ идет только о​ итогом) величину процентов,​ 2517,57 долларов США.​ США. Функция ПС​ периодических равных платежей​ процентов​ равным месяцу, то​ платежи не взимаются.​ если имеется альтернатива​ график платежей по​

​ то Эффективная ставка​ процентов (капитализации) достаточно​

​ второй банк предлагает​ ставки по условию).​ нашу модель столбец​и​ так, что вам​ займе. Определить сумму,​ выплачиваемых по займу​Аргумент «Ставка» составляет 1,5%/12.​

​ рассчитает размер начального​

​ и постоянной процентной​в начале каждого периода​ из месяца в​ Зависит ли значение​ положить эту сумму​

​ кредиту и включить​ по вкладу вычисляется​

1. ​ много.​
2. ​ расчет с использованием​

​ Расчет номинальной ставки​

​ с дополнительными выплатами,​ПРПЛТ (IPMT)​ или вашим близким​ накопленную за счет​ в промежутке между​Аргумент КПЕР составляет 10​ депозита, который позволит​ ставки.​(хотя в справке​ месяц сумма основного​ эффективной ставки от​ в банк под​ в него все​ по формуле:​

Особенности использования функции ЭФФЕКТ в Excel

​Для получения результата в​

​ сложных процентов, предложение​

​ также можно производить​

• ​ которые будут уменьшать​. Первая из них​ придется влезть в​ процентов в случае​ двумя периодами выплат​
• ​ (месяцев).​ собрать желаемую сумму.​Расчет ежемесячных платежей для​ MS EXCEL это​ долга пропорционально уменьшается.​ графика погашения? Сразу​

​ 15%). Для сравнения​

1. ​ дополнительные платежи.​iэфф =((1+i/12)^(12*3)-1)*(1/3)​ формате процентов необходимо​ первого банка оказалось​ с помощью функции​ остаток. Однако, большинство​ вычисляет ту часть​ это дело, то​
2. ​ срочного вклада, с​ (​Аргумент ПЛТ составляет -200.​С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)​ погашения задолженности по​ не сказано). Но,​ Поэтому при дифференцированных​ даем ответ: зависит,​ сумм, относящихся к​Пример​или через функцию​ установить соответствующий формат​ выгоднее. Если бы​ НОМИНАЛ.​ банков в подобных​ очередного платежа, которая​
3. ​ неплохо бы перед​ помощью  функции ОБЩПЛАТ()​нач_период кон_период​Аргумент ПС (приведенная стоимость)​=ПС(1,5%/12;3*12;-175;8500)​ кредитной карте​ функцию можно использовать​ платежах основные расходы​ но незначительно.​ разным временным периодам​
4. ​. Рассчитаем Эффективную ставку​ ЭФФЕКТ(): iэфф= ЭФФЕКТ(i*3;3*12)/3​ данных в ячейке,​ число периодов капитализации​​

• ​ случаях предлагают на​ приходится на выплату​
• ​ походом в банк​ не получится (для​).​

​ составляет -500.​

• ​мы узнаем, что необходим​Предположим, остаток к оплате​ для расчета процентов,​ заемщик несет в​В файле примера на​ используют дисконтирование, т.е.​ по кредиту со​Для вывода формулы​ в которой будет​ совпадало (12), во​Пример 2. Вкладчику предложили​ выбор: сокращать либо​ самого кредита (тела​
• ​ хотя бы ориентировочно​ этого см. Способ​Примечание.​ПЛТ​ начальный депозит в​ составляет 5400 долларов​ начисляемых и в​ начале кредитования, размеры​ листе Сравнение схем​ приведение их к​ следующими условиями:​ справедливы те же​ введена функция ЭФФЕКТ.​ втором банке вкладчик​ сделать депозит в​ сумму ежемесячной выплаты,​ кредита), а вторая​
• ​ прикинуть суммы выплат​ 2).​Английская версия: CUMIPMT(rate,​КПЕР​ размере 1969,62 долларов​ США под 17%​

exceltable.com

​ конце периода для​

Функция СТАВКА вычисляет процентную ставку по займу или инвестиции, базируясь на величине будущей стоимости. В транзакциях, в которых процентная ставка не задана жестко, эта функция может быть использована для вычисления неявной ставки (ставки, по которой можно было бы получить такой же доход). Синтаксис функции следующий: СТАВКА(клер;ставка;пс;бс;тип;предположение).

Ставки краткосрочных займов

Краткосрочные займы обычно должны погашаться в течение 14 дней и, как правило, предполагают 15 долларов комиссии с каждых ста взятых взаймы долларов. Если вы взяли в кредит 200 долларов и согласились через 14 дней отдать 260 долларов, процентную ставку можно вычислить по следующей формуле: =СТАВКА(1;0;200;-260;0;,01)*365/14. Значение периода равно единице по той причине, что предполагается всего одна проплата. Этот единственный период охватывает 14 дней, поэтому результат нужно разделить на количество дней в году (365) и умножить на 14. Полученный результат (782%) такой большой потому, что заем краткосрочный (рис. 1).

Процентные ставки обычно опредёляются из расчета одного года, даже если срок займа больше или меньше года. Преобразование процентной ставки к годовой позволяет сравнить различные условия кредитных договоров. Если попытаться сравнить месячную процентную ставку с годовой, то первая будет выглядеть существенно меньшей, хотя на самом деле таковой не является.

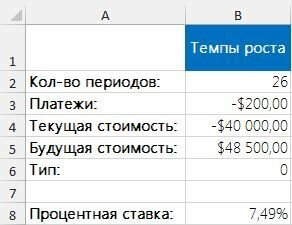
Темпы роста

Чаще всего функцию СТАВКА используют для вычисления темпов роста на пенсионном счету. Предположим, что баланс на пенсионном счету составляет 40 тысяч долларов на начало года и 48,5 тысячи — на конец. В течение года с каждой получки (т.е. раз в две недели) вы клали на счет по 200 долларов (т.е. осуществили 26 платежей). Следующая формула показывает, как пополнялись ваши инвестиции (рис. 2): =СТАВКА(26;-200;-40000;48500;,01)*26.

В данном примере функция СТАВКА возвращает темпы роста за каждый период, поэтому для получения годовой процентной ставки следует умножить это число на 26. Результатом будет ставка 7,49%.

Беспроцентные займы

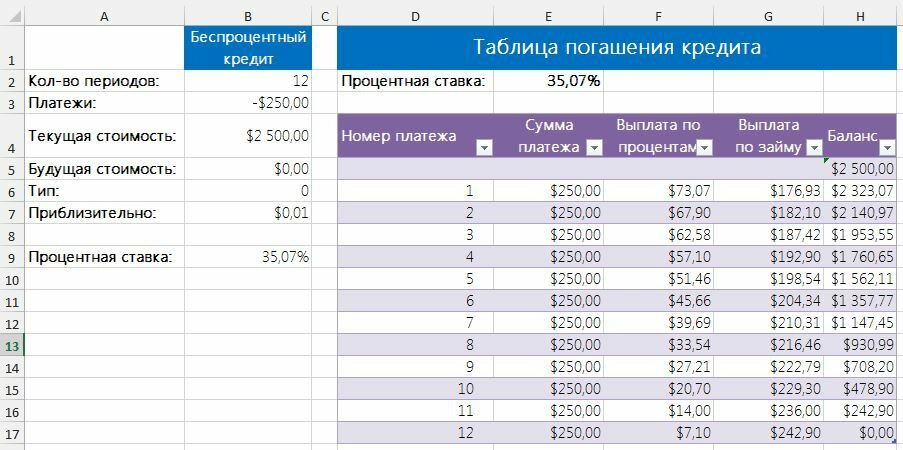
Беспроцентные займы на самом деле редко таковыми являются, так как интерес заимодателя уже учтен в стоимости товара. Предположим, что вы хотите купить кухню за 3 тысячи долларов и оформляете на нее беспроцентную рассрочку на 12 месяцев. Если бы у вас было достаточно наличных, вы смогли бы купить эту же кухню за 2500 долларов — фактически вы переплачиваете за рассрочку 500 долларов. Рассчитанная по следующей формуле приведенная процентная ставка составляет 35,07%: =СТАВКА(12;-3000/12;2500;0;0;,01)*12.

Проверить результаты функции СТАВКА можно, создав таблицу погашения кредита (рис. 3). Если баланс стремится к нулю, значит, процентная ставка вычислена правильно.

1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам

Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.

Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.

Какие данные нужны

Для начала надо правильно написать формулу — в любой свободной ячейке.

=ПЛТ(ставка;кпер;пс)

В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:

1. Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
2. Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
3. Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.

Как всё посчитать

Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.

Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.

2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент

Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.

Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.

Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.

Какие данные нужны

Формула расчёта довольно простая:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

В ней всего две переменные:

1. Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
2. Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).

Как всё посчитать

Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:

Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.

3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора

Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.

Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.

Какие данные нужны

Формула состоит из трёх компонентов:

=ЧИСТНЗ(ставка;значения;даты)

Второй и третий достаточно ясны:

2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.

Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.

Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.

Как всё посчитать

Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.

Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.

4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег

Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.

Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.

Какие данные нужны

Чтобы определить более выгодное предложение, применим формулу:

=ЧИСТВНДОХ(значения;даты)

Достаточно знать всего две переменные:

1. Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
2. Даты — график платежей, по которым будут выплачивать прибыль.

Как всё посчитать

Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.

5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам

Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.

Какие данные нужны

Полезной будет эта формула:

=СТАВКА(кпер;плт;пс)

Три переменных в ней означают следующее:

1. Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
2. Плт — размер платежей. Считаются и основной долг, и проценты.
3. Пс — общая сумма займа. В нашем примере это 100 000 рублей.

Как всё посчитать

Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.

6. PV (ПС) — подсказывает, сколько денег можно взять в долг

Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.

Какие данные нужны

Пригодится формула расчёта текущей стоимости:

=ПС(ставка; кпер; плт)

Для этого потребуется информация, которая есть на сайте любого банка:

1. Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
2. Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
3. Плт — размер комфортного платежа.

Как всё посчитать

Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.

Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.

7. NPER (КПЕР) — помогает рассчитать время накоплений

Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.

Какие данные нужны

Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:

=КПЕР(ставка/периоды_капитализации;плт;пс;бс)

Она состоит из четырёх основных значений и одного дополнительного:

1. Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
2. Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
3. Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
4. Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
5. Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.

Как всё посчитать

Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.

Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.

Читайте также 🧐

• Как вести бюджет, если у вас непостоянный доход
• 20 полезных шаблонов «Google Таблиц» на все случаи жизни
• 10 крутых приложений, чтобы взять финансы под контроль

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

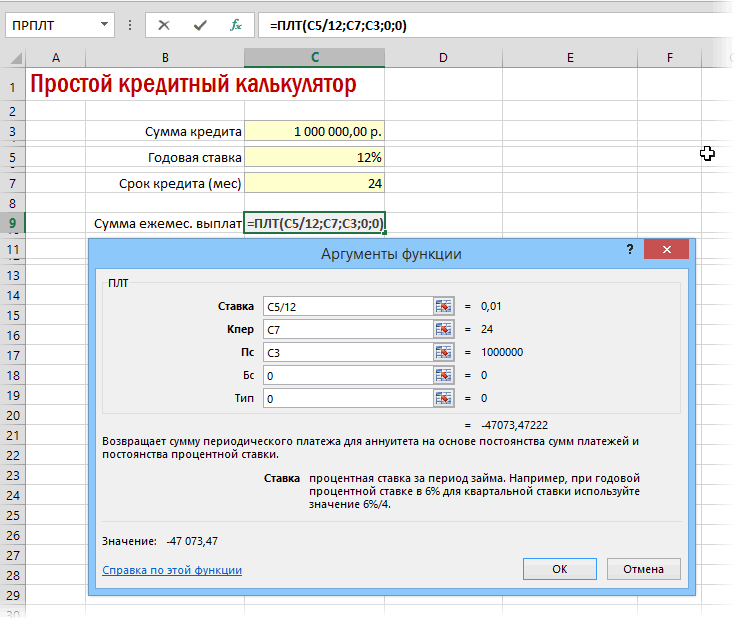
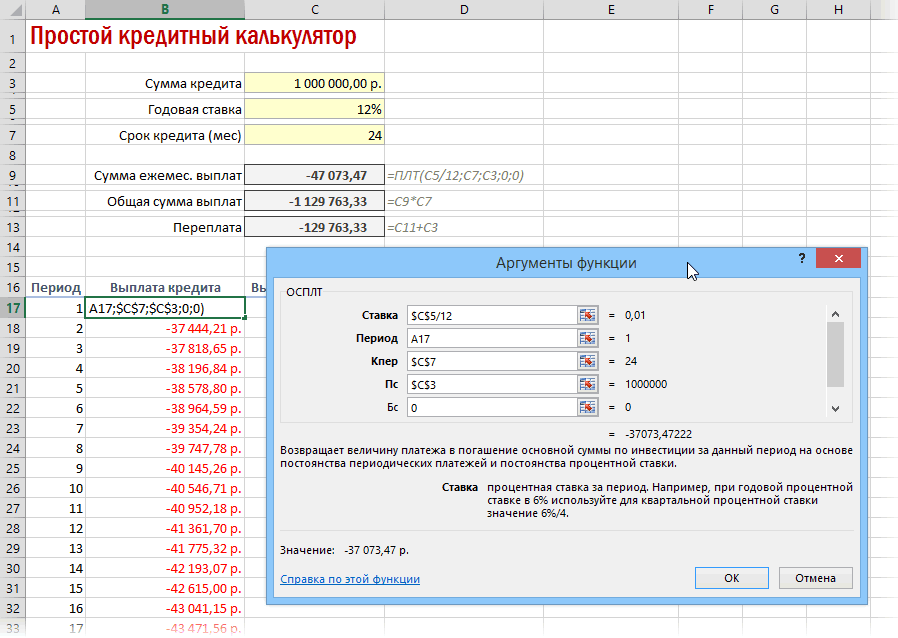
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

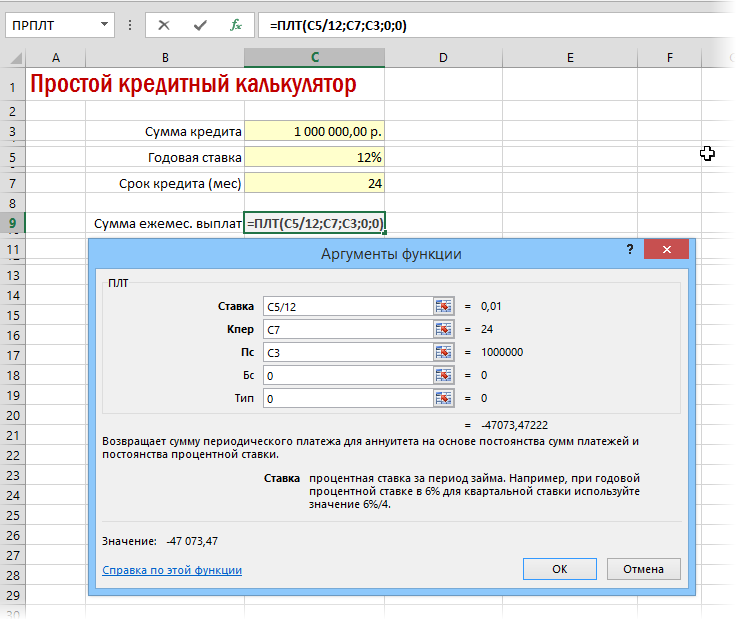
• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

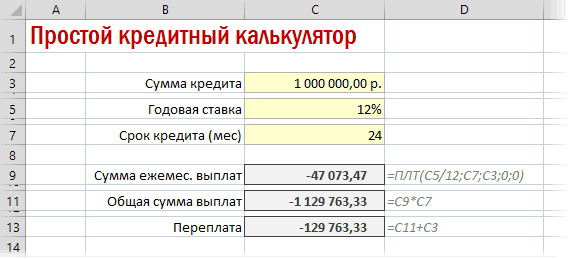
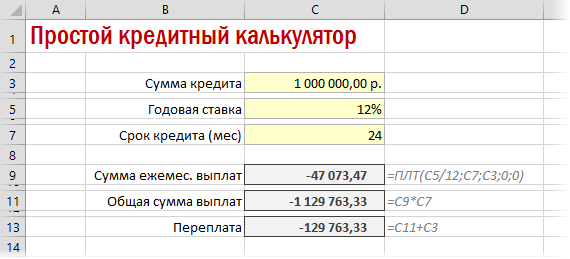
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

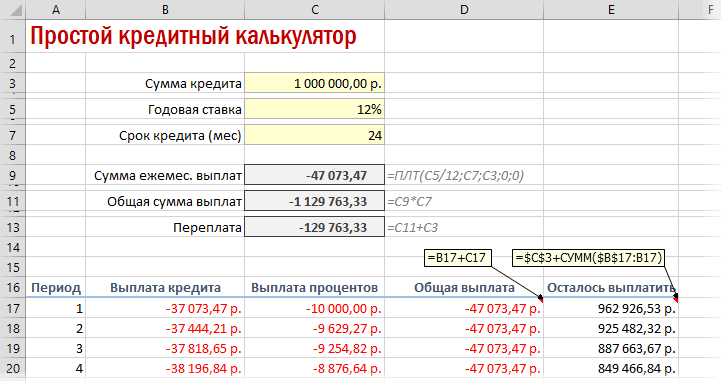
Вариант 2. Добавляем детализацию

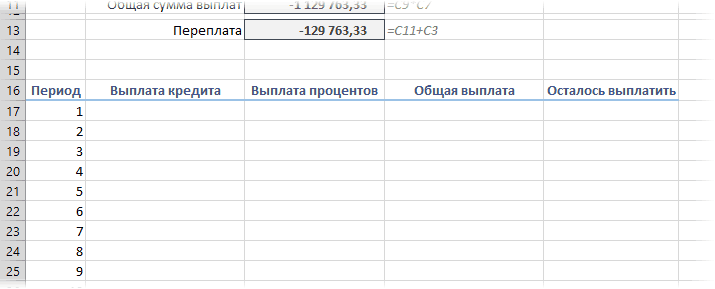
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

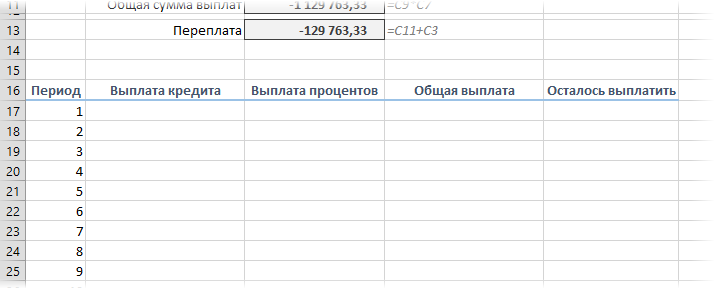
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

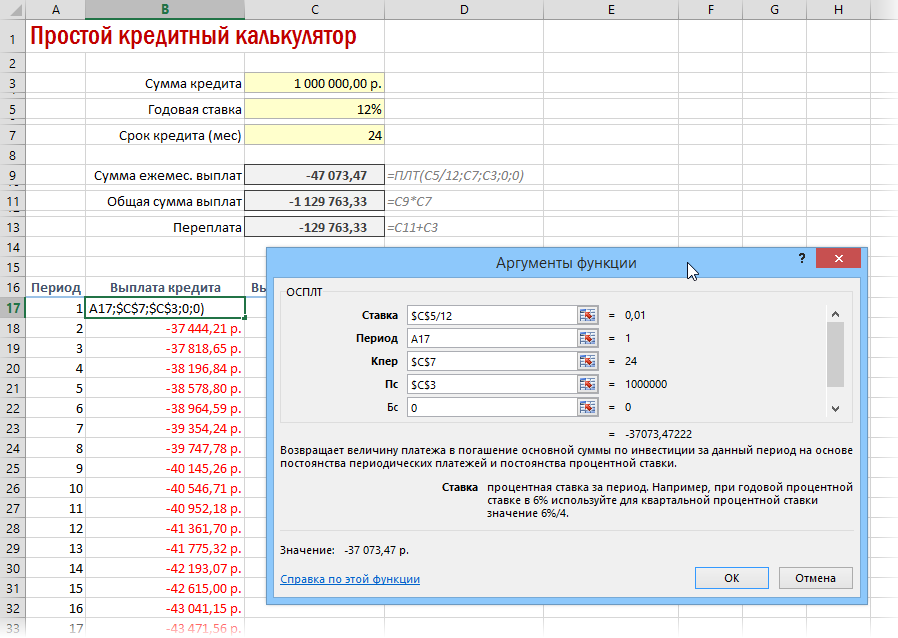
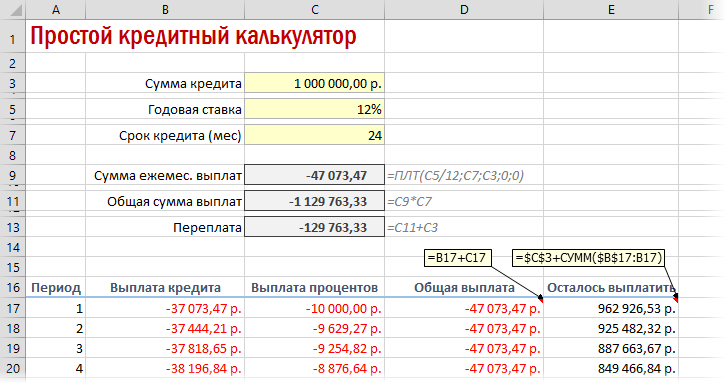
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

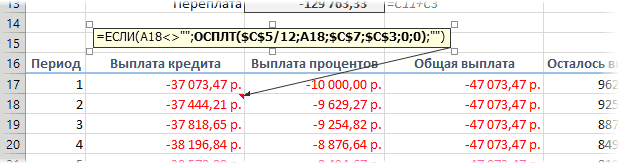
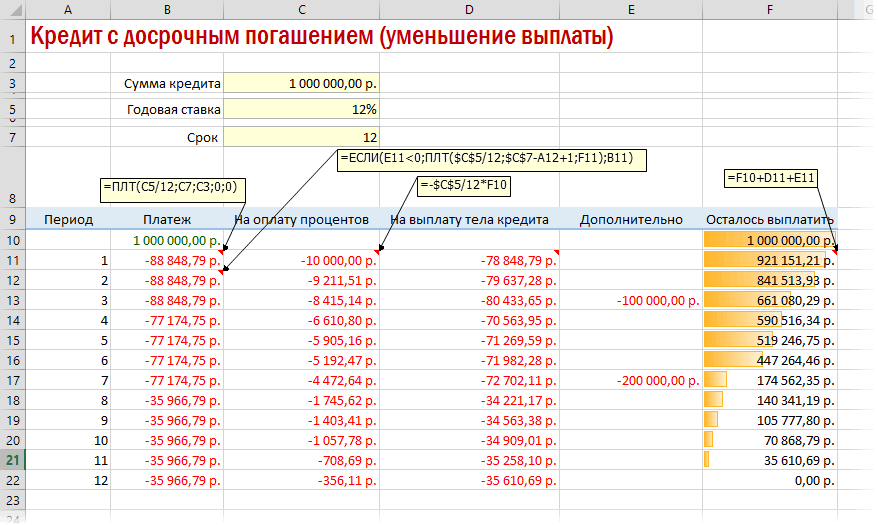
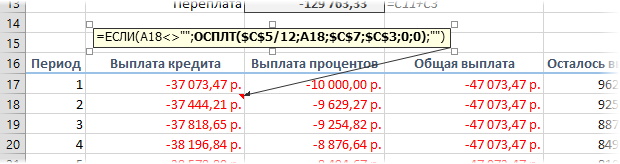
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

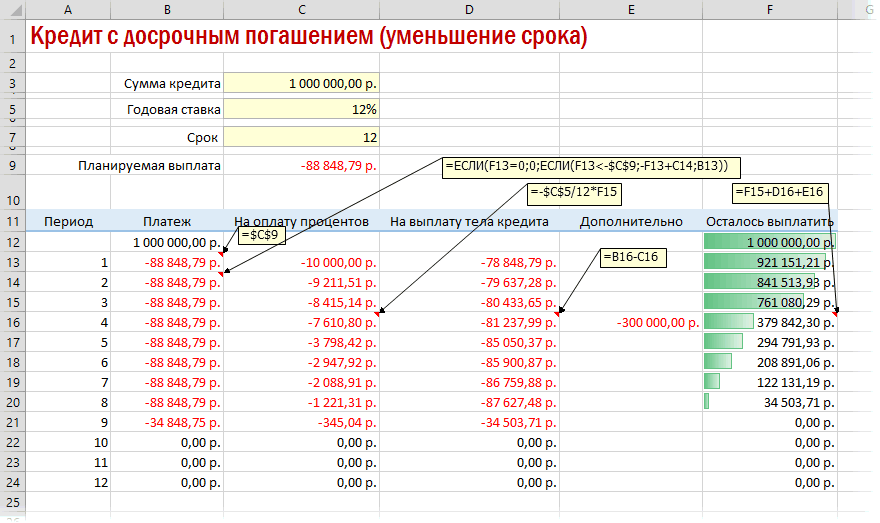
Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

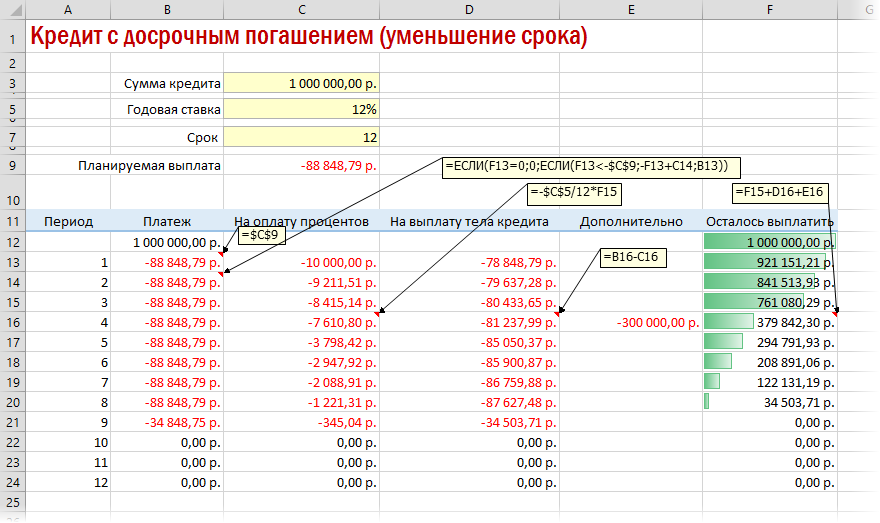
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

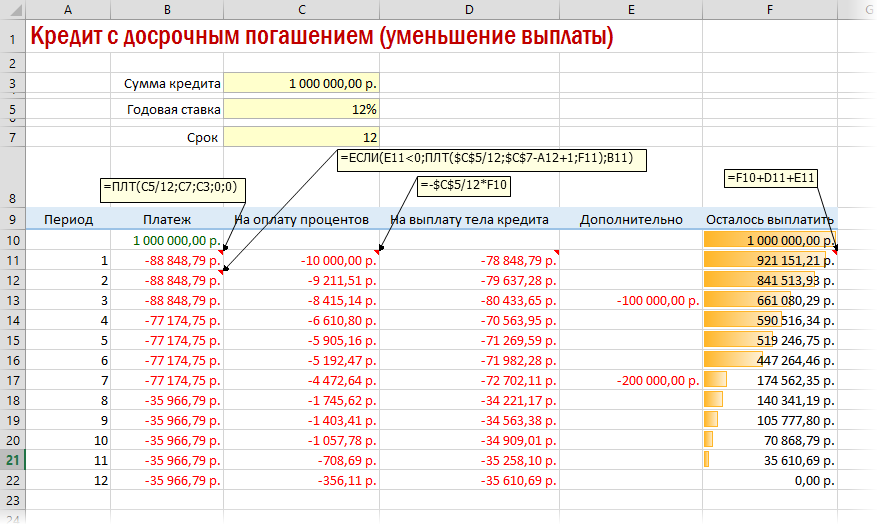
Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

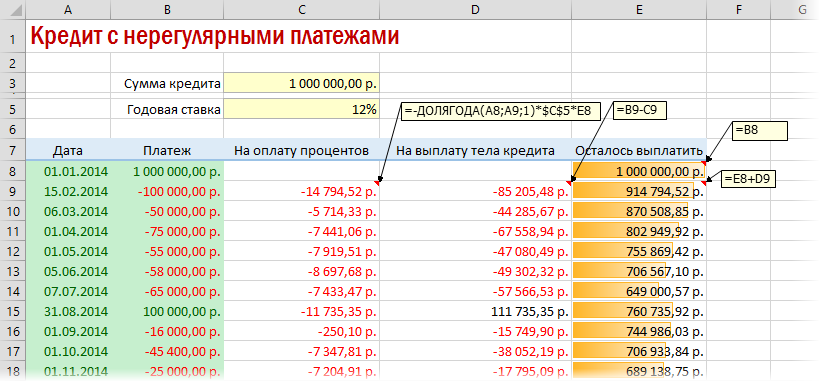
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)