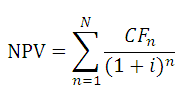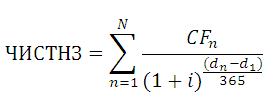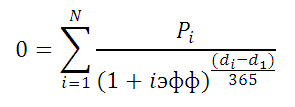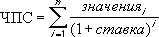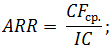Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул
MS
EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют
сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню
(взято из Википедии). Или так:
Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт
cfin.
ru)
Или так:
Текущая
стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика
.
Толковыйсловарь
. —
М
.
:
»
ИНФРА
—
М
«,
Издательство
»
ВесьМир
«.
Дж
.
Блэк
.)
Примечание1
. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется
ЧПС()
, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с
Приведенной стоимостью
.
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма
Приведенных стоимостей
денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет
: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи
Приведенная стоимость
.
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу
сложных процентов
.
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция
ЧПС()
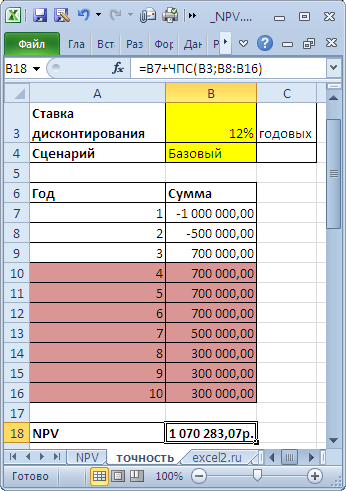
(английский вариант — NPV()). В ее основе используется формула:
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2
. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:
Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)
. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.
Выбор периода дисконтирования для функции ЧПС()
При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.
Примечание3
. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
Определившись со сроками денежных потоков, для функции
ЧПС()
нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.
файл примера, лист NPV
).
В таблице NPV подсчитан двумя способами: через функцию
ЧПС()
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции
ЧПС()
, а нужно просто прибавить к получившемуся результату (см.
файл примера
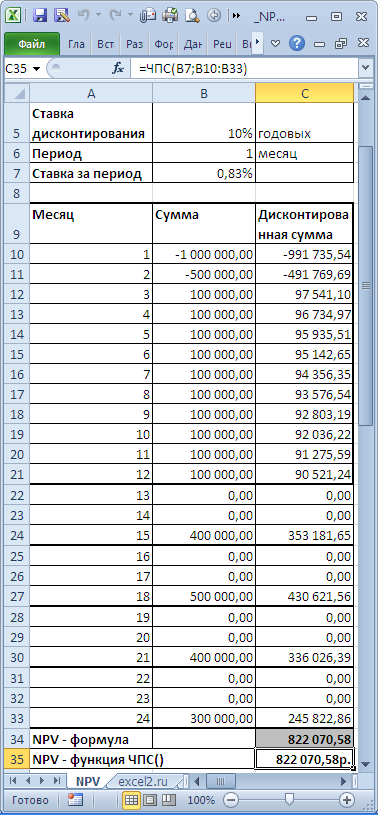
). Сравнение 2-х вариантов дисконтирования приведено в
файле примера
, лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.
файл примера, лист Точность
).
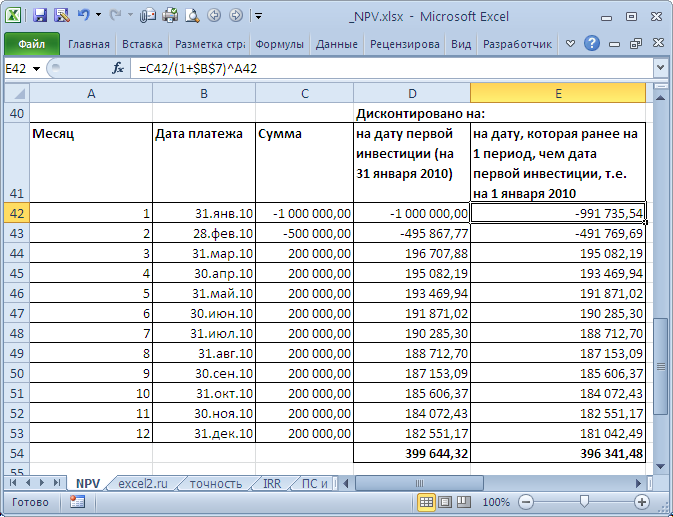
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
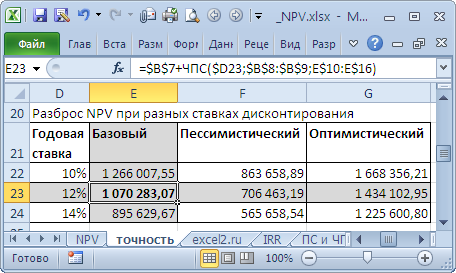
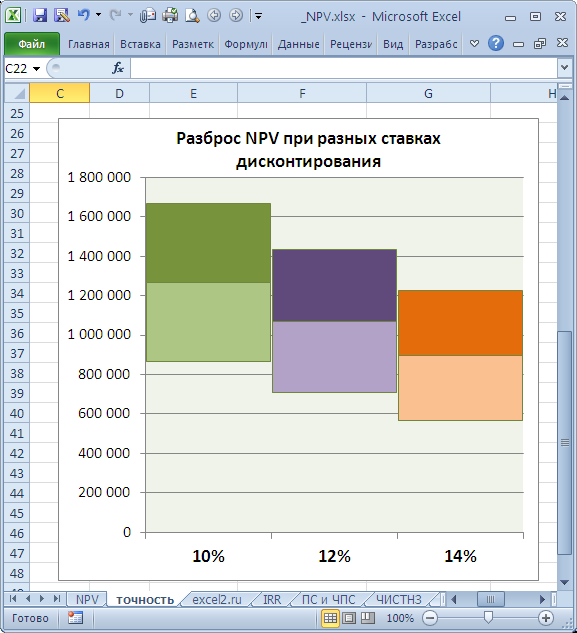
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
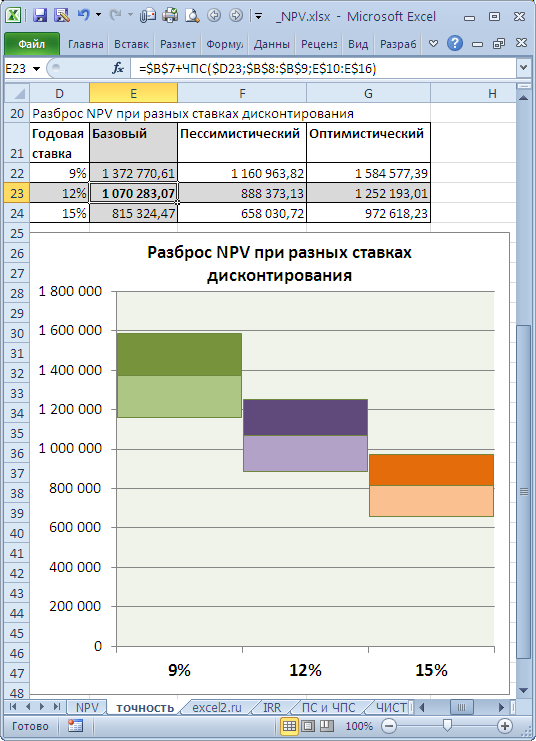
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
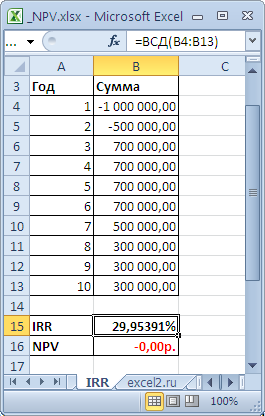
Внутренняя ставка доходности
IRR
(ВСД)
Внутренняя ставка доходности (англ.
internal rate of return
, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.
файл примера, лист IRR
).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
Для расчета IRR используется функция
ВСД()
(английский вариант – IRR()). Эта функция тесно связана с функцией
ЧПС()
. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией
ВСД()
, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:
=ЧПС(ВСД(B5:B14);B5:B14)
Примечание4
. IRR можно рассчитать и без функции
ВСД()
: достаточно иметь функцию
ЧПС()
. Для этого нужно использовать инструмент
Подбор параметра
(поле «Установить в ячейке» должно ссылаться на формулу с
ЧПС()
, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
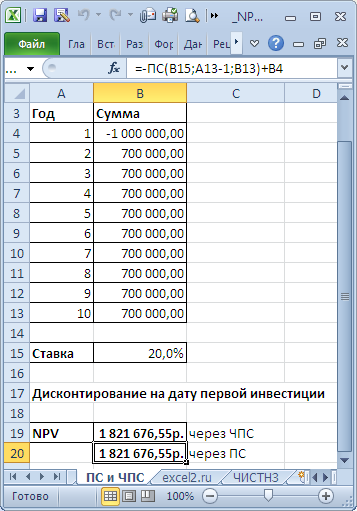
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что
аннуитет
представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию
ПС()
(см.
файл примера, лист ПС и ЧПС
).
В этом случае все денежные потоки (диапазон
В5:В13
, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке
В4
. Ставка дисконтирования расположена в ячейке
В15
со знаком минус. В этом случае формула
=B4+ЧПС(B15;B5:B13)
дает тот же результат, что и
= B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за
любые
промежутки времени, то используется функция
ЧИСТНЗ()
(английский вариант – XNPV()).
Функция
ЧИСТНЗ()
возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от
ЧПС()
является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у
ЧИСТНЗ()
всегда годовая, т.к. указана база 365 дней, а не за период, как у
ЧПС()
. Еще отличие от
ЧПС()
: все денежные потоки всегда дисконтируются на дату первого платежа.
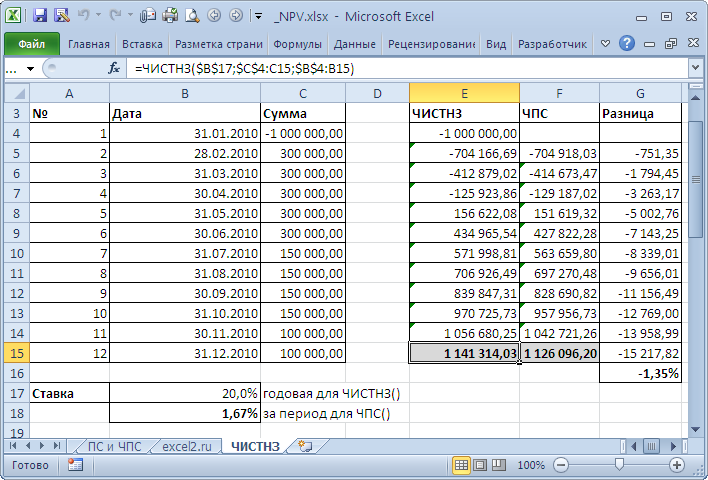
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций
ЧИСТНЗ()
и
ЧПС()
. Эти функции возвращают несколько отличающиеся результаты. Для задачи из
файла примера, Лист ЧИСТНЗ
разница составила порядка 1% (период = 1 месяцу).
Это связано с тем, что у
ЧИСТНЗ()
длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у
ЧПС()
указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет
високосного
года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с
ЧПС()
, у которой имеется родственная ей функция
ВСД()
, у
ЧИСТНЗ()
есть функция
ЧИСТВНДОХ()
, которая вычисляет годовую ставку дисконтирования, при которой
ЧИСТНЗ()
возвращает 0.
Расчеты в функции
ЧИСТВНДОХ()
производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5
. Функция
ЧИСТВНДОХ()
используется для
расчета эффективной ставки по потребительским кредитам
.
Содержание
- Расчет чистого дисконтированного дохода
- Пример вычисления NPV
- Вопросы и ответы
Каждый человек, который серьезно занимался финансовой деятельностью или профессиональным инвестированием, сталкивался с таким показателем, как чистый дисконтированный доход или NPV. Этот показатель отражает инвестиционную эффективность изучаемого проекта. В программе Excel имеются инструменты, которые помогают рассчитать это значение. Давайте выясним, как их можно использовать на практике.
Расчет чистого дисконтированного дохода
Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.
NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.
В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:
=ЧПС(ставка;значение1;значение2;…)
Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.
Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».
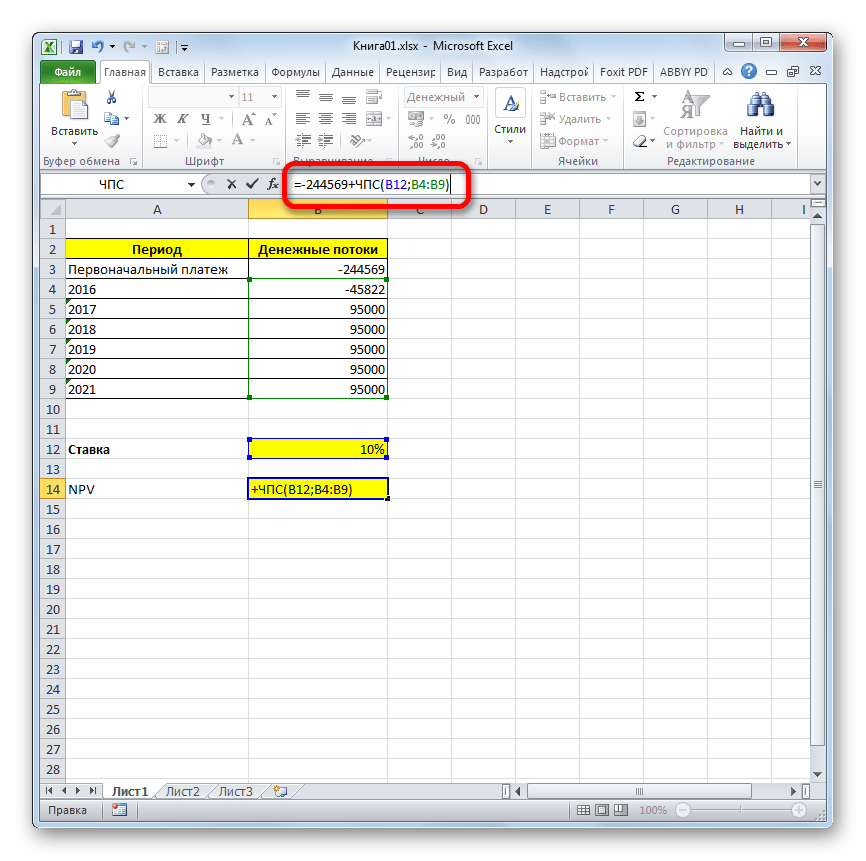
Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:
=Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)
Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».
Пример вычисления NPV
Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.
- Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.
- Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».
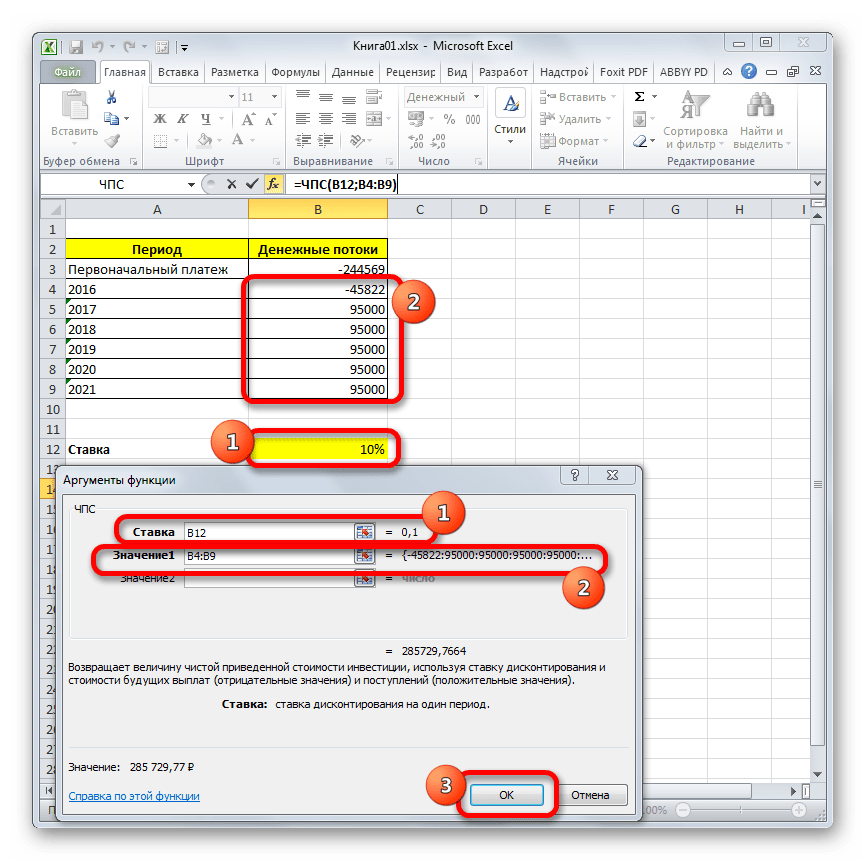
- После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».
В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.
В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.
Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».
- Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.
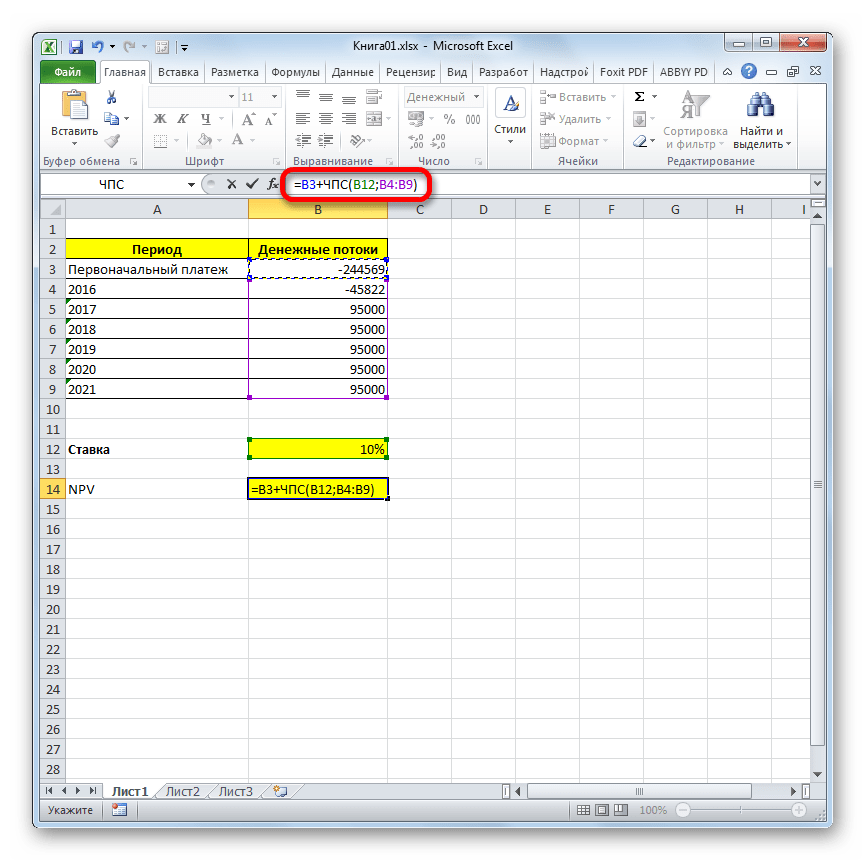
- После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.
Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.
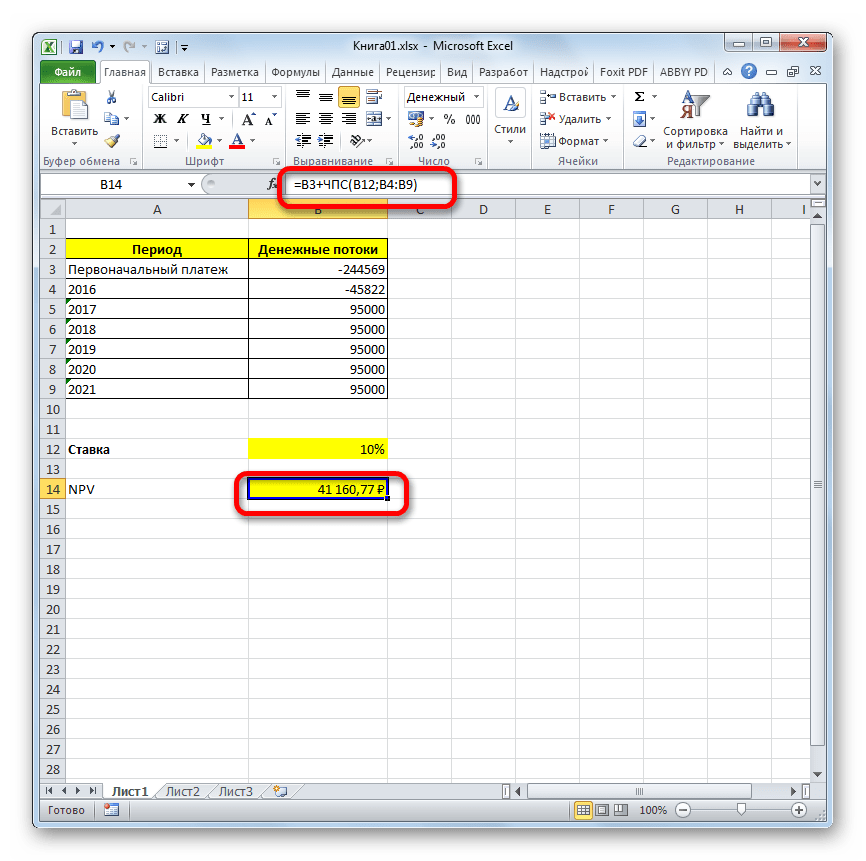
- Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.
Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.
Урок: Финансовые функции в Excel
Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.
For discounted cash flow analysis, the discount rate refers to the interest rate used when calculating the net present value (NPV) of an investment. It represents the time value of money.
NPV is a core component of corporate budgeting and is a comprehensive way to calculate whether a proposed project will add value or not.
For this article, when we look at the discount rate, we will be solving for the rate that results in the NPV equaling zero. Doing so allows us to determine the internal rate of return (IRR) of a project or asset.
Key Takeaways
- The discount rate is the interest rate used to calculate net present value.
- It represents the time value of money.
- Net present value can help companies to determine whether a proposed project may be profitable.
- Net present value is essential to corporate budgeting.
- For an NPV of zero, Excel can find the internal rate of return and use that as the discount rate.
Discount Rate
First, let’s examine each step of NPV in order. The formula is:
NPV = ∑ {After-Tax Cash Flow / (1+r)^t} — Initial Investment
Broken down, each period’s after-tax cash flow at time t is discounted by some rate, shown as r. The sum of all these discounted cash flows is then offset by the initial investment, which equals the current NPV. Any NPV greater than $0 is a value-added project.
In the decision-making process relating to competing yet comparable projects, a project with the highest NPV should tip the scale toward its selection.
The IRR is the discount rate that makes the NPV of future cash flows equal to zero.
The NPV, IRR, and discount rate are all connected concepts. With an NPV, you know the amount and timing of cash flows. You also know the weighted average cost of capital (WACC), which is designated as r when solving for the NPV. With an IRR, you know the same details, and you can solve for the NPV expressed as a percentage return.
The question is, what is the discount rate that sets the IRR to zero? This is the same rate that will give the NPV a value of zero. As you will see below, if the discount rate equals the IRR, then the NPV is zero. Or to put it another way, if the cost of capital equals the return of capital, then the project will break even and have an NPV of 0.
=RATE (nper, pmt, pv, [fv], [type], [guess])
The Excel formula for calculating the discount rate. It’s often used to calculate the interest rate for a loan or to determine the rate of return required to meet a particular investment objective.
Calculating the Discount Rate in Excel
In Excel, you can solve for the discount rate in two ways:
- You can find the IRR and use that as the discount rate, which causes NPV to equal zero.
- You can use What-If analysis, a built-in calculator in Excel, to solve for the discount rate that equals zero.
Method One
To illustrate the first method, we will take our NPV/IRR example. Using a hypothetical outlay, our WACC risk-free rate, and expected after-tax cash flows, we’ve calculated an NPV of $472,169 with an IRR of 57%.
We’ve already defined the discount rate as a WACC that causes the IRR to equal 0. So, we can just take our calculated IRR and put it in place of WACC to get the NPV of 0. That calculation is shown below:
Method Two
Let’s now look at the second method, using Excel’s What-If calculator. This assumes that we did not calculate the IRR of 57%, as we did above, and have no idea what the correct discount rate is.
To get to the What-If solver, go to the Data Tab —> What-If Analysis Menu —> Goal Seek. Then simply plug in the numbers and Excel will solve for the correct value. When you select «OK,» Excel will recalculate WACC to equal the discount rate that makes the NPV zero (57%).
Discount Factor
When working with the discount rate, you may come across the discount factor, as well. They aren’t the same thing although they may be used together in calculations. The discount factor, when multiplied by a cash flow value, discounts that value and provides a present value.
It’s used by Excel to shed added light on the NPV formula and the impact that discounting can have.
Here’s a comparison of the discount rate and the discount factor.
Discount Rate
- Along with time period, it’s used in the formula that calculates the discount factor.
- It represents the time value of money.
- It’s a rate of return determined by a company.
- It’s used in the calculation of present value.
Discount Factor
- As the discount rate increases due to compounding over time, the discount factor increases.
- It facilitates audits of a discounted cash flow model.
- It illustrates the effect of compounding.
- It’s an alternative to using the XNPV and XIRR functions in Excel.
What Is the Formula for the Discount Rate?
The formula for calculating the discount rate in Excel is =RATE (nper, pmt, pv, [fv], [type], [guess]).
What Does the Discount Rate Indicate?
The discount rate represents an interest rate. In discounted cash flow analysis, it’s used in the calculation of the present value of future money. It can tell you the amount of money you’d need today to earn a certain amount in the future.
What Is Net Present Value?
It’s the difference between the present value of cash flows and the present value of cash outlays. It’s used by businesses for corporate budgeting and can help them determine the potential profitability of a proposed project or investment.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.
Описание
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС(ставка; значение1; [значение2],…)
Аргументы функции ЧПС описаны ниже.
-
Ставка Обязательный аргумент. Ставка дисконтирования за один период.
-
Значение1, значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.
-
Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
-
Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.
-
Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.
-
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Замечания
-
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.
-
Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:
-
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.
-
ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,1 |
Годовая ставка дисконтирования |
|
|
-10 000 |
Начальная стоимость инвестиции через один год |
|
|
3000 |
Доход за первый год |
|
|
4200 |
Доход за второй год |
|
|
6800 |
Доход за третий год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A3; A4; A5; A6) |
Чистая приведенная стоимость данной инвестиции |
1 188,44 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,08 |
Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям. |
|
|
-40 000 |
Начальная стоимость инвестиции |
|
|
8000 |
Доход за первый год |
|
|
9200 |
Доход за второй год |
|
|
10000 |
Доход за третий год |
|
|
12000 |
Доход за четвертый год |
|
|
14500 |
Доход за пятый год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A4:A8)+A3 |
Чистая приведенная стоимость данной инвестиции |
1 922,06 ₽ |
|
=ЧПС(A2; A4:A8; -9000)+A3 |
Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году |
(3 749,47 ₽) |
К началу страницы
Нужна дополнительная помощь?
Для привлечения и вложения средств в какое-либо дело инвестору необходимо тщательно изучить внешний и внутренний рынок.
На основании полученных данных составить смету проекта, инвестиционный план, спрогнозировать выручку, сформировать отчет о движении денежных средств. Наиболее полно всю нужную информацию можно представить в виде финансовой модели.
Финансовая модель инвестиционного проекта в Excel
Составляется на прогнозируемый период окупаемости.
Основные компоненты:
- описание макроэкономического окружения (темпы инфляции, проценты по налогам и сборам, требуемая норма доходности);
- прогнозируемый объем продаж;
- прогнозируемые затраты на привлечение и обучение персонала, аренду площадей, закупку сырья и материалов и т.п.;
- анализ оборотного капитала, активов и основных средств;
- источники финансирования;
- анализ рисков;
- прогнозные отчеты (окупаемость, ликвидность, платежеспособность, финансовая устойчивость и т.д.).
Чтобы проект вызывал доверие, все данные должны быть подтверждены. Если у предприятия несколько статей доходов, то прогноз составляется отдельно по каждой.
Финансовая модель – это план снижения рисков при инвестировании. Детализация и реалистичность – обязательные условия. При составлении проекта в программе Microsoft Excel соблюдают правила:
- исходные данные, расчеты и результаты находятся на разных листах;
- структура расчетов логичная и «прозрачная» (никаких скрытых формул, ячеек, цикличных ссылок, ограниченное количество имен массивов);
- столбцы соответствуют друг другу;
- в одной строке – однотипные формулы.
Расчет экономической эффективности инвестиционного проекта в Excel
Для оценки эффективности инвестиций применяются две группы методов:
- статистические (PP, ARR);
- динамические (NPV, IRR, PI, DPP).
Срок окупаемости:
Коэффициент PP (период окупаемости) показывает временной отрезок, за который окупятся первоначальные вложения в проект (когда вернутся инвестированные деньги).
Экономическая формула расчета срока окупаемости:
где IC – первоначальные вложения инвестора (все издержки),
CF – денежный поток, или чистая прибыль (за определенный период).
Расчет окупаемости инвестиционного проекта в Excel:
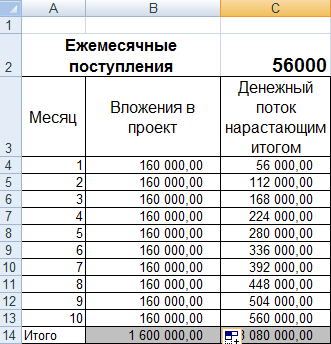
- Составим таблицу с исходными данными. Стоимость первоначальных инвестиций – 160000 рублей. Ежемесячно поступает 56000 рублей. Для расчета денежного потока нарастающим итогом была использована формула: =C4+$C$2.
- Рассчитаем срок окупаемости инвестированных средств. Использовали формулу: =B4/C2 (сумма первоначальных инвестиций / сумма ежемесячных поступлений).
Так как у нас дискретный период, то срок окупаемости составит 3 месяца.
Данная формула позволяет быстро найти показатель срока окупаемости проекта. Но использовать ее крайне сложно, т.к. ежемесячные денежные поступления в реальной жизни редко являются равными суммами. Более того, не учитывается инфляция. Поэтому показатель применяется вкупе с другими критериями оценки эффективности.
Рентабельность инвестиций
ARR, ROI – коэффициенты рентабельности, показывающие прибыльность проекта без учета дисконтирования.
Формула расчета:
где CFср. – средний показатель чистой прибыли за определенный период;
IC – первоначальные вложения инвестора.
Пример расчета в Excel:
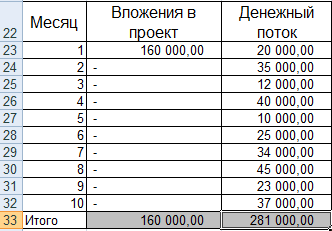
- Изменим входные данные. Первоначальные вложения в размере 160 000 рублей вносятся только один раз, на старте проекта. Ежемесячные платежи – разные суммы.
- Рассчитаем средние поступления по месяцам и найдем рентабельность проекта. Используем формулу: =СРЗНАЧ(C23:C32)/B23. Формат ячейки с результатом процентный.
Чем выше коэффициент рентабельности, тем привлекательнее проект. Главный недостаток данной формулы – сложно спрогнозировать будущие поступления. Поэтому показатель часто применяется для анализа существующего предприятия.
Примеры инвестиционне6ого проекта с расчетами в Excel:
- скачать полный инвестиционный проект
- скачать сокращенный вариант в Excel
Статистические методы не учитывают дисконтирование. Зато позволяют быстро и просто найти необходимые показатели.
Использование Excel для оценки эффективности проекта
Расчет чистого дисконтированного дохода NPV, также называемого ЧДД, несложен, но трудоемок, если считать его вручную.
Мы уже рассматривали пример расчета NPV и IRR по формулам. Там же были приведены формулы всех перечисленных показателей и их расчеты ручным методом .
Теперь поговорим, как рассчитать ЧДД, ВНД (ИРР), срок окупаемости простой и дисконтированный без особых усилий с помощью таблиц Ms Excel. Итак, можно прописать формулы в таблице в экселе для расчета NPV. Что мы и сделаем.
Здесь вы можете бесплатно скачать таблицу Excel для расчета NPV, внутренней нормы доходности (IRR), сроков окупаемости простого и дисконтированного. Мы приведем таблицу для расчета NPV за 25 лет или меньший срок, в таблицу только стоит вставить значения предполагаемого размера инвестиций, размер ставки дисконтирования и величину годовых денежных потоков. И NPV рассчитается автоматически.
Вот эта таблица. Пароль к файлу: goodstudents.ru
Задачу расчета основных показателей эффективности инвестиционного проекта именно с помощью таблиц эксель часто задают преподаватели. В этих ситуациях, либо когда вы ходите быстро рассчитать необходимые вам значения показателей, вы можете использовать шаблон расчета в приведенной таблице.
Теперь давайте поговорим, как воспользоваться данной таблицей для расчета ЧДД, ВНД, срока окупаемости. В ней уже приведен пример расчета NPV.
Пример
Если вам нужно рассчитать NPV за 5 лет. Вам известна ставка дисконтирования 30% (т.е. 0,3). Известны денежные потоки по годам:
100 т.р.
200 т.р.
300 т.р.
350 т.р.
400 т.р.
Размер инвестиций 500 т.р.
В таблице экселя исправим значение ставки дисконтирования на 0,3 (2я строка сверху), исправим значение инвестиций (5я строка, 3й столбец) на 500.
Сотрем денежные потоки и их итог за 25 лет. (также сотрем строки чистых денежных потоков с 6го по 25й год и значение NPV для лишних лет). Вставим известные нам значения за 5 лет. Получим следующие данные.
|
0,3 |
ставка дисконтирования |
|||
|
Годы |
Сумма инвестиций, тыс. руб |
Денежные потоки, тыс. руб(CF) |
Чистые денежные потоки, тыс. руб. |
Чистый дисконтировнный доход, тыс. руб. (NPV) |
|
1 |
500,00 |
100,00 |
76,92 |
-423,08 |
|
2 |
200,00 |
118,34 |
-304,73 |
|
|
3 |
300,00 |
136,55 |
-168,18 |
|
|
4 |
350,00 |
122,54 |
-45,64 |
|
|
5 |
400,00 |
107,73 |
62,09 |
|
|
Итого |
500,00 |
1350,00 |
562,09 |
62,09 |
Как видите нам не пришлось считать NPV самостоятельно, таблица эксель посчитала данный показатель за нас.
Теперь давайте разберемся как посчитать IRR с помощью экселя на конкретном примере. В Ms Excel есть функция, которая называется «подбор параметра». В 2003 экселе эта функция расположена в сервис-> подбор параметра.
Мы уже говорили ранее, что IRR – это такая ставка дисконтирования, при которой NPV равен нулю.
Нажимаем в экселе сервис-> подбор параметра, открывается окошко,
Мы знаем, что ЧДД =0, выбираем значение ячейки с ЧДД за 5й год, присваиваем ему значение 0, изменяя значение ячейки, в которой расположена ставка дисконтирования. После расчета получим.
Итак, NPV равен нулю при ставке дисконтирования равной 35,02%. Т.е. ВНД внутренняя норма доходности (IRR)=35,02%.
Теперь рассчитаем значение срока окупаемости простого и дисконтированного с помощью данной таблицы Эксель.
Срок окупаемости простой:
Мы видим по таблице, что у нас инвестиции 500 т.р. За 2 года мы получим доход 300 т.р. За 3 года получим 600 т.р. Значит срок окупаемости простой будет более 2 и менее 3х лет.
В ячейке F32 (32 строка файла экселя) нажимаем F2 и исправляем, вместо «1+» у нас будет «2+», меняем 1 на 2, и преобразуем формулу следующим образом, вместо « =1+(-(D5-C5)/D6)» у нас будет «=2+(-((D5+D6)-C5)/D7)», другими словами, мы к 2м полным годам прибавили долг по инвестициям на конец второго года, деленный на денежный поток за третий год. Получим 2,66 года.
Срок окупаемости дисконтированный пример расчета:
NPV переходит с минуса на плюс с 4го на 5й год, значит срок окупаемости с учетом дисконтирования будет более 4х и менее 5 лет.
В ячейке F33 (33 строка файла экселя) нажимаем F2 и исправляем, вместо «2+» у нас будет «4+», меняем 2 на 4, и преобразуем формулу следующим образом, вместо «=2+(-F6/E7)» у нас будет «=4+(-F8/E9))», другими словами, мы к четырем полным годам прибавили отношение последнего отрицательного NPV к чистому денежному потоку в следующем году (4+-(-45,64/107,73).
Получим 4,42 года – срок окупаемости с учетом дисконта.
Поэтому если необходимо рассчитать показатели по формулам, то можно посмотреть примеры по ссылке приведенной выше, а здесь мы подробно остановились на расчетах ЧДД, дисконтированных денежных потоков, ВНД, сроков окупаемости с помощью таблиц Excel, что гораздо проще и эффективнее.
Данный пример предназначен для практических занятий. к.э.н., доцент Одинцова Е.В.
Разработка бизнес-процесса — занятие трудоемкое, требующее времени. А если специалисты еще и вручную проводят расчеты, есть вероятность, что полученные данные будут некорректными. Чтобы этого избежать, можно автоматизировать данный процесс. Это позволит снизить риск ошибочного ввода и предоставления информации. Как это сделать в Excel?
Предлагаем следующий алгоритм разработки и автоматизации бизнес-процесса с помощью MS Excel:
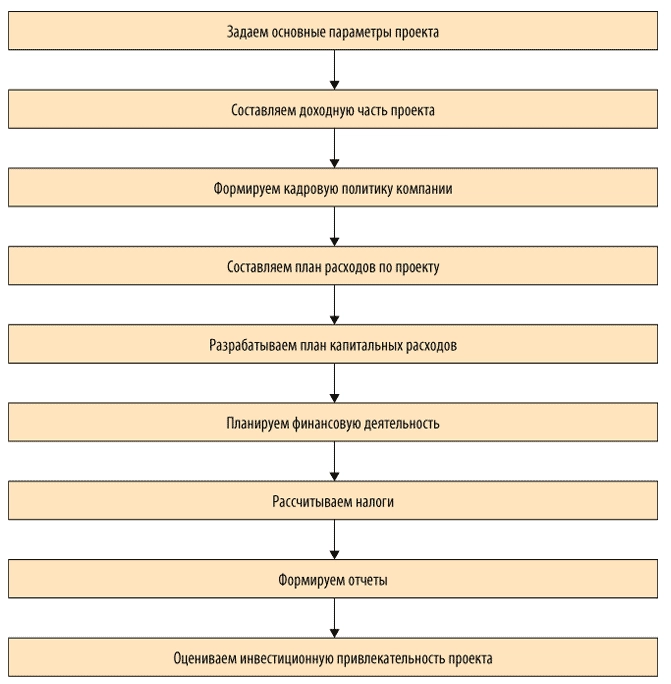
Рассмотрим эти этапы подробнее.
Задаем основные параметры проекта
Предположим, компания «Альфа» планирует построить производственный цех и покрасочное помещение. Устанавливаем для данных объектов начальную проектную мощность, сроки выхода на проектную мощность, годовой темп прироста, выбираем год открытия. Изменяя начальное значение проектной мощности, темпы роста, срок, мощности (старт, темп, срок), получим график выхода на проектную мощность; изменяя год открытия по каждому объекту — календарный план развития данного объекта.
На примере объекта «Производственный цех» задаем формулы:
для расчета максимальной проектной мощности:
=ЕСЛИ(ЕПУСТО($D4);0;$E4*(1+$H4)^$G4),
где $D4 — год открытия объекта;
$E4 — начальная проектная мощность;
$H4 — темп роста;
$G4 — срок выхода на максимальную проектную мощность.
для календарного плана развития:
=ЕСЛИ(ЕПУСТО($D$4);0;ЕСЛИ(ИЛИ($B10=$D$4;$B10>$D$4);1;0)),
где $B10 — год.
Для графика выхода на проектную мощность вводим формулу, представленную на рис. 1. В результате на листе «Сценарий» будут располагаться три таблицы:
- «Сценарий развития компании»;
- «Календарный план развития»;
- «График выхода на проектную мощность, тыс. руб.» (табл. 1).
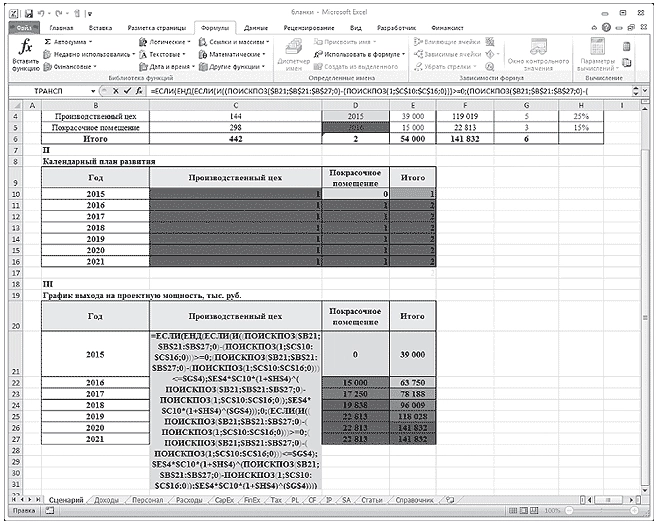
Рис. 1. Формула расчета графика выхода на проектную мощность
Лист «Сценарий»

Как следует из табл. 1, в 2015 г. планируется ввести в эксплуатацию производственный цех, при этом начальная проектная мощность составит 39 000 тыс. руб., срок выхода на максимальную мощность со значением 119 019 тыс. руб. — 5 лет.
Составляем доходную часть проекта (лист «Доходы»)
На листе располагаются следующие таблицы:
- «Ассортиментная политика»;
- «Доля, % от V продаж»;
- «Выручка от реализации с НДС и без НДС, тыс. руб.».
Компания производит низковольтные комплектные устройства, комплектные распределительные устройства и устройства безопасности. Наибольший удельный вес в структуре продаж занимают низковольтные комплектные устройства — порядка 45 %. Выручка от реализации (с НДС) меняется в зависимости от проектной мощности проекта и своего максимального значения — 63 824 тыс. руб. (141 832 x 45 / 100) — достигнет в 2020 г.
Лист «Доходы»
|
I. Ассортиментная политика |
||||||||
|
Номенклатурная группа |
Собственная продукция, % |
Сезонность продаж, мес. |
||||||
|
Низковольтные комплектные устройства |
100% |
12 |
||||||
|
Комплектные распределительные устройства |
100% |
12 |
||||||
|
Устройства безопасности |
100% |
12 |
||||||
|
Итого |
70% |
12 |
||||||
|
Проектная мощность, тыс. руб. |
39 000 |
63 750 |
78 188 |
96 009 |
118 028 |
141 832 |
141 832 |
678 638 |
|
II. Доля, % от V продаж |
||||||||
|
Номенклатурная группа |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Низковольтные комплектные устройства |
45% |
45% |
45% |
45% |
45% |
45% |
45% |
45,00% |
|
Комплектные распределительные устройства |
10% |
10% |
10% |
10% |
10% |
10% |
10% |
10,00% |
|
Устройства безопасности |
15% |
15% |
15% |
15% |
15% |
15% |
15% |
15,00% |
|
Итого |
70% |
70% |
70% |
70% |
70% |
70% |
70% |
70% |
|
III. Выручка от реализации с НДС, тыс. руб. |
||||||||
|
Номенклатурная группа |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Низковольтные комплектные устройства |
17 550 |
28 688 |
35 184 |
43 204 |
53 113 |
63 824 |
63 824 |
305 387 |
|
Комплектные распределительные устройства |
3900 |
6375 |
7819 |
9601 |
11 803 |
14 183 |
14 183 |
67 864 |
|
Устройства безопасности |
5850 |
9563 |
11 728 |
14 401 |
17 704 |
21 275 |
21 275 |
101 796 |
|
Итого |
27 300 |
44 625 |
54 731 |
67 207 |
82 620 |
99 282 |
99 282 |
475 047 |
|
IV. Выручка от реализации без НДС, тыс. руб. |
||||||||
|
Номенклатурная группа |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Низковольтные комплектные устройства |
14 873 |
24 311 |
29 817 |
36 614 |
45 011 |
54 088 |
54 088 |
258 803 |
|
Комплектные распределительные устройства |
3305 |
5403 |
6626 |
8136 |
10 002 |
12 020 |
12 020 |
57 512 |
|
Устройства безопасности |
4958 |
8104 |
9939 |
12 205 |
15 004 |
18 029 |
18 029 |
86 268 |
|
Итого |
23 136 |
37 818 |
46 382 |
56 955 |
70 017 |
84 137 |
84 137 |
402 582 |
Формируем кадровую политику компании (лист «Персонал»)
На этом листе будут сформированы таблицы:
- «Кадровая политика»;
- «Штатное расписание»;
- «ФОТ, налоги и отчисления, тыс. руб.».
Для наглядности задаем значения следующим показателям: инфляция по заработной плате, НДФЛ, страховые взносы (СВ).
Для удобства расчета присваиваем значениям имена:
инфляция по заработной плате — Sindex;
НДФЛ — НДФЛ_;
СВ — Стр_Взносы.
Теперь можем рассчитать фонд оплаты труда по категориям сотрудников, их налоги и отчисления. Для этого задаем формулу (на примере управленческого персонала, отчетный период — 2015 г.):
=($C4*(1+SIndex)^(C$15))*$D4*C9/1000,
где $C4 — среднемесячная заработная плата управленческого персонала (40 000 руб.);
SIndex — инфляция по заработной плате (1 %);
C$15 — порядковый номер периода (2015 году присваиваем значение 0);
$D4 — занятость (12 месяцев);
C9 — численность управленческого персонала (8 чел.).
Получаем таблицу, в которой представлены значения фонда оплаты труда, налоги и отчисления по годам (табл. 1).
Таблица 1. Фонд оплаты труда, налоги и отчисления по категориям персонала
|
Позиция |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
Управленческий персонал |
3840 |
3878 |
3917 |
3956 |
3996 |
4036 |
4076 |
|
Производственные рабочие |
4650 |
4697 |
4743 |
4791 |
4839 |
4887 |
4936 |
|
ИТОГО |
8490 |
8575 |
8661 |
8747 |
8835 |
8923 |
9012 |
|
Страховые взносы + НДФЛ |
4196 |
4238 |
4281 |
4323 |
4367 |
4410 |
4454 |
|
ФОТ с отчислениями |
12 686 |
12 813 |
12 941 |
13 071 |
13 201 |
13 333 |
67 |
Составляем план расходов по проекту
На листе «Расходы» создаем четыре таблицы:
- «Расходы на закупку товарно-материальных ценностей, тыс. руб.»;
- «Расчет себестоимости реализованной продукции, тыс. руб.»;
- «Расчет накладных расходов, тыс. руб.»;
- «Амортизация основных средств (ОС) и нематериальных активов (НА), тыс. руб.».
Лист «Расходы»
|
I. Расходы на закупку товарно-материальных ценностей, тыс. руб. |
||||||||
|
Показатели |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Выручка от реализации, с НДС |
27 300 |
44 625 |
54 731 |
67 207 |
82 620 |
99 282 |
99 282 |
475 047 |
|
Страховой запас, t1 |
2730 |
4463 |
5473 |
6721 |
8262 |
9928 |
9928 |
47 505 |
|
Расходы на приобретение сырья, материалов и покупных комплектующих |
4505 |
7363 |
9031 |
11 089 |
13 632 |
16 382 |
16 382 |
78 383 |
|
Расходы по предоставлению услуг сторонними организациями |
546 |
893 |
1095 |
1344 |
1652 |
1986 |
1986 |
9501 |
|
II. Расчет себестоимости реализованной продукции, тыс. руб. |
||||||||
|
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Выручка от реализации, без НДС |
23 136 |
37 818 |
46 382 |
56 955 |
70 017 |
84 137 |
84 137 |
402 582 |
|
Сырье и материалы, покупные комплектующие |
5784 |
9454 |
11 596 |
14 239 |
17 504 |
21 034 |
21 034 |
100 645 |
|
Заработная плата производственных рабочих |
4650 |
4697 |
4743 |
4791 |
4839 |
4887 |
4936 |
33 543 |
|
Страховые взносы |
1395 |
1409 |
1423 |
1437 |
1452 |
1466 |
1481 |
10 063 |
|
Прочие производственные расходы |
694 |
1135 |
1391 |
1709 |
2100 |
2524 |
2524 |
12 077 |
|
Себестоимость реализации |
12 523 |
16 694 |
19 154 |
22 175 |
25 895 |
29 912 |
29 975 |
156 329 |
|
III |
||||||||
|
1 |
2 |
2 |
2 |
2 |
2 |
2 |
||
|
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Накладные расходы |
14 415 |
14 559 |
14 705 |
14 852 |
15 000 |
15 150 |
15 302 |
103 983 |
|
IV. Амортизация ОС и НА, тыс. руб. |
||||||||
|
Показатель |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
|
Первоначальная стоимость ОС и НА, t1 |
30 900 |
30 900 |
30 900 |
30 900 |
30 900 |
0 |
0 |
|
|
CAPEX |
30 900 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Остаточная стоимость ОС и НА, t1 |
27 810 |
24 720 |
21 630 |
18 540 |
15 450 |
15 450 |
15 450 |
|
|
Амортизация |
3090 |
3090 |
3090 |
3090 |
3090 |
0 |
0 |
Рассмотрим порядок заполнения каждой таблицы подробно.
В таблице «Расходы на закупку товарно-материальных ценностей» важно рассчитать:
- страховой запас;
- расходы на приобретение сырья, материалов и покупных комплектующих;
- расходы по предоставлению услуг сторонними организациями.
Для этого создаем 2 дополнительных столбца, где будет отражена структура данных показателей в выручке.
Итак, страховой запас и расходы по предоставлению услуг сторонними организациями занимают соответственно 10 и 2 % от выручки. Значит, если выручка за 2015 г. планируется в размере 27 300 тыс. руб., то страховой запас составит 2730 тыс. руб. (27 300 x 10 % / 100 %), а расходы по предоставлению услуг сторонними организациями — 546 тыс. руб.
Расходы на приобретение сырья, материалов и покупных комплектующих — это 15 % от выручки. Для расчета показателя «Расходы на приобретение сырья, материалов и покупных комплектующих» суммируем выручку от реализации (27 300) и страховой запас (2730), а затем полученное значение умножаем на 0,15 (15 % / 100 %), получаем 4505 тыс. руб.
Переходим к таблице «Расчет себестоимости реализованной продукции». Здесь все статьи затрат можно представить в укрупненном виде:
- выручка от реализации без НДС;
- сырье и материалы;
- покупные комплектующие;
- заработная плата производственных рабочих;
- страховые взносы;
- прочие производственные расходы.
Например, сырье и материалы, покупные комплектующие и прочие расходы занимают соответственно 25 и 3 % от выручки, или в денежном выражении за 2015 г. соответственно 5784 (23 136 x 25 % / 100 %) и 694 тыс. руб.
Рассчитываем накладные расходы (310 % от заработной платы производственных рабочих). В нашем примере накладные расходы за 2015 г. — 14 415 тыс. руб. (4650 x 310 % / 100 %).
Далее планируем амортизационные отчисления — линейным методом по первоначальной стоимости, которая импортируется в расчет из вкладки «CарEх». Для расчета амортизации вводим следующую формулу:
=B$25*(1/ОС_срок)*100%,
где B$25 — первоначальная стоимость ОС и НА (30 900);
ОС_срок — имя ячейки срока службы оборудования (10 лет).
Так, за 2015 г. амортизация составляет 3090 тыс. руб.
Разрабатываем план капитальных расходов (лист «CapEx»)
Для начала описываем варианты проектного решения. В нашем примере их два:
- вариант 1 — строительство производственных площадей с полной заменой технологического оборудования;
- вариант 2 — строительство производственных площадей с частичной заменой технологического оборудования.
Для каждого варианта составляем смету капитальных затрат (перечень работ и затрат).
Сметный расчет капитальных затрат на строительство производственных площадей
|
Вариант |
1 |
Вариант |
2 |
|
|
Перечень работ и затрат |
Общая стоимость, тыс. руб. |
Перечень работ и затрат |
Общая стоимость, тыс. руб. |
|
|
Строительно-монтажные и проектно-изыскательные работы |
5500 |
Строительно-монтажные и проектно-изыскательные работы |
5500 |
|
|
Оборудование и инвентарь |
25 400 |
Оборудование и инвентарь |
10 500 |
|
|
Итого |
30 900 |
Итого |
16 000 |
Планируем финансовую деятельность (лист «FinEx»)
Здесь главное — определить потребность в финансировании. С этой целью сначала выделяем два показателя:
- инвестиционные затраты;
- оборотный капитал.
Для расчета оборотного капитала за 2015 г. задаем следующую формулу:
=ЕСЛИ(СУММ(($D$10=Data_RE)*($E10=Функция)*Data_2015*Data0)
где Data_RE — имя диапазона столбца С «Отчет» на листе «Статьи»;
Функция — имя диапазона столбца Q «Функция» на листе «Статьи»;
Data_2015 — имя диапазона столбца G «2015» на листе «Статьи»;
Data0 — имя диапазона столбца O «Учет» на листе «Статьи».
Отметим, что при выборе ставки дисконтирования важно знать средневзвешенную стоимость капитала (WACC), которую в данном случае можно рассчитать по формуле:
=СУММ(КЛ*$D$4*(1-НП);ККиЗ*$D$5*(1-НП);СК*$D$6),
где КЛ — имя ячейки $C$4;
НП — имя ячейки $L$6;
ККиЗ — имя ячейки $C$5;
СК — имя ячейки $C$6
Рассчитываем налоги (лист «Тах»)
Для расчета НДС и налога на прибыль запишем макросы, и тогда при нажатии кнопок «Рассчитать НДС» и «Рассчитать налог на прибыль» в таблицах появятся готовые значения. Это достаточно удобно, в том числе при внесении соответствующих корректировок в модели.
Скачайте данные макроса для кнопки «Рассчитать НДС» и «Рассчитать налог на прибыль».
Лист «Тах»
|
I. Налоги по операционной деятельности, тыс. руб. |
||||||||
|
Статья затрат |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Налог на имущество |
612 |
544 |
476 |
408 |
340 |
340 |
340 |
3059 |
|
Транспортный налог |
0 |
|||||||
|
Земельный налог |
0 |
|||||||
|
Итого операционные налоги, тыс. руб. |
612 |
544 |
476 |
408 |
340 |
340 |
340 |
3059 |
|
II. Расчеты по НДС, тыс. руб. |
||||||||
|
Статья затрат |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Исходящий НДС |
4164 |
6807 |
8349 |
10 252 |
12 603 |
15 145 |
15 145 |
72 465 |
|
НДС к возмещению |
9936 |
5682 |
5938 |
6261 |
6667 |
7178 |
7218 |
48 879 |
|
Итого НДС к уплате/возврату, тыс. руб. |
–5771 |
1126 |
2411 |
3991 |
5936 |
7967 |
7927 |
23 586 |
|
III. Налоги с доходов, тыс. руб. |
||||||||
|
Статья затрат |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
Налог на прибыль |
0 |
1931 |
3123 |
4603 |
6442 |
8433 |
8390 |
32 922 |
|
Налог с продаж |
0 |
|||||||
|
Итого налоги с доходов, тыс. руб. |
0 |
1931 |
3123 |
4603 |
6442 |
8433 |
8390 |
32 922 |
Как видим, за 2015 г. компании «Альфа» начислен налог на имущество в размере 612 тыс. руб. (27 810 x 2,2 % / 100 %, где 27 810 — остаточная стоимость основных средств и нематериальных активов; 2,2 % — процентная ставка налога на имущество). При этом НДС к возврату — 5771 тыс. руб. (4164 – 9936), налог на прибыль платить не надо.
Формируем отчеты
На базе рассмотренных таблиц автоматически формируются отчет о финансовых результатах (лист «PL») и отчет о движении денежных средств (лист «CF»).
Отчет о финансовых результатах
|
№ |
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
Итого |
|
+ |
Выручка от реализации продукции, товаров и услуг |
23 136 |
37 818 |
46 382 |
56 955 |
70 017 |
84 137 |
84 137 |
402 582 |
|
— |
Себестоимость реализованной продукции |
–12 523 |
–16 694 |
–19 154 |
–22 175 |
–25 895 |
–29 912 |
–29 975 |
–156 329 |
|
— |
Сырье и материалы, покупные комплектующие |
–5784 |
–9454 |
–11 596 |
–14 239 |
–17 504 |
–21 034 |
–21 034 |
–100 645 |
|
— |
Заработная плата производственных рабочих |
–4650 |
–4697 |
–4743 |
–4791 |
–4839 |
–4887 |
–4936 |
–33 543 |
|
— |
Страховые взносы |
–1395 |
–1409 |
–1423 |
–1437 |
–1452 |
–1466 |
–1481 |
–10 063 |
|
— |
Прочие производственные расходы |
–694 |
–1135 |
–1391 |
–1709 |
–2100 |
–2524 |
–2524 |
–12 077 |
|
+ |
Валовая прибыль |
10 613 |
21 123 |
27 229 |
34 779 |
44 121 |
54 226 |
54 162 |
246 253 |
|
Рентабельность по валовой прибыли, % |
46% |
56% |
59% |
61% |
63% |
64% |
64% |
61% |
|
|
— |
Накладные расходы |
–14 415 |
–14 559 |
–14 705 |
–14 852 |
–15 000 |
–15 150 |
–15 302 |
–103 983 |
|
+ |
EBITDA |
–3802 |
6564 |
12 524 |
19 927 |
29 121 |
39 075 |
38 860 |
142 270 |
|
Рентабельность по EBITDA, % |
–16% |
17% |
27% |
35% |
42% |
46% |
46% |
35% |
|
|
— |
Амортизация |
3090 |
3090 |
3090 |
3090 |
3090 |
3090 |
3090 |
21 630 |
|
+ |
EBIT |
–712 |
9654 |
15 614 |
23 017 |
32 211 |
42 165 |
41 950 |
163 900 |
|
Рентабельность по EBIT, % |
–3% |
26% |
34% |
40% |
46% |
50% |
50% |
41% |
|
|
— |
Проценты по кредитам к уплате |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Прибыль до налогообложения |
–712 |
9654 |
15 614 |
23 017 |
32 211 |
42 165 |
41 950 |
163 900 |
|
Налог на прибыль |
0 |
–1931 |
–3123 |
–4603 |
–6442 |
–8433 |
–8390 |
–32 922 |
|
|
+/- |
Чистая прибыль |
–712 |
7723 |
12 491 |
18 414 |
25 769 |
33 732 |
33 560 |
130 978 |
|
Рентабельность по NP, % |
–3% |
26% |
34% |
40% |
46% |
50% |
50% |
41% |
Отчет о движении денежных средств
|
№ |
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
Остаток на начало периода |
0 |
–27 716 |
–18 440 |
–3573 |
18 232 |
48 643 |
88 371 |
|
|
+/– |
Денежные потоки от текущих операций |
3185 |
9275 |
14 867 |
21 805 |
30 411 |
39 727 |
39 566 |
|
+ |
Поступления — всего |
27 300 |
44 625 |
54 731 |
67 207 |
82 620 |
99 282 |
99 282 |
|
+ |
Выручка от реализации продукции, товаров и услуг |
27 300 |
44 625 |
54 731 |
67 207 |
82 620 |
99 282 |
99 282 |
|
– |
Платежи — всего |
–24 116 |
–35 350 |
–39 864 |
–45 402 |
–52 208 |
–59 555 |
–59 716 |
|
– |
Расходы на приобретение сырья, материалов и покупных комплектующих |
–4505 |
–7363 |
–9031 |
–11 089 |
–13 632 |
–16 382 |
–16 382 |
|
– |
Заработная плата |
–8490 |
–8575 |
–8661 |
–8747 |
–8835 |
–8923 |
–9012 |
|
– |
Расходы по предоставлению услуг сторонними организациями |
–546 |
–893 |
–1095 |
–1344 |
–1652 |
–1986 |
–1986 |
|
– |
Накладные расходы без оплаты труда управленческого персонала |
–10 575 |
–10 681 |
–10 788 |
–10 895 |
–11 004 |
–11 114 |
–11 226 |
|
– |
Расчеты с бюджетом |
0 |
–7838 |
–10 290 |
–13 326 |
–17 084 |
–21 150 |
–21 111 |
|
+/– |
Денежные потоки от инвестиционных операций |
–30 900 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Поступления — всего |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Поступления от продажи внеоборотных активов |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Поступления от продажи акций других организаций |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Прочие поступления |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Платежи — всего |
–30 900 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Расходы в связи с приобретением, созданием, модернизацией, реконструкцией и подготовкой к использованию внеоборотных активов |
–30 900 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Платежи в связи с приобретением акций других организаций |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Прочие платежи |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+/– |
Денежные потоки от финансовых операций |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Поступления — всего |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Получение кредитов и займов |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Денежные вклады собственников |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+ |
Прочие поступления |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Платежи — всего |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Платежи собственникам в связи с выкупом у них акций организаций |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Уплата дивидендов по распределению прибыли в пользу собственников |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
– |
Прочие платежи |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
+/– |
Чистый денежный поток |
–27 716 |
9275 |
14 867 |
21 805 |
30 411 |
39 727 |
39 566 |
|
Остаток на конец периода |
–27 716 |
–18 440 |
–3573 |
18 232 |
127 936 |
Согласно отчету о финансовых результатах в 2015 г. компания понесет убыток в размере 712 тыс. руб. Однако уже в 2016 г. проект будет приносить доход: прибыль составит 7723 тыс. руб., а рентабельность — 26 %. Это достаточно высокий показатель.
Представленные в отчете о движении денежных средств данные позволяют сделать вывод, что в 2016 г. чистый денежный поток ожидается со знаком «+». Однако рост денежных средств прогнозируется только к концу 2018 г.
Оцениваем инвестиционную привлекательность проекта (лист «IP»)
Сначала рассчитываем чистый денежный поток:
|
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
Поток по основной деятельности |
3185 |
9275 |
14 867 |
21 805 |
30 411 |
39 727 |
39 566 |
|
Поток по инвестиционной деятельности |
–30 900 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Поток по финансовой деятельности |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Чистый денежный поток (NCF) |
–27 716 |
9275 |
14 867 |
21 805 |
30 411 |
39 727 |
39 566 |
|
NCF накопленным итогом |
–27 716 |
–18 440 |
–3573 |
18 232 |
48 643 |
88 371 |
127 936 |
|
NCF в периоде дисконтированный |
–25 544 |
7879 |
11 640 |
15 734 |
20 225 |
24 351 |
22 352 |
|
NCF в периоде дисконтированный накопленным итогом |
–25 544 |
–17 665 |
–6026 |
9708 |
29 933 |
54 284 |
76 636 |
Как видим, в 2015 г. NCF составляет –27 716 тыс. руб. (3185 – 30 900), а NCF в периоде дисконтированный — –25 544 тыс. руб. (–27 716) / (1 + 0,085)).
Далее рассчитаем показатели эффективности (внутреннюю норму доходности, чистую приведенную стоимость, срок окупаемости) и оценим стоимость бизнеса.
Расчет показателей эффективности инвестиционного проекта
|
KPI |
Целевые показатели |
Проект |
Δ, +/– |
|
Ставка дисконтирования |
8,5% |
||
|
Ставка капитализации |
3% |
||
|
WACC |
8,5% |
||
|
Внутренняя норма доходности (IRR) |
60,0% |
||
|
Чистая приведенная стоимость (NPV) |
76 636 |
||
|
Чистая терминальная стоимость (NTV) |
418 589 |
||
|
Срок окупаемости (СО), лет |
1 |
||
|
Дисконтированный срок окупаемости (СОд), лет |
3 |
||
|
Срок выхода на текущую окупаемость, лет |
1 |
||
|
Инвестиционная стоимость (EVD) |
495 225 |
Расчет инвестиционной стоимости (EVD)
|
Статья |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
Чистый денежный поток (NCF) |
–27 716 |
9275 |
14 867 |
21 805 |
30 411 |
39 727 |
39 566 |
|
Чистая приведенная стоимость (NPV) |
76 636 |
110 865 |
111 013 |
105 582 |
92 752 |
70 224 |
36 466 |
|
Чистая терминальная стоимость (NTV) |
418 589 |
418 589 |
418 589 |
418 589 |
418 589 |
418 589 |
418 589 |
|
Инвестиционная стоимость (EVD) |
495 225 |
529 454 |
529 603 |
524 172 |
511 341 |
488 814 |
455 056 |
В Excel чистая приведенная стоимость (NPV) определяется формулой ЧПС (d;ЧДПIC), где d — ставка дисконтирования (рис. 2).
Если значение NPV положительное, то проект является прибыльным.
В нашем примере чистая приведенная стоимость в 2015 г. составила 76 636 тыс. руб.
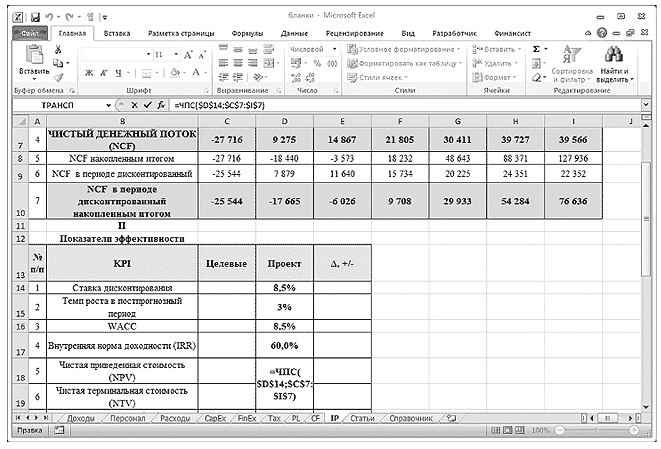
Рис. 2. Пример расчета чистой приведенной стоимости (NPV)
Внутренняя норма доходности (IRR) определяется по формуле ВСД (ЧДПIC;0), где ВСД — внутренняя ставка доходности, и обозначает процентный порог, затраты на капитал выше которого нецелесообразны.
Инвестиционная стоимость бизнеса (EVD) представляет собой сумму чистой приведенной и терминальной стоимости. В нашем примере инвестиционная стоимость составляет 495 225 тыс. руб. (76 636 + 418 589).
Обратите внимание: значение чистой терминальной стоимости зависит от ставки капитализации. Поэтому на листе «IP» пользователь может выбрать ставку капитализации. Изменение ставки капитализации приводит соответственно к изменению чистой приведенной стоимости и, в конечном счете, инвестиционной стоимости бизнеса.
Предложенная модель полностью автоматизированная, что позволяет быстро, а главное — безошибочно проанализировать инвестиционный проект и оценить его. Изменяя те или иные параметры, можно выбрать оптимальный вариант его реализации.
Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.
Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.
Скачать пример
Оценка целесообразности проекта с помощью NPV
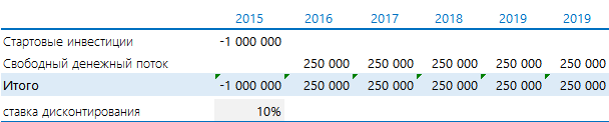
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.
Оцениваем NPV проекта. Напомню формулу этого показателя:
Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:
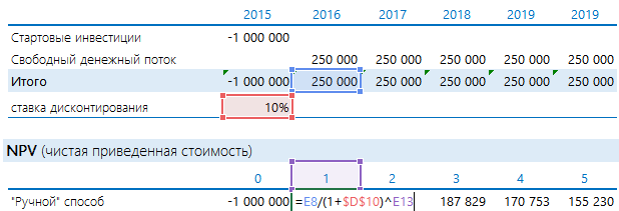
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.
Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.
Получается «-52 303». Проект невыгоден.
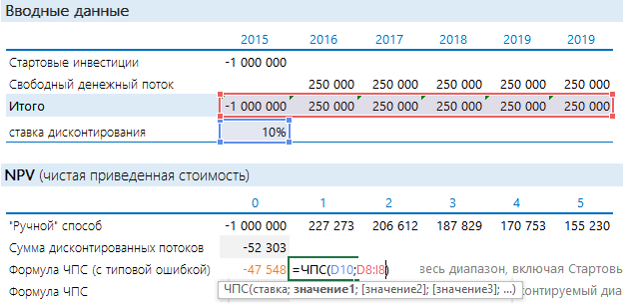
Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):
ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:
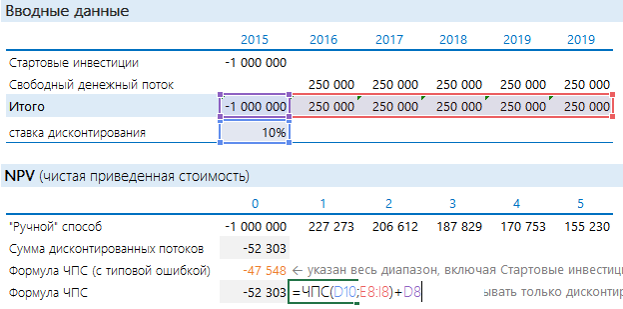
Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:
Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.
Оценка целесообразности проекта с помощью IRR
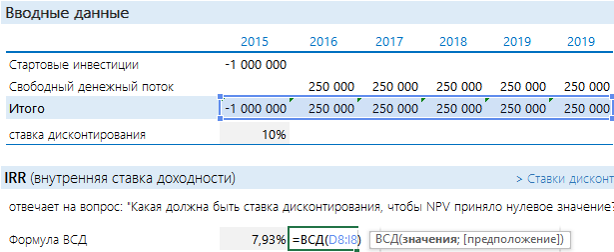
Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования < IRR, то проект стоит принять, если нет – отказаться. Рассчитать IRR с помощью Excel очень просто: подставляем в функцию ВСД итоговый денежный поток.
IRR оказался меньше ставки доходности. Проект невыгодный (тот же вывод, что и при NPV).
NPV и IRR по праву считаются главными экономическими критериями. Их используют и для инвестиционной оценки проектов, и для оценки стоимости существующего бизнеса. В том числе, показатель EVA (Economic Value Added) считается хорошим критерием в том числе потому, что при правильном расчете он равен NPV.
Но кроме всего прочего, NPV и IRR могут быть использованы финансистами в более прикладных вопросах, например, при общении с банками на тему реальной кредитной ставки. Как – давайте посмотрим.
Аннуитеты – любимая банковская цифра
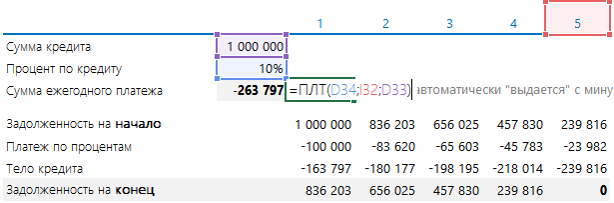
Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:
ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)
В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:
Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.
В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.
Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.
Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:
Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.
Нюансы и тонкости
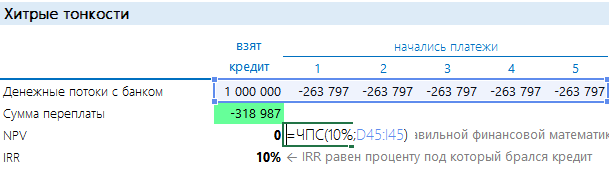
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.
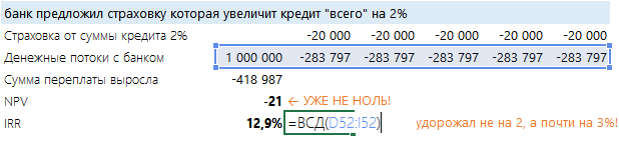
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:
В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…
Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.
Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.
К наиболее типичным методам финансового анализа можно отнести анализ затрат, период окупаемости инвестиций, денежный поток и внутрифирменный коэффициент окупаемости инвестиций. Каждый из этих методов мы рассмотрим далее.
Анализ затрат
Анализ затрат является довольно простым методом. В этом случае вы определяете стоимость производства продукта (которым в нашем случае является проект) и сопоставляете ее с ожидаемыми выгодами. Если выгоды перекрывают затраты, то, скорее всего, данный проект будет принят к исполнению.
При выполнении этого анализа не забывайте включить все затраты. Обычно сюда входит совокупная стоимость таких процессов, как практическая реализация проекта, текущая поддержка, сопровождение (техобслуживание), содержание соответствующего персонала, устранение проблем, которые не удалось решить в ходе выполнения проекта, и т.д. В этой методике полная стоимость проекта рассчитывается не по факту выполненных работ, а на основании результатов, полученных в итоге выполнения этого проекта, и только после того, как они будут внедрены в данной организации.
Период окупаемости инвестиций
Период окупаемости инвестиций — это количество времени, которое требуется для того, чтобы окупились первоначальные инвестиции в данный проект. Совокупная стоимость проекта сравнивается с получаемыми доходами и вычисляется время, которое требуется для того, чтобы полученные доходы превысили затраты на реализацию данного проекта. Когда выполняется сравнение двух или большего числа проектов сходного масштаба и сложности, как правило, выбирается проект с наименьшим периодом окупаемости инвестиций. У этого метода нет «универсальной» формулы, которая позволяла бы быстро найти требуемое решение. Если, например, себестоимость проекта равняется 100 000 долл., а ожидаемые доходы составляют 25 000 долл. в квартал, то период окупаемости инвестиций составит один год.
Дисконтированные (приведенные) денежные потоки
Если вам предложат 1 000 долл. сегодня или те же 1 000 долл. через два года, какой вариант вы предпочтете? Ответ предсказуем, поскольку вложив сейчас эту сумму в банк или какое-либо предприятие, через два года вы будете иметь с нее прибыль. Например, под 6% годовых такая инвестиция на двухлетний период составит 1 123,60 долл. (в нынешних долларах, разумеется).
Метод дисконтированного (приведенного) денежного потока сравнивает стоимость будущих денежных потоков с нынешними долларами. Иными словами, он выполняет операцию, противоположную той, которую мы только что объяснили. Зная, что ваш проект принесет через два года сумму, равную 1 123,60 долл. (это так называемая будущая стоимость — Future Value, или FV), вы бы смогли с помощью метода дисконтированного (приведенного) денежного потока определить нынешнюю стоимость этой суммы. Ответ, конечно же, таков: 1 000 долл.
Чтобы иметь представление о дисконтированных денежных потоках, вы должны знать стоимость соответствующих инвестиций в нынешних долларах, иначе говоря, приведенную стоимостью (Present Value, или PV), которая вычисляется следующим образом: PV=FV/(1+i)n. Эта формула говорит о том, что приведенная стоимость равняется будущей стоимости инвестиций, деленной на один, плюс процентная ставка, возведенная в степень, равную количеству периодов, на которые мы инвестируем нашу сумму.
Вам не нравится математика? Но это же так просто! В Excel предусмотрена встроенная функция для вычисления приведенной стоимости (наряду со множеством других функций, позволяющих выполнять финансовые расчеты). На рисунке ниже показана группа Function Library (Библиотека функций), предусмотренная на вкладке Formulas (Формулы), и часть списка финансовых функций, встроенных в Excel.
Рис. 1. Финансовые функции, представленные в библиотеке функций и перечень финансовых функций
Вернемся, однако, к нашей формуле для вычисления приведенной стоимости инвестиций. Выберите в списке функций элемент PV (в русифицированной версии Excel — ПС (Приведенная стоимость)). На экране появится диалоговое окно Function Arguments (Аргументы функции), показанное на рис. 2.
Рис. 2. Диалоговое окно Function Arguments для функции PV
Диалоговое окно Function Arguments предназначено для ввода значений отдельных элементов выбранной вами функции, которые необходимы для вычисления приведенной стоимости. В текстовом поле Rate (Ставка) этого диалогового окна следует ввести величину процентной ставки за определенный временной период. Вы можете ввести 6% или 0,06 (предполагается, что процент начисляется ежегодно по методу сложных процентов). Если бы процент начислялся ежеквартально (по тому же методу), тогда вам нужно было бы разделить указанную величину процентной ставки на 4, а затем ввести полученный результат в поле Rate (Ставка).
Ниже находится поле Nper (Кпер), в котором вводят количество временных периодов. Мы инвестируем нашу сумму на два года. Величина выплаты (поле Pmt (Плт)) равняется 0, поскольку мы не производим выплат по этой инвестиции, а просто хотим знать величину всей этой суммы в нынешних долларах. Далее находится поле FV (Бс), в котором вводят значение будущей стоимости. В нашем примере будущая стоимость инвестиции равняется -1 123,60 долл. Если в поле FV (Бс) ввести положительное число, то результат вычисления этой функции будет отрицательным. На рис. 3. показано диалоговое окно Function Arguments со значениями аргументов функции PV (Приведенная стоимость), введенных в соответствующие поля.
Рис. 3. Аргументы функции PV
Вместо числовых значений в полях диалогового окна Function Arguments (Аргументы функции) можно дать адрес ячейки, в которой введено нужное вам значение. Предположим, например, что в ячейке С1 введено число 0,06. В этом случае в текстовом поле Rate (Процентная ставка) диалогового окна Function Arguments достаточно указать только адрес упомянутой выше ячейки, т.е. С1. Непосредственно под текстовыми полями диалогового окна Function Arguments представлен результат наших вычислений функции PV (Приведенная стоимость). В нашем случае PV=1000. Помимо диалогового окна Function Arguments аргументы данной функции отображены в строке формул программы Excel, а также в активизированной ячейке (А1 в данном случае) (см. рис. 3.).
Как видите, сначала следует значение процентной ставки, затем количество периодов и будущая стоимость. Обратите внимание, что в данной функции отсутствует значение между двумя запятыми. Это означает, что один из аргументов функции равен нулю (в нашем случае величина выплаты (поле Pmt (Плт)). (В русифицированной версии программы Excel аргументы функций следует отделять друг от друга точкой с запятой (;)) Как только вы
щелкнете на кнопке ОК, в ячейке А1 появится результат вычисления функции, в нашем случае — 1 000 долл.
Для того чтобы воспользоваться функцией PV (ПС), не обязательно перебирать ряд интерфейсных элементов программы. Для этого достаточно просто ввести =pv() в ячейке А1. В результате ваших действий на экране появится экранная подсказка, в которой приведен синтаксис данной функции, т.е. сокращенные названия и очередность ее аргументов (рис. 4).
Рис. 4. Всплывающая подсказка с перечнем аргументов функции PV
Если вы не знаете точно, какие значения следует вводить в качестве аргументов функции, откройте окно справочной системы Excel. В единственном текстовом поле этого окна введите PV (ПС для русифицированной Excel) и нажмите клавишу Enter. Справочная система немедленно отобразит всю необходимую информацию по интересующей вас функции.
Если вы, как и большинство других пользователей, раздражаетесь из-за того, что окно справочной системы Excel время от времени скрывается за вашей электронной таблицей (когда вы пытаетесь выполнять пошаговые инструкции, приведенные в этом окне), выполните следующее: скопируйте, а затем вставьте информацию, представленную в окне справки, в электронную таблицу, а затем, когда вы введете нужные значения в формулу, удалите эту информацию.
Допустим, что ваш комитет по отбору проектов рассматривает три проекта, из которых необходимо выбрать самый подходящий. Ожидается, что проект А принесет через два года 130 000 долл. прибыли; проект В — 140 000 долл. через три года; а проект С — 148 000 долл. через четыре года. Какому из этих проектов должен отдать предпочтение комитет, если свое решение он основывает лишь на использовании метода дисконтированного (приведенного) денежного потока, полагая, что процентная ставка равняется 8%? Самую высокую прибыль обеспечивает проект А. На рис. 5 показаны расчетные формулы по каждому проекту и полученные с их помощью результаты.
Рис. 5. Сравнение проектов с помощью метода дисконтированного (приведенного) денежного потока