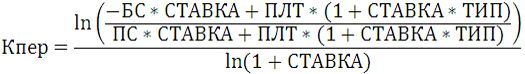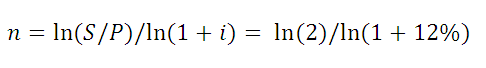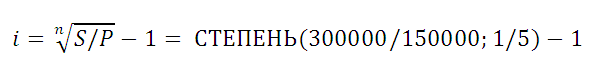Расчет срока вклада в excel

2. Вычисление ренты. Расчетов сроков вклада (займа).

Рассмотрим схему с многократными взносами или выплатами.

Поток платежей, все члены которого имеют одинаковую величину R и разделены равными промежутками времени, называют постоянной рентой.

Один из возможных вариантов такого потока <-Р, -R, -R, . -R, S>, т.е. начальный взнос Р и последующие выплаты R дают в итоге S. Если платежи производятся в конце периодов, то ренту называют обыкновенной, или постнумерандо. Если же платежи происходят в начале периодов, то ренту называют пренумерандо.

Для расчетов используется формулы:

Р — современное значение.

S — будущее значение.

R — периодическая выплата.

r — процентная ставка за период.

n — количество периодов.

type — тип ренты, если type = 0 или опущен, то рента постнумерандо (выплата в конце периода), если type = 1, то рента пренумерандо (выплата в начале периода).

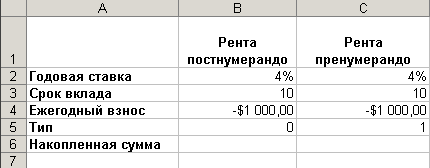
На счет в банке вносится ежегодно сумма 1000 долл. в течение 10 лет 1) в конце каждого года 2) в начале каждого года. Годовая ставка — 4%. Какая сумма будет на счете после 10 лет в обоих случаях?

Перейдите новый лист и переименуйте его в Задача 5. Для проведения расчетов создайте таблицу согласно рис. 9.

Если платежи осуществляются в конце периодов (рента постнумерандо), то тип = 0 (или его можно опустить). В этом случае формула для расчета накопленной суммы будет: =БС(B2;B3;B4;;B5) или = БС( 4%;10; -1000), где ПЛТ (выплата за каждый период)=-1000 $.

Если же сумма вносится в начале года (рента пренумерандо), то формула принимает вид: =БС(C2;C3;C4;;C5) или = БС( 4%;10; -1000; ;1).

Сравните полученные результаты и сделайте вывод.

Сохраните изменения в файле Финансовые расчеты.xls.

Задача №6 (самостоятельно).

Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000 долларов. Какая схема выгоднее?

Примечание. Для расчетов создайте на новом листе Задача 6 таблицу согласно рис. 10.

Сравните полученные результаты и сделайте вывод. Сохраните изменения в файле Финансовые расчеты.xls.

За какой срок в годах сумма, равная 75 000 долл., достигнет 200 000 долл. при начислении процентов по сложной ставке 15% раз в году и поквартально.

Перейдите новый лист и переименуйте его в Задача 7. Для проведения расчетов создайте таблицу согласно рис. 11.

Ставку за квартал в ячейке С3рассчитайте самостоятельно.

Для расчета срока вклада воспользуемся новой финансовой функцией КПЕР, которая возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.

Синтаксис функции кпер.

СТАВКА— процентная ставка за период.

ПЛТ — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам и не включает налогов и сборов.

ПС— приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.

БС— требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент БС опущен, то он полагается равным 0.

Тип— число 0 или 1, обозначающее, когда должна производиться выплата.

Рассчитаем срок вклада, если начисление процентов производится в конце каждого года. Для этого в ячейку В5 введите формулу: =КПЕР(B3;;B2;B4)или=КПЕР(15%;;-75000;200000). В данном случае аргументПЛТопущен, т.к. не производится никаких дополнительных вкладов.

Аналогичным образом в ячейке С5 рассчитайте срок вклада, если начисление процентов производится по кварталам. Обратите внимание, что в данном случае результатом расчета будет количество кварталов. Поэтому полученный результат необходимо разделить на 4.

Сравните полученные результаты и сделайте вывод.

Сохраните изменения в файле Финансовые расчеты.xls.

Задача №8 (самостоятельно).

Ссуда 63 200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб. Рассчитайте срок погашения ссуды.

Примечание. Для расчетов создайте на новом листе Задача 8 таблицу согласно рис. 12.

Сохраните изменения в файле Финансовые расчеты.xls.

Источник

Примеры функции БС в Excel с фиксированной процентной ставкой

Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.

Примеры использования финансовой функции БС в Excel

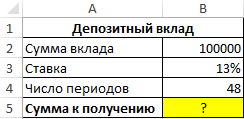
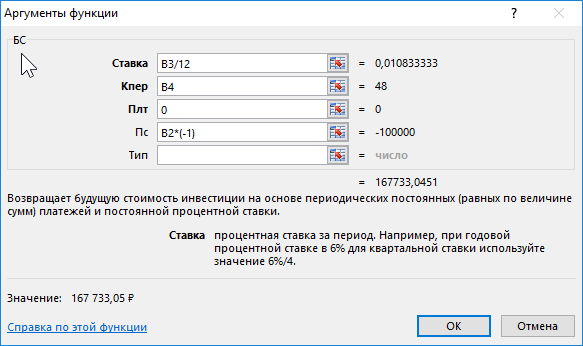
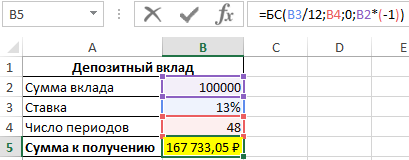
Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?

Формула для расчета:

• B3/12 – ставка за период (капитализация выполняется ежемесячно);
• B4 – число периодов капитализации вклада;
• 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
• B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).

Спустя 4 года вкладчик получит 167 733 рубля.

Расчет суммы долга по кредиту по состоянию на 30-й период погашения

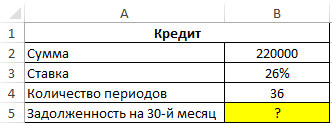
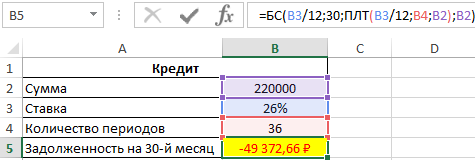
Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?

Формула для расчета:

• B3/12 – месячная процентная ставка;
• 30 – номер периода для расчета остатка задолженности;
• ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
• B2 – тело кредита.

Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.

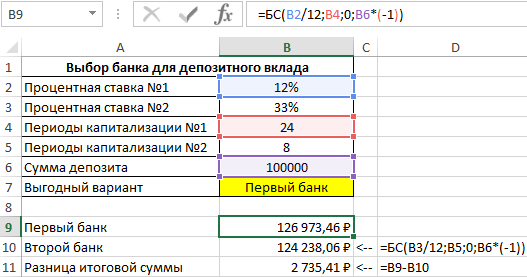
Сравнительный инвестиционный анализ условий депозита в банке

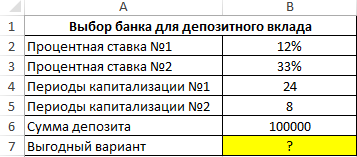
Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:

1. Ставка – 12% годовых, капитализация – ежемесячная.
2. Ставка – 33% годовых, капитализация – ежеквартальная.

Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.

Формула для расчета:

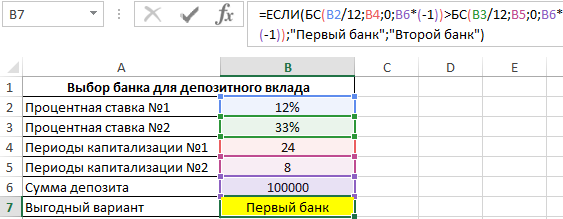
БС(B3/12;B5;0;B6*(-1));»Первый банк»;»Второй банк»)’ >

С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:

Выведем результаты расчетов функций БС и разницу сумм:

Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.

Особенности использования финансовой функции БС в Excel

Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:

=БС( ставка;кпер;плт ;[пс];[тип])

• ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
• кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
• плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
• [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
• [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.

1. При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
2. Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
3. Функция БС использует в расчетах следующую формулу:
4. Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
5. Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
6. Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.

Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).

Источник

Функция КПЕР для расчета количества периодов погашений в Excel

Функция КПЕР в Excel предназначена для расчета количества периодов выплат погашения определенной суммы задолженности при известных значениях процентной ставки (простые проценты), суммы платежа для каждого периода (фиксированное значение), начальной суммы задолженности или общей суммы долга с учетом процентов, и возвращает соответствующее числовое значение.

Примеры как использовать функцию КПЕР в Excel

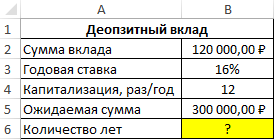
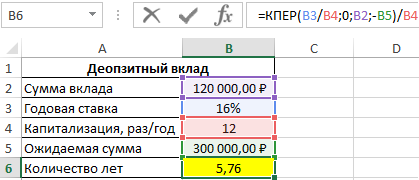
Пример 1. Вкладчик внес депозит под 16% годовых на сумму 120000 рублей с ежемесячной капитализацией вклада (простые проценты). Сколько лет потребуется для накопления 300000 рублей?

Формула для расчета:

• B3/B4 – процентная ставка за период капитализации;
• 0 – числовое значение, характеризующее ежемесячный платеж (дополнительное пополнение депозитного счета не производится);
• B2 – начальная инвестиция;
• -B5 – конечная сумма по окончанию договора.

Возвращенный функцией КПЕР результат разделен на количество периодов капитализации в году для расчета числа лет, необходимых для накопления требуемой суммы. Результат расчетов:

Вкладчик должен оставлять деньги на депозитном счете на протяжении почти 6 лет.

Расчет реальной суммы долга с процентами и переплатой в Excel

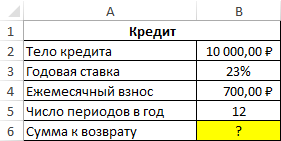
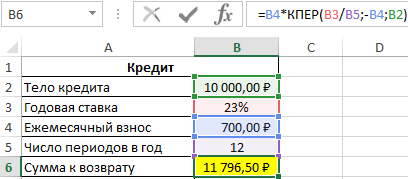
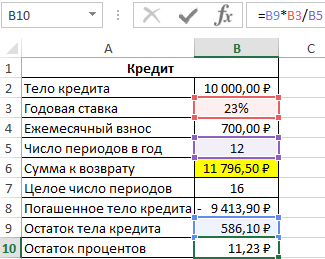
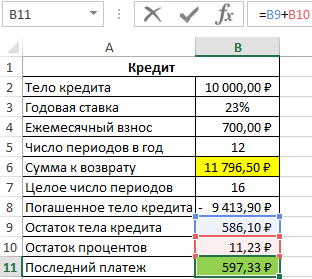
Пример 2. Клиенту банка был выдан кредит на сумму 10000 рублей под 23% годовых с ежемесячной оплатой 700 рублей. Сколько всего денег получит банк по окончанию срока кредитного договора?

Формула для расчета:

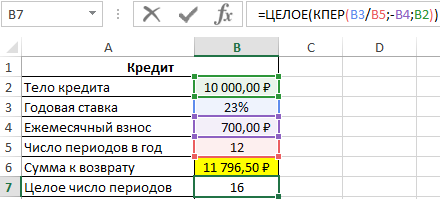
Общая сумма кредита рассчитывается как произведение фиксированной суммы ежемесячного платежа и количества периодов выплат. В данном случае количество периодов равно 16,85 (нецелое число), значит, последняя выплата должна составить меньше 700 рублей. Найдем целое число периодов:

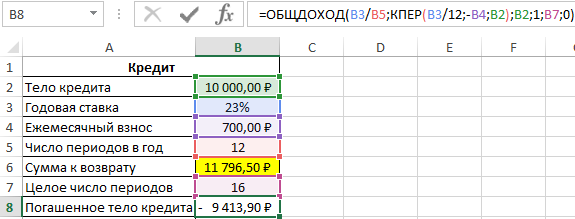
Чтобы определить, какую часть тела кредита было погашено за 16 целых периодов выплат, воспользуемся следующей функцией:

За последний неполный период необходимо вернуть следующую часть тела кредита:

Рассчитаем оставшиеся проценты к уплате:

Так как платеж включает в себя оплату тела кредита и процентов, насчитанных за период, определим размер последнего платежа по формуле:

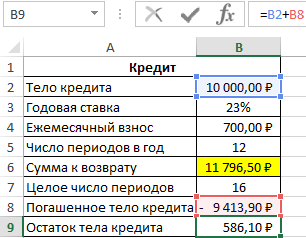
Общая сумма, которую получит банк, составит 11796 рублей, а размер последнего платежа – 597 рублей.

Расчет сроков погашения кредита с помощью функции КПЕР

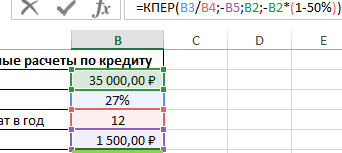
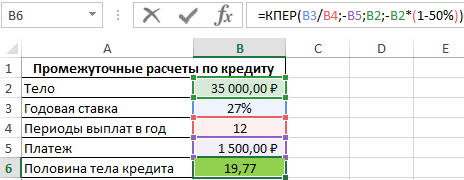
Пример 3. Банк выдал кредит на сумму 35000 рублей под 27% годовых. Размер ежемесячного платежа составляет 1500 рублей. Через сколько месяцев клиент выплатить 50% кредита?

Исходная таблица данных:

На основании тождества аннуитетных платежей (сумма величины платежа в погашение тела кредита за все периоды, тела кредита и будущей стоимости равна нулю, то есть ОБЩДОХОД+ПС+БС=0) используем следующую формулу:

Выражение -B2*(1-50%)) характеризует будущую стоимость и было получено из уравнения:

Для выплаты 50% кредита потребуется вносить ежемесячный платеж на протяжении примерно 20 месяцев.

Особенности использования функции КПЕР в Excel

Функция КПЕР используется для решения финансовых задач совместно с функциями ПЛТ, БС, СТАВКА, ПС и имеет следующую синтаксическую запись:

=КПЕР( ставка;плт;пс ;[бс];[тип])

Описание аргументов (первые три аргумента – обязательные для заполнения):

• ставка – числовое значение, характеризующее ставку за 1 период выплат (для ссуд) или капитализации (для депозитных вкладов). Аргумент может быть указан в виде дробного числа или в качестве значения в процентном формате (например, 14,5% или 0,145 – эквивалентные варианты записи). Если в условии задачи указана годовая ставка, необходимо выполнить пересчет по формуле Rп=Rг/12, где Rп – ставка за период, Rg – годовая ставка, 12 – число месяцев в году.
• плт – числовое значение, соответствующее сумме выплаты за период, которая является фиксированной величиной (простые проценты).
• пс – числовое значение, характеризующее текущую стоимость инвестиции (например, сумма, выданная кредитной организацией в долг клиенту, или сумма средств, положенных на депозитный счет в банк).
• [бс] – числовое значение, соответствующее будущей стоимости инвестиции. Например, данный аргумент может характеризовать сумму, которую получит вкладчик по окончанию действия договора по депозитному вкладу. Если аргумент явно не указан или принимает значение 0 (нуль), функция КПЕР вернет количество периодов выплат до полного погашения задолженности. Аргумент необязателен для заполнения, по умолчанию принимается значение 0.
• [тип] – необязательный аргумент, характеризующий способ выплат (0 – выплата на конец периода, 1 – выплата на начало периода).

1. Функция КПЕР возвращает код ошибки #ЧИСЛО! В случае, если сумма платежа за каждый период меньше, чем произведение начальной суммы инвестиции и ставки за период, при этом будущая стоимость инвестиции равна 0 (ситуация при расчете количества периодов для полного возврата задолженности), а выплата производится в конце периода (то есть, аргумент [тип] или явно указан как 0 (нуль).
2. Указанная выше особенность работы функции КПЕР вытекает из алгоритма, который она использует для расчета:
3. Все аргументы функции КПЕР должны указываться в виде числовых значений или конвертируемых в числа текстовых срок. Иначе рассматриваемая функция будет возвращать код ошибки #ЗНАЧ!.

1. Фактически, функция КПЕР позволяет определить количество периодов, по окончанию последнего из которых будущая стоимость инвестиции примет указанное значение.
2. В случае с кредитом, считается, что задолженность погашена полностью, если будущая стоимость инвестиции равна 0 (нулю).
3. Также функция КПЕР позволяет вычислить количество периодов капитализации депозитного вклада, необходимых для достижения требуемой суммы накоплений.
4. Для расчета количества периодов выплаты задолженности с нулевой процентной ставкой можно использовать формулу =A1/A2, где A1 – будущая стоимость, A2 – фиксированная сумма выплат за период.

Источник

Почему важно иметь под рукой калькулятор вкладов

Если вы думаете сделать вклад, то важно понять, какой доход вы получите к концу срока. Кроме того, важно понимать какая сумма процентов будет выплачиваться каждый месяц. Эти проценты можно тратить и деньги будут работать на вас.

 Loading …

Еще одной важной причиной держать калькулятор вкладов всегда под рукой является необходимость проверки вашего банка. Банк не всегда верно считает и выплачивает проценты по вкладу. Чтоб проверить банк, нужно иметь независимый инструмент для расчета дохода по депозиту.

? Скачать калькулятор вкладов в Excel

Ссылка на калькулятор представлена ниже.
Данный калькулятор подходит для расчета вкладов ВТБ, Сбербанка, банка Тинькофф, Райффайзенбанка и других банков РФ.
Скачать калькулятор в Excel можно по ссылке Калькулятор вкладов Excel.

Профессиональные калькуляторы вкладов

Мы рекомендуем скачать себе на телефон профессиональные мобильные калькуляторы вкладов.
Ниже представлены 2 калькулятора вкладов, которые можно установить на свой телефон. После их установки не нужен Excel. Да и расчёт получается точнее, т.к. есть учёт курсов валют и ключевой ставки ЦБ.

Бесплатный калькулятор вкладов для Windows 10

• Точный расчет вклада любого банка РФ
• Учет пополнений и снятий
• Возможность посчитать несколько вкладов
• Абсолютно бесплатен
• Понятная и подробная статистика
• Возможность учесть фиксированную и плавающую ставку, неснижаемый остаток, макс. дату пополнения

Банковский калькулятор вкладов для Андроид

• Подходит для расчета вкладов любого банка: Тинькофф, Сбербанка, ВТБ, МКБ
• Учитывает при расчете налоги и ставку рефинансирования
• Есть возможность задать пополнения и снятия
• Удобный график выплат и возможность посмотреть ваш доход на сегодня
• Возможность учитывать несколько вкладов и знать сколько денег всего

Основные возможности, которые предоставляет калькулятор вкладов в Excel

1. Расчет вклада с помесячной и годовой капитализацией
2. Расчет валютных и рублевых вкладов.
3.  Расчет суммы вклада в конце срока
4. Расчет процентов по вкладу.
5. Учет налогов, если ставка по вкладу превышает ставку, установленную ЦБ.
6. Достоинства данного калькулятора — что его можно использовать офлайн, т.е. без выхода в интернет.

Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.

Калькулятор вкладов поможет вам правильно выбрать вклад. Просто нужно посчитать и сравнить несколько вкладов. Доходность какого будет лучше, тот и выбрать.
Если у вас один рублевый вклад, а один валютный, то придется провести конверсию по курсу ЦБ.

Также доступна онлайн версия депозитного калькулятора — калькулятор вкладов онлайн

Онлайн версия калькулятора является достаточно точной и позволяет посчитать различные вклады при различных условиях. К примеру вклады  могут иметь плавающую ставку в зависимости от сроков — чем больше срок, тем выше ставка.

Калькулятор позволяте получить результаты расчета в Excel файле. Это полноценный Excel 2003. Можно распечатать ваши расчеты для похода в банк.
Все это можно рассчитать с помощью онлайн версии кредитного калькулятора, просто задаете номер дня и новую ставку.

Далее нажимаем рассчитать и получаем график платежей по вкладу и сумму к получению. Аналогично, если сумма вклада зависит от суммы — устанавливаем переключатель «Плавающая в зависимости от размера» для процентной ставки. Отдельный интерес составляет учет налогов — все вклады, ставка по которым превышает ставку рефинансирования ЦБ + 5 процентов. Для них происходит начисление налога по вкладу в размере 35 процентов от налогооблогаемой части.

Читайте также: Налоги на вклад: как они начисляются? Пример расчета
Следует отменить, что с налогов по ставке 35 процентов нельзя получить налоговый вычет на ипотеку, т.е. хотя это налоги на ваши доходы, которые являются официальными. Банк сам отчисляет налог и автоматически уменьшает доход по вкладу на сумму налогов.

Однако нужно внимательно проверять банк — рассчитывать вклад с помощю указанного выше депозитного калькулятора. Оставляйте свои пожелания к калькулятору вкладов. Все ваши пожелания будут учитываться в доработках .

Популярные вопросы по вкладам

Как рассчитать проценты по вкладу в банке?

Для расчета нужно сумму вклада умножить на число дней, в течение которого был открыт вклад, умножить на ставку по депозиту, деленную на 100%. Полученную сумму нужно разделить на число дней в году(365 или 366). Проще воспользоваться универсальным калькулятором вкладов на нашем сайте.

Что такое процентная ставка по вкладу

Процентная ставка по вкладу — это число, которое определяет доходность вклада. Чем она выше, тем больше доходность. Различают простую и эффективную ставку по вкладу. Ставка по вкладам зависит от ключевой ставки ЦБ.

Что такое капитализация процентов по вкладу?

Капитализация процентов по вкладу — это плюсование процентов, которые начислены за каждый период, к сумме вклада. К примеру, вы положили вклад на 1000 р и получили через месяц доход 10 р, эти 10 рублей плюсуются к сумме вклада — 1000 + 10 = 1010.

На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.

Что значит проценты не капитализируются?

Проценты не капитализируются — это значит проценты не прибавляются к сумме вклада каждый месяц. Обычно они выплачиваются на определенный счет в виде дохода. Их можно снимать и пользоваться этими деньгами. С одной строны это хорошо, сразу получаешь доход. С другой — плохо, т.к. доход по вкладу не растет

Рассмотрим
схему с многократными взносами или
выплатами.

Поток
платежей, все члены которого имеют
одинаковую величину R
и разделены
равными промежутками времени, называют
постоянной
рентой.

Один
из возможных вариантов такого потока
{-Р, -R, -R, …, -R, S},
т.е. начальный
взнос Р и
последующие выплаты R
дают в итоге S.
Если платежи
производятся в конце периодов, то ренту
называют обыкновенной,
или постнумерандо.
Если же платежи
происходят в начале периодов, то ренту
называют пренумерандо.

Для
расчетов используется формулы:

Р
— современное
значение.

S
— будущее
значение.

R
— периодическая
выплата.

r
— процентная
ставка за период.

n
— количество
периодов.

type
— тип ренты, если type
= 0 или опущен,
то рента постнумерандо (выплата в конце
периода), если type
= 1, то рента
пренумерандо (выплата в начале периода).

Задача №5. На счет в банке вносится ежегодно сумма 1000 долл. в течение 10 лет 1) в конце каждого года 2) в начале каждого года. Годовая ставка — 4%. Какая сумма будет на счете после 10 лет в обоих случаях?

Решение.

1. Перейдите
   новый лист и переименуйте его в Задача
   5. Для проведения
   расчетов создайте таблицу согласно
   рис. 9.

Рис.9.

1. Если
   платежи осуществляются в конце периодов
   (рента постнумерандо), то тип = 0 (или его
   можно опустить). В этом случае формула
   для расчета накопленной суммы будет:
   =БС(B2;B3;B4;;B5)
   или = БС(
   4%;10; -1000), где
   ПЛТ (выплата за каждый период)=-1000 $.

2. Если
   же сумма вносится в начале года (рента
   пренумерандо), то формула принимает
   вид: =БС(C2;C3;C4;;C5)
   или = БС( 4%;10;
   -1000; ;1).

3. Сравните
   полученные результаты и сделайте вывод.

1. Сохраните
   изменения в файле Финансовые
   расчеты.xls.

Задача №6 (самостоятельно). Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000 долларов. Какая схема выгоднее?

Примечание.
Для расчетов
создайте на новом листе Задача
6 таблицу согласно
рис. 10.

Рис.10.

Сравните
полученные результаты и сделайте вывод.
Сохраните изменения в файле Финансовые
расчеты.xls.

Задача №7. За какой срок в годах сумма, равная 75 000 долл., достигнет 200 000 долл. при начислении процентов по сложной ставке 15% раз в году и поквартально.

Решение.

1. Перейдите
   новый лист и переименуйте его в Задача
   7. Для проведения
   расчетов создайте таблицу согласно
   рис. 11.

Рис.
11.

1. Ставку
   за квартал в ячейке С3рассчитайте
   самостоятельно.

2. Для
   расчета срока вклада воспользуемся
   новой финансовой функцией КПЕР,
   которая возвращает общее количество
   периодов выплаты для инвестиции на
   основе периодических постоянных выплат
   и постоянной процентной ставки.

Синтаксис функции кпер.

КПЕР(ставка;плт;пс;бс; тип)

СТАВКА—
процентная ставка за период.

ПЛТ —
выплата, производимая в каждый период;
это значение не может меняться в течение
всего периода выплат. Обычно платеж
состоит из основного платежа и платежа
по процентам и не включает налогов и
сборов.

ПС—
приведенная к текущему моменту стоимость
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.

БС—
требуемое значение будущей стоимости
или остатка средств после последней
выплаты. Если аргумент БС опущен, то он
полагается равным 0.

Тип—
число 0 или 1, обозначающее, когда должна
производиться выплата.

1. Рассчитаем
   срок вклада, если начисление процентов
   производится в конце каждого года. Для
   этого в ячейку В5 введите формулу:
   =КПЕР(B3;;B2;B4)или=КПЕР(15%;;-75000;200000).
   В данном случае аргументПЛТопущен, т.к. не производится никаких
   дополнительных вкладов.

2. Аналогичным
   образом в ячейке С5 рассчитайте срок
   вклада, если начисление процентов
   производится по кварталам. Обратите
   внимание, что в данном случае результатом
   расчета будет количество кварталов.
   Поэтому полученный результат необходимо
   разделить на 4.

3. Сравните
   полученные результаты и сделайте вывод.

1. Сохраните
   изменения в файле Финансовые
   расчеты.xls.

Задача №8 (самостоятельно). Ссуда 63 200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб. Рассчитайте срок погашения ссуды.

Примечание.
Для расчетов
создайте на новом листе Задача
8 таблицу согласно
рис. 12.

Рис.12.

Сохраните
изменения в файле Финансовые
расчеты.xls.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.

Примеры использования финансовой функции БС в Excel

Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?

Исходные данные:

Формула для расчета:

Описание аргументов:

• B3/12 – ставка за период (капитализация выполняется ежемесячно);
• B4 – число периодов капитализации вклада;
• 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
• B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).

Результаты расчета:

Спустя 4 года вкладчик получит 167 733 рубля.



Расчет суммы долга по кредиту по состоянию на 30-й период погашения

Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?

Исходные данные:

Формула для расчета:

=БС(B3/12;30;ПЛТ(B3/12;B4;B2);B2)

Описание аргументов:

• B3/12 – месячная процентная ставка;
• 30 – номер периода для расчета остатка задолженности;
• ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
• B2 – тело кредита.

Полученный результат:

Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.

Сравнительный инвестиционный анализ условий депозита в банке

Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:

1. Ставка – 12% годовых, капитализация – ежемесячная.
2. Ставка – 33% годовых, капитализация – ежеквартальная.

Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.

Исходные данные:

Формула для расчета:

С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:

Выведем результаты расчетов функций БС и разницу сумм:

Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.

Особенности использования финансовой функции БС в Excel

Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:

=БС(ставка;кпер;плт;[пс];[тип])

Описание аргументов:

• ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
• кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
• плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
• [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
• [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.

Примечание 1:

1. При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
2. Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
3. Функция БС использует в расчетах следующую формулу:



4. Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
5. Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
6. Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.

Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).

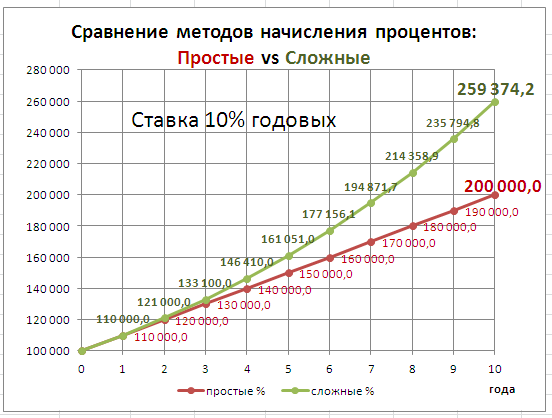
Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по

простым

и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

В

файле примера

приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов

читайте здесь

.

Начисление процентов 1 раз в год

Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу

: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

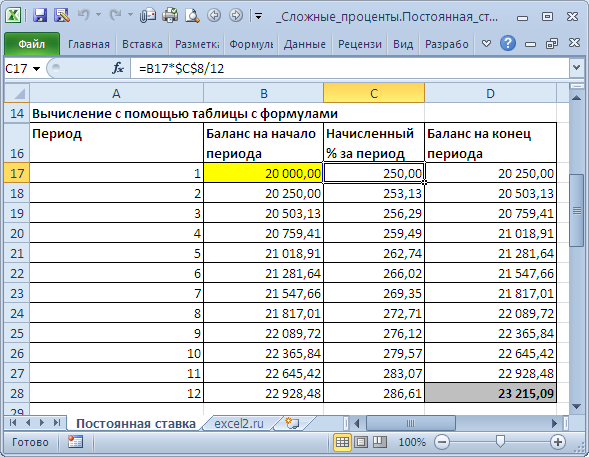
Способ 1. Вычисление с помощью таблицы с формулами

Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В

файле примера

это реализовано на листе

Постоянная ставка

.

За первый период будут начислены проценты в сумме

=20000*(15%/12)

, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов

Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию

СТЕПЕНЬ()

=20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС().

Функция

БС()

позволяет определить

будущую стоимость

инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае

аннуитетных платежей

. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.

=-БС(15%/12;12;;20000)

Или так

=-БС(15%/12;12;0;20000;0)

Примечание .

В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов

используется функция

БЗРАСПИС()

.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.

файл примера

).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

В

файле примера

приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.

Расчет сложных процентов в случае регулярного пополнения вклада

В

файле примера

(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция

БС()

.

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.

1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам

Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.

Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.

Какие данные нужны

Для начала надо правильно написать формулу — в любой свободной ячейке.

=ПЛТ(ставка;кпер;пс)

В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:

1. Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
2. Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
3. Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.

Как всё посчитать

Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.

Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.

2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент

Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.

Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.

Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.

Какие данные нужны

Формула расчёта довольно простая:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

В ней всего две переменные:

1. Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
2. Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).

Как всё посчитать

Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:

Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.

3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора

Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.

Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.

Какие данные нужны

Формула состоит из трёх компонентов:

=ЧИСТНЗ(ставка;значения;даты)

Второй и третий достаточно ясны:

2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.

Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.

Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.

Как всё посчитать

Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.

Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.

4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег

Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.

Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.

Какие данные нужны

Чтобы определить более выгодное предложение, применим формулу:

=ЧИСТВНДОХ(значения;даты)

Достаточно знать всего две переменные:

1. Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
2. Даты — график платежей, по которым будут выплачивать прибыль.

Как всё посчитать

Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.

5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам

Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.

Какие данные нужны

Полезной будет эта формула:

=СТАВКА(кпер;плт;пс)

Три переменных в ней означают следующее:

1. Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
2. Плт — размер платежей. Считаются и основной долг, и проценты.
3. Пс — общая сумма займа. В нашем примере это 100 000 рублей.

Как всё посчитать

Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.

6. PV (ПС) — подсказывает, сколько денег можно взять в долг

Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.

Какие данные нужны

Пригодится формула расчёта текущей стоимости:

=ПС(ставка; кпер; плт)

Для этого потребуется информация, которая есть на сайте любого банка:

1. Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
2. Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
3. Плт — размер комфортного платежа.

Как всё посчитать

Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.

Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.

7. NPER (КПЕР) — помогает рассчитать время накоплений

Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.

Какие данные нужны

Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:

=КПЕР(ставка/периоды_капитализации;плт;пс;бс)

Она состоит из четырёх основных значений и одного дополнительного:

1. Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
2. Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
3. Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
4. Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
5. Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.

Как всё посчитать

Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.

Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.

Читайте также 🧐

• Как вести бюджет, если у вас непостоянный доход
• 20 полезных шаблонов «Google Таблиц» на все случаи жизни
• 10 крутых приложений, чтобы взять финансы под контроль