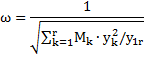tutanhamon
размещено: 14 Января 2009
обновлено: 26 Февраля 2009
Небольшой листик, может быть полезен тем, кто собирает статические ветровые нагрузки на здания и сооружения. Для данного ветрового района, типа местности и значения аэродинамического коэффициента в соотвествии со СНиП 2.01.07-85*, производятся следующие виды расчетов:
1. Построение нормативной и расчетной эпюр ветрового давления по высоте здания.
2. Вычисление интенсивности нормативного и расчетного ветрового давления в конкретной высоте.
3. Вычисление «площади эпюр» между двумя точками по высоте здания, то есть вычисляется суммарная составляющая ветрового давления на любом участке здания по высоте.
Добавлена возможность учитывать пульсационную составляющую ветрового давления.
Пишите комментарии, буду рад любым!..
0.1 МБ
СКАЧАТЬ
Ветровая нагрузка
Опубликовано 15 Дек 2013
Рубрика: О жизни | 26 комментариев

…ветровая нагрузка может создавать угрозу для жизни живых существ и угрозу разрушений для конструкций и сооружений.
Человеку комфортно, когда скорость ветра мала и не превышает 5 м/с. Сильный ветер – это ветер со скоростью более 12 м/с. Ветер со скоростью более 20 м/с – это шторм, а более 30 м/с – ураган.
Энергия ветра.
С точки зрения полезного использования ветровой энергии в энергетике на сегодняшний день оптимальными являются скорости ветра 8…18 м/с. При меньших скоростях ветроэнергетические установки малоэффективны, при больших возникает опасность разрушения конструкций установки.
Так как воздух имеет массу, и эта масса движется с некоторой скоростью относительно поверхности земли, то трудно даже представить, какой колоссальной кинетической энергией обладает окружающее нас воздушное пространство!!!
Чтобы составить представление о величине этой энергии, давайте вырежем из пространства его часть в виде цилиндра, мысленно расположив некий обруч плоскостью перпендикулярно направлению вектора скорости ветра. Площадь сечения обруча – S=1 м2 (диаметр d=1,13 м).
Если на вашем компьютере не установлена программа MS Excel, можно воспользоваться свободно распространяемой программой OOo Calc из пакета Open Office.
Правила форматирования ячеек листа Excel, применяемые в статьях этого блога, можно посмотреть на странице «О блоге».
Включаем Excel и на листе «Энергия ветра» и составляем простую расчетную программу, которая позволит быстро рассчитывать мощность ветроустановок при различных исходных условиях.
Исходные данные:
1. Скорость ветра vв в м/с записываем
в ячейку D3: =10,0
2. Время t в с заносим
в ячейку D5: =1
3. Площадь сечения потока воздуха S в м2 вписываем
в ячейку D6: =1,000
4. Плотность воздуха или удельный вес воздуха при нормальных условиях (атмосферном давлении 101325 Па = 760 мм рт. ст. и температуре +273,15° К = 0° C) γ в кг/м3 вписываем
в ячейку D7: =1,293
5. Коэффициент полезного действия — КПД ветроустановки (реально достигаемые значения не превышают 0,3…0,4) записываем
в ячейку D8: =0,35
Результаты расчетов:
6. При скорости ветра v за время t через сечение обруча пройдет объем воздуха в виде цилиндра V, который вычисляем в м3
в ячейке D10: =D3*D4*D5 =10,000
V=S*vв*t
7. Массу воздуха m в кг, прошедшую через сечение кольца за время t определяем
в ячейке D11: =D6*D9 =12,930
m=γ*V
8. Кинетическую энергию T в Дж, которой обладает движущийся цилиндр воздуха рассчитываем
в ячейке D12: =D10*D3^2/2 =647
T=m*vв2/2
9. Мощность N в КВт, которую мы смогли бы отобрать из этой струи воздуха при заданном КПД, вычисляем
в ячейке D13: =D11/D4*D7/1000 =0,226
N=(T/t)*КПД=(S*γ*vв3/2)*КПД
При реальных КПД ветроэнергетических установок около 0,3…0,4, при скорости ветра vв=10 м/с и диаметре лопастей ветряка d=1,13 м (площадь круга S=1 м2) можно получить мощность порядка N=200…250 Вт. Этой мощности хватит чтобы за час вспахать полсотки земли! Представляете сколько вокруг нас энергии, которую мы никак не научимся эффективно отбирать и преобразовывать?! Сегодняшние ветроэнергетические установки мало-мальски начинают работать при скорости ветра vв>4 м/с, выходя на рабочий режим при скорости vв=9…13 м/с. Однако уже при скорости ветра vв>17 м/с приходится больше заботиться о безопасности окружающих людей, животных, сооружений и сохранности установки, нежели о производстве энергии…
Итак, возможности использования ветра слегка затронули, переходим к проблемам, которые он создает.
Упрощенный расчет в Excel ветровой нагрузки.
Ветровая нагрузка, воздействуя на сооружение, пытается его опрокинуть, разорвать, сдвинуть в направлении действия потока воздуха.
Определим ветровое давление на плоскую стенку перпендикулярную направлению ветра, используя законы и формулы элементарной физики.
В файле Excel на листе «Упрощенный расчет» составляем небольшую расчетную программу, которая позволит рассчитывать ветровую нагрузку на плоскую стенку.
Исходные данные:
1. Скорость ветра vв в м/с записываем
в ячейку D3: =24,0
Скорость ветра необходимо принять для расчетов максимально возможную в данной местности с учетом даже кратковременных порывов, например, для города Омска это 24 м/с.
2. Плотность воздуха γ в кг/м3 вписываем
в ячейку D5: =1,293
3. Ускорение свободного падения на поверхности нашей планеты g в м/с2 записываем
в ячейку D6: =9,81
4. Коэффициент k, учитывающий аэродинамику формы и положения объекта, а также некоторый запас заносим
в ячейку D7: =1.6
Результаты расчетов:
5. Расчетный скоростной напор воздуха на поверхность стенки Q в кг/м2 определяем
в ячейке D9: =D3^2*D5/2/D6 =38,0
Q=vв2*γ/(2*g)
6. Максимальную для данной местности ветровую нагрузку на плоскую поверхность W в кг/м2 рассчитываем
в ячейке D10: =D9*D7 =60,7
W=Q*k
Расчет в Excel ветровой нагрузки по СП 20.13330.2011.
В главе №11 СП 20.13330.2011 «Нагрузки и воздействия» /Актуализированная редакция СНиП 2.01.07-85* от 20.05.2011/ для профессионалов-строителей расписана методика определения ветровой нагрузки. Кроме нормального (перпендикулярного к поверхностям) давления она учитывает силу трения воздуха о неровности поверхностей, пульсации воздушного потока, аэродинамические колебания (флаттер, дивергенцию, галопирование), предусматривает проверку на отсутствие вихревого резонанса. Мы не будем далеко забираться в эти дебри и ограничимся укрупненным расчетом. Если вам необходим полный профессиональный расчет по действующим нормативам, то открывайте СП 20.13330.2011 – и считайте, разобраться в алгоритме не сложно. Дело в том, что расчеты для разных объектов весьма индивидуальны! Могу порекомендовать адрес в Интернете, где расположены ссылки на три бесплатные неплохие программы определения ветровых нагрузок: http://fordewind.org/wiki/doku.php?id=опр_ветра.
Перед началом работы необходимо найти и скачать из Интернета СП 20.13330.2011, включая все приложения.
Часть материалов из СП 20.13330.2011 находятся в файле, который можно скачать по ссылке, размещенной в самом конце этой статьи.
В примечаниях к ячейкам столбца C с исходными данными поместим некоторые важные данные и ссылки на пункты СП 20.13330.2011!!!
В файле Excel на листе «Расчет по СП 20.13330.2011» начинаем составлять программу, которая позволит определять расчетную ветровую нагрузку по второму алгоритму.
Исходные данные:
1. Вписываем коэффициент надежности по нагрузке γf
в ячейку D3: =1,4
2. Определяем тип местности, воспользовавшись примечанием к ячейке C4. Например, наша местность относится к типу B. Выбираем соответствующую строку с записью B в поле с выпадающим списком, расположенном поверх
ячейки D4: =ИНДЕКС(I5:I7;I2) =B
3. Открываем Приложение Ж в СП 20.13330.2011 и по карте «Районирование территории Российской Федерации по давлению ветра» определяем для интересующей нас местности номер ветрового района (карта есть в файле для скачивания). Например, для Санкт-Петербурга и Омска – это II ветровой район. Выбираем соответствующую строку с записью II в поле с выпадающим списком, расположенном поверх
ячейки D5: =ИНДЕКС(G5:G12;G2) =II
О том, как работает функция ИНДЕКС совместно с полем со списком можно прочитать здесь.
4. Задаем эквивалентную высоту объекта над землей ze в м, пользуясь п.11.1.5 СП 20.13330.2011
в ячейке D6: =5
5. Аэродинамический коэффициент c выбираем по приложению Д.1 СП 20.13330.2011, например, для плоской стенки и записываем
в ячейку D7: =1,3
cmax < 2,2 — с наветренной стороны
cmin > -3,4 — с подветренной стороны
Определение двух следующих коэффициентов, влияющих на значение пульсационной составляющей ветровой нагрузки, является очень непростой задачей, требующей расчета частот собственных колебаний объекта! Расчет этот для разных сооружений ведется по различным и очень непростым алгоритмам!!! Я укажу далее лишь примерные возможные диапазоны значений этих коэффициентов. Желающие разобраться досконально с частотами колебаний должны обратиться к другим источникам.
6. Коэффициент пространственной корреляции пульсаций давления ветра ν определяем по п.11.1.11 СП 20.13330.2011 и заносим
в ячейку D8: =0,85
0,38 < ν < 0,95
7. Коэффициент динамичности ξ определяем по п.11.1.8 СП 20.13330.2011 и вписываем
в ячейку D9: =1,20
1,00 ≤ ξ < 2,90
Результаты расчетов:
8. Нормативное значение ветрового давления w0 в кг/м2 считываем
в ячейке D11: =ИНДЕКС(H5:H12;G2) =30
9. Ориентировочную скорость ветра vв в м/с и км/ч определяем соответственно
в ячейке D12: =(D11*9,81*2/1,2929)^0,5 =21,3
vв = (w0 *g*2/γ)^0,5
и в ячейке D13: =D12/1000*60*60 =76,8
vв’= vв/1000*60*60
10. Параметр k10 считываем
в ячейке D14: =ИНДЕКС(K5:K7;I2) =0,65
11. Параметр α считываем
в ячейке D15: =ИНДЕКС(J5:J7;I2) =0,20
12. Параметр ζ10 считываем
в ячейке D16: =ИНДЕКС(L5:L7;I2) =1,06
13. Коэффициент, учитывающий изменение ветрового давления по высоте k (ze) вычисляем
в ячейке D17: =D14*(D6/10)^(2*D15) =0,49
k (ze) = k10*(ze/10)^(2*α)
14. Коэффициент пульсации ветра ζ(ze) вычисляем
в ячейке D18: =D16*(D6/10)^(-D15) =1,22
ζ(ze)= ζ10*(ze/10)^(-α)
15. Нормативное значение средней составляющей ветровой нагрузки wm в кг/м2 рассчитываем
в ячейке D19: =D11*D17*D7 =19,2
wm= w0* k (ze)*c
16. Нормативное значение пульсационной составляющей ветровой нагрузки wp вкг/м2 определяем
в ячейке D20: =D19*D9*D18*D8 =23,9
wp= wm*ξ*ζ(ze)*ν
17. Нормативное значение ветровой нагрузки w вкг/м2 вычисляем
в ячейке D21: =D19+D20 =43,1
w = wm+wp
18. Расчетную ветровую нагрузку W вкг/м2 с учетом коэффициента надежности рассчитываем
в ячейке D22: =D21*D3 =60,3
W = w*γf
Итоги
В расчетах по упрощенной методике и по СП 20.13330.2011 мы получили очень близкие результаты. Хотя во многом это скорее случайное совпадение, обе методики имеют право на жизнь и могут использоваться каждая для решения своих задач. По упрощенному расчету можно быстро сделать оценку нагрузки и при выполнении детального проекта уточнить ветровую нагрузку расчетом по СП 20.13330.2011.
В заключении хочу сказать, что эта статья написана для того, чтобы читающий смог составить общее представление о том, что такое энергия ветра, понять созидательные и разрушительные аспекты темы. Расчет ветровой нагрузки достаточно сложная и многофакторная задача. Я не спроста разместил статью в рубрике «О жизни». Это не справочный материал для инженера-проектировщика! Пользуясь представленными материалами можно приблизительно рассчитать нагрузку на небольшой забор, легкую теплицу или маленькую доску объявлений. Ветровая нагрузка на более серьезные объекты должна быть рассчитана специалистом строго по главе №11 СП 20.13330.2011!
Профессионалам – строителям в комментариях прошу учитывать, что статья написана для широкой аудитории.
Ссылка на скачивание файла: veter (xls 1,97MB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Ветер по-разному влияет на строительные конструкции. Если для одноэтажного котеджа его воздействие минимальное, то для небоскреба или “парусного” рекламного щита нагрузка может стать определяющей. В этой статье подробно описано как вычислить ветровую нагрузку на различные сооружения.
Районы ветровой нагрузки
Первое, с чем нужно определиться – к какому району по давлению ветра относится рассматриваемая местность. Данную информацию можно найти на специальных картах в нормативных документах. Главный нормативный документ, регламентирующий ветровую нагрузку – СП 20.13330*

*Обратите внимание, что СП20.13330 есть 2011 и 2016 года, и карты в этих документах могут отличаются. На момент выхода статьи обязательным является СП 2011г. но в ближайшее время СП 2016г. официально станет действующим и расчет ветровой нагрузки нужно будет проводить по картам нового документа. Расчет ветровой нагрузки так же можно найти по СНиП 2.01.07-85*, но данный расчет не будет действительным т.к. нормы устарели.
Расчет ветровой нагрузки онлайн калькулятор
Полный расчет ветровой нагрузки по СП 20.13330.2011 “Нагрузки и воздействия” приведен ниже. Если с данным расчетом сложно разобраться, то можно воспользоватсья нашим онлайн калькулятором ветровой нагрузки. При возникновении сложностей вы можете заказать расчет написав нам на почту в разделе контакты.

>>> Перейти к онлайн калькулятору ветровой нагрузки <<<
Описание расчета:
- синие ячейки – предназначены для ввода данных.
- зеленые ячейки – расчетные, данные в них рассчитываются автоматически.
- оранжевые ячейки – результат расчета. В данном раcчете результатом является расчетная ветровая нагрузка с учетом пульсационной составляющей.
Пример расчета ветровой нагрузки на здание в онлайн калькуляторе
Ввод данных:
- Ввести тип местности. Тип местности определяется по п. 11.1.6.
- Ввести коэфициент надежности по ветровой нагрузке. По умолчанию равен 1.4 (п.11.1.12).
- Ввести коэфициент надежности по ответственности.
- Ввести нормативное значение ветрового давления. Нормативное значение определяется по таблице 11.1 в зависимости от ветрового района. Ветровой район определяется по карте 3. Справа от ячейки можно выбрать размерность входных и выходных данных (т, кг, кН).
- Ввести размеры здания:
- b-длина здания вдоль основной рамы.
- а-ширина здания поперек основной рамы.
- h-высота здания.
Расчетные ячейки:
Ce – не является ячейкой ввода и поумолчанию заданы все варианты для расчета нагрузки на стены здания. Но изменив эти значения можно посчитать ветровую нагрузку для других конструкций. Расчет Ce для любых конструкций проводится по приложению Д
k(ze) стат. – расчет коэфициента учитывающего изменение ветрового давления для высоте. Онлайн калькулятор считает только при условии: h<d, где d – минимальный размер между а и b
wm – Cтатическое давление. Вычисляется по п. 11.1.3
ζ(ze) – коэффициент пульсации давления ветра Таблица 11.4
Через ρ и χ вычисляется ν по таблице 11.6
wp – динамическая составляющая вычисляется по ф.11.5 принимая во внимание примечание.
В графе суммарное давление вычисляется сумма статической и динамической составляющей. Размерность зависит от размерности выбранной при вводе. Ширина зоны А,Б,С для боковых поверхностей рассчитываются автоматечески исходя из заданных размеров.
Расчет ветровой нагрузки по СП 20.13330.2011 “Нагрузки и воздействия”.
11.1.1 Нормативное значение ветровой нагрузки w следует задавать в одном из двух вариантов. В первом случае нагрузка w представляет собой совокупность:
а) нормального давления we, приложенного к внешней поверхности сооружения или элемента;
б) сил трения wf, направленных по касательной к внешней поверхности и отнесенных к площади ее горизонтальной (для шедовых или волнистых покрытий, покрытий с фонарями) или вертикальной проекции (для стен с лоджиями и подобных конструкций);
в) нормального давления wi, приложенного к внутренним поверхностям сооружений с проницаемыми ограждениями, с открывающимися или постоянно открытыми проемами.
Во втором случае нагрузка w рассматривается как совокупность:
а) проекций wx и wv, внешних сил в направлении осей х и у, обусловленных общим сопротивлением сооружения;
б) крутящего момента wz относительно оси z.
При разработке архитектурно-планировочных решений городских кварталов, а также при планировании возведения зданий внутри существующих городских кварталов рекомендуется провести оценку комфортности пешеходных зон в соответствии с требованиями норм или технических условий.
11.1.2 Нормативное значение ветровой нагрузки w следует определять как сумму средней wm и пульсационной wp составляющих
w = wm + wp (11.1)
При определении внутреннего давления wi пульсационную составляющую ветровой нагрузки допускается не учитывать.
11.1.3 Нормативное значение средней составляющей ветровой нагрузки wm в зависимости от эквивалентной высоты ze над поверхностью земли следует определять по формуле
wm = w0k(ze)c (11.2)
где w0 – нормативное, значение ветрового давления (см. 11.1.4);
k(ze) – коэффициент, учитывающий изменение ветрового давления для высоты ze (см. 11.1.5 и 11.1.6);
с – аэродинамический коэффициент (см. 11.1.7).
11.1.4 Нормативное значение ветрового давления w0 принимается в зависимости от ветрового района по таблице 11.1. Нормативное значение ветрового давления допускается определять в установленном порядке на основе данных метеостанций Росгидромета (см. 4.4). В этом случае w0, Па, следует определять по формуле
(11.3)
где 
Таблица 11.1Таблица ветровых нагрузок в зависимости от ветрового района
|
Ветровые районы (принимаются по карте 3 приложения Ж) |
Iа |
I |
II |
III |
IV |
V |
VI |
VII |
|
w0, кПа |
0,17 |
0,23 |
0,30 |
0,38 |
0,48 |
0,60 |
0,73 |
0,85 |
11.1.5 Эквивалентная высота ze определяется следующим образом.
1. Для башенных сооружений, мачт, труб и т.п. сооружений
ze = z.
2. Для зданий:
а) при h <= d -> ze = h;
б) при d < h <= 2d:
для z >= h – d ->ze = h;
для 0 < z < h – d-> ze = d;
в) при h > 2d:
для z >= h – d -> ze = h;
для d < z < h – d -> ze = z;
для 0 < z <= d -> ze = d.
Здесь z – высота от поверхности земли;
d – размер здания (без учета его стилобатной части) в направлении, перпендикулярном расчетному направлению ветра (поперечный размер);
h – высота здания.
11.1.6 Коэффициент k(ze) определяется по таблице 11.2 или по формуле (11.4), в которых принимаются следующие типы местности:
А – открытые побережья морей, озер и водохранилищ, сельские местности, в том числе с постройками высотой менее 10 м, пустыни, степи, лесостепи, тундра;
В – городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м;
С – городские районы с плотной застройкой зданиями высотой более 25 м.
Сооружение считается расположенным в местности данного типа, если эта местность сохраняется с наветренной стороны сооружения на расстоянии 30h – при высоте сооружения h до 60 м и на расстоянии 2 км – при h > 60 м.
Примечание – Типы местности могут быть различными для разных расчетных направлений ветра.
Таблица 11.2
|
Высота ze, м |
Коэффициент k для типов местности |
||
|
А |
В |
С |
|
|
<=5 |
0,75 |
0,5 |
0,4 |
|
10 |
1,0 |
0,65 |
0,4 |
|
20 |
1,25 |
0,85 |
0,55 |
|
40 |
1,5 |
1,1 |
0,8 |
|
60 |
1,7 |
1,3 |
1,0 |
|
80 |
1,85 |
1,45 |
1,15 |
|
100 |
2,0 |
1,6 |
1,25 |
|
150 |
2,25 |
1,9 |
1,55 |
|
200 |
2,45 |
2,1 |
1,8 |
|
250 |
2,65 |
2,3 |
2,0 |
|
300 |
2,75 |
2,5 |
2,2 |
|
350 |
2,75 |
2,75 |
2,35 |
|
>=480 |
2,75 |
2,75 |
2,75 |
k(ze) = k10(ze/10)2a. (11.4)
Значения параметров k10 и a для различных типов местностей приведены в таблице 11.3.
Таблица 11.3
|
Параметр |
Тип местности |
||
|
А |
В |
С |
|
|
a |
0,15 |
0,20 |
0,25 |
|
k10 |
1,0 |
0,65 |
0,4 |
|
z10 |
0,76 |
1,06 |
1,78 |
11.1.7 При определении компонентов ветровой нагрузки we, wf, wi, wx, wy и wz следует использовать соответствующие значения аэродинамических коэффициентов: внешнего давления се, трения сf, внутреннего давления сi и лобового сопротивления сx, поперечной силы су, крутящего момента сz, принимаемых по приложению Д.1, где стрелками показано направление ветра. Знак «плюс» у коэффициентов се или сt соответствует направлению давления ветра на соответствующую поверхность (активное давление), знак «минус» – от поверхности (отсос). Промежуточные значения нагрузок следует определять линейной интерполяцией.
При определении ветровой нагрузки на поверхности внутренних стен и перегородок при отсутствии наружного ограждения (на стадии монтажа) следует использовать аэродинамические коэффициенты внешнего давления се или лобового сопротивления сх.
Для сооружений повышенного уровня ответственности, а также во всех случаях, не предусмотренных Д.1 приложения Д (иные формы сооружений, учет при надлежащем обосновании других направлений ветрового потока или составляющих общего сопротивления тела по другим направлениям, необходимость учета влияния рядом стоящих зданий и сооружений и т.п. случаях), аэродинамические коэффициенты необходимо принимать на основе результатов продувок моделей сооружений в аэродинамических трубах или по рекомендациям, разработанным специализированными организациями.
Примечания
1 При назначении коэффициентов сх, сv и сm необходимо указать размеры сооружения, к которым они отнесены.
2 Значения аэродинамических коэффициентов, указанных в приложении Д.1, допускается уточнять на основе данных модельных аэродинамических испытаний сооружений.
11.1.8 Нормативное значение пульсационной составляющей ветровой нагрузки wpна эквивалентной высоте ze следует определять следующим образом:
а) для сооружений (и их конструктивных элементов), у которых первая частота собственных колебаний fl, Гц, больше предельного значения собственной частоты fl (см. 11.1.10), – по формуле
wp = wmz(ze)v, (11.5)
где wm – определяется в соответствии с 11.1.3;
z(ze) – коэффициент пульсации давления ветра, принимаемый по таблице 11.4 или формуле (11.6) для эквивалентной высоты ze (см. 11.1.5);
v – коэффициент пространственной корреляции пульсаций давления ветра (см. 11.1.11);
Таблица 11.4
|
Высота ze, м |
Коэффициент пульсаций давления ветра z для типов местности |
||
|
А |
В |
С |
|
|
<= 5 |
0,85 |
1,22 |
1,78 |
|
10 |
0,76 |
1,06 |
1,78 |
|
20 |
0,69 |
0,92 |
1,50 |
|
40 |
0,62 |
0,80 |
1,26 |
|
60 |
0,58 |
0,74 |
1,14 |
|
80 |
0,56 |
0,70 |
1,06 |
|
100 |
0,54 |
0,67 |
1,00 |
|
150 |
0,51 |
0,62 |
0,90 |
|
200 |
0,49 |
0,58 |
0,84 |
|
250 |
0,47 |
0,56 |
0,80 |
|
300 |
0,46 |
0,54 |
0,76 |
|
350 |
0,46 |
0,52 |
0,73 |
|
>= 480 |
0,46 |
0,50 |
0,68 |
z(ze) = z10(ze/10)–a. (11.6)
Значения параметров z10 и a для различных типов местностей приведены в таблице 11.4;
б) для всех сооружений (и их конструктивных элементов), у которых f1 < fl < f2, – по формуле
wp = wmxz(ze)v, (11.7)
где f2 – вторая собственная частота;
- xde1f1;

Здесь w0 (Па) – нормативное значение давления ветра (11.1.4);
k(zэк) – коэффициент, учитывающий изменение давления ветра для высоты zэк (11.1.6);
- gf
Для конструктивных элементов zэк – высота z, на которой они расположены; для зданий и сооружений zэк = 0,7h, где h – высота сооружений;
в) для сооружений, у которых вторая собственная частота меньше предельной, необходимо производить динамический расчет с учетом s первых форм собственных колебаний. Число s следует определять из условия
fs < fl < fs+l;
г) при расчете зданий допускается учитывать динамическую реакцию по трем низшим собственным формам колебаний (двум изгибных и одной крутильной или смешанным крутильно-изгибным).
Примечание – При расчете многоэтажных зданий высотой до 40 м и одноэтажных производственных зданий высотой до 36 м при отношении высоты к пролету менее 1,5, размещаемых в местностях типа А и В (см. 11.1.6), пульсационную составляющую ветровой нагрузки допускается определять по формуле (11.5).
11.1.9 Усилия и перемещения при учете динамической реакции по s собственным формам определяются по формуле

где X – суммарные усилия или перемещения;
Xs – усилия или перемещения по s-й форме колебаний.
11.1.10 Предельное значение частоты собственных колебаний fl, Гц, следует определять по таблице 11.5.
Таблица 11.5
|
Ветровые районы (принимаются по карте 3 приложения Ж) |
fl, Гц |
|
|
||
|
Iа |
0,85 |
2,6 |
|
I |
0,95 |
2,9 |
|
II |
1,1 |
3,4 |
|
III |
1,2 |
3,8 |
|
IV |
1,4 |
4,3 |
|
V |
1,6 |
5,0 |
|
VI |
1,7 |
5,6 |
|
VII |
1,9 |
5,9 |

Значение логарифмического декремента колебаний d следует принимать:
а) для железобетонных и каменных сооружений, а также для зданий со стальным каркасом при наличии ограждающих конструкций d = 0,3;
б) для стальных сооружений футерованных дымовых труб, аппаратов колонного типа, в том числе на железобетонных постаментах d = 0,15.
11.1.11 Коэффициент пространственной корреляции пульсаций давления v следует определять для расчетной поверхности сооружения или отдельной конструкции, для которой учитывается корреляция пульсаций.
Расчетная поверхность включает в себя те части наветренных и подветренных поверхностей, боковых стен, кровли и подобных конструкций, с которых давление ветра передается на рассчитываемый элемент сооружения.
Если расчетная поверхность близка к прямоугольнику, ориентированному так, что его стороны параллельны основным осям (рисунок 11.2), то коэффициент v следует определять по таблице 11.6 в зависимости от параметров r и c, принимаемых по таблице 11.7.
Таблица 11.6
|
r, м |
Коэффициент v при c, м, равном |
||||||
|
5 |
10 |
20 |
40 |
80 |
160 |
350 |
|
|
0,1 |
0,95 |
0,92 |
0,88 |
0,83 |
0,76 |
0,67 |
0,56 |
|
5 |
0,89 |
0,87 |
0,84 |
0,80 |
0,73 |
0,65 |
0,54 |
|
10 |
0,85 |
0,84 |
0,81 |
0,77 |
0,71 |
0,64 |
0,53 |
|
20 |
0,80 |
0,78 |
0,76 |
0,73 |
0,68 |
0,61 |
0,51 |
|
40 |
0,72 |
0,72 |
0,70 |
0,67 |
0,63 |
0,57 |
0,48 |
|
80 |
0,63 |
0,63 |
0,61 |
0,59 |
0,56 |
0,51 |
0,44 |
|
160 |
0,53 |
0.53 |
0,52 |
0,50 |
0,47 |
0,44 |
0,38 |
При расчете сооружения в целом размеры расчетной поверхности следует определять с учетом указаний Д.1 приложения Д, при этом для решетчатых сооружений в качестве расчетной поверхности необходимо принимать размеры расчетной поверхности по его внешнему контуру.
Таблица 11.7
|
Основная координатная плоскость, параллельно которой расположена расчетная поверхность |
r |
c |
|
zoy |
b |
h |
|
zox |
0,4а |
h |
|
хоу |
b |
а |
11.1.12 Коэффициент надежности по ветровой нагрузке следует принимать равным 1,4.
опр_ветра
Определение ветровых нагрузок
Для удобства определения ветровых нагрузок на здания и сооружения разработана книга в MS Excel:
Необходимо ввести исходные данные в зелёные клетки. При наведении курсора на пункт исходных данных появляется подсказка о том, где найти эти данные. Использование данной таблицы предполагает понимание принципа определения ветровых нагрузок по СП.
Примечания:
-
для расчёта башенных сооружений необходимо задать d = 0,1
-
коэф-т пространственной корреляции пульсации определяется автоматически только при включённом запуске макросов
-
коэф-т динамичности необходимо определить вручную — для этого в книге имеются все необходимые таблицы и графики
-
данные, выделенные серым цветом, в расчётах не участвуют (добавлены с целью дальнейшего развития таблицы)
В нижней правой части листа «Расчёт» под графиком реализовано определение нагрузок на торцы плит перекрытий с учётом ширины грузовой площади. Для расчёта необходимо указать отметки плит (отметка от уровня земли).
Полезные ссылки
Особенности расчета металлических решетчатых башен на ветровую нагрузку
В статье рассматриваются некоторые аспекты определения ветровых нагрузок на металлические решетчатые башенные конструкции квадратные в плане, а также особенности расчета последних на ветровое воздействие в ПК ЛИРА-САПР
Определение величины ветровой нагрузки
Ветровую нагрузку следует определять как сумму средней wm и пульсационной wp составляющей. Нормативная величина ветровой нагрузки:
w = wm + wp
Средняя составляющая ветровой нагрузки
Нормативная величина средней составляющей ветровой нагрузки:
wm = w0*k*c
где w0 — нормативное значение ветрового давления; k — коэффициент, учитывающий изменение ветрового давления по высоте; с — аэродинамический коэффициент.
Аэродинамический коэффициент для решетчатых башен и пространственных ферм определяется по формуле:
Ct = Cx(1+η)k1
где Cx — аэродинамический коэффициент отдельностоящей плоской решетчатой конструкции:
Cx = ∑(Cxi*Ai)/Ak
Cxi — аэродинамический коэффициент i-го элемента конструкции; Ai — площадь проекции i-го элемента конструкции; Ak — площадь, ограниченная контуром конструкции.
η — коэффициент, учитывающий давление ветра на подветренную грань. Определяется по табл. В.8 СП 20.13330.2016 в зависимости от относительного расстояния между фермами и коэффициента заполнения ферм.
k1 — коэффициент, зависящий от контура поперечного сечения и направления ветра:
Рис. 1. Значение коэффициента k1 в зависимости от ориентации направления ветра по отношению к башне
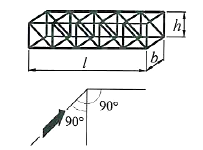
При определении аэродинамического коэффициента решетчатой конструкции Ct принимается, что направление ветра всегда перпендикулярно грани башни:
Рис. 2. Направления ветра по отношению к башне при определении Ct
Таким образом, при определении Ct коэффициент Cx всегда определяется в предположение воздействия ветра на грань, а соответственно ACk — площадь контура грани вне зависимости от угла атаки ветровой нагрузки.
Переход к аэродинамическому коэффициенту Ct при действии ветра на диагональ осуществляется умножением Ct, вычисленного для грани, на коэффициент k1=1.2.
При определении средней составляющей ветровой нагрузки башня разбивается на конечное количество расчетных полей. Далее для каждого расчетного поля определяется площадь, ограниченная контуром Ak; определяется суммарная площадь проекции элементов башни Ai; определяются аэродинамические коэффициенты элементов башни Cxi; определяются коэффициенты Cx, φ, η, k1; определяется аэродинамический коэффициент для решетчатых башен Ct; вычисляется статическая составляющая ветровой нагрузки.
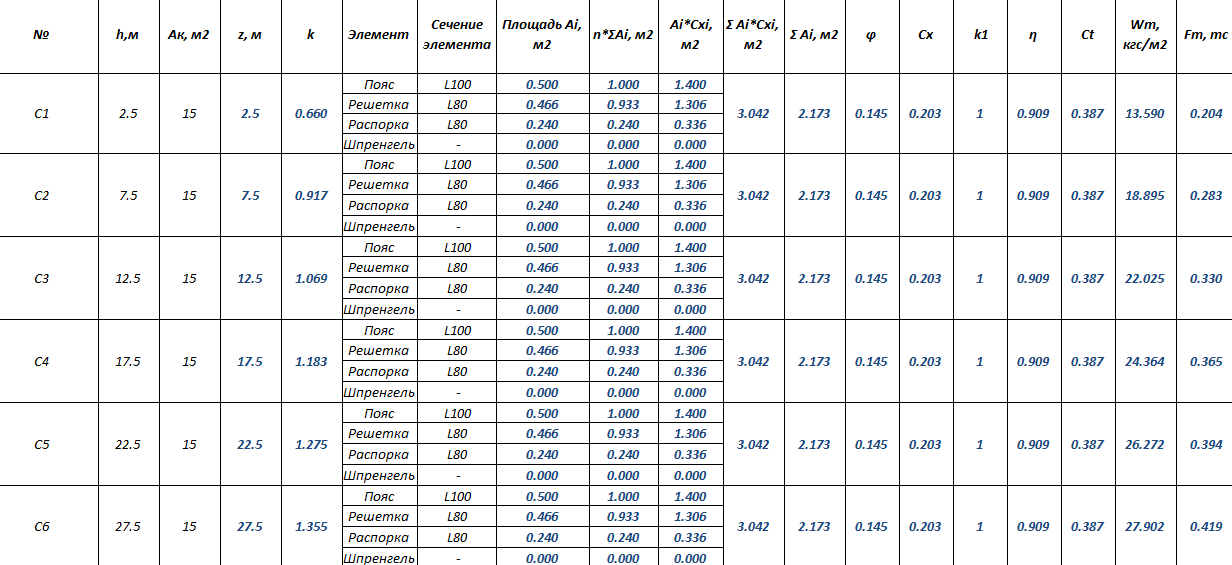
Вычисления удобно выполнять в табличном виде по следующему типу:
Рис. 3. Фрагмент таблицы определения статической составляющей ветровой нагрузки
Пульсационная составляющая ветровой нагрузки
При определении пульсационной составляющей ветровой нагрузки нужно знать собственные формы и частоты колебаний башни.
Известно, что круговая частота колебаний может быть определена по формуле ω=√(k/m), где k и m – соответственно жесткость и масса. Жесткость зависит от момента инерции башни. Для квадратных в плане башен момент инерции при действии ветра на диагональ и на грань одинаковые:
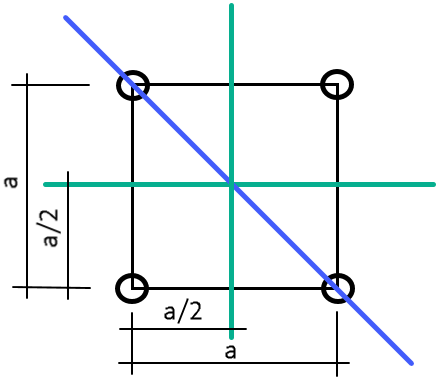
- момент инерции поперечного сечения башни при площади пояса A и размере башни в плане а относительно оси, параллельной грани (зеленой):
Рис. 4. Схема поперечного сечения ствола башни
- момент инерции поперечного сечения башни относительно оси, проходящей через диагональ (синей):
Таким образом, при ветре на диагональ и на грань у квадратной башни одинаковые коэффициент динамичности и ординаты форм колебаний. Поэтому для определения пульсационной составляющей ветровой нагрузки достаточно вычислить частотные характеристики в направлении осей инерции башни, параллельных грани.
В практике проектирования прежних лет пульсационная составляющая ветровой нагрузки определялась только от основной формы колебаний с круговой частотой:
где yk — перемещение точек оси башни при действии единичной силы, приложенной в уровне ее верха; Mk — приведенная к точке масса соответствующего участка башни; y1r — перемещение верха башни от единичной нагрузки.
Пульсационная составляющая ветровой нагрузки в общем случае (динамический анализ) определяется по формуле:
где m — масса башни на уровне Z, отнесенная к площади поверхности, к которой приложена ветровая нагрузка; ξ — коэффициент динамичности (зависит от линейной частоты колебаний f=ω/2π); y — горизонтальное перемещение на уровне Z по форме собственных колебаний; ψ — коэффициент, определяется по формуле:
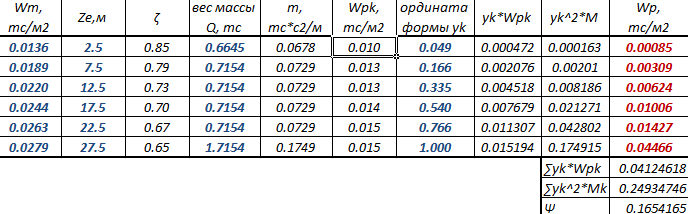
где Mk — масса k-го участка башни; yk — горизонтальное перемещение центра k-го участка (ордината формы колебаний); wpk — равнодействующая пульсационной составляющей ветровой нагрузки на k-й участок:
где ζ — коэффициент пульсаций давления ветра на уровне Z; ν — коэффициент пространственной корреляции пульсаций давления ветра.
Вычисления удобно выполнять в табличном виде по следующему типу:
Рис. 5. Фрагмент таблицы определения пульсационной составляющей ветровой нагрузки
После определения средней (статической) и пульсационной составляющей ветровой нагрузки, определяется полная ветровая нагрузка w=wm+wp. К расчетной модели ветровая нагрузка обычно прикладывается в виде сосредоточенных сил Fi в уровне пересечения поясов с элементами решетки (Fi=w*Ak/n, где n — число узлов).
Далее выполняется определение усилий в элементах башни.
Ветровая нагрузка на металлическую башню должна быть приложена в 2х вариантах — на грань (для определения усилий в решетке) и на диагональ (для определения усилий в поясах).
Усилия в элементах поясов и нагрузки на фундамент квадратной башни при действии ветровой нагрузки определяются от момента Мд и силы Qд – момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на диагональ. При этом усилия в поясах, лежащих на диагонали (поперечной/перпендикулярной ветру), равны нулю, а усилия в поясах по направлению ветровой нагрузки равны между собой по абсолютной величине, но разные по знаку
Усилия в элементах решетки определяются при действии ветровой нагрузки от Мг и Qг — момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на грань.
Пример расчета башни на полную ветровую нагрузку определенную «ручным» способом
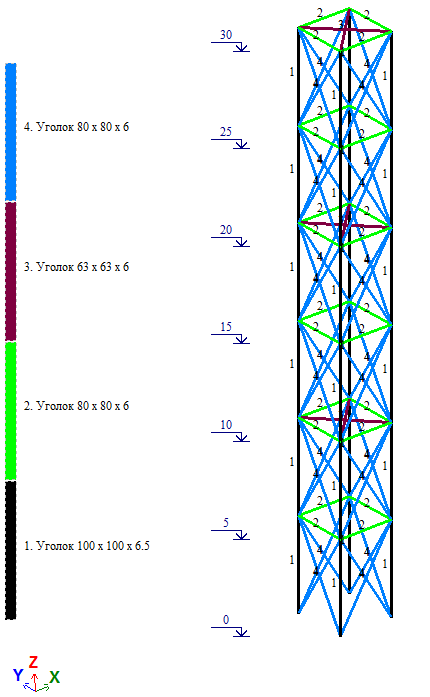
Рассмотрим башню с параллельными поясами высотой 30м. Размер в плане а=3х3м.
Рис. 6. Расчетная модель башни
Нагрузки на башню:
- собственный вес;
- вес оборудования 1тс в уровне верха башни (0.25тс в узел);
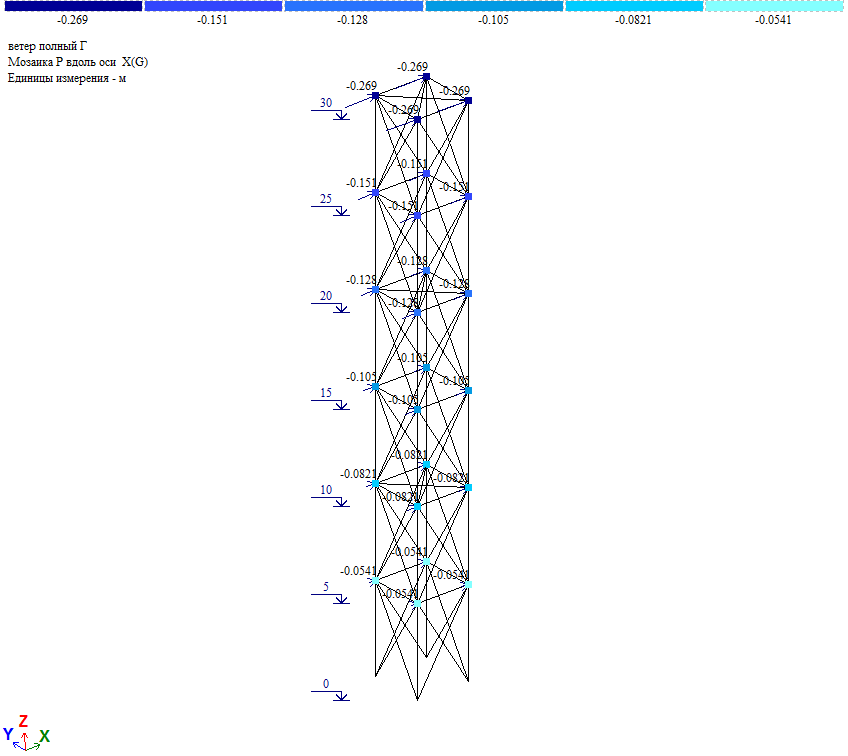
- ветер полный на грань;
- ветер полный на диагональ.
Ветровая нагрузка прикладывается как узловая в уровне верха расчетного поля. Величина полной ветровой нагрузки складывается из статической и пульсационной составляющих. Рассматривается 6 расчетных полей по высоте.
Табл. 1
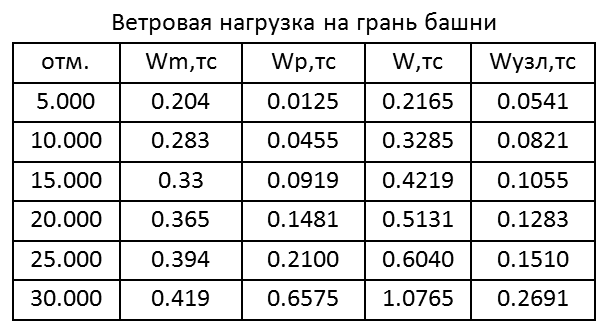
Табл. 2
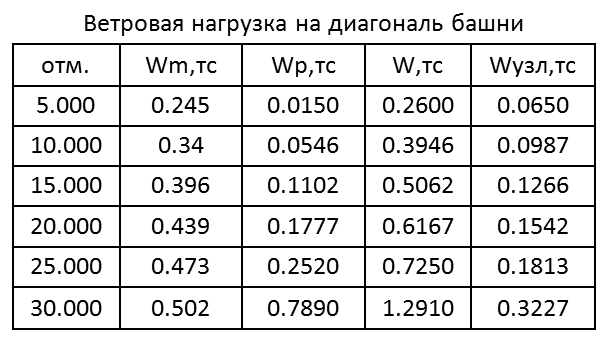
Рис. 7. Схема приложения нагрузок на ствол башни при действии ветра на грань
Рис. 8. Схема приложения нагрузок на ствол башни при действии ветра на диагональ
Ветровая нагрузка на диагональ прикладывается в виде составляющих Х и Y: W(x,y)=W*cos45⁰.
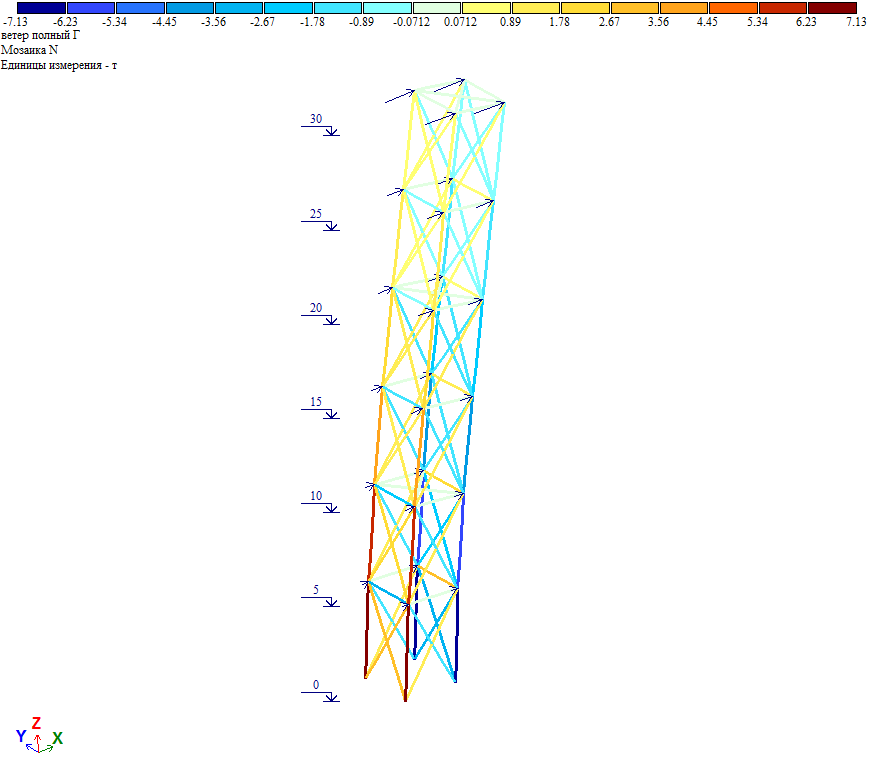
Усилия в элементах башни при действии ветровой нагрузки на грань.
Рис. 9. Усилия от полной ветровой нагрузки при действии ветра на грань
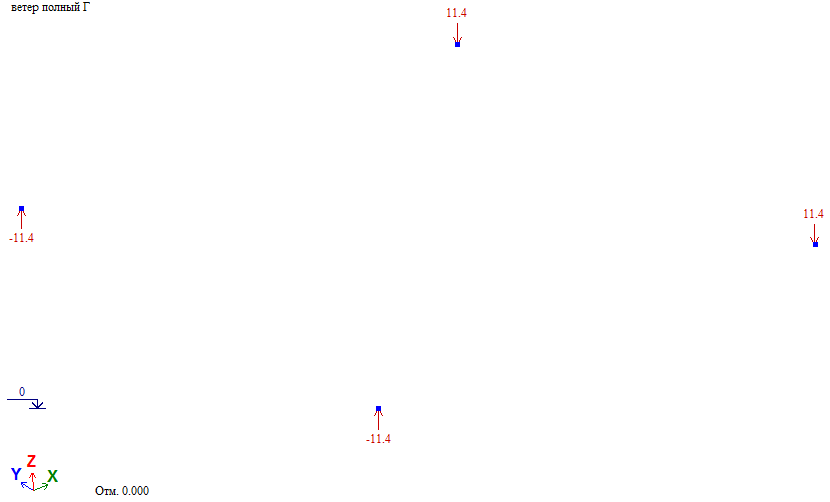
Проверка. Общий момент в основании башни Мг=∑Wiг*Zi=68.35тс*м. Нагрузка на фундамент F=(Мг/а)/2=(68.35/3)/2=11.39тс
Рис. 10. Нагрузки на фрагмент для опорных узлов башни при действии ветра на грань
Как видно результаты программного и «ручного» определения нагрузок на фундаменты сходятся.
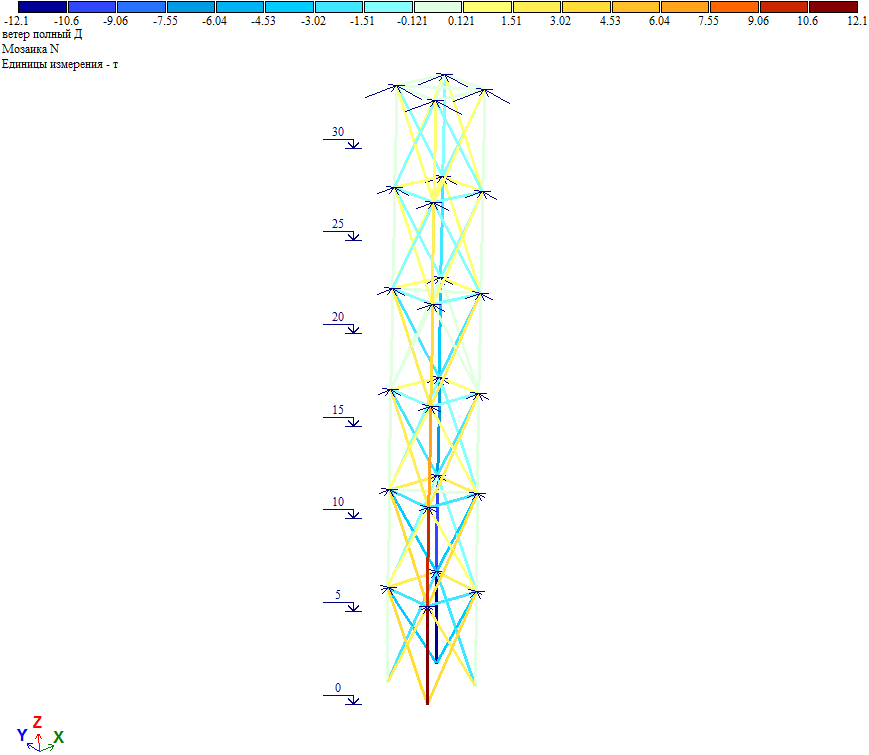
Усилия в элементах башни при действии ветровой нагрузки на диагональ.
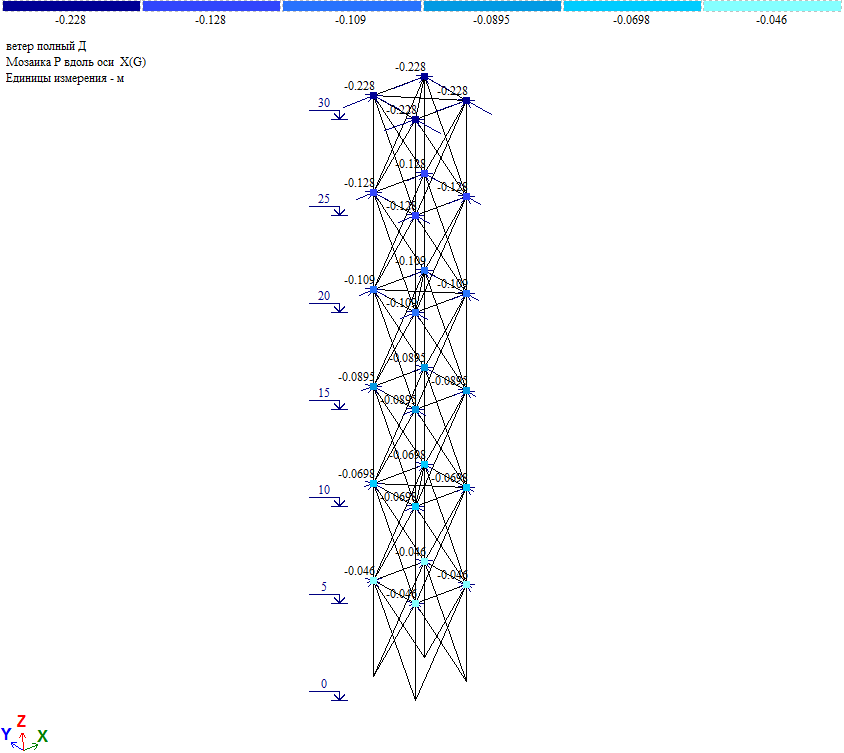
Рис. 11. Усилия от полной ветровой нагрузки при действии ветра на диагональ
Проверка. Общий момент в основании башни Мд=∑Wiд*Zi=82тс*м. Нагрузка на фундамент F=(Мд/а*√2)=(82/3*1.414)=19.33тс
Нагрузки на фрагмент в основании башни:
Рис. 12. Нагрузки на фрагмент для опорных узлов башни при действии ветра на диагональ
Моделирование воздействия ветра в ЛИРА-САПР
При конечноэлементном моделировании башня представляется пространственной фермой. Т.к. жесткость и масса конструкции величины не зависимые от внешней нагрузки, то при определении собственных форм и частот колебаний для разных пульсационных загружений имеет место случай кратных форм колебаний, т.е. форм с одинаковой частотой.
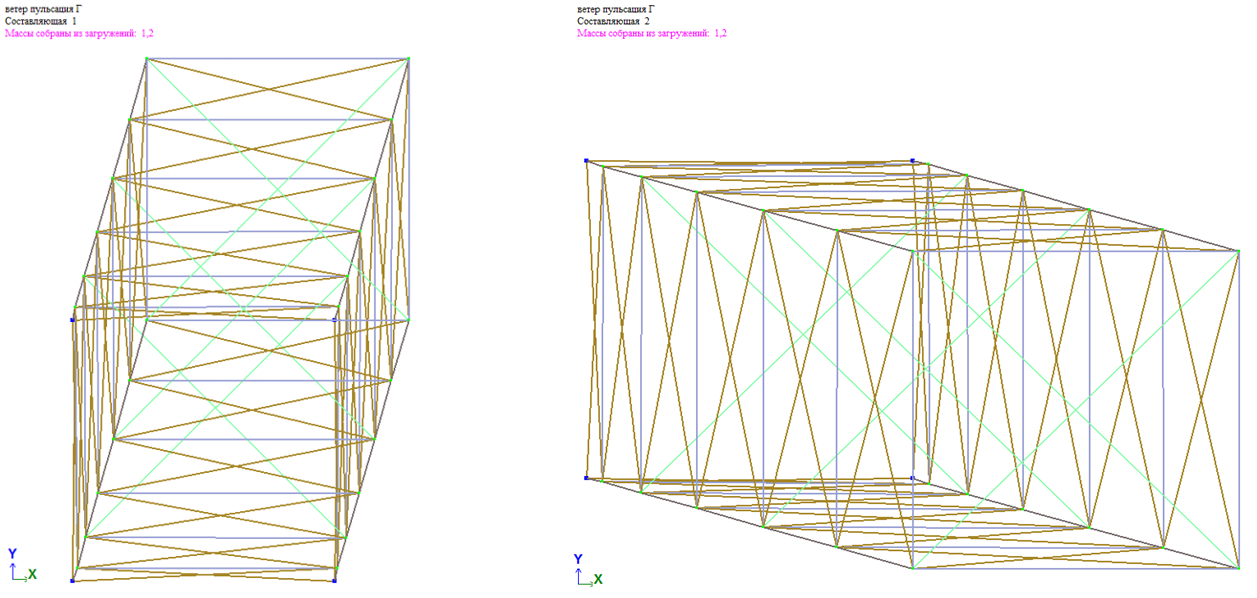
Если частотное уравнение имеет кратные формы, условие ортогональности форм (вдоль граней башни, в данном случае вдоль глобальных осей Х и У) не справедливо. В этом случае существует целое семейство векторов, любая пара из которых может служить собственными векторами для кратных частот. Эта пара будет ортогональна друг другу, но произвольно повернута вокруг вертикально оси башни:
Рис. 13. Пример кратных форм колебаний
Т.к. ординаты форм колебаний учитываются при определении величины пульсационной составляющей ветровой нагрузки, то в случае кратных форм последняя будет зависеть от угла поворота перемещения по кратным формам относительно главных осей сооружения. Если учесть, что угол поворота кратных форм величина случайная, то прогнозировать правильность результатов сложно. В данном случае возможно как уменьшение, так и увеличения вклада ветровой пульсации в усилия в элементах схемы.
Правильный результат будет получен в случае совпадения направления перемещений по одной из кратных форм с направлением ветровой нагрузки.
Для борьбы с кратными формами колебаний применяют разные подходы. Наиболее распространенные из них – изменение геометрии (жесткости) или масс. К примеру, в справке к ПК Abaqus написано:
| «In cases with repeated eigenvalues and eigenvectors, the modal summation results must be interpreted with care. You should add insignificant mass to the structure or perturb the symmetric geometry such that the eigenvalues become unique» | «В случаях с повторяющимися собственными значениями и собственными векторами результаты модального суммирования должны интерпретироваться с осторожностью. Вы должны добавить несущественную массу к конструкции или нарушить симметричную геометрию, чтобы собственные значения стали уникальными» |
При изменении геометрии башня создается прямоугольного сечения с размерами а и k*a (k принимается 1.01-1.05). При изменении масс по одному из направлений прикладываются дополнительные массы (0.01-0.05 от общей массы сооружения по данному направлению).
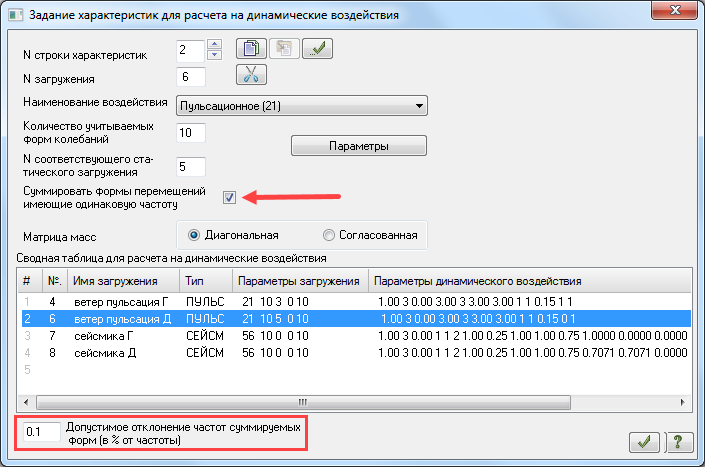
В ЛИРА-САПР версии 2018 появился новый инструмент Суммирование кратных форм. В случае ветровой пульсации направление итоговой формы колебаний принимается по направлению статической составляющей ветровой нагрузки. Так при ветре, заданном на грань, суммарная форма перемещений также будет на грань. При направлении ветра на диагональ, заданном через 2 составляющие вдоль осей X и Y, итоговое направление формы перемещений будет по направлению равнодействующей, т.е. тоже на диагональ.
Рис. 14. Диалог задание характеристик для расчета на динамические воздействия версии 2018
Ниже будут показаны варианты расчета башни на действие пульсационной составляющей ветровой нагрузки с учетом суммирования по формам колебаний и без него. Сравниваться будет НДС схемы при определении величины ветровой пульсации «ручным» способом (см. выше) и программно.
Суммирование кратных форм
К башне, описанной выше, прикладывается статическая составляющая ветровой нагрузки. Пульсационная составляющая определяется программно.
Ветер на грань.
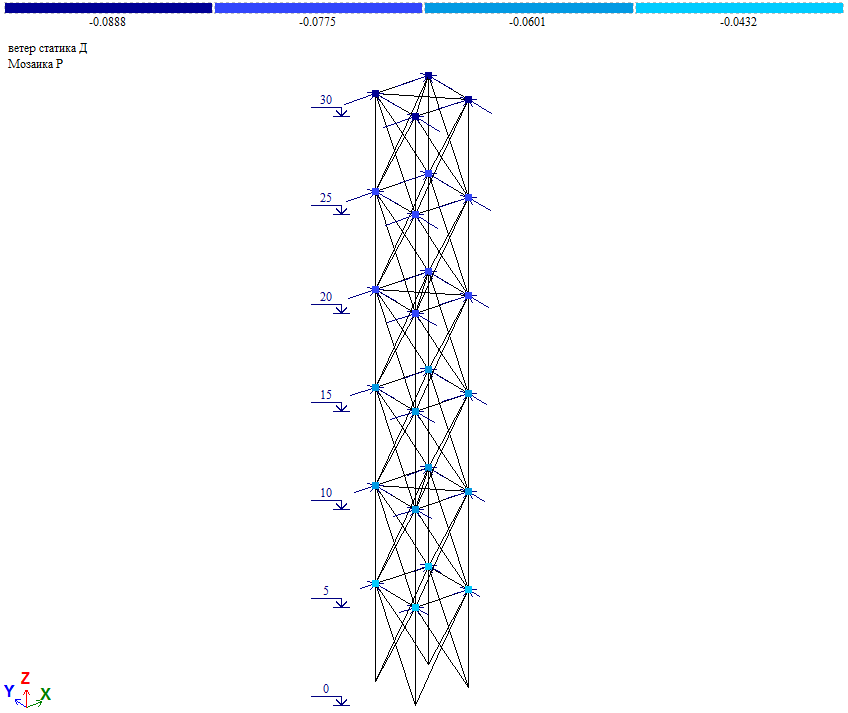
Рис. 15. Схема приложения средней ветровой нагрузки на ствол башни при действии ветра на грань
Величина узловой нагрузки Wm/4 (Wm см. таблицу 2).
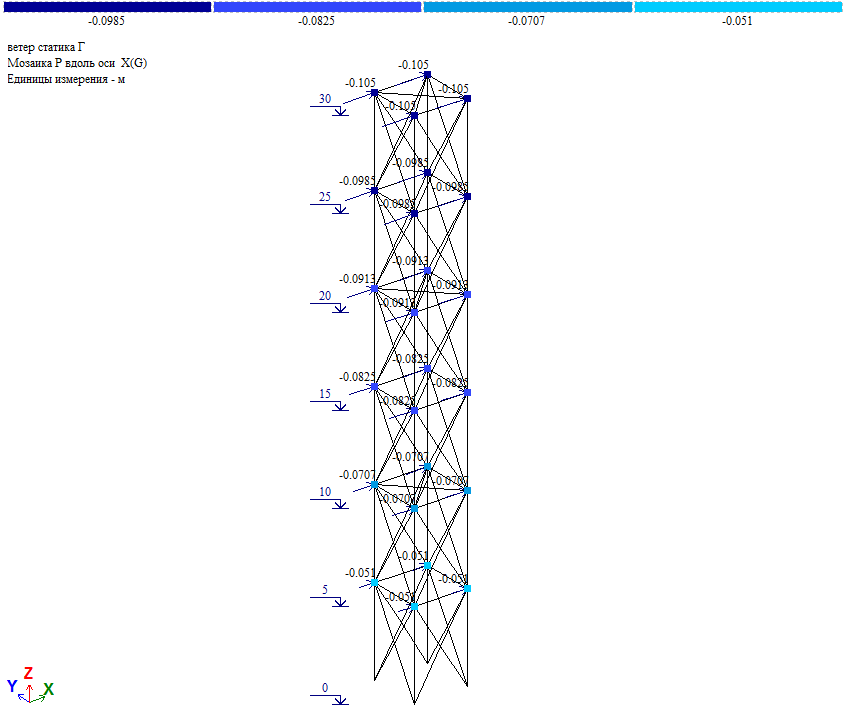
Пульсационная составляющая по результатам расчета:
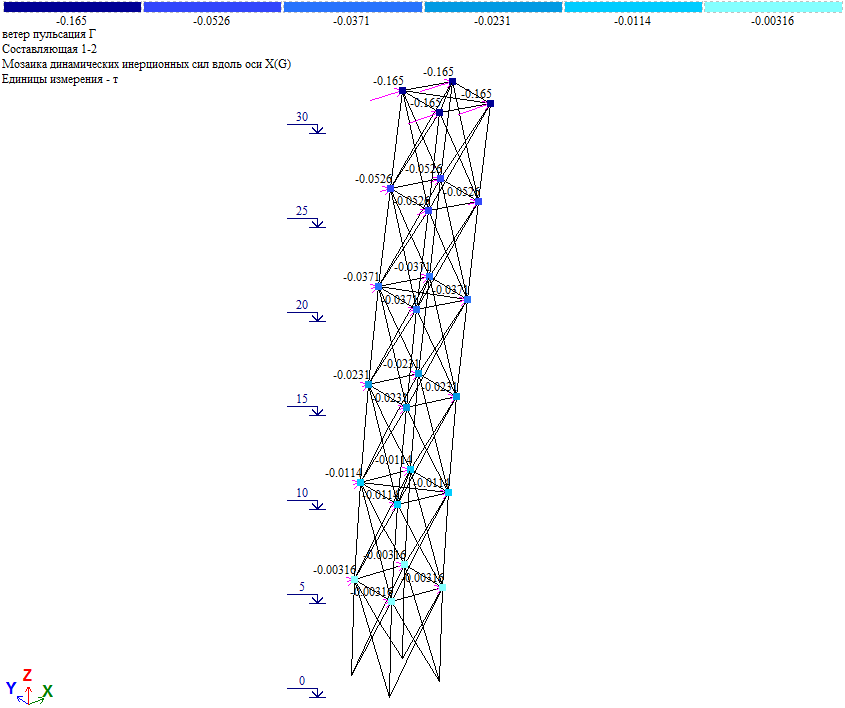
Рис. 16. Пульсационная составляющая ветровой нагрузки при действии ветра на грань
Пульсационная составляющая в уровне отм. +30.000 Wp=0.165*4=0.66тс, что близко к величине нагрузки в таблице 1 (Wp=0.6575тс). Т.е. результаты «ручного» и программного расчета совпадают.
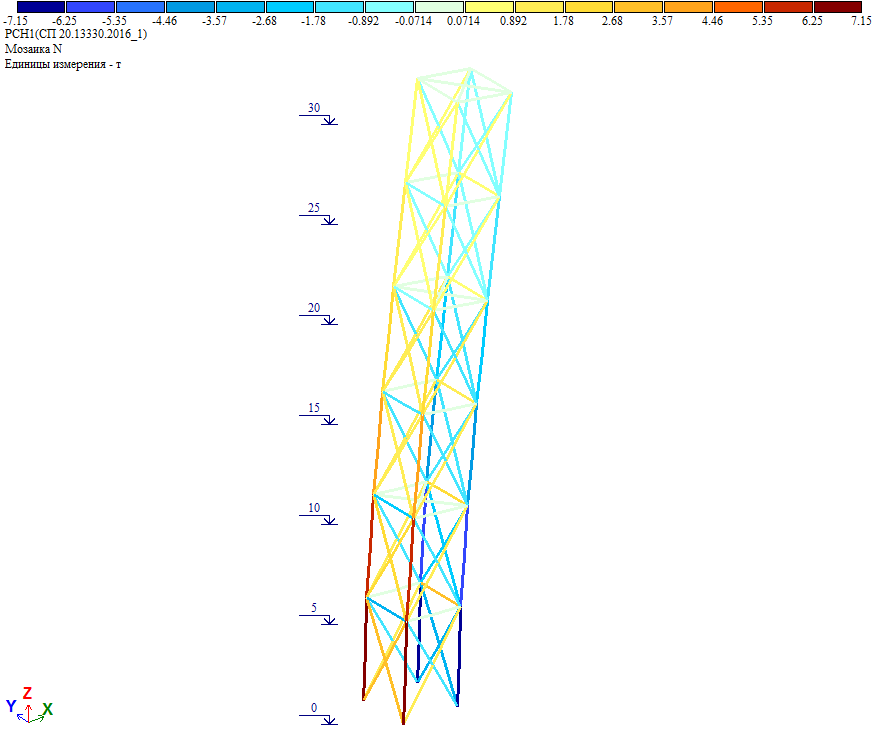
Усилия в элементах башни от полной ветровой нагрузки на грань (получено через РСН):
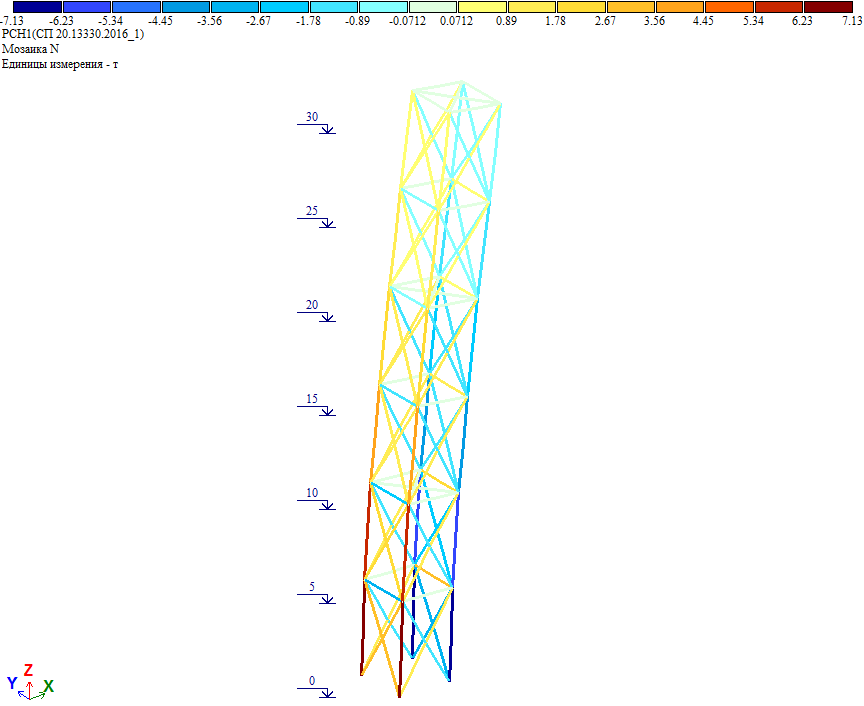
Рис. 17. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на грань
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на грань, определенная «вручную» и приложенная единой нагрузкой.
Ветер на диагональ.
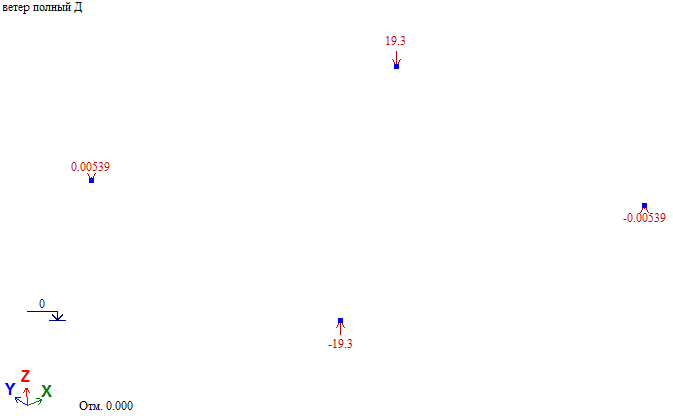
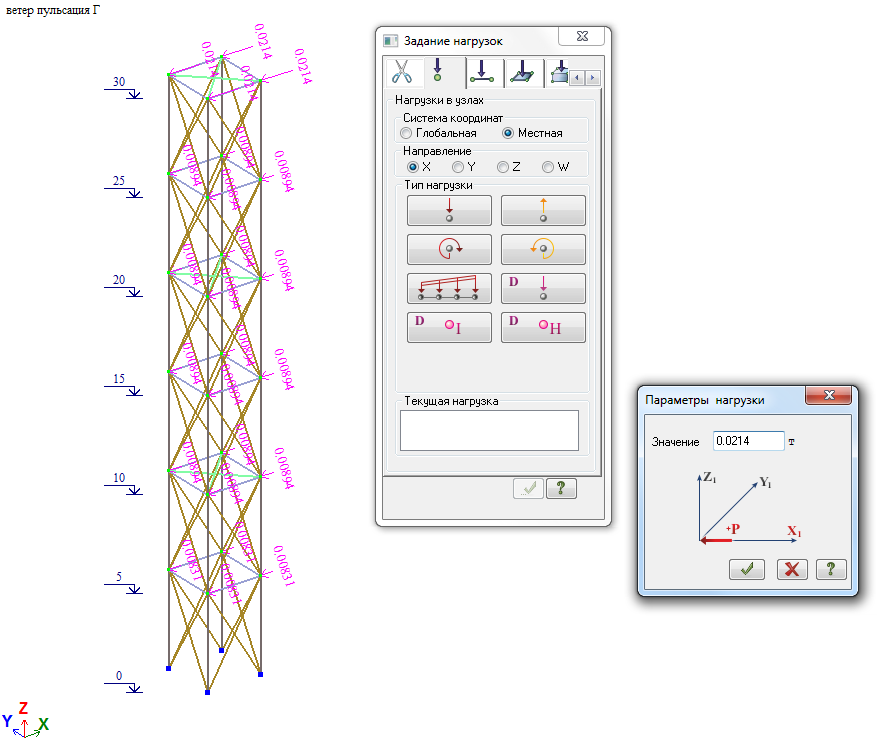
Рис. 18. Схема приложения средней ветровой нагрузки на ствол башни при действии ветра на диагональ
Величина узловой нагрузки (Wm/4)*cos45⁰ (Wm см. таблицу 2).
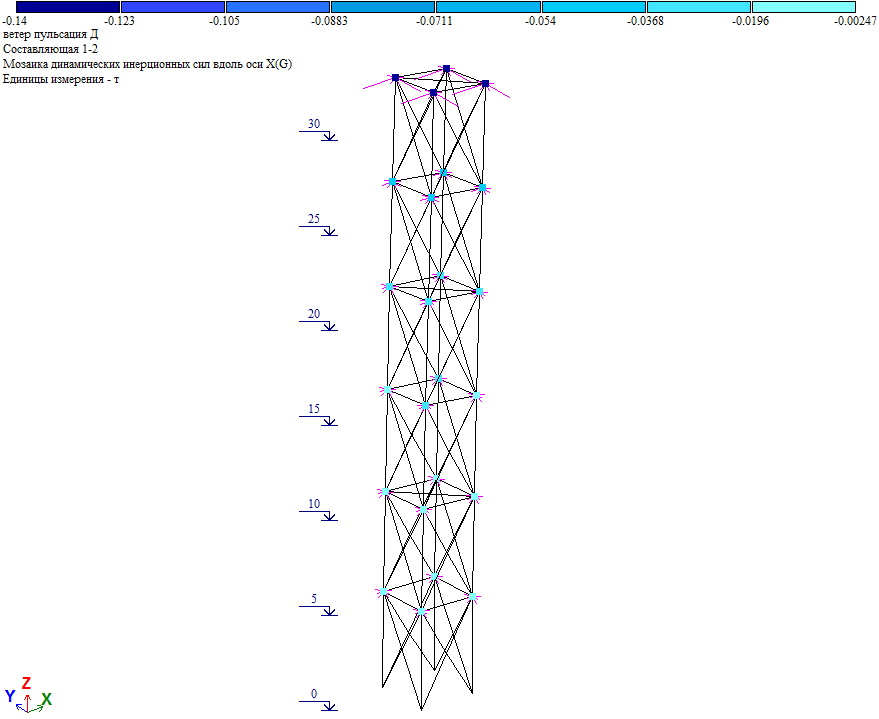
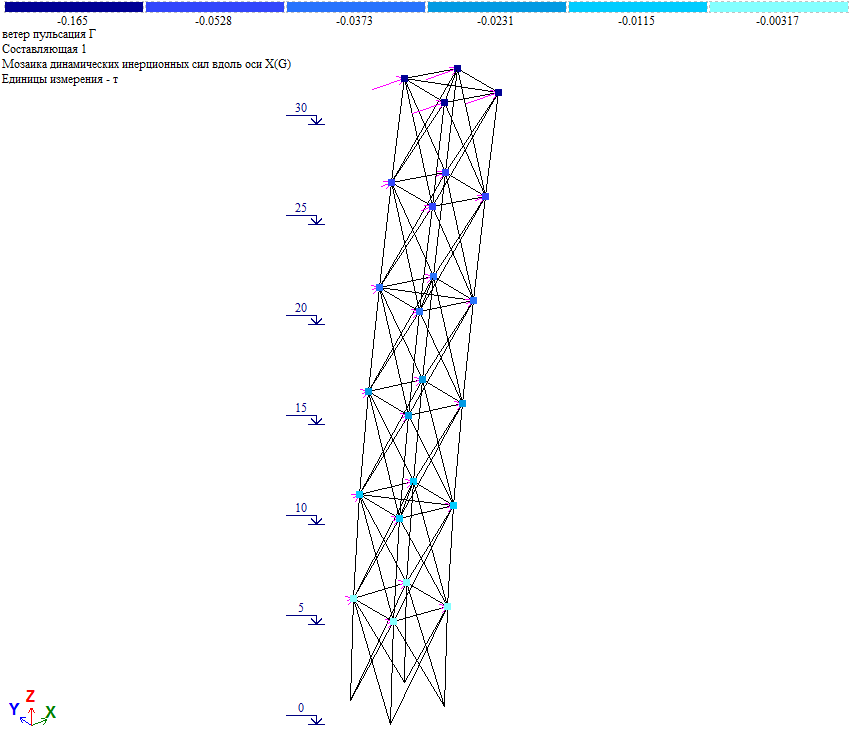
Рис. 19. Пульсационная составляющая ветровой нагрузки при действии ветра на диагональ
Пульсационная составляющая в уровне отм. +30.000 Wp=Wpx/cos45⁰=(0.14*4)/0.7071=0.792тс, что близко к величине нагрузки в таблице 2 (Wp=0.789тс). Т.е. результаты «ручного» и программного расчета совпадают.
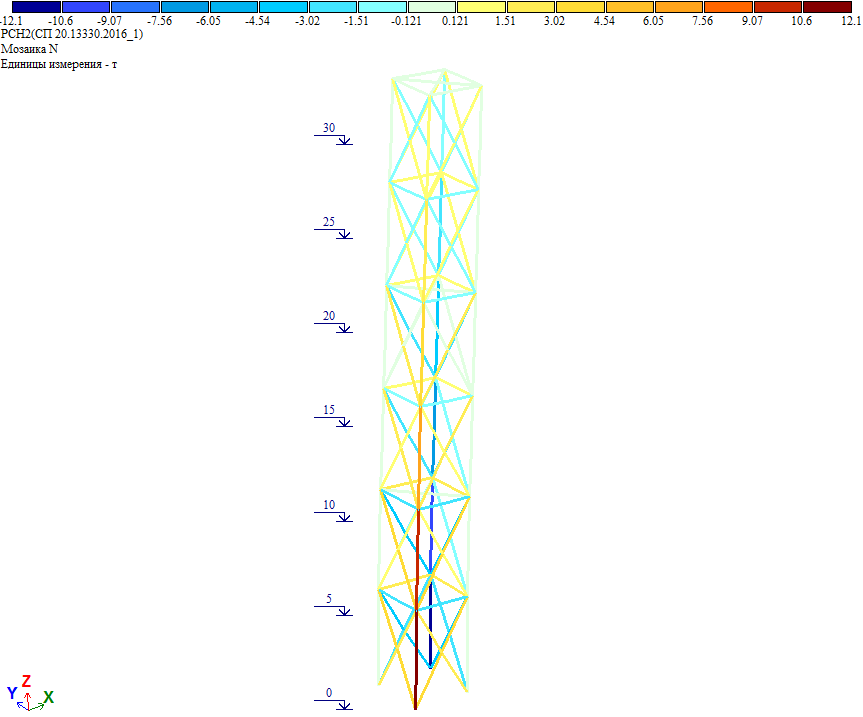
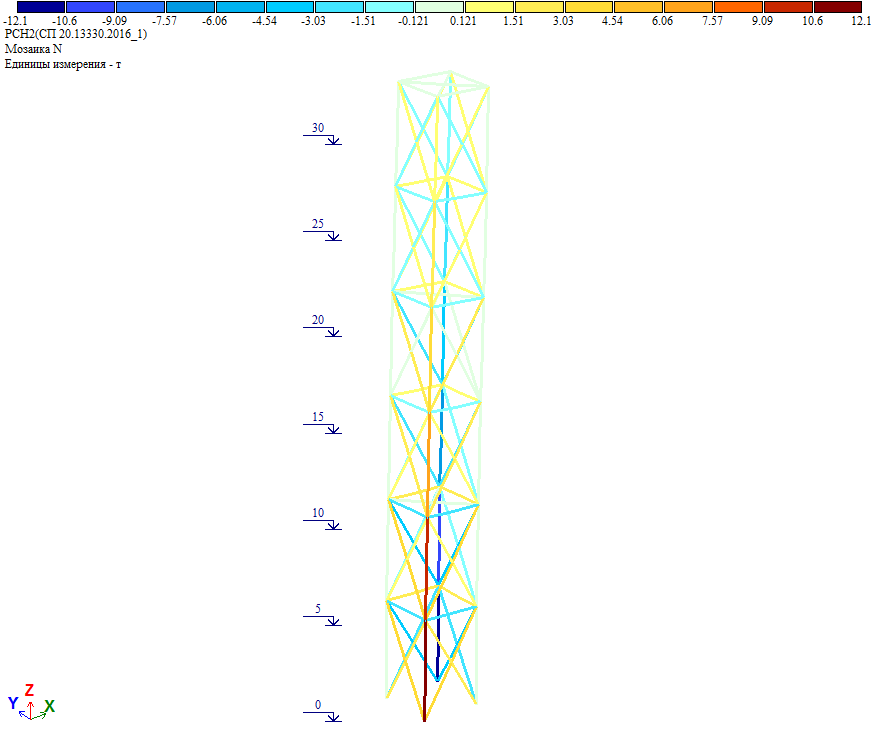
Усилия в элементах башни от полной ветровой нагрузки на диагональ:
Рис. 20. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на диагональ
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на диагональ.
«Управление» кратными формами
При расчете башни без использования функции «Суммировать формы перемещений» кратными формами колебаний следует управлять, чтобы получить ожидаемый результат. Так при ветре на грань следует задать дополнительные веса масс по направлению воздействия ветровой нагрузки:
Рис. 21. Дополнительные узловые веса масс для действия ветра на грань
Величина дополнительных весов масс принимается 0.01-0.05 от общего веса массы сооружения по данному направлению.
Величина суммарной массы представлена в протоколе решения задачи. Т.к. к схеме прикладывается нагрузка вес массы, то массу из протокола расчета следует увеличить в g раз.
В примере выше для каждого уровня принята величина дополнительной массы, пропорциональная массе сооружения на данном уровне.
Рис. 22. Пульсационная составляющая ветровой нагрузки при действии ветра на грань
Рис. 23. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на грань
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия. Максимальное продольное усилие увеличилось на 100%*(7.15-7.13)/7.13=0.28%.
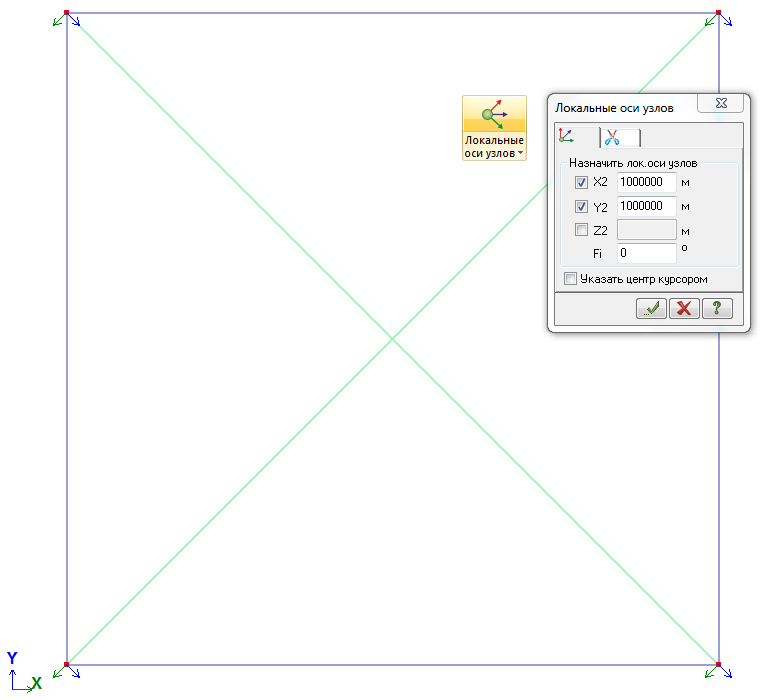
При действии ветра на диагональ следует ввести локальную систему координат узлов по направлению ветра. Для этого нужно отметить узлы, к которым прикладывается нагрузка, вызвать диалог «Локальные оси узлов» и указать в качестве координат точки, из которой будет смотреть ось X2, достаточно большие величины:
Рис. 24. Введение местных осей узлов
В итоге для узлов местные оси Х2 будут параллельны и сонаправлены с ветровым воздействием. Итоговая форма колебаний при определении величины ветровой пульсации также будет совпадать с направлением ветра на диагональ.
Т.к. веса масс при динамическом расчете приложены всегда в локальной системе координат узла (если локальная система координат не вводится, то локальные оси узлов совпадают по направлению с глобальными осями схемы), то при расчете башни на диагональное воздействие ветра следует формировать отдельный файл задачи. В противном случае формы колебаний будут не пригодны для получения корректных пульсационных инерционных сил для загружения ветра на грань. В этом случае результаты расчета двух задач (ветер на грань и на диагональ) можно «склеить» в Метеоре (Вариации моделей). Но всего этого можно избежать, если воспользоваться новой функцией «Суммировать формы перемещений»
Инерционные силы:
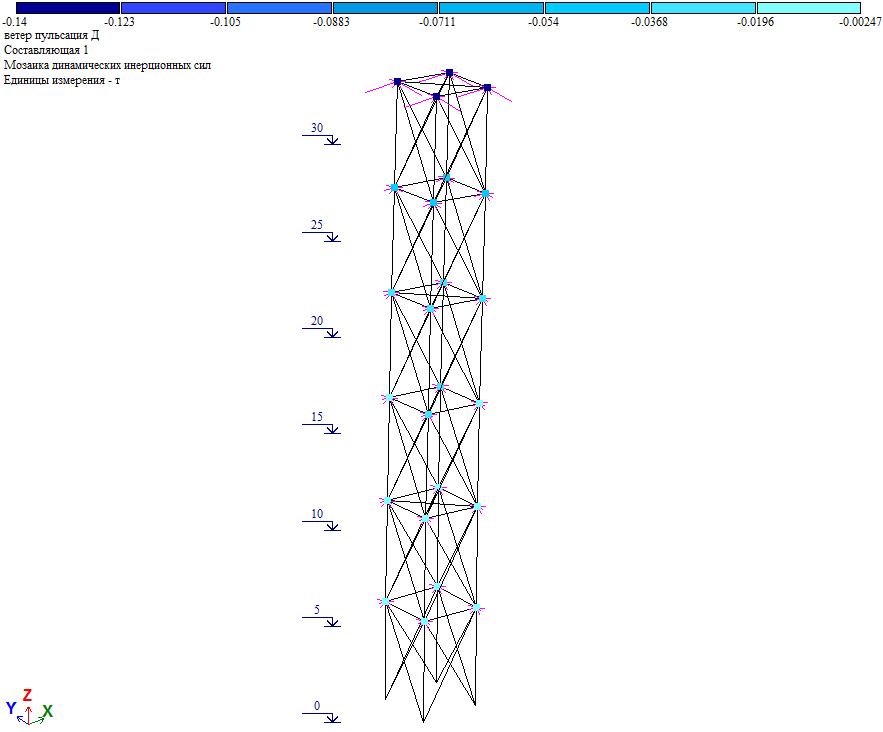
Рис. 25. Пульсационная составляющая ветровой нагрузки при действии ветра на диагональ
Рис. 26. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на диагональ
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия.
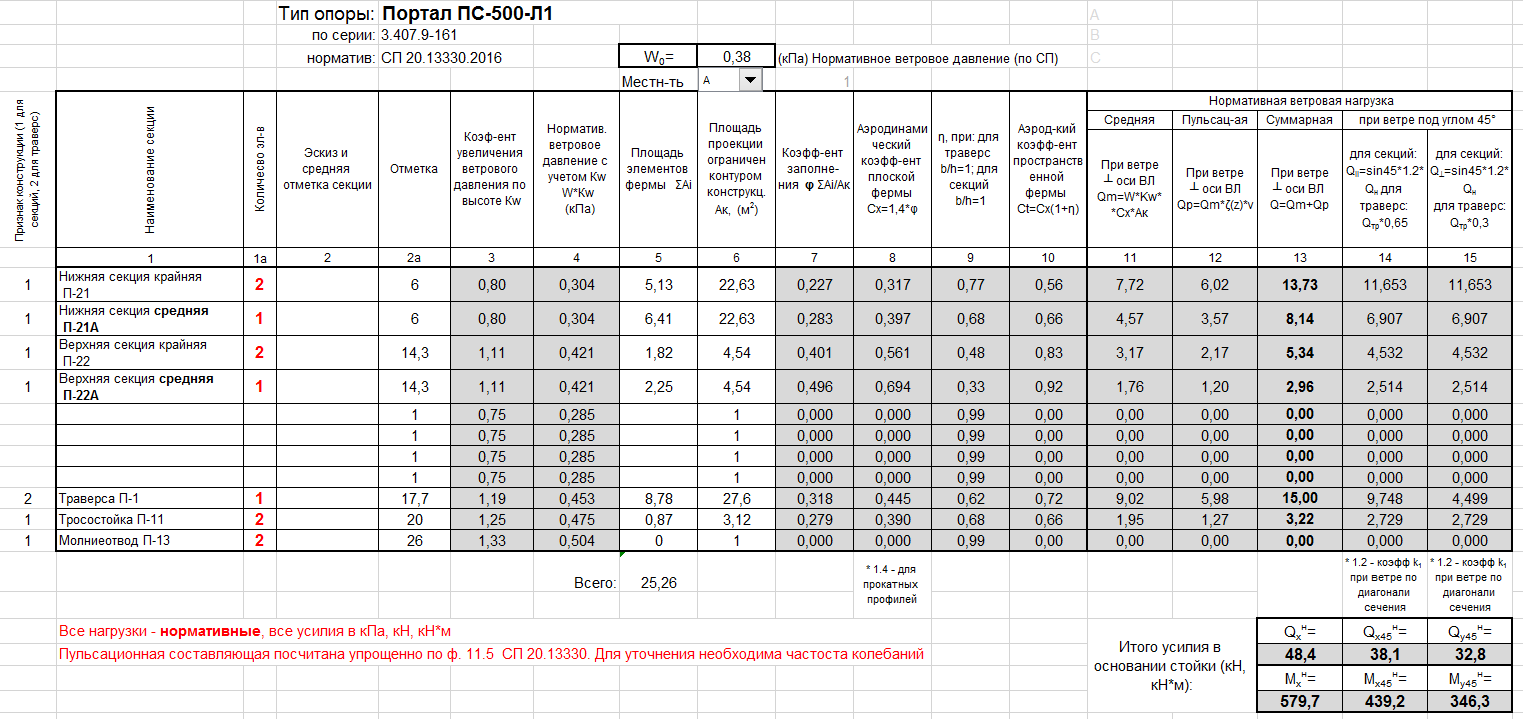
Расчетный файл в формате *.xlsx
Сам расчетный файл в формате *.xlsx можно скачать по ссылке: Ветровая нагрузка на решетчатую опору.xlsx
В файле 2 листа:
- на первом выполняется расчет нагрузок на конструкцию решетчатой опоры по разделу 11 СП 22.13330.2016
- на втором тот же расчет выполняется согласно указаниям ПУЭ издание 7.
В расчетном файле все что закрашено серой заливкой вычисляется автоматически — реализована интерполяция всех коэффициентов к ветровой нагрузке, зависящих от высоты расположения конструкции, типа местности по ветру и от других параметров.
Особенность расчетов —
- Пульсационная составляющая по СП 33.13330-2016 вычисляется приблизительно по ф.11.5 из предположения что первая частота собственных колебаний сооружения больше предельного значения flim. Для точного расчета конструкцию необходиом просчитать на колебания в КЭ программе, например SCAD.
- Для траверс при ветре под 45 градусов приняты эмпирические коэффициенты к ветровому давлению по методике Крюкова-Новгородцева и серий Электросетьпроекта. Пульсационная составляющая ветра в расчете по ПУЭ учитывается коэффициентом 1,5 согласно указаниям данного нормативного документа.
Правильность расчетов проверена на собственном опыте.
При создании файла использовалась программа Microsoft Exel 2013. Более ранние версии могут открыть файл некорректно (не проверял).