Описание презентации по отдельным слайдам:
-
1 слайд
Вычисление производных средствами Excel
Работу выполнил
студент 210 группы
Войцеховский Виктор
Проверил: доцент
Морозов Н.П.
Задание 2 -
2 слайд
Решение
Средствами Excel найти производную функции y=x3 на промежутке x[0,6] с шагом дискретизации x=0,4. построить график производной функции.Необходимо для решения задачи сначала ввести данные в рабочую область таблицы Excel
-
3 слайд
Шаг 1. Составляем таблицу данных
В ячейку А2 вводим левую границу диапазона (0)
В ячейку А3 – левая граница диапазона + шаг построения (=А2+0,4)
Выделив блок ячеек А3:А17, автозаполнением получим все значения аргумента до значения х=6
В диапазоне В2:В17 введем значения функции. Запишем в ячейку В2 формулу = А2^3 и далее автозаполнением копируем эту формулу в данный диапазон. В результате получаем таблицу данных для вычисления производной -
4 слайд
Шаг2. По введенным данным находим значения производной
В ячейку С3 вводим формулу дифференцирования = (В4-В2)/(3*0,4)
Копируем эту формулу в диапазон ячеек С4:С16
Получаем значения производной -
5 слайд
Шаг 3. С помощью мастера диаграмм строим график производной
Краткое описание документа:
Предлагается ряд статей, презентаций лекций и практических занятий по математике по разделу «Дифференциальное исчисление» для студентов вузов и ссузов нетехнических специальностей. Данный цикл занятий стоится на основе учебного пособия профессора Вершининой Лилии Павловны « Математика : математический анализ, линейная алгебра»: учебное пособие / Л.П. Вершинина; М-во культуры РФ, СПб.,Санкт-Петербургский государственный университет культуры и искусств,2009.– 158. Учебные и методические материалы занятий могут быть особенно полезны и интересны школьникам10 и 11 классов, студентам старших курсов ссузов, которые решили продолжать свое образование в гуманитарных (нетехнических)вузах.В данной презентации рассматривается пример вычисления производной с помошью приложения MS Excel.
Нахождение интеграла и производной при помощи Excel
Раскрыть первое сообщение
Как вычислить интеграл в Excel?
Ниже приводится решение интегралов, а также нахождение производной в excel (численное интегрирование и дифференцирование)
Кому-то поможет на лабах
Нахождение производной
Нахождение интеграла
Скачать обе страницы в виде DJVU-файла (54 Кб): mat_task.djvu.zip
DySprozin (написано 12.11.2010 в 23:16)
Кроме форматирования элементов поля ячеек, строк и столбцов часто бывает полезно использовать несколько рабочих листов Excel. Для систематизации и поиска информации в книге удобно присваивать названиям листов собственные имена, отражающие их смысловое содержание. Например, «исходные данные», «результаты расчетов», «графики» и т. п. Это удобно сделать, воспользовавшись контекстным меню. Нажать правую кнопку мышки на ярлычке листа, Переименовать лист и нажать <Enter >.
Для добавления одного или нескольких новых листов в меню Вставка выбрать команду Лист. Чтобы вставить сразу несколько листов нужно выделить ярлычки необходимого числа листов, удерживая <Shift >, затем из меню Вставка выполнить команду Лист. Обратная операция по удалению листов проводится аналогично. Через контекстное меню, где выбирается команда Удалить.
Полезная операция по перемещению листов – левой кнопкой мыши захватить ярлычок листа и переместить его в нужное место. Если при этом нажать <Ctrl>, произойдет перемещение копии листа, а к имени листа добавится число 2 .
Задача 7. Измените формат всей ячейки В2 на: шрифт – Arial 11; расположение – в центре, по нижнему краю; одно слово в строке; формат числа –“0,00”; граница ячейки – двойная линия
|
A |
B |
C |
D |
E |
|
|
1 |
|||||
|
2 |
Показатель |
преломления |
стекла К8 — |
1.5183 |
2.3. Встроенные функции
Программа Excel содержит более 150 встроенных функций для упрощения расчетов и обработки данных. Пример содержимого ячейки с функцией: =В2+SIN(C7), где В2 и С7— адреса ячеек, содержащих числа, а SIN( ) – имя функции. Наиболее используемые функции Excel:
SQRT(25) = 5 – вычисляет квадратный корень из числа (25) РАДИАНЫ(30) = 0,5 — преобразует 30 градусов в радианы ЦЕЛОЕ(8,7) = 8 – округляет до ближайшего меньшего целого ОСТАТ(-3;2) = 1 – оставляет остаток от деления числа(-3) на
делитель(2). Результат имеет знак делителя. ЕСЛИ(E4>0,2;”доп”;”ошиб”) – если число в ячейке Е4 меньше 0,2,
тогда Excel возвращают “доп” (истина), в противном случае – “ошиб”(ложь).
В формуле функции могут быть вложенными друг в друга, но не более 8 раз.
11
При использовании функции главным является определение самой функции и ее аргумента. В качестве аргумента, как правило, указывается адрес ячейки, в которой записана информация.
Определить функцию можно, набрав текст (значки, числа и т.п.) в нужную ячейку, либо воспользоваться Мастером функций. Здесь для удобства поиска все функции разбиты на категории: математические, статистические, логические и другие. Внутри каждой категории они отсортированы в алфавитном порядке.
Мастер функций вызывается командой меню Вставка, Функция
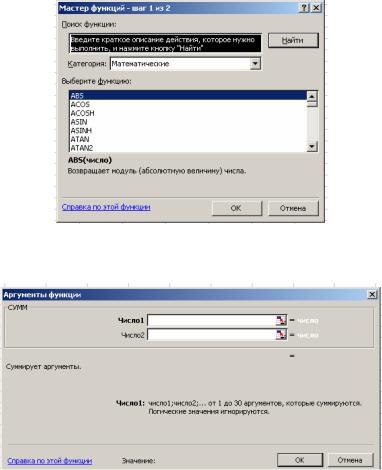
или нажатием пиктограммы ( fx ). В первом появившемся окне Мастера функций (рис.4) определяем Категорию и название конкретной функции, нажимаем <OK>. Во втором окне (рис.5) необходимо определить Аргументы функции. Для этого щелчком кнопки справа от первого диапазона ячеек (Число 1) “прикрываем” окно. Выделяем ячейки, на основе которых будет проводиться вычисление. После этого выделенные ячейки будут занесены в окно первого диапазона . Еще раз нажимаем правую клавишу . Если аргументом является несколько диапазонов ячеек, то действие повторяем. Затем для завершения работы нажимаем <OK>. В исходной ячейке окажется результат вычисления.
Рис. 4. Вид окна Мастер функций
Рис. 5. Окно для задания аргументов выбранной функции
12
Задача 8. Найти среднее значение ряда чисел: 2,5; 2,9; 1,8; 3,4; 6,1;
1,0; 4,4.
Решение. Вводим числа в ячейки, например, С2:С8. Выделяем ячейку С9, в которую записываем функцию =СРЗНАЧ(С2:С8), нажимаем <Enter>, в С9 получаем среднее значение указанных чисел – 3,15.
Задача 9. Применяя условную логическую функцию ЕСЛИ, составить формулу переименования нечетных числе в «осень», четных — «весна».
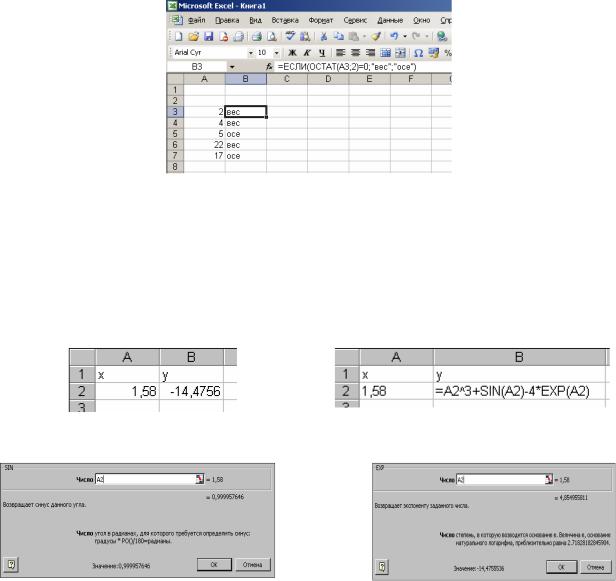
Решение. Выбираем столбец для ввода исходных данных – четных (нечетных) чисел, например, A. В ячейку B3 запишем формулу =ЕСЛИ(ОСТАТ(A3;2)=0;»вес»;»осе»). Копируя ячейку B3 вдоль столбца В, получаем результаты анализа записанных в столбце А чисел. Результаты решения задачи представлены на рис. 6.
Рис. 6. Решение задачи № 9
Задача 10. Вычислить значение функции y = x3 + sinx – 4ex для x = 1,58.
Решение. Разместим данные в ячейки А2 – х, В2 –у. Решение задачи показано на рис.7 в числовом виде слева и формульном – справа. При решении данной задачи следует обратить внимание на вызов функций SIN и экспоненты для ввода аргумента (см. рис.8).
Рис.7. Решение задачи № 10
Рис.8. Окна для ввода аргумента функции SIN и EXP
13
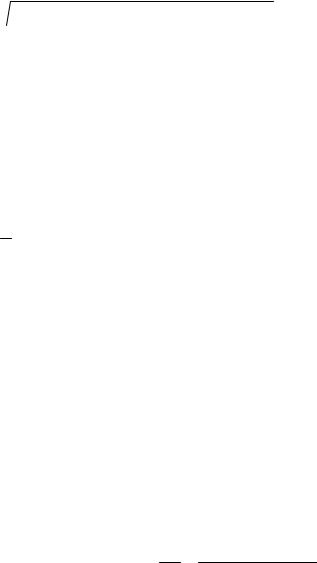
Задача 11. Составьте в Excel математическую модель задачи для расчета функции y= 1/ ((x- 3) · (x+ 4)), при значениях x= 3 и у= -4 выводить на экран «неопределена», численные значения функции – в остальных случаях.
Задача 12. Составьте в Excel математическую модель задачи: 12.1. для вычисления с корнями
а)√ x3· y2· z / √ x·z ; b) (z · √ z )2 ; c) 3√ x2 · 3√x ; d) √ 5·x5·3-1 / √ 20·x·3-1
12.2. для геометрических вычислений а) определить углы прямоугольного треугольника, если известны х – катет, у – гипотенуза ;
b) определить расстояние между двумя точками в декартовой системе координатах XYZ по формуле
d = 
с) определить расстояние от точки (x0,y0) до прямой a x + b y + c = 0 по формуле
d = a x0+b y0+c / √ (a2+b2)
d) определить площадь треугольника по координатам вершин по формуле
S = 12 [(x1 − x3 )(y2 − y3 ) − (x2 − x3 )(y1 − y3 )]
3. Решение задач с применением формул и функций
Задач, которые можно успешно решать с использованием формул и функций Excel, на самом деле много. Рассмотрим задачи, которые в практике наиболее часто решаются с применением электронных таблиц: линейные уравнения и их системы, вычисление численных значений производных и определенных интегралов.
|
3.1.Численное вычисление производной |
и определенного |
|
интеграла |
Производной функции y = f(x) называется отношения ее приращения ∆y к соответствующему приращению ∆x аргумента, когда
∆x→ 0
y = f ( x + x) − f ( x)
x x
(1).
Задача.13. Найти производную функции y = 2x3 + x2 в точке x=3.
14
Решение. Производная, вычисленная аналитическим методом, равна 60. Вычисление производной в Excel проведем по формуле (1). Для этого выполним последовательность действий:
· Проведем обозначения столбцов: Х – аргументы функции, У – значения функции, У ` – производная функции (рис.9).
·Табулируем функцию в окрестности точки х= 3 с малым шагом, например, 0,001 результаты заносим в столбец Х.
Рис. 9. Таблица вычисления производной функции
·В ячейку В2 введем формулу вычисления функции =2*A2^3+A2^2.
·Скопируем формулу до строки 7, получим значения функции в точках табуляции аргумента.
·В ячейку С2 введем формулу вычисления производной =(B3-B2)/ (A3-A2).
·Скопируем формулу до строки 6, получим значения производных в точках табуляции аргумента.
Для значения х= 3 производная функции равна значению 60,019, что близко к значению, вычисленному аналитически.
|
Задача 13. Найти производную функции в указанных точках: |
|||
|
1. |
Y = 2x2 для х = 3 |
2. Y= (1-√x)2 / x для х = 0,01 |
|
|
3. |
Y = Cos(x) для х = 0 |
4. Y= Sin(x) |
для х = π/ 2 |
|
5. |
Y = Cos(x) для х = π/ 2 |
6. Y= Tg(x) |
для х = 0 |
|
7. |
Y = 4/3 x3 – 4x для х = 0,2 |
8. Y= ex ln x для x=1 |
|
9. Y = Cos(x ) / (1- Sin(x)) для х= π /6 |
10. ( a+ b) /(3- 2x) + (5x4— 1) / (a- b) |
|
Определенный интеграл в |
для х = 0 |
|
Excel можно вычислить, используя |
метод трапеций. В методе трапеций область интегрирования разбивается на отрезки с некоторым шагом и площадь под графиком функции на каждом отрезке считается равной площади трапеции. Тогда расчетная формула принимает следующий вид
15
|
b |
|
|
S N = ∫ f (u)du ≈ h N∑−1[f (a + h i) + f (a + h (i + 1))] (2), |
|
|
a |
2 i=0 |
где h= (b- a)/ N – шаг разбиения; N – количество точек разбиения.
Для повышения точности количество точек разбиения удваивается, повторно выполняется расчет интеграла. Дробление исходного интервала прекращают, когда достигнута требуемая точность:
|
Задача 14. Вычислить определенный интеграл ∫3 |
3x 2dx |
|
2 |
|
|
Решение. Для численного вычисления величины определенного |
интеграла выполним следующие действия:
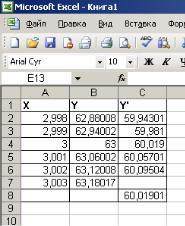
– выберем N= 5, в ячейке F2 рассчитаем h- шаг разбиения (рис. 10);
Рис. 10. Вычисление определенного интеграла
·В первом столбце А записываем номер интервала i ;
·В ячейке B2 запишем формулу =3*(2+F2*A2)^2 для расчета первого слагаемого формулы (2);
·В ячейке С2 запишем формулу =3*(2+F2*(A2+1))^2 для расчета второго слагаемого;
·“Протянем” ячейки с формулами на 4 строки вниз по столбцам;
·В ячейку С7 запишем формулу и вычислим сумму слагаемых ,
·В ячейке С8 запишем формулу и вычислим SN искомое значение определенного интеграла 19,02 (значение SN полученное аналитически
19).
Задача. 15. Вычислить определенный интеграл:
|
3 |
1 |
|
1. Y = ∫2 x d x |
2. Y = ∫2x3dx |
|
0 |
−1 |
|
16 |
|
2 π |
2 |
||||||||||||||
|
3. |
Y = ∫2sin( x)dx |
4. |
Y = ∫ x2dx |
||||||||||||
|
0 |
−2 |
||||||||||||||
|
5. |
5 |
dx |
6. |
1 |
dx |
||||||||||
|
Y = ∫ |
Y = ∫ |
||||||||||||||
|
3x − 2 |
(2x +1) 3 |
||||||||||||||
|
1 |
0 |
||||||||||||||
|
7. |
π |
x |
3x |
2 |
x + 3 |
||||||||||
|
Y = ∫cos |
cos |
dx |
8. |
Y = ∫ |
dx |
||||||||||
|
2 |
2 |
x 2 + 4 |
|||||||||||||
|
0 |
0 |
3.2. Решение линейных уравнений
Линейные уравнения в Excel можно решить, используя функцию Подбор параметра. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки, не возвратит заданное значение.
Рассмотрим процедуру поиска параметра на простом примере решения линейного уравнения с одним неизвестны.
Задача 16. Решить уравнение 10· x — 10 / x = 15.
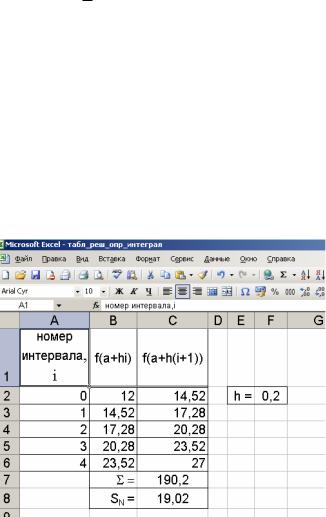
Решение. Для искомого значение параметра – x выберем ячейку A3. Введем в эту ячейку любое число, лежащее в области определения функции (в нашем примере это число не может быть равно нулю). Пусть это будет 3. Это значение будет использовано в качестве начального. В ячейку, например, B3 в соответствии с приведенным уравнением введем формулу =10*A3-10/A3. В результате серии расчетов по данной формуле будет отобрано искомое значение параметра. Теперь в меню Сервис, выбрав команду Подбор параметра, запустим функцию поиска параметра (рис.11, а). Введем параметры поиска:
·В поле Установить в ячейке введем абсолютную ссылку на ячейку $В$3, содержащую формулу.
·В поле Значение введем искомый результат 15.
·В поле Изменяя значение ячейки введем ссылку на ячейку А3, содержащую подбираемое значение, и нажмем <OK>.
По окончании работы функции Подбор параметра на экране появится окно Результат подбора параметра, в котором будут отображены результаты поиска. Найденный параметр 2,000025 появится в ячейке А3, которая была для него зарезервирована.
Обратите внимание на тот факт, что в нашем примере уравнение имеет два решения, а параметр подобран только один. Это происходит потому, что параметр изменяется только до тех пор, пока требуемое значение не будет возвращено. Первый найденный таким образом аргумент и возвращается к нам в качестве результата поиска. Если в качестве
17
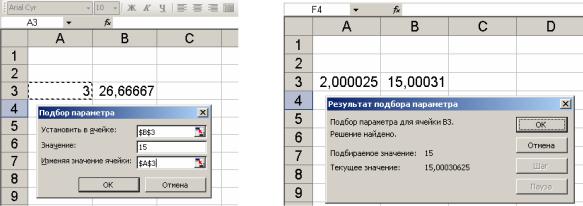
начального значения в нашем примере указать -3, тогда будет найдено второе решение уравнения: -0,5.
а) б)
Рис.11. Решение уравнения: а— ввод данных, б— результат решения
|
Задача 17. Решить уравнения |
||||
|
1. |
5х/ 9- 8= 747x/ 12 |
2. |
(2x+ 2)/ 0.5= 6x |
|
|
3. |
0,5 (2x- 1)+x/ 3= 1/6 |
4. |
7 (4x- 6)+ 3 (7- 8x)= 1 |
|
|
Систему линейных |
уравнений |
можно решать различными |
способами: подстановки, сложения и вычитания уравнений, с использованием матриц. Рассмотрим способ решения канонической системы линейных уравнений (3) с использованием матриц.
a1 x + a2 y + b1= 0
(3)
a3 x + a4 y + b2 =0
Известно, что система линейных уравнений в матричном представлении записывается в виде:
A X = B,
где А – матрица коэффициентов, X– вектор — столбец неизвестных,
В– вектор-столбец свободных членов. Решение такой системы
записывается в виде
X = A-1 B,
где A-1 –матрица, обратная по отношению к А. Это вытекает из того, что при решении матричных уравнений при X должна остаться единичная матрица Е. Умножая слева обе части уравнения АХ = В на А-1, получаем решение линейной системы уравнений.
Задача 18. Решить систему линейных уравнений
2x + y = 3
4x + 5y = 2
18
Решение. Для данной системы линейных уравнений значения соответствующих матрицы и вектора-столбца имеют вид:
|
2 |
1 |
3 |
||||
|
A = |
4 |
5 |
B = |
2 |
||
Для решения задачи выполним действия:
·Выделим блок ячеек, например, А2:В3 и запишем в него элементы матрицы А.
·Выделим блок ячеек, например, С2:С3 и запишем в него элементы матрицы В.
·Выделим блок ячеек, например, D2:D3 для помещения результата решения системы уравнений.
·в ячейку D2 введем формулу = МУМНОЖ(МОБР( А2:В3);С2:С3).
Библиотека Excel в разделе математических функций содержит функции для выполнения операций над матрицами. В частности, это функции:
|
Функция |
Выполняемое действие |
|
|
МОБР (параметр) |
обращение матрицы |
|
|
МОПР (параметр) |
вычисление |
|
|
определителя матрицы |
||
|
МУМНОЖ (список параметров) |
умножение матриц |
Параметрами данных функций могут быть адресные ссылки на массивы, содержащие значения матриц или имена диапазонов и выражения.
Например, МОБР (А1: B2) или МОПР (матрица_1).
· Укажем Excel, что выполняется операция над массивами, для этого нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter>, в ячейках D2 и D3 будет получен результат х = 2,16667; y= — 1,33333.
|
Задача 19. Решите систему линейных уравнений |
||||
|
1. 3x + |
2y = 8 |
2. 5x + y = 7 |
3. 5x + 4y = 22 |
4. 3x — 4y = -17 |
|
5x + |
y = 11 |
4x + 3y = -1 |
3x + y = 9 |
5x + 3y = — 9 |
4. Решение задач оптимизации
Многие проблемы прогнозирования, проектирования и производства сводятся к широкому классу задач оптимизации. Такими задачами являются, например: максимизация выпуска товаров при ограничениях на сырье для производства этих товаров; составление штатного расписания для достижения наилучших результатов при наименьших расходах; минимизация затрат на транспортировку товаров; достижение заданного качества сплава; определение размеров некоторой емкости с учетом стоимости материала для достижения максимального объема; различные
19

задачи, в которые входят случайные величины, и другие задачи оптимального распределения ресурсов и оптимального проектирования.
Решение задач такого вида может быть осуществлено EXCEL с помощью инструмента Поиск решения, который расположен в меню Сервис. Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи надо начинать с построения соответствующей модели. Познакомимся с этими командами на примере.
Задача 20. Предположим, что мы решили производить два вида объективов А и В. Объектив вида А состоит из 3-х линзовых компонентов, вид В – из 4-х . За неделю можно изготовить не более 1800 линз. На сборку объектива вида А требуется – 15 минут, вида В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько объективов А и В надо изготовить, чтобы получить максимальную прибыль, если объектив вида А стоит 3500 рублей, вида В – 4800 рублей.
Решение. Для решения этой задачи необходимо составить и заполнить таблицу в соответствии с рис. 12:
·Переименуем ячейку В2 в x, количество объективов вида А.
·Аналогично переименуем ячейку В3 в y.
· Целевую функцию Прибыль = 3500*x+4800*y введем в ячейку B5. · Затраты на комплектацию равны =3*x+4*y введем в ячейку B7.
· Затраты по времени равны =0,25*x+0,5*y введем в ячейку B8.
|
А |
В |
||
|
1 |
Наименование |
Формулы |
|
|
2 |
А |
“x” |
|
|
3 |
В |
“y” |
|
|
4 |
|||
|
5 |
Прибыль |
= 3500x+ 4800y |
|
|
6 |
|||
|
7 |
Затраты |
на |
= 3x+ 4y |
|
комплектацию |
|||
|
8 |
Затраты по времени |
= 0,25x+ 0,5y |
|
|
9 |
|||
Рис.12. Заполнение таблицы исходными данными
·Выделим ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним ячейки этого окна в соответствии с рис.13.
·Нажмем <Выполнить>; если все сделано правильно, то решение будет таким, как указано ниже.
20
5.1. Вычисление производной функции одного переменного
Известно, что численными приближенными методами производная функции в заданной точке может быть вычислена с использованием формулы конечных разностей. Выражение для вычисления производной функции одного переменного, записанное в конечных разностях, имеет вид:
При достаточно малых приращениях х, можно с приемлемой точностью получить величину производной Для вычисления производной в MS Excel будем использовать приведенную зависимость. Рассмотрим методику вычисления производной на примере упражнения.
Пример 17. Найти производную функции Y= 2x 3 + x 2 в точке x= 3. Производная, вычисленная аналитическим методом, равна 60.
Решение:
1. Ведите в ячейку рабочего листа формулу правой части заданной функцио-нальной зависимости, например в ячейку В2, как показано на рисунке 27 , делая ссылку на ячейку, где будет находиться значение х, например А2: = 2*А2^3+A2^2 2. Определите окрестность точки х=3 достаточно малого размера, например значение слева Х k = 2,9999999, а справа Хk+1 = 3,00000001 и введите эти зна-чения в ячейку А2 и А3 соответственно.
3. В ячейку С2 введите формулу вычисления производной (см рис. 27):
= (В3-В2)/(A3-A2).
Рисунок 27
В результате в ячейке С2 будет вычислено приближенное значение производной заданной функции в точке х=3, величина которой равна 60, что соответствует результату, полученному аналитически.
Как делать производные в Excel
Microsoft Excel не имеет возможности генерировать производное уравнение по заданной формуле, но вы все равно можете использовать программу для вычисления значений как для формулы, так и для ее производной и построения их на графике. Это позволяет сравнивать формулу с ее производной, даже если вы не знаете самой производной. Поскольку Excel берет на себя все вычисления, вы можете использовать этот метод, даже если вы не знаете исчисления.
Введите нижнюю границу горизонтального диапазона, который вы хотите построить, в ячейке A1. Например, чтобы построить график от -2 до 2, введите «-2» в A1 (опуская кавычки здесь и на всех этапах).
Введите расстояние между точками графика в ячейку D1. Чем меньше расстояние, тем точнее будет выглядеть ваш график, но использование слишком большого количества точек может замедлить обработку. Для этого примера введите «0,1», что даст 41 точку графика из -2 и 2. Если вы используете меньший или больший диапазон, измените расстояние соответственно, чтобы получить как минимум несколько десятков точек, но не более нескольких тысяч. .
Введите формулу «= A1 + $ D $ 1» в ячейку A2. Перетащите маркер заполнения в углу ячейки вниз, чтобы повторить формулу для такого количества точек, которое необходимо для достижения желаемого верхнего диапазона.
Поместите исходную формулу в ячейку B1, начиная со знака равенства и заменив переменную на «A1». Например, чтобы использовать уравнение «y = 2x ^ 2», введите «= 2 * A1 ^ 2». Обратите внимание, что Excel не умножает смежные члены автоматически, поэтому для умножения необходимо ввести звездочку.
Дважды щелкните маркер заполнения в ячейке B1, чтобы заполнить все необходимые ячейки в столбце B.
Введите «= (B2-B1) / $ D $ 1» в ячейку C1. Это уравнение находит производную для вашей формулы в каждой точке, используя определение производной «dy / dx»: разница между каждой строкой в столбце B составляет «dy», а значение, которое вы выбрали для D1, представляет «dx». Дважды щелкните маркер заполнения в C1, чтобы заполнить столбец.
Прокрутите вниз и удалите последнее число в столбце C, чтобы избежать неточного значения для последней производной.
Щелкните и перетащите от заголовка столбца A к заголовку C, чтобы выделить первые три столбца. Откройте вкладку «Вставка» на ленте и нажмите «Диаграммы», «Точечная диаграмма», а затем «Точечная диаграмма с плавными линиями» или другой тип диаграммы разброса, если необходимо. Excel отобразит исходную формулу как «Серия 1», а производную — как «Серия 2».
Содержание
- Вычисление производной в Excel
- Минимум теории.
- Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
- Задача:
- Решение:
- Однако.
- Алгоритм нахождения производной
Вычисление производной в Excel

Если функция получена практическими измерениями и задана табличными значениями, то Excel может оказать в этом случае более существенную помощь при выполнении численного дифференцирования и последующей обработке и анализе результатов.
На практике задача вычисления производной методом численного дифференцирования может возникнуть и в механике (при определении скорости и ускорения объекта по имеющимся замерам пути и времени) и в теплотехнике (при расчете теплопередачи во времени). Это также может быть необходимо, например, при бурении скважин для анализа плотности проходимого буром слоя грунта, при решении целого ряда баллистических задач, и т. д.
Похожая ситуация имеет место при «обратной» задаче расчета сложно нагруженных балок, когда по прогибам возникает желание найти значения действующих нагрузок.
Во второй части статьи на «живом» примере рассмотрим вычисление производной по приближенной формуле численного дифференцирования с применением выражений в конечных разностях и разберемся в вопросе – можно ли используя приближения производных конечными разностями по прогибам балки определять действующие в сечениях нагрузки?
Минимум теории.
Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.
Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.
y’ ( x )=lim ( Δy / Δx ) при Δx →0
Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.
tg ( α )= Δy / Δx
Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
На балку длиной 8 метров с шарнирными опорами по краям изготовленную из двух спаренных стальных (Ст3) двутавров 30М опираются 7 прогонов с шагом 1 метр. К центральной части балки крепится площадка с оборудованием. Предположительно усилие от покрытия, передаваемое через прогоны на балку, во всех точках одинаково и равно F1 . Подвесная площадка имеет вес 2* F2 и крепится к балке в двух точках.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.
На следующем скриншоте представлены исходные данные.
Расчетные исходные данные:
3. Погонная масса двутавра 30М:
γ =50,2 кг/м
Сечение балки составлено из двух двутавров:
n =2
Удельный вес балки:
q = γ * n * g =50,2*2*9,81/1000=0,985 Н/мм
5. Момент инерции сечения двутавра 30М:
Ix1 =95 000 000 мм 4
Момент инерции составного сечения балки:
Ix = Ix1 * n =95 000 000*2=190 000 000 мм 4
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R =( q * zmax +8* F1 +2* F2 )/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
В расчете учитывается собственный вес балки!
Задача:
Найти значения изгибающего момента Mxi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Qy , изгибающих моментов Mx , углов поворота Ux оси балки и прогибов Vx по классическим формулам сопромата во всех сечениях с шагом h . (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.
Использованные в расчетах формулы можно посмотреть здесь.
Ссылка для скачивания файла с рассмотренным в статье примером: vychisleniye-proizvodnoy (xls 250,0KB).
Итак, нам известны точные значения моментов и прогибов.
Из теории мы знаем, что:
Угол поворота – это первая производная прогиба U = V’ .
Момент – это вторая производная прогиба M = V’’ .
Сила – это третья производная прогиба Q = V’’’ .
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Итог расчетов мы видим в ячейках M5-M54.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Однако.
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью
1 мкм и стараться максимально уменьшать шаг замеров h , «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$.
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i =4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении ( ε21 =1,813%).
Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Источник
Алгоритм нахождения производной
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
Р.М.Магомедов, Е.В.Маевский
Приближенное вычисление производной функции в заданной точке ( Excel )
Учебно-методические рекомендации для проведения
семинара №5 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Москва 2017
Приближенное вычисление производной
Функции в заданной точке ( Excel )
Введение
Пусть функция 




Простейшими формулами для приближенного численного вычисления производной являются так называемые двухточечные формулы, которые можно получить непосредственно из определения производной: 
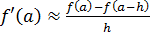
Если зафиксировать функцию и точку 


Более точная оценка получится, если использовать значения функции в трех точках: 



Еще более точными являются формулы, оценивающие производную по большему количеству точек (4 и более). Однако следует иметь в виду, что увеличение количества участвующих в формуле точек усложняет вычисление по формуле и увеличивает ошибку округления, возникающую при этом вычислении. Потому, хотя и возможно теоретически использовать для оценки производной в данной точке весь массив известных значений функции, но на практике этого никогда не делают.
Другой способ уточнения значения производной – уменьшение шага 
Задание 1. Вычислить в Excel приближенно производную функцию в заданной точке по следующему алгоритму.
Алгоритм нахождения производной
1. Составим таблицу значений функции 



1.1. Вводим в диапазон ячеек A3:A23 рабочего листа Excel числа от -10 до 10 с шагом 1, как показано на рисунке. В ячейку C1 вводим число 1. В ячейку B3 вводим формулу для нахождения значений функции 



1.2. Копируем формулу до ячейки B23.
2. В каждой точке 


2.1. В ячейку C3 водим формулу:
2.2. Копируем формулу до ячейки C23.
2.3. Для оформления и построения ломанной в ячейки A2, B2, C2 водим соответственно x, f(x), fᶦ(x) — в 2-х т., как показано на рисунке.
2.4. Выделяем диапазон ячеек A2:C23. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками., как показано на рисунке:
2.5. Нажимаем Ок.
2.6. В результате получиться ломанная как показано на рисунке выше.
3. В каждой точке 

3.1. В ячейку D3 водим формулу:
3.2. Копируем формулу до ячейки D23.
3.3. Для оформления и построения ломанной в ячейку D2 водим fᶦ(x) — в 3-х т., как показано на рисунке.
3.4. Выделяем диаграмму.
3.5. Из контекстного меню выбираем команду Выбрать данные.
3.6. В окне Выбор источника данных задаем команду Добавить.
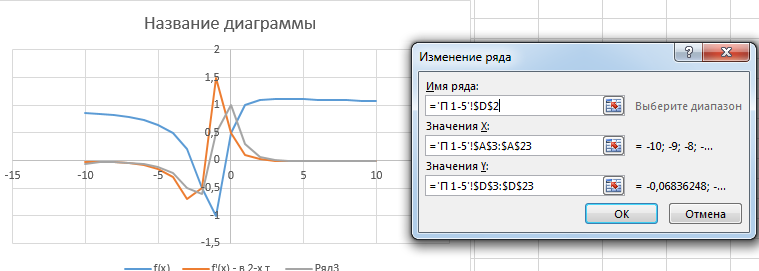
3.7. Заполняем окно Изменение ряда как показано на рисунке:
3.8. В результате получиться ломанная как показано на рисунке выше.
4. Составим таблицу точных значений производной 

4.1. В ячейку E3 водим формулу:
4.2. Копируем формулу до ячейки E23.
4.3. Для оформления и построения ломанной в ячейку E2 водим fᶦ(x) точ, как показано на рисунке.
4.4. Как показано в пункте 3 в область диаграммы добавляем новые данные из диапазона E3:E23.
4.5. В результате должна получиться диаграмма как показано на рисунке:
5. Сравним точные значения производной с приближенными, построив три ломанные на одном графике.
5.1. Выделяем диапазон ячеек A2:A23, C2:E23, как показано на рисунке:
5.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
6. Повторим вычисления пунктов 1-5, взяв величину шага 
6.1. Для этого на новом листе рабочей книги оформляем таблицу как показано на рисунке:
6.2. В ячейке B3 введена формула:
6.3. В ячейке C3 введена формула:
6.4. В ячейке D3 введена формула:
6.5. В ячейке E3 введена формула:
6.6. В ячейке F3 введена формула:
6.7. Выделяем диапазон ячеек A2:A23, D2:F23/
6.8. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
7. Составим таблицу погрешностей двухточечной приближенной формулы, вычисляя разность 
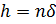


7.1. На новом листе рабочей книги Excel вводим в диапазон ячеек A4:A103 числа от -50, -49,…,-1,1,2,…,50 с шагом 1, как показано на рисунке (начало таблицы):
7.2. В ячейку C1 вводим число 0. В ячейку E1 вводим число 0,01.
7.3. В ячейку В4 вводим формулу:
7.4. В ячейку С4 вводим формулу:
8. Исследуем зависимость погрешности от 
8.1. Выделяем диапазон ячеек A3:A103, C3:C103.
8.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке (см. пункт 9).
9. Повторим шаги 7-8 для погрешности трехточечной формулы 
9.1. В ячейку D4 вводим формулу:
9.2. Выделяем диапазон ячеек A3:A103, C3:D103.
9.3. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
Задание 2. Найти первую производную функции 
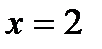

Из вышесказанного известно, что выражение для вычисления производной функции одной переменной в точке x, имеет вид:
где 

Примечание. Количество точек после запятой для выражения h зависить от того с какой заданной точностью нужно вычислить производную, если, например, производную нужно вычислить с точностью до 2 знаков после запятой, то достаточно взять h равной 0,0001.
Решение
Решим задачу двумя способами.
Способ 1
1. Вводим в ячейку C2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – C3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке C4 вычисляем сумму C3=C1+C2.
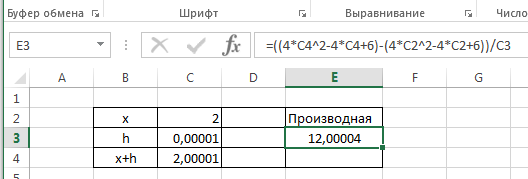
2. В ячейку E3 вводим формулу для вычисления производной:
3. После нажатия клавиши Enter получаем результат вычисления 12,00004 (см. рис.).
Способ 2
1. Зададим окрестность точки 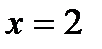

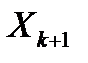
2. Вводим в ячейку рабочего листа формулу правой части заданной функциональной зависимости, например, в ячейку C3, как показано на рис., делая ссылку на ячейку B3, где находится значение х:
3. Копируем эту формулу в ячейку C4.
4. В ячейку E3 вводим формулу вычисления производной (рис.):
В результате вычисления в ячейке E3 будет выведено приближенное значение производной заданной функции в точке 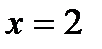
Задание 3. Найти первую производную функции 

Из вышесказанного известно, что выражение для вычисления первой производной функции одной переменной в точке x, имеет вид:
где 
Решение
1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное =3*пи()/4, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В3 вычисляем сумму В3=В1+В2.
2. В ячейку E3 вводим формулу для вычисления производной:
3. После нажатия клавиши Enter получаем результат вычисления 0,0000213 (см. рис.).
Задание 4. Найти вторую производную функции 
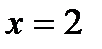
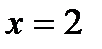
Из математики известно, что выражение для вычисления второй производной функции одной переменной в точке 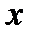
где 

Решение
1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В4 вычисляем сумму В3=В1+В2.
2. В ячейку E3 вводим формулу для вычисления второй производной:
3. После нажатия клавиши Enter получаем результат вычисления 44,00003917 (см. рис.).
Источник


![РешениеСредствами Excel найти производную функции y=x3 на промежутке x[0,6] с... РешениеСредствами Excel найти производную функции y=x3 на промежутке x[0,6] с...](https://documents.infourok.ru/a2b611ad-f095-49a1-a436-4514378a929a/0/slide_02.jpg)