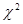Рассмотрим понятие процентиля, функцию
ПРОЦЕНТИЛЬ.ВКЛ()
, процентиль-ранг и построим кривую процентилей.
Сначала разберемся на примерах, что такое
процентиль
, затем рассмотрим соответствующие функции MS EXCEL.
Задача.
Проектируют койку на круизном лайнере. Необходимо, чтобы 95% пассажиров помещались на койке в полный рост. Как вычислить длину койки?
Для решения задачи потребуется найти рост, ниже которого 95% населения. Для этого нужно сделать
репрезентативную выборку
, скажем, из 2000 человек,
отсортировать значения выборки по возрастанию
, потом определить значение с позицией равной 1901 (2000*95%+1). Пусть найденный рост оказался равен 190 см.
Ответ
: Длина койки должна быть 190 см (+ запас для комфортного размещения на койке).
Значение 190 см называется 95%-й
процентилью
данной
выборки
, т.е. 95% опрошенных людей имеет рост <190 см.
Примечание
: Найденное значение (190см) является
оценкой
95%-й
процентили
всей
генеральной совокупности
, из которой взята
выборка
.
СОВЕТ
: Понятие
процентиля
связано с понятием
квантиля функции распределения
. Поэтому имеет смысл освежить в памяти понятия
функции распределения и обратной функции
.
На основании вышесказанного сформулируем определение для
процентили
:
K-й Процентиль представляет такое собой значение
Х
в наборе данных, которое разделяет набор на две части: одна часть содержит K процентов данных,
меньших Х
, а другая часть содержит все остальные значения набора (т.е. 1-
K
процентов данных б
о
льших Х).
Приведем алгоритм для нахождения
k
-й процентили выборки:
-
отсортировать значения
выборки
по возрастанию (пусть в
выборке
всего N значений); -
найти такую позицию в списке
, для которой k% значений оказалось бы меньше этого значения. Это можно сделать с помощью формулы N*k%+1 (затем,
округлить его до целого
);
-
значение, находящееся в этой позиции, и будет
k
-й процентилью
(примерно), т.к. k% значений массива данных будет меньше этого значения.
Примечание
: Более точный алгоритм расчета
процентилей
дан ниже в разделе про функцию
ПРОЦЕНТИЛЬ.ВКЛ()
.
Еще одна
задача
.
Зачет «автоматом» поставят только тем студентам, которые в течение семестра набрали в течение семестра больше баллов, чем 90%-я Процентиль (другими словами 10% лучшим студентам поставят зачет «автоматом»).
Так как порог установлен в
процентилях
, то заданному % студентов придется сдавать экзамен вне зависимости от набранных баллов (т.е. 90% студентов в любом случае будут сдавать экзамен). А вот если бы порог был установлен в абсолютных значениях, например, 380 баллов из 400, то вполне вероятна ситуация, когда половине студентов поставили бы «автоматом» (если бы они, конечно, набрали бы больше 380 баллов). Или наоборот, при общих слабых результатах ни один студент не получил бы зачет «автоматом». Установка порога в
процентилях
создает предпосылки здоровой конкуренции (или, наоборот, сговора: даже если никто особо не учился, то в любом случае 10% получат зачет «автоматом»).
Решим эту задачу, используя заданные значения
выборки
. Пусть всего 120 студентов, значения баллов за семестр разместим в диапазоне
A8:A127
(см.
Файл примера
, лист
Пример-Студенты
). Максимальный суммарный балл = 400. Порог получения зачета «автоматом» — больше баллов, чем 90%-я
Процентиль
.
Понятно, чтобы определить тех студентов, которые получат зачет «автоматом» нужно отсортировать их по набранным баллам и отобрать 10% (т.е. 12 студентов) с максимальными баллами. Но, чтобы студенты сами определились, начинать ли им готовиться к экзамену или нет, достаточно сообщить им проходной балл (90%-ю
процентиль
). Рассчитаем этот проходной балл.
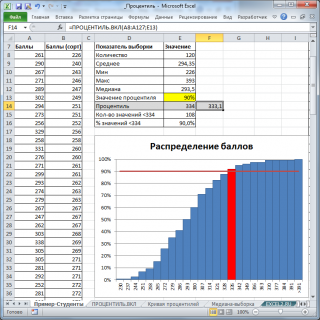
Для наглядности построим
Гистограмму распределения с накоплением
.
90%-ю
процентиль
можно найти с помощью формулы
=НАИМЕНЬШИЙ(A8:A127;ЦЕЛОЕ(120*0,9)+1)
Эта формула создана на основе алгоритма, приведенного выше. Результат формулы — 334 балла.
Как видно из рисунка выше, количество значений массива (студентов), у которых баллы хуже, действительно равно 108 (90% от 120). Следовательно, как и предполагалось, 12 студентов получат зачет «автоматом».
Примечание
:
Найденное значение
процентили
334 является приблизительным. Точное значение дает формула
=ПРОЦЕНТИЛЬ.ВКЛ(A8:A127;0,9)
, которое равно 331,4. О том как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
читайте ниже.
Как показывает опыт, для данных выборки
K
-я
процентиль
не всегда отделяет точно
К
процентов значений, которые меньше ее. Например, в нашем примере найдем 80%-ю
процентиль.
Оказывается, что только 79% значений меньше 80%-й
процентили
(318). Это происходит из-за округления. Для
выборок
с большим количеством значений (>100) обычно наблюдается хорошее соответствие. Повторы значений также могут привести к несоответствию значения
процентиля
и соответствующего % значений (см. ниже).
Примечание
:
Процентили
часто называют
перцентилями
(с этим соглашается и MS WORD) или
центилями
. В версии MS EXCEL 2007 и более ранних использовалась функция
ПЕРСЕНТИЛЬ()
, которая оставлена для совместимости. Но, начиная с версии EXCEL 2010, появились функции
ПРОЦЕНТИЛЬ.ВКЛ()
и
ПРОЦЕНТИЛЬ.ИСКЛ()
– английское название PERCENTILE.EXC(), а
Условное форматирование
предлагает настроить правило с использованием именно
процентилей
. В свою очередь,
надстройка Пакет Анализа
имеет инструмент
Ранг и Персентиль
.
Google также отдает предпочтение
процентилям
, выдавая гораздо больше результатов на запрос «процентиль», чем на запрос «перцентиль» (на начало 2016 года).
Таким образом, для
процентилей
используется 3 названия:
процентиль
(MS EXCEL, Google)
, персентиль
(MS EXCEL)
, перцентиль
(MS WORD)
.
Ниже детально рассмотрим как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
и создадим ее аналог с помощью альтернативной формулы. Также рассмотрим функцию
ПРОЦЕНТРАНГ.ВКЛ()
и
кривую процентилей
.
СОВЕТ
:
Нижеследующие разделы следует читать пользователям, владеющими базовыми понятиями
математической статистики (случайная величина, функция распределения)
.
Функция
ПРОЦЕНТИЛЬ.ВКЛ()
Начиная с версии MS EXCEL 2010 для расчета
процентилей
используется функция
ПРОЦЕНТИЛЬ.ВКЛ()
– английское название PERCENTILE.INC(). В более ранних версиях MS EXCEL использовался ее аналог — функция
ПЕРСЕНТИЛЬ()
.
Напомним определение
процентиля
, данное выше:
K-й Процентиль представляет такое собой значение
Х
в наборе данных, которое разделяет набор на две части: одна часть содержит K% данных,
меньших Х
, а другая часть содержит все остальные значения набора (т.е. 1-
K
% данных б
о
льших Х).
Разберем детально как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
.
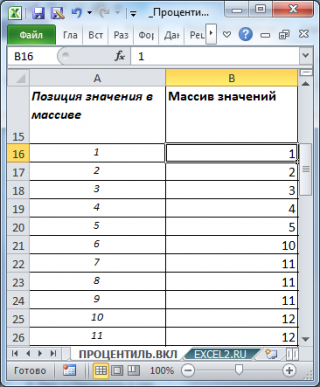
Пусть имеется массив значений (
выборка
). В массиве 49 значений, массив расположен в диапазоне
B15:B63
, имеются
повторы значений
, массив для удобства
отсортирован по возрастанию
(см.
файл примера
, лист
ПРОЦЕНТИЛЬ.ВКЛ
).
Рассчитаем 0,08-ю
процентиль
(
8%-процентиль
) с помощью формулы
=ПРОЦЕНТИЛЬ.ВКЛ(B15:B63; 0,08)
. Получим, что 0,08-я
процентиль
равна 4,84.
Проанализируем, что мы получили.
-
Во-первых, значения 4,84 нет в массиве (есть 4 и 5), т.е. функция
ПРОЦЕНТИЛЬ.ВКЛ()
интерполирует значения. -
Во-вторых, процент значений меньших 4,84 равен не точно 8%, а 8,16%=4/49*100% (т.к. всего 4 значения в массиве меньше 4,84). Это произошло, т.к. в
выборке
относительно мало значений. -
Другой причиной расхождения могут стать повторы. Например, заменив, первые 4 значения в массиве (т.е. 1; 2; 3; 4) числом 5, мы получим вместо 8,16% — 0%. Это произошло потому, что теперь 0,08-я
процентиль
равна 5, а в
выборке
нет ни одного значения меньше 5.
Как видно из рисунка ниже первое значение (
минимальное
, равное 1) является 0-й
процентилью
.
Соответственно, 1-й
процентилью
(100%
процентилью
), является
максимальное значение
равное 120 (см.
файл примера
лист ПРОЦЕНТИЛЬ.ВКЛ).
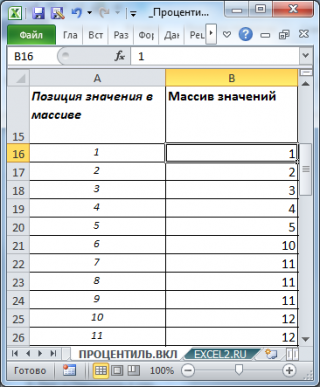
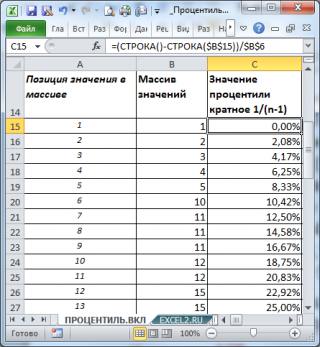
Как видно из рисунка, следующее за минимальным значением (т.е. число 2) является 0,0208-й
процентилью
. Значение 0,0208 или 2,08% — это (k-1)*1/(n-1), где n – это количество значений в массиве (в нашем массиве n=49), а k – это позиция числа в массиве (в данном случае k=2, где 2 – это позиция, а не само число).
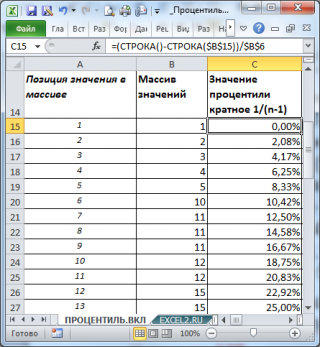
Поясним эту формулу. Для вычисления
процентили
принимается, что весь диапазон значений массива (от мин до макс) разбит n значениями на равные интервалы (их всего n-1). Соответственно, 1/(n-1), это «ширина» интервала (весь диапазон равен 1 или 100%). Обратите внимание, что «ширина» интервала не зависит от данных, а только от их количества. В нашем случае «ширина» интервала равна 0,0208 или 2,08%.
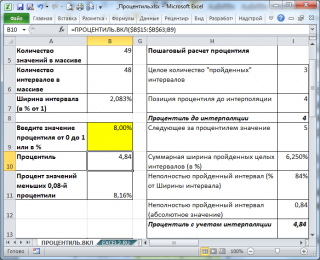
Приведем алгоритм расчета
12,50%-процентили
функцией
ПРОЦЕНТИЛЬ.ВКЛ()
(см. ячейку
С21
):
ПРОЦЕНТИЛЬ.ВКЛ()
определяет «ширину» интервала (в долях или процентах): =1/(49-1)=0,0208;-
подсчитывает
Количество интервалов
, которые были укладываются в 12,50%, т.е. =12,50%/2,08%=6 (значение
процентиля
кратно ширине интервала, т.е. делится нацело); - 6-й интервал располагается между числами массива 10 и 11. Верхняя граница последнего 6-го интервала равна 11;
-
Следовательно,
12,50%-я процентиль
равна 11 (см. ячейку
B
21
).
По аналогии с
непрерывной функцией распределения
(см.
статью про квантили
), получается, что 12,50% значений должно быть меньше полученного числа 11 (в соответствии с определением
процентиля
). Фактически получается, что таких значений 6 (1; 2; 3; 4; 5; 10) и процент значений меньших 11 равен 12,24%=6/49 (причины расхождения: повторы и небольшое количество значений).
Если значение
процентиля
не кратно ширине интервала (ширина интервала равна 1/(n-1)), то имеет место интерполирование. Например, вспомним результат вычисления
0,08-й процентили
равный 4,84. Значение
процентили
(т.е. не результат, а %) равно 0,08 (8%), что соответствует 3-м целым интервалам (8%/2,08%=
3
,84) и некой доли (0,84) от ширины следующего интервала. Границами этого «неполного» интервала являются значения 4 (
0,0625-я процентиль
) и 5 (
0,0833-я процентиль
). Т.к. разница между 5 и 4 равна 1, то умножая «пройденную» долю интервала (0,84) на длину интервала в абсолютных значениях (=5-4=1), получаем 0,84. В итоге получаем 4,84: 4 – левая граница интервала + часть следующего (5-4)*0,84.
Если бы в массиве вместо 5 было значение 6, то значение
0,08-й процентили
было бы равно 5,68 (4 – левая граница интервала + (6-4)*0,84=1,68).
Альтернативный расчет
процентили
с помощью формул приведен в
файле примера
.
Примечание
: Некоторые значения
процентилей
имеют специальные названия:
-
25-я
процентиль
называется 1-й квартилью; -
50-я
процентиль
называетсяМедианой
(2-я квартиль);
-
75-я
процентиль
называется 3-й квартилью.
Функция
ПРОЦЕНТРАНГ.ВКЛ()
и Кривая процентилей
Функция
ПРОЦЕНТРАНГ.ВКЛ()
используется для оценки относительного положения значения в массиве. Для заданного значения функция вычисляет сколько значений в массиве меньше или равно ему. Точнее — какой процент значений массива меньше или равен ему. Результат функции называется
процентиль-ранг (percentile rank)
. Понятно, что для максимального значения
процентиль-ранг
равен 0,00%, а для наименьшего — 100% (все значения массива меньше или равны ему).
Функция
ПРОЦЕНТРАНГ.ВКЛ()
, английская версия – PERCENTRANK(), является, в каком-то смысле, обратной функции
ПРОЦЕНТИЛЬ.ВКЛ()
: т.е. задавая в качестве аргумента значение из массива, функция
ПРОЦЕНТРАНГ.ВКЛ()
вернет
значение процентили
кратной 1/(n-1).
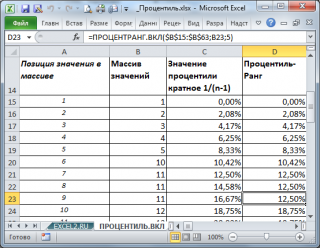
Как видно из рисунка выше, для повторяющихся значений функция
ПРОЦЕНТРАНГ.ВКЛ()
вернет, естественно, одинаковые значения. Также поступает функция
РАНГ.РВ()
или
РАНГ()
(см. статью
Функция РАНГ() в MS EXCEL
).
Действительно, функции
РАНГ.РВ()
и
ПРОЦЕНТРАНГ.ВКЛ()
очень похожи. Первая
возвращает позицию числа в массиве
в зависимости от его значения. Вторая, в принципе, делает тоже самое, но результат выводится в % от общего количества значений в массиве.
Как видно из картинки выше, чтобы получить
процентиль-ранг
необходимо значение ранга уменьшить на 1 и разделить на n-1. Значение
ранга
, естественно, должно быть
отсортировано по возрастанию
.
По
выборке
можно оценить
функцию распределения
Генеральной совокупности
, из которой взята данная
выборка.
Для этой цели построим
Кривую процентилей
(percentile curve или percentile rank plot).
Кривая
процентилей
представляет собой график зависимости
процентиль-ранга
от значений
выборки
.
Возьмем
выборку
состоящую из 100 значений (см.
файл примера
лист
Кривая процентилей
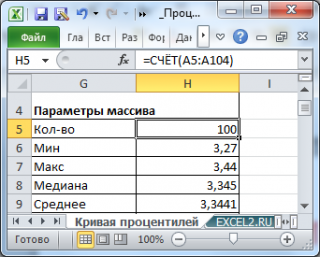
). Значения содержатся в диапазоне
А5:А104
.
Сначала построим
таблицу частот
для каждого из значений
выборки
.
Примечание
: В отличие от
Гистограммы
, где
кумулятивная
таблица частот
строится для интервалов значений,
таблицу частот
для
Кривой
процентилей
строят для
каждого
из значений
выборки
.
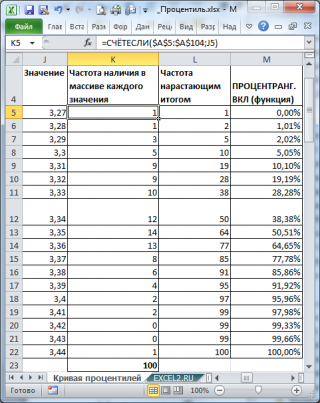
Из таблицы видно (столбец
Частота нарастающим итогом
), что
примерно
1 процент значений меньше или равен значения 3,27,
примерно
2 процента на уровне или ниже 3,28, 5 процентов на уровне или ниже 3,29, и так далее. График
Кривой
процентилей
для этих данных приведен на картинке ниже.
СОВЕТ
: Про построение графиков см. статью
Основные типы диаграмм
.
Следует отметить, что использование данных из таблицы приведет к точечному виду кривой (так как
процентиль-ранг
будет изменяться скачком для каждого значения
выборки
). Поэтому, сглаженная кривая, построенная на основе этих данных будет лучше представлять оцениваемую
функцию распределения
(пунктирная кривая).
Построив пунктирную кривую, становится ясно, зачем нам пришлось вводить понятие
процентиль-ранга: процентиль-ранг
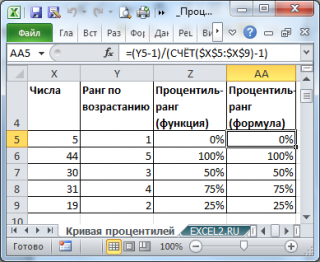
– является приблизительной вероятностью выбрать случайную величину меньше или равную соответствующему значению (сравните с определением функции распределения). Это, в частности следует из расчета
процентиль-ранга
по формуле
=СЧЁТЕСЛИ($A$5:$A$104;»<«&A5)/ (СЧЁТ($A$5:$A$104)-1)
Обратите внимание, что при построении
Кривой процентилей
никакие значения из
выборки
не были удалены или сгруппированы. В этом смысле, построение
Кривой процентилей
это более точная процедура для оценки вида
функции распределения
, чем построение
Гистограммы данных
(так как информация не теряется в процессе построения). Правда, для этого требуется достаточно большая выборка (лучше >100 значений).
Примечание
: Формула
=(РАНГ.РВ(A5;$A$5:$A$104;1)-1)/ (СЧЁТ($A$5:$A$104)-1)
эквивалентна формуле
=ПРОЦЕНТРАНГ.ВКЛ($A$5:$A$104;A5;5)
17 авг. 2022 г.
читать 2 мин
Вы можете использовать функцию ПРОЦЕНТРАНГ в Excel, чтобы вычислить ранг значения в наборе данных в процентах от общего набора данных.
Эта функция использует следующий базовый синтаксис:
=PERCENTRANK( A2:A16 , A2 )
В этом конкретном примере вычисляется процентильный ранг значения A2 в диапазоне A2:A16 .
В Excel также есть две другие функции процентиля:
- PERCENTRANK.INC : вычисляет процентильный ранг значения, включая наименьшее и наибольшее значения.
- PERCENTRANK.EXC : вычисляет процентильный ранг значения, исключая наименьшее и наибольшее значения.
В следующих примерах показано, как использовать эти функции на практике.
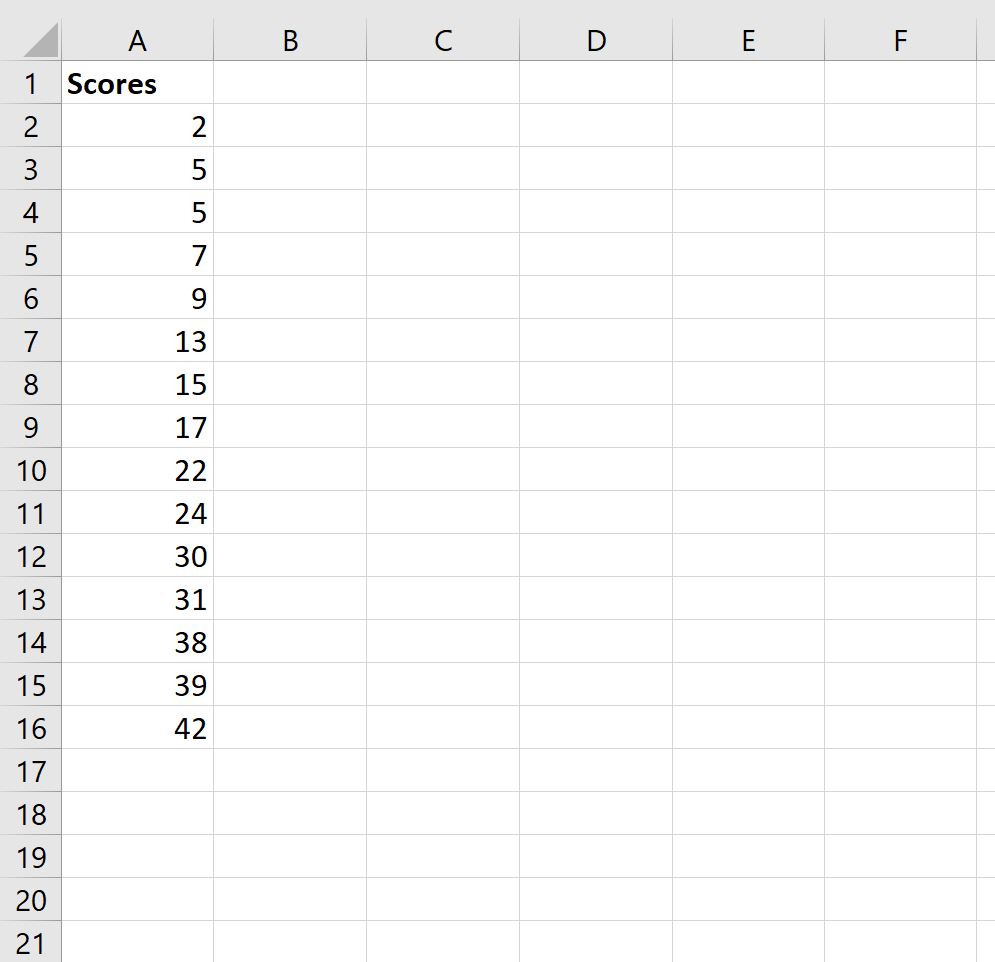
Пример: вычисление процентиля в Excel
Предположим, у нас есть следующий набор данных, который показывает результаты экзаменов, полученные 15 учениками в определенном классе:
Теперь предположим, что мы хотели бы вычислить процентильный ранг оценки каждого учащегося.
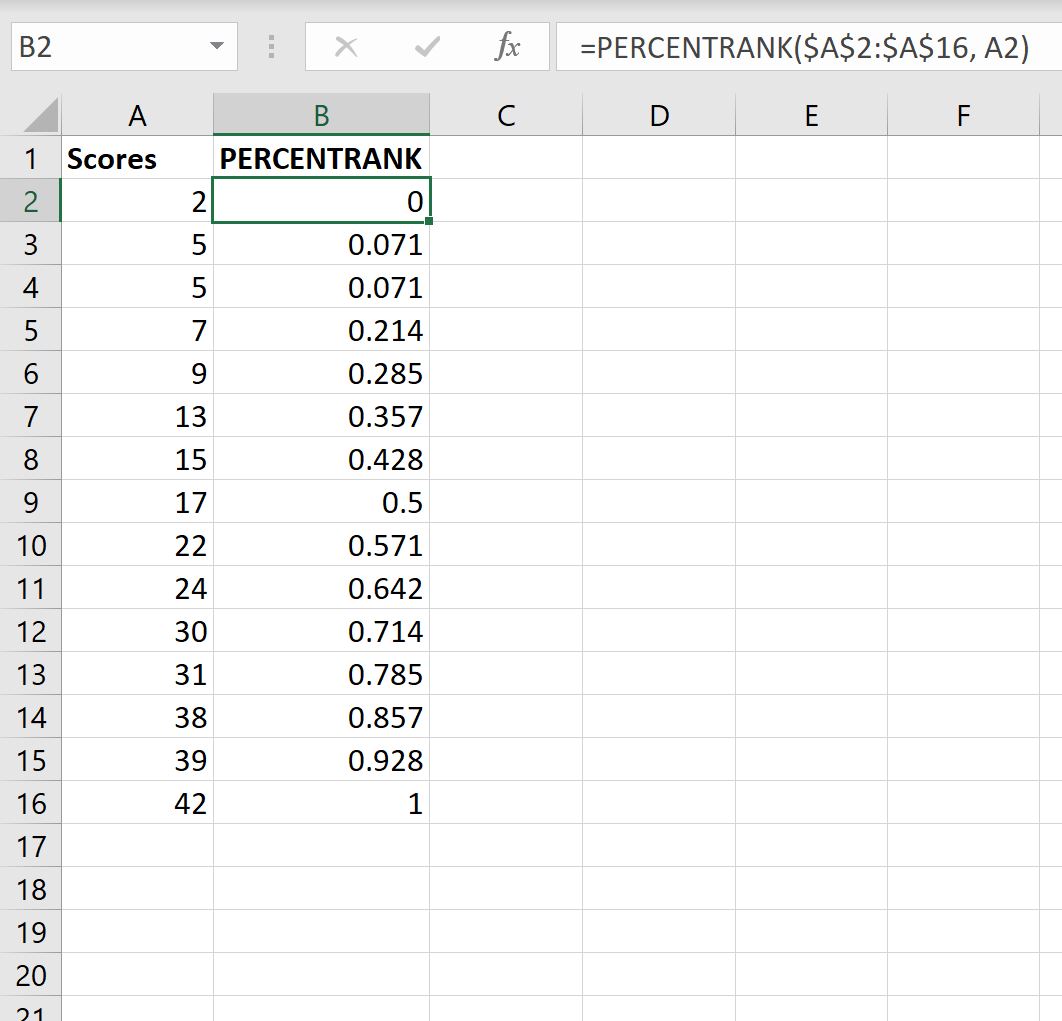
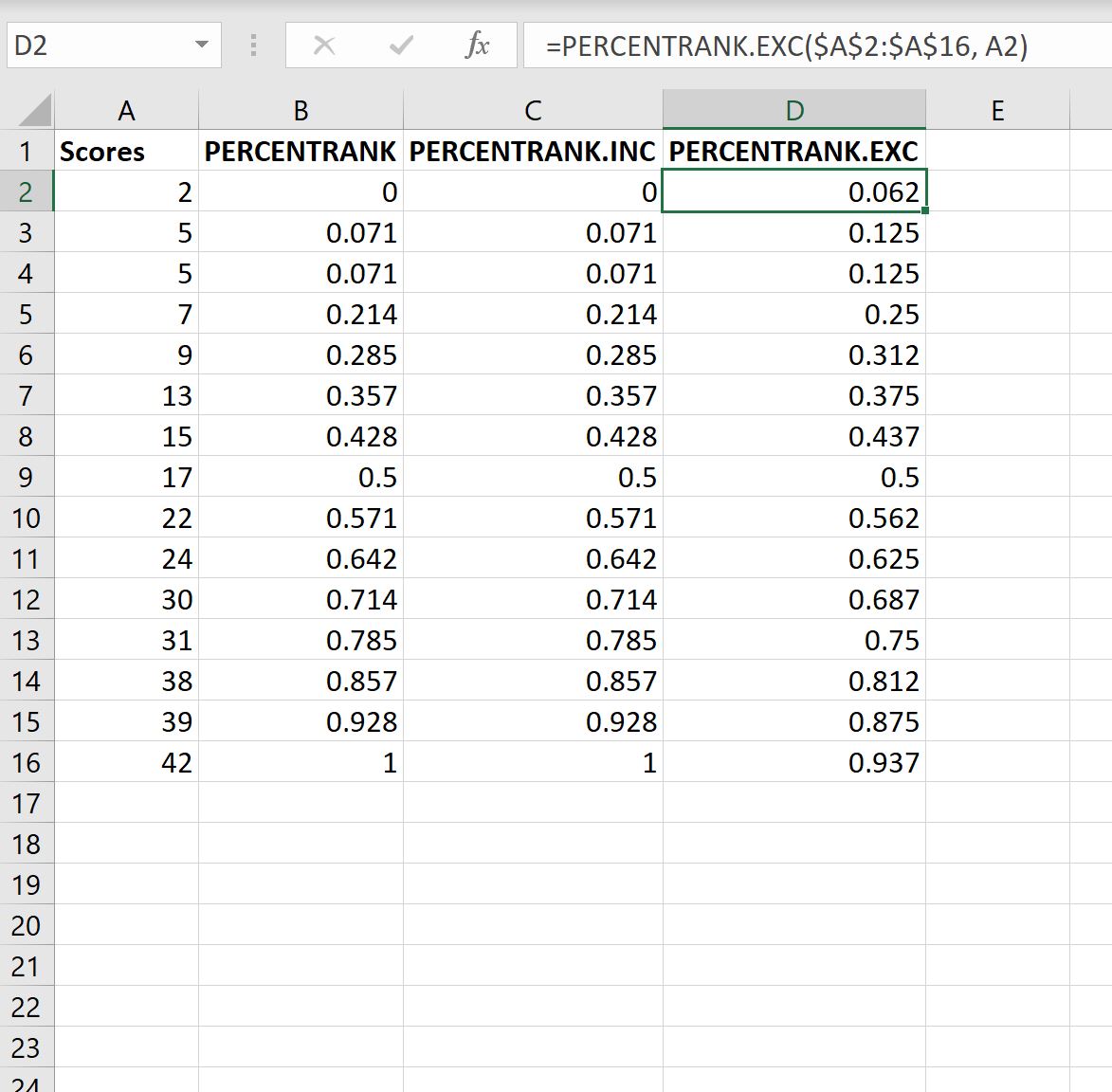
Мы можем ввести следующую формулу в ячейку B2:
=PERCENTRANK( $A$2:$A$16 , A2 )
Затем мы можем скопировать и вставить эту формулу в каждую оставшуюся ячейку в столбце B:
Вот как интерпретировать каждое значение процентного ранга:
- Учащийся, набравший 2 балла, занял 0 процентиль (или 0%) в классе.
- Учащиеся, набравшие 5 баллов, заняли процентиль 0,071 (или 7,1%) в классе.
- Учащийся, набравший 7 баллов, занял процентиль 0,214 (или 21,4%) в классе.
И так далее.
Обратите внимание, что когда мы используем функцию PERCENTRANK , наименьшее значение в наборе данных всегда будет иметь процентильный ранг 0, а самое большое значение в наборе данных всегда будет иметь процентильный ранг 1.
На следующем снимке экрана также показано, как использовать функции PERCENTRANK.INC и PERCENTRANK.EXC :
Здесь следует отметить две вещи:
1. Функция ПРОЦЕНТИЛЬ.ВКЛ возвращает точно такие же значения, что и функция ПРОЦЕНТИЛЬ .
2. Функция ПРОЦЕНТИЛЬ.ИСКЛ не возвращает значение 0 и 1 для наименьшего и наибольшего значений в наборе данных соответственно.
Полную документацию по функции ПРОЦЕНТРАНГ в Excel вы можете найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как преобразовать Z-баллы в процентили в Excel
Как рассчитать среднее и стандартное отклонение в Excel
Как рассчитать межквартильный диапазон в Excel
Процентильная шкала определяет позицию определенного значения среди других данных в базе. Процентили в первую очередь используются для описания стандартных результатов тестов. Если же результат в стандартном тесте находится в 90-ом процентиле – это значит, что данный результат является выше чем 90% результатов показателей которые принимают участие в тесте. Другими словами, результат находится среди 10% самых высоких показателей, использованных в тесте.
Пример вычисления формулы процентиля в Excel
Перцентили (они же процентили или персентили) часто применяются в анализе данных. Они являются инструментом для оценки результатов на фоне целой группы данных. С их помощью можно, например, определить персентильную классификацию работника по его годовому обороту.
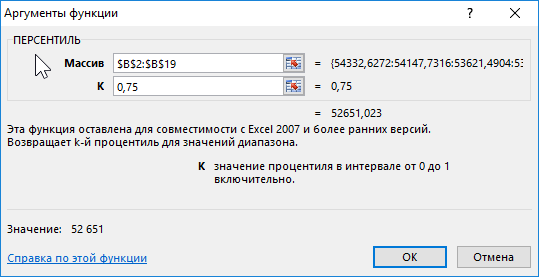
В программе Excel персентильную классификацию можно легко определить при использовании функции ПЕРСЕНТИЛЬ. Данная функция имеет 2 аргументы:
- Массив – диапазон исходных данных.
- К – значение найденного процентиля (чаще всего число в десятичной дроби диапазоном от 0 и до 1).
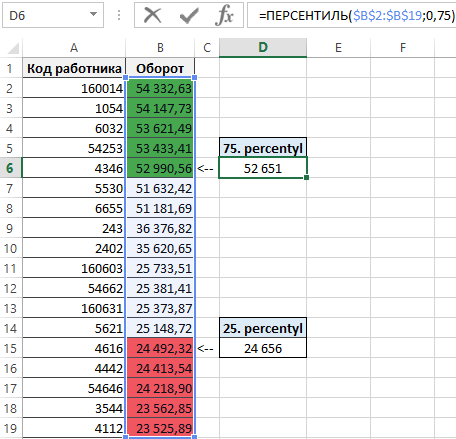
В примере, изображенном ниже на рисунке ячейка D6 содержит значение, которое является результатом вычисления ниже указанной формулы – число 0,75 процентиля данных диапазоне ячеек $B$2:$B$19:
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовые обороты превышают 52651 работает лучше, чем 75% всех остальных сотрудников.
Ячейка D15 содержит результат вычисления формулы, которая возвращает число 25 процентиля данных в диапазоне ячеек $B$2:$B$19.
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовой оборот не превышает 24656 находится среди 25% самых слабых сотрудников.
В данном примере используется условное форматирование использующие выше приведенные значения перцентилей. Значения больше чем 75 перцентиля выделены зеленым цветом, а значения меньше чем 25 перцентиля выделены красным цветом.
Два правила условного форматирования для одного диапазона ячеек в Excel
Чтобы создать описанную схему автоматического выделения ячеек по условию пользователя, выполните целый ряд следующих действий шаг за шагом:
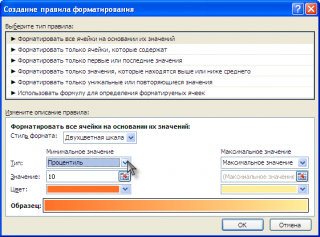
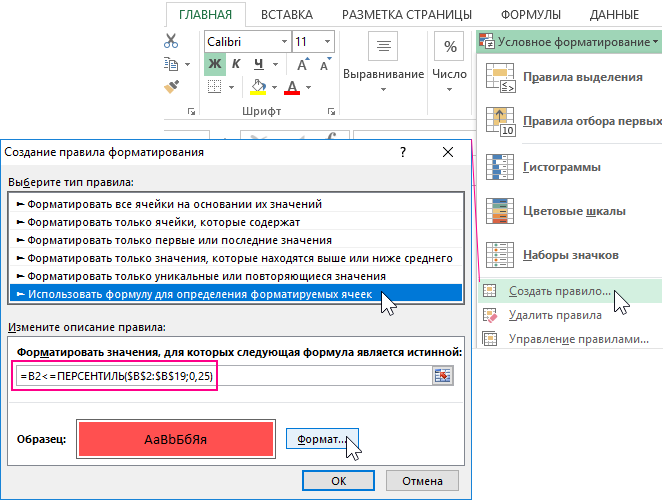
- Выделите диапазон ячеек B2:B19, которые будут автоматически выделятся цветом по условию формулы и выберите инструмент: «ГЛАВНАЯ»-«Условное форматирование»-«Создать правило». В результате чего высветится окно как ниже на рисунке:
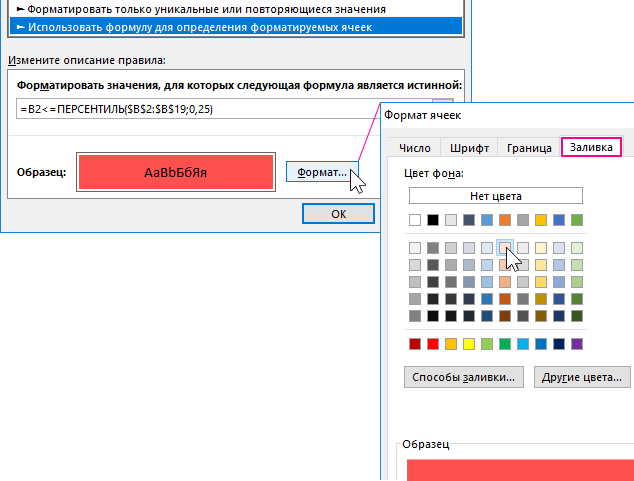
- В верхней части окна находится список опций. Выберите из него опцию «Использовать формулу для определения форматируемых ячеек». Данная опция служит для преобразования формата в ячейках в зависимости от их значений с помощью определенной формулы с логическим выражением. Если в результате вычисления формулы будет возвращено логическое значение ИСТИНА, тогда к текущей ячейке будет применено условное форматирование.
- В полю ввода введите формулу с логическим выражением, которая представлена ниже в этом разделе. Данная формула проверяет: если значение в целевой ячейке B2 меньше чем значение 25 перцентиля, тогда ей присваивается новый формат красного цвета фона для экспонирования.
=B2<=ПЕРСЕНТИЛЬ($B$2:$B$19;0,25)
- Нажмите на кнопку «Формат». Появится окно «Формат ячеек», в котором находятся все опции для форматирования шрифта, границы и фона ячеек. Главное укажите красный фон заливки. После указания своих пользовательских опций форматирования нажмите на кнопки ОК на все открытых окнах чтобы подтвердить и применить все изменения.
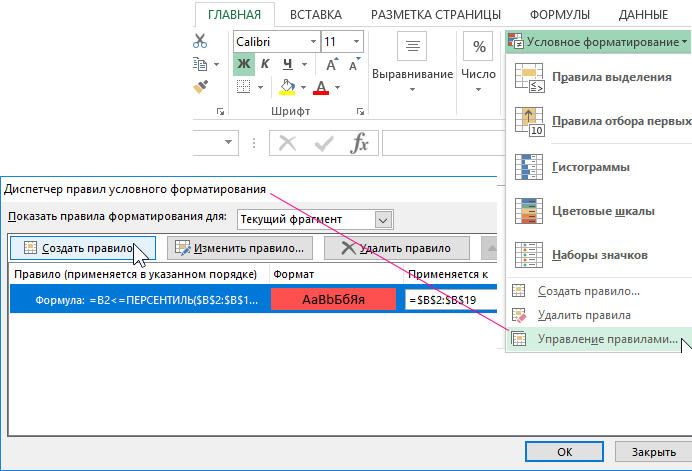
- Снова выделите диапазон ячеек B2:B19 и на этот раз уже выберите инструмент «ГЛАВНАЯ»-«Условное форматирование»-«Управление правилами». В результате появится окно «Диспетчер правил условного форматирования», где находится наше первое правило. Для создания второго правила в этом же окне нажмите на кнопку «Создать правило».
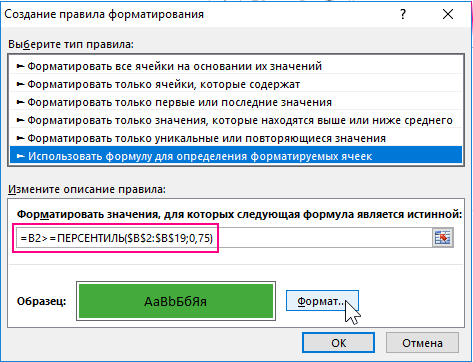
- И снова в появившемся окне «Создание правила форматирования» выберите опцию «Использовать формулу для определения форматируемых ячеек».
- В полю ввода формул на этот раз введите другую формул представленную на этом шаге. Данная формула проверяет: если значение в целевой ячейке B2 больше чем 75 персентиля, тогда применить для нее новый формат (зеленый фон).
- Снова нажмите на кнопку «Формат» где на этот раз следует указать зеленый фон заливки для ячеек. После чего нажмите на кнопку ОК для всех открытых окон.
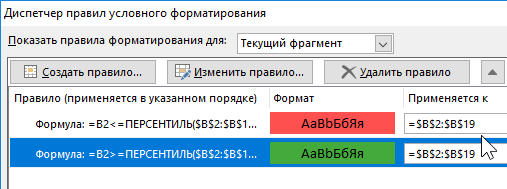
В результате к одному и тому же диапазону ячеек одновременно применяется 2 правила условного форматирования. В следствии чего одна группа значений выделена красным цветом значение которых меньше 25% показателей, а вторая группа – зеленым >75%.
Содержание
- ПРОЦЕНТИЛЬ Обзор функций
- Функция ПРОЦЕНТИЛЬ Синтаксис и входные данные:
- Что такое функция ПРОЦЕНТИЛЬ?
- ПРОЦЕНТИЛЬ — это функция «совместимости»
- Что такое процентиль?
- Как использовать функцию ПРОЦЕНТИЛЬ
- Два метода расчета процентилей
- PERCENTILE.INC
- Линейная интерполяция
- PERCENTILE.EXC
- PERCENTILE в Google Таблицах
- PERCENTILE примеров в VBA
Скачать пример рабочей книги
Загрузите образец книги
В этом руководстве показано, как использовать Функция ПРОЦЕНТИЛЬ в Excel в Excel для расчета процентиля.
ПРОЦЕНТИЛЬ Обзор функций
Функция PERCENTILE вычисляет k-й процентиль.
Чтобы использовать функцию PERCENTILE Excel Worksheet, выберите ячейку и введите:
(Обратите внимание, как появляются входные данные формулы)
Функция ПРОЦЕНТИЛЬ Синтаксис и входные данные:
| 1 | = ПРОЦЕНТИЛЬ (массив; k) |
множество — Массив чисел.
k — Значение процентиля от 0 до 1.
Что такое функция ПРОЦЕНТИЛЬ?
ПРОЦЕНТИЛЬ — одна из статистических функций Excel. Он возвращает k-й процентиль заданного диапазона данных.
ПРОЦЕНТИЛЬ — это функция «совместимости»
В Excel 2010 Microsoft заменила PERCENTILE двумя вариантами: PERCENTILE.INC и PERCENTILE. ИСКЛ.
PERCENTILE по-прежнему работает, поэтому старые таблицы, в которых он используется, будут работать в обычном режиме. Однако, если вам не требуется, чтобы таблица оставалась совместимой со старыми версиями Excel, следует использовать PERCENTILE.INC или PERCENTILE.EXC.
Мы обсудим все три, чтобы вы поняли все до мелочей.
Что такое процентиль?
Процентиль показывает, как значение сравнивается с другими значениями в заданном диапазоне. Когда значение находится на k-м процентиле, это означает, что оно выше, чем k% других значений в группе.
Например, если вы мужчина, живущий в США, и ваш рост 6 футов (180 см), вы находитесь в 71-м процентиле — вы выше 71% других мужчин в США. Если вы женщина и рост 180 см, то вы находитесь в группе 99th процентиль — вы выше 99% других женщин.
Когда вы имеете дело с процентилями, обратите внимание, что 50th процентиль равен медиане <> данных.
Функция Excel PERCENTILE сообщает вам, какова точка отсечения для данного процентиля, то есть, насколько высоким должно быть значение, чтобы оно попадало в k-й процентиль.
Как использовать функцию ПРОЦЕНТИЛЬ
Используйте PERCENTILE так:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13; F3) |
Вот несколько друзей, которые решили вычислить 80th процентиль роста их группы, и мы видим результат — 183,4 см.
Первый аргумент функции — это диапазон данных — их высота, которую мы выложили в C4: C13.
Следующий аргумент — процентиль. В этом примере я поместил процентиль в ячейку F3, а затем указал на эту ячейку в функции. Таким образом, легко изменить процентиль и увидеть новые результаты.
Однако вы можете ввести процентиль непосредственно в формулу, если хотите. Вы можете определить его как десятичную дробь, например:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13; .8) |
Или в процентах, например:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13, 80%) |
И все они возвращают одно и то же значение.
Что нужно знать о PERCENTILE:
- Если определяемый вами процентиль не является числом, функция вернет #VALUE! ошибка
- Если процентиль меньше 0 или больше 1, вы получите # ЧИСЛО! ошибка
- Текст и пустые ячейки в диапазоне данных будут проигнорированы.
Два метода расчета процентилей
Давайте на секунду расставим наши данные по порядку:
Вы можете задаться вопросом, почему 80th процентиль не 183, так как Чендлер — 8th самый высокий человек в группе.
Что ж, на самом деле существует множество способов математического вычисления процентиля, но нет стандартизированного или предпочтительного метода для всех ситуаций. Это то, о чем статистики спорят в научных статьях.
Excel предлагает два способа сделать это, что приводит нас к PERCENTILE.INC и PERCENTILE.EXC.
Функция PERCENTILE.INC в Excel аналогична функции PERCENTILE. Часть «INC» — это сокращение от «включающий», потому что она может вычислять любой действительный процентиль (то есть что-либо от 0% до 100%).
Вы используете это так:
| 1 | = ПРОЦЕНТИЛЬ.INC (C4: C13; F3) |
Как видите, он возвращает тот же результат, что и ранее PERCENTILE.
Итак, возвращаясь к тому, почему 80th процентиль не в точности равен росту Чендлера. Помните, что здесь мы выполняем инклюзивный расчет, поэтому мы включаем все значения k от 0 до 1 (или от 0% до 100%).
Это означает, что наша самая короткая подруга Дженис находится на нулевой отметке.th процентиль, а Ричард, самый высокий, — это 100 человек.th процентиль. Все другие друзья имеют равные приращения между двумя, и это приращение равно 1 / (n-1), где n — количество точек данных в диапазоне.
В нашем случае это:
Это означает, что Чендлеру на самом деле не 80.th процентиль, он на 77,777th процентиль. Если мы подставим это число в PERCENTILE.INC, мы должны получить рост Чендлера …
… И мы делаем.
Линейная интерполяция
Теперь, когда указанное вами значение k не кратно 1 / (n-1), PERCENTILE.INC будет применять процесс, называемый линейной интерполяцией, для вычисления результата. Это звучит сложно, но в основном это означает, что Excel выберет одно из двух значений.
Так почему же мы получили 183,4, когда попросили 80?th процентиль раньше?
Расчет работает следующим образом:
- 80th процентиль падает между Чендлером и Россом, Чендлер на 77,777th процентиль и Росс на 88,888-м месте.
- 80th процентиль на 2,222% опережает рост Чендлера
- Мы знаем, что расстояние между высотами Чендлера и Росса составляет 11%.
- 222% / 11,111% = 20% после округления. Теперь мы знаем, что 80th процентиль — это 20% расстояния между высотами Росса и Чендлера.
- Разница между ростом Росса в 185 см и ростом Чендлера в 183 см составляет 2 см.
- 20% 2 см составляет 0,4 см
- Добавьте это к росту Чендлера, и мы получим 183,4 см.
PERCENTILE.EXC
Вы используете PERCENTILE.EXC практически таким же образом:
| 1 | = ПРОЦЕНТИЛЬ.ИСКЛ (C4: C13; F3) |
Итак, у нас одинаковые данные, нам нужен одинаковый процентиль, но мы получили разные результаты. Это почему?
Это связано с тем, что PERCENTILE.EXC исключает первое и последнее значения при вычислении интервалов процентилей. См. ниже:
Вместо того, чтобы интервал равнялся 1 / (n-1), с PERCENTILE.EXC интервал равен 1 / (n + 1), или в данном случае 9,091%.
Все остальное работает так же, как и с PERCENTILE.INC. Опять же, 80th процентиль находится между Чендлером и Россом, поэтому Excel применяет тот же метод линейной интерполяции:
- 80th процентиль падает между Чендлером и Россом, Чендлер на 72,727th процентиль и Росс на 81,818-м месте.
- 80th процентиль на 7,272% опережает рост Чендлера
- Мы знаем, что расстояние между высотами Чендлера и Росса составляет 9,091%.
- 272% / 9,091% = 80% после округления. Теперь мы знаем, что 80th процентиль — это 80% расстояния между высотами Росса и Чендлера.
- Разница между ростом Росса в 185 см и ростом Чендлера в 183 см составляет 2 см.
- 80% 2 см составляет 1,6 см
- Добавьте это к росту Чендлера, и мы получим 184,6 см.
PERCENTILE в Google Таблицах
Функция ПРОЦЕНТИЛЬ в Google Таблицах работает точно так же, как и в Excel:
PERCENTILE примеров в VBA
Вы также можете использовать функцию ПРОЦЕНТИЛЬ в VBA. Тип:application.worksheetfunction.percentile (массив, k)
Для аргументов функции (массив и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.
Вернуться к списку всех функций в Excel
Процентили
— это характеристики набора данных, которые выражают ранги элементов массива в виде чисел от 1 до 100, и являются показателем того, какой процент значений находится ниже определенного уровня.
Например, значение 30-й процентили указывает, что 30% значений располагается ниже этого уровня.
На конкретном примере поясним понятие процентиля:
Пример 1 . Группа студентов из 20 человек получила на экзамене по статистике следующие балы: три студента — 5 баллов, 8 студентов — 4 балла, 6 студентов — 3 бала и 3 студента — 2 балла. Вычислить процентиль успеваемости каждого студента.
Решение.
Формула процентиля
Процентиль = n(x≤X)/N*100
n(x≤X) — число студентов, получивших бал не менее X ,
X — количество балов конкретного студента, процентиль которого находим ,
N — число всех студентов .
Для удобства вычислений ранжируем выборку балов от максимального значения до минимального ( в порядке убывания): 5,5,5,4,4,4,4,4,4,4,4,3,3,3,3,3,3,2,2,2
Допустим нам необходимо определить процентиль студента Иванова получившего на экзамене 5 баллов:
Находим n(x≤X)=n(x≤5)=20 — т.е. 20 студентов получили бал не выше 5, тода
Процентиль (Иванова) = 20/20*100=100
Допустим необходимо определить процентиль студента Петрова получившего на экзамене 4 балла:
Находим n(x≤X)=n(x≤4)=17 — т.е. 17 студентов получили бал не выше 4, тода
Процентиль (Петрова) = 17/20*100=85
Допустим необходимо определить процентиль студента Сидорова получившего на экзамене 3 балла:
Находим n(x≤X)=n(x≤3)=9 — т.е. 9 студентов получили бал не выше 3, тода
Процентиль (Иванова) = 9/20*100=45
После расчета процентиля можно составить таблицу стандартизации. Для наших баллов она будет выглядеть следующим образом:
Алгоритм расчета процентилей
1. Для каждого человека посчитать, какое количество человек набрало столько же или меньше баллов.
2. Посчитать сколько процентов составляет это количество от всей выборки.
Процентиль – это процент людей из выборки, набравших столько же или меньше баллов, чем конкретный человек.
Процентиль является достаточно распространенной шкалой стандартизации, среди психологов, социологов, биологов, медиков и т.д., т.к. очень удобен и понятен. Его диапазон от 1 до 100.
Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать, как ранговые градации, общее число которых равно 100, с той лишь разницей, что при ранжировании принято начинать отсчет сверху, т.е. с лучшего члена группы, получающего ранг 1. В случае же процентилей отсчет ведется снизу, поэтому, чем ниже процентиль, тем хуже позиция индивида.
Процентиль может использоваться для стандартизации как нормально распределенных случайных величин СВ, так и данных с ненормальным распределением.
Расчет процентилей в Excel
Для расчета процентилей нам понадобится функция СЧЕТЕСЛИ.
Для расчета, для каждого значения нужно ввести формулу:
=(СЧЁТЕСЛИ(диапазон;условие)*100)/N , где N – количество человек.
Процентили в EXCEL
Рассмотрим понятие процентиля, функцию ПРОЦЕНТИЛЬ.ВКЛ() , процентиль-ранг и построим кривую процентилей.
Сначала разберемся на примерах, что такое процентиль , затем рассмотрим соответствующие функции MS EXCEL.
Задача. Проектируют койку на круизном лайнере. Необходимо, чтобы 95% пассажиров помещались на койке в полный рост. Как вычислить длину койки?
Для решения задачи потребуется найти рост, ниже которого 95% населения. Для этого нужно сделать репрезентативную выборку , скажем, из 2000 человек, отсортировать значения выборки по возрастанию , потом определить значение с позицией равной 1901 (2000*95%+1). Пусть найденный рост оказался равен 190 см. Ответ : Длина койки должна быть 190 см (+ запас для комфортного размещения на койке).
Значение 190 см называется 95%-й процентилью данной выборки , т.е. 95% опрошенных людей имеет рост 100) обычно наблюдается хорошее соответствие. Повторы значений также могут привести к несоответствию значения процентиля и соответствующего % значений (см. ниже).
Примечание : Процентили часто называют перцентилями (с этим соглашается и MS WORD) или центилями . В версии MS EXCEL 2007 и более ранних использовалась функция ПЕРСЕНТИЛЬ() , которая оставлена для совместимости. Но, начиная с версии EXCEL 2010, появились функции ПРОЦЕНТИЛЬ.ВКЛ() и ПРОЦЕНТИЛЬ.ИСКЛ() – английское название PERCENTILE.EXC(), а Условное форматирование предлагает настроить правило с использованием именно процентилей . В свою очередь, надстройка Пакет Анализа имеет инструмент Ранг и Персентиль . 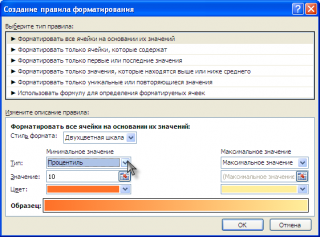
Таким образом, для процентилей используется 3 названия: процентиль (MS EXCEL, Google) , персентиль (MS EXCEL) , перцентиль (MS WORD) .
Ниже детально рассмотрим как работает функция ПРОЦЕНТИЛЬ.ВКЛ() и создадим ее аналог с помощью альтернативной формулы. Также рассмотрим функцию ПРОЦЕНТРАНГ.ВКЛ() и кривую процентилей .
СОВЕТ : Нижеследующие разделы следует читать пользователям, владеющими базовыми понятиями математической статистики (случайная величина, функция распределения) .
Функция ПРОЦЕНТИЛЬ.ВКЛ()
Начиная с версии MS EXCEL 2010 для расчета процентилей используется функция ПРОЦЕНТИЛЬ.ВКЛ() – английское название PERCENTILE.INC(). В более ранних версиях MS EXCEL использовался ее аналог — функция ПЕРСЕНТИЛЬ() .
Напомним определение процентиля , данное выше: K-й Процентиль представляет такое собой значение Х в наборе данных, которое разделяет набор на две части: одна часть содержит K% данных, меньших Х , а другая часть содержит все остальные значения набора (т.е. 1- K % данных б о льших Х).
Разберем детально как работает функция ПРОЦЕНТИЛЬ.ВКЛ() .
Пусть имеется массив значений ( выборка ). В массиве 49 значений, массив расположен в диапазоне B15:B63 , имеются повторы значений , массив для удобства отсортирован по возрастанию (см. файл примера , лист ПРОЦЕНТИЛЬ.ВКЛ ).
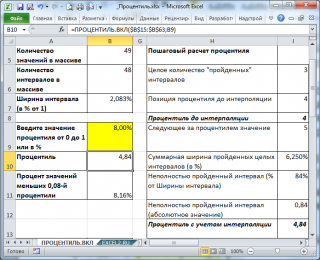
Рассчитаем 0,08-ю процентиль ( 8%-процентиль ) с помощью формулы =ПРОЦЕНТИЛЬ.ВКЛ(B15:B63; 0,08) . Получим, что 0,08-я процентиль равна 4,84.
Проанализируем, что мы получили.
- Во-первых, значения 4,84 нет в массиве (есть 4 и 5), т.е. функция ПРОЦЕНТИЛЬ.ВКЛ() интерполирует значения.
- Во-вторых, процент значений меньших 4,84 равен не точно 8%, а 8,16%=4/49*100% (т.к. всего 4 значения в массиве меньше 4,84). Это произошло, т.к. в выборке относительно мало значений.
- Другой причиной расхождения могут стать повторы. Например, заменив, первые 4 значения в массиве (т.е. 1; 2; 3; 4) числом 5, мы получим вместо 8,16% — 0%. Это произошло потому, что теперь 0,08-я процентиль равна 5, а в выборке нет ни одного значения меньше 5.
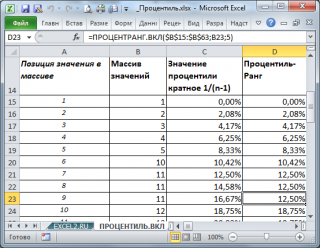
Как видно из рисунка ниже первое значение ( минимальное , равное 1) является 0-й процентилью .
Соответственно, 1-й процентилью (100% процентилью ), является максимальное значение равное 120 (см. файл примера лист ПРОЦЕНТИЛЬ.ВКЛ).
Как видно из рисунка, следующее за минимальным значением (т.е. число 2) является 0,0208-й процентилью . Значение 0,0208 или 2,08% — это (k-1)*1/(n-1), где n – это количество значений в массиве (в нашем массиве n=49), а k – это позиция числа в массиве (в данном случае k=2, где 2 – это позиция, а не само число).
Поясним эту формулу. Для вычисления процентили принимается, что весь диапазон значений массива (от мин до макс) разбит n значениями на равные интервалы (их всего n-1). Соответственно, 1/(n-1), это «ширина» интервала (весь диапазон равен 1 или 100%). Обратите внимание, что «ширина» интервала не зависит от данных, а только от их количества. В нашем случае «ширина» интервала равна 0,0208 или 2,08%.
Приведем алгоритм расчета 12,50%-процентили функцией ПРОЦЕНТИЛЬ.ВКЛ() (см. ячейку С21 ):
- ПРОЦЕНТИЛЬ.ВКЛ() определяет «ширину» интервала (в долях или процентах): =1/(49-1)=0,0208;
- подсчитывает Количество интервалов , которые были укладываются в 12,50%, т.е. =12,50%/2,08%=6 (значение процентиля кратно ширине интервала, т.е. делится нацело);
- 6-й интервал располагается между числами массива 10 и 11. Верхняя граница последнего 6-го интервала равна 11;
- Следовательно, 12,50%-я процентиль равна 11 (см. ячейку B21 ).
По аналогии с непрерывной функцией распределения (см. статью про квантили ), получается, что 12,50% значений должно быть меньше полученного числа 11 (в соответствии с определением процентиля ). Фактически получается, что таких значений 6 (1; 2; 3; 4; 5; 10) и процент значений меньших 11 равен 12,24%=6/49 (причины расхождения: повторы и небольшое количество значений).
Если значение процентиля не кратно ширине интервала (ширина интервала равна 1/(n-1)), то имеет место интерполирование. Например, вспомним результат вычисления 0,08-й процентили равный 4,84. Значение процентили (т.е. не результат, а %) равно 0,08 (8%), что соответствует 3-м целым интервалам (8%/2,08%= 3 ,84) и некой доли (0,84) от ширины следующего интервала. Границами этого «неполного» интервала являются значения 4 ( 0,0625-я процентиль ) и 5 ( 0,0833-я процентиль ). Т.к. разница между 5 и 4 равна 1, то умножая «пройденную» долю интервала (0,84) на длину интервала в абсолютных значениях (=5-4=1), получаем 0,84. В итоге получаем 4,84: 4 – левая граница интервала + часть следующего (5-4)*0,84.
Если бы в массиве вместо 5 было значение 6, то значение 0,08-й процентили было бы равно 5,68 (4 – левая граница интервала + (6-4)*0,84=1,68).
Альтернативный расчет процентили с помощью формул приведен в файле примера .
Примечание : Некоторые значения процентилей имеют специальные названия:
- 25-я процентиль называется 1-й квартилью;
- 50-я процентиль называется Медианой (2-я квартиль);
- 75-я процентиль называется 3-й квартилью.
Функция ПРОЦЕНТРАНГ.ВКЛ() и Кривая процентилей
Функция ПРОЦЕНТРАНГ.ВКЛ() используется для оценки относительного положения значения в массиве. Для заданного значения функция вычисляет сколько значений в массиве меньше или равно ему. Точнее — какой процент значений массива меньше или равен ему. Результат функции называется процентиль-ранг (percentile rank) . Понятно, что для максимального значения процентиль-ранг равен 0,00%, а для наименьшего — 100% (все значения массива меньше или равны ему).
Функция ПРОЦЕНТРАНГ.ВКЛ() , английская версия – PERCENTRANK(), является, в каком-то смысле, обратной функции ПРОЦЕНТИЛЬ.ВКЛ() : т.е. задавая в качестве аргумента значение из массива, функция ПРОЦЕНТРАНГ.ВКЛ() вернет значение процентили кратной 1/(n-1).
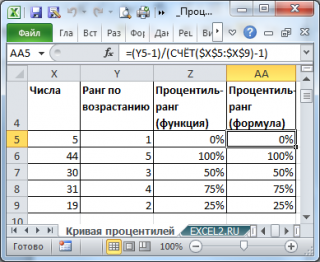
Как видно из рисунка выше, для повторяющихся значений функция ПРОЦЕНТРАНГ.ВКЛ() вернет, естественно, одинаковые значения. Также поступает функция РАНГ.РВ() или РАНГ() (см. статью Функция РАНГ() в MS EXCEL ).
Действительно, функции РАНГ.РВ() и ПРОЦЕНТРАНГ.ВКЛ() очень похожи. Первая возвращает позицию числа в массиве в зависимости от его значения. Вторая, в принципе, делает тоже самое, но результат выводится в % от общего количества значений в массиве.
Как видно из картинки выше, чтобы получить процентиль-ранг необходимо значение ранга уменьшить на 1 и разделить на n-1. Значение ранга , естественно, должно быть отсортировано по возрастанию .
По выборке можно оценить функцию распределения Генеральной совокупности , из которой взята данная выборка. Для этой цели построим Кривую процентилей (percentile curve или percentile rank plot). 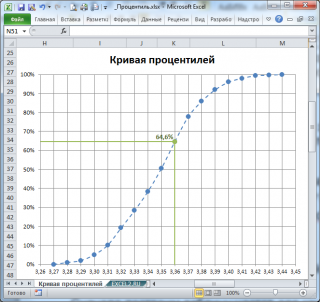
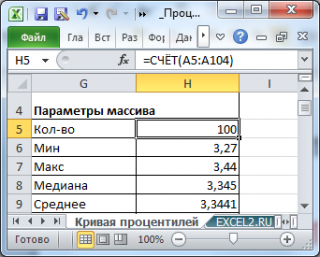
Возьмем выборку состоящую из 100 значений (см. файл примера лист Кривая процентилей ). Значения содержатся в диапазоне А5:А104 .
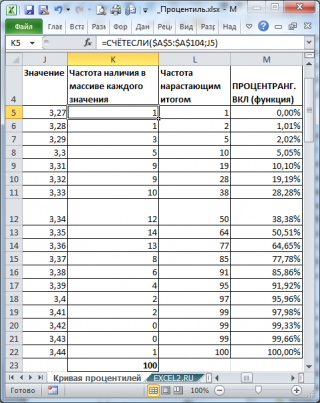
Сначала построим таблицу частот для каждого из значений выборки .
Примечание : В отличие от Гистограммы , где кумулятивная таблица частот строится для интервалов значений, таблицу частот для Кривой процентилей строят для каждого из значений выборки .
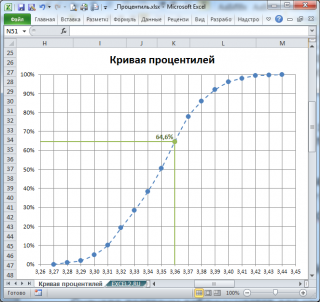
Из таблицы видно (столбец Частота нарастающим итогом ), что примерно 1 процент значений меньше или равен значения 3,27, примерно 2 процента на уровне или ниже 3,28, 5 процентов на уровне или ниже 3,29, и так далее. График Кривой процентилей для этих данных приведен на картинке ниже.
СОВЕТ : Про построение графиков см. статью Основные типы диаграмм .
Следует отметить, что использование данных из таблицы приведет к точечному виду кривой (так как процентиль-ранг будет изменяться скачком для каждого значения выборки ). Поэтому, сглаженная кривая, построенная на основе этих данных будет лучше представлять оцениваемую функцию распределения (пунктирная кривая).
Построив пунктирную кривую, становится ясно, зачем нам пришлось вводить понятие процентиль-ранга: процентиль-ранг – является приблизительной вероятностью выбрать случайную величину меньше или равную соответствующему значению (сравните с определением функции распределения). Это, в частности следует из расчета процентиль-ранга по формуле =СЧЁТЕСЛИ($A$5:$A$104;» 100 значений).
Примечание : Формула =(РАНГ.РВ(A5;$A$5:$A$104;1)-1)/ (СЧЁТ($A$5:$A$104)-1) эквивалентна формуле =ПРОЦЕНТРАНГ.ВКЛ($A$5:$A$104;A5;5)
КВАРТИЛЬ: какие формулы расчета использует Excel
Квартиль — одна из статистик, используемая при описании выборок (подробнее о различных статистиках см. Определение среднего значения, вариации и формы распределения. Описательные статистики). В то время как медиана разделяет упорядоченный массив пополам, квартили разбивают набор данных на четыре части. Первый квартиль – это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше значения первого квартиля. Третий квартиль — это число, разделяющее выборку также на две части: 75% элементов меньше, а 25% — больше третьего квартиля.
Рис. 1. 5-числовые сводки: М – медиана, Н1 и Н2 – сгибы (они же квартили)
Скачать заметку в формате Word или pdf, примеры в формате Excel (файл содержит код VBA).
Для расчета квартилей в Excel2007 и более ранних версиях использовалась функция КВАРТИЛЬ. Начиная с версии Excel2010 применяются две функции: КВАРТИЛЬ.ВКЛ и КВАРТИЛЬ.ИСКЛ (функция КВАРТИЛЬ оставлена для совмещения с более ранними версиями Excel; эта функция возвращает те же значения, что и КВАРТИЛЬ.ВКЛ). Эти две функции возвращают различные значения, но я нигде не нашел, какой алгоритм они используют при расчетах. Замечу, что для корректной работы функций данные можно не упорядочивать.
Изучение литературы показало, что в отличие от большинства других статистик, единодушия в методике расчета квартилей нет)) Я нашел упоминание о девяти различных подходах…
Начнем с метода Джона Тьюки, описанного им в, уже ставшем классическом, труде Анализ результатов наблюдений. Разведочный анализ, изданном в 1977 г. Он начинает с введения трех сводок, характеризующих выборку: минимальное, максимальное значения и медиана. Далее он продолжает: «Если мы хотим добавить еще два числа, чтобы образовать 5-числовую сводку, то естественно определять их подсчетом до половины расстояния от каждого из концов к медиане. Процесс нахождения медианы, а затем и этих новых значений можно представить себе, как складывание листа бумаги. Поэтому эти новые значения естественно назвать сгибами» (англ. – hinge; рис. 1). Мы их называем квартилями.
Такие рисунки выглядят очень аккуратно, если число элементов выборки N = 4k + 1, например, 9, 13, 17… Но как быть, если в выборке 12 или 19 элементов? Наглядную картину представил Jon Peltier в серии заметок в своем блоге. Упорядочим элементы случайной выборки и разместим их над линейкой (рис. 2; случайная выборка, элементы которой упорядочены называется вариационным рядом). Серые числа под линейкой – индекс ряда (Джон зачем-то в качестве выборки – над линейкой – взял ряд целых чисел; наверное, чтобы запутать нас). Красное число над рядом – значение сводки; если оно дробное, значит полученное значение является интерполяцией между соседними значениями. Мы определяем медиану, как среднее значение набора данных, а первую квартиль – как медиану нижней половины данных.
Рис. 2. Инклюзивные квартили
Когда Джон Тьюки впервые предложил такой подход, он решил, что медиана (если число элементов в выборке нечетное) должна быть включена как в нижнюю (левую на рисунке), так и в верхнюю половинку данных при определении медиан этих половинок, то есть сгибов. Поэтому такой подход и называется инклюзивным (с включением).
Эксклюзивный подход. Некоторым статистикам не нравится, что медиана учитывается дважды. Они решили, что сгибы должны быть определены как медианы верхней и нижней половин набора данных, из которых срединное значение исключено (рис. 3). Такой взгляд отстаивали Moore и McCabe, или кратко M&M. Если набор данных содержит четное количество значений, инклюзивные и эксклюзивные квартили равны, так как нет элемента выборки (соответствующего центральной медиане), который можно было бы включить или исключить из рассмотрения. Для нечетного числа элементов, инклюзивные сгибы всегда ближе к медиане.
Рис. 3. Эксклюзивные квартили
Третий подход – компромисс между Тьюки и М&M – называется Эмпирическая функции распределения или Интегральная функция распределения (английская аббревиатура CDF). В случае нечетного числа значений в наборе данных, следует включить или исключить медиану, ориентируясь на то, чтобы оставшиеся половинки содержали нечетное число элементов. Например, если в выборке 9 элементов, медиану следует включить, а при 11 элементах – исключить. В обоих случаях половинки будут содержать по 5 элементов. Преимущество этого компромисса заключается в том, что в качестве значения квартиля всегда получается один из элементов набора данных (а не среднее значение двух соседних элементов). CDF является методом по умолчанию в статистическом пакете SAS.
Все возможные случаи N. Мы не всегда можем изобразить данные в W-образной форме, как на рис. 1, поэтому удобнее пользоваться линейкой. В общем случае возможны четыре варианта по числу элементов в выборке: N = 4k, N = 4k + 1, N = 4k + 2, N = 4k + 3… и три подхода к расчету квартилей: Тьюки, M&M, CDF (рис. 4–7).
Рис. 4. Число элементов в выборке N = 4k; все три метода дают одинаковые значения квартилей
Рис. 5. Число элементов в выборке N = 4k + 1; M&M дает значения, отстоящие дальше от медианы
Рис. 6. Число элементов в выборке N = 4k + 2; все три метода дают одинаковые значения квартилей
Рис. 7. Число элементов в выборке N = 4k + 3
Методы интерполяции. Помимо трех описанных выше методов, применяют и целый ряд индексных алгоритмов. Мы рассмотрим три из них. Первый индекс во всех методах равен 0, а последний – N–1, N, N + 1. Например, для N=8 индексированные ряды представлены на рис. 8.
Рис. 8. Индексные ряды на основе N–1, N и N + 1 для N = 8
Положение перцентиля р – доля длины индексной линии, или р(N–1), рN, р(N+1), соответственно. р = 0,25 соответствует первому квартилю, а р = 0,75 – третьему. Ниже наглядно представлен расчет квартилей при различном числе элементов в выборке и трех методах интерполяции на основе N–1, N и N + 1 (рис. 9, 11–13). Обратите внимание, что рассчитанные числа (по формулам справа от линеек) являются не значениями квартилей, а значениями индексов квартилей. Над линейками показано значение квартилей для ряда значений <1, 2, 3, 4, 5, 6, 7, 8>.
Рис. 9. Число элементов в выборке N = 4k
Если, например, наша выборка <2, 3, 5, 8, 11, 12, 14, 17>, то расчет квартилей на основе N–1-метода даст индексы 1,75, 3,5 и 5,25, и значения квартилей 4,5, 9,5 и 12,5 (рис. 10).
Рис. 10. От индексов к значениям квартилей для N–1-метода и N = 4k
Рис. 11. Число элементов в выборке N = 4k + 1
Рис. 12. Число элементов в выборке N = 4k + 2
Рис. 13. Число элементов в выборке N = 4k + 3
Какой алгоритм считать стандартным для вычисления квартилей?
В 1996 году Роб Дж. Хиндман и Янан Фан опубликовали статью в American Statistician под названием Квантили выборок в статистических пакетах. В ней они рассматривали различные алгоритмы расчета квантилей (квартили – это частный случай квантилей). Их целью было указать методологию, которая могла бы стать стандартом для поставщиков статистического программного обеспечения, чтобы расчет квартилей не зависел от типа пакета. В статье они описали девять методов для расчета квантилей. Таблица показывает некоторые статистические пакеты и используемые в них алгоритмы (рис. 14; таблица, этот раздел заметки и код VBA ниже базируются на тексте с сайта Bacon Bits). Обратите внимание, что R и Maple применяют весь спектр алгоритмов.
Рис. 14. Алгоритмы, используемые в статистических пакетах
Кстати, Хиндман и Фан в завершении своей статьи рекомендовали метод 8 в качестве стандарта для статистических пакетов. По их мнению, этот метод оценки квантиля не зависит от распределения, что делает его наиболее приемлемым для расчета.
Расчет квартилей в Excel
Функция Excel КВАРТИЛЬ.ИСКЛ использует следующую формулу для расчета квартилей:
где Qp – p-й квантиль: p = 0 – для минимального значения, 0,25 – для первого квартиля, 0,5 – для медианы, 0,75 – для третьего квартиля, 1 – для максимального значения;
x – индекс квантиля (может быть дробным); x = (n+1)p, где n – число элементов в выборке; обратите внимание на (n+1), поэтому метод и называется N+1-интерполяция;
i – индекс элемента в упорядоченной выборке; самое большое целое всё еще меньшее, чем x;
Формула для КВАРТИЛЬ.ВКЛ отличается только методом расчета х: x = (n-1)p+1; обратите внимание на (n–1), поэтому метод называется N–1-интерполяция. Подробнее с работой формул можно ознакомиться в приложенном Excel-файле на листе Формулы.
Расчет квартилей в R и SAS
Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R!). Квантиль при i-м методе расчета:
где i – номер метода, 1 ≤ i ≤ 9, (j–m)/n ≤ p = 0 And i
Инструменты Excel для построения интервальных оценок параметров распределений
Все, рассмотренные в этом разделе инструменты вычисляют значения квантилей как значения функций, обратных соответствующим функциям распределения. Все эти функции – библиотечные функции Excel из группы функций «Статистические»,.
Функция вычисления критических точек распределения Лапласа
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) стандартного нормального распределения.
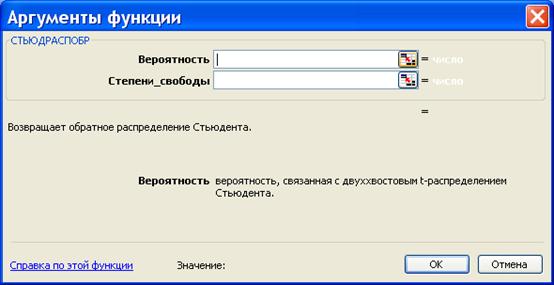
Функция вычисления критических точек распределения Стьюдента
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения Стьюдента с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
Важно знать, что функция Excel СТЬЮДРАСПОБР( p , k ) возвращает значение t , при котором P (| x | > t ) = p , x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы.
Поэтому решение уравнения 
Функция вычисления критических точек распределения
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения 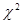
В Excel функция распределения случайной величины определена нестандартно: F x ( x ) = P ( x > x ). Поэтому для вычисления квантиля 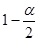
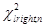
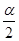
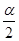
Вычислить процентиль в Excel 2010
Это мой список ниже. Я пытаюсь вычислить 95% звонков, которые вернулись за сколько миллисекунд.
Что означают приведенные выше данные-это-
Теперь я должен выяснить 95% percentile из приведенных выше данных. Что означает 95% времени, звонки возвращались в эти миллисекунды.
Может ли кто-нибудь сказать мне, как это сделать в Excel листе? Спасибо за помощь
Я использую Excel 2010. Я скопировал оба столбца в моем листе Excel, как это делается, чтобы вычислить процент.
Обновление:-
С списке ниже, я получаю 95 percentil Е 66. Так что это означает 95% времени, звонки вернулись в 66 milliseconds , что, наверное, неправильно. Это выглядит для меня 95% времени, звонки вернулись в
Я использую эту формулу-
3 Ответа
Дополнительный столбец упростит вычисления, но вы можете вычислить без него, если хотите.
Предполагая, что миллисекунды в A2:A21 и количество вызовов в B2:B21 можно использовать эту формулу массива
подтверждено с помощью CTRL + SHIFT + ENTER
или эта версия без массива
Я получаю результат 63 с обоими — изменение на 0.75 (75-й процентиль) , и вы получаете 59
Установите новый столбец «количество вызовов в момент времени или ниже» и попросите его вычислить сумму количества вызовов текущей строки плюс все номера вызовов в более высоких строках (более низкие времена). Затем установите столбец рядом с тем, который называется «Percentile», и вычислите его, разделив «Number of Calls at or Below Time» на общее количество принятых вызовов. Независимо от того, какая первая строка показывает процентиль выше, чем 95%, это та, которая содержит 95-й процентиль.
Получите стандартное отклонение времени в миллисекундах и используйте его для (95%
2 x std) подсчитайте количество вызовов ниже
2 стандартных отклонений?
Похожие вопросы:
Я пытаюсь вычислить 95th Percentile из наборов данных, которые я заполнил в моем ниже ConcurrentHashMap . Мне интересно узнать, сколько звонков вернулось в 95-й процентиль времени Моя карта будет.
Я пытаюсь вычислить процентиль для каждого значения в столбце a от DataFrame x . Есть ли лучший способ написать следующий фрагмент кода? x[pcta] = [stats.percentileofscore(x[a].values, i) for i in.
Нам нужно вычислить процентиль (95-й и 99-й) в отчете SSRS на основе общего набора данных, который возвращает агрегированные данные с интервалом в 15 минут. Процентиль должен быть за день в целом.
Этот вопрос здесь, похоже, не помогает: вычисление процентилей (Ruby ) Я хотел бы вычислить 95-й процентиль (или, действительно, любой другой желаемый процентиль) из массива чисел. В конечном счете.
//I have a list of students List Students < lond StudentId; double Marks; int Rank; double Percentile; >Я снабжен идентификатором и метками, и мне нужно вычислить ранг и процентиль.
Я пытаюсь подсчитать, сколько звонков вернулось за 95 процентиль времени. Ниже приведен мой результирующий набор. Я работаю с Excel 2010 Milliseconds Number 0 1702 1 15036 2 14262 3 13190 4 9137 5.
я пытаюсь вычислить 95-й процентиль для нескольких значений качества воды, сгруппированных по водоразделу. например. Watershed WQ 50500101 62.370661 50500101 65.505046 50500101 58.741477 50500105.
Я пытаюсь вычислить процентиль столбца в A DataFrame? Я не могу найти ни одной функции percentile_approx в функциях агрегации Spark. Например, в Hive у нас есть percentile_approx, и мы можем.
Я хочу вычислить 95-й процентиль распределения. Я думаю, что я не могу использовать proc means , потому что мне нужно значение, в то время как выход proc means -это таблица. Я должен использовать.
У меня есть dataframe со столбцом, который имеет числовые значения. Этот столбец плохо аппроксимируется нормальным распределением. Учитывая другое числовое значение, а не в этом столбце, как я могу.