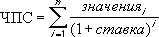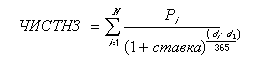Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.
Описание
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС(ставка; значение1; [значение2],…)
Аргументы функции ЧПС описаны ниже.
-
Ставка Обязательный аргумент. Ставка дисконтирования за один период.
-
Значение1, значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.
-
Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
-
Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.
-
Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.
-
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Замечания
-
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.
-
Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:
-
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.
-
ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,1 |
Годовая ставка дисконтирования |
|
|
-10 000 |
Начальная стоимость инвестиции через один год |
|
|
3000 |
Доход за первый год |
|
|
4200 |
Доход за второй год |
|
|
6800 |
Доход за третий год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A3; A4; A5; A6) |
Чистая приведенная стоимость данной инвестиции |
1 188,44 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,08 |
Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям. |
|
|
-40 000 |
Начальная стоимость инвестиции |
|
|
8000 |
Доход за первый год |
|
|
9200 |
Доход за второй год |
|
|
10000 |
Доход за третий год |
|
|
12000 |
Доход за четвертый год |
|
|
14500 |
Доход за пятый год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A4:A8)+A3 |
Чистая приведенная стоимость данной инвестиции |
1 922,06 ₽ |
|
=ЧПС(A2; A4:A8; -9000)+A3 |
Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году |
(3 749,47 ₽) |
К началу страницы
Нужна дополнительная помощь?
Рассчитаем
Приведенную (к текущему моменту) стоимость
инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.
Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и
Будущей стоимости
важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты:
простые проценты
,
сложные проценты
или
аннуитет
(в
файле примера
приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание
. В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция
ПС()
используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить
ПС()
рассчитать Приведенную стоимость и по методу простых процентов (см.
файл примера
).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета
Будущей стоимости
(FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя
формулу наращения для сложных процентов
.
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,
т.е. PV = FV / (1+i)^n
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
Сложные проценты (несколько сумм)
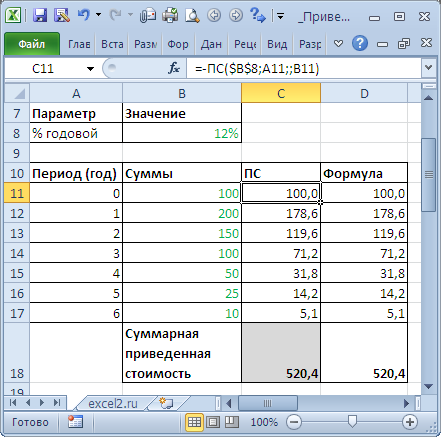
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции
ПС()
или альтернативной формулы PV = FV / (1+i)^n
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см.
файл примера
).
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью
Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость
, где приведен расчет с помощью функции
ПС()
, а также вывод альтернативной формулы).
Здесь разберем другую задачу (см.
файл примера
):
Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?
Решение может быть найдено с помощью функции
ПС()
:
=ПС(12%/12;12;20000;-1000000;0)
= 662 347,68р.
Аргумент
Ставка
указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент
Кпер
– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент
Плт
— это 20000р., т.е. величина дополнительных взносов. Аргумент
Бс
— это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент
перечисляет
эти средства банку, а будущую сумму вклада клиент
получит
от банка. Это очень важное замечание касается всех
функций аннуитета
, т.к. в противном случае можно получить некорректный результат. Результат функции
ПС()
– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше
=ПС(12%/12;12;20000)
= -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость
= БС(12%/12;12;; 225 101,55+662 347,68)
= -1000000,0р., что и требовалось доказать.
Определение Приведенной стоимости в случае платежей произвольной величины
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция
ЧПС()
. Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция
ЧИСТНЗ()
. Об этих расчетах читайте в статье
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL
.
Present value (PV) is the current value of an expected future stream of cash flow. Present value can be calculated relatively quickly using Microsoft Excel.
The formula for calculating PV in Excel is =PV(rate, nper, pmt, [fv], [type]).
Key Takeaways
- Present value (PV) is the current value of a stream of cash flows.
- PV analysis is used to value a range of assets from stocks and bonds to real estate and annuities.
- PV can be calculated in Excel with the formula =PV(rate, nper, pmt, [fv], [type]).
- If FV is omitted, PMT must be included, or vice versa, but both can also be included.
- NPV is different from PV, as it takes into account the initial investment amount.
Formula for PV in Excel
Again, the formula for calculating PV in Excel is
=PV(rate, nper, pmt, [fv], [type]).
The inputs for the present value (PV) formula in excel includes the following:
- RATE = Interest rate per period
- NPER = Number of payment periods
- PMT = Amount paid each period (if omitted—it’s assumed to be 0 and FV must be included)
- [FV] = Future value of the investment (if omitted—it’s assumed to be 0 and PMT must be included)
- [TYPE] = When payments are made (0, or if omitted—assumed to be at the end of the period, or 1—assumed to be at the beginning of the period)
Some keys to remember for PV formulas is that any money paid out (outflows) should be a negative number. Money in (inflows) are positive numbers.
NPV vs. PV Formula in Excel
While you can calculate PV in Excel, you can also calculate net present value (NPV). Present value is discounted future cash flows. Net present value is the difference between PV of cash flows and PV of cash outflows.
The big difference between PV and NPV is that NPV takes into account the initial investment. The NPV formula for Excel uses the discount rate and series of cash outflows and inflows.
Key differences between NPV and PV:
- The PV formula in Excel can only be used with constant cash flows that don’t change.
- NPV can be used with variable cash flows.
- PV can be used for regular annuities (payments at the end of the period) and annuities due (payments at the beginning of the period).
- NPVs can only be used for payments or cash flows at the end of the period.
Example of PV Formula in Excel
If you expect to have $50,000 in your banking account 10 years from now, with the interest rate at 5%, you can figure out the amount that would be invested today to achieve this.
You can label cell A1 in Excel «Years.» Besides that, in cell B1, enter the number of years (in this case 10). Label cell A2 «Interest Rate» and enter 5% in cell B2 (0.05). Now in cell A3, label it “Future Value” and put $50,000 into cell B3.
The built-in function PV can easily calculate the present value with the given information. Enter «Present Value» into cell A4, and then enter the PV formula in B4, =PV(rate, nper, pmt, [fv], [type], which, in our example, is «=PV(B2,B1,0,B3).»
Since there are no intervening payments, 0 is used for the «PMT» argument. The present value is calculated to be ($30,695.66), since you would need to put this amount into your account; it is considered to be a cash outflow, and so shows as a negative. If the future value was shown as an outflow, then Excel will show the present value as an inflow.
PV in Excel.
Special Considerations
For the PV formula in Excel, if the interest rate and payment amount are based on different periods, adjustments must be made. A popular change that’s needed to make the PV formula in Excel work is changing the annual interest rate to a period rate. That’s done by dividing the annual rate by the number of periods per year.
For example, if your payment for the PV formula is made monthly then you’ll need to convert your annual interest rate to monthly by dividing by 12. As well, for NPER, which is the number of periods, if you’re collecting an annuity payment monthly for four years, the NPER is 12 times 4, or 48.
What Is the Difference Between Present Value (PV) and Future Value (FV)?
Present value uses the time value of money to discount future amounts of money or cash flows to what they are worth today. This is because money today tends to have greater purchasing power than the same amount of money in the future. Taking the same logic in the other direction, future value (FV) takes the value of money today and projects what its buying power would be at some point in the future.
Why Is Present Value Important?
Present value is important in order to price assets or investments today that will be sold in the future, or which have returns or cash flows that will be paid in the future. Because transactions take place in the present, those future cash flows or returns must be considered but using the value of today’s money.
When Might You Need to Calculate Present Value?
Present value calculations are quite common. Any asset that pays interest, such as a bond, annuity, lease, or real estate, will be priced using its net present value. Stocks are also often priced based on the present value of their future profits or dividend streams using discounted cash flow (DCF) analysis.
Функция ЧИСТНЗ предназначена для расчета приведенной стоимости на основе данных о имеющихся денежных потоках и датах проведения этих платежей (непериодические платежи), и возвращает соответствующее числовое значение.
Функции ЧИСТНЗ и ЧПС рассчитывают один и тот же экономический параметр, однако вторая может быть использована только для определения приведенной стоимости для ряда периодических финансовых потоков (проводимых через определенные промежутки времени, например, через 365 дней).
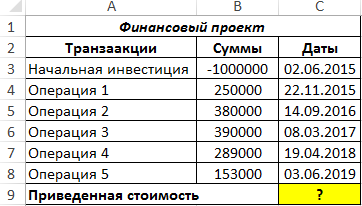
Пример расчета приведенной стоимости проекта в Excel
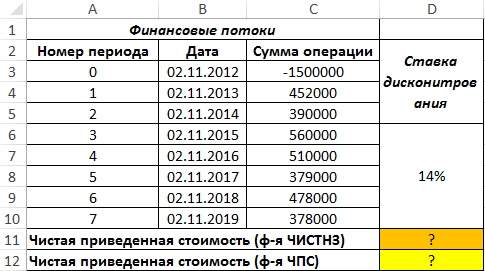
Пример 1. Определить значение чистой приведенной стоимости для проекта, начальные затраты на реализацию которого составили 1 млн у. е. Длительность проекта составила 5 лет, ставка дисконтирования – 13%.
Вид таблицы данных:
Для определения искомого значения используем функцию:
Описание аргументов:
- 0,13 – числовое значение ставки дисконтирования (13%);
- B3:B8 – диапазон ячеек с числовыми данными о денежных потоках;
- C3:C8 – диапазон ячеек с датами совершения финансовых операций.
Результат:
Это был базовый пример использования функции ЧИСТНЗ в Excel
Расчет приведенной стоимости денежного потока в Excel
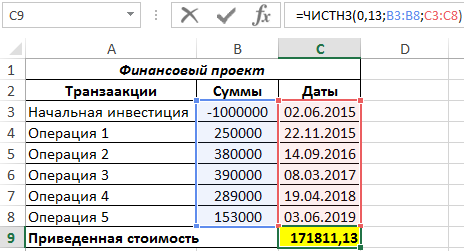
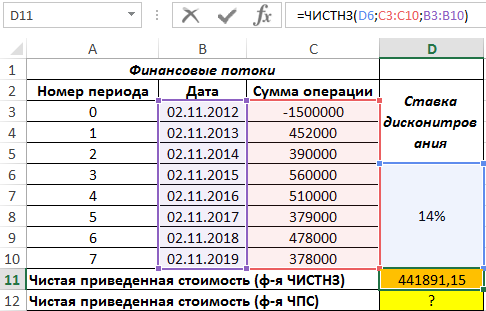
Пример 2. Рассчитать значение чистой приведенной стоимости для финансовых потоков, представленных в таблице, с использованием функции ЧПС, сравнить данные, применив функцию ЧИСТНЗ, объяснить расхождения в полученных результатах.
Вид таблицы данных:
Вначале рассчитаем значение приведенной стоимости с использованием рассматриваемой функции:
В результате получим:
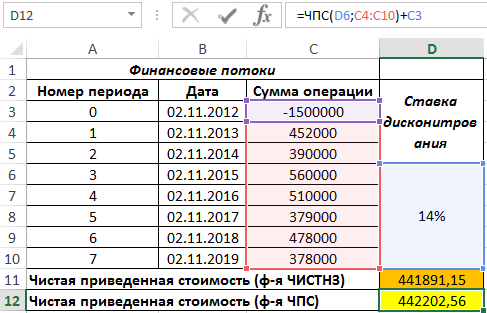
Если бы в табличном редакторе Excel отсутствовала формула ЧИСТНЗ, кроме ручного способа можно было бы рассчитать приведенную стоимость с помощью функции ЧПС следующим образом:
Поскольку функция ЧПС учитывает только платежи, к результатам ее вычислений добавлено значение первоначальных затрат (+C3).
Результат вычислений:
Как видно, результаты немного различны. Это обусловлено тем, что функция ЧИСТНЗ учитывает реальное количество дней в году (в високосном году дней больше на 1). Несмотря на то, что все платежи производились 2-го числа 11 месяца ежегодно, их нельзя считать периодичными, поскольку в списке дат есть високосный год и реальное число дней между 2.11.2016 и 2.11.2017 равен 366 дней. Функция ЧИСТНЗ в подобных расчетах дает более точный результат.
Правила использования функции ЧИСТНЗ в Excel
Функция имеет следующую синтаксическую запись:
=ЧИСТНЗ(ставка;значения;даты)
Описание аргументов:
- ставка – обязательный для заполнения, принимает числовое значение ставки дисконтирования для исследуемого потока финансовых движений.
- значения – обязательный для заполнения, принимает ссылку на диапазон ячеек, содержащих данные о денежных потоках. Фактически, это столбец, в котором приведен график платежей. Указанные значения могут быть как затратами, так и поступлениями. Любая затрата указывается в виде отрицательного числового значения (например, — 10000). Для корректных расчетов хотя бы одно число в графике платежей должно быть отрицательным. Дисконтирование выплат осуществляется на основе года длительностью в 365 дней.
- даты – обязательный для заполнения, принимает ссылку на ячейки с датами, соответствующим моментам совершения финансовых операций (расходы или получение прибыли). Первая дата соответствует началу графика платежей. Последующие должны являться более поздними датами относительно первой. Периодичность дат – необязательное условие. Например, 1-й платеж может быть совершен 1.01.2018, 2-й – 3.07.2018, 3-й – 14.09.2018 и т. д.
Примечания:
- Для корректных расчетов значения в столбце, передаваемые в качестве аргумента даты, должны быть записаны с использованием функции ДАТА. Если они указаны в виде числовых значений (например, записанная в Excel дата 03.06.2019 соответствует числу 43619), дробные части таких чисел будут усечены (например, 43619,3 будет считаться равным 43619).
- Любое значение, переданное в качестве любого из трех аргументов, должно являться числом (или данными типа ДАТА – аргумент даты). Если этой условие не соблюдено, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
- Если любая из дат, содержащихся в столбце с датами совершения платежей, является более ранней датой, чем момент осуществления первого платежа, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
- Если число ячеек в столбцах с данными о платежах и соответствующими им датами различны, функция ЧИСТНЗ вернет ошибку #ЧИСЛО!
Для проверки значений, вычисленных с использованием функции ЧИСТНЗ, можно использовать формулу:
Эта формула положена в основу алгоритма расчета рассматриваемой функции. Аргументы:
- d0 – дата начальной выплаты (принимается как нулевая выплата, в отличие от функции ЧПС, где начальная выплата является 1-й, чем в первую очередь и обуславливаются различия в результатах вычислений);
- di – дата, соответствующая последней финансовой операции по графику;
- Pi – сумма платежа последней финансовой операции по графику.
Содержание
- Предварительные данные о чистой приведенной стоимости
- Особенности использования функции ЧПС
- Пример расчета чистой приведенной стоимости
Расчет чистой приведенной стоимости в Excel подводит закономерный итог нашим обстоятельным публикациям, посвященным теме приведенной стоимости вообще и чистой приведенной стоимости (NPV) – в частности.
Помимо специальных калькуляторов и таблиц, наиболее эффективным на текущий момент представляется расчет чистой приведенной стоимости именно средствами Excel, хотя бы потому, что это легко, удобно и отвечает современным представлениям об эффективных расчетах.
В сегодняшней статье мы разберем стандартную функцию ЧПС, используемую для нахождения значений чистой приведенной стоимости в таблицах Microsoft Excel, уделив внимание ее синтаксису и приведя несколько наглядных примеров ее практического применения.
Предварительные данные о чистой приведенной стоимости
Освежить свои представления о приведенной и чистой приведенной стоимости можно соответственно здесь и здесь.
Ради экономии вашего (прежде всего) времени ограничусь лишь напоминанием общеизвестной формулы, которую нам придется впоследствии увязывать со стандартной функцией Excel.
Как мы помним, когда речь идет о расчете чистой приведенной стоимости n-ного количества денежных потоков, мы прибегаем к помощи следующей весьма изящной математической конструкции:
Здесь Pi обозначает численное значение денежного потока (которое, кстати говоря, может иметь и отрицательное значение, когда речь идет об оттоках денежных средств), а r – некоторая процентная ставка (ставка дисконтирования).
Разработчики Excel позаботились о том, чтобы предельно упростить стоящую перед нами задачу расчета данного показателя, разработав функцию ЧПС, имеющую следующий формат:
=ЧПС (r, P1, P2, …).
Обязательными в этой функции являются только два параметра: r – размер процентной ставки и P1 – денежный поток в 1-ом периоде. Остальными параметрами можно пренебречь.
Всего формула позволяет обработать 254 значения Pi.
Значения P1, P2, …, Pnмогут быть положительными (в случае ПОСТУПЛЕНИЯ денежных средств) или отрицательными (когда имеют место будущие ВЫПЛАТЫ).
В свою очередь, результат функции ЧПС будет напрямую зависеть от исследуемых эмпирических данных и, как следствие, может принимать как положительные, так и отрицательные значения.
Особенности использования функции ЧПС
Ввести одномоментно 254 значения в одну ячейку бывает весьма утомительно.
Лучше заранее заполнить численными значениями некоторый диапазон, а затем подставлять в формулу ЧПС ссылки на входящие в диапазон ячейки.
Такой подход позволит легко комбинировать данные и исправлять возможные ошибки.
Следует помнить, что для расчета функции ЧПС важен ПОРЯДОК, в котором следуют значения P1, P2, …, Pn. Изменение этого порядка приведет к разным значениям нашей функции.
Предполагается также, что расчет производится для случая, когда выплаты или поступления отстоят друг от друга на один и тот же период (неделя, месяц, год и т.д.), то есть имеет место равномерное распределение денежных потоков во времени.
Все аргументы должны иметь численный формат. Ошибочно введенные в формулу ЧПС буквенные значения или символы при расчетах будут проигнорированы.
Пример расчета чистой приведенной стоимости
Не смею больше испытывать ваше терпение и предлагаю немедля окунуться в завораживающий мир расчета чистой приведенной стоимости с помощью функции ЧПС.
Итак, обещанный пример. Внимательно смотрим на иллюстрацию ниже:
Организуйте на листе вашей таблицы Excel размещение данных, аналогичных вышеприведенным.
Здесь важно заполнить ячейки A1, A2, A3, A4 и A5 конкретными числовыми данными, а в ячейку A7 поместить (важен каждый символ) выражение =ЧПС(A1; A2; A3; A4; A5).
Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5.
Соответствующий диапазон, естественно, вы можете расширить или сузить, как вам заблагорассудится, а результирующее значение поместить в любую другую удобную для вас ячейку.
Здесь главное – понять принцип.
Обратите внимание, что значение в ячейке A3 имеет отрицательное значение (-5350).
Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций).
Значения всех следующих аргументов являются положительными, так как мы имеем дело с поступлениями, символизирующими отдачу от наших инвестиций.
Заметим также, что наша функция в ячейке A7 может иметь и более краткий вид: =ЧПС(A1; A2:A5).
Такая запись соответствует синтаксическим стандартам Excel и позволяет сэкономить в ряде случаев и время, и нервы…
Итоговое значение (4110,00р) в денежном формате отображено во все той же ячейке A7.
Обязательно ВРУЧНУЮ проработайте приведенный выше пример.
Вы получите очень важный навык расчета реального финансового показателя – чистой приведенной стоимости – с помощью таблиц Excel.
Если вы планируете серьезно погрузиться в мир инвестиций, вам придется кое-что уметь и кое в чем разбираться.
Умение считать не на бумажке, а с использованием современного программного обеспечения – один из таких навыков.
Дополнительная информация по теме представлена в статье Расчет NPV в Excel (пример).
Удачных инвестиций!
На чтение 7 мин Просмотров 23.6к.
Приведенную стоимость рассчитывают с целью определения сегодняшней цены инвестиций, доход от которых будет получен в будущем периоде. То есть, показатель отражает текущую стоимость активов с учетом доходности.
Содержание
- Понятие приведенной стоимости
- Зачем рассчитывают приведенную стоимость
- Расчет приведенной стоимости
- Формула для вычисления приведенной стоимости
- Пошаговый алгоритм расчета приведенной стоимости
- Пример вычисления приведенной стоимости
- Альтернативные методы расчета приведенной стоимости
- Расчет приведенной стоимости в Excel
Понятие приведенной стоимости
Приведенная стоимость (далее ПД) представляет собой значение доходности вложений на сегодняшний день. Если говорить простыми словами, приведенная стоимость – это объем денежных средств, которые инвестор получит в будущем периоде, переведенный в стоимость на сегодняшний день.
Кроме понятия «приведенная стоимость», в экономике существует такой термин, как «чистая приведенная стоимость» (далее ЧПД). ЧПД – это совокупность финансовых оборотов от вложений, переведенных в стоимость на момент проведения анализа.
Чистая приведенная стоимость отличается от ПД тем, что при определении первого показателя учитываются первоначальные финансовые вложения. То есть, сумма, которую компания инвестировала для получения дохода, отнимается из будущей стоимости актива, приведенной к значению на сегодняшний день.
Зачем рассчитывают приведенную стоимость
Приведенную стоимость рассчитывают с целью определения объема денежных средств, которые инвестор получит в будущем в стоимостной оценке на дату проведения анализа. Например, сегодня компания вложила 1 млн. рублей в развитие проекта. Неизвестно, сколько предприятие получит от реализации программы. Однако данное значение можно вычислить при помощи формулы расчета приведенной стоимости.
Как правило, в будущем денежные средства имеют совсем иную цену, в сравнении с днем сегодняшним. А особенностью вычисления приведенной стоимости считается тот факт, что анализ отражает сумму дохода в стоимости на сегодняшний день. Для этого будущий доход дисконтируется.
Расчет приведенной стоимости
Расчет приведенной стоимости значительно отличается от вычисления будущей доходности. Для того, чтобы вычислить приведенную стоимость, для начала, необходимо найти будущую доходность. Именно от этой суммы отталкивается аналитик, производящий анализ. Будущая стоимость в дальнейшем приводится к сегодняшнему значению путем дисконтирования.
Важно! Результат расчета приведенной стоимости показывает не сумму средств, которую инвестор получит в будущем, а объем финансов, необходимых для инвестирования.
То есть, вычисляя показатель ПС, сначала нужно понять, сколько инвестор хочет заработать от вложений. Затем можно приступать к расчетам при помощи арифметической формулы. Итог анализа – это и есть сумма, которой компания должна располагать на сегодняшний день, чтобы получить задуманный объем дохода.
Формула для вычисления приведенной стоимости
Анализ приведенной стоимости строится на расчете показателя. Его вычисление реализуется при помощи формул. Вид арифметического выражения напрямую зависит от метода начисления процентов: простого или сложного:
- Метод простых процентов предполагает расчет приведенной стоимости в традиционном порядке. Объем ожидаемых доходов дисконтируют в обычном порядке.
- Прием сложных процентов предполагает присоединение суммы процентов прошлого периода к общему объему финансов. Данную операцию в экономической теории называют капитализацией.
В связи с этим, каждый период денежный поток, поддающийся дисконтированию, должен быть разным:
| Метод определения приведенной стоимости | Формула | Расшифровка формулы |
| Простые проценты | БС / (1 + СД)н | БС – будущая стоимость;
СД – ставка дисконтирования; Н – число периодов инвестирования |
| Сложные проценты | БС / (1 + СДп)н*м | БС – будущая стоимость;
СДп – ставка дисконтирования за период; Н – число периодов инвестирования; М – число капитализаций в год |
Важно! Оценивая результаты расчета приведенной стоимости методом простых и сложных процентов, нужно опираться на наименьший результат. Это означает, что для получения одной и той же суммы дохода компании придется вложить меньше собственных средств.
Кроме ПС, можно определить показатель чистой приведенной стоимости. Вычисления проводятся также при помощи формулы:
(БС / (1 + СД)н) – ПИ,
где БС – будущая стоимость (предполагаемый доход);
СД – ставка дисконтирования (процентная ставка по договору);
Н – число периодов инвестирования;
ПИ – объем первоначальных вложений.
Таким образом, чистая приведенная стоимость — это ПС за исключением суммы инвестирования в проект.
Пошаговый алгоритм расчета приведенной стоимости
Для расчета ПС рекомендуется использовать пошаговую инструкцию, которая поможет избежать ошибок:
- Определяем период инвестирования. То есть, промежуток времени, через который инвестор планирует получить определенный доход.
- Вычисляем объем прибыли от инвестирования при условии соблюдения договора. Обычно показатель берется из документации по планированию.
- Находим ставку дисконтирования. Она определяется путем деления процентной ставки доходности на 100. В случае применения методики сложных процентов, определяем число случаев капитализации за 1 год.
- Рассчитываем приведенную стоимость путем замены буквенных выражений формулы на соответствующие числовые значения.
Сам процесс вычисления не сложен. Труднее исключить допущение ошибок, так как будущую доходность принято считать путем сложения денежных потоков.
Пример вычисления приведенной стоимости
Приведем пример вычисления приведенной стоимости на основании следующих условий. Компания планирует получить доход 1 млн. рублей от помещения денежных средств на депозит сроком на 5 лет. Банк предлагает два варианта начисления процентов: сложный (12% годовых) и простой (10% годовых). Перед заключением договора необходимо выбрать оптимальный метод. Для этого рассчитывается приведенная стоимость приемом сложных и простых процентов.
В первую очередь, определим приведенную стоимость методом простых процентов:
1 млн. руб. / (1 + 0,1)5 = 951465, 68 руб.
Таким образом, чтобы через 5 лет получить доход в размере 1 млн. рублей под 10% годовых, необходимо вложить 951465, 68 рублей. Теперь найдем приведенную стоимость методом сложных процентов. Допустим, проценты начисляются каждый месяц, пополнений не предусмотрено:
1 млн. руб. / (1 + 0,12 / 12)5 * 12 = 550375,73 руб.
Получается, что вложив 550375,73 руб. под сложные проценты 12% годовых, через 5 лет компания сможет иметь доход 1 млн. рублей Таким образом, гораздо выгоднее поместить средства на депозит под сложные проценты, так как при условии получения одинакового дохода за аналогичный промежуток времени необходимо вложить гораздо меньше средств.
Чтобы рассчитать чистую приведенную стоимость, из ожидаемого дохода нужно отнять рассчитанный показатель ПС:
- ЧПС методом простых процентов: 1 млн. руб. – 951465,68 руб. = 48534,32 рубля;
- ЧПС методом сложных процентов: 1 млн. руб. – 550375,73 = 449624,27 рублей.
Таки образом, можно сделать вывод о том, что чистая приведенная стоимость методом сложных процентов гораздо выше, чем при альтернативном варианте.
Альтернативные методы расчета приведенной стоимости
Альтернативным методом расчета приведенной стоимости является автоматизированный прием, основанный на использовании специализированных программ. Существует масса сервисов, которые помогают безошибочно рассчитать показатель. Если подобных инструментов нет, можно использовать стандартный Excel.
Excel – это программа, входящая в стандартный пакет Microsoft Office. Сервис наделен множествами функций, которые позволяют безошибочно проводить расчеты в автоматическом режиме по заданным параметрам. Главная сложность использования Excel заключается в неумении пользователей применять встроенные сервисы.
Основным достоинством расчета приведенной стоимости в Excel является то, что программа имеет функцию вычисления данного показателя. Поэтому нет необходимости вводить формулу. Достаточно выбрать инструмент и выделить участвующие в расчете ячейки.
Расчет приведенной стоимости в Excel
Вычисление приведенной стоимости в Excel производится при помощи встроенного инструмента. Нет необходимости вводить сложные формулы. Достаточно выбрать опцию и отразить ячейки, принимающие участие в анализе. Определение ПС в Excel имеет следующий алгоритм:
- создаем таблицу (начиная с 4 и далее строки), состоящую из трех столбцов – период, сумма периода и приведенная стоимость;
- в ячейках первого столбца отражаем последовательность периодов, в ячейках второго – сумму денежных потоков;
- третий столбец посвящен приведенной стоимости по временным промежуткам;
- чуть выше таблицы, например, в первой строке, прописываем значение ставки дисконтирования, во второй – итоговое значение приведенной стоимости, но ячейка, посвященная результату показателя, будет пустой;
- итоговую приведенную стоимость также необходимо отобразить в заключительной ячейке столбца показателя;
- после того, как все данные введены, можно приступать к указанию формул.
Положительной особенностью Excel является тот факт, что программа имеет встроенный инструмент для расчета приведенной стоимости. Достаточно найти функцию и выделить ячейки, необходимые для расчета. Сама формула для вычисления и результат сформируются автоматически.
Важно! Для расчета чистой приведенной стоимости отражение временных промежутков нужно начинать с нулевого года с отрицательным значением суммы инвестиций.
В дальнейшем, автоматически сформированную формулу нужно видоизменить, добавив сумму ячейки первоначальных вложений. Конечный результат ПС должен быть всегда положительным.
Все ближе дата обязательного перехода на ФСБУ 25/2018. Учитывая разъяснения Минфина, переходить на него придется довольно большому числу участников рынка долгосрочной аренды и лизинга. В этой статье разберем особенности учета неоперационной аренды и лизинга у получателя таких услуг по ФСБУ 25/2018. Расчеты по приведенной стоимости для арендатора и лизингополучателя по ФСБУ 25/2018 с 2022 года для бухгалтерского учета аренды (лизинга) на примере и с формулами Excel.
Получатель лизинга или услуг по аренде должен применять в учете те же базовые принципы, что и тот, кто предоставляет объект в лизинг или аренду.
Подробно о том, зачем нужно отражение по дисконтированной стоимости, мы рассказали в первых разделах статьи: “ФСБУ 25/2018: расчеты по приведенной стоимости у арендодателя и лизингодателя с 2022 года и как удобнее считать в Excel“.
Рекомендуем арендаторам тоже ознакомиться.
Здесь же мы только сформулируем кратко, что должен показать пользователю отчетности по ФСБУ арендатор или лизингополучатель.
В отчетности нужно раскрыть, что взять объект в лизинг или аренду для арендатора выгоднее, чем взять кредит и купить такой же объект.
Из этого вытекают и все нюансы расчетов по ФСБУ 25/2018 для арендаторов и лизингополучателей.
Как определить ставку дисконтирования арендатору
Поскольку арендатор (далее будем понимать в широком смысле – как арендатора и по финансовой аренде, он же лизингополучатель) отталкивается от альтернативного варианта – взять кредит и купить аналог вместо аренды или лизинга – то и в качестве ставки дисконтирования ему достаточно взять ставку по банковским кредитам. Только следует помнить, что кредиты надо выбирать сопоставимые по сумме и сроку пользования объектом аренды (лизинга).
Если подобные привлеченные кредиты уже есть на момент заключения договора аренды – ставку надо брать по ним. Если своих кредитов нет – нужно взять те, которые можно было бы взять (например, в банках, в которых размещены счета, или в банках, которые специализируются на выдаче таких кредитов). О таких вариантах написано в п. 15 ФСБУ 25/2018.
Как посчитать первоначальную оценку обязательства по аренде
Обязательство по аренде у арендатора (лизингополучателя) представляет собой кредиторскую задолженность по уплате лизинговых платежей в будущем.
Первоначальная оценка обязательства (ПОО) – это суммарная дисконтированная стоимость платежей по договору на дату получения предмета лизинга (п. 10 и 14 ФСБУ 25/2018, п. 3 информационного сообщения Минфина России от 25.01.2019 № ИС-учет-15).
Для арендатора должно соблюдаться равенство:
ПОО = ПСЛП = СС предмета – Авансы (выплаченные) – НЛС
Где:
- ПСЛП – приведенная стоимость будущих лизинговых платежей;
- СС предмета – справедливая стоимость предмета аренды (стоимость покупки лизингодателем при лизинге);
- НЛС – негарантированная ликвидационная стоимость
Таким образом, первоначальную величину обязательства по лизингу можно рассчитать прямым путем (без дисконтирования будущих платежей) по формуле (п. 3 и 6 Рекомендации Р-65/2015-КпР “Ставка дисконтирования”):
ПОО = Стоимость приобретения предмета лизингодателем – Авансы
Напомним, что все значения фигурируют без НДС.
Если переход права собственности на предмет аренды не предусмотрен или неизвестна негарантированная ликвидационная стоимость, обязательство по аренде вычисляют как приведенную стоимость будущих лизинговых платежей.
ПОО = Н / (1 + r) + Н / (1 + r)2 + … + Н / (1 + r)t
Где:
- П – приведенная стоимость лизинговых платежей;
- Н – номинальная величина одного лизингового платежа без НДС;
- r – ставка дисконтирования за период;
- t – количество периодов до последнего платежа.
По сути предлагается каждый лизинговый платеж отдельно дисконтировать и сложить результаты.
Пример
Пусть заключен договор лизинга, по которому 01.01.2022 передан предмет. Лизингополучатель платит ежеквартально, в начале квартала. Для упрощения расчетов примем, что выкупной стоимости отдельно нет. По завершении договора предмет лизинга остается у лизингополучателя.
Лизингодатель купил предмет за 1 млн руб.
Лизингополучатель платит ежеквартально, до 5-го числа первого месяца квартала – 105 000 рублей.
Срок договора – 3 года.
(этот пример – зеркальный приведенному в статье про расчеты для лизингополучателя, на которую дана ссылка выше)
Лизингополучатель может последовать указаниям ФСБУ и действовать «прямым» методом – продисконтировать каждый платеж, взяв ставку дисконтирования по банковским кредитам.
Пусть ставка банков 11,5% годовых. Для дисконтирования ежеквартальных платежей ее нужно сделать ставкой для квартала:
11,5% / 4 = 0,02875
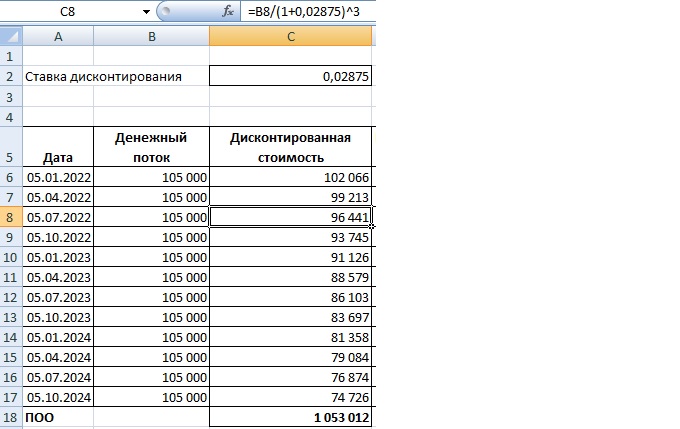
Далее вносим формулы в таблицу платежей в Excel.
Сумма, получившаяся по всем дисконтированным платежам, – это и есть первоначальная оценка обязательства по аренде.
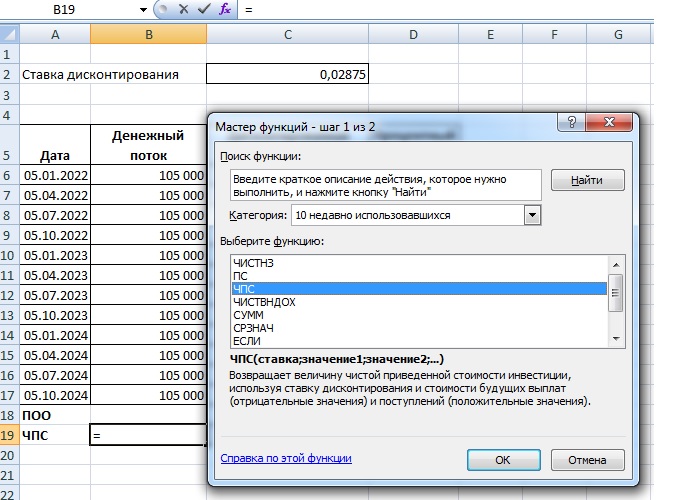
Есть возможность не вычислять ее по каждому платежу, а воспользоваться формулой ЧПС.
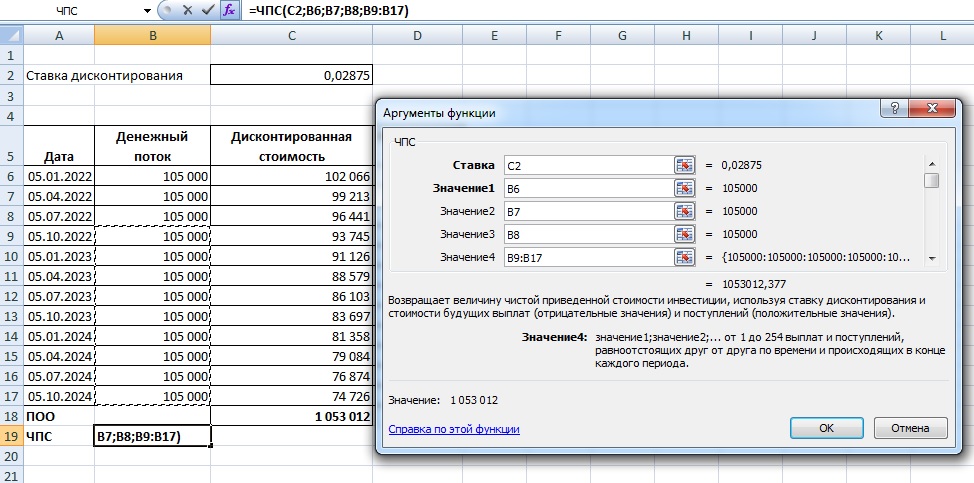
Обратите внимание, как вносить значения: первые 3 ячейки – первые 3 значения из списка, а далее можно вносить суммой, выделяя нужный диапазон.
Получившийся по ЧПС результат – тот же, что и при обсчете каждого платежа в отдельности.
Таким же образом можно обсчитать по ЧПС стоимость обязательства на любую конкретную дату, учитывая в формуле платежи, которые еще не уплатили.
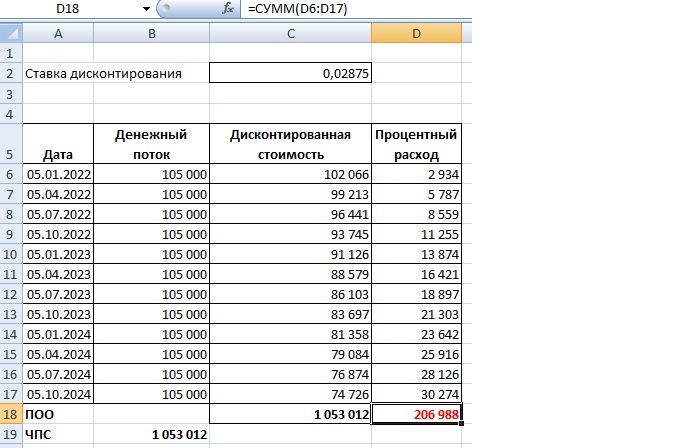
Из расчетов легко вычислить и процентный расход, подлежащий учету у арендатора.
У арендодателя сумма процентного дохода по примеру – 260 000 рублей.
У арендатора – 206 988 рублей. Остаток «уходит» в приведенную стоимость предмета аренды.
Именно так получают данные для сравнения. В нашем примере фактическая стоимость предмета у лизингодателя – 1 000 000, а для лизингополучателя после дисконтирования предмет стоит на 1 053 012 (есть переплата 53 012). Что как раз и покажет пользователю, что сделка для лизингополучателя невыгодна. И рациональнее было бы взять кредит у банка и купить аналогичный предмет.
Расчет величины права пользования активом
Получатель арендованного (лизингового) имущества объектом ОС его не признает. Вместо этого, по ФСБУ 25/2018 ему надо в активах в противовес обязательству по аренде признать право пользования активом (ППА).
ППА при этом тоже учитывают на счете 01 (отдельном субсчете) по фактической стоимости, которую формируют на счете 08.
В ППА включают (п. 13 ФСБУ 25/2018):
- ПОО (его мы уже научились определять);
- авансы по договору, перечисленные до даты получения предмета договора включительно;
- расходы, связанные с поступлением предмета и приведением его в состояние, пригодное для использования;
- оценочное обязательство в связи с предстоящими расходами на демонтаж предмета лизинга, его перемещение, восстановление окружающей среды, если возникновение такого обязательства обусловлено получением лизингового имущества.
Проще говоря, берем ПОО, корректируем на величину денег, которые к моменту передачи предмета уже уплачены, добавляем расходы, которые уже понесли или можем понести в будущем в связи с этим предметом. Получаем ППА для признания.
Напомним, что НДС везде исключают и в расчет берут только «чистые» суммы.
Подводим итоги
Арендатору для вычислений по ФСБУ 25/2018 достаточно знать банковскую ставку по кредиту, который он мог бы взять для покупки аналогичного объекта, и видеть условия договора.
Дисконтирует арендатор только поток своих будущих платежей по аренде. Для этого ему наиболее подходит формула ЧПС в Excel.
Приведенная стоимость — это текущая стоимость ожидаемого будущего потока денежных средств. Идея проста. Например, предположим, что вы стремитесь сэкономить 10 000 долларов на сберегательном счете через пять лет после сегодняшнего дня, а процентная ставка составляет 3% в год. Вам нужно будет выяснить, сколько нужно инвестировать сегодня или текущую стоимость. Формула для текущей стоимости: PV = FV ÷ (1 + r) ^ n; где FV — будущая стоимость, r — процентная ставка, а n — количество периодов. Используя информацию из приведенного выше примера, PV = 10 000 ÷ (1 + 0,03) ^ 5 или 8 626,09 долларов США, что является суммой, которую вам нужно будет инвестировать сегодня.
В Microsoft Excel есть встроенная функция для нахождения текущего значения с учетом необходимых аргументов. Например, если вы ожидаете, что через 10 лет на вашем банковском счете будет 50 000 долларов при процентной ставке 5%, вы можете рассчитать сумму, которую нужно было бы инвестировать сегодня для достижения этой цели. Используя Excel, введите «Год» в ячейку A1. В ячейке B1 введите количество лет, в данном случае 10. В ячейке A2 введите «Процентная ставка» и введите 5% в ячейку B2. Теперь в ячейке A3 введите «Будущая стоимость» и 50 000 долларов в ячейку B3. Встроенная функция PV может легко вычислить текущую стоимость с заданной информацией. Введите «Текущее значение» в ячейку A4, в ячейку B2 введите «= PV (B2, B1, 0, B3)». Поскольку промежуточных платежей нет, в качестве аргумента «pmt» используется 0. Приведенная стоимость рассчитана равной (30 695,66 долларов США), поскольку вам нужно будет положить эту сумму на свой счет; это считается оттоком денежных средств и поэтому отображается как отрицательный. Если будущая стоимость была показана как отток, тогда Excel покажет текущую стоимость как приток.
Расскажем простыми словами, что это такое NPV (Net Present Value). Покажем формулы и методы расчета чистой приведенной стоимости всех денежных потоков инвестиционного проекта с помощью ставки дисконтирования.
Откройте счет
в БКС Мир Инвестиций
Зачем нужно считать NPV (Net Present Value)
NPV (чистая приведенная стоимость) — это метод, который позволяет вычислить ожидаемую доходность с учетом изменения ценности денежных потоков (дисконтирования).
Финансовый показатель нужен для того, чтобы сопоставить будущую прибыль с текущими вложениями. Таким образом можно оценить, стоит ли инвестировать в тот или иной проект, окупятся ли вложенные средства и насколько вероятен риск убытков. Также с помощью NPV сравнивают инвестиционные проекты, чтобы выявить из них более привлекательный по критерию прибыльности.
Преимущества и недостатки подсчета чистой приведенной стоимости
Главное преимущество NPV состоит в том, что с помощью показателя можно произвести оценку инвестиционной привлекательности проекта. При расчетах допустимо учитывать дополнительные составляющие: срок жизни проекта и распределение денежных потоков во времени. Также одним из плюсов NPV является возможность складывать показатели различных проектов.
Основные недостатки NPV — это сложность расчетов и относительно низкая достоверность. Если говорить об ожидаемой прибыли, которую планирует получить инвестор, то показатель может отразить ее некорректно. Все дело в ряде факторов, влияющих на точность расчетов: например, ставка дисконтирования имеет свойство меняться, как и показатель инфляции. Эти риски можно принимать во внимание при проведении расчетов, но вместе с ними возрастает и сложность вычислений.
На практике организации чаще используют другой показатель для оценки проектов — IRR (внутренняя норма доходности). Он позволяет определить максимальную ставку кредита, которая позволительна для того, чтобы инвестиционный проект не был убыточным.
Формула расчета
Рассмотрим формулу, по которой можно рассчитать NPV:
где:
n — временной отрезок, за который производится расчет;
Pk — денежный поток за выбранный интервал времени;
i — ставка дисконтирования;
IC — капитал, вложенный на этапе первоначальных инвестиций.
Денежные потоки инвестиционного проекта
Денежные потоки — это разница между доходами и расходами компании или проекта.
Одним из самых сложных пунктов при расчете NPV является учет всей массы денежных потоков. Для этого необходимо соотнести размер первоначально вложенного капитала, а также ожидаемую прибыль и планируемые расходы в будущем.
Сложность состоит в том, что при подсчете денежных потоков следует учесть множество нюансов: экономическую ситуацию, наличие спроса, если ваш инвестиционный проект связан с производством, конкурентную составляющую и так далее.
Также необходимо произвести расчеты, которые связаны с потенциальными операционными расходами. В свою очередь, они напрямую зависят от ряда факторов: размера заработной платы сотрудников, занятых в проекте, стоимости сырьевого обеспечения, динамики курсов валют и других показателей.
Ставка дисконтирования простыми словами
Ставка дисконтирования — это инструмент для прогнозирования, который позволяет оценить доходность будущих инвестиций. При этом полученный результат выражается в текущей стоимостной величине.
Если говорить простыми словами, то ставка дисконтирования позволяет рассчитать стоимость будущего дохода по меркам настоящего времени. Это эталонная величина, которая используется для приведения будущих денежных потоков к одному знаменателю. Например, чтобы оценить, стоит ли инвестировать финансовые средства в тот или иной инструмент и какой доход он принесет в будущем по отношению к настоящему моменту.
Как рассчитать NPV
Рассмотрим, как рассчитать чистую приведенную стоимость, на примере. Допустим, капитал, инвестированный в качестве стартовых вложений, составит 500 тысяч рублей. Временной интервал, за который будут производиться вычисления, — 1 год. Также необходимо определить ставку дисконтирования: в нашем примере она будет равна 10% (показатель рассчитывается как коэффициент, поэтому его значение мы определим как 0,1). Дополнительно следует предположить, какой размер денежных поступлений планируется: например: 300 тысяч рублей.
300 000 ₽ / (1+0,1) – 500 000 ₽ = –227 273 ₽
В итоге мы получили число, которые выражает чистую прибыль за годовой период. Так как ниже нуля, то данный инвестиционный проект можно назвать убыточным на выбранном отрезке времени. Но если мы увеличим количество таких периодов, то получит другое значение.
Рассчитаем NPV за 3 года, учитывая, что в каждом из них ставка дисконтирования будет уменьшаться.
300 000 ₽ / (1+0,1) + 300 000 ₽ / (1+0,1)² + 300 000 ₽ / (1+0,1)³ + 300 000 ₽ / (1+0,1)⁴ – 500 000 ₽ = 518 952 ₽
Сумма, полученная в результаты вычислений, положительная, а это означает, что по прошествии трех лет данный инвестиционный проект окупится и будет приносить прибыль.
Пример расчета в MS Excel
Для быстроты и удобства можно также применить инструмент таблицы в MS Excel. Этот метод позволит не производить вычисления самостоятельно и поможет избежать возможных ошибок, возможных при расчетах вручную. Для начала заполните все поля таблицы необходимыми данными.
Затем используйте ЧПС — специальную функцию для вычисления NPV. Для этого в ячейку B10 необходимо добавить формулу, приведенную на картинке ниже.
Таблица произведет расчеты самостоятельно, и вы увидите результат в ячейке B10.
Полученная сумма в нашем примере отрицательное. Это значит, что инвестиционный проект невыгоден и не окупиться за 3 года.
Популярные ошибки при расчете
Игнорирование сопутствующих расходов
Допустим, инвестор планирует приобрести оборудование для производства автомобильных деталей и продавать их по определенной стоимости. В этом случае необходимо учесть расходы на износ и амортизацию оборудования, а это — дополнительные деньги в качестве трат. Если не учесть их при вычислении, NPV будет ошибочным;
Завышенные ожидания от проекта
При расчете NPV следует опираться на реалистичные прогнозы, ведь доходность зависит от множества факторов. Недальновидно ожидать, что приток пользователей вашего проекта будет динамично расти, а вместе с ним и размер прибыли. Ведь у каждого бизнеса есть периоды простоя: например, из-за фактора сезонности;
Некорректное значение ставки дисконтирования
Для расчета показателя используется ряд методов, каждый из которых учитывает различные исходные данные. Спустя некоторое количество времени значения могут меняться (например, уровень инфляции), соответственно, рассчитанная ранее чистая приведенная стоимость станет неактуальной.
Выводы для инвестора
Метод чистой приведенной стоимости используется, чтобы рассчитать ожидаемую доходность инвестиционного проекта и сроки его окупаемости;
Для вычисления NPV понадобится учесть ряд показателей: стартовый капитал, вложенный в проект в качестве персональных инвестиций, ставку. дисконтирования, временной отрезок и денежные потоки за выбранный период;
Для более корректного результата необходимо включить в расчете все предполагаемые риски, с которыми можно столкнуться в ходе проекта.
Инвестируйте из любой точки мира, покупайте и продавайте валюту по выгодному курсу, пользуйтесь умными подсказками и качественной аналитикой.
Приложение БКС Мир инвестиций
Отсканируйте QR-код и скачайте приложение
Прогноз цены: как применять технический и фундаментальный анализ рынка
Как составить личный финансовый план. Пошаговая инструкция