Может пригодиться в расчетах студентам и инженерам, сам я довольно часто использую некоторые из этих расчётов.

хоть бы намекнули в чем суть расчетов. а то качать и смотреть всем то не хочется 
Список вложенных файлов
___________________________
1. algebra.XLS Расчет квадратного уравнения несколькими способами
2. boltkruk.XLS Расчет прочности нагруженных болтовых соединений
3. circle.XLS Расчет параметров круга
4. dm1cepr.XLS Расчет цепной передачи по методике Чернавского
5. dm1cher.XLS Расчет червячного редуктора Чернавского
6. dm1klrem.XLS Расчет клиноременной передачи по методике Чернавского
7. dm1kon.XLS Расчет конического прямозубого редуктора по методике Чернавского
8. dm1kos.XLS Расчет цилиндрического косозубого редуктора по методике Чернавского
9. dm1plrem.XLS Расчет плоскоременной передачи по методике Чернавского
10. dm1podc.XLS Расчет подшипников цилиндрического редуктора по методике Чернавского
11. dm1porem.XLS Расчет поликлиновой передачи по методике Чернавского
12. dm1pr.XLS Расчет цилиндрического прямозубого редуктора по методике Чернавского
13. dm1privd.XLS Расчет КПД привода и мощности электродвигателя по методике Чернавского
14. dm1shpon.XLS Расчет прочности шпоночного соединения по методике Чернавского
15. dm1val1.XLS Предварительный расчет валов по методике Чернавского
16. dm2cher.XLS Расчет червячного редуктора по методике Дунаева
17. dm2kon.XLS Расчет конического прямозубого редуктора по методике Дунаева
18. dm2kos.XLS Расчет цилиндрического косозубого редуктора по методике Дунаева
19. dm2privd.XLS Расчет КПД и мощности электродвигателя по методике Дунаева
20. dm2shpon.XLS Расчет прочности шпоночного соединения по методике Дунаева
21. dm3podc.XLS Расчет подшипников цилиндрического редуктора по методике Шейнблита
22. dm3privd.XLS Расчет КПД и мощности электродвигателя по методике Шейнблита
23. dm4klrem.XLS Расчет клиноременной передачи по методике Эрдеди
24. dm4plrem.XLS Расчет плоскоременной передачи по методике Эрдеди
25. dm4shpon.XLS Расчет прочности шпоночного соединения по методике Эрдеди
26. dm5klrem.XLS Расчет клиноременной передачи по методике Иванова
27. dmmufta.XLS Расчет муфты
28. electro.XLS Электротехника — расчет сопротивления резистора
29. manyangl.XLS Геометрия — расчет многоугольников
30. mechanic.XLS Механика — расчет реакций опор
31. physic.XLS Физика — расчет движения тела, брошенного под углом к горизонту
32. piramida.XLS Геометрия — расчет пирамиды
33. plita.XLS Механика — расчет нагрузок кронштейновых и балочных конструкций
34. rezba.XLS Расчет резьбовых соединений
35. ring.XLS Геометрия — расчет кольца
36. romb.XLS Геометрия — расчет ромба
37. square.XLS Геометрия — расчет квадрата
38. svarka.XLS Расчет сварных соединений
39. vint4.XLS Расчет передачи винт-гайка
40. zaklepka.XLS Расчет клепаных соединений
___________________________________________________
Один файл
GPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Не могу отправить из-за ограничений размеров файлов, если Администратор мне поможет это исправить, то и его выложу.
Или предложите куда его выложить, чтобы смогли скачать.
Цитата: VIO от 22.03.08, 10:32:09
…
Один файлGPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Не могу отправить из-за ограничений размеров файлов, если Администратор мне поможет это исправить, то и его выложу.
Или предложите куда его выложить, чтобы смогли скачать.
Да хоть куда: _www.slil.ru например.
Пожалуйста, там он будет висеть 1 месяц
http://slil.ru/25613893
GPM.XLS Расчет узлов грузоподъемных машин по методике Казака
Расчёт для общего развития хороший 
Только жаль, что разбросан. Но это на мой вкус.
Не знаю что и предложить?
Может администратор, что предложит?
VIO
Спасибо за файлы!
Как я понял это из книги А.Дубина «Машиностроительные расчеты в среде Excel 97/2000»
Просто книга у меня есть, а дискету куда-то потерял.
Ещё раз спасибо!
Цитата: Игорьтек от 26.03.08, 14:15:41
VIO
Спасибо за файлы!
Как я понял это из книги А.Дубина «Машиностроительные расчеты в среде Excel 97/2000»
Просто книга у меня есть, а дискету куда-то потерял.
Ещё раз спасибо!
Правильно, купил думал освою VBA, но как-то времени не хватает.

Народ
Может кто обновит ссылку ?
Вы не могли бы залить все одним файлом
В том числе и самый большой ?
VIO!
Перезалейте, пожалуйста, GPM.XLS Расчет узлов грузоподъемных машин по методике Казака ( Расчет8.zip ), а то ссылки уже не работают.
- Форум пользователей ПО АСКОН
-
►
Профессиональные вопросы -
►
Конструирование -
►
Расчеты в Excel
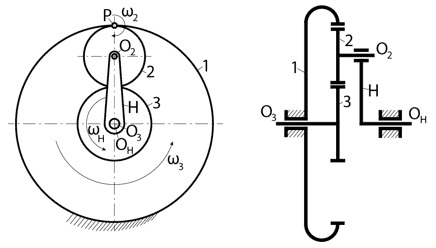
Добрый день, в данной статье я попытаюсь описать мой опыт и сформированный мной метод по разработке планетарного редуктора.
Недавно стал обладателем 3d-принтера Flsun QQ-S и начал потихоньку переводить пластик на всякие интересности и непотребства.
Как и у многих других посетителей сайта 3dtoday у меня периодически возникают вопросы: каковы пределы прочности пластика и что можно напечатать?
На одном из русскоязычных youtube-каналов нашел целый плейлист от пользователя, который на 3d-принтере распечатал лебедку, чтобы поднимать в гаражном погребе картошку и соленья с вареньями ссылка) И здесь возникает идея повторения данной самоделки от этапа конструирования, чтобы прокачать свои умения по моделированию, до печати и сборки изделия, с последующими испытаниями лебедки.
В данном абзаце необходимо немного отпрыгнуть в сторону и прояснить определенные моменты, которые привели к написанию данной статьи.
После покупки принтера возникает определенная коллизия, которую каждый решает для себя владелец 3d-принтера. В чем моделировать изделие? Если только для себя и друга, то один набор софта, а если попытаться окупить стоимость принтера или хотя бы пластика, то количество доступных вариантов резко сужается. Я имею ввиду пользоваться софтом согласно пользовательскому соглашению. А так хочется все же окупить свою игрушку)) И здесь стоит выбор между светлой и темной стороной силы. Для себя же я принял ключевое решение моделировать в только в лицензионном софте, т.е. софт должен предоставляться разработчиком или бесплатно, или оплачиваться в тех лимитах, в которых мне позволяет разгуляться жаба. Пользоваться коммерческим, платным софтом можно, но только в пределах ознакомительного периода и только для ознакомления, после чего программа будет удаляться.
В ходе перебора доступных решений на рынке, как отечественного, так и зарубежного производства, был выбран Fusion 360. Приходится признать, что Autodesk умеет подсаживать привлекать новых пользователей.
Теперь возвращаемся к лебедке, в данной лебедке используется несколько ступеней планетарного редуктора для понижения количества оборотов, выдаваемых двигателем с соответствующим увеличением вращающего момента на выходном валу.
Для того, чтобы начать конструировать планетарную передачу я исследовал глубины Fusion 360 для поиска функции, которая по заданным мной параметрам смоделирует и выведет в рабочую область уже готовую модель зубчатого зацепления. Наивный) Такая функция припасена для платных больших программ.
После чего я начал штудировать опыт более опытных товарищей, обитающих на этом сайте. В ходе изучения материалов, я сформировал для себя следующие выводы (если не прав, то поправьте меня):
-
в основном моделируются отдельные шестерни, которые печатаются;
-
моделирование происходит по принципу построения зуба и круговым массивом формируем контур шестерни, который затем выдавливается;
-
используются генераторы профиля шестерни в разнообразных редакторах, которые так же затем выдавливаются.
Исследовав генераторы, я пришел к любопытным выводам, что они или простые и бесплатные. или более-менее функциональные и стали платные (например https://geargenerator.com/). Причем последний, несмотря на свой неплохой функционал, не может сгенерировать необходимый мне планетарный редуктор.
Обобщив свой опыт и опыт многих других, установил, что для проектировании планетарного редуктора необходимо провести геометрический расчет редуктора (модуль, число зубьев элементов передачи, число сателлитов, делительные диаметры, проверка собираемости передачи). Причем свободного софта для расчета этих параметров, я не нашел. По просторам рунет ходит excel файл только для расчета цилиндрической передачи.
На основе чего возникла идея следующего алгоритма:
-
вычисляем геометрические параметры планетарного редуктора
-
на основе расчета во Fusion формируем шестерни
-
перемещаем их, как нам надо и используем их для моделирования изделия
-
профит
Теперь начинаем копать, как рассчитывается планетарный редуктор. Не буду утомлять подробностями, для расчета в excel подготовил небольшую табличку, которая помогает рассчитать зацепление. Для пользования табличкой необходимо в excel подключить надстройку ‘Поиск решения’.
Сразу пояснение, в текущем виде происходит подбор зацепления по передаточному соотношению и числу зубьев солнечной шестерни, если необходимо, чтобы число зубьев солнечной шестерни не менялось, то в инструкции (в файле указано, как это сделать)
Как ею пользоваться и весь алгоритм действий по созданию зацепления:
1. Открываем файл
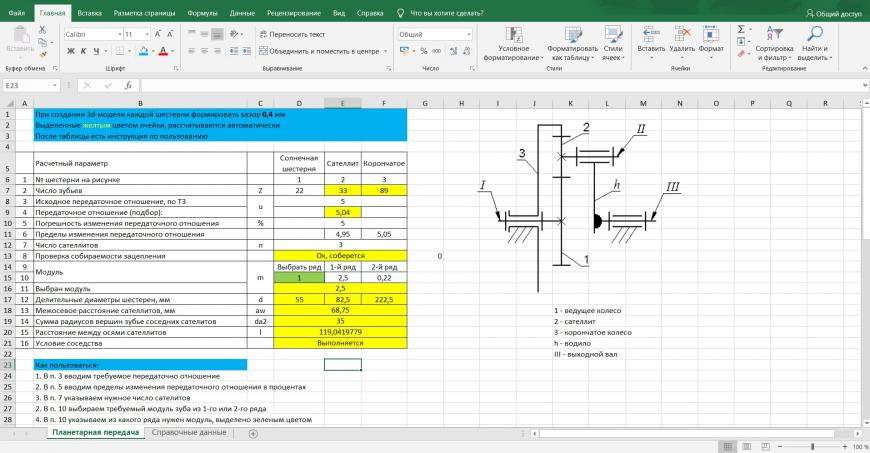
2. Согласно инструкции заполняем начальные условия
3. Вкладка ‘Данные’, вызываем ‘Поиск решения’, нажимаем ‘Найти решение’.
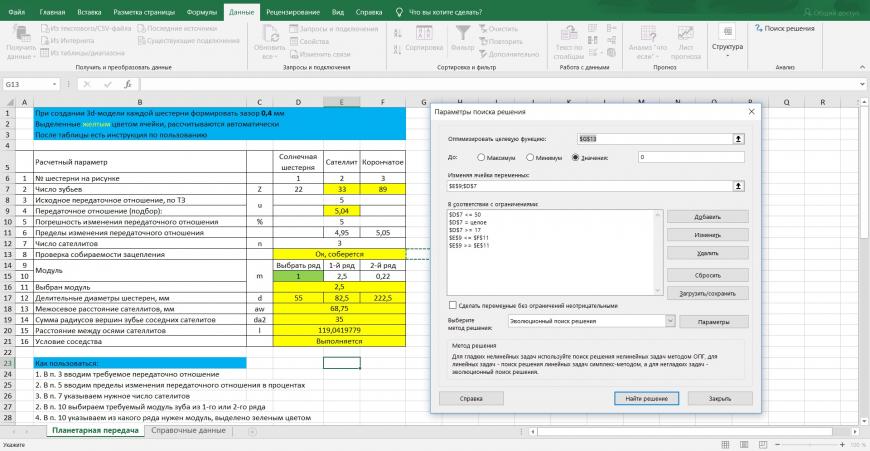
4. Получаем требуемые параметры. Нас здесь интересуют числа зубьев элементов передачи, число сателитов и межосевое расстояние сателлитов (это радиус, на котором располагаются оси сателлитов)
5. Открываем fusion и переходим во Fusion App-store, где ищем и устанавливаем следующие дополнения: Helical Gear и FM Gears
Фишка в чем, Helical Gear — дополнение, формирующее косозубые передачи, но в нем можно поставить угол наклона зубьев равный 0 и получить прямозубую передачу, а FM Gears позволяем сформировать корончатую передачу, так же в Helical Gear можно установить зазор зацепления, а в FM Gear нельзя.
6. Запускаем Helical Gear и окне заполняем параметры либо солнечной, либо сателлита Helix Angle — угол наклона зубьев — 0, Module
— модуль зацепления, Teeth — число зубьев по расчету, Gear Thickness — толщина зуба, здесь еще важен параметр Backlash — зазор зацепления ставим 0,4 мм. Ставим галочку Preview и видим нашу красивую шестеренку, затем жмем Ок и шестеренка создается в виде компонента в начале координат.
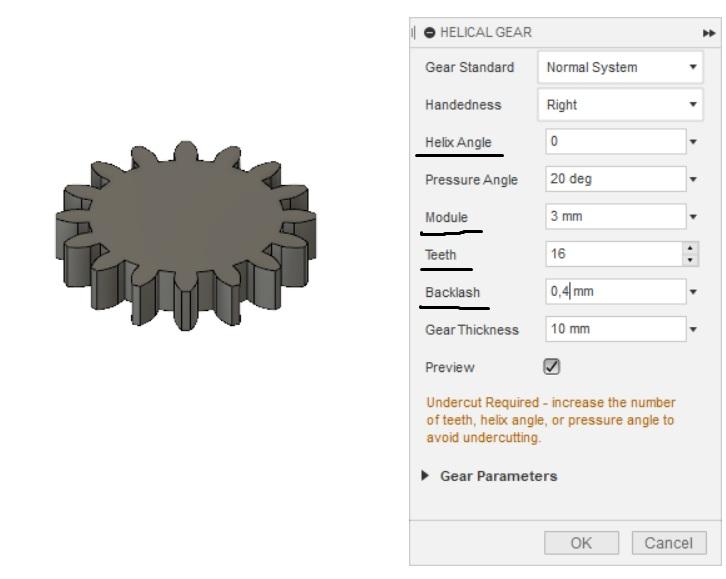
7. Такую операцию делаем и для другой шестерни, так же указываем зазор 0,4 мм.
8. Затем из размещаем в пространстве согласно назначению, солнечная в центре, сателлит на расстоянии радиуса сателлита
9. Создаем корончатую шестерню. Запускаем дополнение FM Gear и переходим на вкладку Internal Gear, заполняемые параметры аналогичны предыдущему дополнению, но здесь нет зазора и необходимо выставить наружный диаметр корончатой шестерни. Не волнуйтесь, если диаметр будет не соответствующий, то система выдаст предупреждение и тогда его надо будет просто увеличить. Жмем Ок и видим результат в виде созданного компонента.
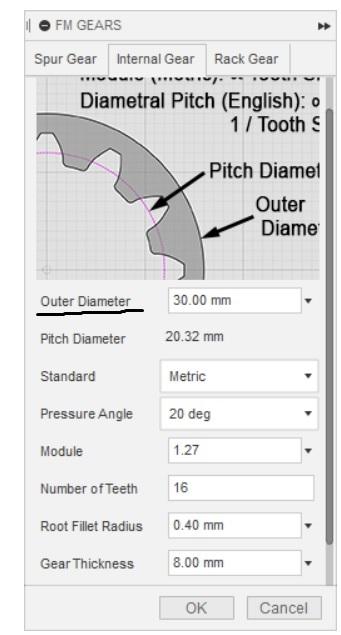
10. Обратите внимание, что шестерни после создания располагаются в перпендикулярных плоскостях, с центрами в начале координат. Поэтому поворачиваем их, как нам надо.

11. Создаем зазор в зацеплении корончатой шестерни, из опыта печати, без этого зазора шестерня не налезла на сателлиты)). Для этого раскрываем компонент корончатой шестерни, проще всего на плоскости шестерни создать новый эскиз спроецировать на него профиль зуба, затем командой Offset создать смещение на 0,4 мм, затем круговым массивом создать профиль шестерни и выдавить твердое тело.
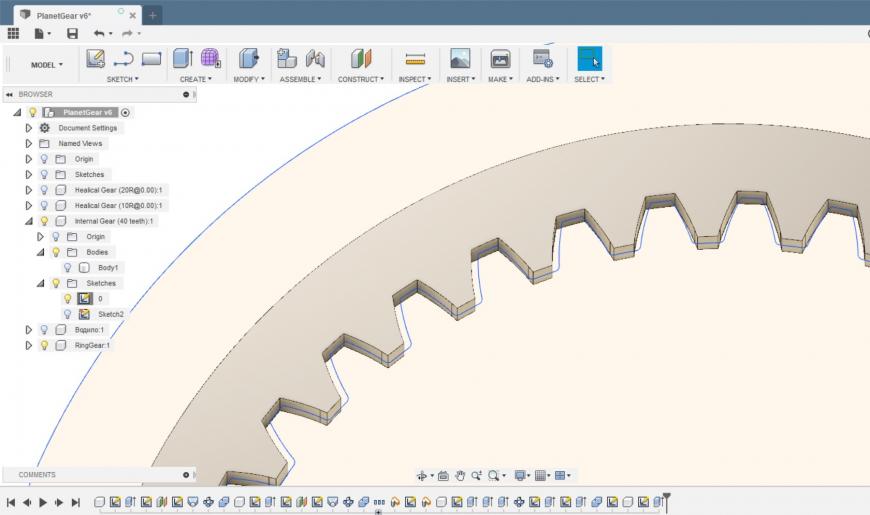
12. Можно дополнительно заморочиться и красиво повернуть шестерни, чтобы зубья не пересекались, но это уже для эстетов.
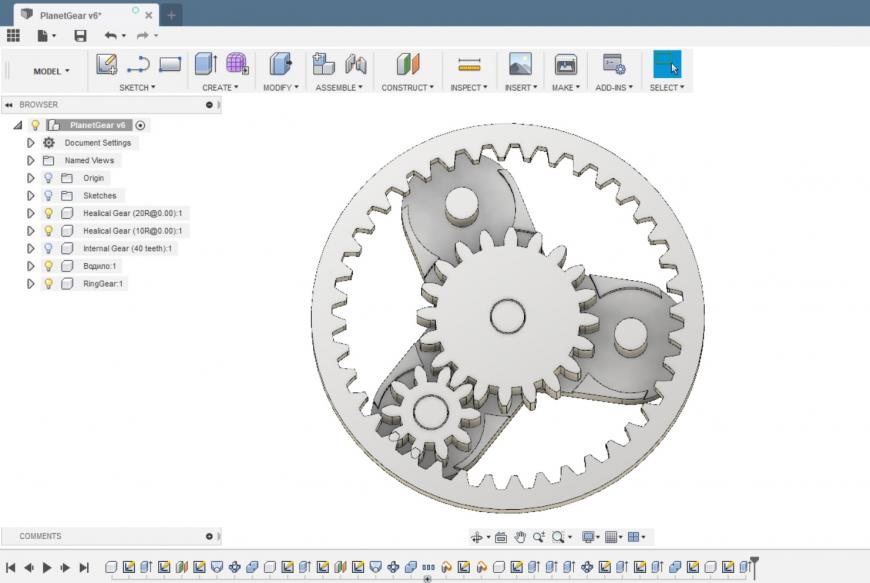
13. Дальше остается самое простое. Смоделировать водило, перегнать модели в STL и отправить их на слайсер.
Распечатываем и собираем зубчатое зацепление.

На фотографии планетарная передача, которая была рассчитана с помощью данной экселевской таблички и собрана по окончании печати.
Что сказать, зазоры между солнечной шестерней и сателлилами 0,4 каждое колесо оказался нормальный, между корончатой шестерней и сателлитом оказался великоват, т.к. при разработки я поставил смещение корончатой передачи 0,5 мм.
По итогу, данный способ создания планетарного зацепления имеем место быть. Так же я знаю, что взрослые пакеты умеют все это строить и рассчитывать в автоматическом режиме. Но, при подходе пользования только лицензионным софтом для проектирования и не тратиться лишнего на лицензии, он себя оправдывает. Если кто знает более простой метод создания планетарного редуктора, то дайте знать, буду рад ознакомиться и применять))
Далее в планах создания аналогичных табличек для расчета конической передачи и цилиндрической зубчатой передачи.
Файл экселя прилагаю. Только пока не знаю, как залить его на 3dtoday.
Планетарная передача — вид зубчатой передачи, применяемой в механических и автоматических трансмиссиях. Помимо преобразования вращения «планетарка» способна суммировать и раскладывать мощности. Зная о планетарном механизме: что это такое, как работает, по каким критериям оценивают редуктор, станет понятно устройство и характеристики АКПП. В случае поломки расчёт передачи поможет выбрать надёжный и долговечный механизм.
Планетарные зубчатые передачи
Общие сведения о планетарных передачах
Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.
Наибольшее распространение получила простая одинарная планетарная передача (рис. 1), которая состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального колеса 3 с внутренними зубьями; сателлитов 2 – колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (на рис. 1 число сателлитов с = 3), и водила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом. В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).
При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлитов 2 относительно собственных осей, а обкатывание сателлитов по колесу 3 перемещает их оси и вращает водило Н. Сателлиты таким образом совершают вращение относительно водила и вместе с водилом вокруг центральной оси, с. е. совершают движение, подобное движению планет. Поэтому такие передачи и называют планетарными.
При неподвижном колесе 3 движение передают чаще всего от колеса 1 к водилу Н, можно передавать движение от водила Н к колесу 1.
В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.
Разновидности планетарных передач
Существует много различных типов и конструкций планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную передачу, схема которой показана на рисунке 1. Эта передача конструктивно проста, имеет малые габариты. Находит применение в силовых и вспомогательных приводах. КПД планетарной передачи η = 0,96…0,98 при передаточных числах u = 3…8.
Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. На рис. 2,а планетарная передача составлена из двух последовательно соединенных однорядных планетарных передач. В этом случае суммарное передаточное число u = u1×u2 ≤ 64, а КПД равен η = η1×η2 = 0,92…0,96.
На рисунке 2, б показана схема планетарной передачи с двухрядным (двухвенцовым) сателлитом, для которой при передаче движения от колеса 1 к водилу Н при n4 = передаточное число определяется из зависимостей:
В этой передаче u = 3…19 при КПД η = 0,95…0,97.
Как упоминалось выше, планетарные передачи, у которых все звенья подвижны, называют дифференциальными или просто дифференциалами.
Неизбежные погрешности изготовления приводят к неравномерному распределению нагрузки между сателлитами. Для выравнивания нагрузки в передачах с тремя сателлитами одно из центральных колес выполняют самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения. Высокие требования предъявляются к прочности и жесткости водила, при этом его масса должна быть минимальной. Обычно водила выполняют литыми или сварными.
Достоинства и недостатки планетарных передач
Основными достоинствами планетарных передач являются:
Не лишены планетарные передачи и недостатков:
Область применения планетарных передач
Планетарные передачи применяют как редукторы в силовых передачах и приборах, в коробках передач автомобилей и другой самоходной техники, при этом передаточное число такой КПП может изменяться путем поочередного торможения различных звеньев (например, водила или одного из колес), в дифференциалах автомобилей, тракторов и т. п.
Широкое применение планетарные передачи нашли в автоматических коробках передач автомобилей благодаря удобству управления передаточными числами (переключением передач) и компактности. Можно встретить планетарные передачи и в механизмах привода ведущих колес современных велосипедов. Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор, мотор-колесо).
Передаточное число планетарных передач
Здесь существенное значение имеет знак передаточного числа. Передаточное число считают положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 1 имеем:
где z – числа зубьев колес.
В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1.
В качестве примера определим передаточное число для планетарной передачи, изображенной на рис. 1, при передаче движения от колеса 1 к водилу Н. Мысленная остановка водила в этой передаче равноценна вычитанию его частоты nН из частоты вращения колес. Тогда для обращенного механизма этой передачи имеем:
Для планетарной передачи, у которой колесо 3 закреплено в корпусе неподвижно ( n3 = ), колесо 1 является ведущим, а водило Н – ведомым. Тогда получим передаточное число такой передачи:
Подбор чисел зубьев планетарных передач
В отличие от обычных зубчатых передач расчет планетарных начинают с подбора чисел зубьев на колесах и сателлитах. Рассмотрим последовательность подбора чисел зубьев на примере планетарной передачи, изображенной на рис. 1.
Число зубьев z1 центральной шестерни 1 задают из условия неподрезания ножки зуба: z1 ≥ 17. Принимают z1 = 24 при Н ≤ 350 НВ; z1 = 21 при Н ≤ 52 HRC и z1 = 17 при Н > 52 HRC.
Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу u :
Конструктивные особенности
Как поменять редуктор на ваз 2106
Основой любого редуктора является зубчатое зацепление, передающее вращательный момент и изменяющее число оборотов вала. Для цилиндрических зацеплений характерна возможность вращаться в обе стороны. При необходимости ведомый вал с колесом подключается к двигателю и становится ведущим. Они в данной конструкции расположены параллельно, горизонтально и вертикально. Устройство цилиндрических редукторов может быть самое разное, но оно обязательно включает в свою конструкцию:
- ведущий;
- ведомый вал;
- шестерню;
- колесо;
- подшипники;
- корпус;
- крышки;
- систему смазки.
В простейшем одноступенчатом редукторе одна пара находится в зацеплении – шестерня и колесо. Если ступеней 2 и больше, соответственно увеличивается количество деталей. Появляются промежуточные оси. Для изменения направления вращения, в кинематическую схему включают паразитку, промежуточную шестерню с количеством зубьев как у ведущей.
Корпус и крышка отливаются из чугуна или делаются сварными из низкоуглеродистого листа толщиной 4 – 10 мм в зависимости от габаритов и мощности узла. Сварными делают маленькие редуктора. Остальные имеют крепкий литой корпус.
Характеристика цилиндрических редукторов
Количество зацеплений, тип зуба и взаимное расположение валов для всех видов оборудования описывает ГОСТ Редукторы цилиндрические. В нем указаны типоразмеры всех деталей, которые могут применяться в цилиндрических редукторах при различных количествах ступеней. Максимальное передаточное число одной пары 6,5. Общее многоступенчатого редуктора может быть до 70.
Больше чем у цилиндрического редуктора может быть передаточное число у червячной передачи,оно может достигать 80. При этом они компактные, но используются редко из-за низкого КПД. У цилиндрических одноступенчатых редукторов КПД 99 – 98%, самый высокий из всех видов передач.Отличаются червячные и цилиндрические редукторы расположением валов. Если у цилиндрических они параллельные, то червяк располагается к колесу под углом. Следовательно валы ведущий и ведомый выходят из перпендикулярно расположенных боковых стенок корпуса.
Для смазки достаточно залить масло в поддон, чтобы нижние шестерни в него частично погрузились. При вращении зубья захватывают масло и разбрызгивают его на другие детали.
Проектирование и порядок расчета
Расчет будущего редуктора начинается с определения передаточного момента и подборки его из нормированных пар. После этого уточняются диаметры деталей и межосевое расстояние валов. Составляется кинематическая схема, определяется оптимальная форма корпуса и крышки, номера подшипников. В сборочный чертеж входит кинематическая схема двухступенчатого редуктора, система смазки и способы ее контроля, типы подшипников и места их установки.
ГОСТ 16531-83 описывает все возможные виды и типоразмеры зубчатых колес, которые могут применяться в цилиндрических редукторах с указанием модуля, количества зубьев и диаметра. По размеру шестерни подбирается вал. Его прочность рассчитывается с учетом вращательного момента на скручивание и изгиб. Определяется минимальный размер, умножается на коэффициент прочности. Затем выбирается ближайший больший нормализованный размер вала. Шпонка рассчитывается только на срез и подбирается аналогично.
По диаметру вала выбирается подшипник. Его тип определяется направлением зуба. При косозубой передаче ставят упорные, более дорогие. Прямозубая передача не нагружает их в осевом направлении, и однорядные шарикоподшипники работают по несколько тысяч часов.
Схема сборки указывается на чертеже внизу и подробно расписывается в технологической документации, которая выдается в производство вместе с чертежами. На главном чертеже с общим видом в таблице указываются технические характеристики редуктора, которые затем переносятся в паспорт:
- количество ступеней;
- передаточное число;
- число оборотов ведущего вала;
- мощность на выходе;
- КПД;
- габариты;
- вес.
Дополнительно могут указываться вертикальное расположение зацепления, направление вращение вала и способ установки: фланцевый или на лапах.
Планетарные редукторы.
Редукторы с зубчатыми передачами, в которых имеются колеса с перемещающимися осями, называются планетарными. Планетарные передачи позволяют получить большие передаточные числа редукторов при малом числе зубчатых колес. Габариты планетарных редукторов меньше, чем габариты обычных редукторов при одинаковых передаточных числах и нагрузках. Планетарные передачи несколько сложнее в изготовлении.
K FL — коэффициент долговечности:
NFе — эквивалентное число циклов напряжений:
где KFej — коэффициент приведения переменного режима работы к постоянному.
K FС — коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При нереверсивной (односторонней) нагрузке 3, с. 15 K FС = 1 . При реверсивной симметричной нагрузке:
где г FС — коэффициент, учитывающий влияние химико-термической обработки.
В соответствии с [11 табл. 13] и для солнечной шестерни и для сателлита:
Определяем уFPj по формуле (2).
3.2 Определяем межосевое расстояние между солнечным колесом и сателлитом
Кинематические схемы планетарных редукторов.
Планетарные передачи с одновенцовыми (рис. 1 ) и двухвенцовыми (рис. 3) сателлитами, а также многоступенчатые передачи (рис. 2) имеют средние передаточные числа (2…30) и высокий КПД (0,9…0,97).
Одноступенчатый планетарный редуктор.
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, водило Н — ведомое. Центральное колесо 3 закреплено в корпусе.
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 1.
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, водило Н2 — ведомое. Центральные колеса 3 и 6 закреплены в корпусе.
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 2.
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, водило Н — ведомое. Центральное колесо 4 закреплено в корпусе. Колеса 2 и 3 жестко соединены между собой.
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 3.
Рис. 4
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, центральное колесо 5 — ведомое. Центральное колесо 3 закреплено в корпусе, колеса 2 и 4 жестко соединены между собой.
Ведущий и ведомый валы вращаются при D5 D3 — в противоположные стороны.
Планетарные передачи с тремя центральными колесами (рис. 4) имеют большие передаточные числа (100… 200). С увеличением передаточного числа КПД резко снижается.
Двухступенчатый планетарный редуктор с кривошипом.
Планетарные передачи с кривошипами (рис. 5,6) имеют большие передаточные числа (100…200), но сравнительно низкие КПД.
Рис. 5
Валы расположены параллельно установочной плоскости корпуса.
Водило Н — ведущее, центральное колесо 4 — ведомое. Центральное колесо 2 закреплено в корпусе, колеса 1 и 3 жестко соединены между собой.
Ведущий и ведомый валы вращаются при D3 D2 — в противоположные стороны.
Одноступенчатый планетарный редуктор с кривошипом.
Рис. 6
Валы расположены параллельно установочной плоскости корпуса.
Водило Н — ведущее, вал с кривошипами К — ведомый. Центральное колесо 2 закреплено в корпусе.
Ведущий и ведомый валы вращаются в разные стороны.
Износ
Что касается срока службы и амортизации, то в линейных механизмах планетарных систем распределение нагрузки заметно среди основных компонентов.
Термическая и циклическая усталость могут повышаться в них за счет ограниченного распределения нагрузки и того факта, что планетарные передачи могут вращаться довольно быстро по их осям. Более того, при высоких скоростях и передаточных отношениях планетарного механизма, центробежные силы могут значительно увеличить величину движения. Также следует заметить, что по мере снижения точности производства и увеличения количества сателлитов тенденция к дисбалансу возрастает.
Эти устройства и их системы могут даже подвергнуться износу или амортизации. Некоторые конструкции будут чувствительны даже к небольшим дисбалансам и способны потребовать качественные и дорогие компоненты сборки. Точным расположением планетных штифтов вокруг оси солнечной шестерни может быть ключ.
Другие схемы планетарных механизмов, которые помогают балансировать нагрузки, включают использование плавающих подузлов или «мягких» креплений, чтобы обеспечить максимально долговечное движение солнца или эпицентра.
Планетарный редуктор: принцип работы, характеристики и разновидности этого устройства
Двухступенчатый планетарный редуктор представляет собой конструкцию, составленную из шестеренок и других рабочих элементов, которые приводятся в движение посредством зубчатой передачи. При этом двигаются они по принципу, который заложен в механике вращения планет – вокруг одного центра. По этой причине центральная шестерня именуется «солнечной», промежуточные — «сателлитами», а внешняя с внутренним зубчатым сцеплением — «коронной». Кроме этого, самый простой планетарный редуктор состоит из водила. Оно предназначено для фиксации сателлитов относительно друг друга, чтобы они двигались вместе.
Степени свободы
Так называется совокупность координат вращения, позволяющая определить положение системы в пространстве в данный момент времени. Фактически каждый планетарный механизм имеет степеней свободы не менее двух. То есть угловые скорости вращения любого звена в таких устройствах не связаны линейно, как в других зубчатых передачах. Это позволяет получать на выходе угловые скорости не такие, какие есть на входе. Объяснить это можно тем, что в дифференциальной связи в планетарном механизме находятся три элемента в любом ряду, а остальные будут связаны с ним линейно, посредством какого-либо одного элемента ряда. Теоретически можно создать планетарные системы с тремя и более степенями свободы. Но на практике они оказываются неработоспособными.
Назначение и конструкция редуктора
Служит редуктор для обеспечения понижения передачи и при этом повышения силы крутящего момента. Для обеспечения работы этого механизма вращающийся вал присоединяется к его ведомому элементу.
Это устройство в классическом исполнении состоит из червячных или зубчатых пар, центрирующих подшипников, различных уплотнений, сальников и т.д. Примером планетарного редуктора является шариковый подшипник. Корпус устройства сложен из двух элементов:
Смазка всех составных элементов этого устройства производится путем разбрызгивания масла, но в некоторых особенных устройствах это осуществляется при помощи масляного насоса в принудительном порядке.
Принцип работы
То, как будет функционировать этот агрегат зависит от кинематической схемы привода. Так подводку вращательного движения можно осуществлять к любому элементу этой системы, а снятие производить с какого-либо из оставшихся. Передаточное число зависит от того, согласно какой схемы организована подводка и съем вращательного движения.
Понимание того, как работает подобный редуктор, позволяет оценить сложность ремонта и восстановления.
Разновидности планетарных редукторов
В зависимости от количества ступеней, которые они имеют планетарные редукторы подразделяют на:
Одноступенчатые более простые и при этом компактнее, меньше по размерам в сравнении с многоступенчатыми, обеспечивают более широкие возможности по передаче крутящего момента, достижения разных передаточных чисел. Обладающие несколькими ступенями являются достаточно громоздкими механизмами, при этом диапазон передаточных чисел, которые ими могут быть обеспечены, существенно меньше.
В зависимости от сложности конструкции они могут быть:
Кроме этого, планетарные редукторы в зависимости от формы корпуса, используемых элементов и внутренней конструкции могут быть:
Через них может передаваться движение между параллельными, пересекающимися и перекрещивающимися валами.
Расположение элементов
Самая простая форма планетарного механизма включает в себя три комплекта передач с разной степенью свободы. Указанные выше сателлиты вращаются вокруг своих осей и одновременно вокруг солнца, остающегося на месте. Эпицикл связывает планетарный механизм снаружи и тоже вращается посредством поочередного сцепления зубьев (его и сателлитов). Такая конструкция способна в одной плоскости изменять крутящий момент (угловые скорости).
В простом планетарном механизме может вращаться солнце и сателлиты, а эпицентр оставаться фиксированным. В любом случае, угловые скорости всех составляющих не хаотичны, а имеют линейную зависимость друг от друга. По мере поворота носителя, обеспечивается низкоскоростной выход с высоким крутящим моментом.
То есть суть планетарной передачи заключается в том, что такая конструкция способна изменять, раскладывать и складывать крутящий момент и проводимую угловую скорость. Вращательные движения при этом происходят в одной геометрической оси. Устанавливается необходимый элемент трансмиссии различных транспортных средств и механизмов.
Характеристики основных разновидностей этого устройства
Цилиндрические
Самые распространенные. Коэффициент полезного действия этих устройств достигает 95%. Они могут обеспечивать передачу достаточно больших мощностей. Передача движения осуществляется между параллельными и соосными валами. Они могут оснащаться прямозубными, косозубными и шевронными зубчатыми колесами. Коэффициент передачи может колебаться в пределах от 1,5 до 600.
Конические
Такое название они носят потому, что в них используются шестеренки, которые имеют коническую форму. Это обеспечивает плавность сцепки и способность выдерживать достаточно большие нагрузки. Могу иметь одну, две и три ступени. Валы в этой разновидности редукторов могут располагаться как горизонтально, так и вертикально.
Волновые
Они представляют собой конструкцию с гибким промежуточным числом. Состоят они из генератора волн, эксцентрика или кулачка, который обеспечивает растяжение гибкого колеса до достижения его контакта с неподвижным. При этом гибкое колесо имеет наружные зубья, а неподвижное — внутренние.
К достоинствам такого типа редукторов относится:
Они могут быть одно- и многоступенчатыми. Высокоскоростные оснащены подшипниками скольжения, а низкоскоростные — подшипниками качения.
Сайт использует cookie-файлы, для наилучшего представления содержимого сайта.
Подробнее…


Проектирование планетарного механизма
Исходные данные
Передаточное отношение*:
Количество сателлитов:
Допустимая погрешность, %:
Число решений:
Однорядный
Двухрядный
смешанное зацепление
Двухрядный
два внешних зацепления
Двухрядный
два внутренних зацепления
Введите код:
Подтвердите, что вы не робот.
* Передаточное отношение указывается в сторону повышения.
Ограничения передаточных отношений и механический КПД каждого планетарного редуктора размещены в таблице.
Пример проведения расчета
Расчет зубчатой передачи
Опубликовано 22 Июн 2013
Рубрика: Механика | 118 комментариев

…тип передачи (прямозубая, косозубая или шевронная), вид передачи (с внешним зацеплением или внутренним), график нагрузки (режим работы – доля времени действия максимальных нагрузок), материал и термообработку шестерни и колеса, схему расположения передачи в редукторе и в общей схеме привода.
На основании вышеперечисленных исходных данных при помощи многочисленных таблиц, разнообразных диаграмм, коэффициентов, формул определяются основные параметры зубчатой передачи: межосевое расстояние, модуль, угол наклона зубьев, число зубьев шестерни и колеса, ширины зубчатых венцов шестерни и колеса.
В детальном алгоритме расчетов — около пятидесяти смысловых программных шагов! При этом часто при работе приходится возвращаться на несколько шагов назад, отменять принятые ранее решения и вновь двигаться вперед, понимая, что, возможно, придется вновь вернуться. Найденные в результате такой кропотливой работы расчетные значения межосевого расстояния и модуля необходимо в конце расчетов округлить до ближайшего большего значения из стандартизованного ряда…
То есть, считали-считали, а в конце — «бац» — и просто на 15…20% результаты увеличили…
Студентам в курсовом проекте по «Деталям машин» такой расчет делать нужно! В реальной жизни инженера, я думаю, это не всегда целесообразно.
В предлагаемой вашему вниманию статье я расскажу как быстро и с приемлемой для практики точностью выполнить проектировочный расчет зубчатой передачи. Работая инженером-конструктором, я довольно часто применял изложенный ниже алгоритм в своей работе, когда не требовалась высокая точность прочностных расчетов. Так бывает при единичном изготовлении передачи, когда проще, быстрее и дешевле спроектировать и изготовить зубчатую пару с некоторым излишним запасом прочности. Используя предлагаемую программу расчета, можно легко и достаточно быстро проверить результаты, полученные, например, с помощью другой аналогичной программы или убедиться в правильности «ручных» расчетов.
По сути, данная статья является в какой-то мере продолжением темы, начатой в посте «Расчет привода тележки». Там результатами расчета были: передаточное число привода, статический момент сопротивления движению, приведенный к валу колеса и статическая мощность двигателя. Для нашего расчета они будут частью исходных данных.
Проектировочный расчет цилиндрической зубчатой передачи будем выполнять в программе MS Excel.
Начинаем. Обращаю ваше внимание, что материалом для всех зубчатых колес выбираем Сталь40Х или Сталь45 с твердостью HRC 30…36 (для шестерни – «потверже», для колеса – «помягче», но в этом диапазоне) и допустимыми контактными напряжениями [σH]=600МПа. В практике – это наиболее распространенный и доступный материал и термообработка.
Расчет в примере будет выполнен для косозубой передачи. Общая схема зубчатой передачи изображена на представленном далее рисунке.
Запускаем Excel. В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные и уточненные пользователем (принятые) расчетные данные. В ячейках со светло-желтой заливкой считываем результаты расчетов. В ячейках со светло-зеленой заливкой помещены мало подверженные изменениям исходные данные.
Заполняем ячейки исходными данными:
1. Коэффициент полезного действия передачи КПД (это КПД эвольвентного зубчатого зацепления и КПД двух пар подшипников качения) пишем
в ячейку D3: 0,931
2. Значение интегрального коэффициента K, зависящего от типа передачи (смотри примечание к ячейке D4), записываем
в ячейку D4: 11,5
3. Угол наклона зубьев (предварительный) bп в градусах выбираем из рекомендованного диапазона в примечании к ячейке D5 и вводим
в ячейку D5: 15,000
4. Передаточное число uп, определенное в предварительных расчетах, записываем
в ячейку D6: 4,020
5. Записываем мощность на быстроходном валу передачи P1 в Ваттах
в ячейку D7: 250
6. Частоту вращения быстроходного вала n1 в оборотах в минуту вводим
в ячейку D8: 1320
Программа расчета зубчатой передачи выдает первый блок расчетных параметров:
7. Вращательный момент на быстроходном валу T1 в Ньютонах умноженных на метр
в ячейке D9: =30*D7/(ПИ()*D8)=1,809
T1=30*P1/(3,14*n1)
8. Мощность на тихоходном валу передачи P2 в Ваттах
в ячейке D10: =D7*D3=233
P2=P1*КПД
9. Частота вращения тихоходного вала n2 в оборотах в минуту
в ячейке D11: =D8/D6=328
n2=n1/uп
10. Вращательный момент на тихоходном валу T2 в Ньютонах умноженных на метр
в ячейке D12: =30*D10/(ПИ()*D11)=6,770
T2=30*P2/(3,14*n2)
11. Расчетный диаметр делительной окружности шестерни d1р в миллиметрах
в ячейке D13: =D4*(D12*(D6+1)/D6)^0,33333333=23,427
d1р=K*(T2*(uп+1)/uп )^0,33333333
12. Расчетный диаметр делительной окружности колеса d2р в миллиметрах
в ячейке D14: =D13*D6=94,175
d2р= d1р*uп
13. Максимальный расчетный модуль зацепления m(max)р в миллиметрах
в ячейке D15: =D13/17*COS (D5/180*ПИ())=1,331
m(max)р=d1р/17*cos(bп)
14. Минимальный расчетный модуль зацепления m(min)р в миллиметрах
в ячейке D16: =D15/2 =0,666
m(min)р=m(max)р/2
15. Выбираем модуль зацепления m в миллиметрах из диапазона рассчитанных выше значений и из стандартизованного ряда, приведенного в примечании к ячейке В17 и записываем
в ячейку D17: 1,250
Далее в диалоговом режиме пользователя и программы определяем следующие основные параметры зубчатой передачи:
16. Расчетная ширина зубчатого венца колеса b2р в миллиметрах
в ячейке D18: =D13*0,6=14,056
b2р= d1р*0,6
17. Округляем ширину зубчатого венца колеса b2 в миллиметрах и вводим
в ячейку D19: 14,000
18. Программа определяет ширину зубчатого венца шестерни b1 в миллиметрах
в ячейке D20: =D19+4=18,000
b1=b2+4
19. Далее находится расчетное число зубьев шестерни z1р
в ячейке D21: =D13*COS (D5/180*ПИ())/D17 =18,1
z1р=d1р*cos(bп)/m
20. Округляем полученное выше значение числа зубьев шестерни z1 и записываем
в ячейку D22: 19
21. Далее по аналогии — расчетное число зубьев колеса z2р
в ячейке D23: =D22*D6 =76,4
z2р=z1*uп
22. Округленное число зубьев колеса z2 записываем
в ячейку D24: 77
23. Уточняем расчетом передаточное число (окончательное) u
в ячейке D25: =D24/D22=4,053
u=z2/z1
24. Рассчитываем отклонение передаточного числа окончательного от предварительного delta в процентах и сравниваем с допустимыми значениями, приведенными в примечании к ячейке D26
в ячейке D26: =(D25/D6-1)*100=0,81
delta=u/uп-1
25. Далее программа находит расчетное межосевое расстояние зубчатой передачи awр в миллиметрах
в ячейке D27: =D17*(D22+D24)/(2*COS (D5/180*ПИ())=62,117
awр=m*(z1+z2)/(2*cos(bп))
26. Округляем в большую сторону расчетное значение межосевого расстояния зубчатой передачи по стандартизованному ряду, приведенному в примечании к ячейке D28, и вводим окончательное межосевое расстояние aw в миллиметрах
в ячейку D28: 63,000
27. В завершение программа уточняет угол наклона зубьев зубчатой передачи b в градусах
в ячейке D27: =ЕСЛИ(D5=0;0;ACOS (D17*(D22+D24)/(2*D28))/ПИ()*180)=17,753
b=arccos(m*(z1+z2)/(2*aw))
Итак, мы выполнили по упрощенной схеме проектировочный расчет зубчатой цилиндрической передачи, целью которого было определение основных габаритных параметров на основе заданных силовых.
Далее конструктору для выполнения чертежей элементов передачи необходимо выполнить геометрический расчет зацепления. Но это, возможно, тема другого поста.
Ссылка на скачивание файла: raschet-zubchatoi-peredachi (xls 38,5KB).
Другие статьи автора блога
На главную


























