Создадим модель для определения оптимального размера партии товара, при котором общие переменные затраты минимальны. Затраты связаны с процедурой заказа и хранением партии на складе, и зависят от размера партии. Также учтем ограничение, связанное с размером склада. Расчет будем проводить с помощью надстройки Поиск решения. Для простейшего случая задачи приведем аналитическое решение.
Задача основана на EOQ-модели (Economic Order Quantity, Экономичный размер заказа). Сначала рассмотрим классическую EOQ-модель, затем добавим ограничение, связанное с размером склада и найдем решение с помощью
Поиска решения
. (пример с сайта
www.solver.com
)
EOQ-модель
Изделия на склад поступают регулярно одинаковыми партиями размера Q (в каждой партии Q изделий), а со склада выходят по одному изделию (продаются или запускаются в производство). Предполагается, что количество изделий на складе уменьшается равномерно от Q до 0, а затем, происходит мгновенное пополнение склада новой партией (на величину Q) и так несколько раз в течение года, где D – это величина годового спроса на изделия. Соответственно, пополнение происходит D/Q раз в год. В этой модели 2 источника затрат:
- затраты, связанные с процедурой закупки партии товара;
- затраты на хранение изделий на складе.
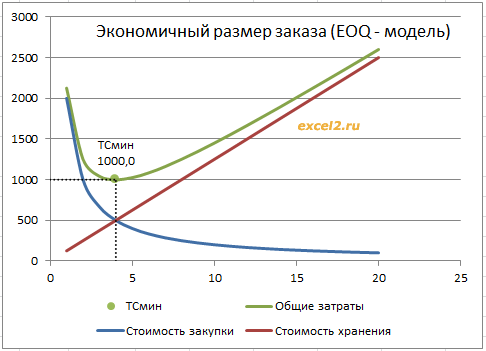
Стоимость процедуры закупки одной партии фиксирована и равна K, она включает затраты на погрузку, разгрузку, доставку и пр. Суммарная стоимость закупки всех партий в течение года =K*D/Q. Годовая стоимость хранения одного изделия =h (включает содержание склада, охлаждение, страховку и пр.). Среднее количество изделий, хранящееся на складе =Q/2 (т.к. количество равномерно убывает от Q до 0), годовая стоимость хранения изделий =h*Q/2. Обратим внимание, что чем больше размер партии Q, тем выше расходы на хранение (=h*Q/2), но меньше стоимость закупки (=K*D/Q). Для определения оптимального размера партии (Q*) существует аналитическое решение. Общие затраты на хранение и закупку (TC): TC=K*D/Q+h*Q/2
После дифференцирования по Q определим Q* — размер партии, при которой TC минимальны.
Q*=SQRT(2*D*K/h) — формула Уилсона. На рисунке ниже приведены графики стоимости закупки, стоимости хранения и суммарные затраты (см.
файл примера
).
К сожалению, рассмотренная модель зачастую не отражает более сложную окружающую нас действительность: спрос подвержен изменениям, время исполнения закупочной процедуры не постоянно, на складе оставляют некий переменный запас изделий и др. В следующей модели мы учтем ограниченность размера склада. Для определения оптимального размера партии в данном случае нельзя будет применить Формулу Уилсона, но задачу можно решить с помощью
Поиска решения
. Покажем, как это сделать.
EOQ-модель с ограничением по объему склада
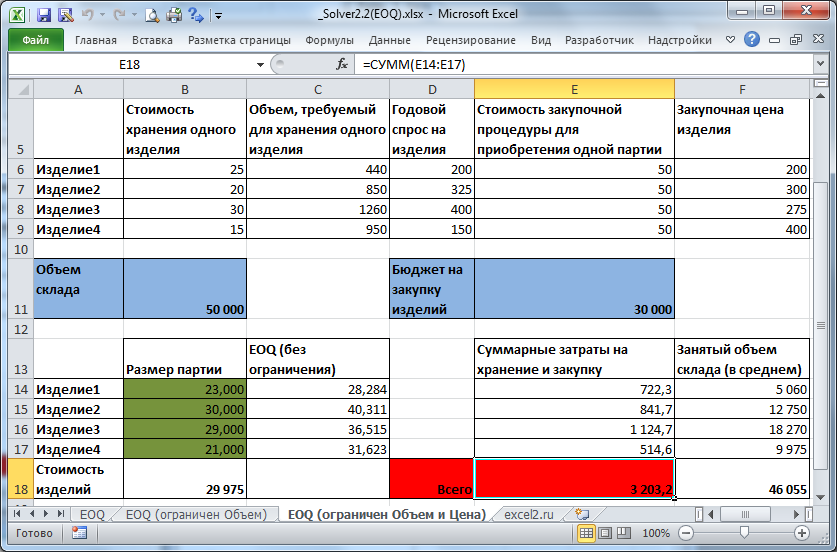
Усложним предыдущую задачу, добавив ограничение на объем склада, и рассмотрим поставку и хранение сразу 4-х разных изделий. У каждого изделия своя стоимость хранения и стоимость закупочной процедуры.
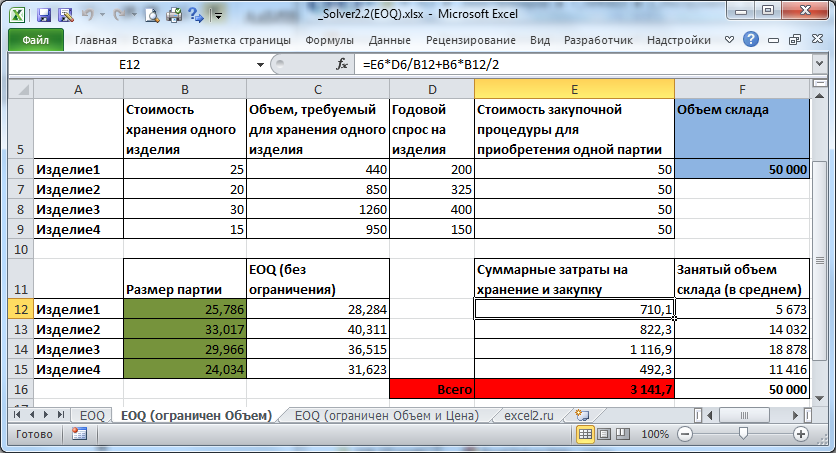
На рисунке ниже приведена модель, созданная для решения этой задачи (см.
файл примера, лист EOQ (ограничен объем)
).
Переменные (выделено зеленым)
. В качестве переменных модели следует взять количество изделий в партии (4 переменных для каждого изделия).
Ограничения (выделено синим)
. Объем склада не должен быть меньше, чем общий объем партий.
Примечание
. Т.к. партии разных изделий приходят независимо друг от друга и количество изделий равномерно убывает от Q до 0, то в среднем количество изделий, находящихся на складе, будет равно половине партии (это допущение необходимо для сравнения с EOQ моделью).
Целевая функция (выделено красным)
.
Общая стоимость закупки и хранения, д.б. минимальна.
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
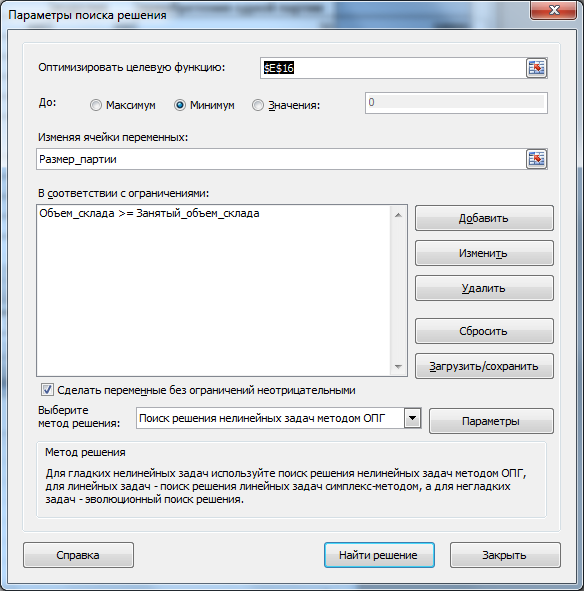
Обратите внимание, что модель не линейная: Целевая функция (TC) зависит от переменных (Q) по нелинейному закону: TC=K*D/Q+h*Q/2 Поэтому в окне
Поиска решения
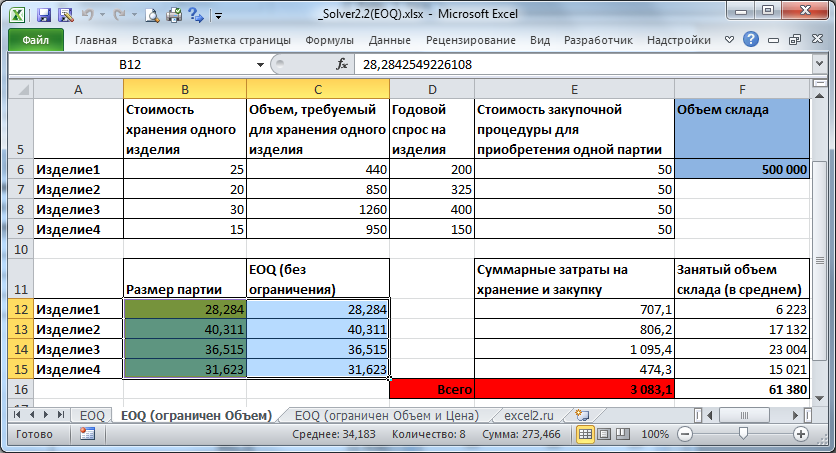
выберите метод для решения нелинейных задач. Формулы модели не должны содержать ошибок, поэтому не оставляйте ячейки переменных пустыми: в качестве начальных условий будут взяты 0 значения, что вызовет ошибку #ДЕЛ/0! Если ослабить ограничение (взять большой объем склада, скажем 500 000), то найденное решение будет близко или даже совпадать с расчетами, выполненными по Формуле Уилсона.
EOQ-модель с ограничением по объему склада и закупочной цене
Усложним предыдущую задачу, добавив ограничение на стоимость закупки изделий. Также потребуем, чтобы количество изделий в партиях было четным числом (см.
файл примера, лист EOQ (ограничен объем и цена)
).
В параметрах
Поиска решения
можно установить Целочисленную оптимальность =0. При Целочисленной оптимальности =5% решение начинает сильно зависеть от начальных условий (установите сначала переменные равным 1, затем =26). В первом случае будет найдено решение 23, 30, 30, 20, а во втором 24, 31, 30, 19. Дело в том, что целевая функция в обоих случаях будет отличаться совсем незначительно (гораздо менее 5%).
Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Лабораторная
работа Часть 1. Подбор параметра
Создайте таблицу
(цена и объем выбрать можете произвольно), а остальные столбцы рассчитайте по
формулам:
|
Курс |
55 |
|||
|
Наименование |
Цена в $ |
Объем заказа |
Сумма в $ |
Сумма в руб. |
|
оргтехника |
||||
|
ПК |
89 |
6 |
534 |
29 370,00 ₽ |
|
Ноутбуки |
69 |
10 |
690 |
37 950,00 ₽ |
|
Принтеры |
57 |
13 |
741 |
40 755,00 ₽ |
|
Ксероксы |
83 |
5 |
415 |
22 825,00 ₽ |
|
сканеры |
77 |
9 |
693 |
38 115,00 ₽ |
|
ИТОГО |
375 |
43 |
3073 |
169 015,00 ₽ |
Эта
таблица, в которой объемы заказов являются желаемыми. Видно, что итоговая сумма
169015,00 руб. Допустим у нас ограниченный бюджет на закупку оргтехники в
размере 150 000 руб. Возникает вопрос в том, что объем заказа нужно
сокращать.
Например, мы считаем
что для нас допустимым является уменьшить число принтеров. Чтобы автоматически
найти до какого количества можно сократить число принтеров, воспользуемся
«подбором» параметра.
Выделите ячейку с
объемом принтеров. Найдите функцию «подбор параметра» на вкладке «данные». Если
его нет, то через кнопку «Офис» и «параметры эксель» найдите эту функцию и
добавьте ее:
Далее запустив данную функцию увидите окно:
В котором нужно указать ячейку где
рассчитывается стоимость всего заказа. В поле «значение» установите значение
равное 150 000 (это помним ограничение по бюджету). Изменяемой ячейкой
естественно должна быть ячейка в которой указывает объем заказыаемых принтеров.
Нажмите Ок.
В итоге:
Видим, что число заказываемых принтеров 6.9,
следовательно не более 6 целых принтеров мы можем заказать , чтобы уложиться в
бюджет.
Задания. Теперь выполните подбор параметра для «курса валюты» при котором бы все
заявленные объемы могли быть приобретены в рамках данного бюджета в
150 000 руб. Также выполните подбор параметра для ячейки «цена ПК» при
которой можно было бы уложиться в указанный бюджет в размере 145 000 руб,
не изменяя исходных объемов заказа.
Часть
2. Расчет оптимальных значений (поиск оптимальных значений).
Необходимо решить задачу оптимизации. Возьмем
задачу линейного программирования, в которой есть целевая функция (критерий) Z, и три ограничения.
Условие
задачи: Завод производит два вида продукции:
велосипеды и мотоциклы. При этом цех по сборке велосипедов имеет мощность 100
тыс. штук в год, цех по сборке мотоциклов – 30 тыс. Одна группа механических
цехов завода может производить либо детали для 120 тыс. велосипедов, либо
детали для 40 тыс. мотоциклов, либо другую комбинацию деталей, ограниченную
этими данными. Другая группа механических цехов может выпускать детали либо для
80 тыс. велосипедов, либо для 60 тыс. мотоциклов, либо любую допустимую их
комбинацию. В результате реализации каждой тысячи велосипедов завод получает
прибыль в 2 тыс. рублей, а каждой тысячи мотоциклов – 3 тыс. рублей.
Математический
вид задачи:
,
.
В
качестве переменных задачи естественно взять количества велосипедов и
мотоциклов, выпускаемых заводом в год (в тыс. штук): и
.
В
екселе решение задачи будет выглядеть так:
В
итоге необходимо решить данную задачу средствами ексель. Воспользуемся
«надстройкой» называемой «поиск решения». «Поиск решения» должна быть во
вкладке «данные». Если ее нет. Установите ее, через кнопку «офис»-«параметры Ексель»-«надстройки». Здесь поиск решения будет
отображаться среди неактивных настроек:
Выберите ее и нажмите «перейти». Получим:
Выбираем «поиск решения». Ставим галочку и
нажимаем ОК. Далее происходит установка этой надстройки. Подождите.
Затем на вкладке данные появится возможность
вызвать данную функцию:
Запустите ее. Видим:
Здесь укажите тип задачи (максимизация или
минимизация) в нашем случае – максимизация примбыли, а в целевой ячейке,
укажите ячейку в которой рассчитывается целевая функция Z.
Это в нашем примере ячейка D1. В ней должна быть формула
для расчета целевой функции (обратите внимание, что она соответствует
математической записи задачи):
Где B4 и В5 это ячейки
для значений переменных х1 и х2:
Эти две ячейки (B4 и В5)
нужно указать здесь:
Далее в поле «Ограничение» указываем ячейки в
которых рассчитываются ограничения:
Формулы для ячеек с ограничениями:
Т.е. при добавлении ограничения, видим:
Где указыается ячейка для ограничения и
значение (число) чем значение ограничивается, в нашем случае 1 (см.
математическую запись задачи).
После того, как все ограничения введены
получим решения нажав «выполнить»
Видим:
Максимум прибыли равно 163.333. При этом нужно
выпускать 66.6 велосипедов, и 10 мотоциклов.
Решить задачи самостоятельно в ексель:
1. ,

Ответ:
2. ,

Ответ:
3. ,

Ответ:
4. ,

.
5. ,

Расчет точки заказа товара на основании:
- статистики продаж
- периодичности заказов
- сроков поставки
Персентиль VS формула Вильсона
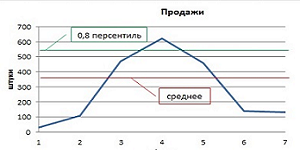
Для расчета оптимальной партии заказа, оптимальной точки заказа, оптимального времени заказа в классической логистике используется формула Вильсона (Уильсона). Однако, формула Вильсона была разработана для крупных промышленных предприятий и подходит для условий, когда расход продукции постоянен, продукция однородна. В реальности продажи бывают разными:
То есть, для современной торговой компании формула Вильсона не подходит. Также не подходит формирование страхового запаса на базе расчета средней арифметической, т.к. такой уровень запаса не обеспечивает всплески продаж. В то же время держать на складе избыточный запас в расчете на всплески продаж, которых может и не быть — неэффективное замораживание оборотных средств.
При расчетах страховых запасов более 10.000 наименований (SKU) с неравномерными продажами оправдана другая методика расчета точки заказа — с помощью функции MS Excel -ПЕРСЕНТИЛЬ (скачать файл). Персентиль позволяет установить процент продаж, обеспеченных страховым запасом. В рассматриваемом примере берется 0.8 Персентиль, т.е. товарными запасами будут обеспечены 80% продаж:
Если Вам нужно обеспечить запасами большее или меньшее количество возможных продаж, просто поменяйте процент продаж обеспеченности продаж в строке 1 (это второй аргумент в функции Персентиль). Например, аргумент, равный «0,95» обеспечит 95% возможных продаж, рассчитанных на основании статистики. Значение аргумента может быть задано в диапазоне от 0% до 100% продаж.

|
Формула для заказа товара |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Коэффициент оборачиваемости = Расход/Средний запас за период
Средний запас за период = (остаток на начало + остаток на конец) /2
для вашего примера первая формула
Показывает, за сколько раз обернулся средний товарный запас за период. Чем ниже КО, тем хуже.
Если периодов больше 1, то неплохо брать средний запас за период более детально, так точнее видна фактическая оборачиваемость (если приход в конце периода, а в 90% дней был 0, то средний запас может быть слишком большим, а расход просто не успеть раскрутиться)
Но коэффициент оборачиваемости не поможет вам спланировать минимальный запас, если по Коэффициенту оборачиваемости не установлен критерий. Наример, он должен быть не ниже 1. Или не ниже 0,5 — зависит от отрасли и кучи других вещей, в том числе аппетитов начальства.
Общий подход, который можно в экселе спланировать:
Тов.Запас на начало периода д.б. равен запасу на период поставки + страховой запас.
То есть вам нужно знать как минимум:
1. Срок поставки (от размещения заказа до прихода на склад)
2. План продаж на этот период
3. Возможное отклонение плана продаж и срока поставки
Тогда общая формула будет примерно такая:
Мин. ТЗ на нач.мес. = (Среднедневной план продаж)*(срок поставки в днях)+Страховой_запас
Страховой_запас = Возможное отклонение плана продаж за период + запас на возможное отклонение срока поставки
Запас на возможное отклонение срока поставки = (Возможное количество дней задержки поставки)*(Среднедневной план продаж)
Запас на возможное отклонение плана продаж = (Возможное отклонение плана продаж в %)*(Вероятность этого отклонения)*(Среднедневной план продаж)*(срок поставки в днях)
Последнее встречается в + редко, так что можно проигнорировать. Обычно идет недовыполнение плана, поэтому образуются излишки сами по себе.
Но страховой запас может быть установлен и директивно — должно быть в запасе 20% от плана, и хоть тресни.
Ну и этот Мин.ТЗ может быть округлен вверх до некоего минимального нормативного запаса — кратно какой-то упаковке, партии, или просто «должно быть всегда не меньше Х, иначе никто не придет покупать»