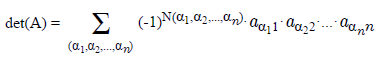Расчет определителя матрицы excel - Word и Excel - помощь в работе с программами

Вычислим определитель (детерминант) матрицы с помощью функции

МОПРЕД()

или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).

Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.

Для вычисления определителя в MS EXCEL есть специальная функция

МОПРЕД()

. В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см.

файл примера

).

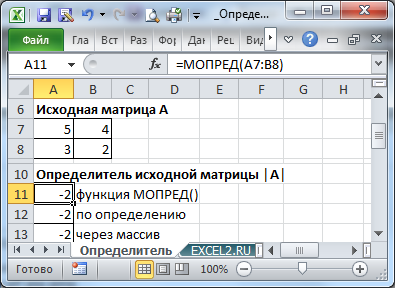
Массив может быть задан не только как интервал ячеек, например

A7:B8

, но и как

массив констант

, например

=МОПРЕД({5;4:3;2})

. Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на

именованный диапазон

Для матриц порядка 2 можно определитель можно вычислить без использования функции

МОПРЕД()

. Например, для вышеуказанной матрицы выражение

=A7*B8-B7*A8

вернет тот же результат.

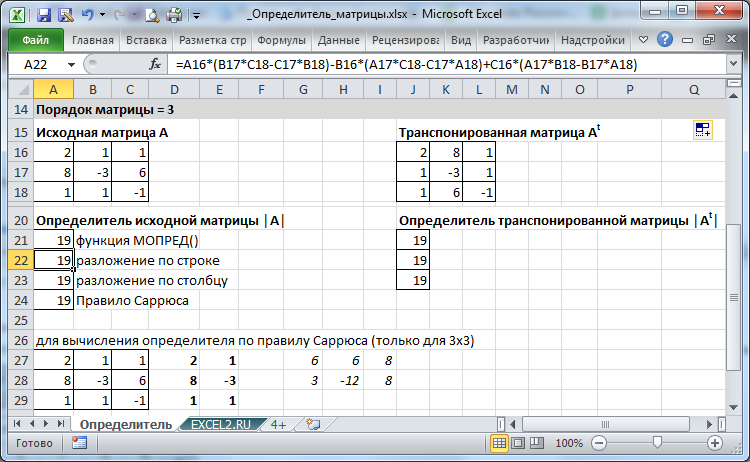
Для матрицы порядка 3, например размещенной в диапазоне

A16:C18

, выражение усложняется

=A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18)

(разложение по строке).

В

файле примера

для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.

Свойства определителя

Теперь о некоторых свойствах определителя (см.

файл примера

):

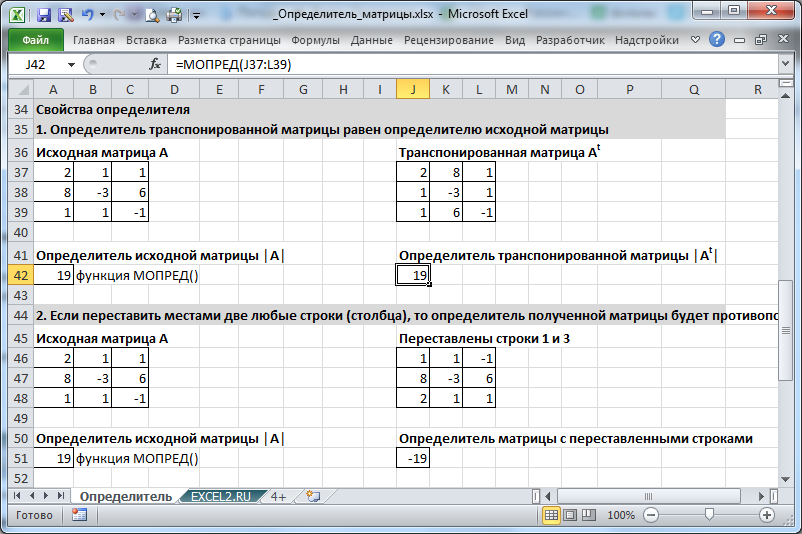
Определитель

транспонированной матрицы

равен определителю исходной матрицы
Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет

равен определителю исходной матрицы, умноженному на

k
Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
det(А)=1/det(А
^-1
), где А
^-1
—

матрица обратная

матрице А (А — квадратная невырожденная матрица).

Вычисление определителя матрицы по определению (до 6 порядка включительно)

СОВЕТ

: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция

МОПРЕД()

.

Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции

МОПРЕД()

) придется вспомнить определение:

Определителем квадратной матрицы порядка

n

х

n

является сумма, содержащая

n!

слагаемых (

=ФАКТР(n)

). Каждое слагаемое представляет собой произведение

n

элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы

А

. Перед

k-ым

слагаемым появляется коэффициент

(-1)

, если элементы матрицы

А

в произведении упорядочены по номеру строки, а количество инверсий в

k-ой

перестановке множества номеров столбцов нечетно.

где (

α
₁
,

α
₂
,…,

α
_n
) — перестановка чисел от 1 до

n

, N(

α
₁
,

α
₂
,…,

α
_n
) — число

инверсий в перестановке

, суммирование идёт по всем возможным перестановкам порядка

n

.

Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.

Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:

а21*а12*а33
а21*а32*а13
а11*а32*а23
а11*а22*а33
а31*а22*а13
а31*а12*а23

а21, а12 и т.д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее

транспонированной матрицы

равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).

Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения (

в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы

А

),

а в нашем слагаемом нет элемента из строки 3.

Примечание

: Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок:

(1, 2, 3),

(1, 3, 2),

(2, 3, 1),

(2, 1, 3),

(3, 1, 2),

(3, 2, 1). См. статью

Перестановки без повторений: Комбинаторика в MS EXCEL

Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).

СОВЕТ

: Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье

Перебор всех возможных Перестановок в MS EXCEL

Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.

Примечание

:

Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.

Сложив все слагаемые: (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.

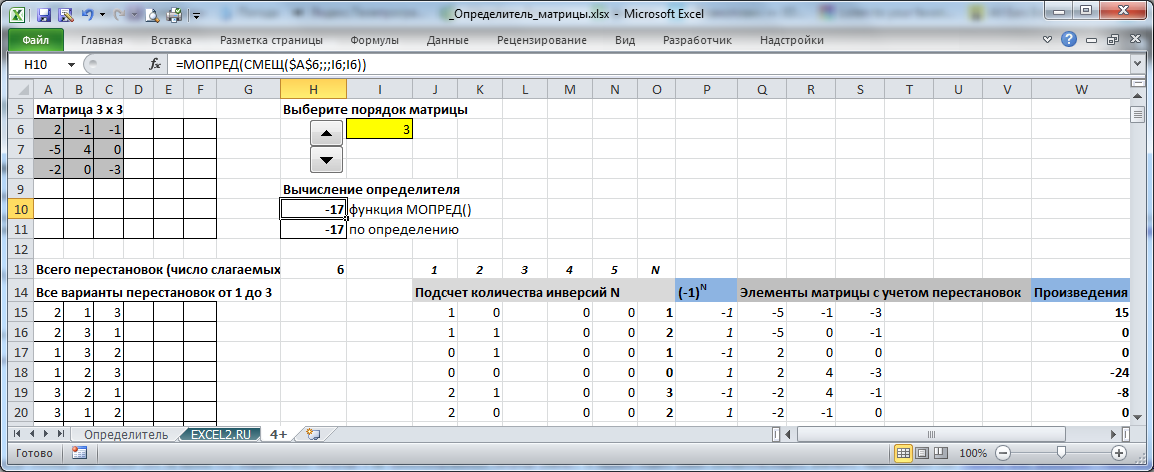
В

файле примера на листе 4+,

и

зменяя порядок матрицы с помощью

элемента управления Счетчик

, можно вычислить определитель матрицы до 6 порядка включительно.

Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования

МОПРЕД()

не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование MDETERM
в Microsoft Excel.

Описание

Возвращает определитель матрицы (матрица хранится в массиве).

Синтаксис

МОПРЕД(массив)

Аргументы функции МОПРЕД описаны ниже.

Массив Обязательный. Числовой массив с равным количеством строк и столбцов.

Замечания

Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например {1;2;3:4;5;6:7;8;9}, как имя для интервала или массива.
Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.
- Если какая-либо ячейка в массиве пуста или содержит текст.
- Если количество строк в массиве не равно количеству столбцов.
Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:

МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)

Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.
Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.

Пример

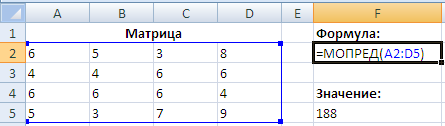
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Данные	Данные	Данные
1	3	8	5
1	3	6	1
1	1	1	0
7	3	10	2
Формула	Описание	Результат
=МОПРЕД(A2:D5)	Определитель приведенной выше матрицы.	88
=МОПРЕД({3;6;1:1;1;0:3;10;2})	Определитель матрицы, представленной в виде массива констант.	1
=МОПРЕД({3;6:1;1})	Определитель матрицы в массиве констант.	-3
=МОПРЕД({1;3;8;5:1;3;6;1})	Возвращает сообщение об ошибке, так как массив имеет разное количество строк и столбцов.	#ЗНАЧ!

Нужна дополнительная помощь?

Источник

Функция МОПРЕД в Excel используется для работы с прямоугольными матрицами. Задаваемыми в качестве статических массивов или диапазонов ячеек с числовыми данными, и вычисляет детерминант (определитель) исследуемой матрицы.

Матрица – математический объект, состоящий из совокупности строк из столбцов, каждый элемент которых содержит определенное числовое значение. Детерминант – один из основных вычисляемых параметров матрицы, характеризующих ее ключевые свойства.

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

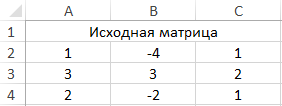
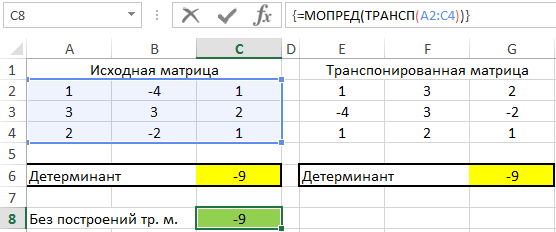
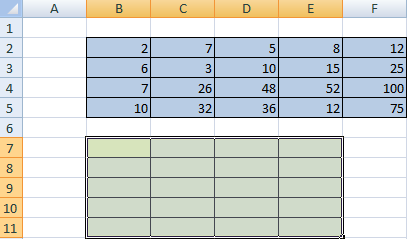
Пример 1. Одним из свойств матриц является то, что определитель (детерминант) исходной матрицы соответствует определителю транспонированной матрицы. Доказать справедливость этого суждения с использованием средств Excel.

Вид таблицы с данными:

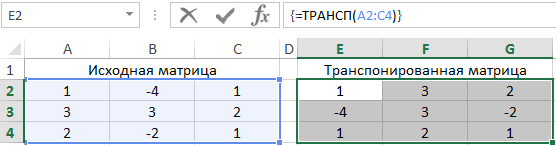
Для получения транспонированной матрицы выделим соответствующий по количеству строк и столбцов диапазон ячеек и используем следующую формулу (формула массива CTRL+SHIFT+Enter):

=ТРАНСП(A2:C4)

A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

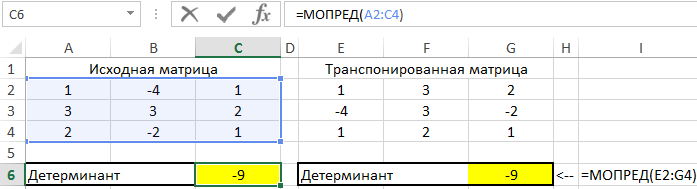
Рассчитаем детерминант для каждой матрицы отдельно:

=МОПРЕД(A2:C4)

=МОПРЕД(E2:G4)

A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Полученные результаты:

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

=МОПРЕД(ТРАНСП(A2:C4))

Результат вычислений:

В результате вычислений формул Excel детерминант – доказан!

Решение системы линейных уравнений по методу Крамера в Excel

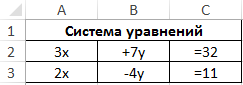
Пример 2. Решить систему линейных уравнений с использованием метода Крамера. Для расчета необходимо найти определители нескольких матриц.

Вид таблицы данных:

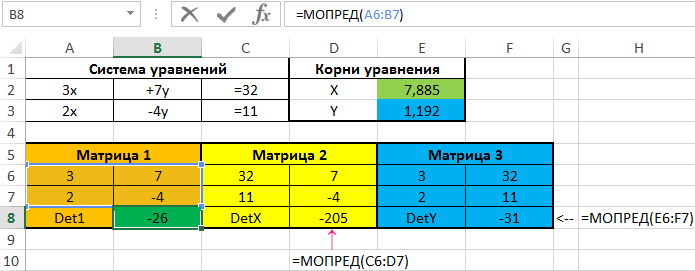
Для нахождения решений методом Крамера выделим три матрицы.

Если детерминант первой матрицы равен нулю, исходная система уравнений имеет бесконечное число решений. Проверим это условие с помощью формулы:

=МОПРЕД(A6:B7)

Результат вычислений:

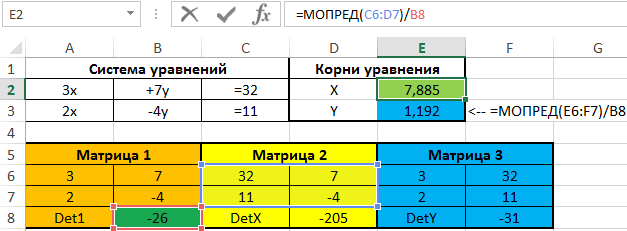
Так как детерминант основной матрицы (Матрица 1) не равен нулю, система имеет единственное решение. Для нахождения значения переменных X и Y используем формулы:

=МОПРЕД(C6:D7)/B8

=МОПРЕД(E6:F7)/B8

Результаты вычислений:

Принцип работы функции МОПРЕД в Excel

Функция МОПРЕД имеет следующую синтаксическую запись:

=МОПРЕД(массив)

Единственным аргументом рассматриваемой функции является массив, который обязателен для заполнения. Он может быть указан в виде статического массива или ссылки на диапазон ячеек.

Примечания:

Диапазон ячеек или статический массив должен иметь равное количество строк и столбцов, иначе результатом работы функции МОПРЕД будет код ошибки #ЗНАЧ!.
Если диапазон ячеек или массив, переданные в качестве аргумента рассматриваемой функции, содержат текстовые данные или пустые значения, в результате будет возвращен код ошибки #ЗНАЧ!.
Функция МОПРЕД значительно упрощает процесс расчета детерминанта матрицы. Пользователь Excel может выполнить расчеты самостоятельно. Например, для прямоугольной матрицы, значения которой находятся в диапазоне A1:C3 рассчитать детерминант можно следующим способом: A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1).
Точность расчетов функции МОПРЕД составляет примерно 1E-16, то есть до 16 знаков после запятой. Для более точных расчетов (что требуется крайне редко) используют другие методы определения детерминанта матрицы.
Значение детерминанта используют для поиска решений системы линейных уравнений.

Источник

Для того, чтобы вычислить определитель матрицы в Excel совершенно необязательно производить сложные вычисления суммируя различные произведения элементов матрицы. Рассмотрим простой способ вычисления определителя матрицы.

Вычислить определитель матрицы второго порядка достаточно просто, третьего порядка уже куда сложнее, а с расчетом определителя четвертого порядка точно справится не каждый.
Однако с помощью Excel эта задача легко решается вне зависимости от порядка матрицы.

Предположим нам необходимо найти определитель следующей матрицы:

Если искать определитель вручную, то нам потребуется произвести расчет для 24 (в общем случае в определитель матрицы порядка n входит n! слагаемых) элементов определителя, поэтому прибегнем к решению с помощью инструментов Excel.
В Excel есть стандартная функция МОПРЕД, которая позволяет вычислить определитель матрицы.

Описание функции МОПРЕД

МОПРЕД([массив])
Возвращает определитель матрицы (матрица хранится в массиве).

Массив (обязательный аргумент) — квадратная матрица (массив), т.е. матрица с равным количеством строк и столбцов.

Пример вычисления определителя матрицы в Excel

В качестве аргумента функции МОПРЕД выделяем диапазон ячеек A2:D5 и в результате получаем:

Удачи вам и до скорой встречи на страницах блога Tutorexcel.ru!

Поделиться с друзьями:

Поиск по сайту:

Источник

Содержание

Определитель матрицы в Excel
Как найти определитель матрицы в Excel
Описание функции МОПРЕД
Пример вычисления определителя матрицы в Excel
Функция МОПРЕД для нахождения детерминанта матрицы в Excel
Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel
Решение системы линейных уравнений по методу Крамера в Excel
Принцип работы функции МОПРЕД в Excel
Функция МОПРЕД
Описание
Синтаксис
Замечания
Пример
Операции с матрицами в Excel
Формулы массива
Что можно делать с матрицами
Транспонирование
Сложение
Умножение
Обратная матрица
Поиск определителя матрицы
Несколько примеров
Умножение и деление
Метод 1
Метод 2
Сложение и вычитание
Метод 1
Метод 2
Пример транспонирования матрицы
Поиск обратной матрицы
Выводы

Определитель матрицы в Excel

Вычислить определитель матрицы второго порядка достаточно просто, третьего порядка уже куда сложнее, а с расчетом определителя четвертого порядка точно справится не каждый.
Однако с помощью Excel эта задача легко решается вне зависимости от порядка матрицы.

Как найти определитель матрицы в Excel

Предположим нам необходимо найти определитель следующей матрицы:

Описание функции МОПРЕД

МОПРЕД([массив])
Возвращает определитель матрицы (матрица хранится в массиве).

Массив(обязательный аргумент) — квадратная матрица (массив), т.е. матрица с равным количеством строк и столбцов.

Пример вычисления определителя матрицы в Excel

В качестве аргумента функции МОПРЕД выделяем диапазон ячеек A2:D5 и в результате получаем:

Источник

Функция МОПРЕД для нахождения детерминанта матрицы в Excel

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

Вид таблицы с данными:

A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

Рассчитаем детерминант для каждой матрицы отдельно:

A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

В результате вычислений формул Excel детерминант – доказан!

Решение системы линейных уравнений по методу Крамера в Excel

Вид таблицы данных:

Для нахождения решений методом Крамера выделим три матрицы.

Принцип работы функции МОПРЕД в Excel

Функция МОПРЕД имеет следующую синтаксическую запись:

Диапазон ячеек или статический массив должен иметь равное количество строк и столбцов, иначе результатом работы функции МОПРЕД будет код ошибки #ЗНАЧ!.
Если диапазон ячеек или массив, переданные в качестве аргумента рассматриваемой функции, содержат текстовые данные или пустые значения, в результате будет возвращен код ошибки #ЗНАЧ!.
Функция МОПРЕД значительно упрощает процесс расчета детерминанта матрицы. Пользователь Excel может выполнить расчеты самостоятельно. Например, для прямоугольной матрицы, значения которой находятся в диапазоне A1:C3 рассчитать детерминант можно следующим способом: A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1).
Точность расчетов функции МОПРЕД составляет примерно 1E-16, то есть до 16 знаков после запятой. Для более точных расчетов (что требуется крайне редко) используют другие методы определения детерминанта матрицы.
Значение детерминанта используют для поиска решений системы линейных уравнений.

Источник

Функция МОПРЕД

В этой статье описаны синтаксис формулы и использование MDETERM в Microsoft Excel.

Описание

Возвращает определитель матрицы (матрица хранится в массиве).

Синтаксис

Аргументы функции МОПРЕД описаны ниже.

Массив Обязательный. Числовой массив с равным количеством строк и столбцов.

Замечания

Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например <1;2;3:4;5;6:7;8;9>, как имя для интервала или массива.

Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.

Если какая-либо ячейка в массиве пуста или содержит текст.

Если количество строк в массиве не равно количеству столбцов.

Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:

МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)

Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.

Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.

Пример

Источник

Операции с матрицами в Excel

Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.

Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

Выделить набор ячеек, где будут выводиться значения.
Непосредственно введение формулы.
Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

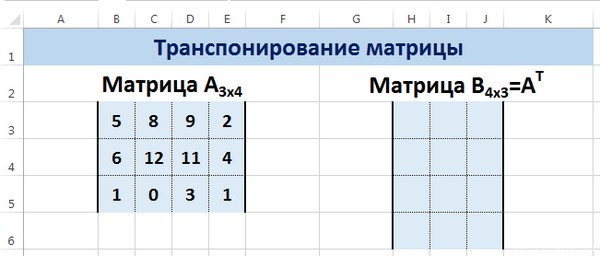
Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.

Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.

Далее есть несколько методов, как можно осуществить транспонирование.

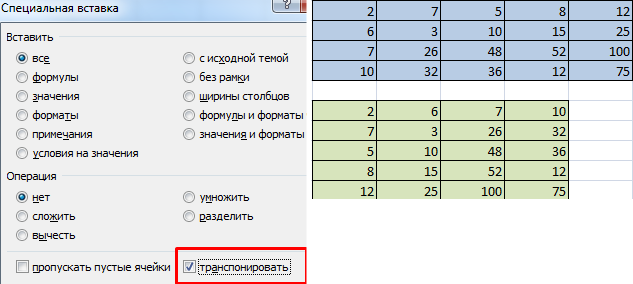
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.

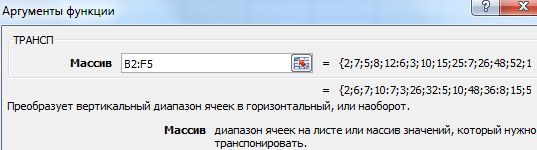
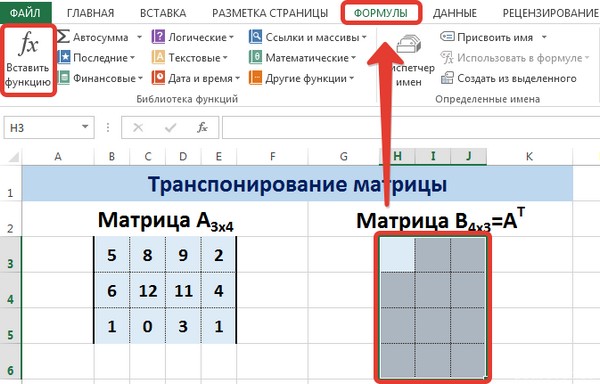
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП . Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.

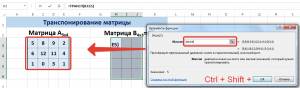
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

Выделить набор ячеек, отведенных под транспонированную матрицу.
Нажать клавишу F2.
Нажать на горячие клавиши Ctrl + Shift + Enter.

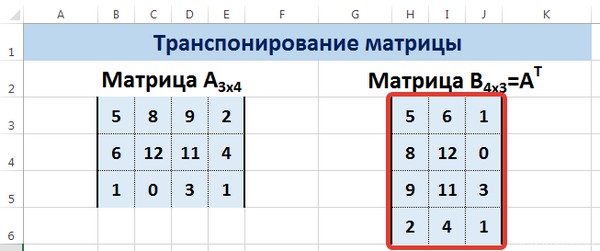
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

Сложение

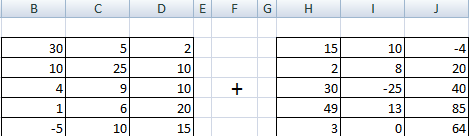
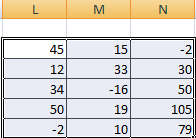
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.

В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.

=Первый элемент первой матрицы + Первый элемент второй матрицы

Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.

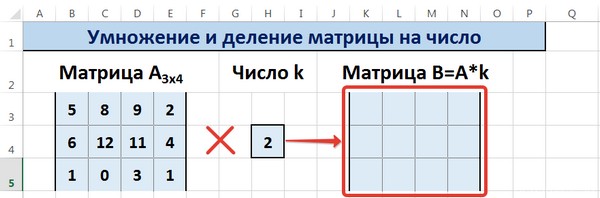
Умножение

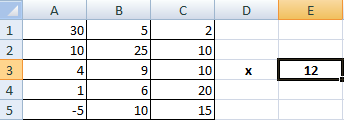
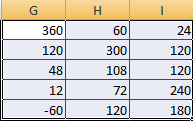
Предположим, у нас есть такая таблица, которую следует умножить на 12.

Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.

При этом важно указывать абсолютные ссылки на ячейки.

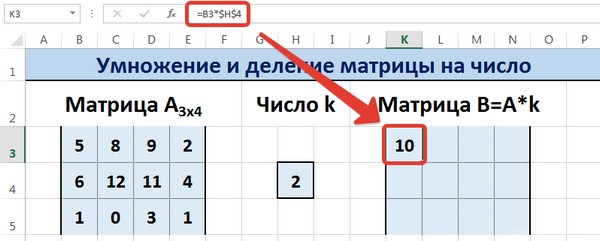
Итого, получится такая формула.

=A1*$E$3

Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.

Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.

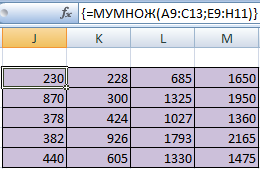
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.

Обратная матрица

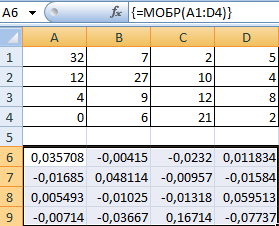
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР .

Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4) . В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.

Поиск определителя матрицы

Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД .

Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)

Несколько примеров

Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.

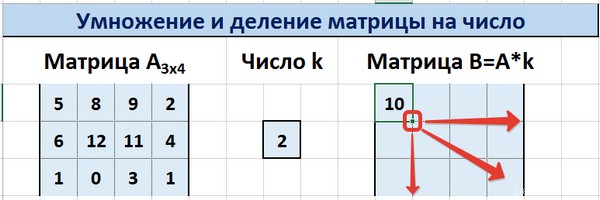
Умножение и деление

Метод 1

Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.

Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.

Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.

Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.

Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.

Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.

Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.

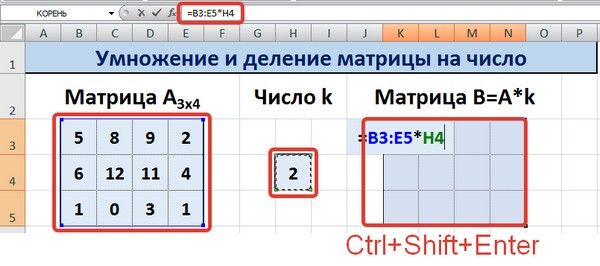
Метод 2

Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.

Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.

Деление осуществляется аналогичным образом, только знак * нужно заменить на /.

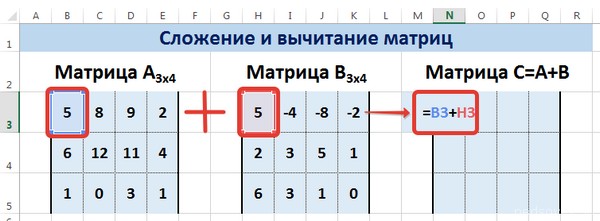
Сложение и вычитание

Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.

Метод 1

Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.

Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:

Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.

Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.

Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.

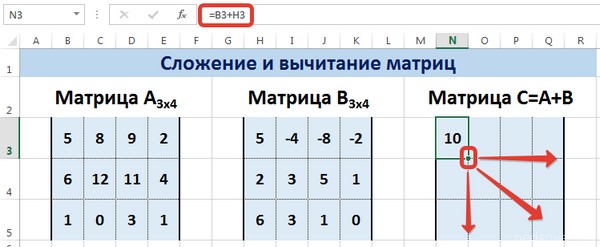
Метод 2

Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.

Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.

Пример транспонирования матрицы

Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП() .

Выделяем диапазон для ячеек матрицы АТ.

Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП . После этого свои действия подтверждаются кнопкой ОК.

Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».

Важно . Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.

В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.

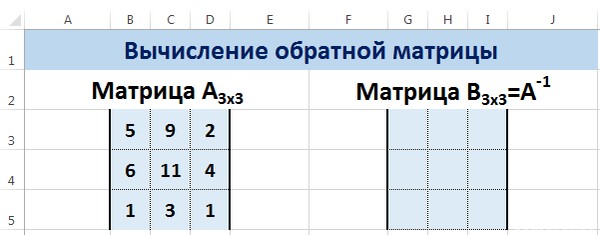
Поиск обратной матрицы

Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР() .

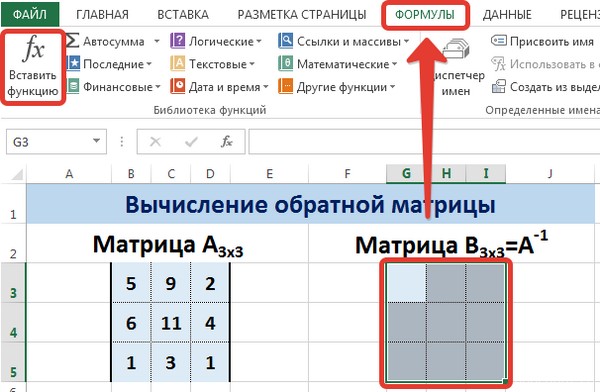
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».

Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР . После того, как мы ее выберем, нужно нажать на клавишу ОК . Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.

Выводы

Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.

Источник