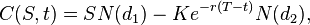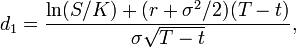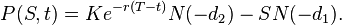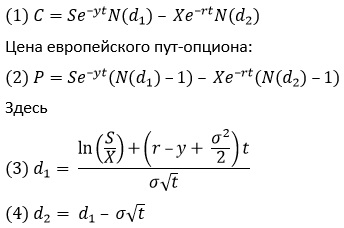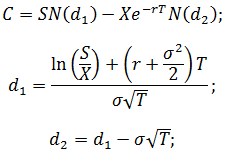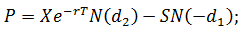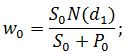Время на прочтение
5 мин
Количество просмотров 37K
Статья адресована и будет полезна в первую очередь тем, кто начал изучать опционы и хочет разобраться в их ценообразовании. Ну и во вторую очередь тем, кто ещё не использует инструмент VBA в своих расчётах в екселе, но хочет научиться — вы увидите, как это на самом деле просто.
Основы опционов
Для начала кратко о сути и ценообразовании опционов. Опцион имеет четыре основных параметра:
1. Базовый актив
2. Тип опциона (Колл или Пут)
3. Цена страйка (цена исполнения опциона)
4. Дата экспирации (истечения) опциона
Для покупателя опциона он представляет собой право
купить (опцион Колл) или продать (опцион Пут) базовый актив по цене страйка в день экспирации.
Для продавца опциона он представляет собой обязанность
продать (опцион Колл) или купить (опцион Пут) базовый актив по цене страйка в день экспирации. Фактически опцион представляет собой страховку от изменения цены базового актива (БА) от момента сделки до даты экспирации — в роли страховщика выступает продавец (в случае неблагоприятного изменения цены БА он выплачивает страховку покупателю опциона), а страхователем является покупатель опциона (он платит за страховку продавцу).
Как и цена страховки цена опциона полностью определяется вероятностью «страхового случая», т.е. исполнения опциона (исполнения права покупателя опциона). Основные составляющие, которые влияют эту вероятность и на цену опциона, на стоимость страховки, которую платит покупатель и получает продавец:
- Разница между ценой страйка и ценой базового актива. Т.е. при покупке Колла, чем выше его страйк, тем он дешевле (т.к. снижается вероятность того, что на момент экспирации БА будет выше цены страйка)
- Волатильность базового актива. Чем выше волатильность (грубо размах колебаний цены) БА, тем выше вероятность достичь страйка до экспирации.
- Время до экспирации. Чем больше времени до экспирации опциона, тем при покупке Колла выше вероятность что за это время цена базового актива уйдёт выше страйка, соответственно цена опциона выше.
При этом зависимость цены опциона по каждой из этих трёх составляющих нелинейная. Ставшая общепринятой формула оценки опционов с учётом этих основных факторов была выведена Фишером Блэком и Майроном Шоулзом в 1973 году.
Формула Блэка-Шоулза имеет следующий вид (подробно можно посмотреть в Википедии):
Цена (европейского) опциона call:
Цена (европейского) опциона put:
Обозначения:
C(S,t) — текущая стоимость опциона call в момент t до истечения срока опциона (до экспирации);
S — текущая цена базового актива;
N(x) — вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения);
K — цена исполнения опциона;
r — безрисковая процентная ставка;
T — t — время до истечения срока опциона;

Греки опционов
Для оценки чувствительности цены опциона к цене БА, волатильности, и времени до экспирации, применяют коэффициенты, называемые Греками (коэффициенты в основном обозначаются греческими буквами, за исключением «веги»).
Греки в модели Блэка-Шоулза вычисляются следующим образом:
1. Дельта (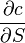
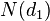
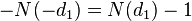
2. Гамма ( 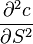
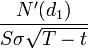
3. Вега ( 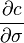

4. Тета ( 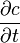
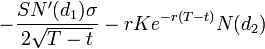
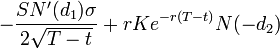
Вышеприведенные формулы верны для общего случая, в том числе для случая опционов на акции. Для расчёта опционов на фьючерсные контракты безрисковая ставка r не применяется. Т.к. на Московской бирже торгуются опционы на фьючерсы, далее в расчётах процентную ставку не учитываем.
Реализация модели в MS Excel
Итак, реализация модели Блэка-Шоулза в Excel+VBA.
Для удобства создадим функцию для каждой переменной из модели БШ. В каждой функции будут входные переменные:
S — цена БА
X — цена страйка
d — число дней до экспирации
y — число дней в году
v — волатильность
OptionType — тип опциона «Call» или «Put» (только для расчета цены и дельты)
Запись обычной функции в VBA выглядит следующим образом:
Function НазваниеФункции(входные переменные через запятую)
… вычисления…
НазваниеФункции =… вычисления…
End Function
Такую функцию можно вызывать как из других функций, так и из листа Excel.
Функции записываются в созданный Модуль (запускаем VBA в Excel, например нажатием Alt+F11, выбираем Insert -> Module):
Function d_1(S, X, d, y, v)
T = d / y
d_1 = (Log(S / X) + (0.5 * (v ^ 2)) * T) / (v * (T ^ 0.5))
End FunctionFunction d_2(S, X, d, y, v)
T = d / y
d_2 = d_1(S, X, d, y, v) — v * (T ^ 0.5)
End FunctionFunction Nd_1(S, X, d, y, v)
Nd_1 = Application.NormSDist(d_1(S, X, d, y, v))
End FunctionFunction Nd_2(S, X, d, y, v)
Nd_2 = Application.NormSDist(d_2(S, X, d, y, v))
End FunctionFunction N_d_1(S, X, d, y, v)
N_d_1 = Application.NormSDist(-d_1(S, X, d, y, v))
End FunctionFunction N_d_2(S, X, d, y, v)
N_d_2 = Application.NormSDist(-d_2(S, X, d, y, v))
End FunctionFunction N1d_1(S, X, d, y, v)
T = d / y
N1d_1 = 1 / (2 * Application.Pi()) ^ 0.5 * (Exp(-0.5 * d_1(S, X, d, y, v) ^ 2))
End FunctionFunction OptionPrice(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
OptionPrice = S * Nd_1(S, X, d, y, v) — X * Nd_2(S, X, d, y, v)
ElseIf OptionType = «Put» Then
OptionPrice = X * N_d_2(S, X, d, y, v) — S * N_d_1(S, X, d, y, v)
End If
End FunctionFunction Delta(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v))
ElseIf OptionType = «Put» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v)) — 1
End If
End FunctionFunction Theta(S, X, d, y, v)
T = d / y
Theta = -((S * v * N1d_1(S, X, d, y, v)) / (2 * (T ^ 0.5))) / y
End FunctionFunction Gamma(S, X, d, y, v)
T = d / y
Gamma = N1d_1(S, X, d, y, v) / (S * (v * (T ^ 0.5)))
End FunctionFunction Vega(S, X, d, y, v)
T = d / y
Vega = (S * (T ^ 0.5) * N1d_1(S, X, d, y, v)) / 100
End Function
Готовый Excel-файл можно скачать по ссылке.
Теперь в екселевской ячейке можем вызывать любую прописанную нами функцию, например введя в ячейке =OptionPrice(«Put»;76870;90000;13;365;0.47) мы получим теоретическую цену опциона Пут при цене базового актива 76870, страйке 90000, предполагаемой волатильности 45% и за 13 дней до экспирации.
Некоторые моменты, которые хотелось бы отметить
- Полученные в нашей программе значения теорцены практически идентичны тем, что транслирует Мосбиржа, это значит что биржа в своих расчётах использует именно модель БШ.
- На самом деле опцион (как и страховка) не имеет истинной справедливой стоимости — она для каждого своя, и зависит от того какая предполагается волатильность или например какое учитывать число дней (учитывать ли выходные, с каким весом учитывать разные дни недели, сколько дней в году использовать в формуле) и т.д.
- Греки обладают замечательным свойством — чтобы получить значение греков для портфеля фьючерсов и опционов нужно просто сложить соответствующие греки для отдельных активов портфеля. Т.е. мы легко можем рассчитать, например, сколько нужно купить/продать базовых фьючерсов чтобы общая стоимость портфеля не изменялась при изменении цены этого фьючерса (т.н. выравнивание Дельты или дельта-хеджирование).
- Не смотря на свою распространённость, модель БШ основана на допущении, что доходность актива имеет нормальное распределение, что на реальном рынке не выполняется никогда.
Итог
Итак, мы получили рабочий опционный калькулятор на VBA, который можно использовать как для изучения свойств опционов (строить диаграммы зависимостей цены и греков от разных параметров рынка), так и использовать для торговли и построения более сложных программ.
Содержание
- Пояснение-дисклеймер от Excellentricks: автор сайта критично относится к криптовалютам и к используемым в статье ниже подходам (и явным ошибкам), статья приведена, как иллюстрация сопряжения элементов Excel и имитационного моделирования, поэтому некоторые формулы, написанные с применением MathJax отображаются некорректно (полную версию можно прочитать по ссылке внизу статьи на хабре).
- Введение
- Определение опциона
- Как продавец оценивает премию по опциону
- Эталонный расчет — модель Блэка — Шоулза
- Логнормальное распределение
- Расчет премии по формуле Б-Ш
- Историческая волатильность
- Расчет премии в Excel
- Расчет премии для “ненормального” ценового распределения
- Моделирование “реальной” цены
Пояснение-дисклеймер от Excellentricks: автор сайта критично относится к криптовалютам и к используемым в статье ниже подходам (и явным ошибкам), статья приведена, как иллюстрация сопряжения элементов Excel и имитационного моделирования, поэтому некоторые формулы, написанные с применением MathJax отображаются некорректно (полную версию можно прочитать по ссылке внизу статьи на хабре).
Введение
На волне хайпа криптовалют проскакивают новости о торговле биткойном на мировых биржах CME и NASDAQ. Для меня это знаковое событие: руки корпораций, надувавших пузыри доткомов и ипотек, дотянулись и до золота шифропанков — криптовалют. А в арсенале этих самых корпораций мощный рычаг — производные финансовые инструменты, или деривативы.
Находясь под впечатлением прочитанных не так давно историй взлетов и метаморфоз рынков деривативов — прежде всего, фьючерсных и опционных контрактов, я заинтересовался нетривиальным ценообразованием опционов. Мне открылось, что, хотя интернет полон рерайтов статей, толкующих знаменитую формулу Блэка-Шоулза, практических инструментов — web-сайтов, технологических программ или банальных руководств для программиста — не математика, по данному вопросу в интернете недостает. Пришлось вспомнить азы тервера и адаптировать строгие математические описания в популярном, понятном, прежде всего, мне самому, формате.
Определение опциона
Опцион — контракт, дающий покупателю право (но не обязанность!) купить или продать торгуемый на рынке актив по указанной им (покупателем контракта) цене. Продавец опциона назначает покупателю премию — свое вознаграждение за предоставленную покупателю опциона возможность купить или продать актив в определенный срок по определенной цене.
Пример опционного контракта:
- покупатель опциона хочет получить право купить 10 Ethereum (ETH) по цене $470 за 1 ETH через 30 дней.
- текущая цена Ethereum равна $450.
Допустим, через 30 дней рыночный курс Ethereum вырастет до $500. Покупатель опциона сможет купить 10 Ethereum (10 ETH) по оговоренной в контракте цене $470. После чего, покупатель, желающий сейчас же извлечь выгоду из своей сделки, тут же продаст Ethereum по цене $500, заработав:
10 x (500 — 470) = 300 (USD).
Если же цена Ethereum окажется ниже $470, покупатель опциона просто откажется от невыгодной сделки.
Беспроигрышное предложение! Разумеется, за такую чудесную возможность продавец запросит какую-то сумму — премию по опциону.
Итак, спецификация опционного контракта:
- в данном примере покупатель приобрел европейский call опцион в объеме 10 ETH со страйк-ценой $470 USD с экспирацией через 30 дней.
- “Европейский” — в данном контексте означает, что покупатель опциона может совершить сделку по указанной цене строго на определенную дату — на момент экспирации опциона. Существуют также “американские” опционы, где покупатель контракта может исполнить его в любое время до момента экспирации, но рассмотрение американских опционов выходит за рамки статьи.
- Покупатель опциона получает право купить актив (Ethereum) по указанной цене. Опцион на покупку актива определен как call-опцион, на продажу — put-опцион.
- Цена, по которой покупатель опциона имеет право приобрести актив — в нашем примере $470 — называется страйк-ценой.
- Сумма, которую покупатель опциона уплатит продавцу, называется премией.
Размер премии по опциону и есть предмет нашего небольшого исследования.
Как продавец оценивает премию по опциону
Рассчитать величину премии — такую, чтобы и самому не остаться в накладе, и не отпугнуть потенциального покупателя “задранным” ценником — настоящее искусство. По крайней мере, было таковым до поры. Пока в 1973 году два математика не явили свету изящную формулу, названную их именами — формула Блэка-Шоулза. Об этой формуле и ее влиянии на рынок деривативов написана даже популярная книга — “Кванты. Как волшебники от математики заработали миллиарды и чуть не обрушили фондовый рынок”. Конечно, реальная история несколько сложнее, чем “тьма невежества — вжух! — формула”… Но меня интересуют не столь глобальные процессы, а непосредственно вопрос: насколько формула Блэка-Шоулза применима для оценки “справедливой” премии по опциону, рассчитанной для популярных у трейдеров криптовалютных контрактов?
Модель Блэка-Шоулза описывает некий “стандартизированный” рынок. Выхолощенный, избавленный от резких ценовых перепадов, живущий годами в одном ритме. Разумеется, формула, выведенная для “идеального” рынка, не так хорошо работает на практике, как в теории.
Как принято у трейдеров — там, где недостает теории, обращаются к эмпирике. К трейдерской “чуйке”, к “опыту”. Как программист, я негодую от такого невежества. Потому приведу свое решение: чужие выкладки, немного тервера, магия Excel и, в самом конце, исходники на C#.
Эталонный расчет — модель Блэка — Шоулза
Википедия снабдит нас формулой. Задав значения переменных опционного контракта и зная параметры торгового актива, мы можем подсчитать “справедливую” премию.
Для дальнейших расчетов нам нужны “идеальные” данные — ценовой ряд, обладающий нужными характеристиками.
Реальная цена, как я уже отмечал, может быть дамой непостоянной: то топчется на месте, то вдруг лихо срывается с места в карьер. Нам же нужен образец идеальной серии ценовых данных как эталон для последующих вычислений.
Логнормальное распределение
Модель Б-Ш (давайте уже сократим имена авторов в названии) предполагает, что ценовой ряд описывает логнормальное распределение. Что это означает? Приведу пример:
в столбце A — цена абстрактного актива ABS/USD, pipi.
Столбец B содержит натуральный логарифм от частного pipi и pi−1pi−1.
Логнормальное распределение описывает ценовой ряд, производный ряд от которого, полученный как натуральный логарифм частного от деления текущего значения с предыдущим, имеет нормальное распределение. Сложно. Поясню на нашем примере: если значения в столбце B распределены согласно нормальному закону, то значения столбца A описывает логнормальное распределение.
Как нам получить “логнормальный” ценовой ряд? MS Excel, который я уже использовал для примера, умеет генерировать случайные числа, имеющие равномерное (увы, не нормальное) распределение. Есть несложная методика, по которой мы сможем получить ряд нормально распределенной СВ из равномерно распределенной СВ. Методика называется “метод обратной функции”. Не вдаваясь в детали метода, отмечу следующий его важный аспект:
- метод обратной функции позволяет получить СВ с произвольным, заданным функцией (таблицей), законом распределения, получая на входе СВ, равномерно распределенную в диапазоне от 0 до 1.
Нам нужна обратная интегральная (как ее еще называют, кумулятивная) функция нормального распределения. Такая есть в Excel: функция “НОРМ.ОБР”.
Функция НОРМ.ОБР принимает значения: вероятность, среднее, стандартное отклонение.
- Вероятность — то самое значение, от которого мы строим нашу функцию. Строго больше 0 и строго меньше 1. Сгенерируем 999 значений от 0.001 до 0.999 с шагом 0.001 в столбце A. Значения из столбца A и пойдут на вход функции НОРМ.ОБР.
- Среднее — математическое ожидание нашей СВ. Напомню, мы генерируем величину, пропорциональную динамике нашего ценового актива ABS/USD. Положительные значения соответствуют росту цены (pi>pi−1⟹ln(pi/pi−1)>0pi>pi−1⟹ln(pi/pi−1)>0), отрицательные — падению. Если мы зададим параметр “среднее” большим нуля, наш актив будет, скорее всего, расти (программист говорит: проведем миллион итераций и гарантированно увидим конечную цену, превышающую начальное значение). Наш выбор — среднее, равное 0. Что означает “нейтрально дрейфующую” цену ABS/USD.
- Стандартное отклонение. О нем тоже пойдет речь впоследствии. Величина, характеризующая волатильность нашего актива. Примем ее равной 0.5% или 0.005. Что примерно соответствует изменению цены в день на ± 0.5% в среднем.
Как интерпретировать эти данные? Возьмем первую пару чисел:
“СВ примет значение -0.015451 или меньше с вероятностью 0.001 (0.1%)”.
Вторая пара: “СВ примет значение -0.014391 или меньше с вероятностью 0.002 (0.2%)”. И т.д.
Метод обратной функции: мы случайным образом выбираем число в диапазоне от 0 до 1 (столбец A) и находим соответствующее ему значение обратной кумулятивной функции распределения (столбец B). Или же, в нашем случае, просто случайным образом выбираем число из столбца B.
Т.е., выбираем значение N в диапазоне от 0 до 999 и читаем содержимое ячейки BN+2BN+2:
- Формула ячейки B2: =НОРМ.ОБР(A2;0;0,005)
- Формула ячейки C2: =СЛУЧМЕЖДУ(0;999)
- Формула ячейки D2: =ДВССЫЛ(СЦЕПИТЬ(«B»;C2+2))
Вот мы и получили нормально распределенную случайную величину с математическим ожиданием 0 и среднеквадратичным отклонением 0.005.
В столбце D может быть сколько угодно значений. Нам понадобится 3650 значений — мы собираемся моделировать дневные изменения цены ABS/USD за 10 лет. Осталось сгенерировать собственно цену ABS/USD.
В столбце D мы имеем ряд величин ∆, а ∆, по формуле логнормального распределения, определена как
Δi=ln(pi/pi−1)∆i=ln(pi/pi−1)
Значит, цены ABS/USD, последующая и предшествующая, будут связаны функцией
pi=pi−1∗eΔpi=pi−1∗e∆
Перенесем столбец D на новый лист, скопировав его, а затем вставив значения, начиная с ячейки A3.
Теперь укажем начальную цену ABS/USD равную 1000 (USD за 1 ABS) — введем “1000” в ячейку B2:
В ячейку B3 введем “=B2*EXP(A3)” и скопируем это значение во все последующие ячейки — B4:B3652.
На этом подготовка исходных данных, наконец, завершена. Столбец B содержит ценовой ряд нашего эталонного актива ABS/USD. Ряд, обладающий характеристиками логнормального распределения со среднеквадратичным отклонением, равным 0.005 (0.5%). У меня получились такие значения:
Нет никакой гарантии, что у вас, если вы проделаете ровно те же вычисления в MS Excel, получатся ровно те же значения, так как исходные данные — случайная величина. И все же — согласитесь, график вполне походит на биржевую сводку?
Расчет премии по формуле Б-Ш
Раз уж у нас есть “эталонные” данные, проведем “эталонный” расчет. Мы считаем премию по “ванильному” европейскому CALL-опциону:
- текущая цена (S) равна 1000,
- страйк (X) равен 1000. Страйк равен текущей цене, такой опцион на сленге именуется “ванильным”,
- экспирация через 30 дней (T),
- объем сделки — один контракт.
Наш инструмент ABS — не акция, не облигация и не иная ценная бумага. Никаких дивидендов за обладание ABS владельцу не полагается.
Та самая формула — формула расчета премии за европейский опцион Call (значение C):
C=SN(d1)−Xe−rTN(d2)C=SN(d1)−Xe−rTN(d2)
d1=ln(SX)+(r+σ22)TσT−−√d1=ln(SX)+(r+σ22)TσT
d2=d1−σT−−√d2=d1−σT
Разберем параметры формулы.
- S и X нам уже известны — текущая (1000 USD) и страйк (1000 USD) цены актива, соответственно.
- T — время до экспирации, выраженное, как часть года. К примеру, наш контракт ABS торгуется 365 дней в году, подобно криптовалютным контрактам. Экспирация произойдет через 30 дней, следовательно, T = 30/365 ~ 0.082. Другой пример — опцион на EURUSD на Чикагской бирже, торгуется приблизительно 265 дней в году. Считаем количество торговых дней до конкретной даты — до дня экспирации. Скажем, мы посчитали 23 торговых дня. В таком случае параметр T будет равен 23/265 или примерно 0.087.
- r — безрисковая процентная ставка. Как мы уже отмечали, для актива ABS она равна 0.
- σ (сигма) — историческая волатильность актива. Здесь потребуется небольшое отступление.
Историческая волатильность
За волатильность мы берем среднеквадратичное отклонение (СКО), пересчитанное на годичный интервал. Приведу очередную формулу из Википедии:
S0=1n−1∑i=1n(xi−x¯¯¯)2−−−−−−−−−−−−−−−√S0=1n−1∑i=1n(xi−x¯)2
Как нам посчитать среднеквадратичное отклонение цен ABS/USD в MS Excel?
- Столбец C содержит разность текущего и предыдущего значения цен ABS, поделенную на предыдущее значение и умноженную на 100%.
- Ячейка D2 содержит среднее значение из столбца C.
- Столбец E содержит квадраты разности ценового отклонения (столбец C) и среднего значения ценового отклонения (ячейка D2, вторая строка “зафиксирована” в формуле символом $).
- Ячейка G2 — дисперсия, сумма квадратов отклонений, деленная на количество значений за вычетом 1 (SIC!).
- Наконец, ячейка H2 содержит искомое СКО — корень из дисперсии (G2).
Часть вычислений можно пропустить: достаточно посчитать столбец C (величины отклонений в процентах) и воспользоваться функцией Excel для нахождения среднеквадратичного (стандартного) отклонения — что мы и определили в ячейке I2 — функция “СТАНДОТКЛОН.В”.
Осталось пересчитать значение СКО (σ) на интервал один год. Наш ABS/USD торгуется 365 дней в году. Значение σ, рассчитанное для одного дня, надо умножить на корень квадратный из 365:
σY=σ365−−−√=0,4943%×19,105=9,443%σY=σ365=0,4943%×19,105=9,443%
Откуда взялся квадратный корень в формуле пересчета дневного значения среднеквадратичного отклонения в годовое? Заинтересовавшихся адресую в интернет, искать модель случайного блуждания, random walk (RW).
Расчет премии в Excel
Теперь, когда мы определили все параметры формулы Блэка — Шоулза, введем их значения и функции в Excel:
Сразу отмечу: значения T и σ я указываю в абсолютных величинах, не в процентах.
- Формула коэффициента d1 =(LN(B2/B3)+B4*(B6+B5*B5/2))/(B5*КОРЕНЬ(B4))
- d2 =H2-B5*КОРЕНЬ(B4)
- N(d1) =НОРМ.РАСП(H2;0;1; ИСТИНА)
- N(d2)=НОРМ.РАСП(H3;0;1; ИСТИНА)
- Наконец, премия CALL-опциона: =B2*СТЕПЕНЬ(2,71818;-B7*B4)*K2-B3*СТЕПЕНЬ(2,71818;-B6*B4)*K3
“Справедливая” премия за ванильный European CALL-опцион ABS/USD со страйком 1000 и экспирацией через 30 дней составила $10.80 за один контракт.
Расчет премии для “ненормального” ценового распределения
Выше утверждалось, что ценовая модель Б-Ш адекватна для логнормального распределения ценового ряда. Но насколько близок “реальный” рынок по своим характеристикам подобному закону распределения СВ? Точнее, насколько рынок далек от него?
Наш гипотетический актив ABS/USD характеризуется нормальным распределением логарифмов от частного соседних (текущая и предыдущая) цен. График плотности вероятности появления больших и малых отклонений цены (логарифмов) имеет классическую для нормального распределения форму, примерно такую:
Иначе говоря, имеет форму колокола, с “крутой” вершиной и “плечами”, или “хвостами”, быстро приближающимися к оси абсцисс по мере удаления от среднего значения (0).
Каким эмпирическим наблюдениям могли бы соответствовать для реального рынка эти самые “хвосты” нормального распределения?
Большие отклонения цены возможны, но имеют крайне низкую вероятность. Для графика, приведенного выше, можно сказать, что отклонение цены на +2% и более имеет вероятность 5%. А отклонение цены на +3% и более имеет уже околонулевую вероятность — какие-то незначительные доли процента.
“Реальному” рынку свойственно несколько иное поведение. А конкретно: большинство ценовых изменений лежат в довольно узком диапазоне, при этом, однако, существенна вероятность значительных ценовых колебаний. График плотности вероятностей ценовых отклонений для “реального” рынка примет вид приблизительно такой:
Повлияет ли тот факт, что характеристики распределения дневных отклонений цены для “реального” рынка отличаются от модели Б-Ш на точность расчета?
Очевидно, повлияет. Вопрос — насколько сильно будет ошибаться формула Б-Ш в своей оценке “справедливой” премии?
Моделирование “реальной” цены
Сейчас моя задача — генерировать новый ценовой ряд. Ценовой ряд, логарифмы от частного соседних цен в котором подчиняются некоторому “ненормальному” распределению — распределению, отличающемуся “толстыми хвостами”. Более того, я немного усложню себе задачу.
Итоговый ценовой ряд должен характеризоваться той же величиной исторической волатильности, что и ценовой ряд ABS/USD, построенный нами ранее.
Для примера приведу две кривых плотности распределения СВ: нормальное распределение (коричневая линия) и “реальное” распределение (синяя линия) — то, что мы хотим получить. С толстыми и длинными хвостами:
В нормальном распределении мы можем варьировать один параметр — среднеквадратичное отклонение (σ). Вот как выглядят два графика плотности нормального распределения с σ, равной 1 и 0.4 соответственно:
Оба графика — не совсем то, что нам бы хотелось. Тонкое “тело” графика для параметра σ = 0,4 — близко к желаемому. Но нам бы хотелось “хвостов” потолще. Иначе говоря — большой процент отклонений, концентрирующихся в окрестностях среднего значения (0), при все еще значимой вероятности больших (2% и более) ценовых отклонений.
Решение: сложить два графика. Я получу ту самую зависимость, что привел выше на рисунке как “реальную” плотность вероятности распределения цен.
Сейчас мы складывали значения функции плотности нормального распределения. Как же построить распределение, плотность которого будет соответствовать сумме двух функций нормального распределения с параметрами σ = 1 и σ = 0,4?
Очевидно (исправлено):
- сложить две (обратные) интегральные функции плотности нормального распределения,
- подставить в получившуюся функцию аргумент — равномерно распределенную СВ.
Проделаю примерно те же вычисления, что и раньше, при генерации ряда ABS/USD. Но теперь заполню два столбца функцией “НОРМ.ОБР”. Результирующая величина должна иметь годовое среднеквадратичное отклонение, равное 9.44% — как и в предыдущем примере. Этого я добьюсь, проведя несколько итераций подбора параметров, так как результат (сгенерированная выборка) недетерминирован:
- Столбцы C (R1), D (R2) содержат обратную функцию нормального распределения с параметрами 0.005 и 0.0015 соответственно.
- Столбец E (R ) — взвешенную сумму двух этих величин — 0,8 x R1 + 0,65 x R2.
- Столбец F (RND) — случайное число в диапазоне от 2 до 1000.
- Наконец, столбец G(∆) — случайным образом выбранную из столбца E (R ) ячейку. То распределение, которого мы добивались.
Осталось применить к полученному ряду формулу:
xi=xi−1∗eΔixi=xi−1∗e∆i
Сумму двух нормально распределенных случайных величин копируем в столбец A. В столбце B, как и раньше, мы умножаем предыдущее значение цены (начинается от 1000) на экспоненту от СВ из столбца A.
В итоге у меня получился следующий график цены WRD/USD:
Премия за опцион CALL для WRDUSD на тех же условиях контракта, что мы уже рассчитали ранее, останется неизменной, так как параметры в формуле Б-Ш не менялись. Напомню цифры: премия за ванильный European CALL-опцион WRD/USD со страйком 1000 и экспирацией через 30 дней составила $10.80 за один контракт.
Мы располагаем двумя активами, динамика цен на которые выражается разными законами:
| ABS/USD | WRD/USD | |
| Закон распределения цен | логнормальное распределение | «Реальное» распределение |
| Премия по формуле Б-Ш | $10.80 | $10.80 |
| “Справедливая” премия | ? | ? |
На этом этапе возможностей MS Excel мне уже недостает (их не достаёт автору статьи, а не автору https://Excellentricks.ru), пора переходить к программированию.
В начале 70-х годов прошлого века экономисты Фишер Блэк, Майрон Шоулз и Роберт Мертон вывели формулу ценообразования опционов Блэка–Шоулза, которая позволяет получить оценку европейских колл- и пут-опционов. За свою работу Шоулз и Мертон были удостоены Нобелевской премии по экономике в 1997 г. (Блэк умер до 1997 г., а Нобелевская премия не присуждается посмертно.) Их научный труд произвел революцию в области корпоративных финансов. В данной заметке приведены основные положения этой важной научной работы, а также показано, как рассчитать стоимость опциона с помощью Excel.[1]
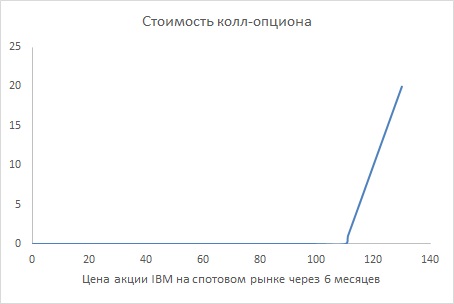
Рис. 1. Стоимость колл-опциона
Скачать заметку в формате Word или pdf, примеры в формате Excel
Основные сведения об опционах
Колл-опцион дает владельцу опциона право купить акцию (или иной актив, например, валюту) по цене исполнения. Пут-опцион дает владельцу опциона право продать акцию по цене исполнения.
Американский опцион может быть исполнен не позднее даты, известной как дата исполнения (часто называемой датой истечения срока действия опциона). Европейский опцион может быть исполнен только в последний день срока его действия.
Давайте рассмотрим итоги сделки по приобретению шестимесячного европейского колл-опциона на акции IBM с ценой исполнения 110 долларов. Пусть P — это курс акции IBM через шесть месяцев. Выигрыш от колл-опциона на эти акции составит 0 долларов, если P < 110 (зачем исполнять опцион, если цена акций на спотовом рынке ниже цены исполнения!?), и (P – 110) долларов, если P > 110. Если значение P больше 110 долларов, владелец может исполнить опцион, купив акцию за 110 долларов и немедленно продав ее на спотовом рынке за P долларов, и тем самым получить прибыль (P – 110) долларов. На рис. 1 представлен выигрыш по этому колл-опциону. Выигрыш можно записать как формулу в Excel =МАКС(0;Р-110). Если Р ≤ 110, говорят опцион не в деньгах.
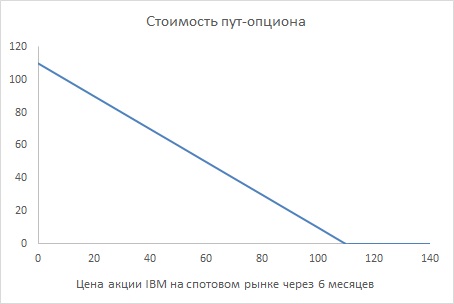
Ситуация с пут-опциона противоположна (рис. 2). Выигрыш по пут-опциону составит 0 долларов, если P > 110, и (110 – Р) долларов, если P < 110. Для значений P меньше 110 долларов владелец опциона может купить акцию за P долларов и немедленно продать ее за 110 долларов, реализуя опцион. Это принесет прибыль (110 – P) долларов. Если P больше 110 долларов, покупать акцию за P долларов и продавать за 110 долларов невыгодно, так что владелец не исполнит пут-опцион. Формула выигрыша =МАКС(0;110-Р).
Рис. 2. Стоимость пут-опциона
Параметры, определяющие цену опциона
При создании модели ценообразования Блэк, Шоулз и Мертон показали, что цена опциона зависит от следующих параметров:
- Текущая цена акции (или иного актива).
- Цена исполнения опциона.
- Время (в годах) до истечения срока действия опциона (называемое сроком опциона).
- Процентная ставка (в год с учетом сложных процентов) на безрисковые инвестиции (как правило, в казначейские векселя) в течение всего срока инвестирования. Например, если трехмесячные казначейские векселя приносят 5% дохода, безрисковая ставка вычисляется как ln(1 + 0,05). (Взятие логарифма преобразует простую процентную ставку в ставку с учетом сложных процентов.) Сложные проценты означают, что в каждый момент времени проценты приносят проценты.
- Годовая ставка (в процентах от курса акции), по которой выплачиваются дивиденды. Если акция приносит каждый год 2% своей стоимости в качестве дивидендов, норма дивидендов составляет 0,02.
- Волатильность акции (измеряемая в годовом исчислении). Годовая волатильность акции, например, 30% означает, что (приближенно) стандартное отклонение относительного годичного изменения курса акции составит примерно 30%. Во времена интернет-пузыря в конце 1990-х годов волатильность акций многих интернет-компаний превышала 100%. Этот важный параметр можно вычислить двумя способами.
В формуле ценообразования Блэка–Шоулза курс акции должен соответствовать логарифмически нормальному распределению.
Оценка волатильности акции на основе исторических данных
Для оценки исторической волатильности акции необходимо выполнить следующие шаги:
- Определить прибыль (убыток) по акции за несколько лет.
- Определить для каждого месяца ln(1 + прибыль).
- Определить стандартное отклонение для ln(1 + прибыль). Это вычисление дает ежемесячную волатильность.
- Умножить ежемесячную волатильность на для преобразования ежемесячной волатильности в годовую.
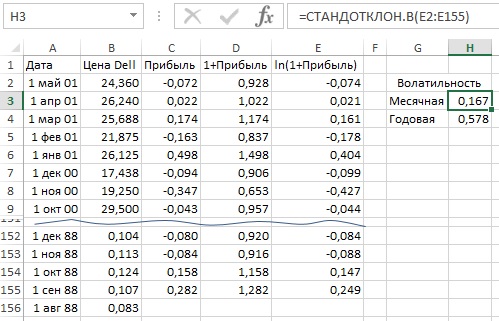
На рис. 3 приведены данные ежемесячной стоимости акций компании Dell за период с августа 1988 г. по май 2001 г. Прибыль равна разности цен за две соседние даты. Ежемесячная волатильность в ячейке Н3 определена по формуле =СТАНДОТКЛОН.В(E2:E155). (Если вам интересно в чем различие между двумя формулами Excel: СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г, см. здесь.) В ячейке Н4 используется формула =КОРЕНЬ(12)*H3. Годовая волатильность акций Dell составляет 57,8%.
Рис. 3. Вычисление исторической волатильности стоимости акций Dell
Формулу Блэка–Шоулза в Excel
Цена европейского колл-опциона вычисляется по формуле:
N(x) — вероятность того, что нормальная случайная величина со средним значением 0 и стандартным отклонением σ=1, меньше или равна x. Например, N(-1) = 0,16, N(0) = 0,5, N(1) = 0,84 и N(1,96) = 0,975. Нормальная случайная величина со средним значением 0 и стандартным отклонением 1 называется нормированной случайной величиной, распределенной по нормальному закону. Нормальное интегральное распределение в Microsoft Excel вычисляет функция НОРМ.СТ.РАСП. Формула =НОРМ.СТ.РАСП(x;ИСТИНА) возвращает вероятность того, что нормированная случайная величина, распределенная по нормальному закону, меньше или равна х. Например, формула =НОРМ.СТ.РАСП(-1;ИСТИНА), дает в результате 0,16. Это значение показывает, что нормальная случайная величина со средним значением 0 и стандартным отклонением 1 с вероятностью 16% примет значение менее -1.
S — текущий курс акции; t — срок опциона (в годах); X — цена исполнения; r — годовая безрисковая ставка (предполагается, что эта ставка постоянно вычисляется с учетом сложных процентов); σ — годовая волатильность акции; y — процент от стоимости акции, выплачиваемый в качестве дивидендов.
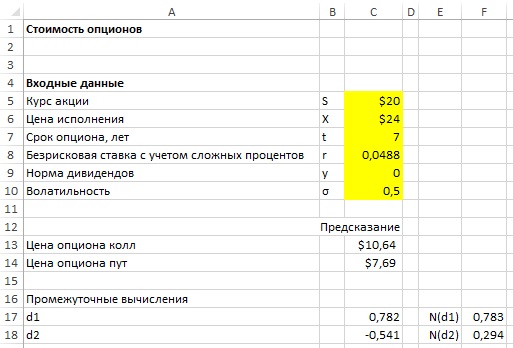
На рис. 4 находится шаблон, который вычисляет цену для европейских колл- и пут-опционов. Введите значения параметров в ячейки С5:С10 и получите цену европейского колл-опциона в С13, а цену европейского пут-опциона в С14. В качестве примера предположим, что акция Cisco сегодня продается за 20 долларов и вы выпустили семилетний европейский колл-опцион. Пусть годовая волатильность акции Cisco равна 50%, и безрисковая ставка в течение семилетнего периода исчисляется исходя из 5% в год. С учетом сложных процентов она преобразуется в ln(1+0,05) = 0,0488. Компания Cisco не выплачивает дивиденды, так что годовая норма дивидендов равна 0. Цена колл-опциона составляет 10,64 долл. Семилетний пут-опцион с ценой исполнения 24 доллара будет стоить 7,69 долларов.
Рис. 4. Определение цены европейских колл- и пут-опционов
Чувствительность стоимости опционов к росту основных параметров
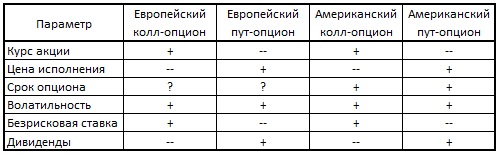
Как правило, влияние изменения входных параметра на цену колл- или пут- опциона соответствует указанному на рис. 5.
Рис. 5. Влияние роста входных параметров на стоимость опционов
Повышение сегодняшнего курса акции всегда повышает цену колл-опциона и снижает цену пут-опциона.
Повышение цены исполнения всегда повышает цену пут-опциона и снижает цену колл-опциона.
Увеличение срока опциона всегда повышает цену американского опциона. В случае выплаты дивидендов увеличение срока опциона может или повысить, или понизить цену европейского опциона.
Увеличение волатильности всегда повышает цену опциона.
Повышение безрисковой ставки повышает цену колл-опциона, поскольку более высокие ставки имеют тенденцию к увеличению темпов роста курса акции (что хорошо для колл-опциона). Эта ситуация отменяет тот факт, что в результате более высокой процентной ставки выигрыш по опциону уменьшается. Повышение безрисковой ставки всегда понижает цену пут-опциона, поскольку более высокие темпы роста курса акции, как правило, наносят ущерб пут-опциону, и будущий выигрыш по пут-опциону уменьшается. Как и в предыдущем случае, при этом предполагается, что процентные ставки не влияют на текущие курсы акций, однако это не так.
Дивиденды, как правило, снижают темпы роста курса акции, поэтому увеличенные дивиденды снижают цену колл-опциона и повышают цену пут-опциона.
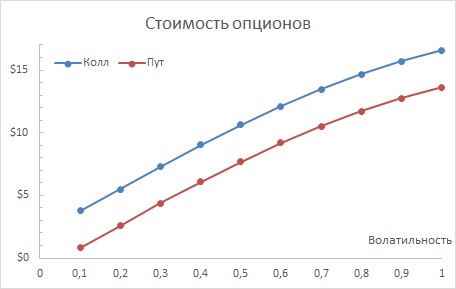
Конкретное влияние изменения параметров на цену колл- и пут-опционов можно исследовать с помощью таблицы данных (рис. 6), см. также Анализ чувствительности в Excel (анализ «что–если», таблицы данных).
Рис. 6. Анализ чувствительности опционов от волатильности
Оценка волатильности акции по формуле Блэка–Шоулза
Выше было показано, как на основе исторических данных оценить годовую волатильность акций. Проблема с оценкой исторической волатильности состоит в том, что анализ выполняется на основе прошлого. А в действительности требуется оценить волатильность акций на основе ожиданий. Подход на основе подразумеваемой волатильности просто оценивает волатильность акции как значение волатильности, при котором цена по формуле Блэка–Шоулза соответствует рыночной цене опциона. Иными словами, подразумеваемая волатильность получает значение волатильности, вытекающее из рыночной цены опциона.
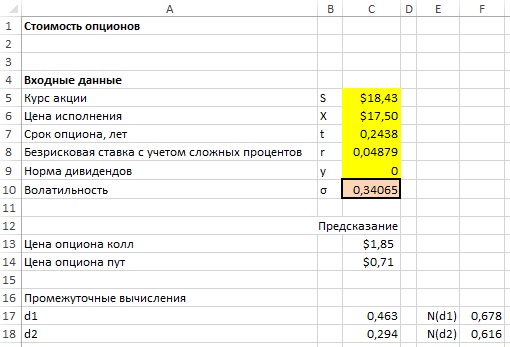
Для вычисления подразумеваемой волатильности можно воспользоваться инструментом Подбор параметра и описанными ранее входными параметрами (см. рис. 4). 22 июля 2003 г. акция Cisco продавалась за 18,43 долларов. В октябре 2003 г. колл-опцион с ценой исполнения 17,50 долларов продавался за 1,85 долларов. Срок действия этого опциона истекал 18 октября (через 89 дней в будущем). Таким образом, срок действия опциона составляет 89/365 = 0,2438 лет. Предположительно, Cisco не выплачивает дивиденды. Пусть ставка для казначейских векселей составляет 5%, и соответствующая безрисковая ставка равна ln(1 + 0,05) = 0,04879. Для определения волатильности акции Cisco, которая подразумевается ценой опциона, введите в ячейки B5:B10 (рис. 7) релевантные параметры.
Рис. 7. Вычисление волатильности акции Cisco согласно подразумеваемой волатильности
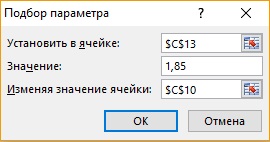
Далее в диалоговом окне Подбор параметра (Меню Данные –> Анализ «что-если»), показанном на рис. 8, определите волатильность (значение в ячейке B10), при которой цена опциона (формула в С13) достигает значения 1,85 долларов.
Как показано на рис. 7, этот опцион подразумевает годовую волатильность для Cisco в размере 34%.
Рис. 8. Настройки в диалоговом окне Подбор параметра
На сайте http://www.ivolatility.com/ и http://www.ivolatility.ru/ предоставляются оценки волатильности любой акции, как исторические, так и подразумеваемые.
Реальные опционы
Ценообразование опционов может повлиять на повышение эффективности долгосрочных инвестиций компании или на процесс принятия финансовых решений. Использование ценообразования опционов для оценки фактических инвестиционных проектов называется реальными опционами. Идею реальных опционов приписывают Джуди Левен, в прошлом финансовому директору компании Merck. По существу, реальные опционы позволяют назначить явную цену для управленческой гибкости, которую часто упускают из вида при традиционном составлении плана долгосрочных инвестиций. Рассмотрим два примера.
Пусть вы являетесь владельцем нефтяной скважины. Сегодня наиболее правдоподобное предположение о стоимости нефти в скважине — 50 млн. долларов. Через 5 лет (оставаясь владельцем скважины) вам предстоит принять решение о разработке нефтяной скважины, которая обойдется вам в 70 млн. долларов. Бизнесмен с сомнительной репутацией готов купить скважину сегодня за 10 млн. долларов. Следует ли продать скважину?
Безусловно, цена нефти через 5 лет может вырасти. Даже если предположить, что цена нефти будет расти на 5% в год, через 5 лет нефть будет стоить 63,81 млн долларов. Традиционный план долгосрочного инвестирования предполагает, что нефть обесценится, поскольку стоимость ее разработки превышает стоимость нефти в скважине. Но не торопитесь — через 5 лет цена нефти в скважине будет другой, т.к. многие вещи (такие как мировая цена на нефть) могут измениться. Существует вероятность, что через 5 лет нефть будет стоить не меньше 70 млн. долларов. Если через 5 лет нефть будет стоить 80 млн. долларов, разработка скважины через пять лет принесет 10 млн долларов.
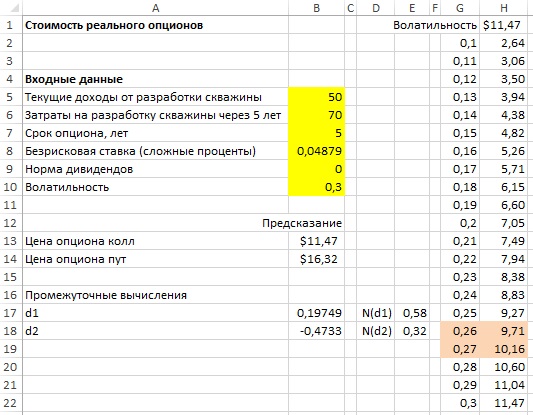
По сути, вы владеете пятилетним европейским колл-опционом на эту скважину, т.к. выигрыш от скважины через 5 лет такой же, как выигрыш по европейскому колл-опциону с курсом акции 50 млн. долларов, ценой исполнения 70 млн. долларов и сроком опциона 5 лет. Можно предположить, что годовая волатильность подобна волатильности акции типичной нефтяной компании (например, 30%). Если использовать безрисковую ставку 4,879%, можно определить, что цена такого колл- опциона составляет 11,47 млн. долларов (рис. 9). Из этого следует, что вы не должны продавать скважину за 10 млн. долларов.
Рис. 9. Реальный опцион на нефтяную скважину
Конечно, фактическая волатильность для этой нефтяной скважины неизвестна. По этой причине с помощью таблицы данных с одним входом определим, как цена опциона зависит от оценки волатильности (см. рис. 9). Как видно из таблицы, пока волатильность скважины составляет, по меньшей мере, 27%, опцион на нефтяную скважину стоит более 10 млн. долларов.
В качестве второго примера рассмотрим биотехнологическую компанию по производству лекарств, разрабатывающую лекарственный препарат для фармацевтической фирмы. В биотехнологической компании в настоящее время предполагают, что цена разрабатываемого препарата составляет 50 млн. долларов. Безусловно, цена лекарственного препарата со временем может понизиться. Для защиты от резкого падения цены биотехнологической компании требуется, чтобы препарат через 5 лет имел гарантированную цену 50 млн. долларов. Если страховая компания собирается подписать такое обязательство, какая справедливая цена должна быть назначена?
По существу, биотехнологическая компания запрашивает платеж в 1 млн. долларов для каждого миллиона долларов, на который цена препарата упадет ниже уровня 50 млн. долларов, через 5 лет. Это эквивалентно пятилетнему пут-опциону на цену лекарственного препарата. Предположим, что ставка по казначейскому векселю составляет 5% и годовая волатильность для акций сопоставимых компаний равна 40% (рис. 10), тогда цена этого опциона — 10,51 млн. долларов. Такой тип опциона часто называют опционом на отказ от проекта, но он эквивалентен пут-опциону. (На рис. 10 таблица данных показывает, как цена опциона отказа от проекта зависит от предполагаемой волатильности, составляющей 30–45% от цены лекарственного препарата.)
Рис. 10. Вычисление стоимости пут-опциона отказа от проекта
[1] Заметка написана на основе материалов из книги Уэйн Л. Винстон. Microsoft Excel 2013. Анализ данных и бизнес-моделирование, глава 78.
In finance, option pricing is a term used for estimating the value of an option contract using all known inputs. Monte Carlo Simulation is a popular algorithm that can generate a series of random variables with similar properties to simulate realistic inputs. In this guide, we’re going to show you how to calculate Option Pricing using Monte Carlo Simulations in Excel.
Download Workbook
Monte Carlo Simulation
Monte Carlo simulation is a special type of probability simulation which is mainly used to determine the risk factors by observing the cluster of possible results. First developed for finding the possible outcomes of a solitaire game, Monte Carlo takes its name from the famous casino in Monaco.
The simulation takes random values of the inputs within constraints and the results are recorded as more iterations are run. Then, you get a rather big pool of answers created from all those random inputs.
We can simulate the possible future stock prices and then use them to find the discounted expected option payoffs.
Using the statistical formulas NORM.S.INV and VBA, we can generate random variables in normal distribution and run the simulation as many times as necessary..
European-style Options Pricing
In this example, we are going to be using the Black-Scholes formula to calculate a European-style option pricing model, which restricts its options execution until the expiration date. There are two major types of options: calls and puts.
- Call is an option contract between the buyer and the seller of the call option, to exchange a security at a set price.
- Put is an option contract which gives the purchaser of the put option the right to sell an asset, at a specified price, by a specified date to the seller of the put.
The Black-Scholes formula is a popular approach for calculating European put and call options. In its simplest form, the Black-Scholes model involves underlying assets of a risk-free rate of return and a risky share price. The following equation shows how a stock price varies over time:
St = Stock price at time t
r = Risk-free rate
t = time
σ = T he volatility of the stock’s returns; this is the square root of the quadratic variation of the stock’s log price process
ε = random generated variable from a normal distribution
δ = Dividend yield which was not in the Black-Scholes model originally. The original model was for pricing options on non-paying dividends stocks.
Once the formula is run thousands or million times, you will have the set of St values. The payoff values can be calculated with the following formula, where K is the strike price:
Calculating Option Pricing with VBA
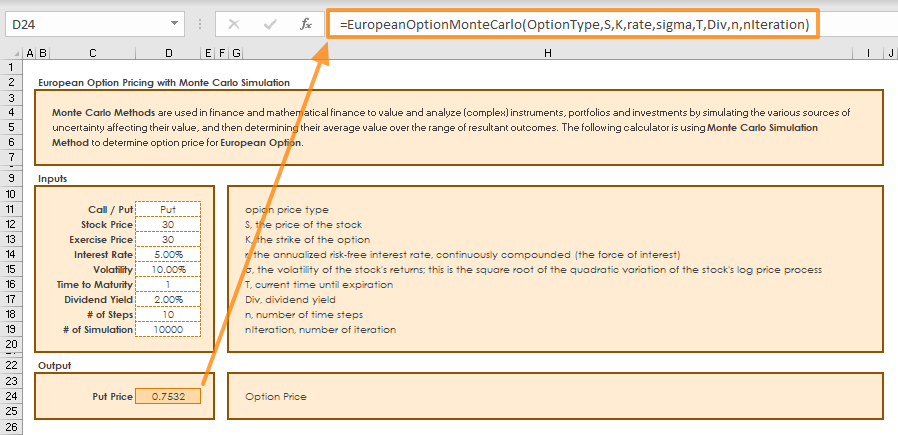
Let’s pass these formulations into a VBA code. We are going to create a user defined function (UDF) which can be used as a built-in function like SUM or VLOOKUP. Our function name is “EuropeanOptionMonteCarlo”.
Public Function EuropeanOptionMonteCarlo(OptionType As String, S As Double, K As Double, r As Double, sigma As Double, T As Double, Div As Double, N As Double, nIt As Double)
Dim i As Integer, j As Integer
Dim Payoff() As Double, St As Double, dt As Double, e As Double, price As Double
ReDim Payoff(1 To nIt)
dt = T / N
Randomize 'new seed for random number generation
For i = 1 To nIt
St = S
For j = 1 To N
e = WorksheetFunction.NormSInv(Rnd()) 'random factor
St = St * Exp((r - Div - sigma ^ 2 / 2) * dt + sigma * Sqr(dt) * e) 'European option formula
Next j
If OptionType = "Call" Then 'Call or Put
Payoff(i) = WorksheetFunction.Max(St - K, 0) * Exp(-r * T)
ElseIf OptionType = "Put" Then
Payoff(i) = WorksheetFunction.Max(K - St, 0) * Exp(-r * T)
End If
Next i
For i = 1 To nIt
price = price + Payoff(i) 'Total of iterations
Next i
EuropeanOptionMonteCarlo = price / nIt 'Return average of iterations as the function's result
End Function
Once the UDF is ready, we are ready to see the result in Excel.
Всем привет!
У опционных трейдеров очень часто возникает вопрос, как тестировать опционные стратегии? Попробую описать самый простой способ.
И так. Нам понадобится:
1.Excel (уменя Microsoft Office Excel 2003)
2.Данные с биржи РТС (ftp://ftp.rts.ru/pub/FORTS/volat_coeff/) вфайле ftp://ftp.rts.ru/pub/FORTS/volat_coeff/Volat_description.doc подробно описан формат данных.
3.Конвертор. Необходимо извлечь и обработать нужные нам данные.
Приступим.
Создаем на диске папку option (у меня она будет на диске h:)
Скачиваем в неё файл ftp://ftp.rts.ru/pub/FORTS/volat_coeff/201303.7z. В нем данные за март 2013 года. Распаковываем архив в эту же папку.
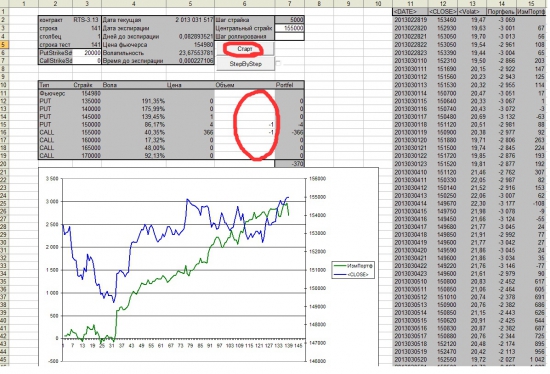
Открываем Excel. Создаем новый файл. Называем лист «1». Сохраняем его как Конвертор.xls. На листе «1» создаем кнопку и называем ее, например, Старт. Кнопка должна исполнить функцию StartSplitTextFile.
В ячейке A1 указываем путь к нужному файлу H:optiom201303.csv. В ячейке A2 указываем необходимый нам контракт RTS-3.13. Создаем лист «2» потом он нам пригодится.
Жмем кнопку старт и ждем (ждать придется долго, минуты 3). После работы конвертора будет создан файл 201303(1).csv. Открываем его в Excel. Выделяем столбцы D:K, жмем Ctrl+F, выбираем вкладку Заменить. Заменяем точку на запятую. Выделяем столбцы A:K, жмем Ctrl+C, переходим к файлу Конвертор.xls, выбираем лист «2», ячейку A1 и жмем Ctrl+V.
У нас получилось 5080 строк. А нам столько надо? Допустим нам нужны данные только каждый час. Удалим все лишнее. Создадим на листе «2» кнопку «1 час». Она оставит нам только нужные данные. (140 строк).
Все, данные готовы, можем писать тестер.
Создаем файл тестер.xls. Одну страничку называем «архив», вторую тест. В архив вставляем очищенные данные из файла конвертор.
Приступаем к самому интересному. Нам понадобятся формулы кривой улыбки биржи РТС, и формула расчета стоимости опциона.
Идем на сайт РТС за формулой.
1) http://fs.rts.ru/files/5570
2) http://fs.rts.ru/files/5562
Осталось самую малость, написать все это на VB.
Создаем функции Volat и OPrice. Первая будет рассчитывать текущую волатильность опциона, а вторая его цену.
Создаем кнопку старт, StepByStepи CheckBox. Пишем небольшой код и… Ура! Все работает.
Если нужно прогнать не сразу, а шаг за шагом, есть кнопка StepByStep. Ставим галочку рядом с кнопкой, жмем Старт, и дальше StepByStep.
Кстати расчет прошел за 3 секунды.
Кому интересно, пишите комментарии. Позднее, всем заинтересовавшимся скину ссылки на сами файлы.
Simplified
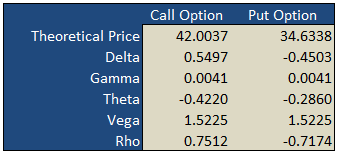
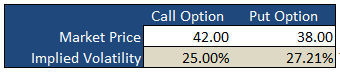
On the «basic» worksheet tab you will find a simple option calculator that generates fair values and option Greeks for a single call and put according to the underlying inputs you select. The white areas are for your user input while the shaded green areas are the model outputs.
Implied Volatility
Underneath the main pricing outputs is a section for calculating the implied volatility for the same call and put option. Here, you enter the market prices for the options, either last paid or bid/ask into the white Market Price cell and the spreadsheet will calculate the volatility that the model would have used to generate a theoretical price that is in-line with the market price i.e. the «implied» volatility.
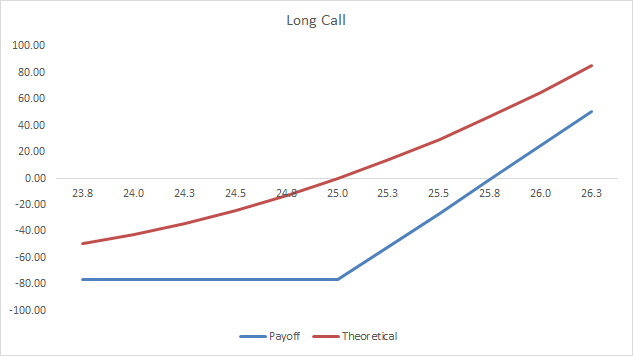
Payoff Graphs
The PayoffGraphs tab gives you the profit and loss profile of basic option legs; buy call, sell call, buy put and sell put. You can change the underlying inputs to see how your changes effect the profit profile of each option.
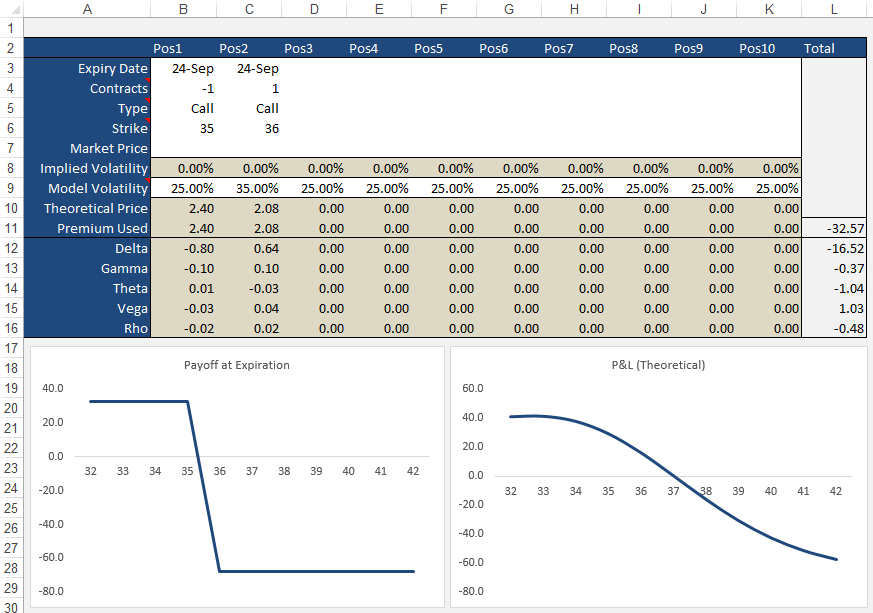
Strategies
The Strategies tab allows you to create option/stock combinations of up to 10 components. Again, use the while areas for your user input while the shaded areas are for the model outputs.
Formulas
Theoretical and Greek Prices
Use this Excel formula for generating theoretical prices for either call or put as well as the option Greeks:
=OTW_BlackScholes(Type, Output, Underlying Price, Exercise Price, Time, Interest Rates, Volatility, Dividend Yield)
- Type
- c = Call, p = Put, s = Stock
- Output
- p = theoretical price, d = delta, g = gamma, t = theta, v = vega, r = rho
- Underlying Price
- The current market price of the stock
- Exercise Price
- The exercise/strike price of the option
- Time
- Time to expiration in years e.g. 0.50 = 6 months
- Interest Rates
- As a percentage e.g. 5% = 0.05
- Volatlity
- As a percentage e.g. 25% = 0.25
- Dividend Yield
- As a percentage e.g. 4% = 0.04
A Sample formula would look like =OTW_BlackScholes(c, p, 25, 26, 0.25, 0.05, 0.21, 0.015).
Implied Volatility
=OTW_IV(Type, Underlying Price, Exercise Price, Time, Interest Rates, Market Price, Dividend Yield)
Same inputs as above except:
- Market Price
- The current market last, bid/ask of the option
Example: =OTW_IV(p, 100, 100, 0.74, 0.05, 8.2, 0.01)
Support
If you’re having troubles getting the formulas to work, please check out the support page or send me an email.
If you’re after an online version of an option calculator then you should visit Option-Price.com
Just to note that much of what I have learnt that made this spreadsheet possible was taken from the highly acclaimed book on financial modeling by Simon Benninga — Financial Modeling — 3rd Edition
If you’re an Excel junkie, you’ll love this book. There are loads of real world problems that Simon solves using Excel. The book also comes with a disk that contains all the exercises Simon illustrates. You can find a copy of Financial Modeling at Amazon of course.
Модель ценообразования опционов (Option Pricing Model, OPT) может быть эффективно использована для любых производных финансовых инструментов. Вывод формулы ценообразования опционов позволили на практике использовать их преимущества, об этом свидетельствует небывалый рост объема торгов по производным ценным бумагам. Модель Блэка- Шоулза основывается на следующих предположениях:
- Дивиденды не выплачиваются по базовому активу опциона колл;
- Нет транзакционных издержек, связанных с продажей или покупкой акций или опциона;
- Безрисковая процентная ставка постоянная и не меняется со временем;
- Разрешение короткой продажи без ограничений;
- Опцион колл исполняется только к по истечению срока опциона;
- Доходности ценных бумаг подчинены логнормальному закону распределения (очень важное предположение!).
Использование опционов позволяет минимизировать возможные риски неблагоприятного изменения курсовой стоимости. Для того что бы застраховать базовый актив необходимо купить опцион, можно сказать, что цена опциона представляет собой некоторую надбавку к первоначальной стоимости базового актива. Формула расчета цены опциона «колл» представлена ниже:
где: S – цена базового актива; Х – цена исполнения опциона; T –срок погашения опциона; r- процентная ставка; σ –стандартное отклонение доходностей акций; N – величина стандартного нормального распределения.
По теореме о паритете «пут-колл», что бы рассчитать стоимость опциона «пут» с тем же базовым активом и тем же сроком исполнения воспользуемся формулой:
На практике часто случается ситуация, когда на рынке нет подходящего опциона «пут» для нашего базового актива, так же иногда возникает необходимость застраховать не один актив, например акцию, а целый инвестиционный портфель. На индексные портфели, которые повторяют динамику рыночного индекса (RTSI, S&P&100, S&P500 ) скорей всего найдутся соответствующие опционы, но для большинства инвестиционных портфелей их нет.
Для того, что бы решить данную проблему воспользуемся моделью ценообразования опционов Блека – Шоулза (Скоулза). Как мы помним, опцион «пут» представляет собой совокупность базового актива (инвестиционный портфель) и безрисковой ценной бумаги, где доли вложенных средств в этот портфель постоянно корректируются. Под безрисковыми ценными бумагами будем подразумевать вложения в облигации.
И так, попробуем смоделировать страхование инвестиционного портфеля, используя модель ценообразования Блека- Шоулза, где в соответствии ей будем распределять средства нашего инвестиционного портфеля между акциями и облигациями.
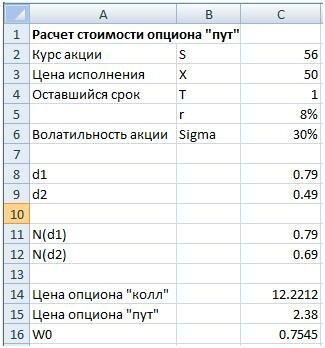
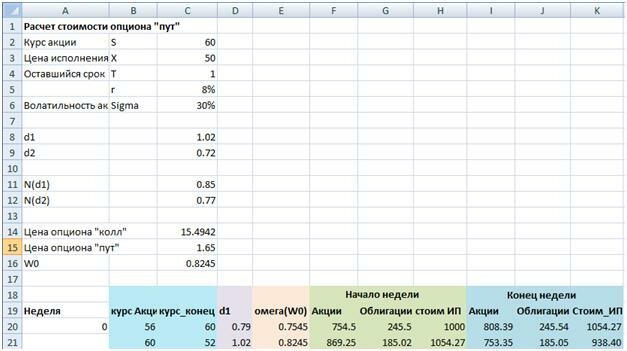
Предположим мы располагаем капиталом в1000$ и решаемся вложится в акцию(инвестиционный портфель) на срок 1 год. Сейчас акция стоит 56$, смоделируем страхование вложения в акцию, что бы по истечению одного года стоимость акции составила не менее 50$. Так же предположим, что на рынке нет опционов, дающих нам такое страхование. Поэтому создадим собственный опцион за счет вложения средств в акции и безрисковые облигации. Безрисковая процентная ставка составляет 8%. Волатильность акций составляет 30%.
Для облегчения расчетов воспользуемся пакетом Excel. Для расчета доли вложения в акции воспользуемся формулой:
Для расчета долей облигаций в нашем инвестиционном портфеле необходимо 1-w0.
Рассчитаем стоимость опциона «пут»(P0) и другие необходимые переменные по приведенным в начале статьи формулам.
S= первоначальная стоимость акции;
Х= цена исполнения опциона;
Т= срок исполнения опциона;
r= процентная ставка по безрисковым облигациям;
Sigma = волатильность акции;
d1= (LN(C2/C3)+(C5+0.5*C6^2)*C4)/(C6*КОРЕНЬ(C4)); d2=C8-C6*КОРЕНЬ(C4); N(d1) =НОРМСТРАСП(C8); N(d2) =НОРМСТРАСП(C9); Цена опциона «колл»=C2*C11-C3*EXP(-C5*C4)*C12; Цена опциона «пут»= C14-C2+C3*EXP(-C5*C4); W0 =C2*C11/(C2+C15) - доля капитала вложенного в акции.
Далее рассчитаем размер инвестированного капитала в акции и облигации. Данные по курсу акции на начало недели, конец недели, d1 и омеги (W0) заносим в таблицу. Так как вначале мы располагали 1000$, то в акции необходимо будет вложить Н20*W0 средств, объем средств по облигациям составит (1-W0)*Н20. К концу недели курс акций составил 60$, то есть рост составил 60/56=1.07. Стоимость акций увеличилась =(60/56)*F20 и стала составлять 808.39$. Рост стоимости облигаций постоянен и через неделю составил 1,00154 = exp^((1/52)0,008). Совокупная стоимость инвестиционного портфеля рассчитывается как сумма стоимости акций и облигаций на конец недели.
Далее рассчитаем следующую неделю. Возьмем курс акции на начало недели 60$, тогда стоимость ИП на начало недели будет составлять 1054.27$. Далее рассчитаем омегу (W0), и распределение капитала между акциями и облигациями. Предположим, что курс на конец недели снизился и составил 52$, стоимость пакета вложенного в акции сократится в 52/60 раз и составит 753.35$, пакет облигаций вырастет и составит 185.05$. Суммарная стоимость инвестиционного портфеля к концу недели составит 938.40$.
Далее можно смоделировать изменение курса с помощью генератора случайных чисел из надстройки «Анализ данных» -> «Генератор случайных чисел».
Смоделируем различный курс акций и заполним далее таблицу. У нас получится следующая картина. Помимо расчетов долей для распределения акций и облигаций рассчитаем изменения доходности инвестиционного портфеля при пассивном управлении, то есть изменения стоимости портфеля при однократном вложении без распределения средств между акциями и облигациями. В колонке «М» по формуле проведем расчет:
Стоимость ИП при пассивном управлении=M20+M20*(C21-B21)/B21;
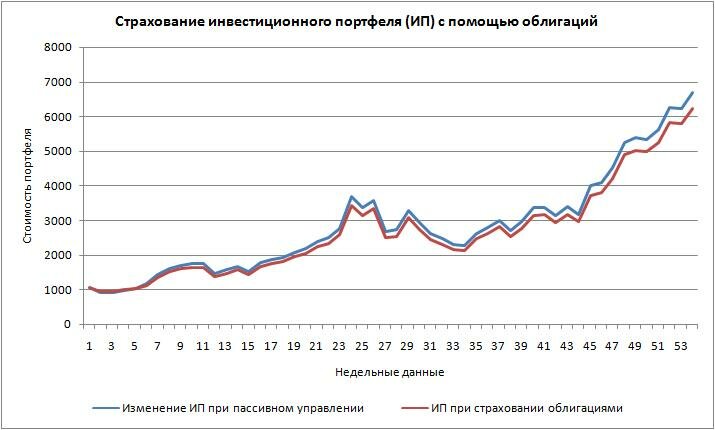
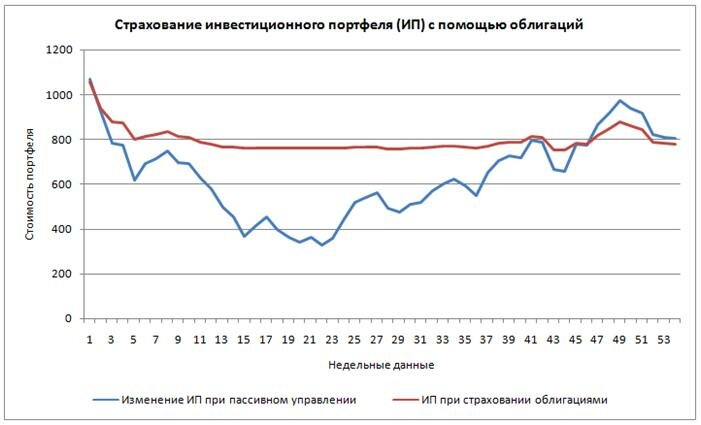
Построим график изменения динамики инвестиционного портфеля с пассивным управлением и со страхованием с помощью облигаций по опционной модели Блэка –Шоулза. Как видно, при снижении стоимости акции, портфель с пассивным управлением копировал динамику стоимости акции, портфель же с использованием страхования показал меньшую просадку депозита.
Если использовать страхование на растущем рынке, когда наблюдается рост стоимости акции, то использование данной схемы страхования снизит прибыль портфеля. На рисунке ниже, показана динамика портфеля с использованием страхования и без него.
Заключение: Использование страхования с помощью облигаций на основе модели опционного ценообразования Блэка –Шоулза позволяет значительно снизить просадки капитала. На растущем рынке, где значительных убытков не наблюдается, использование страховки отразится на меньшем росте такого портфеля, так как часть средств будет вложена в облигации, обладающих меньшей доходностью.