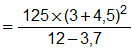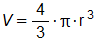Есть задачка. Нужно составить формулу в Excel. Есть горизонтальное хранилище формой «шаровый сегмент — цилиндр — шаровый сегмент». Дано: длина хранилища, уровень жидкости в хранилище, диаметр цилиндрической части и высота шарового сегмента. Задача в следующем: нужно в Excel`e написать формулу по расчету объема жидкости в хранилище. Если кто-нить может помочь — не будьте равнодушными. Мне очень очень нужна эта формула. Заранее благодарен.
to Serge 007
Цитата: Serge 007 от 06.09.2010, 20:20
А одного форума мало?
Сергей, ну не согласен я с Вами…
Дублировать темы на 1-ом форуме — нельзя
а регистрироваться и задавать вопросы на разных форумах — никто не запрещал
to GhostR
Вы второй раз наступаете на одни и те же грабли
уважайте свое и чужое время. никто Вам не будет сидеть и составлять за Вас таблицы. составьте сами какая вам нужна
ВОТ ТАК ЕСТЬ и ВОТ ТАК ХОЧУ
и еще один небольшой совет. Все граммотные програмисты знают друг друга и все общаются на всех форумах
дублирование вопроса на другом сайте — это не факт что там другие «знатоки » и они умнее чем здесь
Выкладываю образец файла.
Цитата: 0mega от 06.09.2010, 22:39
Все граммотные програмисты знают друг друга и все общаются на всех форумах
дублирование вопроса на другом сайте — это не факт что там другие «знатоки » и они умнее чем здесь
Я вовсе не хотел сказать что тут или там «знатоки» умнее или наоборот. Я всего лишь прошу помочь.
Если я правильно понял, то мало данных: еще нужно знать радиус шарового сегмета
Отдельное спасибо можно на QiWi-кошелек 909-771-53-87 или ЯД 41001136675053
Цитата: _Boroda_ от 07.09.2010, 13:14
Не очень понятно как цепляются между собой цилиндр и шары? Если радиус шара больше радиуса цилиндра, то все нормально. На сечении мест сцепки будет выглядеть как хорда, перпендикулярная горизонтальной плоскости. А вот если R шара меньше R цилиндра (как и указано в условии), то как-то не рисуется у меня в голове эта картинка. Возможно, это просто я что-то не догоняю. Покажите рисунок Вашего хранилища.
Радиус шара по-любому больше радиуса цилиндрической части. Рисунок у Михаил С. постом ниже верный, только 152.5 — это радиус, а не диаметр.
Цитата: Михаил С. от 07.09.2010, 15:17
Если я правильно понял, то мало данных: еще нужно знать радиус шарового сегмета
Увы радиус шара не реально померять рулеткой, нужны чертежи. Но, я точно знаю что каким-то образом можно и без радиуса шара посчитать, т.к. метрологи берут именно те размеры что я дал, а радиус шара они точно не учитывают.
Вообще то я не прав — имеем три точки — начало, конец и высоту дуги — дуга орпеделяется однозначно…
Задача чисто геомеотрическая, я геометрию изучал примерно 30 лет назад, счас подзабыл… смотрите справочники по определению объемов цилиндрических и сферическх тел….
Отдельное спасибо можно на QiWi-кошелек 909-771-53-87 или ЯД 41001136675053
Может и я на что сгожусь … Если сгодился, можете меня по+благодарить+.
нарисовал для наглядности:
Для горизонтального цилиндра с плоскими днищами все понятно, формула есть и она работает. В Excel она выглядит так:
=(A2*B2^2*(ACOS((B2-C2)/B2)-((B2-C2)/B2)*(1-((B2-C2)/B2)^2)^0,5))/1000000
где:
А2 — длина цилиндра
B2 — радиус
C2 — высота наполнения емкости
А математически как на вложенном файле:
З.Ы. Добавить бы к этой формуле сферические сегменты по обе стороны
Люди помогите закинуть в Excel такой интеграл:
V2 = 2*int_(R-B)^R dx*int_(R-h)^R dy*sqrt(R^2 — x^2 — y^2)
R — в ячейке A1
B — в B1
h — в C1
V2 — в D1
это решение по определению объема жидкости в сферической части хранилища.
Общая формула
=PI()*r^2*h
Резюме
Чтобы вычислить объем цилиндра, вы можете использовать функцию PI вместе с оператором экспоненты (^). В показанном примере формула в D5, скопированная ниже, имеет следующий вид:
=PI()*B5^2*C5
который возвращает объем цилиндра с радиусом, указанным в столбце B, и высотой, указанной в столбце C. Единицы измерения обычно обозначаются буквой «u», а результирующий объем является кубическими единицами (u 3 ).
Объяснение
В геометрии формула для расчета объема цилиндра выглядит так:
Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с функцией PI, которая возвращает число 3,14159265358979 с точностью до 15 цифр:
=PI() // returns 3.14159265358979
Чтобы возвести число в квадрат в Excel, вы можете использовать оператор возведения в степень (^):
=A1^2
Или вы можете использовать функцию POWER:
=POWER(A1,2)
Переписывая формулу объема цилиндра математическими операторами Excel, получаем:
=PI()*B5^2*C5
Или с помощью функции POWER:
=PI()*POWER(B5,2)*C5
Результат одинаков для обеих формул. В соответствии с порядком операций в Excel, возведение в степень выполняется перед умножением.
Формула объема в таблице в Excel помогает быстро посчитать объем нужной фигуры, а сделать это можно при помощи инструкции выше.
- Параллелепипед;
- Сфера;
- Пирамида;
- Цилиндр;
- Конус.
Видеоинструкция
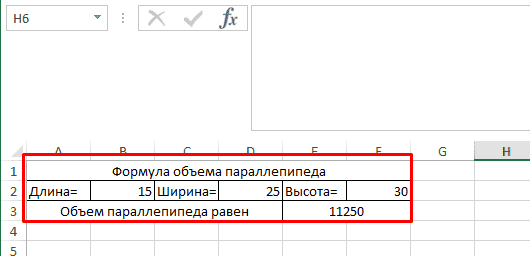
Формула объема параллелепипеда в Excel
Для этого потребуется использовать формулу:
=(Длина)*(Ширину)*(Высоту)
Пример можно скачать ниже:
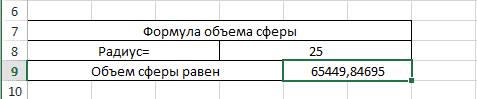
Сфера
Для шара можно воспользоваться конструкцией:
=(4/3)*ПИ()*(D8^3)
Пример:
Пирамида
В этом случае можно воспользоваться:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример:
Цилиндр
Задачу с данной фигурой можно решить через:
=ПИ()*C14*C14*F14
Пример:
Конус
В случае с конусом объем вычисляется через формулу:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример:
Опубликовано 02 Авг 2013
Рубрика: Справочник Excel | 5 комментариев

…Оказывается — очень многое.
Надстройка «Поиск решения» позволяет найти оптимальные значения аргументов в задачах «на экстремум» и иных задачах оптимизации функции нескольких переменных при заданных ограничивающих условиях. Слишком мудрено? Давайте рассмотрим практический пример — и все станет просто и понятно!
При проектировании и изготовлении любой емкости для хранения газов, жидкостей, сыпучих твердых материалов разработчик часто стремится получить максимальный объем при минимальной площади поверхности — при этом наиболее рационально и с пользой расходуется материал. Безусловно, в погоне за экономией материалов нельзя забывать вопросы прочности и жесткости стенок резервуара, а так же вопросы технологичности последующих эксплуатации и обслуживания емкости.
Формулируем условие задачи:
Из имеющегося в наличии стального листа толщиной 4 мм стандартных размеров 1,5 м на 6,0 м необходимо сварить бак для воды (дно и боковые стенки без крышки), например, на дачу максимального объема, оптимальной формы, с удобным и простым раскроем, с минимальной трудоемкостью изготовления.
Конечно, всем известно, что максимальный объем при минимальной площади поверхности имеет шар, но сложность и трудоемкость его изготовления, а так же неудобства эксплуатации и обслуживания «съедают» всю выгоду от минимального расхода материала. К тому же реальный коэффициент использования материала из-за криволинейного раскроя далек от единицы. Емкости-шары применяют для хранения газов под давлением для обеспечения равномерного распределения возникающих в стенке сосуда напряжений и исключения зон концентрации напряжений, приводящих к разрушению объектов. При поиске решения для нашей задачи мы шар рассматривать не будем.
Для решения поставленной задачи привлечем в помощь Excel.
При отсутствии на вашем компьютере программы MS Excel можно выполнить расчет в программе Calc из бесплатного пакета Open Office. Надстройке «Поиск решения» MS Excel в OOo Calc соответствует «Решатель».
Исходные данные — в ячейках со светло-бирюзовой заливкой, результаты расчетов — в ячейках со светло-желтой заливкой. Результаты работы надстройки «Поиск решения» — в ячейках с золотистой заливкой.
Открываем лист Excel и заполняем таблицу с параметрами прямоугольной листовой заготовки:
1. Толщину листа S в миллиметрах заносим
в ячейку D3: 4,000
2. Ширину листа В в метрах пишем
в ячейку D4: 1,500
3. Длину листа L в метрах пишем
в ячейку D5: 6,000
Предварительные расчеты в Excel выполняем по формулам:
4. Площадь поверхности (с одной стороны) A0 в метрах квадратных считаем
в ячейке D6: =D4*D5=9,000
A0=B*L
5. Массу G в килограммах (для справки) рассчитываем
в ячейке D7: =D3/10*D4*100*D5*100*7,85/1000=282,600
G=S*B*L*7,85

Первой проанализируем цилиндрическую форму емкости с круговым дном:
1. Записываем формулу для расчета площади поверхности A1 в квадратных метрах
в ячейку G13: =ПИ()*E13^2/4+ПИ()*E13*F13
A1=3.14*y^2/4+3.14*y*z
2. Записываем формулу для расчета объема бака V в кубических метрах
в ячейку H13: =ПИ()*E13^2/4*F13
V=3.14*y^2/4*z
3. Вызываем диалоговое окно надстройки «Поиск решения» (в Excel 2003: Сервис – Поиск решения…) и заполняем так, как на снимке экрана, представленном ниже.
Мы хотим получить в целевой ячейке H13 (V — объем бака) максимальное значение, изменяя значения ячеек E13 (y — диаметр бака) и F13 (z — высота бака). При этом мы сообщаем Excel ограничения: E13 (диаметр бака) и F13 (высота бака) – это положительные числа, а значение в ячейке G13 (A1 — площадь поверхности) равно значению в ячейке D6 (A0 — площадь листа-заготовки).
Таким образом, мы сформулировали задачу поиска диаметра и высоты цилиндрического бака из конкретного количества материала для получения максимального объема. О том, что это цилиндр с круглым дном, но без крышки «сказано» в формулах расчета A1 и V.
4. Нажимаем кнопку «Выполнить» окна Поиск решения». Окно «Поиск решения» исчезает и появляется окно «Результаты поиска решения». При этом найденные значения мгновенно отображается в соответствующих ячейках:
5. Диаметр бака y в метрах считываем
в ячейке E13: 1,954
6. Высоту бака z в метрах считываем
в ячейке F13: 0.977
7. Площадь поверхности бака A1 в метрах квадратных считываем
в ячейке G13: 9.000
8. Объем бака V в метрах кубических считываем
в ячейке H13: 2.932
9. Нажимаем на кнопку «ОК» — сохраняем найденное решение
10. Анализируем полученные результаты и делаем выводы:
— цилиндрическая емкость с дном и без крышки имеет максимальный объем и минимальную площадь поверхности при диаметре в два раза большем высоты;
— сделать технологически приемлемый и экономичный раскрой листа 1,5 м на 6,0 м для изготовления бака диаметром 1,954 м и высотой 0,977 м достаточно сложно (практически невозможно раскроить без отходов).
Попробуем изменить ограничения: зададим высоту бака z=1.5 м – по ширине исходного листа, а диаметр y=L/(3.14+1) – из условия, что в длину исходного листа должны вложиться донышко и стенка. Площадь поверхности A1 – положительное число. Раскрой деталей при этом будет предельно прост.
1. Формулу для расчета диаметра бака y в метрах записываем
в ячейку E14: =D5/(ПИ()+1)=1.449
2. Высоту емкости z в метрах заносим
в ячейку F14: 1.500
3. Копируем формулу для расчета площади поверхности A1 в квадратных метрах
в ячейку G14: =ПИ()*E14^2/4+ПИ()*E14*F14=8.475
4. Копируем формулу для расчета объема бака V в кубических метрах
в ячейку H14: =ПИ()*E14^2/4*F14=2.473
5. Анализируем полученные результаты и делаем вывод:
— в сравнении с предыдущим вариантом мы получили высокотехнологичный раскрой, минимум сварных швов, но «расплатились» за это уменьшением объема бака на 15,7%.
Далее выполним анализ формы емкости в виде параллелепипеда:
По сути — это тоже цилиндр с прямоугольным дном в основании.
Работаем с надстройкой «Поиск решения» по расписанному выше алгоритму. Отличие только в том, что переменных теперь не две, а три – ширина x, длина y, высота z. И формулы для расчета площади поверхности и объема для параллелепипеда другие:
A1=x*y+2*x*z+2*y*z
V=x*y*z
Я не буду подробно расписывать все шаги работы с параллелепипедом – они аналогичны расписанной выше по шагам работе с круговым цилиндром! Изучите самостоятельно результаты в таблице по баку-параллелепипеду максимального объема без крышки.
Лучшими решениями поставленной в начале статьи задачи с точки зрения математики без учета технологичности раскроя и трудоемкости изготовления являются варианты №1 и №3.
Лучшими практическими решениями задачи являются, безусловно, варианты №2, №5 и №6!
Какие можно сделать в итоге выводы?
1. При изготовлении цилиндрической емкости без крышки для наиболее эффективного использования материала следует высоту бака делать равной радиусу основания!
2. При изготовлении цилиндрической емкости без крышки с высотой равной радиусу основания для наиболее эффективного использования материала следует в качестве заготовки брать прямоугольный лист с отношением сторон 1/(1+3,14/2)=1 / 2,57!
3. При изготовлении емкости в виде параллелепипеда без крышки для наиболее эффективного использования материала следует основание делать квадратным, а высоту бака делать равной половине размера основания!
4. При изготовлении емкости в виде параллелепипеда без крышки с квадратным основанием и высотой равной половине размера основания для наиболее эффективного использования материала следует в качестве заготовки брать прямоугольный лист с отношением сторон 1/3!
5. Чем больше емкость по размерам, тем меньше нужно квадратных метров листового материала на кубический метр объема!
6. Замечательный инструмент в Excel «Поиск решения» — легко и просто решает задачи с несколькими переменными! Рекомендую!!!
7. Чтобы «хранить» на даче два с половиной кубических метра воды, можно купить тринадцать двухсотлитровых металлических бочек. Места они займут, конечно, много, но обойдутся в три раза дешевле…
Ссылка на скачивание файла: poisk-resheniya-v-excel (xls KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Как рассчитать объем и площадь в Excel
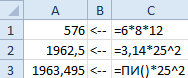
В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.
В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.
В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.14). Поэтому значения ячеек A2 и A3 немного отличаются.
Вычисление арифметических формул в Excel
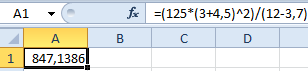
Допустим нам нужно в Excel вычислить формулу:
Чтобы получить результат вычисления ее нужно просто записать в одну строку: =(125*(3+4,5)^2)/(12-3,7).
Данная формула содержит 5 арифметических действий: суммирование, вычитание, умножение, деление и поднесение к степени (^). Если мы записываем все в одно строку, то нужно соблюдать правила арифметической последовательности. Для этого нужно использовать скобки.
Формула для вычисления объема сферы в Excel
Например, нам нужно регулярно вычислить объемы сфер с разными радиусами.
Формула вычисления объема сферы выгладит так:
Предыдущие примеры плохо подходят для решения данной задачи, так как они не используют переменных значений в формулах, а только константы. Из-за этого при смене радиуса нужно переписывать формулу. Но Excel позволяет нам использовать эффективное решение:
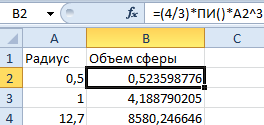
- В ячейку B2 запишем формулу вычисления объема сферы в одну строку: =(4/3)*ПИ()*A2^3 (A2 – это ссылка на ячейку).
- В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.