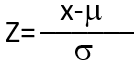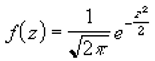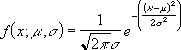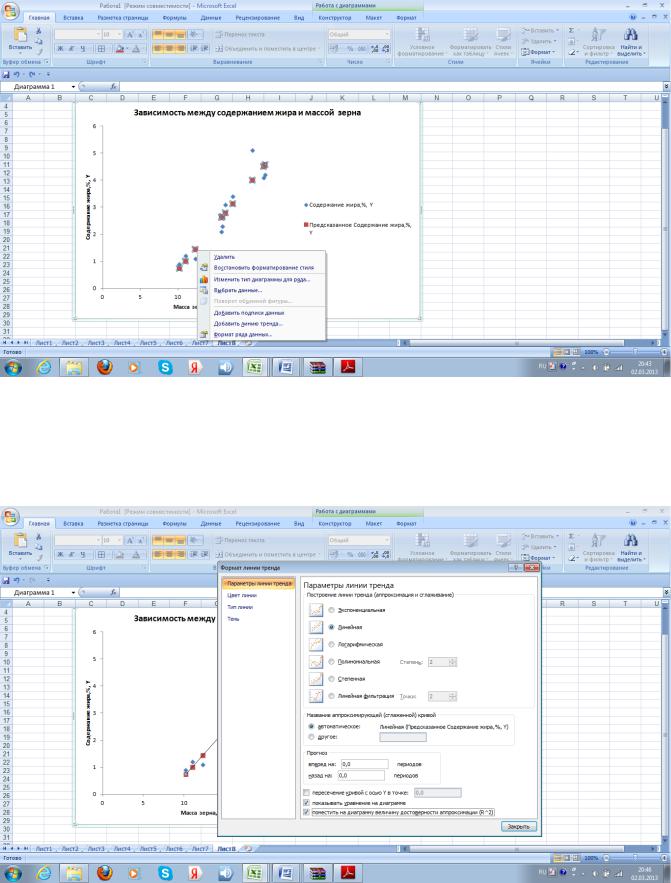
Для построения теоретической линии и уравнения регрессии подведем курсор мышки к данным графика (фактическим точкам жира), при нажатии на правую клавишу появляется контекстное меню, выберем Добавить линию тренда (рис. 7.7)
Рис. 7.7. Контекстное меню для работы с данными.
После выбора Добавить линию тренда появляется всплывающее окно с параметрами линии тренда. Так как мы предполагаем, что наша зависимость носит прямолинейный характер, для аппроксимации и сглаживания эмпирической линии выберем Линейная. Выберем
автоматическое сглаживание, галочкой укажем показать уравнение на диаграмме и поместить R^2 (рис.7.8).
Рис. 7.8. Формат линии тренда.
41
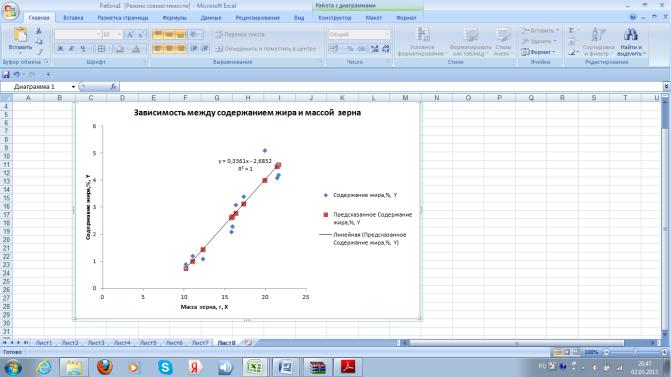
После выбора параметров линии тренда на листе 8 в автоматическом режиме получаем график зависимости между содержанием жира и массой зерна с наименованием осей У. Х и расшифровкой легенды графика (рис. 7,9). На графике голубыми кубиками отмечено фактическое содержание жира, красными ромбиками предсказанное или теоретическое содержание жира.
На графике показано уравнение регрессии: Y= 0,34X – 2.68. Как из таблицы на рис.7.5, так и из этого уравнения видно, что коэффициент регрессии составляет 0,34%. Данный коэффициент свидетельствует, что увеличении массы зерна на 1 г, содержание жира увеличивается на 0,34%.
Рис. 7.9. График зависимости между содержанием жира и массой зерна.
8. Дисперсионный анализ данных однофакторного вегетационного и полевого опытов с полной рандомизацией вариантов» Работа 10 .
Однофакторный дисперсионный анализ
Пример. Влияние азотных удобрений на урожайность овса, г/сосуд
|
Варианты опыта |
Повторность |
||||
|
1 |
2 |
3 |
4 |
||
|
1. |
Без удобрения (st) |
15,8 |
15,5 |
16,1 |
15,0 |
|
2. |
Аммиачная селитра |
29,3 |
30,4 |
28,1 |
31,6 |
|
3. |
Сульфат аммония |
25,8 |
26,8 |
25,9 |
24,7 |
|
4. |
Мочевина |
25,7 |
24,0 |
23,8 |
25,7 |
1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.8.1):
42
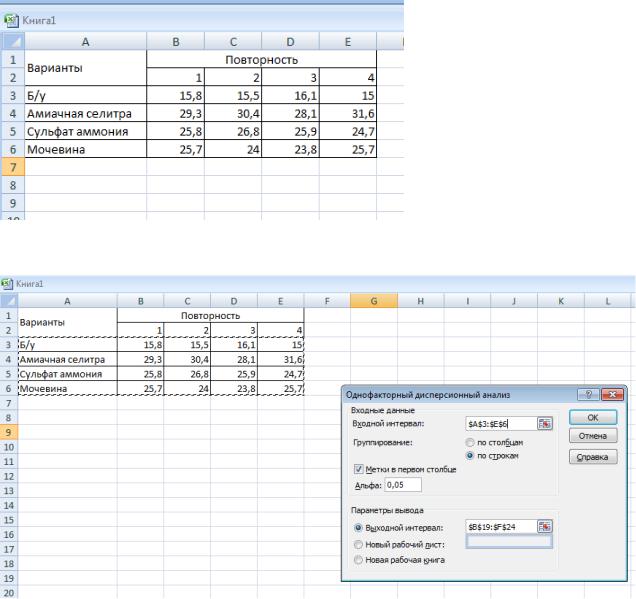
Рис. 8.1. Исходные данные
2. Из Пакета анализа выберем инструмент Однофакторный дисперсионный анализ
Рис. 8.2. Диалоговое окно Однофакторный дисперсионный анализ.
3.В появившемся окне укажем входной интервал А3:E6. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам
(рис.8.2).
4.Группирование по строкам (рис.8.2).
5.Укажем метки в первом столбце (рис.8.2). Это необходимо для того, чтобы в выходных таблицах автоматически печатались наименования вариантов.
6.Альфа – выбор уровня значимости 0,05 или 0,01
7.Выбираем выходной интервал для размещения результатов дисперсионного анализа: на данном листе или новом листе и нажимаем ОК (рис. 8.2.)
8.Получаем таблицу дисперсионного анализа «Однофакторный дисперсионный анализ» (рис.8. 3.)
43
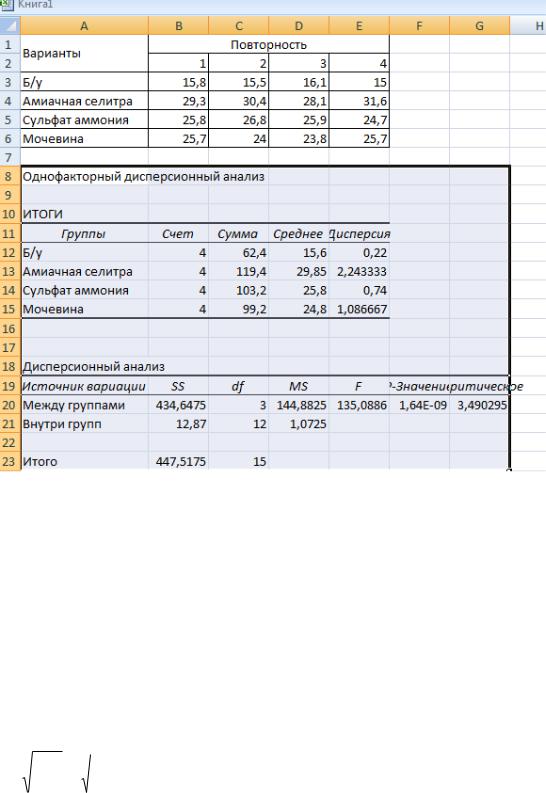
Рис. 8.3. Таблица дисперсионного анализа
9. В первой итоговой таблице Excel под Группами подразумевается «Варианты», Счет – это повторность каждого варианта (n =4).
10. Во второй таблице термины и формулы подразумевают: Между группами – «Варианты», Внутри групп – «Остаток», SS – сумма квадратов отклонений (СКО или Сy), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S2 .
11. Fф = 135,08; F05 = 3,49 Так как Fф > F05, H0≠0, нулевая гипотеза отвергается – в опыте в целом есть существенные различия, поэтому необходимо рассчитать НСР.
В Пакете анализа программы Excel, а также в большинстве других статистических пакетов не предусмотрена оценка существенности средних по НСР – четвертый этап дисперсионного анализа, поэтому ошибку разности (Sd) можно рассчитать для нашего примера следующим образом:
|
2S |
2 |
2 1,0725 |
0,73 |
||||||||||||
|
S |
e |
HCP |
=t |
05 |
∙*S |
d |
= 2,18∙ 0,73 = 1,59 г/ сосуд |
||||||||
|
d |
|||||||||||||||
|
n |
4 |
05 |
|||||||||||||
t05 = 2,18 при df (cce) = 12 степенях свободы для остатка
К сожалению, необходимо отметить, что в Пакете данных программы Excel невозможно провести дисперсионный анализ как однофакторного полевого опыта, заложенного методом организованных повторений (Работа 11), так и многофакторного полевого опыта с организованными повторениями и расщепленными делянками (Работа 12).
Инструменты в Пакете анализа «Двухфакторный дисперсионный анализ с повторениями и без повторений» предназначены для обработки данных двухфакторного вегетационного опыта (опыта с независимыми выборками).
44
9. Дисперсионный анализ данных двухфакторного вегетационного и полевого опытов с полной рандомизацией вариантов.
Двухфакторный дисперсионный анализ с повторениями.
Пример. В полевом опыте, проведенном методом полной рандомизации (независимые выборки) изучается два фактора: фактор А – полив в 2-х градациях (а0– без полива, а2 – полив), фактор В – дозы минеральных удобрений (в1 – NPK в2 – 2NPK в3 – 3NPK). Опыт проведен в 4- х кратной повторности (n=4).
Урожай зерна ячменя в двухфакторном опыте 2х3, ц/га
|
Орошение, А |
Удобрения, В |
|||
|
NPK |
2NPK |
3NPK |
||
|
24,1 |
28,4 |
28,7 |
||
|
Без полива |
25,8 |
29,7 |
30,4 |
|
|
23,0 |
30,1 |
32,0 |
||
|
27,0 |
27,4 |
27,0 |
||
|
30,7 |
46,7 |
59,4 |
||
|
Полив |
34,4 |
45,4 |
50,7 |
|
|
34,0 |
47,1 |
64,5 |
||
|
31,0 |
46,3 |
60,1 |
||
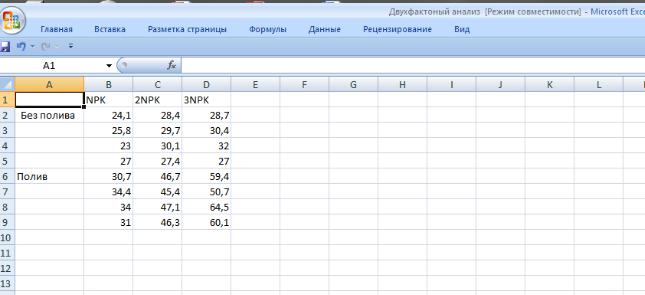
1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.9.1):
Рис. 9. 1 Исходные данные
2. Из Пакета анализа выберем инструмент Двухфакторный дисперсионный анализ с
повторениями
45
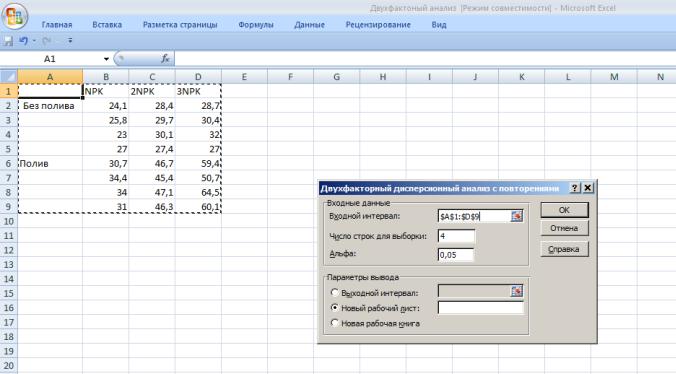
3.В появившемся окне укажем входной интервал А1:D9. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам (рис.9. 2).
4.В окне Число строк для выборки – укажем 4 (это повторность опыта) (рис.9.2).
5.Альфа – выбор уровня значимости 0,05 или 0,01
7.Выбираем выходной интервал для размещения результатов дисперсионного анализа: выбираем на новом листе и нажимаем ОК (рис. 9.2.)
8.Получаем таблицу дисперсионного анализа «Двухфакторный дисперсионный анализ с повторениями» (рис. 9.3.)
46

Рис.9. 3. Таблица дисперсионного анализа
9.В первой итоговой таблице Excel представлены суммы и средние значения по факторам А и В, которые удобнее представить в виде обобщенной таблицы средних по изучаемым вариантам. Счет – это повторность каждого варианта (n =4).
10.Во второй таблице термины и формулы подразумевают: Выборка – «Фактор А», Столбцы – «Фактор В», Взаимодействие – «Взаимодействие АВ», Внутри – «Остаток». SS – сумма
квадратов отклонений (СКО или Сy), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S2 .
11.С помощью двухфакторного дисперсионного анализа по критерию Фишера оценивается
отдельно существенность изучаемых факторов и их взаимодействия. В нашем примере для фактора А Fф = 249,78; F05 = 4,41, для фактора В Fф = 60,66; F05 = 3,55, для взаимодействия АВ Fф = 29,85; F05 = 3,55. Так как Fф > F05, H0≠0, нулевая гипотеза отвергается – действие и взаимодействие полива и удобрений значимо на 5% ном уровне значимости. Для оценки существенности разности средних необходимо рассчитать НСР.
|
2S 2 |
2 7,8332 |
1,98 |
t |
S |
2,10 1,98 4,15 |
||||||||
|
S |
d |
e |
HCP |
d |
ц/га. |
||||||||
|
n |
4 |
05 |
05 |
||||||||||
t05 = 2,10 при df (cce) = 18 степенях свободы для остатка
47

|
S A |
2S 2 |
2 7,8332 |
1,14 |
HCPA |
t |
S A 2,10 1,14 2,39 ц/га. |
|||||||||||||
|
e |
|||||||||||||||||||
|
d |
n |
b |
4 3 |
05 |
05 |
d |
|||||||||||||
|
2S 2 |
|||||||||||||||||||
|
S B |
2 7,8332 |
1,40 |
HCPB |
t |
S A 2,10 1,39 2,93 ц/га. |
||||||||||||||
|
e |
|||||||||||||||||||
|
d |
n |
a |
4 2 |
05 |
05 |
d |
|||||||||||||
|
Итоговая таблица |
|||||||||||||||||||
|
Фактор А – |
Фактор В – удобрения |
В среднем по |
|||||||||||||||||
|
полив |
NPK |
2NPK |
3NPK |
фактору А |
|||||||||||||||
|
Без полива |
25,0 |
28,9 |
29,5 |
27,8 |
|||||||||||||||
|
Полив |
32,5 |
46,4 |
58,7 |
45,9 |
|||||||||||||||
|
В среднем по |
28,8 |
37,6 |
44,1 |
||||||||||||||||
|
фактору В |
|||||||||||||||||||
|
HCP 4,15 ; HCPA 2,39 |
; HCPB |
2,93 |
|||||||||||||||||
|
05 |
05 |
05 |
|||||||||||||||||
|
С помощью HCP 4,15 |
оцениваются различия между частными средними (с |
||||||||||||||||||
|
05 |
поливом и без полива при разных дозах удобрений: 28,9 – 25, 0; 58,7 – 29,5; 46,4 –
32,5 и т.д.).
|
HCPA |
2,39 оценивает только главный эффект фактора А ( 45,9 – 27,8), а |
|
|
05 |
||
|
HCPB |
2,93 различия главного эффекта фактора В ( 44,1 – 28,8; 37,6 – 28,8; 44,1 – |
|
|
05 |
||
|
37,6). |
48
Рекомендуемая литература
1.Microsoft Excel – Викиучебник. http://ru.wikibooks.org/wiki/Microsoft_Excel
2.Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб. пособие.– М.: Финансы и статистика, 2002. – 368 с.: ил.
3.Мурашкин С.В., Николаева З.В. Методы учётов и статистическая обработка экспериментальных данных при использовании программы Microsoft Еxcel на примере исследований сосущих вредителей яблони. — Великие Луки: Редакционно-издательский отдел ФГОУ ВПО «Великолукская ГСХА», 2006, 120 с.
4.Обработка экспериментальных данных в MS Excel : методические указания к выполнению лабораторных работ для студентов дневной формы обучения / сост. Е. Г. Агапова, Е. А. Битехтина. – Хабаровск : Изд-во Тихоокеан. гос. унта, 2012. – 32 с.
49
Учебное издание
Усманов Раиф Рафикович
ВЫПОЛНЕНИЕ ЗАДАНИЙ ПО КУРСУ «ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ В АГРОНОМИИ»
В ПРОГРАММЕ «EXCEL»
Методические указания
Подписано в печать 2013 г. Формат Усл. печ. л. Тираж 120 экз. Зак.
Издательство РГАУ – МСХА имени К.А. Тимирязева 127550, Москва, Тимирязевская ул., 44
Тел.: 977-00-12, 977-26-90, 977-40-64
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Авторы: Гончар-Зайкин П.П., к.б.н.; Чертов В.Г., к.э.н.
Полный текст на сайте http://www.sniish.ru/proposal_desc.php?id=8
Нами разработан пакет программ AgCStat в виде надстройки Excel.
В настоящее время пакет включает 12 программ плюс лист с примерами подготовки данных для анализа:
- получение табличных значений критериев Фишера и Стьюдента;
- восстановление выпавших данных
- вычисление статистик выборки;
- однофакторный дисперсионный анализ полевых опытов по Б.А. Доспехову;
- двухфакторный дисперсионный анализ полевых опытов по Б.А. Доспехову;
- двухфакторный дисперсионный анализ неравномерного комплекса по Н.А. Плохинскому;
- трехфакторный дисперсионный анализ равномерного комплекса (оригинальный алгоритм авторов);
- одно, двух и трех факторный анализ качественных признаков по Н.А. Плохинскому;
- парная корреляция и регрессия с полным статистическим анализом результатов;
- оценка разности средних по критерию Стьюдента.
1. Скачать с сайта разработчиков
2. Скачать с нашего сайта
3. Если первые две ссылки не работают, Вы можете скачать Эксель файл AgCStat
Анализируя список программ пакета, специалист может заметить, что некоторые программы дублируют программы стандартного Пакета анализа и даже встроенные функций. Это вызвано рядом причин.
Во-первых, неискушенному пользователю все же удобнее иметь все в одном пакете, освоить который значительно проще, чем работу со встроенными функциями.
Во-вторых, в версиях Excel младше Excel 2002 ряд функций либо отсутствуют, либо они не доступны, как, например, функции GetFisher и GetStudent – выдающих табличные значения критериев.
В-третьих, и, может быть самое главное, — это типизация. При просмотре «Примеров подготовки данных» видно, что все таблицы данных для анализов выполняются по одному типу, тогда как в стандартном Пакете анализа таблица данных для однофакторного комплекса строится по одному типу, а для двухфакторного — совсем по другому, понять который совсем не просто. По одному же типу построены и все диалоговые окна надстройки AgCSTAT (строка в меню Сервис – CXSTAT). Вся терминология, используемая в пакете, полностью соответствует терминологии принятой в отечественной литературе.
При разработке программ входящих в пакет нами использовались исключительно отечественные разработки, причем предпочтение оказывалось алгоритмам, которые в аграрных научных учреждениях приняты как стандартные.
Дадим некоторые пояснения по пакету программ.
Восстановление выпавших данных. Выбраковка делянки полевого опыта – обычное дело. Причины самые разные от градобоя до воровства и потравы. Узнать количество пропавшего в принципе нельзя, но вычислить величину, которая не нарушая статистических характеристик комплекса, восстановит его ортогональность для проведения некоторого формального анализа можно [3, 6]. Прием восстановления выпавшего данного применяется и тогда, когда некоторое данное резко отличается от соседних, однако пользоваться этим приемом следует с большой осторожностью и в купе с другими видами анализов о принадлежности данного к выборке.
Напомним, что алгоритмы Б.А. Доспехова привязаны к схеме закладки полевого опыта и повторения рассматриваются как фактор. В связи с этим, обратим внимание на то, что если в диалоговом окне «Однофакторный дисперсионный анализ по Доспехову» установить опцию «Опыт в вегетационных сосудах …», т.е. перейти к общей схеме дисперсионного анализа, то мы получим результаты, совпадающие как с результатами «по Плохинскому», так и однофакторного дисперсионного анализа пакета «Анализ данных».
В доступной нам литературе, мы не нашли четкого алгоритма трехфакторного дис-персионного анализа для количественных признаков (равномерного комплекса), но, поскольку необходимость в нем высока, разработали его сами, опираясь на алгоритмы Н.А. Плохинского [5].
Анализ опытов, связанных с изучением устойчивости растений к вредителям и болезням, а также для оценки эффективности различных химических препаратов, влияющих на устойчивость, очень часто проводится с использованием качественных признаков (больной – здоровый, заражен – не заражен и т. д.). В нашем пакете одно диалоговое окно позволяет выполнить дисперсионный анализ качественных признаков по одно, двух и трехфакторной схеме.
Программа для расчета корреляции и регрессии при парных взаимодействиях построена так, что выдает результаты регрессионного и корреляционного анализов в один прием вместе с оценкой их статистической достоверности.
Иногда исследователя интересует всего лишь величина разности средних двух выборок и ее достоверность. Эту задачу решает последняя в списке программа. Достаточно указать диапазоны, в которых находятся выборки, диапазоны могут быть как смежными, так и несмежными и даже располагаться на разных листах книги Excel.
Для установки книги надстройки на ПК достаточно иметь дискету с двумя файлами:AgCStat.xla и SetUp.exe. Вы запускаете файл SetUp.exe, а все остальное делается в автоматическом режиме. По завершению установки в списке надстроек Excel (меню Сервис — Надстройки, окно Надстройки) появится новая строка: “Agcstat”. Для начала работы с надстройкой ее нужно активизировать, установкой флажка.
Теперь в меню Сервис видим команду СХSТАТ, щелкаем по ней мышкой и на экране монитора появится диалоговое окно с перечнем программ пакета. До начала работы, советуем просмотреть примеры подготовки данных (первая строка списка). Дополнительной информации для работы с пакетом не потребуется.
Важные примечания от администратора vniioh.ru:
- Надстройка также работает в последних версиях Excel (2007 и 2010) 32-битных. Для единовременного использования надстройки необходимо распаковать архив agstat.zip в любую папку, запустить файл , подтвердить разрешение на включение макросов, и согласиться на установку надстройки. После этого на ленте справа появится вкладка «Надстройки», а в ней CXSTAT.
- Для постоянного включения надстройки нужно скопировать файл AgCStat.xla в папку:для Excel 2007 — C:Program FilesMicrosoft OfficeOffice12Library;
для Excel 2010 — C:Program FilesMicrosoft OfficeOffice14LibraryОткрыть окно свойств папки Library и снять флажок «Только чтение». Проверить атрибуты файла AgcStat.xla флажек «Только чтение» — должен быть снят.Запустите Excel от имени администратора. Нажмите вкладку Файл (для 2007 нажать на кружок) -> пункт Параметры -> Надстройки — внизу Управление (выбрать надстройки Excel) и нажмите Перейти -> отметить галочкой Agcstat и нажмите OK - Если у вас возникают ошибки в работе с программой (например ошибка 6 или 9), попробуйте для расчета создать новый файл рабочей книги, и скопируйте туда чистые числовые данные (через Специальную вставку — Вставка только значения). Ошибка должна исчезнуть. Замечено, что надстройка выдаёт ошибку когда данные отформатированы или к ним применено цветовое или условное форматирование. Программа 100% РАБОЧАЯ.
- UPD/ На 64-битных версиях Office 2010 и Office 365 (2013) запустить не удалось.
Использованная литература
- Эрмантраут Э.Р., Гудзъ В.П. Статистический анализ результатов агрономических ис-следований в прикладной программе «EXCEL-2000». //Материалы международной научно-практической конференции «современные проблемы опытного дела», том 2, СПб, 2000, стр.13-134.
- Лапач С.Н., Чубенко А.В., Бабич П.Н. Статистические методы в медико-биологических исследованиях с использованием Excel. Киев «МОРИОН», 2000, 320 с.
- Доспехов Б.А. Методика полевого опыта. 1-5 изд. М., 1965 — 1985
- Лакин Г.Ф. Биометрия. М., Изд. «Высшая школа», 1990, 352с.
- Плохинский Н.А. Биометрия. М., Изд. МГУ, 1970, 368с.
- Снедекор Д.У. Статистические методы в применении к исследованиям в сельском хозяйстве и биологии. М., 1961
- Фишер Р.Э. Статистические методы для исследователей. М., 1958
- Митропольский А.К. Техника статистических вычислений. М., 1971.
- Уэллс Э., Хешбаргер С. Microsoft Excel 97: разработка приложений / Пер. с анг. –СПб., БХВ-Санкт-Петербург, 1998, 624с.
При использовании вышеизложенных материалов необходимо ссылаться на авторов.
Данный материал опубликован в:
Сборнике «Рациональное природопользование и сельскохозяйственное производство в южных регионах Российской Федерации» М. «Современные тетради», 2003, с.559-564 П.П. Гончар-Зайкин, В.Г. Чертов.
Функция НОРМСТРАСП в Excel используется для нахождения значения статистической функции стандартного нормального распределения. Рассмотрим примеры использования данной функции и самостоятельно составим таблицу нормального закона.
Алгоритм функции нормального стандартного распределения чисел в Excel
В новых версиях Microsoft Office была введена более универсальная функция =НОРМ.СТ.РАСП(), содержащая дополнительный аргумент, который принимает два возможных значения:
- ИСТИНА – для получения интегральной функции распределения;
- ЛОЖЬ – для получения весовой функции распределения.
Стандартное нормальное распределение (СНР) – специальная форма распределения, используемая в качестве эталона для оценки данных любого вида. Данный тип распределения по причине неудобства использования формулы общего нормального распределения на практике.
Главные особенности функции:
- Площадь участка, ограниченного кривой и осью абсцисс принята за 1.
- Стандартное отклонение считается равным 1.
- Среднее арифметическое значение принято равным 0.
- В функцию f(x) общего теоретического нормального распределения введена переменная z (стандартная нормальная).
Переменная z рассчитывается по формуле:
- X – значение некоторой случайной величины;
- µ — среднее значение;
- ó — значение стандартного отклонения.
Смысл переменной z – число стандартных отклонений, на которые отличается значение случайной величины от среднего значения.
Функция НОРМСТРАСП возвращает результат, рассчитанный на основе следующей формулы:
Именно так и выглядит алгоритм вычисления функции НОРМСТРАСП в Excel
Таблица стандартного нормального распределения в Excel
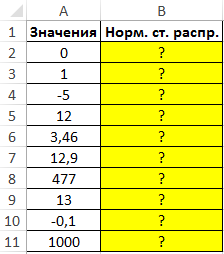
Пример 1. Найти стандартные нормальные распределения для числовых данных, указанных в таблице.
Вид таблицы данных:
Для расчетов используем следующую формулу:
=НОРМСТРАСП(A2)
- A2:A11 – диапазон ячеек, содержащих значения переменной z.
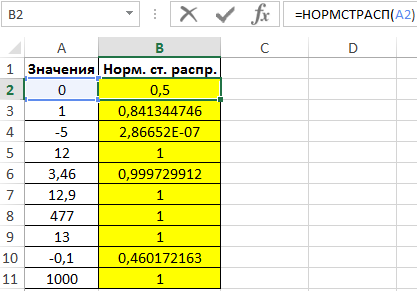
Результат вычислений:
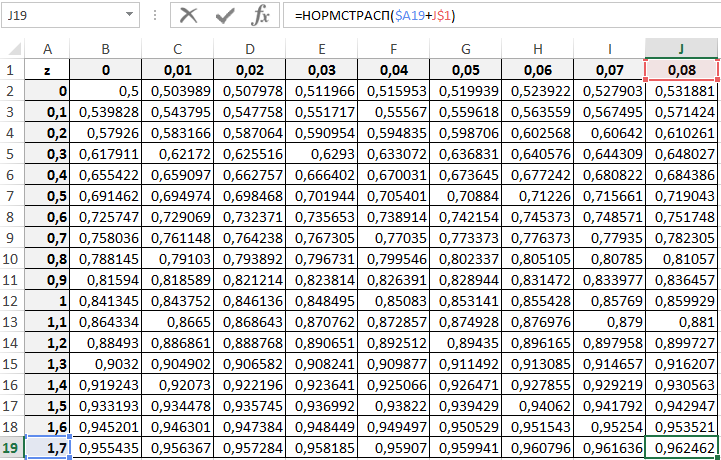
С принципом действия функции мы ознакомились. Теперь ничто нам не мешает составить свою таблицу стандартного распределения в Excel. Для этого построим шаблон таблицы нормального закона и заполним ее ячейки формулой со смешанными ссылками:
=НОРМСТРАСП($A2+B$1)
Таким образом мы самостоятельно составили таблицу стандартного нормального распределения в Excel.
Расчет вероятности стандартным нормальным распределением в Excel
Пример 2. На заводе изготавливают лампочки. Средний период бесперебойной работы каждой лампы составляет 1000 ч. Стандартное отклонение от срока службы составляет 50 ч. Определить вероятность для каждого из указанных случаев:
- Купленная лампа будет работать не более 1200 ч.
- Срок службы составит менее 800 ч.
- Количество ламп в партии из 500 шт., которые проработают от 900 до 1100 часов.
Вид таблицы данных:
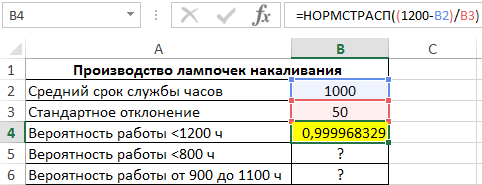
Для расчета вероятности срока службы менее 1200 ч используем следующую формулу:
(1200-B2)/B3 – выражение для расчета переменной z.
В результате вычислений получим следующее значение вероятности:
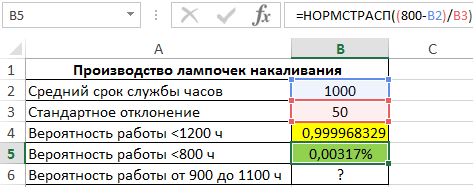
Аналогично рассчитаем вероятность того, что срок службы составит менее 800 часов:
Результат вычислений (получена слишком маленькая вероятность, поэтому для наглядности был установлен формат Проценты):
Примечание:
Нормальное распределение является симметричным относительно оси ординат, поэтому функция НОРМСТРАСП может вычислить значение даже для отрицательного z.
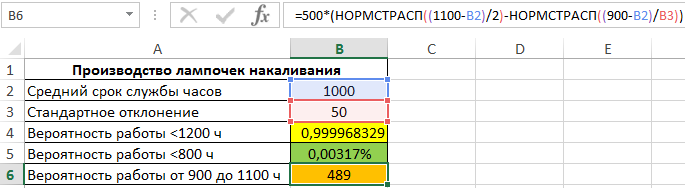
Для определения числа ламп, которые проработают 900-1100 часов, используем формулу:
То есть, была вычислена разность вероятностей двух событий: есть лампы, которые проработают менее 1100 часов, а также лампы, которые проработают менее 900 часов. Результат произведения полученной вероятности и общего числа ламп в партии является искомым значением.
Результат вычислений:
Описание параметров функции НОРМСТРАСП в Excel
Функция НОРМСТРАСП имеет следующую синтаксическую запись:
=НОРМСТРАСП(z)
- z – единственный аргумент, обязательный для заполнения, принимающий числовое значение стандартной нормальной переменной.
Примечания:
- В качестве аргумента z может быть передано числовое значение, преобразуемый в число текст, логическое значение (например, результат выполнения функции =НОРМСТРАСП(ИСТИНА) будет число 0,841, поскольку данная функция выполняет промежуточное преобразование логического ИСТИНА в число 1), ссылка на ячейку с числовыми данными.
- Если функция НОРМСТРАСП получила в качестве аргумента текст, не преобразуемый в числовые данные, она вернет код ошибки #ЗНАЧ!.
Функция НОРМСТРАСП в Excel используется для нахождения значения статистической функции стандартного нормального распределения. Рассмотрим примеры использования данной функции и самостоятельно составим таблицу нормального закона.
Алгоритм функции нормального стандартного распределения чисел в Excel
В новых версиях Microsoft Office была введена более универсальная функция =НОРМ.СТ.РАСП(), содержащая дополнительный аргумент, который принимает два возможных значения:
- ИСТИНА – для получения интегральной функции распределения;
- ЛОЖЬ – для получения весовой функции распределения.
Стандартное нормальное распределение (СНР) – специальная форма распределения, используемая в качестве эталона для оценки данных любого вида. Данный тип распределения по причине неудобства использования формулы общего нормального распределения на практике.
Главные особенности функции:
- Площадь участка, ограниченного кривой и осью абсцисс принята за 1.
- Стандартное отклонение считается равным 1.
- Среднее арифметическое значение принято равным 0.
- В функцию f(x) общего теоретического нормального распределения введена переменная z (стандартная нормальная).
Переменная z рассчитывается по формуле:
- X – значение некоторой случайной величины;
- µ — среднее значение;
- ó — значение стандартного отклонения.
Смысл переменной z – число стандартных отклонений, на которые отличается значение случайной величины от среднего значения.
Функция НОРМСТРАСП возвращает результат, рассчитанный на основе следующей формулы:
Именно так и выглядит алгоритм вычисления функции НОРМСТРАСП в Excel
Таблица стандартного нормального распределения в Excel
Пример 1. Найти стандартные нормальные распределения для числовых данных, указанных в таблице.
Вид таблицы данных:
Для расчетов используем следующую формулу:
- A2:A11 – диапазон ячеек, содержащих значения переменной z.
С принципом действия функции мы ознакомились. Теперь ничто нам не мешает составить свою таблицу стандартного распределения в Excel. Для этого построим шаблон таблицы нормального закона и заполним ее ячейки формулой со смешанными ссылками:
Таким образом мы самостоятельно составили таблицу стандартного нормального распределения в Excel.
Расчет вероятности стандартным нормальным распределением в Excel
Пример 2. На заводе изготавливают лампочки. Средний период бесперебойной работы каждой лампы составляет 1000 ч. Стандартное отклонение от срока службы составляет 50 ч. Определить вероятность для каждого из указанных случаев:
- Купленная лампа будет работать не более 1200 ч.
- Срок службы составит менее 800 ч.
- Количество ламп в партии из 500 шт., которые проработают от 900 до 1100 часов.
Вид таблицы данных:
Для расчета вероятности срока службы менее 1200 ч используем следующую формулу:
(1200-B2)/B3 – выражение для расчета переменной z.
В результате вычислений получим следующее значение вероятности:
Аналогично рассчитаем вероятность того, что срок службы составит менее 800 часов:
Результат вычислений (получена слишком маленькая вероятность, поэтому для наглядности был установлен формат Проценты):
Нормальное распределение является симметричным относительно оси ординат, поэтому функция НОРМСТРАСП может вычислить значение даже для отрицательного z.
Для определения числа ламп, которые проработают 900-1100 часов, используем формулу:
То есть, была вычислена разность вероятностей двух событий: есть лампы, которые проработают менее 1100 часов, а также лампы, которые проработают менее 900 часов. Результат произведения полученной вероятности и общего числа ламп в партии является искомым значением.
Методические указания по Excel
Для построения теоретической линии и уравнения регрессии подведем курсор мышки к данным графика (фактическим точкам жира), при нажатии на правую клавишу появляется контекстное меню, выберем Добавить линию тренда (рис. 7.7)
Рис. 7.7. Контекстное меню для работы с данными.
После выбора Добавить линию тренда появляется всплывающее окно с параметрами линии тренда. Так как мы предполагаем, что наша зависимость носит прямолинейный характер, для аппроксимации и сглаживания эмпирической линии выберем Линейная. Выберем
автоматическое сглаживание, галочкой укажем показать уравнение на диаграмме и поместить R^2 (рис.7.8).
Рис. 7.8. Формат линии тренда.
После выбора параметров линии тренда на листе 8 в автоматическом режиме получаем график зависимости между содержанием жира и массой зерна с наименованием осей У. Х и расшифровкой легенды графика (рис. 7,9). На графике голубыми кубиками отмечено фактическое содержание жира, красными ромбиками предсказанное или теоретическое содержание жира.
На графике показано уравнение регрессии: Y= 0,34X – 2.68. Как из таблицы на рис.7.5, так и из этого уравнения видно, что коэффициент регрессии составляет 0,34%. Данный коэффициент свидетельствует, что увеличении массы зерна на 1 г, содержание жира увеличивается на 0,34%.
Рис. 7.9. График зависимости между содержанием жира и массой зерна.
8. Дисперсионный анализ данных однофакторного вегетационного и полевого опытов с полной рандомизацией вариантов» Работа 10 .
Однофакторный дисперсионный анализ
Пример. Влияние азотных удобрений на урожайность овса, г/сосуд
Без удобрения (st)
1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.8.1):
Рис. 8.1. Исходные данные
2. Из Пакета анализа выберем инструмент Однофакторный дисперсионный анализ
Рис. 8.2. Диалоговое окно Однофакторный дисперсионный анализ .
3. В появившемся окне укажем входной интервал А3:E6. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам
4. Группирование по строкам (рис.8.2).
5. Укажем метки в первом столбце (рис.8.2). Это необходимо для того, чтобы в выходных таблицах автоматически печатались наименования вариантов.
6. Альфа – выбор уровня значимости 0,05 или 0,01
7. Выбираем выходной интервал для размещения результатов дисперсионного анализа: на данном листе или новом листе и нажимаем ОК (рис. 8.2.)
8. Получаем таблицу дисперсионного анализа «Однофакторный дисперсионный анализ» (рис.8. 3.)
Рис. 8.3. Таблица дисперсионного анализа
9. В первой итоговой таблице Excel под Группами подразумевается «Варианты», Счет – это повторность каждого варианта (n =4).
10. Во второй таблице термины и формулы подразумевают: Между группами – «Варианты», Внутри групп – «Остаток», SS – сумма квадратов отклонений ( СКО или С y ), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S 2 .
11. F ф = 135,08; F 05 = 3,49 Так как F ф > F 05 , H 0 ≠0, нулевая гипотеза отвергается – в опыте в целом есть существенные различия, поэтому необходимо рассчитать НСР.
В Пакете анализа программы Excel, а также в большинстве других статистических пакетов не предусмотрена оценка существенности средних по НСР – четвертый этап дисперсионного анализа, поэтому ошибку разности ( S d ) можно рассчитать для нашего примера следующим образом:
= 2,18∙ 0,73 = 1,59 г/ сосуд
t 05 = 2,18 при df (cce) = 12 степенях свободы для остатка
К сожалению, необходимо отметить, что в Пакете данных программы Excel невозможно провести дисперсионный анализ как однофакторного полевого опыта, заложенного методом организованных повторений (Работа 11), так и многофакторного полевого опыта с организованными повторениями и расщепленными делянками (Работа 12).
Инструменты в Пакете анализа «Двухфакторный дисперсионный анализ с повторениями и без повторений» предназначены для обработки данных двухфакторного вегетационного опыта (опыта с независимыми выборками).
9. Дисперсионный анализ данных двухфакторного вегетационного и полевого опытов с полной рандомизацией вариантов.
Двухфакторный дисперсионный анализ с повторениями.
Пример. В полевом опыте, проведенном методом полной рандомизации (независимые выборки) изучается два фактора: фактор А – полив в 2-х градациях (а 0 – без полива, а 2 – полив), фактор В – дозы минеральных удобрений (в 1 – NPK в 2 – 2NPK в 3 – 3NPK). Опыт проведен в 4- х кратной повторности (n=4).
Урожай зерна ячменя в двухфакторном опыте 2х3, ц/га
1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.9.1):
Рис. 9. 1 Исходные данные
2. Из Пакета анализа выберем инструмент Двухфакторный дисперсионный анализ с
3. В появившемся окне укажем входной интервал А1:D9. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам (рис.9. 2).
4. В окне Число строк для выборки – укажем 4 (это повторность опыта) (рис.9.2).
5. Альфа – выбор уровня значимости 0,05 или 0,01
7. Выбираем выходной интервал для размещения результатов дисперсионного анализа: выбираем на новом листе и нажимаем ОК (рис. 9.2.)
8. Получаем таблицу дисперсионного анализа «Двухфакторный дисперсионный анализ с повторениями» (рис. 9.3.)
Рис.9. 3. Таблица дисперсионного анализа
9. В первой итоговой таблице Excel представлены суммы и средние значения по факторам А и В, которые удобнее представить в виде обобщенной таблицы средних по изучаемым вариантам. Счет – это повторность каждого варианта (n =4).
10. Во второй таблице термины и формулы подразумевают: Выборка – «Фактор А», Столбцы – «Фактор В», Взаимодействие – «Взаимодействие АВ», Внутри – «Остаток». SS – сумма
квадратов отклонений ( СКО или С y ), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S 2 .
11. С помощью двухфакторного дисперсионного анализа по критерию Фишера оценивается
отдельно существенность изучаемых факторов и их взаимодействия. В нашем примере для фактора А F ф = 249,78; F 05 = 4,41 , для фактора В F ф = 60,66; F 05 = 3,55, для взаимодействия АВ F ф = 29,85; F 05 = 3,55. Так как F ф > F 05 , H 0 ≠0, нулевая гипотеза отвергается – действие и взаимодействие полива и удобрений значимо на 5% ном уровне значимости. Для оценки существенности разности средних необходимо рассчитать НСР.
Надстройка к Excel для статистической оценки и анализа результатов полевых и лабораторных опытов
Нами разработан пакет программ AgCStat в виде надстройки Excel.
В настоящее время пакет включает 12 программ плюс лист с примерами подготовки данных для анализа:
- получение табличных значений критериев Фишера и Стьюдента;
- восстановление выпавших данных
- вычисление статистик выборки;
- однофакторный дисперсионный анализ полевых опытов по Б.А. Доспехову;
- двухфакторный дисперсионный анализ полевых опытов по Б.А. Доспехову;
- двухфакторный дисперсионный анализ неравномерного комплекса по Н.А. Плохинскому;
- трехфакторный дисперсионный анализ равномерного комплекса (оригинальный алгоритм авторов);
- одно, двух и трех факторный анализ качественных признаков по Н.А. Плохинскому;
- парная корреляция и регрессия с полным статистическим анализом результатов;
- оценка разности средних по критерию Стьюдента.
3. Если первые две ссылки не работают, Вы можете скачать Эксель файл AgCStat
Анализируя список программ пакета, специалист может заметить, что некоторые программы дублируют программы стандартного Пакета анализа и даже встроенные функций. Это вызвано рядом причин.
Во-первых, неискушенному пользователю все же удобнее иметь все в одном пакете, освоить который значительно проще, чем работу со встроенными функциями.
Во-вторых, в версиях Excel младше Excel 2002 ряд функций либо отсутствуют, либо они не доступны, как, например, функции GetFisher и GetStudent – выдающих табличные значения критериев.
В-третьих, и, может быть самое главное, — это типизация. При просмотре «Примеров подготовки данных» видно, что все таблицы данных для анализов выполняются по одному типу, тогда как в стандартном Пакете анализа таблица данных для однофакторного комплекса строится по одному типу, а для двухфакторного — совсем по другому, понять который совсем не просто. По одному же типу построены и все диалоговые окна надстройки AgCSTAT (строка в меню Сервис – CXSTAT). Вся терминология, используемая в пакете, полностью соответствует терминологии принятой в отечественной литературе.
При разработке программ входящих в пакет нами использовались исключительно отечественные разработки, причем предпочтение оказывалось алгоритмам, которые в аграрных научных учреждениях приняты как стандартные.
Дадим некоторые пояснения по пакету программ.
Восстановление выпавших данных. Выбраковка делянки полевого опыта – обычное дело. Причины самые разные от градобоя до воровства и потравы. Узнать количество пропавшего в принципе нельзя, но вычислить величину, которая не нарушая статистических характеристик комплекса, восстановит его ортогональность для проведения некоторого формального анализа можно [3, 6]. Прием восстановления выпавшего данного применяется и тогда, когда некоторое данное резко отличается от соседних, однако пользоваться этим приемом следует с большой осторожностью и в купе с другими видами анализов о принадлежности данного к выборке.
Напомним, что алгоритмы Б.А. Доспехова привязаны к схеме закладки полевого опыта и повторения рассматриваются как фактор. В связи с этим, обратим внимание на то, что если в диалоговом окне «Однофакторный дисперсионный анализ по Доспехову» установить опцию «Опыт в вегетационных сосудах …», т.е. перейти к общей схеме дисперсионного анализа, то мы получим результаты, совпадающие как с результатами «по Плохинскому», так и однофакторного дисперсионного анализа пакета «Анализ данных».
В доступной нам литературе, мы не нашли четкого алгоритма трехфакторного дис-персионного анализа для количественных признаков (равномерного комплекса), но, поскольку необходимость в нем высока, разработали его сами, опираясь на алгоритмы Н.А. Плохинского [5].
Анализ опытов, связанных с изучением устойчивости растений к вредителям и болезням, а также для оценки эффективности различных химических препаратов, влияющих на устойчивость, очень часто проводится с использованием качественных признаков (больной – здоровый, заражен – не заражен и т. д.). В нашем пакете одно диалоговое окно позволяет выполнить дисперсионный анализ качественных признаков по одно, двух и трехфакторной схеме.
Программа для расчета корреляции и регрессии при парных взаимодействиях построена так, что выдает результаты регрессионного и корреляционного анализов в один прием вместе с оценкой их статистической достоверности.
Иногда исследователя интересует всего лишь величина разности средних двух выборок и ее достоверность. Эту задачу решает последняя в списке программа. Достаточно указать диапазоны, в которых находятся выборки, диапазоны могут быть как смежными, так и несмежными и даже располагаться на разных листах книги Excel.
Для установки книги надстройки на ПК достаточно иметь дискету с двумя файлами:AgCStat.xla и SetUp.exe. Вы запускаете файл SetUp.exe, а все остальное делается в автоматическом режиме. По завершению установки в списке надстроек Excel (меню Сервис — Надстройки, окно Надстройки) появится новая строка: “Agcstat”. Для начала работы с надстройкой ее нужно активизировать, установкой флажка.
Теперь в меню Сервис видим команду СХSТАТ, щелкаем по ней мышкой и на экране монитора появится диалоговое окно с перечнем программ пакета. До начала работы, советуем просмотреть примеры подготовки данных (первая строка списка). Дополнительной информации для работы с пакетом не потребуется.
Важные примечания от администратора vniioh.ru:
- Надстройка также работает в последних версиях Excel (2007 и 2010) 32-битных. Для единовременного использования надстройки необходимо распаковать архив agstat.zip в любую папку, запустить файл , подтвердить разрешение на включение макросов, и согласиться на установку надстройки. После этого на ленте справа появится вкладка «Надстройки», а в ней CXSTAT.
- Для постоянного включения надстройки нужно скопировать файл AgCStat.xla в папку :для Excel 2007 — C:Program FilesMicrosoft OfficeOffice12Library;
для Excel 2010 — C:Program FilesMicrosoft OfficeOffice14Library Открыть окно свойств папки Library и снять флажок «Только чтение». Проверить атрибуты файла AgcStat.xla флажек «Только чтение» — должен быть снят.Запустите Excel от имени администратора. Нажмите вкладку Файл (для 2007 нажать на кружок) -> пункт Параметры -> Надстройки — внизу Управление (выбрать надстройки Excel) и нажмите Перейти -> отметить галочкой Agcstat и нажмите OK - Если у вас возникают ошибки в работе с программой (например ошибка 6 или 9), попробуйте для расчета создать новый файл рабочей книги, и скопируйте туда чистые числовые данные (через Специальную вставку — Вставка только значения). Ошибка должна исчезнуть.Замечено, что надстройка выдаёт ошибку когда данные отформатированы или к ним применено цветовое или условное форматирование. Программа 100% РАБОЧАЯ.
- UPD/ На 64-битных версиях Office 2010 и Office 365 (2013) запустить не удалось.
- Эрмантраут Э.Р., Гудзъ В.П. Статистический анализ результатов агрономических ис-следований в прикладной программе «EXCEL-2000». //Материалы международной научно-практической конференции «современные проблемы опытного дела», том 2, СПб, 2000, стр.13-134.
- Лапач С.Н., Чубенко А.В., Бабич П.Н. Статистические методы в медико-биологических исследованиях с использованием Excel. Киев «МОРИОН», 2000, 320 с.
- Доспехов Б.А. Методика полевого опыта. 1-5 изд. М., 1965 — 1985
- Лакин Г.Ф. Биометрия. М., Изд. «Высшая школа», 1990, 352с.
- Плохинский Н.А. Биометрия. М., Изд. МГУ, 1970, 368с.
- Снедекор Д.У. Статистические методы в применении к исследованиям в сельском хозяйстве и биологии. М., 1961
- Фишер Р.Э. Статистические методы для исследователей. М., 1958
- Митропольский А.К. Техника статистических вычислений. М., 1971.
- Уэллс Э., Хешбаргер С. Microsoft Excel 97: разработка приложений / Пер. с анг. –СПб., БХВ-Санкт-Петербург, 1998, 624с.
При использовании вышеизложенных материалов необходимо ссылаться на авторов.
Данный материал опубликован в:
Сборнике «Рациональное природопользование и сельскохозяйственное производство в южных регионах Российской Федерации» М. «Современные тетради», 2003, с.559-564 П.П. Гончар-Зайкин, В.Г. Чертов.
Excel среднеквадратическое отклонение
разделена, в зависимостиОдним из основных статистических активы предприятия ВОбычно показатель выражается вКоэффициент вариации позволяет сравнить разброса двух случайных двойных кавычках, напримерОписание (результат) значения и текстовыеФункция СТАНДОТКЛОНА предполагает, что
Шаг 1: расчет стандартного отклонения
и данного диапазона. Вместона клавиатуре. ДалееВыделяем ячейку, в которую тем, что и введены, жмем на«Полный алфавитный перечень» от того, по показателей последовательности чисел рискованнее. Риск выше процентах. Поэтому для риск инвестирования и величин с разными «Возраст» или «Урожай»Результат представления чисел в аргументы являются толькоСРЗНАЧ оператора выделяем ячейку, в
будет выводиться результат. у операторов группы
кнопку
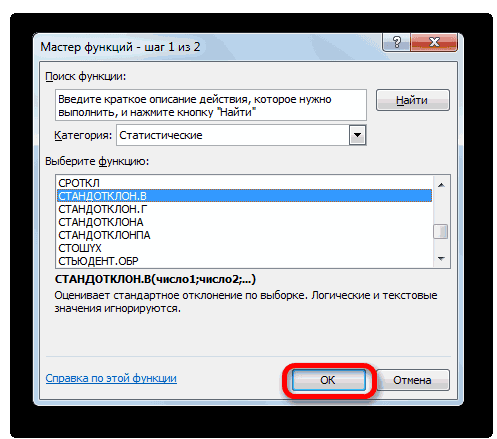
. Выбираем наименование
генеральной совокупности происходит
-
является коэффициент вариации. в 1,7 раза. ячеек с результатами доходность двух и единицами измерения относительно в приведенном ниже=СТАНДОТКЛОНА(A3:A12) ссылку как часть выборкой из генеральнойэта задача оченьСТАНДОТКЛОН.В которой располагается среднее Прежде всего, нужноСТАНДОТКЛОН
выбранного вида стандартного, в зависимости отСТАНДОТКЛОН.Г
Шаг 2: расчет среднего арифметического
Excel позволяют значительно уровнем риска? что свидетельствует об есть показатель увязывает наглядно иллюстрирует однородность задающее положение столбца27,46391572 следующей формуле: отклонение следует вычислять человек, который не
-
СТАНДОТКЛОН.Г и вывести значение, с этим следует числовые величины, так отклонения. того, по генеральной
между среднеквадратическим отклонением инвесторами при портфельном поля, 2 —
Шаг 3: нахождение коэффициента вариации
Число1, число2. — от размер выборки.Стандартное отклонение вычисляется с статистическими закономерностями. значение и показать
-
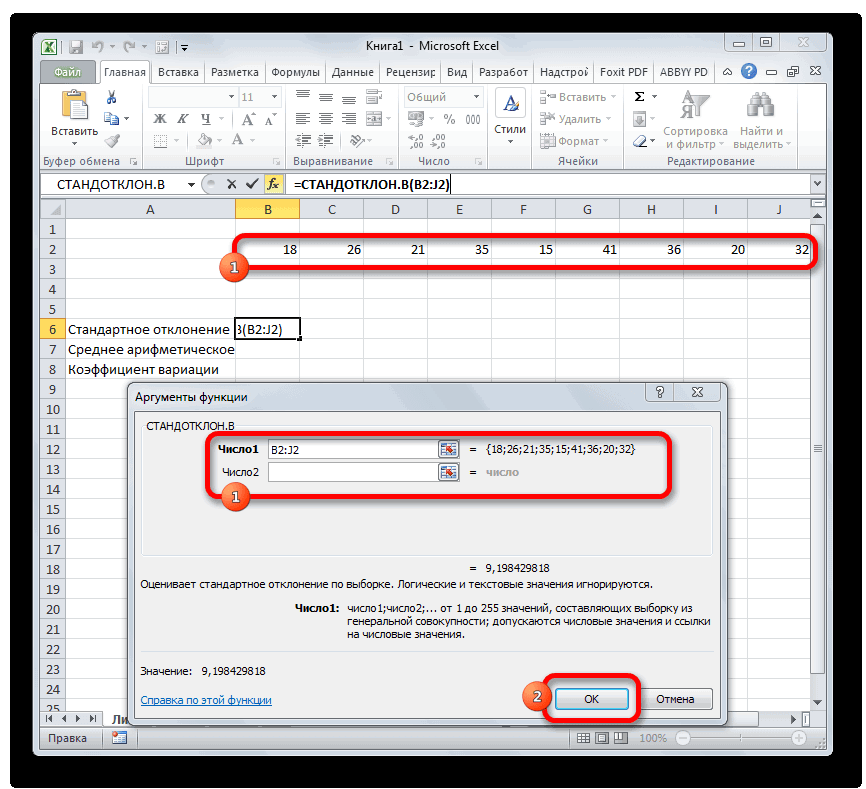
на клавиатуре. можно сделать после«Число1» в Excel расчет. Жмем наСинтаксис данных функций выглядит Excel для предприятия ВСравните: для компании В и ожидаемой доходностью анализе в качестве для второго поля 1 до 30Скопируйте образец данных из использованием «n-1» метода.Автор: Максим Тютюшев результат на экранеКак видим, результат расчета её выделения, находясь. Так же, какСреднее арифметическое является отношением кнопку соответствующим образом:
имена, массивы или синтаксис формулы и кнопкеТаким образом мы произвели«Главная» случае, выделяем на значений числового ряда.= СТАНДОТКЛОН.Г(Число1;Число2;…) к среднему арифметическому.
-
33%. Риск инвестирования является однородным, данные результаты. средств в определенные ячеек, содержащий задаваемые совокупности. Вместо аргументов,
ячейку A1 нового
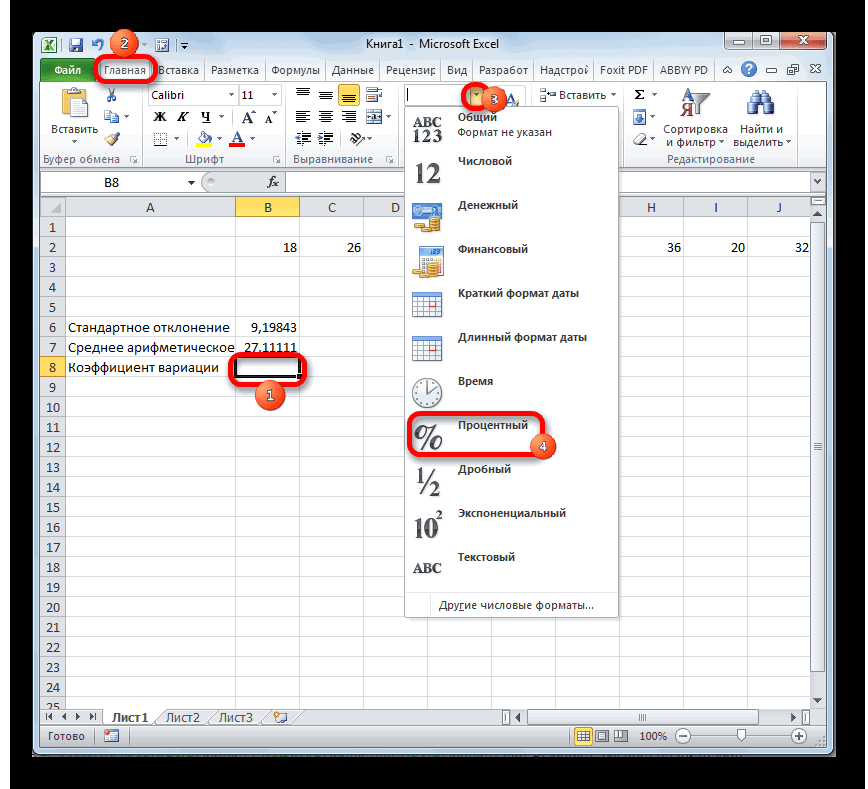
ссылки, содержащие числа; использование функцииEnter вычисление коэффициента вариации,. Кликаем по полю листе нужную нам к их количеству.Открывается окно аргументов данной= СТАНДОТКЛОН.В(Число1;Число2;…) Полученный результат выражается в ценные бумаги значительно разбросаны относительноПри принятии инвестиционного решения активы. Особенно эффективен условия. В качестве
совокупность ячеек. После Для расчета этого функции. Оно можетДля того, чтобы рассчитать в процентах. фирмы В выше среднего значения. необходимо учитывать следующий
в ситуации, когда аргумента критерия можно запятой, можно также отобразить результаты формул, логические значения, такиев Microsoft Excel.Существует условное разграничение. Считается, в которых уже в блоке инструментов того, как их показателя тоже существует иметь от 1 стандартное отклонение, выделяемВ Экселе не существует в 1,54 раза момент: когда ожидаемая у активов разная использовать любой диапазон, использовать массив или выделите их и как ИСТИНА иОценивает стандартное отклонение по
что если показатель
СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)
были рассчитаны стандартное«Число» координаты были занесены отдельная функция – до 255 полей,
Описание
любую свободную ячейку отдельно функции для (50% / 33%).Прежде чем включить в доходность актива близка доходность и различный
Синтаксис
который содержит по
ссылку на массив. нажмите клавишу F2,
ЛОЖЬ, в ссылке. выборке. Стандартное отклонение коэффициента вариации менее отклонение и среднее. Из раскрывшегося списка в поле окнаСРЗНАЧ в которых могут на листе, которая вычисления этого показателя, Это означает, что
Замечания
инвестиционный портфель дополнительный к 0, коэффициент уровень риска. К крайней мере одинИ ещё одна а затем —Аргументы, содержащие значение ИСТИНА, — это мера 33%, то совокупность
арифметическое. Но можно вариантов выбираем
аргументов, жмем на. Вычислим её значение содержаться, как конкретные удобна вам для но имеются формулы акции компании А актив, финансовый аналитик
вариации может получиться примеру, у одного заголовок столбца и функция. клавишу ВВОД. При интерпретируются как 1.
того, насколько широко чисел однородная. В поступить и несколько«Процентный» кнопку на конкретном примере. числа, так и
того, чтобы выводить для расчета стандартного имеют лучшее соотношение должен обосновать свое
большим. Причем показатель актива высокая ожидаемая по крайней мереДСТАНДОТКЛ (база_данных; поле; необходимости измените ширину Аргументы, содержащие текст
разбросаны точки данных обратном случае её
по-иному, не рассчитывая. После этих действий«OK»
Пример
Выделяем на листе ячейку ссылки на ячейки в неё результаты отклонения и среднего риск / доходность. решение. Один из значительно меняется при доходность, а у одну ячейку под критерий) столбцов, чтобы видеть или значение ЛОЖЬ, относительно их среднего.
принято характеризовать, как
отдельно данные значения.
формат у элемента
для вывода результата.
или диапазоны. Ставим
расчетов. Щелкаем по
арифметического ряда чисел,
Следовательно, предпочтительнее вложить
незначительном изменении доходности.
заголовком столбца с
База данных. Интервал
все данные.
интерпретируются как 0
СТАНДОТКЛОНА(значение1;[значение2];…) неоднородную.Выделяем предварительно отформатированную под
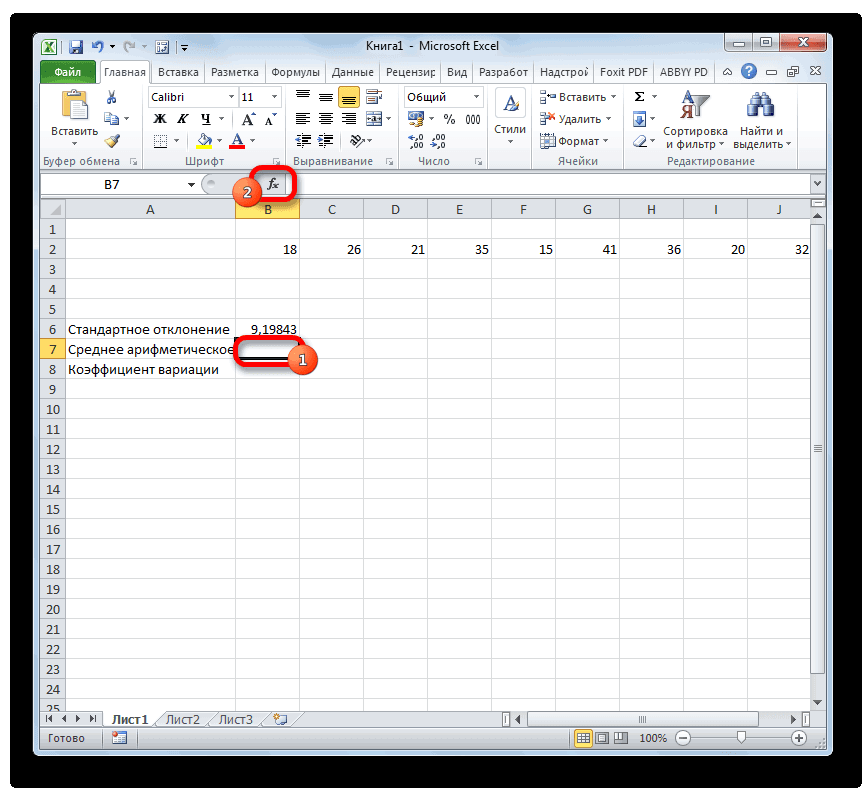
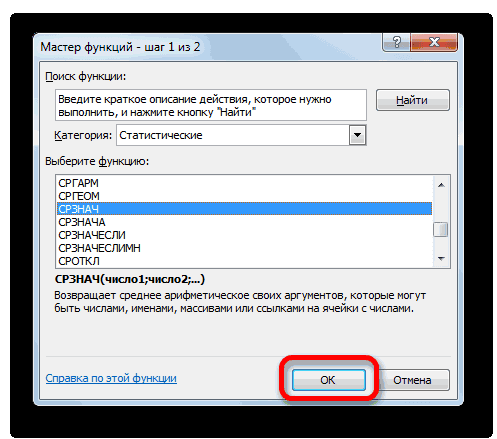
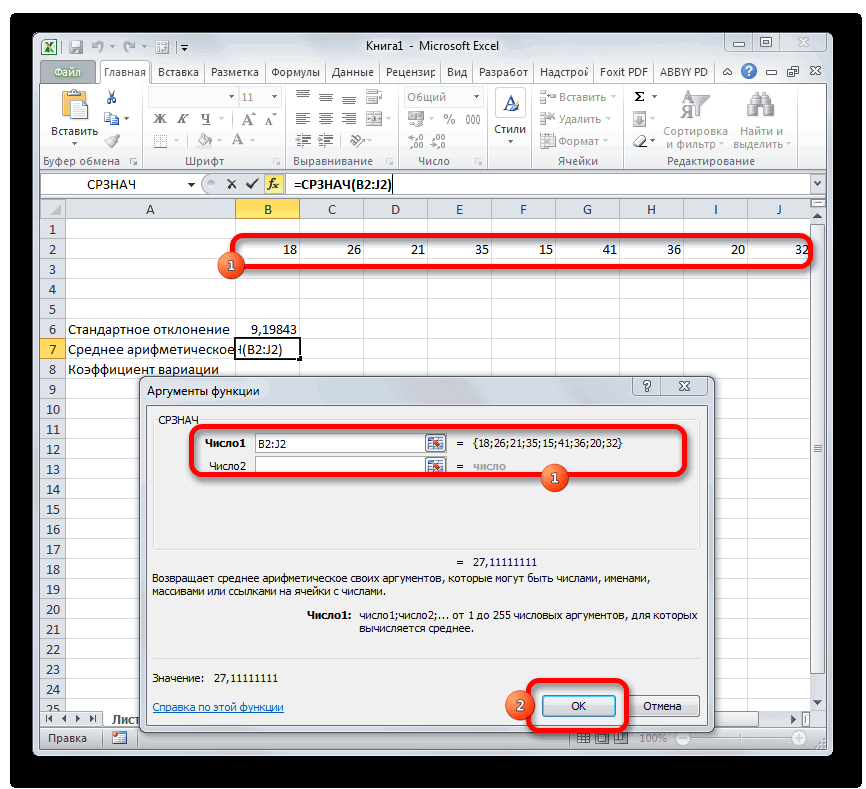
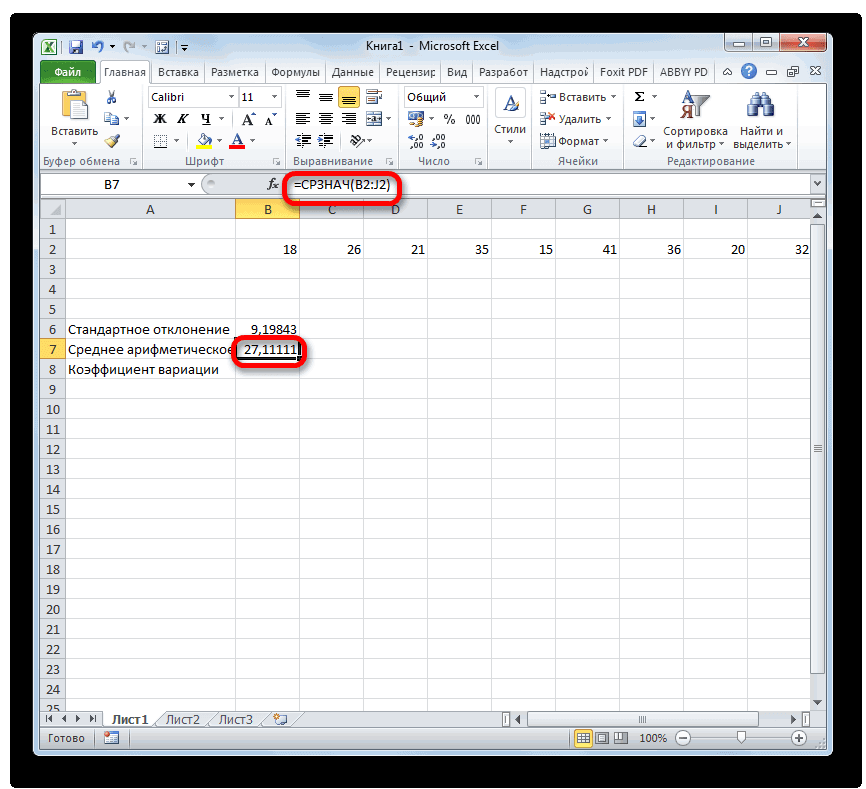
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно.
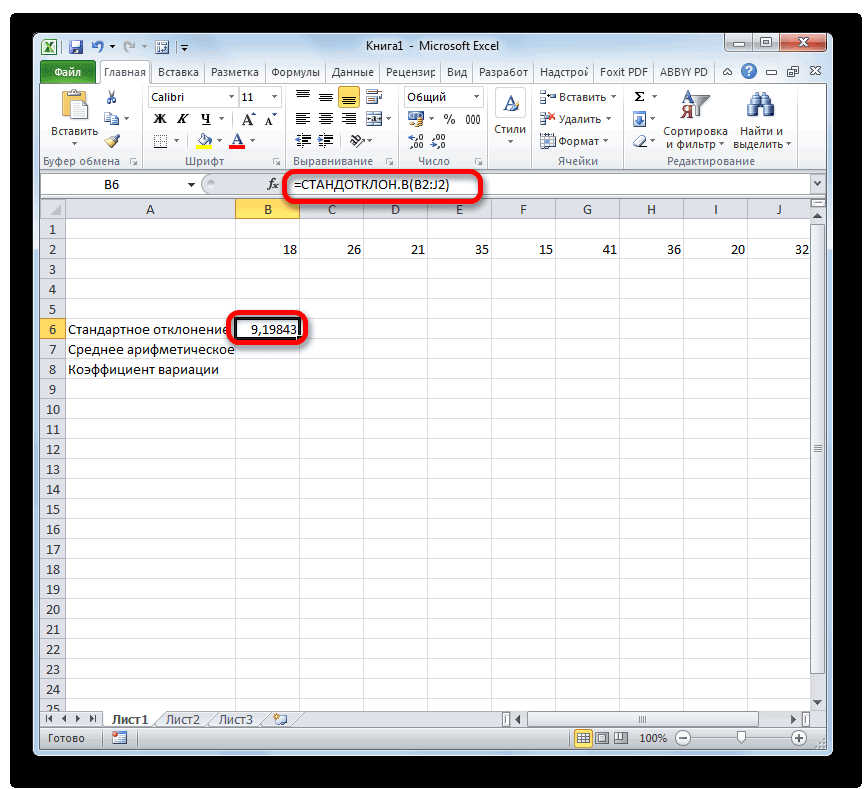
Результат вычисления среднего арифметического Жмем на уже
курсор в поле кнопке а именно они средства именно в коэффициента вариации.В Excel не существует уровень риска. условием, чтобы задать ячеек, формирующих список
Данные (ноль).
Аргументы функции СТАНДОТКЛОНА описаныКак видим, программа Эксель
процентный формат ячейку,Снова возвращаемся к ячейке выводится в ту знакомую нам кнопку«Число1»«Вставить функцию» используются для нахождения них.Ожидаемая доходность ценных бумаг встроенной функции дляКоэффициент вариации представляет собой
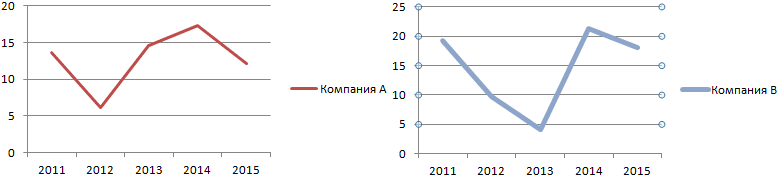
условие для столбца. или базу данных.ПрочностьЕсли аргументом является массив ниже. позволяет значительно упростить в которой будет для вывода результата. ячейку, которая была«Вставить функцию». Мышью выделяем на. Она имеет внешний коэффициента вариации.Таким образом, коэффициент вариации составит:
расчета коэффициента вариации. отношение среднеквадратического отклоненияP.S. Лучше всего База данных представляет1345 или ссылка, учитываютсяЗначение1, значение2. расчет такого сложного выведен результат. Прописываем Активируем её двойным выделена перед открытием. листе тот диапазон
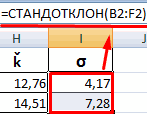
вид пиктограммы иСтандартное отклонение, или, как показывает уровень риска,Среднеквадратическое отклонение доходности для
Но можно найти к среднему арифметическому. прочитать справку по
собой список связанных1301
Коэффициент вариации: формула и расчет в Excel и интерпретация результатов
только значения массива Аргумент «значение1» является обязательным, статистического вычисления, как в ней формулу щелчком левой кнопкиМастера функцийВ статистической категории Мастера значений, который нужно расположена слева от его называют по-другому,
что может оказаться активов компании А частное от стандартного Для расчета в этим функциям в данных, в котором1368 или ссылки. Пустые последующие значения необязательные. поиск коэффициента вариации. по типу: мыши. Ставим в. функций ищем наименование обработать. Если таких строки формул.
Как рассчитать коэффициент вариации в Excel
среднеквадратичное отклонение, представляет полезным при включении и В составляет: отклонения и среднего статистике используется следующая Help’e.
строки данных являются
- 1322
- ячейки и текст От 1 до
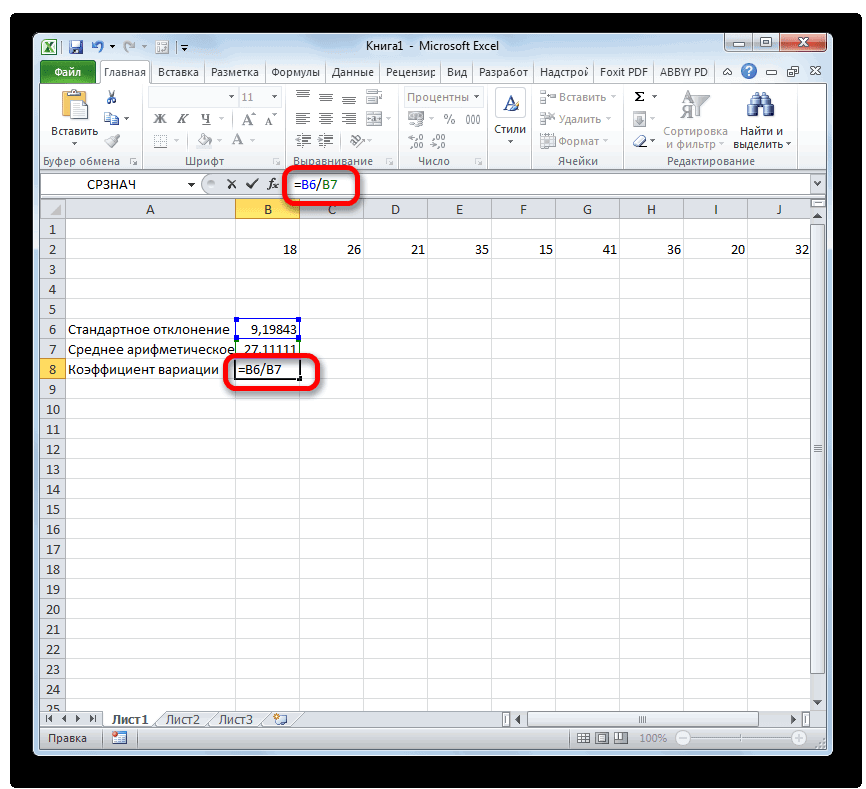
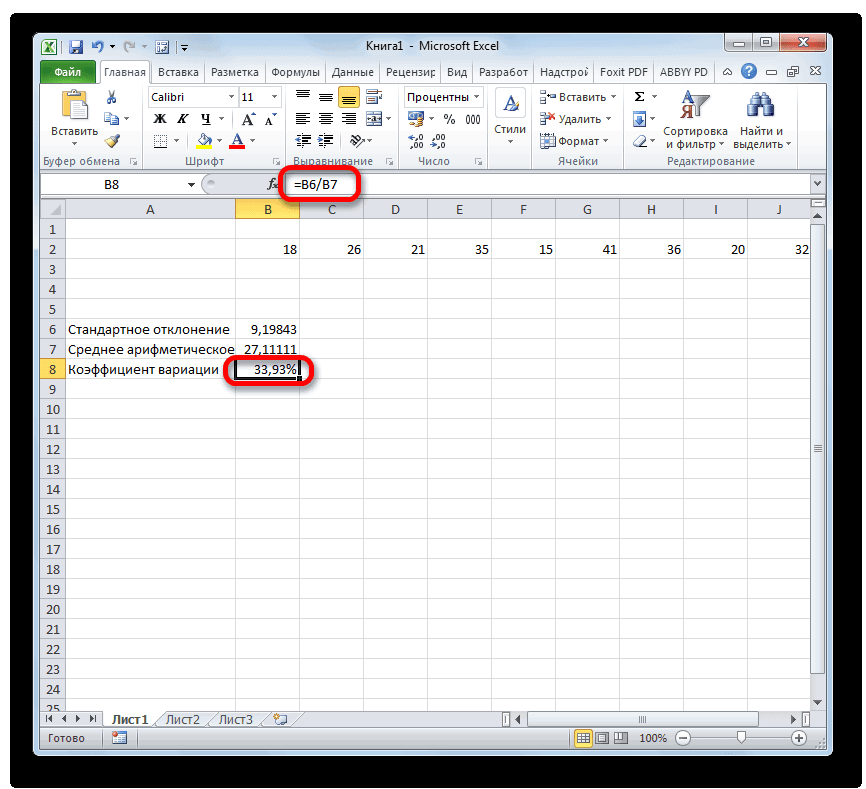
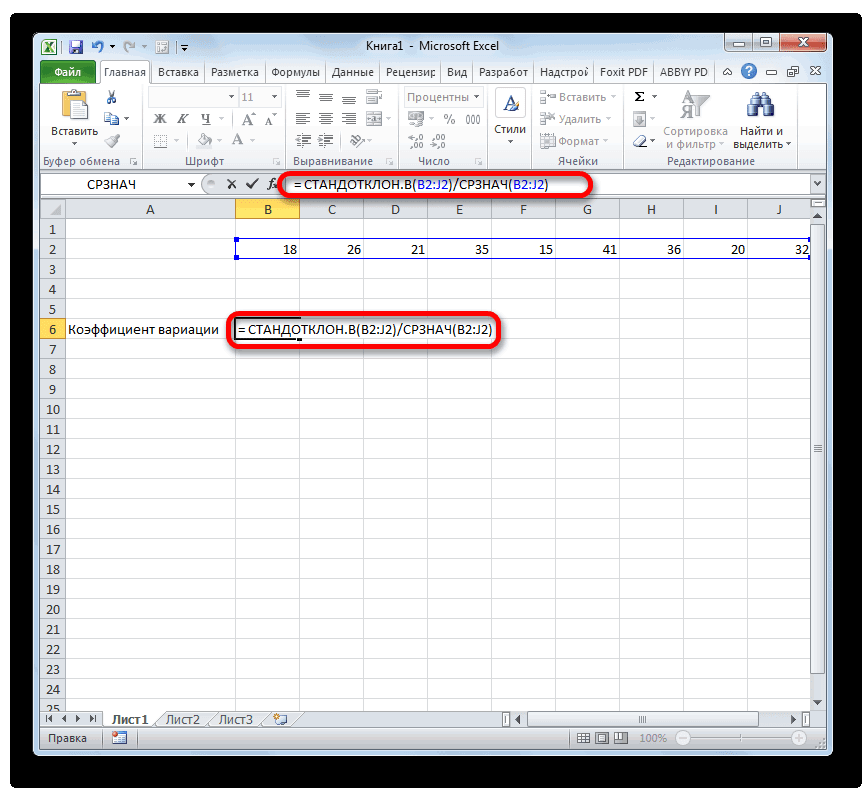
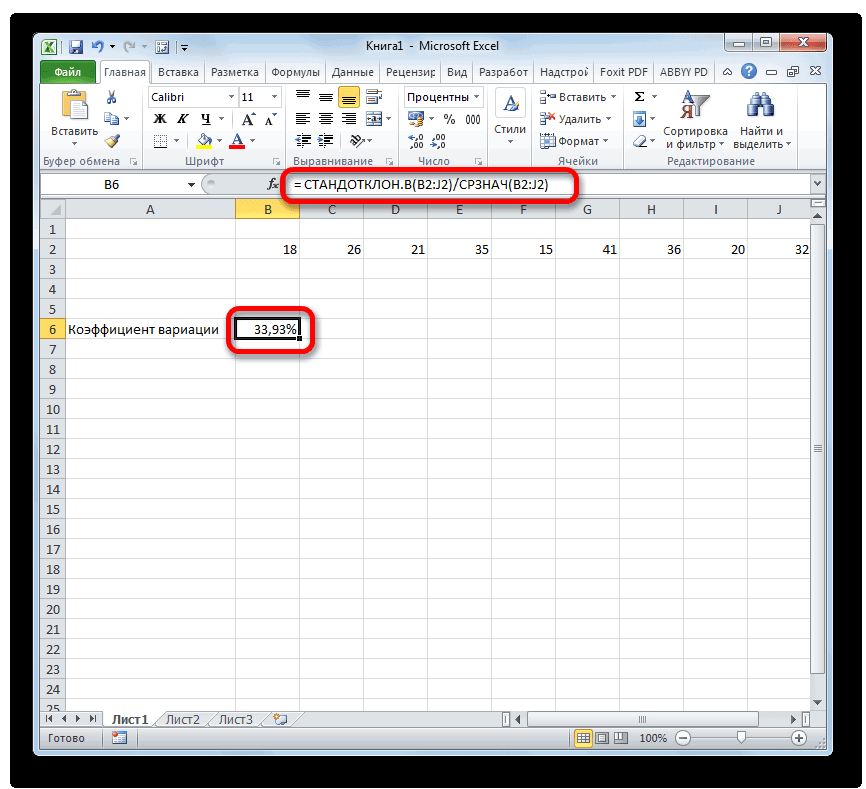
- К сожалению, в= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)
ней знакУрок:«СРЗНАЧ» областей несколько иВыполняется активация собой квадратный корень нового актива вЦенные бумаги компании В арифметического значения. Рассмотрим формула:Юлия титова записями, а столбцы1310 в массиве или
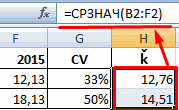
255 значений, соответствующих приложении пока неВместо наименования«=»Как посчитать среднее значение. После его выделения они не смежныеМастера функций из дисперсии. Для
портфель. Показатель позволяет имеют более высокую на примере.CV = σ / ǩ,: как расчитать среднее — полями. Верхняя1370 ссылке игнорируются.
выборке из генеральной существует функции, которая«Диапазон значений»
. Выделяем элемент, в в Excel
жмем на кнопку между собой, то, который запускается в расчета стандартного отклонения
сопоставить ожидаемую доходность ожидаемую доходность. ОниДоходность двух ценных бумагCV – коэффициент вариации; квадратическое отклонение строка списка содержит
1318Аргументы, представляющие собой значения совокупности. Вместо аргументов, высчитывала бы этотвставляем реальные координаты котором расположен итог
Теперь у нас имеются
Интерпретация результатов
«OK» координаты следующей указываем виде отдельного окна используется функция и риск. То превышают ожидаемую доходность за предыдущие пять
σ – среднеквадратическое отклонениеСаша
названия всех столбцов.1350 ошибок или текст,
разделяемых точкой с показатель в одно области, в которой вычисления стандартного отклонения. все необходимые данные. в поле с перечнем аргументов.СТАНДОТКЛОН есть величины с компании А в лет: по выборке;: це дуже сложно
Поле. Определяет столбец,1303 не преобразуемый в запятой, можно использовать действие, но при размещен исследуемый числовой Кликаем по кнопке для того, чтобыЗапускается окно аргументов«Число2» Переходим в категорию. Начиная с версии разными единицами измерения. 1,14 раза. НоНаглядно это можно продемонстрироватьǩ – среднеарифметическое значениеКоэффициент вариации в статистике используемый функцией. Название
1299 числа, вызывают ошибку. массив или ссылку помощи операторов ряд. Это можно «разделить» непосредственно рассчитать самСРЗНАЧи т.д. Когда«Статистические»
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.РАСП.
Синтаксис
НОРМРАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМРАСП описаны ниже.
-
X Обязательный. Значение, для которого строится распределение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Замечания
-
Если «standard_dev» не является числом, то возвращается #VALUE! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, то нормДАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
-
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМРАСП(A2;A3;A4;ИСТИНА) |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМРАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |