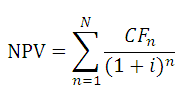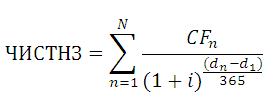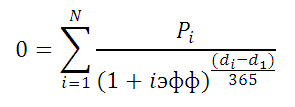Расчет npv онлайн калькулятор excel

Сегодняшняя публикация будет полезна тем, кто уже знает, что такое NPV и с помощью каких формул этот показатель рассчитывается, но нуждается в простых подручных инструментах, позволяющих рассчитывать NPV быстрее, нежели вручную или с помощью обычных калькуляторов.

Им в помощь многофункциональная среда Excel, позволяющая рассчитать NPV с помощью табличной организации данных либо же с применением специальных финансовых функций.

Разберем гипотетический пример, который решим посредством применения уже известной нам формулы расчета NPV, а затем повторим наши вычисления, используя возможности Excel.

Задача на нахождение NPV

Пример. Первоначальные инвестиции в проект A составляют 10000 рублей. Ежегодная процентная ставка – 10 %. Динамика поступлений с 1-го по 10-ый годы представлена в нижеследующей таблице:

Период	Притоки	Оттоки
0		10000
1	1100
2	1200
3	1300
4	1450
5	1600
6	1720
7	1860
8	2200
9	2500
10	3600

Для наглядности cответствующие данные можно представить графически:

Необходимо рассчитать показатель NPV.

Стандартное решение. Для решения задачи будем использовать уже известную нам формулу NPV:

Просто подставляем в нее известные значения, которые затем суммируем. Для этих вычислений нам пригодится калькулятор:

NPV = -10000/1,1⁰ + 1100/1,1¹ + 1200/1,1² + 1300/1,1³ + 1450/1,1⁴ + 1600/1,1⁵ + 1720/1,1⁶ + 1860/1,1⁷ + 2200/1,1⁸ + 2500/1,1⁹ + 3600/1,1¹⁰ = 352,1738 рублей.

Расчет NPV в Excel (пример табличный)

Этот же пример мы можем решить, организовав соответствующие данные в форме таблицы Excel.

Выглядеть это должно примерно так:

Для того чтобы получить нужный результат, мы должны соответствующие ячейки заполнить нужными формулами.

Ячейка	Формула
E4	=1/СТЕПЕНЬ(1+$F$2/100;B4)
E5	=1/СТЕПЕНЬ(1+$F$2/100;B5)
E6	=1/СТЕПЕНЬ(1+$F$2/100;B6)
E7	=1/СТЕПЕНЬ(1+$F$2/100;B7)
E8	=1/СТЕПЕНЬ(1+$F$2/100;B8)
E9	=1/СТЕПЕНЬ(1+$F$2/100;B9)
E10	=1/СТЕПЕНЬ(1+$F$2/100;B10)
E11	=1/СТЕПЕНЬ(1+$F$2/100;B11)
E12	=1/СТЕПЕНЬ(1+$F$2/100;B12)
E13	=1/СТЕПЕНЬ(1+$F$2/100;B13)
E14	=1/СТЕПЕНЬ(1+$F$2/100;B14)
F4	=(C4-D4)*E4
F5	=(C5-D5)*E5
F6	=(C6-D6)*E6
F7	=(C7-D7)*E7
F8	=(C8-D8)*E8
F9	=(C9-D9)*E9
F10	=(C10-D10)*E10
F11	=(C11-D11)*E11
F12	=(C12-D12)*E12
F13	=(C13-D13)*E13
F14	=(C14-D14)*E14
F15	=СУММ(F4:F14)

В результате в ячейке F15 мы получим искомое значение NPV, равное 352,1738.

Чтобы создать такую таблицу нужно затратить 3-4 минуты. Excel позволяет найти нужное значение NPV быстрее.

Расчет NPV в Excel (функция ЧПС)

Поместим в ячейку B17 (или любую другую свободную ячейку) формулу:

=ЧПС(F2/100;C5:C14)-D14

Мы мгновенно получим точное значение NPV в рублях (352,1738р.).

Наша формула ссылается на ячейки F2 (у нас там указана процентная ставка – 10 %; для использования в функции ЧПС нужно разделить ее на 100), диапазон значений C5:C14, где размещены данные о притоках денежных средств, и на ячейку D14, содержащую размер первоначальных инвестиций.

Таковы особенности функции ЧПС, рассчитывающей NPV без учета первоначальных инвестиций.

Тем, кто не прочь поэкспериментировать с функцией ЧПС, а также вычислением NPV с помощью табличной организации данных, предлагаю скачать исходник с примерами, рассмотренными в настоящей статье по ссылке.

Расчет NPV в Excel: заключение

Расчет NPV в Excel (читается: эксель) позволяет избежать трудоемких вычислений вручную или за счет использования громоздких программных комплексов и получить нужный результат в считанные секунды.

Расчет NPV в Excel (видео):

Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.

Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.

Скачать пример

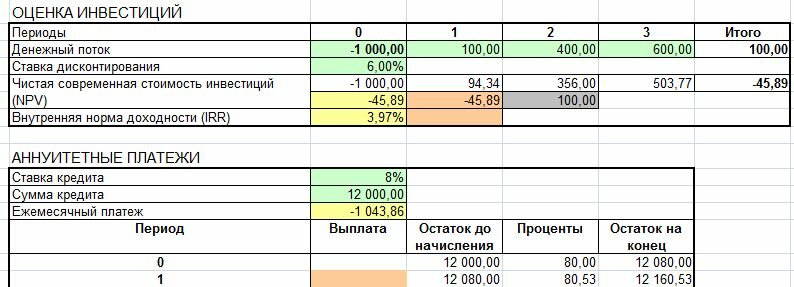
Оценка целесообразности проекта с помощью NPV

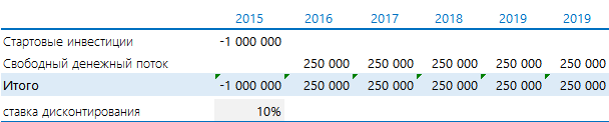
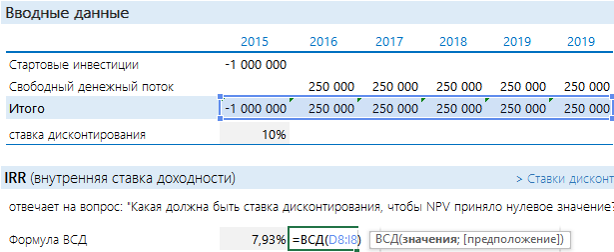
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.

Оцениваем NPV проекта. Напомню формулу этого показателя:

Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:

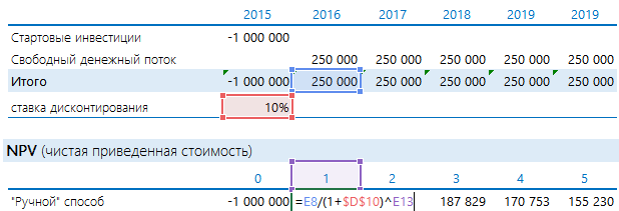
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.

Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.

Получается «-52 303». Проект невыгоден.

Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):

ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)

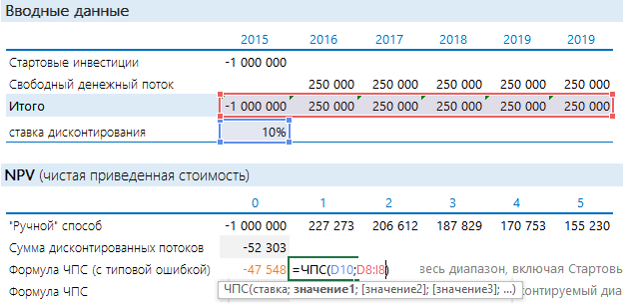
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:

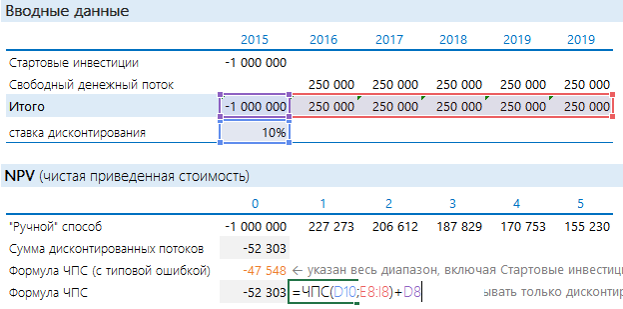
Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:

Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.

Оценка целесообразности проекта с помощью IRR

Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования < IRR, то проект стоит принять, если нет – отказаться. Рассчитать IRR с помощью Excel очень просто: подставляем в функцию ВСД итоговый денежный поток.

IRR оказался меньше ставки доходности. Проект невыгодный (тот же вывод, что и при NPV).

NPV и IRR по праву считаются главными экономическими критериями. Их используют и для инвестиционной оценки проектов, и для оценки стоимости существующего бизнеса. В том числе, показатель EVA (Economic Value Added) считается хорошим критерием в том числе потому, что при правильном расчете он равен NPV.

Но кроме всего прочего, NPV и IRR могут быть использованы финансистами в более прикладных вопросах, например, при общении с банками на тему реальной кредитной ставки. Как – давайте посмотрим.

Аннуитеты – любимая банковская цифра

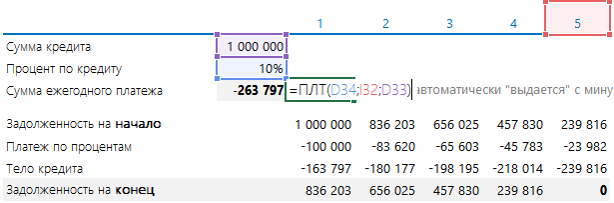
Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:

ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)

В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:

Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.

В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.

Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.

Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:

Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.

Нюансы и тонкости

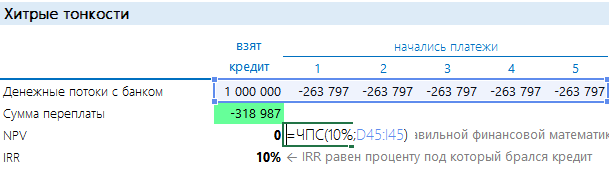
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.

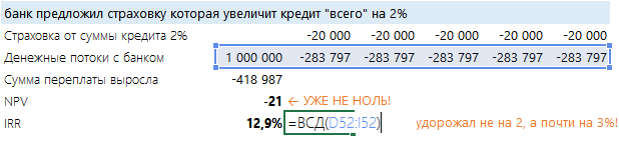
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:

В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…

Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.

Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.

Каждый человек, который серьезно занимался финансовой деятельностью или профессиональным инвестированием, сталкивался с таким показателем, как чистый дисконтированный доход или NPV. Этот показатель отражает инвестиционную эффективность изучаемого проекта. В программе Excel имеются инструменты, которые помогают рассчитать это значение. Давайте выясним, как их можно использовать на практике.

Расчет чистого дисконтированного дохода

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:

=ЧПС(ставка;значение1;значение2;…)

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».

Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

=Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

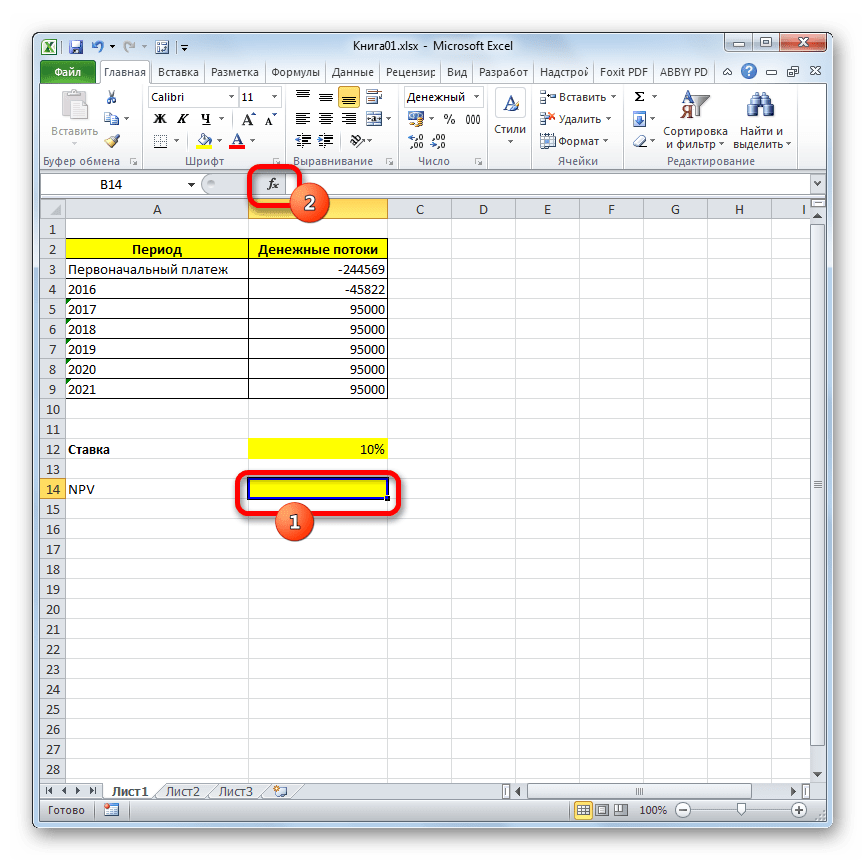
1. Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.



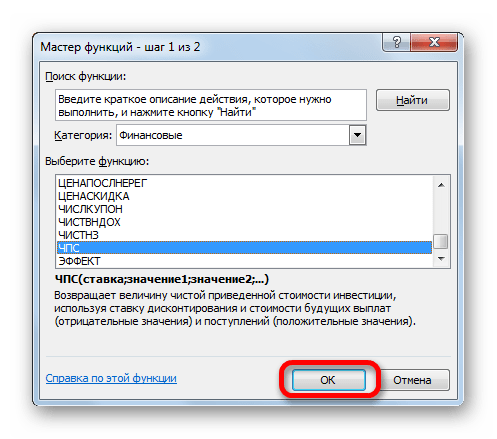
2. Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».



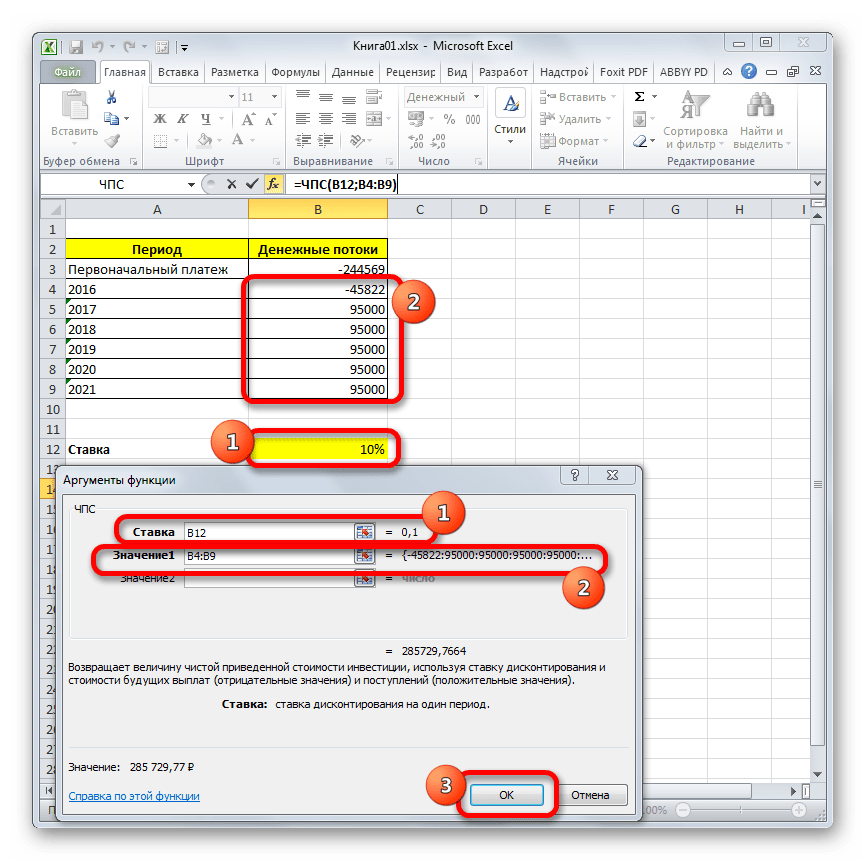
3. После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».

   В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

   

   В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

   Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».



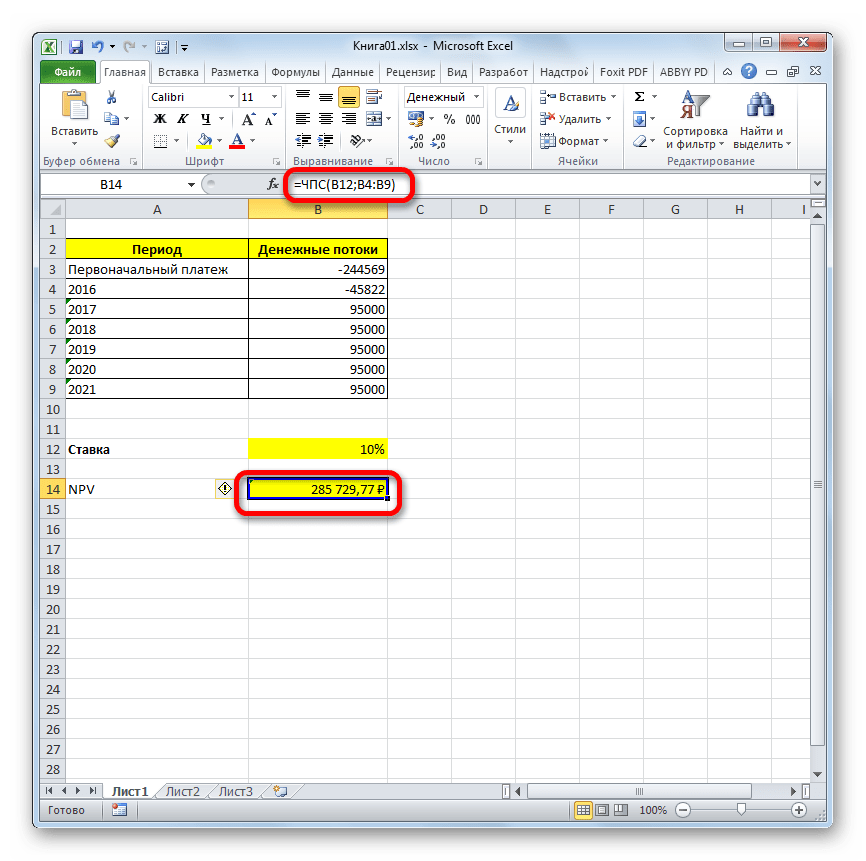
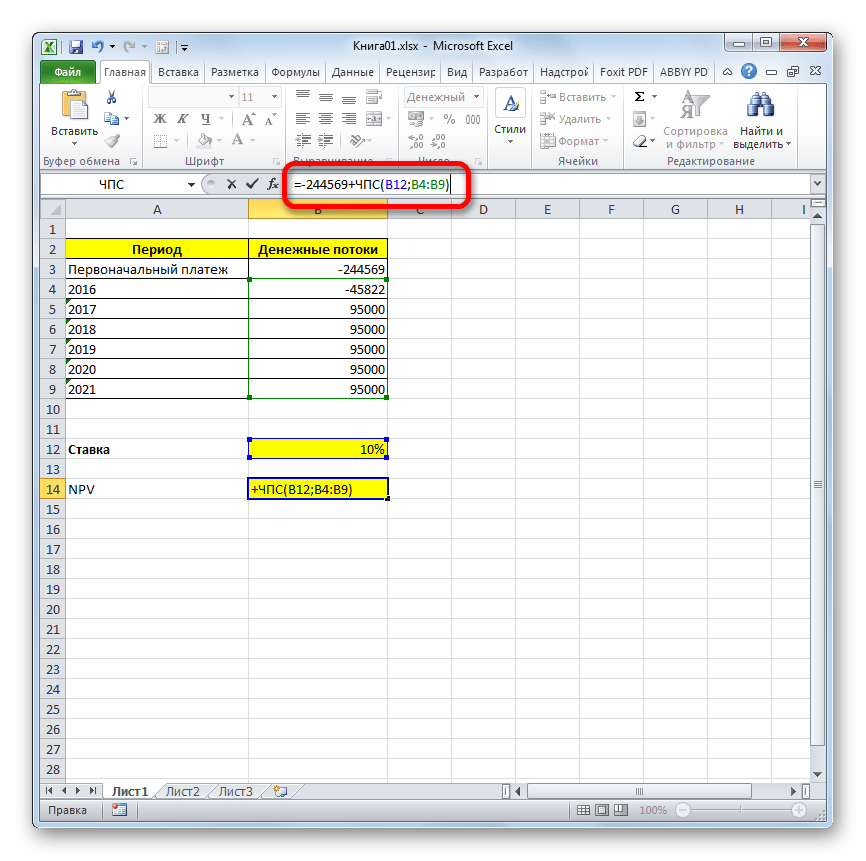
4. Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.



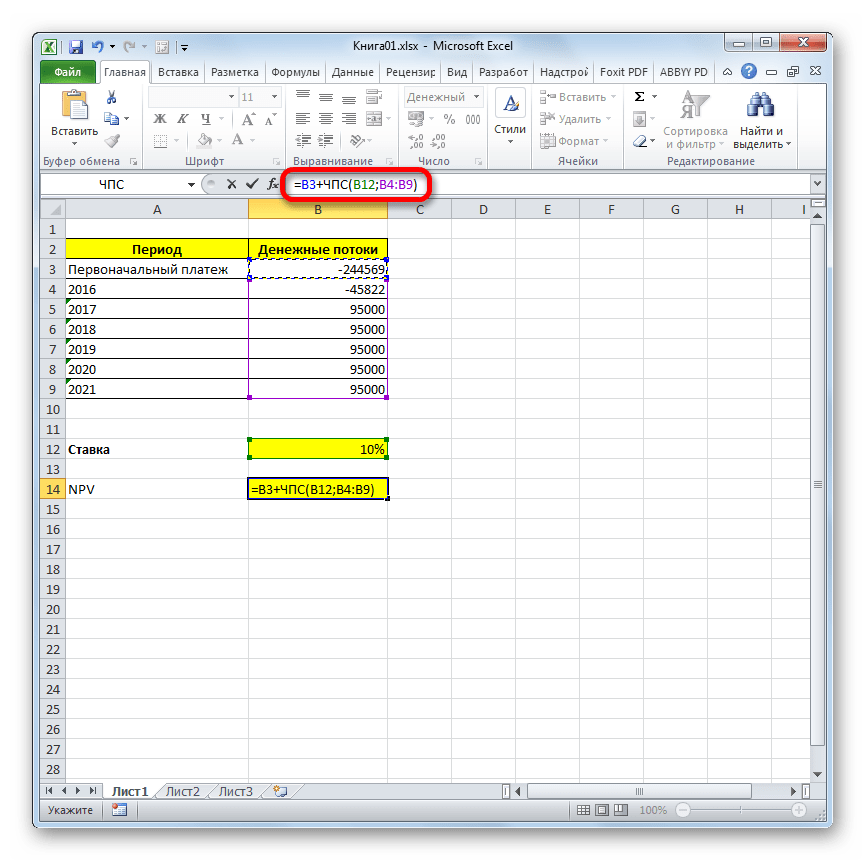
5. После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.
   

   Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.



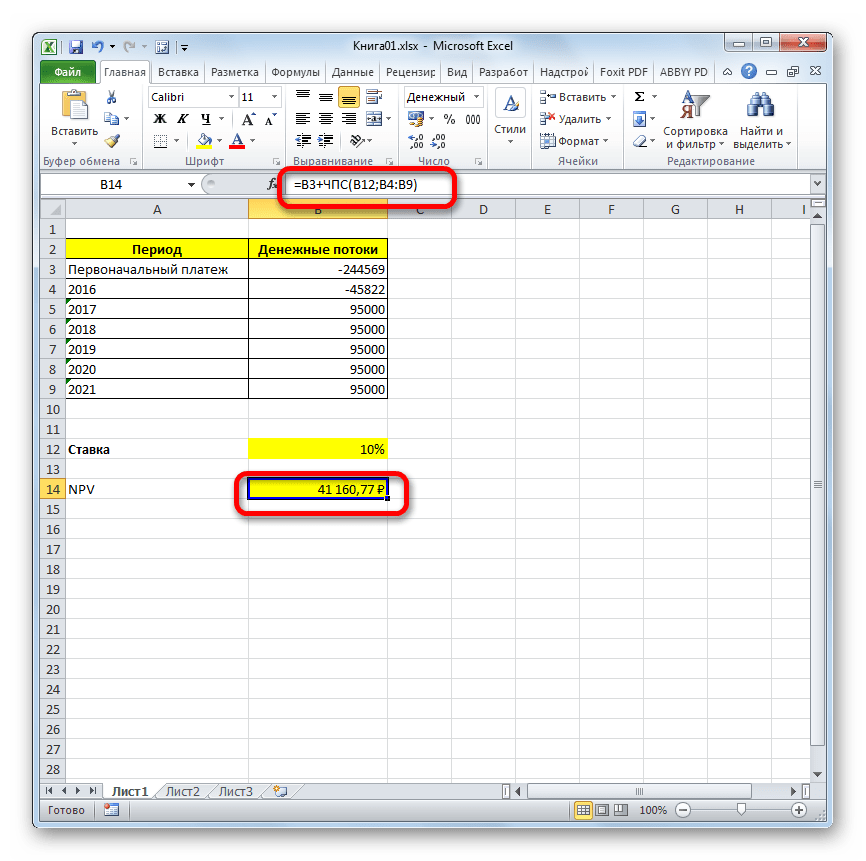
6. Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.

Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Урок: Финансовые функции в Excel

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

Онлайн калькулятор рассчитывает NPV (чистую приведенную стоимость) для инвестиционного проекта с заданными денежными потоками для соответствующих временных периодов.

NPV, чистый дисконтированный доход (Net Present Value) — сумма предполагаемого потока платежей, приведенная к текущей (на настоящий момент времени) стоимости. Приведение к текущей стоимости приводится по заданной ставке дисконтирования.

Обозначения

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул

MS

EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют

сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню

(взято из Википедии). Или так:

Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт

cfin.

ru)

Или так:

Текущая

стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика

.

Толковыйсловарь

. —

М

.

:

»

ИНФРА

—

М

«,

Издательство

»

ВесьМир

«.

Дж

.

Блэк

.)

Примечание1

. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется

ЧПС()

, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с

Приведенной стоимостью

.

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма

Приведенных стоимостей

денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет

: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи

Приведенная стоимость

.

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу

сложных процентов

.

Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция

ЧПС()

(английский вариант — NPV()). В ее основе используется формула:

CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2

. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:

Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)

. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.

Выбор периода дисконтирования для функции ЧПС()

При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.

Примечание3

. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции

ЧПС()

нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы  ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.

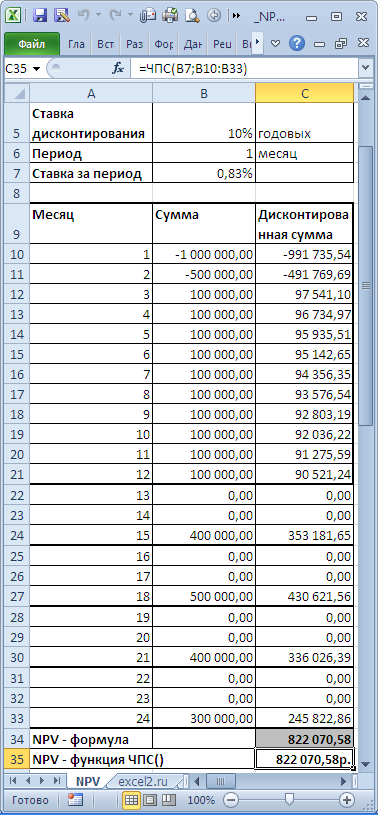
файл примера, лист NPV

).

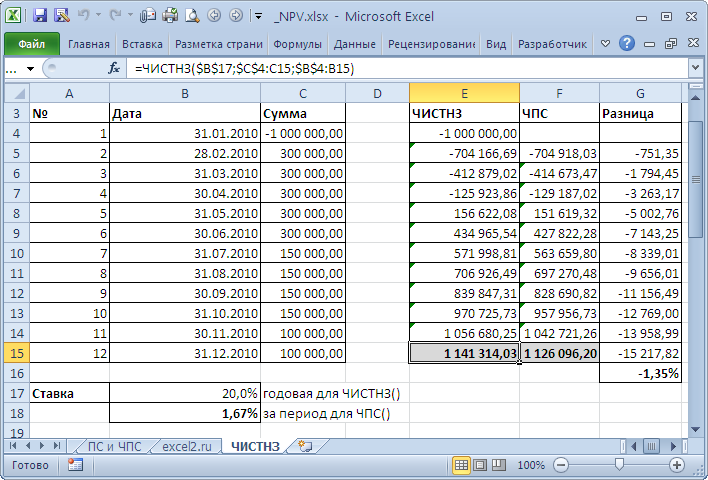
В таблице NPV подсчитан двумя способами: через функцию

ЧПС()

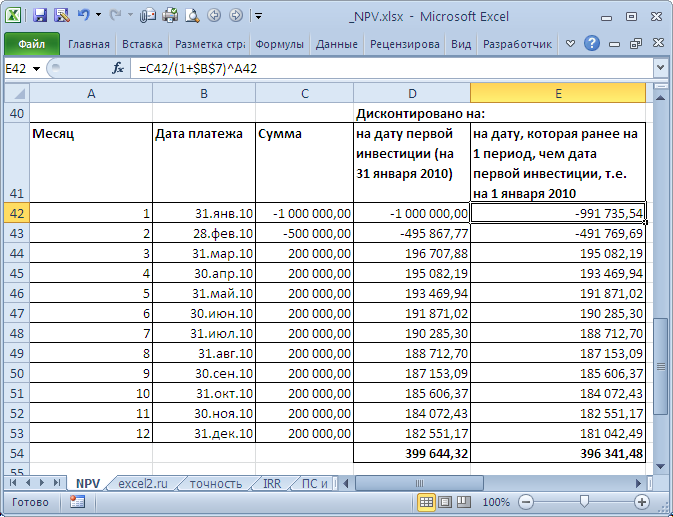
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции

ЧПС()

, а нужно просто прибавить к получившемуся результату (см.

файл примера

). Сравнение 2-х вариантов дисконтирования приведено в

файле примера

, лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.

файл примера, лист Точность

).

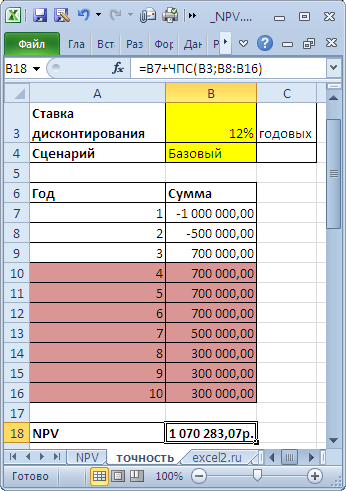
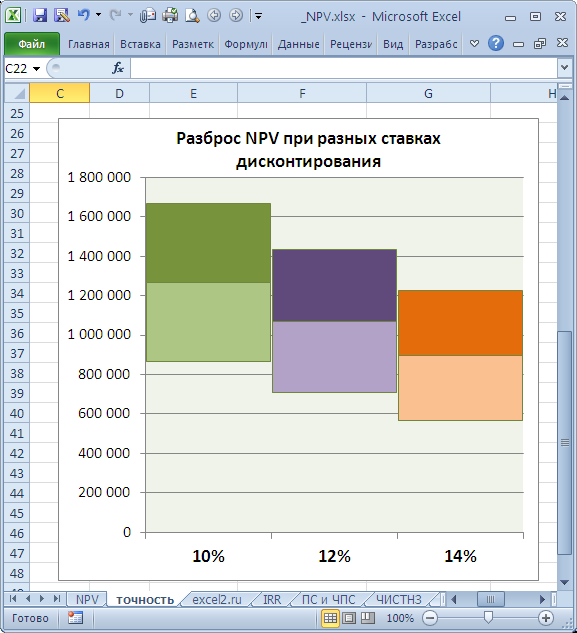
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

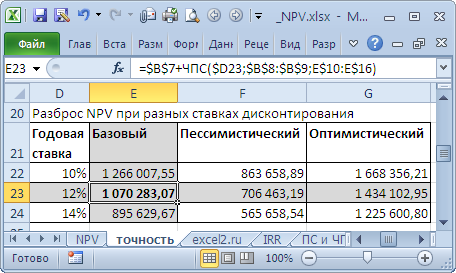
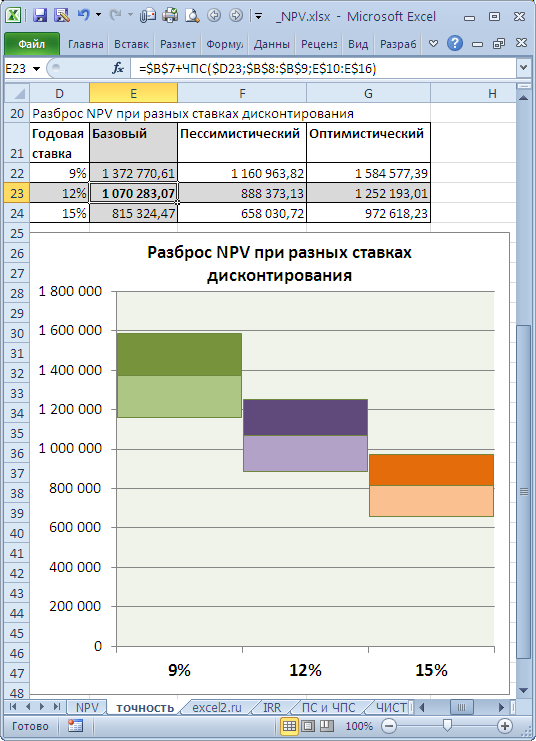
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

Внутренняя ставка доходности

IRR

(ВСД)

Внутренняя ставка доходности (англ.

internal rate of return

, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.

файл примера, лист IRR

).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Для расчета IRR используется функция

ВСД()

(английский вариант – IRR()). Эта функция тесно связана с функцией

ЧПС()

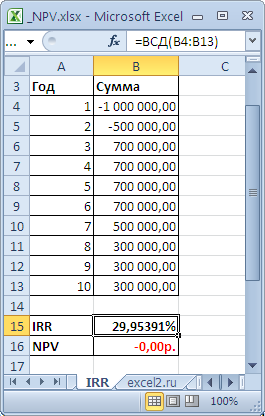
. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией

ВСД()

, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:

=ЧПС(ВСД(B5:B14);B5:B14)

Примечание4

. IRR можно рассчитать и без функции

ВСД()

: достаточно иметь функцию

ЧПС()

. Для этого нужно использовать инструмент

Подбор параметра

(поле «Установить в ячейке» должно ссылаться на формулу с

ЧПС()

, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

Напомним, что

аннуитет

представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию

ПС()

(см.

файл примера, лист ПС и ЧПС

).

В этом случае все денежные потоки (диапазон

В5:В13

, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке

В4

. Ставка дисконтирования расположена в ячейке

В15

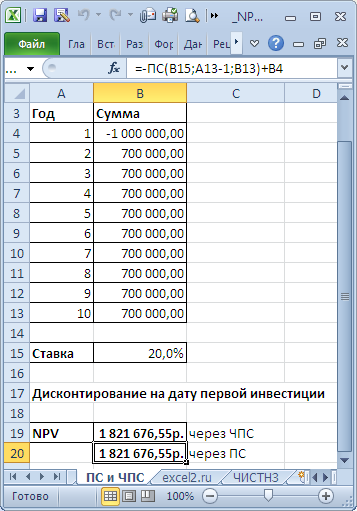
со знаком минус. В этом случае формула

=B4+ЧПС(B15;B5:B13)

дает тот же результат, что и

= B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за

любые

промежутки времени, то используется функция

ЧИСТНЗ()

(английский вариант – XNPV()).

Функция

ЧИСТНЗ()

возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от

ЧПС()

является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у

ЧИСТНЗ()

всегда годовая, т.к. указана база 365 дней, а не за период, как у

ЧПС()

. Еще отличие от

ЧПС()

: все денежные потоки всегда дисконтируются на дату первого платежа.

В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций

ЧИСТНЗ()

и

ЧПС()

. Эти функции возвращают несколько отличающиеся результаты. Для задачи из

файла примера, Лист ЧИСТНЗ

разница составила порядка 1% (период = 1 месяцу).

Это связано с тем, что у

ЧИСТНЗ()

длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у

ЧПС()

указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет

високосного

года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с

ЧПС()

, у которой имеется родственная ей функция

ВСД()

, у

ЧИСТНЗ()

есть функция

ЧИСТВНДОХ()

, которая вычисляет годовую ставку дисконтирования, при которой

ЧИСТНЗ()

возвращает 0.

Расчеты в функции

ЧИСТВНДОХ()

производятся по формуле:

Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Примечание5

. Функция

ЧИСТВНДОХ()

используется для

расчета эффективной ставки по потребительским кредитам

.

Написано admin в 24 января, 2012. Опубликовано в Инвестиционное проектирование

Теги:excel, анализ, инвестиции, расчет, финансы

Trackback с вашего сайта.