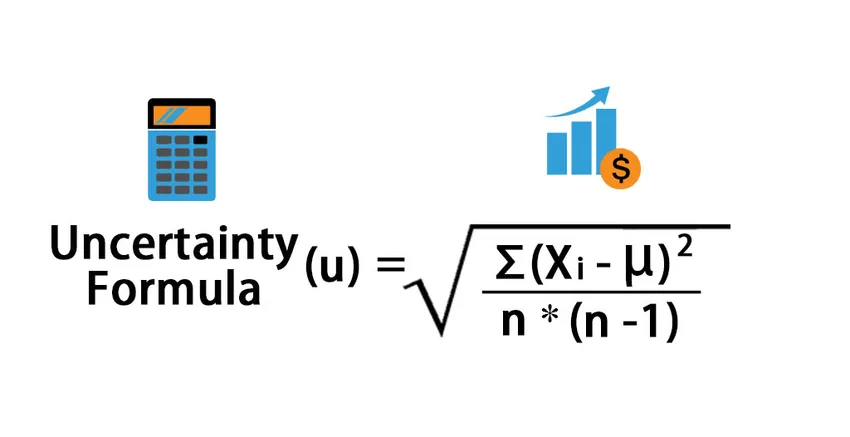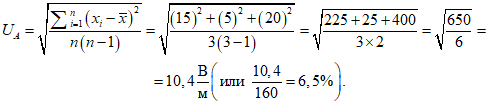© 2015-2022 — K-Tree.ru • Электронный учебник
По любым вопросам Вы можете связаться по почте info@k-tree.ru
Копия материалов, размещённых на данном сайте, допускается только по письменному разрешению владельцев
сайта.
- Что такое формула неопределенности?
Формула неопределенности (Содержание)
- формула
- Примеры
Что такое формула неопределенности?
В статистическом смысле термин «неопределенность» связан с измерением, где он относится к ожидаемому изменению значения, которое получается из среднего значения нескольких показаний, из истинного среднего значения набора данных или показаний. Другими словами, неопределенность можно рассматривать как стандартное отклонение среднего значения набора данных. Формула для неопределенности может быть получена путем суммирования квадратов отклонения каждой переменной от среднего значения, затем деления результата на произведение числа чтений и количества чтений минус один, а затем вычисление квадратного корня из результата, Математически формула неопределенности представлена в виде
Uncertainty (u) = √ (∑ (x i – μ) 2 / (n * (n – 1)))
Где,
- x i = i- е чтение в наборе данных
- μ = среднее значение набора данных
- n = количество чтений в наборе данных
Примеры формулы неопределенности (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет неопределенности.
Вы можете скачать этот шаблон формулы неопределенности Excel здесь — Шаблон формулы неопределенности Excel
Формула неопределенности — пример № 1
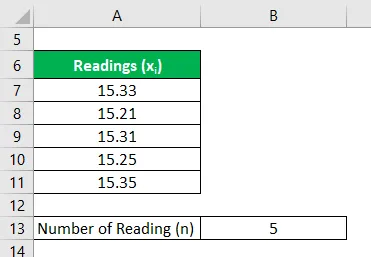
Давайте возьмем пример забега на 100 м в школьном соревновании. Гонка была рассчитана с использованием пяти разных секундомеров, и каждый секундомер записывал немного разные сроки. Показания составляют 15, 33 секунды, 15, 21 секунды, 15, 31 секунды, 15, 25 секунды и 15, 35 секунды. Рассчитайте неопределенность времени на основе предоставленной информации и представьте время с уровнем достоверности 68%.
Решение:
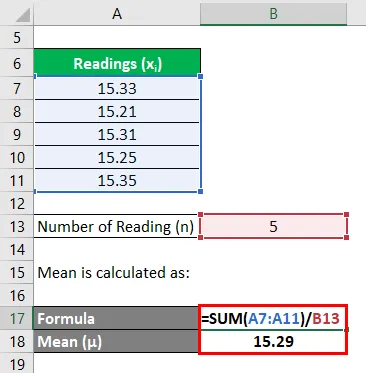
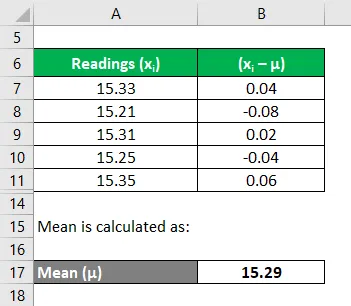
Среднее значение рассчитывается как:
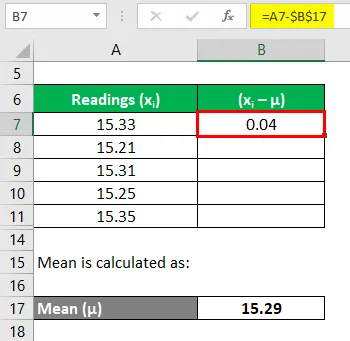
Теперь нам нужно рассчитать отклонения каждого чтения
Аналогично рассчитайте все показания
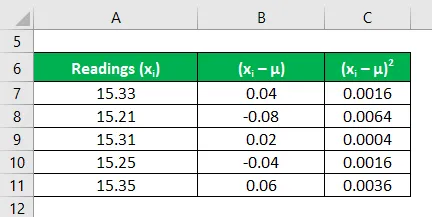
Рассчитайте квадрат отклонений каждого показания
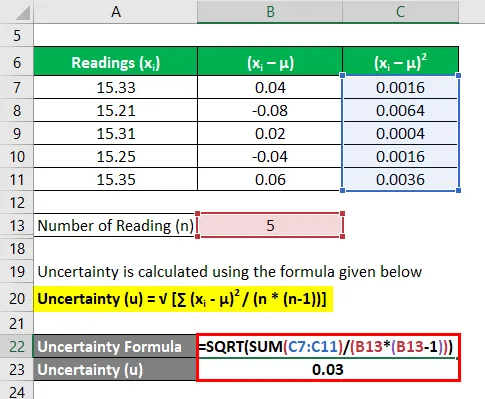
Неопределенность рассчитывается по формуле, приведенной ниже
Неопределенность (u) = √ (∑ (x i — μ) 2 / (n * (n-1)))
- Неопределенность = 0, 03 секунды
Время при уровне достоверности 68% = μ ± 1 * u
- Измерение при уровне достоверности 68% = (15, 29 ± 1 * 0, 03) секунды
- Измерение при уровне достоверности 68% = (15, 29 ± 0, 03) секунды
Следовательно, неопределенность набора данных составляет 0, 03 секунды, а время может быть представлено как (15, 29 ± 0, 03) секунды при уровне достоверности 68%.
Формула неопределенности — пример № 2
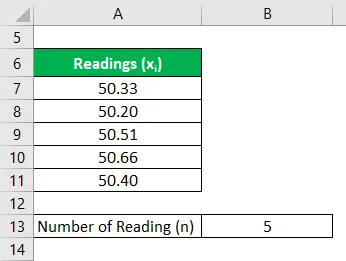
Давайте возьмем пример Джона, который решил продать свою недвижимость, которая является бесплодной землей. Он хочет измерить доступную площадь имущества. Согласно назначенному геодезисту, были взяты 5 чтений — 50, 33 акра, 50, 20 акра, 50, 51 акра, 50, 66 акра и 50, 40 акра. Выразите измерение земли с 95% и 99% уровнем достоверности.
Решение:
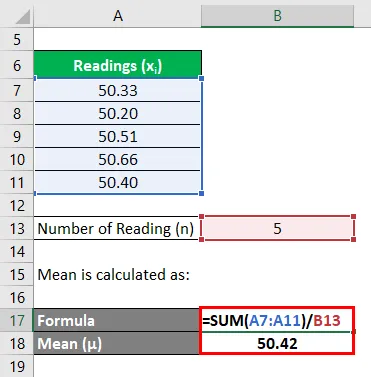
Среднее значение рассчитывается как:
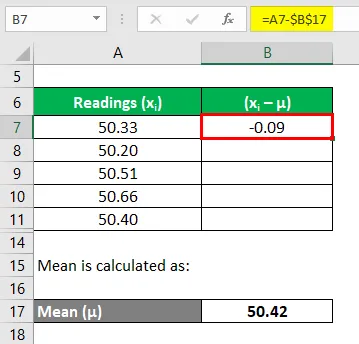
Теперь нам нужно рассчитать отклонения каждого чтения
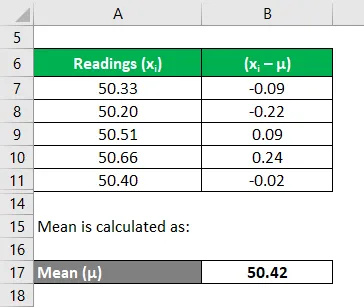
Аналогично рассчитайте все показания
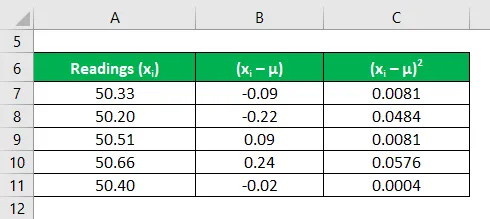
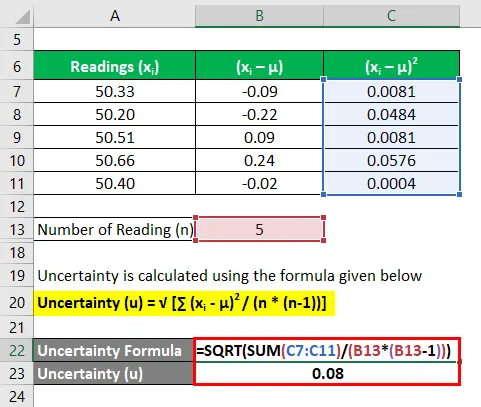
Рассчитайте квадрат отклонений каждого показания
Неопределенность рассчитывается по формуле, приведенной ниже
Неопределенность (u) = √ (∑ (x i — μ) 2 / (n * (n-1)))
- Неопределенность = 0, 08 акра
Измерение при уровне достоверности 95% = μ ± 2 * u
- Измерение при уровне достоверности 95% = (50, 42 ± 2 * 0, 08) акр
- Измерение при уровне достоверности 95% = (50, 42 ± 0, 16) акр
Измерение при уровне достоверности 99% = μ ± 3 * u
- Измерение при уровне достоверности 99% = (50, 42 ± 3 * 0, 08) акр
- Измерение при уровне достоверности 99% = (50, 42 ± 0, 24) акр
Следовательно, погрешность показаний составляет 0, 08 акра, и измерение можно представить как (50, 42 ± 0, 16) акра и (50, 42 ± 0, 24) акра при уровне достоверности 95% и 99%.
объяснение
Формула для неопределенности может быть получена с помощью следующих шагов:
Шаг 1: Во-первых, выберите эксперимент и переменную, которую нужно измерить.
Шаг 2: Затем соберите достаточное количество показаний для эксперимента путем повторных измерений. Показания будут формировать набор данных, и каждое чтение будет обозначаться как x i .
Шаг 3: Затем определите количество чтений в наборе данных, которое обозначено как n.
Шаг 4: Затем рассчитайте среднее значение показаний, суммируя все показания в наборе данных, а затем разделите результат на число показаний, доступных в наборе данных. Среднее обозначается через µ.
μ = ∑ x i / n
Шаг 5: Затем рассчитайте отклонение для всех показаний в наборе данных, которое представляет собой разницу между каждым показанием и средним значением, т.е. (x i — μ) .
Шаг 6: Затем вычислите квадрат всех отклонений, т.е. (x i — μ) 2 .
Шаг 7: Затем суммируйте все квадратичные отклонения, т.е. ∑ (x i — μ) 2 .
Шаг 8: Затем указанная выше сумма делится на произведение числа чтений и количества чтений минус один, то есть n * (n — 1) .
Шаг 9: Наконец, формула для неопределенности может быть получена путем вычисления квадратного корня из вышеуказанного результата, как показано ниже.
Неопределенность (u) = √ (∑ (x i — μ) 2 ) / (n * (n-1))
Актуальность и использование формулы неопределенности
С точки зрения статистических экспериментов концепция неопределенности очень важна, поскольку помогает статистику определять изменчивость показаний и оценивать измерения с определенным уровнем достоверности. Тем не менее, точность неопределенности так же хороша, как и показания, полученные измерителем. Неопределенность помогает в оценке наилучшего приближения для измерения.
Рекомендуемые статьи
Это было руководство к формуле неопределенности. Здесь мы обсудим, как рассчитать неопределенность, используя формулу вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Примеры для расчета абсолютной стоимости
- Калькулятор формулы допустимой погрешности
- Как рассчитать коэффициент текущей стоимости с помощью формулы?
- Руководство по формуле снижения относительного риска
145 сообщений в этой теме
- Назад
- 1
- 2
- 3
- 4
- 5
- 6
- Далее
-
Страница 1 из 6
Рекомендуемые сообщения
-
- Жалоба
- Поделиться
Часто приносят приборы в калибровку,при этом необходимо
вычислять неопределенность.
Существуют ли какие нибудь программы ускоряющие
этот трудоёмкий процесс ?
Самое трудное это вычисление средних значений калибруемого прибора (по 10 измерениям),
и вычисление средне квадратического отклонения
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
Ответы
144 -
Создана
6 л -
Последний ответ
5 л
Лучшие авторы в этой теме
-
30
-
24
-
23
-
16
Загружено фотографий
-
- Жалоба
- Поделиться
Цитата
Самое трудное это вычисление средних значений калибруемого прибора (по 10 измерениям),
и вычисление средне квадратического отклонения
Это выполняет Excel
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
А где найти формулу что бы вставить её в Эксель ?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
23 минуты назад, Victor1956 сказал:
А где найти формулу что бы вставить её в Эксель ?
В Экселе же: fx — СТАНДОТКЛОН( )
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
А где найти формулу что бы вставить её в Эксель ?
Извините что задаю такие вопросы,плохо знаю Эксель.
Можно немного поподробнее как в Экселе вычислить
среднее арифметическое из 10 измерений и среднее квадратическое
из 10 измерений ?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Степан Иванович, извиняюсь, что ссылкой Вас кидаю. Но этот ресурс будет для Вас полезен — http://www.planetaexcel.ru/
как писать формулы: встаете в ячейку, в значение строки формул пишите «=» далее руками набираете «СРЗНАЧ». Открываются скобки — выбираете нужный диапазон, в котором хотите найти среднее.
все другие функции по аналогии.
Это самая база. Читайте книги, форумы.
Изменено 17 Февраля 2017 пользователем Planck
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
27 минут назад, Victor1956 сказал:
Можно немного поподробнее как в Экселе вычислить
среднее арифметическое из 10 измерений и среднее квадратическое
из 10 измерений ?
Подробнее не могу
Форум СР СКО.xlsx
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
1 час назад, efim сказал:
есть примерчик, ср знач м/вычислить по разному
Возможности Excel безграничны. И по СКО можно полностью формулу забить со всеми действиями, и округлить результат по- разному и многое другое.
По обработке результатов измерений по калибровке (к примеру, электронных лабораторных весов) в свое время «здорово» помог в плане значительного сокращения времени на расчеты и оформление — внес результаты измерений и ИТОГ сразу же. Забьешь допускаемые значения и годно, или не годно по этому параметру напишет в отдельной ячейке ДА или НЕТ.
Формула СКО 1.xlsx
Изменено 17 Февраля 2017 пользователем владимир 332
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
Спасибо всем,это уже кое что.
А есть в экселе формула позволяющая вычислить стандартную неопределённость по типу А ?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
Может быть я что то делаю неправильно гляньте на формулы которыми я пользуюсь :
Изменено 30 Мая 2017 пользователем Victor1956
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
48 минут назад, Victor1956 сказал:
А Вы, простите, ВНИИМ им. Менделеева представляете?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
Нет
Изменено 30 Мая 2017 пользователем Victor1956
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
В 17.02.2017 в 16:36, Victor1956 сказал:
…
Изменено 30 Мая 2017 пользователем 5ive
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
К тому же на форуме, в режиме обмена мнениями и знаниями,
можно быстрее разобраться с любыми вопросами.
Изменено 30 Мая 2017 пользователем Victor1956
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Обратите внимание, СКО и стандартное отклонение, которое считает Эксель СТАНДОТКЛОН( ) — это не совсем одно и то же.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
9 часов назад, Victor1956 сказал:
В метрологических службах предприятий есть специалисты
более эрудированные чем в НИИ.
Вот для начала я как специалист рекомендую вам перестать считать неопределенность при поверке. Может вы данный частотомер и калибруете, но встречал ваши протоколы поверки с расчетом неопределенности. Зачем?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
ГОСТ 8.736 -2011 ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения.
Изменено 18 Февраля 2017 пользователем владимир 332
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
11 часов назад, Victor1956 сказал:
Может быть я что то делаю неправильно гляньте на формулы которыми я пользуюсь :
4 часа назад, Alex Aliev сказал:
Обратите внимание, СКО и стандартное отклонение, которое считает Эксель СТАНДОТКЛОН( ) — это не совсем одно и то же.
Эксель СТАНДОТКЛОН( ) считает именно среднееквадратическое отклонение (СКО) п.5.3 Формула (3) ГОСТ 8.736-2011.
В Вашем протоколе калибровки, Степан Иванович, Sч это среднее квадратическое отклонение среднего арифметического (оценка измеряемой величины) п.5.4 Формула (4) ГОСТ 8.736-2011, она в корень квадратный из числа измерений (10) меньше СКО.
ГОСТ 8.736-2011 Измерения многократные обработка РИ..pdf
Изменено 18 Февраля 2017 пользователем владимир 332
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
Формула 5.3 не подходит для неопределенности,в знаменателе должно быть n(n-1).
То есть в экселе нет подходящей под мой случай формулы ?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
В 18.02.2017 в 02:32, 5ive сказал:
Вот для начала я как специалист рекомендую вам перестать считать неопределенность при поверке. Может вы данный частотомер и калибруете, но встречал ваши протоколы поверки с расчетом неопределенности. Зачем?
При поверке никакую неопределенность не приводят,неопределенность только при калибровке.
Изменено 30 Мая 2017 пользователем Victor1956
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
3 часа назад, Victor1956 сказал:
Формула 5.3 не подходит для неопределенности,в знаменателе должно быть n(n-1).
То есть в экселе нет подходящей под мой случай формулы ?
Почему же Эксель позволяет забить любую формулу
(СТАНДОТКЛОН.В( )/ КОРЕНЬ (10))*1000
По Вашим данным посчитал по формуле (4) п. 5.4 ГОСТ 8.736-2011, которая абсолютно идентична Вашей формуле по определению Fч в протоколе калибровки. Можно и неопределенности посчитать, если забить формулы по их определению. а уж оформление протокола за Вами. Можно весь протокол в Экселе сделать.
Но на все это нужно время, зато потом «красота».
ПК ЧЗ-63.xlsx
Изменено 18 Февраля 2017 пользователем владимир 332
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Автор
-
- Жалоба
- Поделиться
Владимир 332 — спасибо,здорово у вас получилось !
Только я всё равно ничего не понял — какую формулу нужно вбить конкретно.
Кстати, n(n-1) можно заменить на число 90,эта величина будет постоянной
(если 10 измерений.)
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
15 минут назад, Victor1956 сказал:
Владимир 332 — спасибо,здорово у вас получилось !
Только я всё равно ничего не понял — какую формулу нужно вбить конкретно.
Кстати, n(n-1) можно заменить на число 90,эта величина будет постоянной
(если 10 измерений.)
Victor1956! В этом случае ничего вбивать не надо, я уже все «вбил». В любой табличке вбиваете показания и г-н эксель все посчитает. Единственное, «жирное не трогайте» — формула там и в верхней строчке виден алгоритм. Попробуйте. Впрочем чего объяснять, » подводных камней хватает». Всего я Вам не объясню никогда… У Вас один выход изучать Эксель, альтернативы нет, калькулятор «не катит», такова она современная жизнь.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
1 час назад, владимир 332 сказал:
У Вас один выход изучать Эксель, альтернативы нет, калькулятор «не катит», такова она современная жизнь.
Калькулятор который с кнопочками, в режиме статистика, для весов специального класса точности точно не катит. Надо 12 разрядный. А вот стандартный Виндовс подойдет точно
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Назад
- 1
- 2
- 3
- 4
- 5
- 6
- Далее
- Страница 1 из 6
Присоединиться к обсуждению
Вы можете ответить сейчас, а зарегистрироваться позже.
Если у вас уже есть аккаунт, войдите, чтобы ответить от своего имени.
ПРИМЕР РАСЧЕТА РАСШИРЕННОЙ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
1.1. Для расчета расширенной неопределенности измерений напряженности ЭП ПЧ 50 Гц в таблице представлены (в качестве примера) исходные данные.
При измерениях напряженности ЭП ПЧ использован прибор с допускаемой основной относительной погрешностью измерений — 20%.
В результате измерений уровней ЭП ПЧ в соответствии с пунктами 3.1 — 3.3 представлены значения (В/м) в таблице.
Таблица
Пример значений при измерении уровней ЭП ПЧ
|
Точки измерений ЭП ПЧ |
Точка N 1 |
Точка N 2 |
Точка N 3 |
|||||||||
|
Высота проведения измерений, м |
0,5 |
1,0 |
1,5 |
2,0 |
0,5 |
1,0 |
1,5 |
2,0 |
0,5 |
1,0 |
1,5 |
2,0 |
|
Полученные результаты, В/м |
90 |
100 |
80 |
90 |
110 |
175 |
130 |
90 |
90 |
60 |
80 |
90 |
|
100 |
80 |
110 |
110 |
60 |
165 |
120 |
100 |
100 |
70 |
115 |
140 |
|
|
80 |
90 |
80 |
70 |
100 |
140 |
110 |
80 |
110 |
80 |
105 |
100 |
|
|
Усредненные значения уровней напряженности ЭП ПЧ, В/м |
90 |
90 |
90 |
90 |
90 |
160 |
120 |
90 |
100 |
70 |
100 |
110 |
В точке N 2 таблицы на высоте 1,0 м получено максимальное из усредненных значений уровней напряженности ЭП ПЧ, вычисленное по формуле:
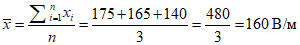
Вычисляем стандартную неопределенность по типу «А» для источников неопределенности случайного характера:
Вычисляем неопределенность систематического характера, вызванную погрешностью прибора (приборная погрешность), стандартную неопределенность по типу Б:
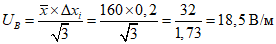
где — пределы допускаемой приборной погрешности, в качестве значения напряженности ЭП ПЧ берем полученное среднее значение 160 В/м с учетом погрешности 20% прибора.
Вычисляем суммарную стандартную неопределенность:
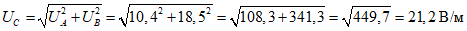
Для доверительной вероятности (вероятности охвата) P = 0.95 задаем коэффициент охвата k = 2 <4>, поскольку полученные значения являются арифметическими средними нормально распределенными независимыми повторными наблюдениями (при n > 10 каждой измеренной величины, полученной с учетом современных средств измерений, которые производят серию измерений усредняя полученные результаты) и вычисляем расширенную неопределенность измерений:
———————————
<4> Для одностороннего охвата применяется коэффициент — 1,65.
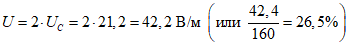
С учетом расширенной неопределенности получаем следующий результат измерений, который вносится в протокол:
160 +/- 42,4 В/м.
1.2. Расчет расширенной неопределенности измерений напряженности МП ПЧ 50 Гц проводится аналогично п. 1.1 приложения к настоящим МУК.
Скачать документ целиком в формате PDF
Как рассчитать неопределенность в Excel?
Чтобы открыть панель «Полосы ошибок форматирования», дважды щелкните полосу погрешностей, отображаемую на диаграмме. Если категория «Параметры полос погрешностей» еще не выбрана, выберите ее сейчас. После этого у вас будет возможность изменить процент, значение стандартного отклонения или даже выбрать уникальное для вас значение из ячейки, которая могла быть результатом статистической формулы.
Какова формула расчета неопределенности?
Формула относительной неопределенности или относительной ошибки используется для расчета неопределенности измерения по сравнению с размером измерения. Формула ее определения следующая: относительная неопределенность = абсолютная ошибка/измеренное значение.
Как рассчитать расширенную неопределенность в Excel?
Расширенная неопределенность рассчитывается из стандартной неопределенности путем ее умножения на коэффициент охвата k. Наиболее распространенным способом выражения неопределенности результатов измерений и анализов является использование расширенной неопределенности на уровне k = 2.
Является ли неопределенность тем же самым, что и стандартное отклонение?
Дисперсия или ее квадратный корень, известный как стандартное отклонение, могут использоваться для измерения степени неопределенности. Стандартная ошибка статистики — это другое название ее стандартного отклонения, и последнее является более распространенным из двух. Изменчивость порождает явление неопределенности.
Является ли неопределенность ошибкой?
Разница между фактическим значением и значением, которое было измерено, называется ошибкой. Неопределенность — это сообщаемое значение, которое находится в пределах диапазона значений, в пределах которого, как утверждается, находится истинное значение.
рассчитать неопределенность в excel
Существуют сомнения относительно точности большинства статистических данных — даже при соблюдении процедур и использовании эффективного оборудования для тестирования. Excel позволяет рассчитывать неопределенность на основе стандартного отклонения образца.
В Excel есть статистические формулы, которые мы можем использовать для расчета неопределенности. И в этой статье мы рассчитаем среднее арифметическое, стандартное отклонение и стандартную ошибку. Мы также рассмотрим, как мы можем построить эту неопределенность на графике в Excel.
Мы будем использовать следующие примеры данных с этими формулами.
Эти данные показывают пять человек, которые сделали измерение или чтение некоторого вида. Имея пять разных показаний, мы не уверены в том, что является реальной ценностью.
Среднее арифметическое значений
Если у вас есть неопределенность в отношении диапазона различных значений, взятие среднего значения (среднее арифметическое) может служить разумной оценкой.
Это легко сделать в Excel с помощью функции AVERAGE.
Мы можем использовать следующую формулу на примере данных выше.
= СРЗНАЧ (В2: В6)
Стандартное отклонение значений
Функции стандартного отклонения показывают, насколько широко распространены ваши данные из центральной точки (среднее значение, которое мы вычислили в последнем разделе).
Excel имеет несколько различных функций стандартного отклонения для различных целей. Двумя основными являются STDEV.P и STDEV.S.
Каждый из них будет рассчитывать стандартное отклонение. Разница между ними заключается в том, что STDEV.P основан на том, что вы предоставляете ему всю совокупность ценностей. STDEV.S работает с меньшей выборкой из этой совокупности данных.
В этом примере мы используем все пять наших значений в наборе данных, поэтому мы будем работать с STDEV.P.
Эта функция работает так же, как и AVERAGE. Вы можете использовать формулу ниже на этом образце данных.
= STDEV.P (В2: В6)
Результат этих пяти различных значений составляет 0,16. Это число говорит нам, насколько обычно каждое измерение отличается от среднего значения.
Рассчитать стандартную ошибку
Рассчитав стандартное отклонение, мы можем найти стандартную ошибку.
Стандартная ошибка — это стандартное отклонение, деленное на квадратный корень из числа измерений.
Приведенная ниже формула рассчитает стандартную ошибку для данных нашего образца.
= Д5 / SQRT (COUNT (В2: В6))
Использование панелей ошибок для представления неопределенности в диаграммах
В Excel очень просто отобразить на графике стандартные отклонения или границы неопределенности. Мы можем сделать это, добавив панели ошибок.
Ниже у нас есть столбчатая диаграмма из выборочного набора данных, показывающая популяцию, измеренную за пять лет.
Выбрав диаграмму, нажмите «Дизайн»> «Добавить элемент диаграммы».
Затем выберите один из доступных типов ошибок.
Вы можете показать стандартную ошибку или величину стандартного отклонения для всех значений, как мы рассчитывали ранее в этой статье. Вы также можете отобразить процентное изменение ошибки. По умолчанию это 5%.
Для этого примера мы решили показать процент.
Есть еще несколько вариантов, чтобы настроить ваши панели ошибок.
Дважды щелкните панель ошибок на диаграмме, чтобы открыть панель «Формат ошибок». Выберите категорию «Параметры панели ошибок», если она еще не выбрана.
Затем вы можете отрегулировать процентное значение, значение стандартного отклонения или даже выбрать пользовательское значение из ячейки, которое могло быть создано статистической формулой.
Excel является идеальным инструментом для статистического анализа и отчетности. Он предоставляет множество способов для расчета неопределенности, чтобы вы получили то, что вам нужно.