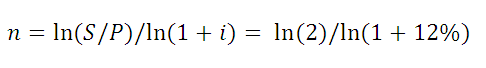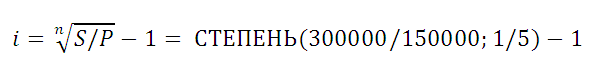Расчет начисления процентов по вкладам excel

Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.

Примеры использования функции ЭФФЕКТ в Excel

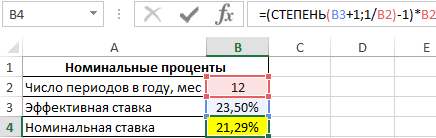
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.

Исходная таблица данных:

Связь между значениями эффективной и номинальной ставок описывается следующей формулой:

=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2

Полученный результат:

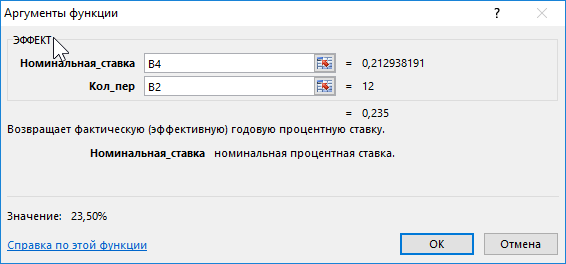
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:

Описание аргументов:

• B4 – полученное выше числовое значение номинальной ставки;
• B2 – число периодов погашения.

Результат:

Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.



Формула расчета процентов по вкладу в Excel

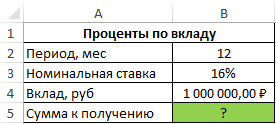
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.

Исходные данные:

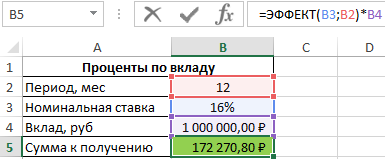
Формула для расчета:

=ЭФФЕКТ(B3;B2)*B4

Описание аргументов:

• B2 – число периодов капитализации;
• B3 – номинальная ставка;
• B4 – сумма вклада.

Результат расчетов:

Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.

Как посчитать проценты на депозит в Excel для выбора вклада

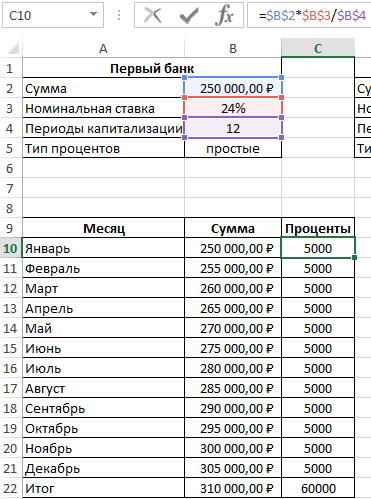
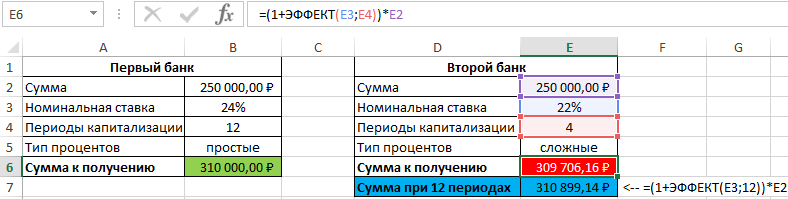
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:

1. Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
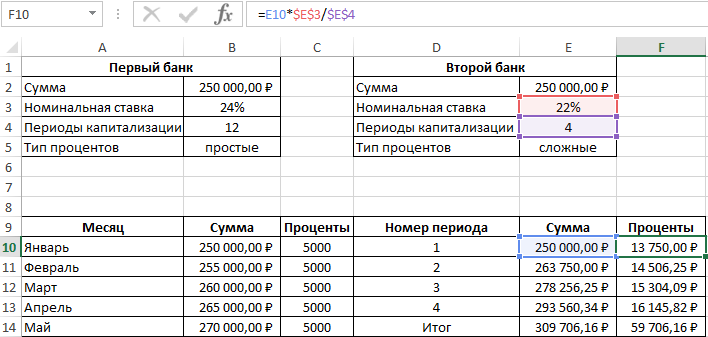
2. Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.

Определить выгодный вариант, отобразить схему выплат.

Исходные данные:

В первом случае таблица выплат выглядит так:

Проценты – постоянная величина, рассчитываемая по формуле:

=$B$2*$B$3/$B$4

Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):

• $B$2 – начальная сумма вклада;
• $B$3 – годовая ставка;
• $B$4 – число периодов капитализации вклада.

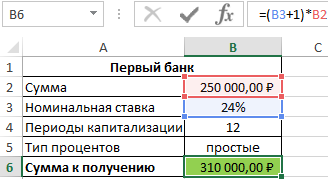
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.

Таблица начисления процентов по условиям второго банка:

В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):

=L3*$E$3/$E$4

При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.

Для быстрого расчета итоговой суммы используем формулы:

1. Первый банк:



2. Второй банк:

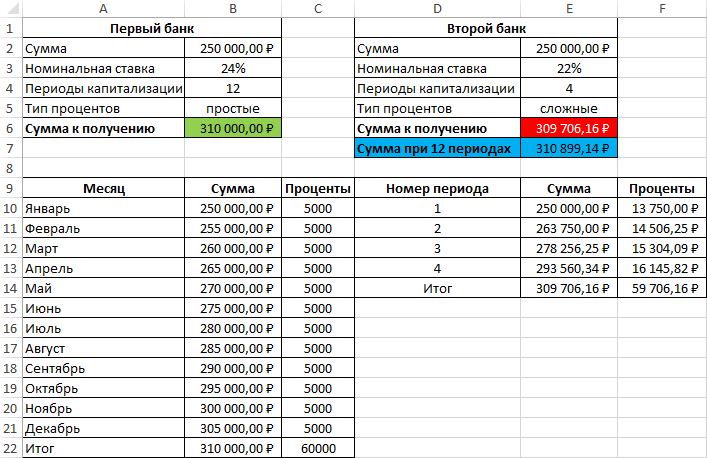
Результаты расчетов:

Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.

Особенности использования функции ЭФФЕКТ в Excel

Функция имеет следующий синтаксис:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

Описание аргументов:

• номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
• кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.

Примечания 1:

1. Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
2. Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
3. Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
4. Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:

• A1 – номинальная годовая ставка;
• A2 – число периодов, в которые происходит начисление сложных процентов.

Примечания 2:

• Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
• Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
• Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.

В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.

За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f _{x ,} слева от строки ввода значений и адресов ячеек.

В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.

Составляющим формулы расчета будущей стоимости FV = PV(1+r)ⁿ в Excel соответствуют следующие функции:

Общее название	Функция в Excel	Краткое описание
FV (Future Value)	БС (Будущая Стоимость)	Будущая сумма вклада
PV (Present Value)	ПС (Текущая Стоимость)	Текущая стоимость вклада
n	КПЕР (Количество Периодов)	Число периодов начисления процентов по вкладу
r	СТАВКА	Процентная ставка по вкладу

Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.

Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.

Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:

• если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
• если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.

В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).

А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.

Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:

• капитализироваться;
• капитализироваться ежемесячно.

Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.

• Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.

А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!

А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.

Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.

• Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.

Обучение торговле на бирже

Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по

простым

и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

В

файле примера

приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов

читайте здесь

.

Начисление процентов 1 раз в год

Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу

: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

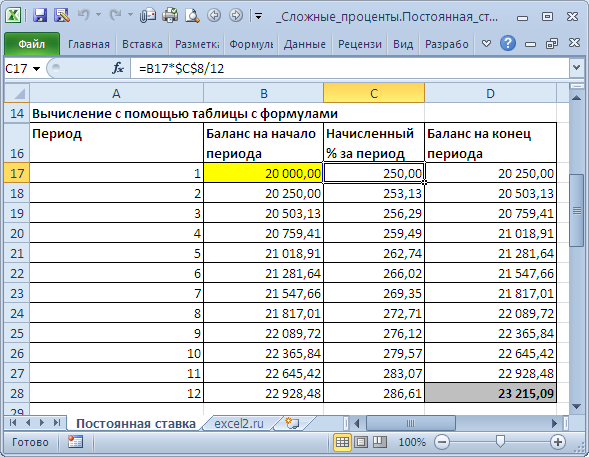
Способ 1. Вычисление с помощью таблицы с формулами

Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В

файле примера

это реализовано на листе

Постоянная ставка

.

За первый период будут начислены проценты в сумме

=20000*(15%/12)

, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов

Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию

СТЕПЕНЬ()

=20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС().

Функция

БС()

позволяет определить

будущую стоимость

инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае

аннуитетных платежей

. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.

=-БС(15%/12;12;;20000)

Или так

=-БС(15%/12;12;0;20000;0)

Примечание .

В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов

используется функция

БЗРАСПИС()

.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.

файл примера

).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

В

файле примера

приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.

Расчет сложных процентов в случае регулярного пополнения вклада

В

файле примера

(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция

БС()

.

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.

Почему важно иметь под рукой калькулятор вкладов

Если вы думаете сделать вклад, то важно понять, какой доход вы получите к концу срока. Кроме того, важно понимать какая сумма процентов будет выплачиваться каждый месяц. Эти проценты можно тратить и деньги будут работать на вас.

 Loading …

Еще одной важной причиной держать калькулятор вкладов всегда под рукой является необходимость проверки вашего банка. Банк не всегда верно считает и выплачивает проценты по вкладу. Чтоб проверить банк, нужно иметь независимый инструмент для расчета дохода по депозиту.

? Скачать калькулятор вкладов в Excel

Ссылка на калькулятор представлена ниже.
Данный калькулятор подходит для расчета вкладов ВТБ, Сбербанка, банка Тинькофф, Райффайзенбанка и других банков РФ.
Скачать калькулятор в Excel можно по ссылке Калькулятор вкладов Excel.

Профессиональные калькуляторы вкладов

Мы рекомендуем скачать себе на телефон профессиональные мобильные калькуляторы вкладов.
Ниже представлены 2 калькулятора вкладов, которые можно установить на свой телефон. После их установки не нужен Excel. Да и расчёт получается точнее, т.к. есть учёт курсов валют и ключевой ставки ЦБ.

Бесплатный калькулятор вкладов для Windows 10

• Точный расчет вклада любого банка РФ
• Учет пополнений и снятий
• Возможность посчитать несколько вкладов
• Абсолютно бесплатен
• Понятная и подробная статистика
• Возможность учесть фиксированную и плавающую ставку, неснижаемый остаток, макс. дату пополнения

Банковский калькулятор вкладов для Андроид

• Подходит для расчета вкладов любого банка: Тинькофф, Сбербанка, ВТБ, МКБ
• Учитывает при расчете налоги и ставку рефинансирования
• Есть возможность задать пополнения и снятия
• Удобный график выплат и возможность посмотреть ваш доход на сегодня
• Возможность учитывать несколько вкладов и знать сколько денег всего

Основные возможности, которые предоставляет калькулятор вкладов в Excel

1. Расчет вклада с помесячной и годовой капитализацией
2. Расчет валютных и рублевых вкладов.
3.  Расчет суммы вклада в конце срока
4. Расчет процентов по вкладу.
5. Учет налогов, если ставка по вкладу превышает ставку, установленную ЦБ.
6. Достоинства данного калькулятора — что его можно использовать офлайн, т.е. без выхода в интернет.

Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.

Калькулятор вкладов поможет вам правильно выбрать вклад. Просто нужно посчитать и сравнить несколько вкладов. Доходность какого будет лучше, тот и выбрать.
Если у вас один рублевый вклад, а один валютный, то придется провести конверсию по курсу ЦБ.

Также доступна онлайн версия депозитного калькулятора — калькулятор вкладов онлайн

Онлайн версия калькулятора является достаточно точной и позволяет посчитать различные вклады при различных условиях. К примеру вклады  могут иметь плавающую ставку в зависимости от сроков — чем больше срок, тем выше ставка.

Калькулятор позволяте получить результаты расчета в Excel файле. Это полноценный Excel 2003. Можно распечатать ваши расчеты для похода в банк.
Все это можно рассчитать с помощью онлайн версии кредитного калькулятора, просто задаете номер дня и новую ставку.

Далее нажимаем рассчитать и получаем график платежей по вкладу и сумму к получению. Аналогично, если сумма вклада зависит от суммы — устанавливаем переключатель «Плавающая в зависимости от размера» для процентной ставки. Отдельный интерес составляет учет налогов — все вклады, ставка по которым превышает ставку рефинансирования ЦБ + 5 процентов. Для них происходит начисление налога по вкладу в размере 35 процентов от налогооблогаемой части.

Читайте также: Налоги на вклад: как они начисляются? Пример расчета
Следует отменить, что с налогов по ставке 35 процентов нельзя получить налоговый вычет на ипотеку, т.е. хотя это налоги на ваши доходы, которые являются официальными. Банк сам отчисляет налог и автоматически уменьшает доход по вкладу на сумму налогов.

Однако нужно внимательно проверять банк — рассчитывать вклад с помощю указанного выше депозитного калькулятора. Оставляйте свои пожелания к калькулятору вкладов. Все ваши пожелания будут учитываться в доработках .

Популярные вопросы по вкладам

Как рассчитать проценты по вкладу в банке?

Для расчета нужно сумму вклада умножить на число дней, в течение которого был открыт вклад, умножить на ставку по депозиту, деленную на 100%. Полученную сумму нужно разделить на число дней в году(365 или 366). Проще воспользоваться универсальным калькулятором вкладов на нашем сайте.

Что такое процентная ставка по вкладу

Процентная ставка по вкладу — это число, которое определяет доходность вклада. Чем она выше, тем больше доходность. Различают простую и эффективную ставку по вкладу. Ставка по вкладам зависит от ключевой ставки ЦБ.

Что такое капитализация процентов по вкладу?

Капитализация процентов по вкладу — это плюсование процентов, которые начислены за каждый период, к сумме вклада. К примеру, вы положили вклад на 1000 р и получили через месяц доход 10 р, эти 10 рублей плюсуются к сумме вклада — 1000 + 10 = 1010.

На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.

Что значит проценты не капитализируются?

Проценты не капитализируются — это значит проценты не прибавляются к сумме вклада каждый месяц. Обычно они выплачиваются на определенный счет в виде дохода. Их можно снимать и пользоваться этими деньгами. С одной строны это хорошо, сразу получаешь доход. С другой — плохо, т.к. доход по вкладу не растет

Разберем  различные формулы расчета процентов в Excel, для этого рассмотрим реальные практические примеры, формулы и типовые финансовые задачи.

Формула расчета процентов. Как посчитать проценты в Экселе?

Проценты (латин. pro centum) – являются неотъемлемой частью финансовой математики и используются в банковском секторе, финансах, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность предприятия, ставку по банковским кредитам и займам, налоговые ставки и т.д. Можно привести в подтверждение важности процентов в финансовом мире высказывание А. Энштейна: «Сложные проценты – самая мощная сила в природе». Перед тем как рассмотреть формулы расчета процентов введем основные термины и понятия.

• Капитал (англ. Capital, Principal) – является базой относительно которого вычисляют процент.
• Частота начисления процентов – период выплат процентов на капитал.
• Процентная ставка (англ. Rate) – размер процента или доля капитала, который будет выплачен.
• Период вложения (англ. Period) – временной интервал передачи капитала банку или другому финансовому институту.

Итак, рассмотрим различные эконометрические задачи с процентами.

Формула расчета доли

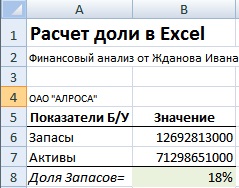
Расчет доли часто необходим в бухгалтерском и финансовом учете, где необходимо определить долю тех или иных видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО «АЛРОСА».

Пример задачи. Необходимо рассчитать долю «Запасов» в структуре «Активов» предприятия. Для этого воспользуемся формулой:

Доля запасов в Активах =B6/B7

Для того чтобы в ячейке полученные доли имею процентный вид можно воспользоваться сочетанием клавиш «Ctrl» + «Shift» + «%».

Формула расчета размера процента от капитала

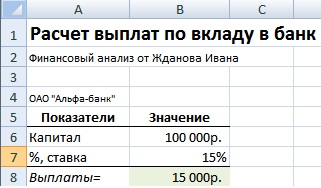
Рассмотрим вторую постоянно встречающуюся экономическую задачу: расчет абсолютного значения процента по капиталу.

Пример задачи. Необходимо определить размер выплаты банка ОАО «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь следующий вид:

Выплаты по вкладу в банке =B6*B7

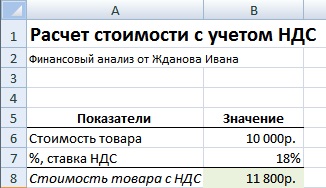
Формула расчета размера капитала с процентами

Пример задачи. Требуется рассчитать итоговую стоимость товара с НДС (налог на добавленную стоимость), тогда как стоимость товара без НДС составляет 10000 руб., процентная ставка налога равна 18%.  Формула расчета стоимости товара с учетом НДС рассчитывается по формуле:

Стоимость товара с учетом НДС =B6*(1+B7)

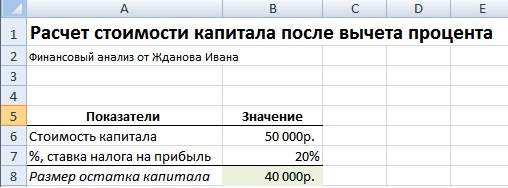
Формула уменьшения размера капитала на процент

Пример задачи. Необходимо рассчитать размер капитала после вычета налога на прибыль, процентная ставка налога равна 24%, текущее значение капитала равно 50000 руб. Формула расчета остатка капитала после вычета налога следующая:

Остаток капитала =B6-B6*B7

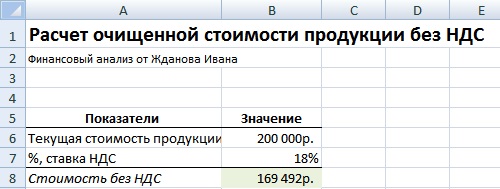
Формула расчета очищенной стоимости капитала (продукции)

Пример задачи. Необходимо рассчитать начальную стоимость продукции без НДС (налог на добавленную стоимость), текущая стоимость продукции составляет 200000 руб., процентная ставка налога 18%. Формула расчета процентов следующая:

Стоимость продукции без НДС=B6/(1+B7)

Формула расчета простых процентов по банковскому вкладу

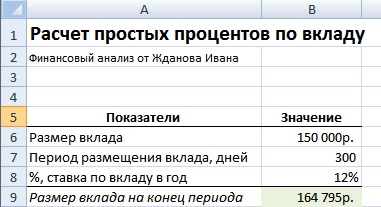
При использовании простых процентов выплаты по вкладу осуществляются только в конце срока (периода) размещения.

Пример задачи. Требуется рассчитать размер выплат по банковскому вкладу, на который начисляется простые проценты. Размер вклада составляет 150000 руб., годовая процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel следующая:

Размер банковского вклада на конец периода размещения =(1+B8*300/365)*B6

Формула расчета сложных процентов по банковскому вкладу

Сложные проценты отличаются от простых тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.

Пример задачи. Необходимо рассчитать размер банковского вклада, который был размещен по сложный процент. Первоначальный размер депозита составляет 100000 руб., годовая процентная ставка равна 14%, период начисления процентов – каждые 4 месяца, срок размещения вклада 1 год.

Формула расчета сложных процентов:

Размер вклада со сложными процентами на конец года =B6*(1+B8*B9/B7)^4

Метод сложных процентов имеет широкое использование в финансовом анализе и применяется для дисконтирования денежных потоков. Более подробно о методе дисконтирования читайте в статье: «Дисконтирование денежных потоков (DCF). Формула. Расчет в Excel«.

Видео-урок: «Примеры расчета простых и сложных процентов»

Резюме

Расчет процентов является неотъемлемой частью финансовой математики и всей экономики в целом. Навык быстрого расчета процентов в Excel позволяет экономить время при оценке будущей стоимости капитала.

Автор: к.э.н. Жданов Иван Юрьевич

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Чтобы рассчитывать доходность банковских вкладов, нужно разобраться с простыми и сложными процентами.

• Простые проценты (P — principal) начисляют на первоначальный вклад в конце отчетного периода. 
• Частота начисления процентов — период времени, в конце которого банк пересчитывает сумму на вкладе.
• Период вложения — время, на которое сделан вклад. При этом за период вложения проценты могут начисляться несколько раз.
• Процентная ставка (r — rate) — собственно величина, на которую умножается сумма на вкладе с определённой частотой.

Например, при начислении процентов раз в год по вкладу в 10 тыс. рублей под 12% годовых в конце мы получим прибыль 10 000 х 0,12 = 1200 рублей. 

Сложные проценты — это когда проценты начисляются не только на основной капитал, но и на полученную в предыдущих периодах прибыль. То есть, с определённой периодичностью сумма вклада пересчитывается и начисляются, в том числе, проценты на проценты. Сумма растёт по экспоненте.

Сложные проценты могут называть по-разному:

• эффективные проценты;
• проценты на проценты;
• композиционный процент;
• норма доходности с учетом капитализации;
• норма доходности с учетом реинвестирования.

Расчёт сложных и простых процентов на реальном примере

Предположим, есть два брата, и у обоих на руках есть первоначальный капитал в размере 10 000 рублей. Они решают сделать вклад на 20 лет. 

Первый брат делает вклад на депозитный счет с простой процентной ставкой 9%, а второй делает вклад на счет со сложной процентной ставкой 8%.

Начисление процентов происходит в конце каждого года. 

Итак имеем:

• P₀ = 10 000 руб.,
• r₁ = 9%,
• r₂ = 8%,
• t = 20 лет.

Формула расчета простых процентов:

Формула расчета сложных процентов:

t — число реинвестиций (капитализаций) в течение одного года. В нашем примере t = 1, поскольку начисление процентов происходит только раз в год.

В Excel рост капитала двух братьев будет выглядеть следующим образом. 

• Период — год от момента открытия вклада. 
• Капитал — сумма, на которую начисляются проценты в конце года. 
• Процент — проценты по вкладу за этот год. В первом случае процент считаем от первоначального капитала, каждый год прибыль одинаковая. Во втором случае процент начисляется на весь капитал, то есть на первоначальную сумму плюс проценты за все прошлые годы — прибыль постоянно реинвестируется.
• Баланс — итого на счёте в конце года.

Если хотите узнать больше о работе в Excel, то рекомендуем записаться на наш обширный онлайн-курс «Академия Excel».

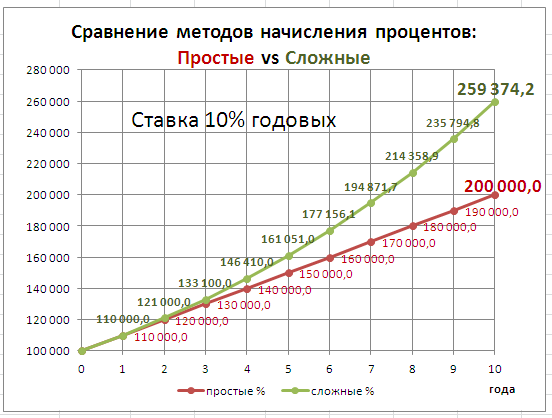
Можно заметить, что первые несколько лет вклад с простыми процентами выгоднее за счёт более высокой процентной ставки. Но затем ситуация меняется, и даже при меньшей ставке второй брат получил через 20 лет 466% от первоначальной суммы, а первый брат — 280%.

На рисунке ниже показан рост капитала при различных видах процента.

Корректировки на ситуацию вокруг

Чтобы получить высокую доходность при сложном проценте, необходимо ждать длительное время. С этим могут быть сложности в реальных условиях российской экономики (например: кризисы 1998 г., 2008 г., 2014 г. и т.д.). 

Кроме того, уровень инфляции постепенно растёт, и прибыль по вкладам, особенно с более низкой ставкой при сложных процентах, может свестись к нулю.

Читайте также: О курсе «Excel Academy»

По норме доходность акции значительно превосходят доходность по банковским вкладам, но это более рискованный инструмент. С другой стороны, многие российские банки получают прибыль как раз за счёт активной деятельности на фондовом рынке — то есть несут те же риски, но прибыль вы получаете меньше. 

Таким образом, банковские вклады могут выступать в роли сохранения первоначальной ценности капитала (с небольшим риском), и никак не являются механизмом получения прибыли. Чтобы капитал рос в имеющихся условиях, целесообразнее самостоятельно заниматься инвестированием в развивающиеся отрасли.

Это тоже интересно:

Правда и вымысел о финансовой безграмотности россиян

Как работать с дублями в Excel?

Что должен уметь финансист будущего: технические навыки и инструменты

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

MS Office

Мультипликаторы для оценки бизнеса

Содержание статьи Основные методы сравнительного подхода к оценке бизнеса — метод рынка капитала и метод сделок, применение которых предполагают обязательный этап — расчет оценочных мультипликаторов…

Разбор структуры капитала «Райффайзенбанк»

Содержание статьи Капитал банка является обязательным условием образования и функционирования любого коммерческого банка. Капитал формируется из собственных средств акционеров или участников банка. Основной функцией…