Расчет на продавливание excel

Сложно назвать программой. Скорее шаблончик. Расчеты для колонн внутри площади плиты и для колонны у края. Расчеты выполнены по методике Научно-технического отчета ГУП «НИИ ЖБ» по теме «Разработка методики расчета и конструирования монолитных железобетонных безбалочных перекрытий, фундаментных плит и ростверков на продавливание» (Есть в Download). Выложил для темы Продавливание, выбор распределительных систем.

• Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
• Регистрация

• Узнайте сколько стоит уникальная работа конкретно по Вашей теме:
• Сколько стоит заказать работу?

Расчет плиты на продавливание. Расчет фундаментной плиты на продавливание колонной

На данный момент, 29.08.2017, программа производит расчёт на продавливание по СП 63 c учётом равномерно распределённой поперечной
арматуры при прямоугольных или квадратных колоннах.
Новое:
— усовершенствована защита от «дурака»;
— расчёт с учётом равномерно распределённой поперечной арматуры;
— загрузка и сохранение данных.
Ведутся работы по добавлению следующийх пунктов расчёта:
— расчёт с концентрированным поперечным армированием;
— расчёт при наличии капители;
— расчёт при наличии отверстий;
— расчёт около стен без поперечной арматуры;
— расчёт около стен c поперечной арматурой;
— расчёт при колонне круглого поперечного сечения + радиальное армирование;
— расчёт при колонне сложного сечения.
— отгибы и жёсткое армирование;
— изменение меры угла угла плиты;
— возможности изменения положения площадки относительно края плиты;
— возможности изменения положения площадки относительно угла плиты;
— масштабирование изображений.

Загрузить файл	Сохранить файл

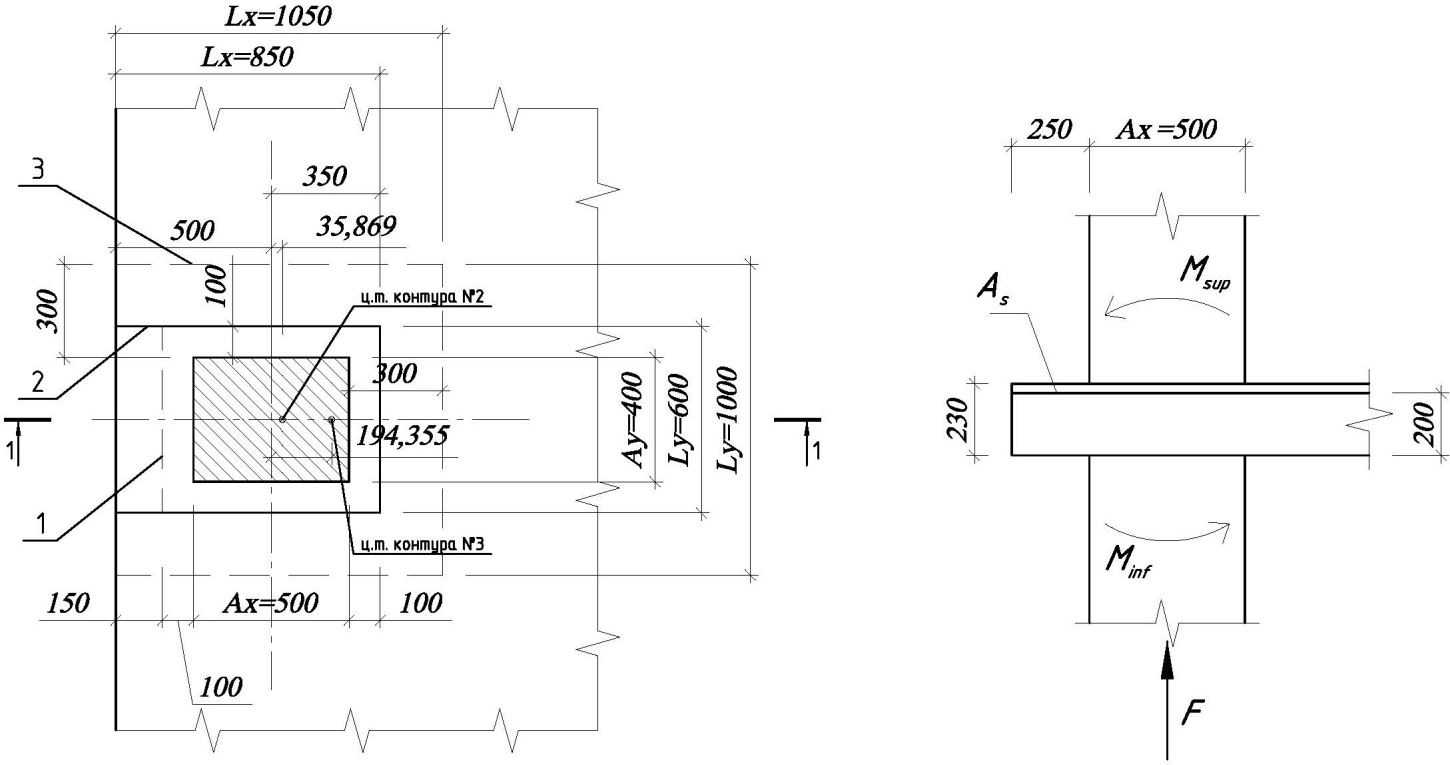
Пример продавливание у края плиты (СП)

1 – замкнутый расчетный контур №1, 2 – незамкнутый расчетный контур №2, 3 – незамкнутый расчетный контур №3.

Расчет плиты плоского монолитного перекрытия на продавливание

Цель: Проверка режима расчета на продавливание в постпроцессоре «Железобетон» вычислительного комплекса SCAD

Задача: Проверить правильность анализа прочности на продавливание бетонного элемента при действии сосредоточенной силы и изгибающего момента в случае расположения площадки приложения нагрузки у края плиты.

Соответствие нормативам: СНиП 52-101-2003, СП 63.13330.2012.

Файл с исходными данными:
SCAD 41 SP-2003.spr,
SCAD 41 SP-2012.spr 
отчет – SCAD 41 SP-2003.doc
отчет – SCAD 41 SP-2012.doc

Исходные данные:

h = 230 мм	Толщина плиты
h0 = 200 мм	Усреднённая рабочая высота плиты
a×b = 500×400 мм	Размеры сечения колонн
F = 150 кН	Нагрузка, передающаяся с перекрытия на колонну
Msup = 80 кН∙м	Момент в сечении колонны по верхней грани плиты
Minf = 90 кН∙м	Момент в сечении колонны по нижней грани плиты
x0 = 500 мм	Расстояние от центра сечения колонны до свободного края плиты
Класс бетона	В25

Аналитическое решение:

В данном случае необходимо проверить прочность трех контуров расчетного поперечного сечения:Аналитическое решение:

контур №1 – замкнутый контур вокруг сечения колонны на расстоянии 0,5h₀ от контура колонны;

контур №2 – незамкнутый контур вокруг сечения колонны на расстоянии 0,5h₀ от контура колонны с продлением контура до свободного края плиты;

контур №3 – незамкнутый контур вокруг сечения колонны на расстоянии 1,5h₀ от контура колонны (контура поверочного расчета без учета арматуры).

1. Замкнутый контур №1:

L_x = A_x + h₀ = 500 + 200 = 700 mm = 0,7 m,

L_y = A_y + h₀ = 400 + 200 = 600 mm = 0,6 m,

Периметр расчетного контура поперечного сечения:

u = 2(L_x + L_y) = 2 (0,7 + 0,6) = 2,6 m.

Площадь расчетного контура поперечного сечения:

A_b = uh₀ = 2,6 х 0,2 = 0,52 m².

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,52 = 546 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

[
I_{bx} =2frac{L_{y}^{3} }{12}+2L_{x} left( {frac{L_{y} }{2}} right)^{2}=
quad
2frac{0,6^{3} }{12}+2cdot 0,7left( {frac{0,6}{2}} right)^{2}=quad 
0,162 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{bx} =frac{I_{bx} }{y_{max } }==
quad
frac{0,162}{0,3}=quad 0,54  м^{2}.
]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:[
I_{by} =2frac{L_{x}^{3} }{12}+2cdot L_{y} left( {frac{L_{x} }{2}} 
right)^{2}=
quad
2frac{0,7^{3} }{12}+2cdot 0,6left( {frac{0,7}{2}} right)^{2}=quad 
0,204 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{by} =frac{I_{by} }{x_{max } }==
quad
frac{0,204}{0,35}=quad 0,583 м^{2}.
]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 1,217 х 0,2 = 255,57 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,547 х 0,2 = 114,87 кНм.

M_y = M_y — Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 кНм.

Для СНиП 52-101-2003:

[
frac{M_{x} }{M_{bx,ult} }le frac{F}{F_{b,ult} };
quad
frac{M_{y} }{M_{by,ult} }le frac{F}{F_{b,ult} }
]
(
frac{M_{y} }{M_{by,ult} }=frac{55,85}{114,87}=0,486le frac{F}{F_{b,ult} 
}=frac{150}{651}=0,23 )- условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,275
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]

[
К1 = 0,275 + 0 + 0,275 = 0,55
]

Для СП 63.13330.2012:

[
frac{M_{x} }{M_{bx,ult} } + frac{M_{y} }{M_{by,ult} } le 0,5 frac{F}{F_{b,ult} } 
]

( frac{M_{y} }{M_{by,ult} }=frac{85}{122,4}=0,694le 0,5frac{F}{F_{b,ult} 
}=frac{150}{546}=0,5cdot 0,275=0,1375quad ) – условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,1375
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]

[
К1 = 0,275 + 0 + 0,1375 = 0,413
]

Незамкнутый контур №2:

L_x =A_x +h₀ + 150 = 500 + 200 + 150 = 850 мм = 0,85 м,

L_y =A_y +h₀ = 400 + 200 = 600 мм = 0,6 м,

Периметр расчетного контура поперечного сечения:

u = 2L_x + L_y = 2х0,85 + 0,6 = 2,3 м.

Площадь расчетного контура поперечного сечения:

_Ab = uh₀ = 2,3 х 0,2 = 0,46 м².

Координата Х центра тяжести незамкнутого контура относительно левого края плиты:

[
X=frac{425cdot 850cdot 2+850cdot 600}{850cdot 2+600}=535,869 мм
]

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,46 = 483 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

[
I_{bx} =frac{L_{y}^{3} }{12}+2L_{x} left( {frac{L_{y} }{2}} right)^{2}=
quad
frac{0,6^{3} }{12}+2cdot 0,85left( {frac{0,6}{2}} right)^{2}=quad 
0,171 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{bx} =frac{I_{bx} }{y_{max } }=
quad
frac{0,171}{0,3}=quad 0,57 м^{2}.
]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:

[
I_{by} =2frac{L_{x}^{3} }{12}+2L_{x} (0,075+0,035869)^{2}+L_{y} left( 
{0,35-0,035869} right)^{2}=
2frac{0,85^{3} }{12}+2cdot 0,85(0,075+0,035869)^{2}+0,6left( 
{0,35-0,035869} right)^{2}=0,183 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{by} =frac{I_{by} }{x_{max } }=
quad
frac{0,183}{0,535869}=quad 0,341 м^{2}.
]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 0,57 х 0,2 = 119,7 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,341 х 0,2 = 71,6 кНм.

M_y = M_y — Fe₀ = 85 – 150х0,035869 = 85 – 5,38 = 79,62 кНм.

Для СНиП 52-101-2003:

[
frac{M_{x} }{M_{bx,ult} }le frac{F}{F_{b,ult} };
quad
frac{M_{y} }{M_{by,ult} }le frac{F}{F_{b,ult} }
]

( frac{M_{y} }{M_{by,ult} }=frac{79,62}{71,6}=1,112le frac{F}{F_{b,ult} 
}=frac{150}{483}=0,311 )  – условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,311
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]
[
К1 = 0,311+0+0,311 = 0,622
]

Для СП 63.13330.2012:

[
frac{M_{x} }{M_{bx,ult} }+frac{M_{y} }{M_{by,ult} }le 
0,5frac{F}{F_{b,ult} }
]
( frac{M_{y} }{M_{by,ult} }=frac{79,62}{71,6}=1,112le 0,5frac{F}{F_{b,ult} 
}=frac{150}{483}=0,5cdot 0,311=0,155 ) – условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,155
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]
[
К1 = 0,311 + 0 + 0,155 = 0,466
]

Незамкнутый контур №3:

L_x = A_x + 1,5h₀ + 250 = 500 +1,5х200 + 250 = 1050 мм = 1,05 м,

L_y = A_y + 2·1,5h₀ = 400 + 2х1,5х200 = 1000 мм = 1,0 м,

Периметр расчетного контура поперечного сечения:

u = 2L_x + L_y = 2х1,05 + 1,0 = 3,1 м.

Площадь расчетного контура поперечного сечения:

A_b = uh₀ = 3,1 х 0,2 = 0,62 м².

Координата Х центра тяжести незамкнутого контура относительно левого края плиты:

[
X=frac{525cdot 1050cdot 2+1050cdot 1000}{1050cdot 2+1000}=694,355 мм
]

Предельное усилие, воспринимаемое бетоном:

F_b,ult = R_btA_b = 1,05 х10³ х 0,62 = 651 кН.

Момент инерции расчетного контура относительно оси Х, проходящей через его центр тяжести:

[
I_{bx} =frac{L_{y}^{3} }{12}+2L_{x} left( {frac{L_{y} }{2}} right)^{2}=
quad
frac{1,05^{3} }{12}+2cdot 1,05left( {frac{1,0}{2}} right)^{2}=quad 
0,608 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{bx} =frac{I_{bx} }{y_{max } }=
quad
frac{0,608}{0,5}=quad 1,217 м^{2}.
]

Момент инерции расчетного контура относительно оси Y, проходящей через его центр тяжести:

[
I_{by} =2frac{L_{x}^{3} }{12}+2L_{x} (0,194355-0,025)^{2}+L_{y} left( 
{1,05-0,694355} right)^{2}=
2frac{1,05^{3} }{12}+2cdot 1,05(0,194355-0,025)^{2}+1,0left( 
{1,05-0,694355} right)^{2}=0,38 м^{3}.
]

Момент сопротивления расчетного контура бетона

[
W_{by} =frac{I_{by} }{x_{max } }=
quad
frac{0,38}{0,694355}=quad 0,547 м^{2}.
]

Изгибающий момент, который может быть воспринят бетоном в расчетном поперечном сечении:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 1,217 х 0,2 = 255,57 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,547 х 0,2 = 114,87 кНм.

M_y = M_y — Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 кНм.

Для СНиП 52-101-2003:

[
frac{M_{x} }{M_{bx,ult} }le frac{F}{F_{b,ult} };
quad
frac{M_{y} }{M_{by,ult} }le frac{F}{F_{b,ult} }
]

( frac{M_{y} }{M_{by,ult} }=frac{55,85}{114,87}=0,486le frac{F}{F_{b,ult} 
}=frac{150}{651}=0,23 ) – условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,23
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]
[
К1 = 0,23 + 0 + 0,23 = 0,46
]

Для СП 63.13330.2012:

[
frac{M_{x} }{M_{bx,ult} }+frac{M_{y} }{M_{by,ult} }le 
0,5frac{F}{F_{b,ult} }
]

( frac{M_{y} }{M_{by,ult} }=frac{55,85}{114,87}=0,486le 
0,5frac{F}{F_{b,ult} }=frac{150}{651}=0,5cdot 0,23=0,115 )  – условие не выполняется.

Принимаем

[
frac{M_{y} }{M_{by,ult} }=frac{F}{F_{b,ult} }=0,155
]

Прочность плиты при продавливании:

[
K1=left[ {frac{F}{F_{b,ult} }} right.+left. {frac{M_{x} }{M_{bx,ult} 
}+frac{M_{y} }{M_{by,ult} }} right]le 1,0
]
[
К1 = 0,23 + 0 + 0,115 = 0,345
]

Результаты расчета SCAD:

Узел № 5

Коэффициент надежности по ответственности γ_n = 1
Бетон
Вид бетона: Тяжелый
Класс бетона: B25

Коэффициенты условий работы бетона
γb1	учет нагрузок длительного действия	1
γb2	учет характера разрушения	1
γb3	учет вертикального положения при бетонировании	1
γb4	учет замораживания/оттаивания и отрицательных температур	1

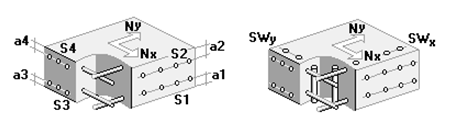
Расстояние до ц.т. арматуры
a1	a2	a3	a4
мм	мм	мм	мм
30	30	0	0

Результаты расчета
Расчетный случай – крайняя колонна
Длина контура верхнего основания пирамиды продавливания — 1800 мм
Длина контура нижнего основания пирамиды продавливания — 2300 мм

Сравнение решений (по СНиП 52-101-2003)

Проверено по СНиП	Проверка	Коэффициент использования
п.6.2.49	Прочность без учета армирования	0,62

Проверка	прочность на продавливание по незамкнутому контуру бетонного элемента при действии сосредоточенной силы и изгибающих моментов (в том числе дополнительных от внецентренного приложения силы относительно контура продавливания) с векторами вдоль осей X,Y (площадка приложения у края плиты)
Аналитическое решение	0,622
SCAD	0,62
Отклонение, %	0,1 %

Сравнение решений (по СП 63.13330.2012)

Проверено по СП	Проверка	Коэффициент использования
п.8.1.49	Прочность без учета армирования	0,47

Проверка	прочность на продавливание по незамкнутому контуру бетонного элемента при действии сосредоточенной силы и изгибающих моментов (в том числе дополнительных от внецентренного приложения силы относительно контура продавливания) с векторами вдоль осей X,Y (площадка приложения у края плиты)
Аналитическое решение	0,466
SCAD	0,47
Отклонение, %	0,1 %