17 авг. 2022 г.
читать 2 мин
U-критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30).
Он считается непараметрическим эквивалентом двухвыборочного t-критерия .
В этом руководстве объясняется, как выполнить U-критерий Манна-Уитни в Excel.
Пример: U-критерий Манна-Уитни в Excel
Исследователи хотят знать, приводит ли обработка топлива к изменению среднего расхода топлива на галлон автомобиля. Чтобы проверить это, они проводят эксперимент, в котором измеряют расход на галлон 12 автомобилей с обработкой топлива и 12 автомобилей без нее.
Поскольку размеры выборки малы и они подозревают, что распределение выборки не является нормальным, они решили выполнить U-критерий Манна-Уитни, чтобы определить, есть ли статистически значимая разница в милях на галлон между двумя группами.
Выполните следующие шаги, чтобы провести U-критерий Манна-Уитни в Excel.
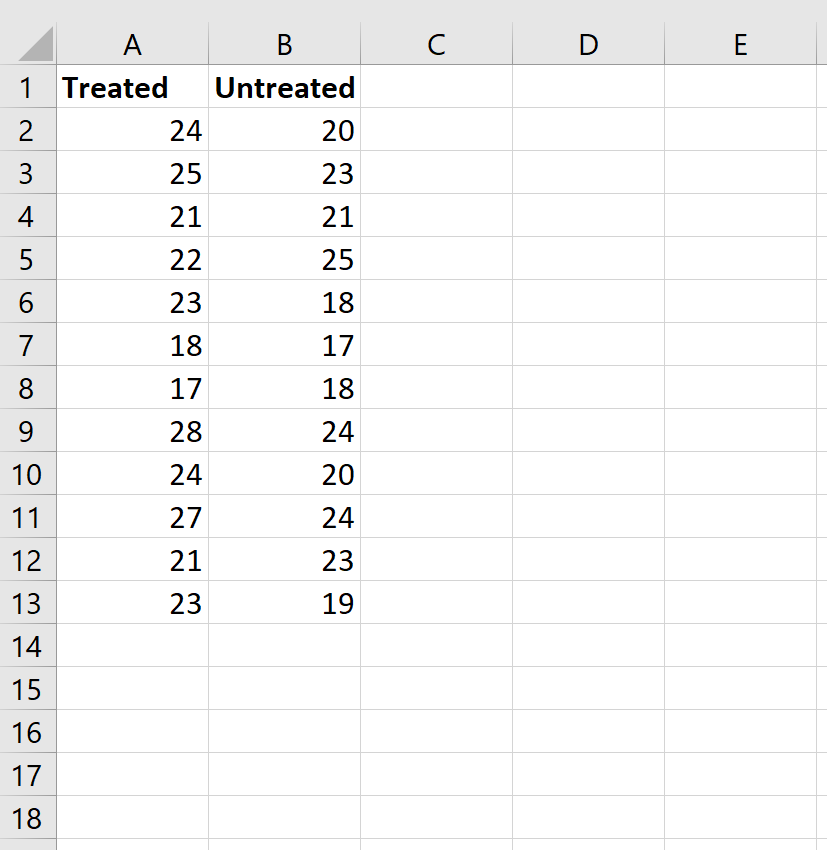
Шаг 1: Введите данные.
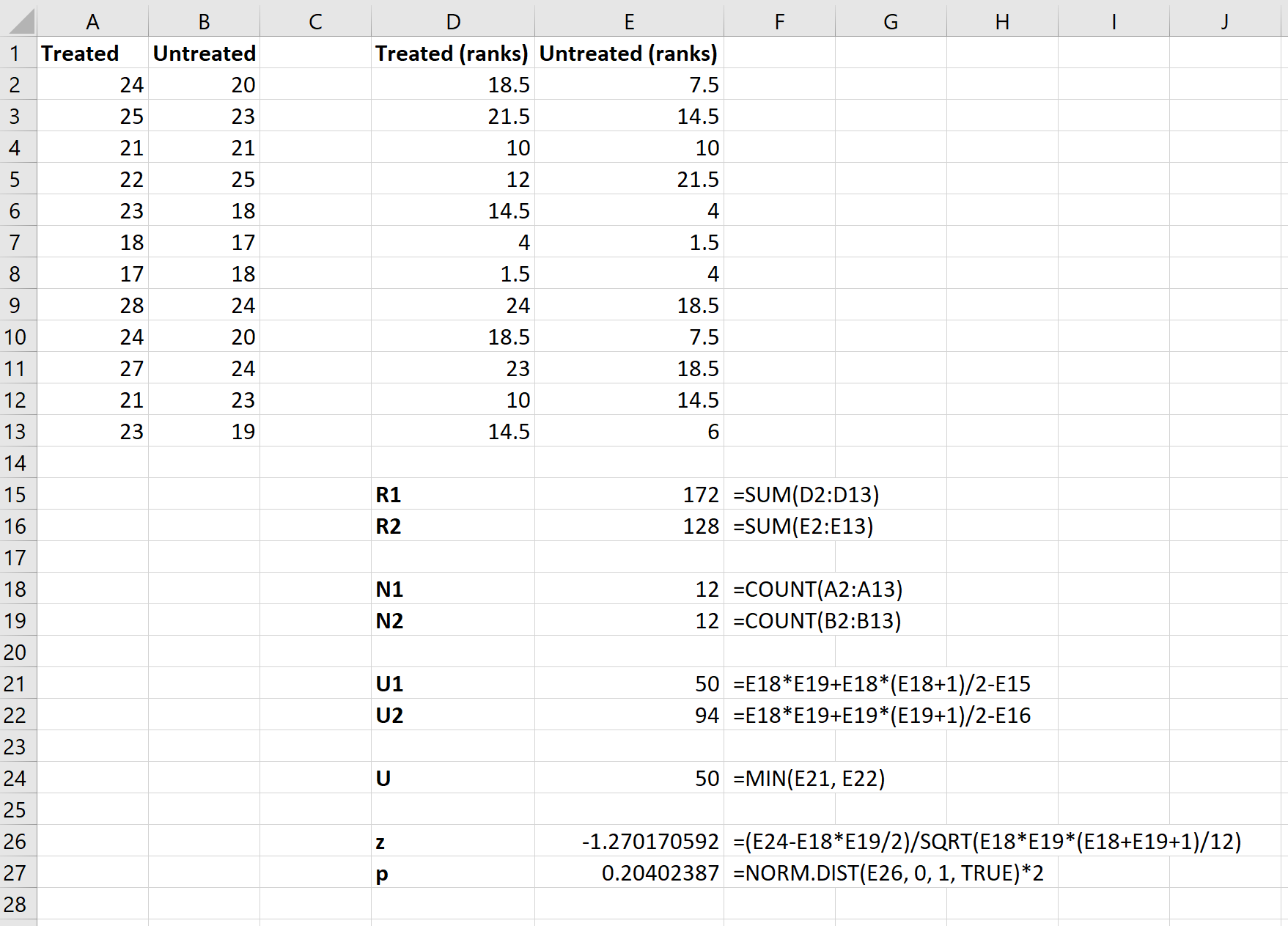
Введите данные следующим образом:
Шаг 2: Рассчитайте ранги для обеих групп.
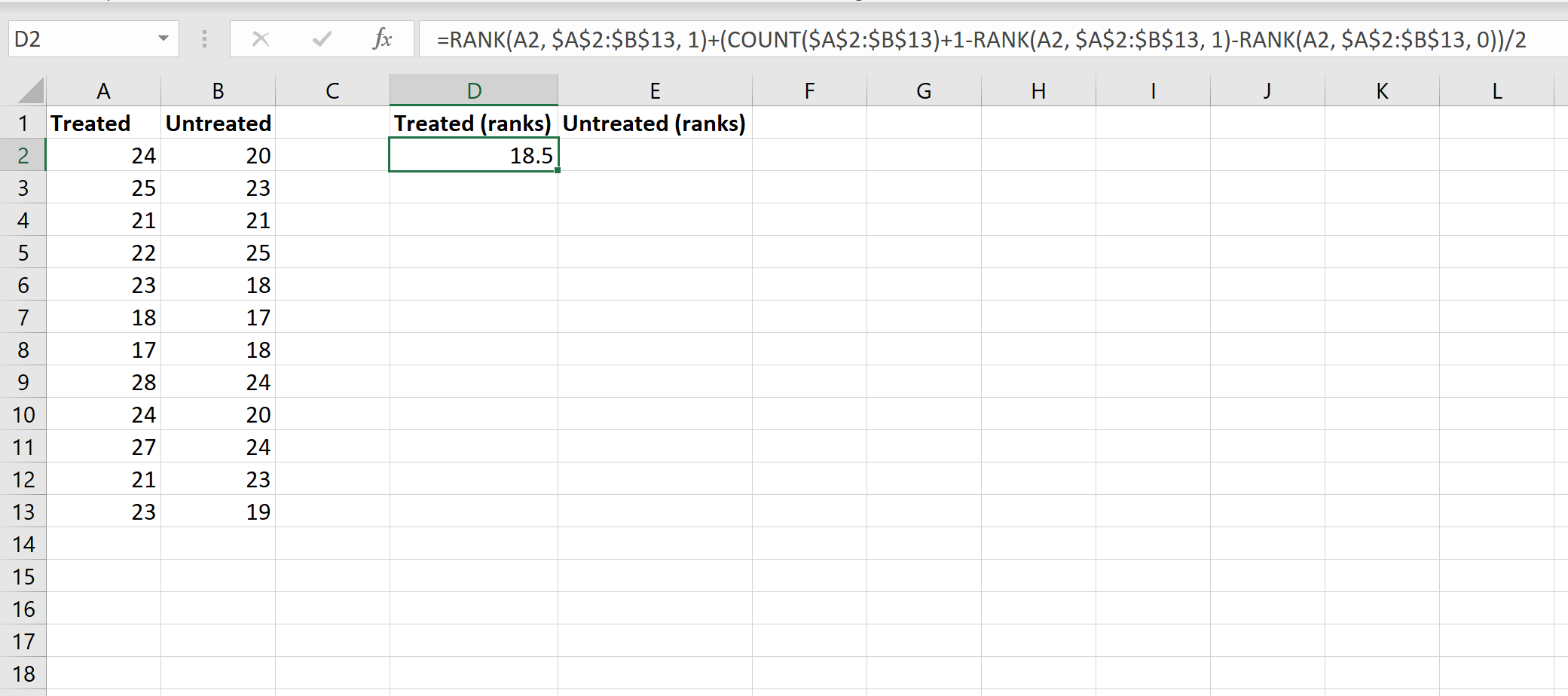
Далее мы рассчитаем ранги для каждой группы. На следующем изображении показана формула, используемая для расчета ранга первого значения в группе обработанных:
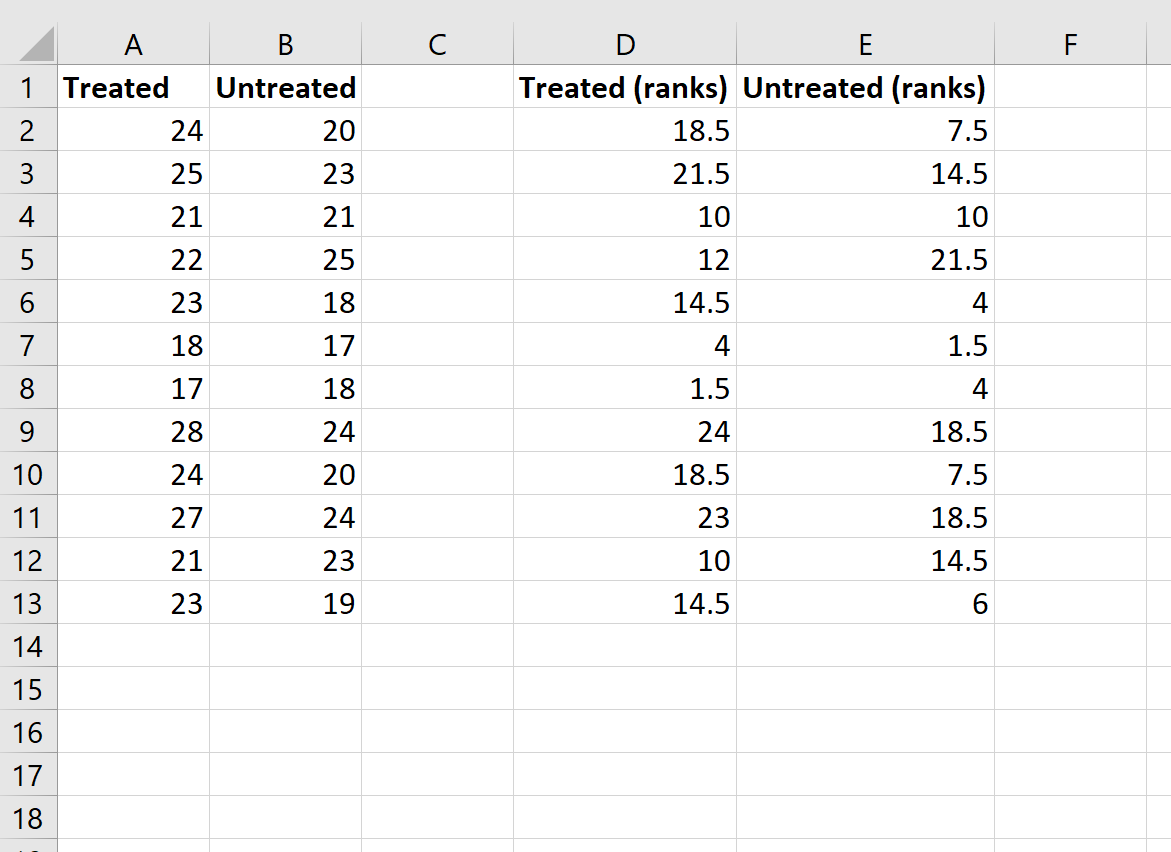
Хотя эта формула довольно сложна, вам нужно ввести ее только один раз. Затем вы можете просто перетащить формулу во все остальные ячейки, чтобы заполнить ранги:
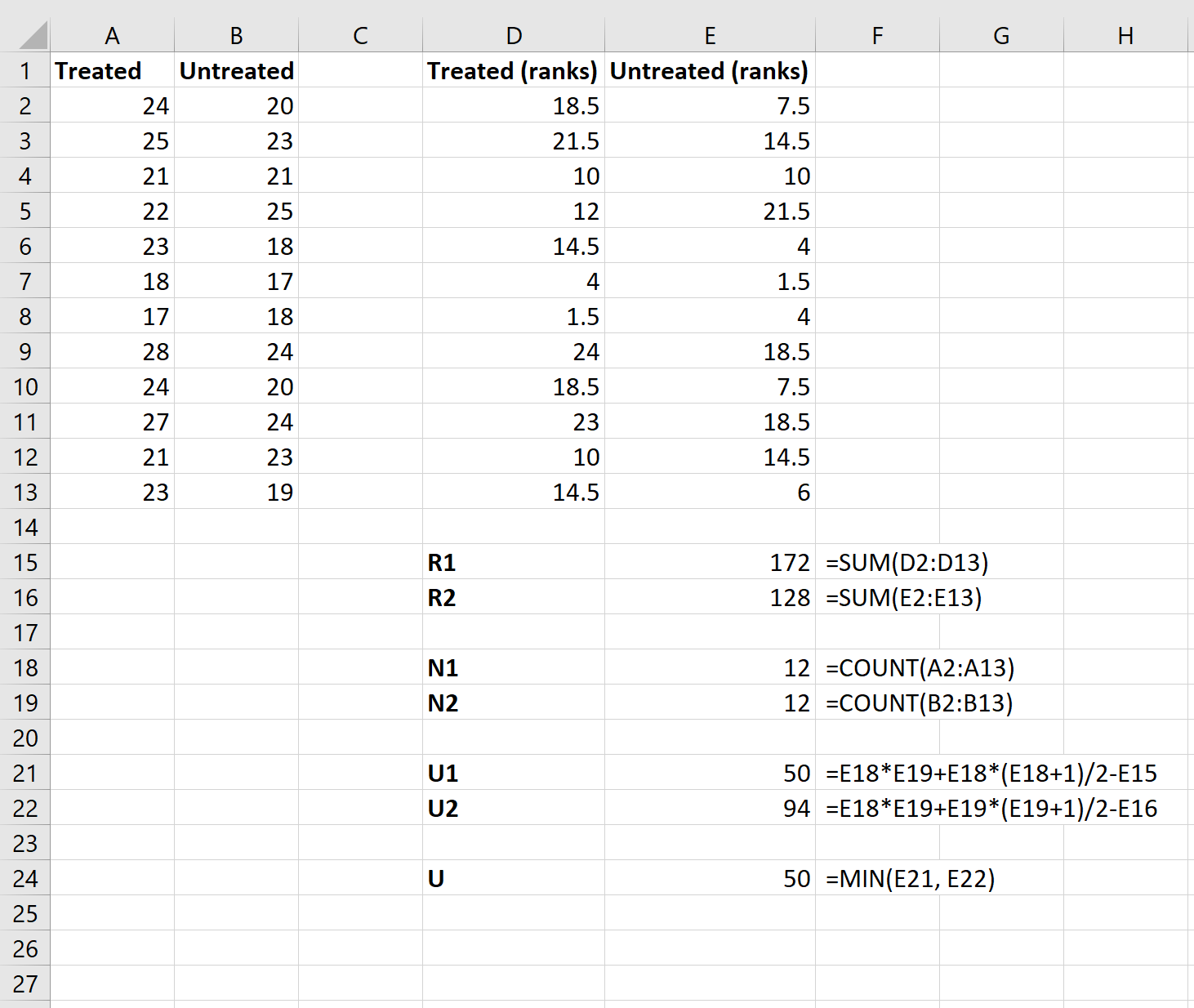
Шаг 3: Рассчитайте необходимые значения для тестовой статистики.
Затем мы будем использовать следующие формулы для расчета суммы рангов для каждой группы, размера выборки для каждой группы, статистики U-теста для каждой группы и общей статистики U-теста:
Шаг 4: Рассчитайте статистику теста z и соответствующее значение p.
Наконец, мы будем использовать следующие формулы для расчета статистики теста z и соответствующего значения p, чтобы определить, должны ли мы отклонить или не отклонить нулевую гипотезу:
Нулевая гипотеза теста утверждает, что две группы имеют одинаковое среднее значение расхода топлива на галлон. Поскольку p-значение теста ( 0,20402387 ) не меньше нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу.
У нас нет достаточных доказательств, чтобы сказать, что истинное среднее значение расхода на галлон отличается между двумя группами.
Перейти к содержимому
Онлайн калькулятор непараметрического критерия U Манна-Уитни позволяет получить расчет сразу на сайте. Итоговое описание состоит из таблиц, графиков и текстовых выводов. Его можно сказать в формате Word, а таблицы в Excel.
Читать далее Онлайн расчет критерия U-Манна-Уитни
В данном видео описан пошаговый алгоритм расчета критерия U Манна-Уитни в программе SPSS.
Читать далее [Видео] Алгоритм расчета критерия U Манна-Уитни в SPSS
В этом обучающем видео представлена интерпретация результатов расчета критерия U Манна-Уитни в программе SPSS.
Читать далее [Видео] Интерпретация результатов расчета критерия U Манна Уитни в SPSS
В данной таблице представлены критические значения критерия U-Манна-Уитни для уровня значимости 0,05 и уровня значимости 0,01.
Читать далее Таблица критических значений критерия U-Манна-Уитни
Для того, чтобы рассчитать непараметрический критерий U Манна-Уитни для независимых выборок используя статистически пакет SPSS необходимо сделать следующий шаги:
Читать далее Расчет критерия U Манна-Уитни в SPSS
Непараметрический критерий U Манна-Уитни применяется для сравнения средних значений двух независимых выборок.
Условия применения:
Читать далее Непараметрический критерий U Манна-Уитни
This tutorial will help you run and interpret a Mann-Whitney test on two independent samples in Excel using XLSTAT.
What is a Mann-Whitney test?
The Mann-Whitney test is a non parametric test that allows to compare two independent samples.
Three researchers, Mann, Whitney, and Wilcoxon, separately perfected a very similar non-parametric test which can determine if the samples may be considered identical or not on the basis of their ranks.
This test can only be used to study the relative positions of the samples. For example, if we generate a sample of 500 observations taken from an N(0,1) distribution and a sample from a distribution of 500 observations from an N(0,4) distribution, the Mann-Whitney test will find no difference between the samples.
The results proposed by XLSTAT are based on the U statistic of Mann-Whitney.
Dataset for running a Mann-Whitney test in Excel
The data are from [Fisher M. (1936), The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, 179 -188] and correspond to 100 Iris flowers, described by four variables (sepal length, sepal width, petal length, petal width) and their species. The original dataset contains 150 flowers and 3 species, but we have isolated for this tutorials the observations belonging to the versicolor and virginica species. Our goal is to test if for the four variables, there is a clear difference between the two species.
The goal of this tutorial is to compare the two species with respect to the four variables independently.
Setting up a Mann-Whitney test on two independent samples
Once XLSTAT-Pro is activated, select the XLSTAT / Nonparametric tests / Comparison of two samples (Wilcoxon, Mann-Whitney, …) command.
Once you’ve clicked the button, the dialog box appears. You can then select the data on the Excel sheet. Select the one column per variable option because, we have 4 columns of data and one column corresponding to the species identifiers.
In the options tab, we suppose that the difference between samples is equal to 0. Note that exact p-value can be computed with XLSTAT.
After you have clicked on the OK button, the results are displayed on a new Excel sheet (because the Sheet option has been selected for outputs).
Interpreting the results of a Mann Whitney test on two independent samples
The first results displayed are the statistics for the various samples. For each variable, we obtain a test result.
We can see that for the first variable, the null hypothesis of equality is rejected. We can consider that the sepal length is significantly different from one specie to the other.
Results for the other variables are also available in the output.
Not sure you chose the right test? This guide will let you know.
Was this article useful?
- Yes
- No
Mann-Whitney Test in Excel Using QI Macros
When to Use the Mann-Whitney Test
A Mann-Whitney test (equivalent to Wilcoxon Rank Sum Test) compares the differences between two independent samples to determine if they differ in location.
Use Mann-Whitney or Wilcoxon Rank Sum tests instead of Mood’s Median Test, as they provide more accurate results.
Note: Excel does not do statistical tests of non-normal (i.e., not «bell shaped») data. QI Macros, adds this functionality with a set of of non-parametric test templates.
Mann-Whitney Example
A professor wants to compare the grades of students who attended live lectures vs video-taped lectures. Scores of students attending video lectures is in column A; live lectures in column B.
To conduct a test using QI Macros he will:
- Click on the QI Macros menu > Stat Templates > Mann Whitney
- Input the data for Sample 1 (Video Taped Lectures) into column A and the data for Sample 2 (Live Lectures) into column B.
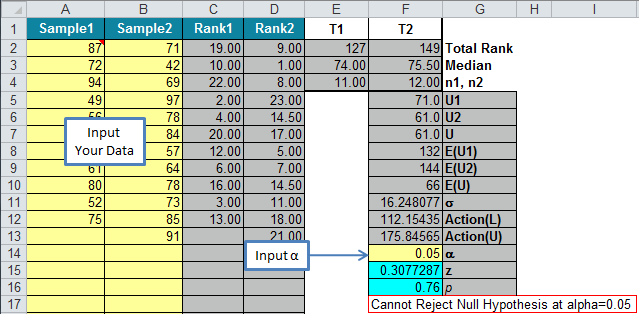
- QI Macros will perform the calculations and display the results in columns C:G.
- QI Macros will also interpret the results for you. Cell F7 indicates that we cannot reject the null hypothesis (accept the null hypothesis):
Interpreting the Mann Whitney Test Results: Since p (0.758) is greater than alpha (0.05) we cannot reject the null hypothesis (accept the null hypothesis) that video instruction is as good as live instruction.
Tip: As you enter additional rows of data in columns A and B, the formulas in columns C and D should be automatically extended. If they do not extend, you can extend them yourself using copy and paste.
NOTE: If p < 0.05 Reject the Null Hypothesis.
Why Choose QI Macros Statistical Software for Excel?
Easy to Use
- Works Right in Excel
- Interprets p-values for You
- Accurate No-Worry Results
- Free Training Anytime
Proven and Trusted
- 100,000 Users in 80 Countries
- Celebrating 20th Anniversary
- Five Star CNET Rating — Virus Free
Affordable
- Only $349 USD
Quantity Discounts Available - No annual fees
- Free Technical Support
-
-
May 31 2012, 09:25
- Литература
- Общество
- Психология
- Cancel
Сделал черновой вариант расчета U-критерия Манна-Уитни в MS Excel. Вроде работает правильно, но я особо не проверял. Да, и в этом варианте нет поправки на связки (повторяющиеся наблюдения). Будет корректно работать при n1 и n2 >20 и минимальном количестве повторяющихся наблюдений.
Обновленная версия реализации в MS Excel — форму отчета приблизил к форме отчета в SPSS.
См. также Полезные книги по математико-статистической обработке данных психологического исследования.
Originally published at В поиске предельных смыслов. You can comment here or there.